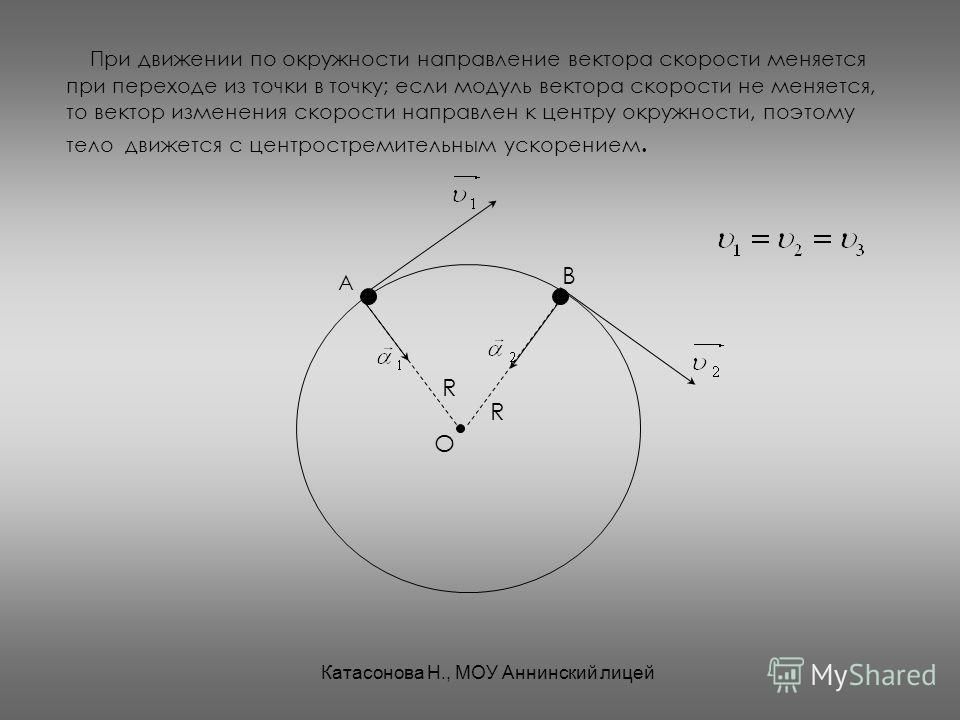
Куда направлено ускорение
☰
Ускорение — это быстрота изменения скорости. В системе СИ ускорение измеряется в метрах за секунду в квадрате (м/с2), то есть показывает, на сколько изменяется скорость тела за одну секунду.
Если, например, ускорение тела равно 10 м/с2, то это значит, что за каждую секунду скорость тела увеличивается на 10 м/с. Так, если до начала ускорения тело двигалось с постоянной скоростью 100 м/с, то после первой секунды движения с ускорением его скорость составит 110 м/с, после второй — 120 м/с и т. д. В данном случае скорость тела постепенно увеличивалась.
Но скорость тела может постепенно и уменьшаться. Обычно так происходит при торможении. Если то же тело, двигавшееся с постоянной скоростью 100 м/с, начинает уменьшать свою скорость на 10 м/с в каждую секунду, то через две секунды его скорость будет равна 80 м/с. А через 10 с тело вообще остановится.
Во втором случае (при торможении) мы можем сказать, что ускорение является отрицательной величиной.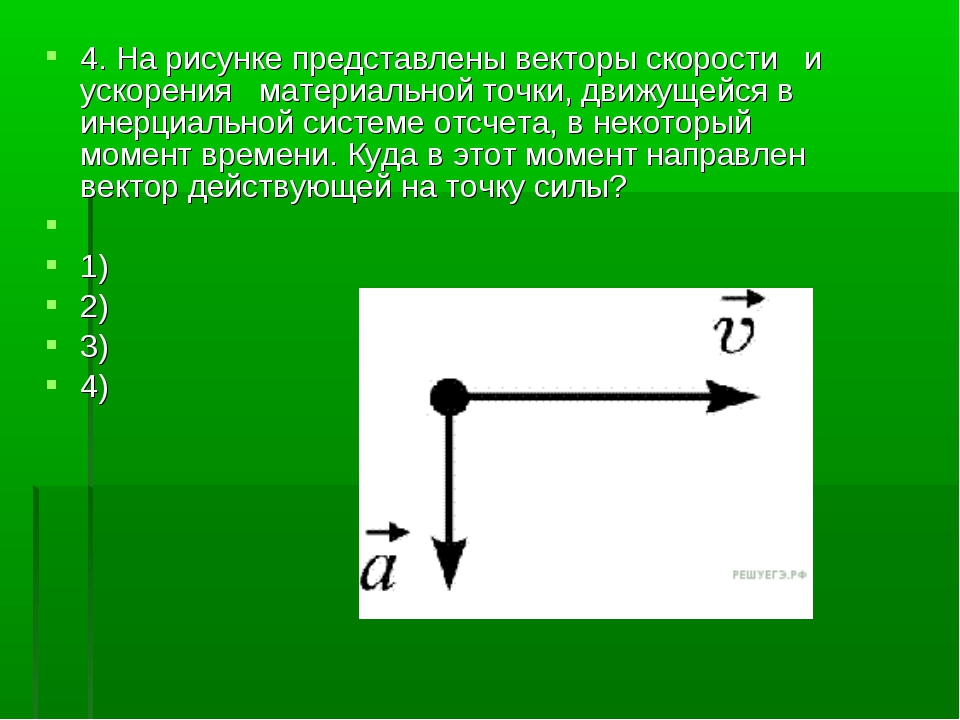
Поскольку ускорение может принимать как положительные, так и отрицательные значения, то это значит, что ускорение является векторной величиной.
Из рассмотренных примеров мы могли бы сказать, что при разгоне (увеличении скорости) ускорение положительная величина, а при торможении — отрицательная. Однако не так все просто, когда мы имеем дело с системой координат. Здесь скорость тоже оказывается величиной векторной, способной быть как положительной, так и отрицательной. Поэтому то, куда направлено ускорение, зависит от направления скорости, а не от того, уменьшается скорость или увеличивается под действием ускорения.
Если скорость тела направлена в положительном направлении оси координат (скажем, X), то тело за каждую секунду времени увеличивает свою координату. Так, если в момент начала измерения тело находилось в точке с координатой 25 м и начало двигаться с постоянной скоростью 5 м/с в положительном направлении оси X, то через одну секунду тело будет находиться в координате 30 м, через 2 с — 35 м. Вообще, чтобы найти координату тела в определенный момент времени, надо к начальной координате прибавить скорость умноженную на количество прошедшего времени. Например, 25 м + 5 м/с · 7 с = 60 м. В данном случае тело через 7 секунд окажется в точке с координатой 60. Здесь скорость — положительная величина, так как координата увеличивается.
Так, если в момент начала измерения тело находилось в точке с координатой 25 м и начало двигаться с постоянной скоростью 5 м/с в положительном направлении оси X, то через одну секунду тело будет находиться в координате 30 м, через 2 с — 35 м. Вообще, чтобы найти координату тела в определенный момент времени, надо к начальной координате прибавить скорость умноженную на количество прошедшего времени. Например, 25 м + 5 м/с · 7 с = 60 м. В данном случае тело через 7 секунд окажется в точке с координатой 60. Здесь скорость — положительная величина, так как координата увеличивается.
Скорость отрицательна, когда ее вектор направлен в отрицательном направлении оси координат. Пусть тело из предыдущего примера начало двигаться не в положительном, а в отрицательном направлении оси X с постоянной скоростью. Через 1 с тело будет в точке с координатой 20 м, через 2 с — 15 м и т. д. Теперь чтобы найти координату, надо из начальной вычесть скорость умноженную на время. Например, где будет тело через 8 с? 25 м — 5 м/с · 8 с = -15 м.
Назовем первый случай (когда тело двигается в положительном направлении оси X) A, а второй случай B. Рассмотрим, куда будет направлено ускорение при торможении и разгоне в обоих случаях.
В случае A при торможении ускорение направлено в противоположном скорости направлении. Так как скорость положительная величина, то ускорение — будет отрицательной, то есть вектор ускорения будет направлен в отрицательном направлении оси X.
В случае B при разгоне направление ускорения будет совпадать с направлением скорости, а значит ускорение будет направлено в отрицательном направлении оси X (ведь туда же направлена и скорость). Обратите внимание, несмотря на то, что ускорение отрицательно, оно все же увеличивает модуль скорости.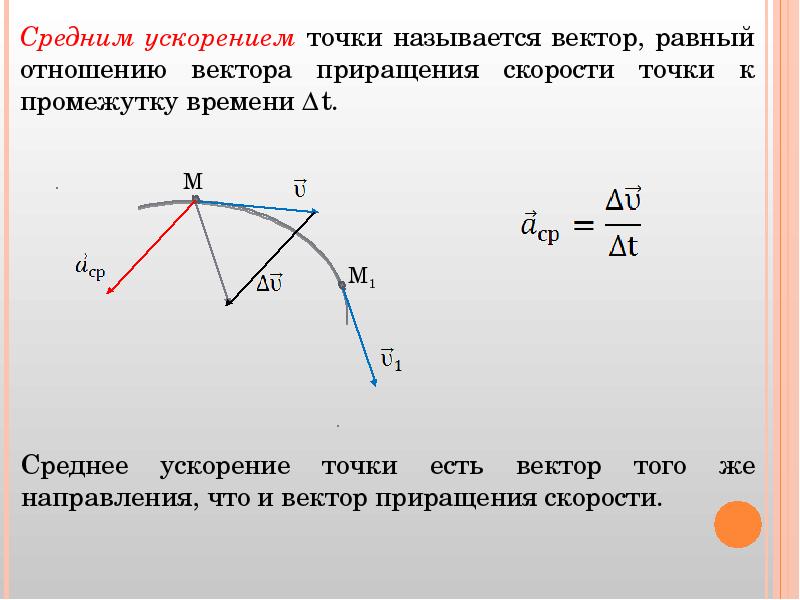
В случае B при торможении ускорение направлено противоположно скорости. Так как скорость имеет отрицательное направление, то ускорение окажется положительной величиной. Но при этом будет уменьшать модуль скорости. Например, начальная скорость была -20 м/с, ускорение равно 2 м/с2. Скорость тела через 3 с, окажется равной -20 м/с + 2 м/с2 · 3 с = -14 м/с.
Таким образом, ответ на вопрос «куда направлено ускорение» зависит от того, по отношению к чему оно рассматривается. По отношению к скорости ускорение может быть направлено в ту же сторону, что и скорость (при разгоне), или в противоположную сторону (при торможении).
В системе координат положительное и отрицательное ускорение само по себе ничего не говорит от том, тормозило ли тело (уменьшало свою скорость) или разгонялось (увеличивало скорость). Надо смотреть на то, куда направлена скорость.
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
где – вектор ускорения.
Направление вектора ускорения совпадает с направлением изменения скорости
Δ = — 0 (здесь 0 – это начальная скорость,
то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость 0. В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = — 0. Тогда определить ускорение можно так:
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени –
это физическая величина, равная пределу, к которому стремится среднее ускорение при
стремлении промежутка времени к нулю.
Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями аХ, aY, aZ).
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
v21то направление вектора ускорения противоположно направлению вектора скорости 2. Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а
Рис. 1.9. Мгновенное ускорение.
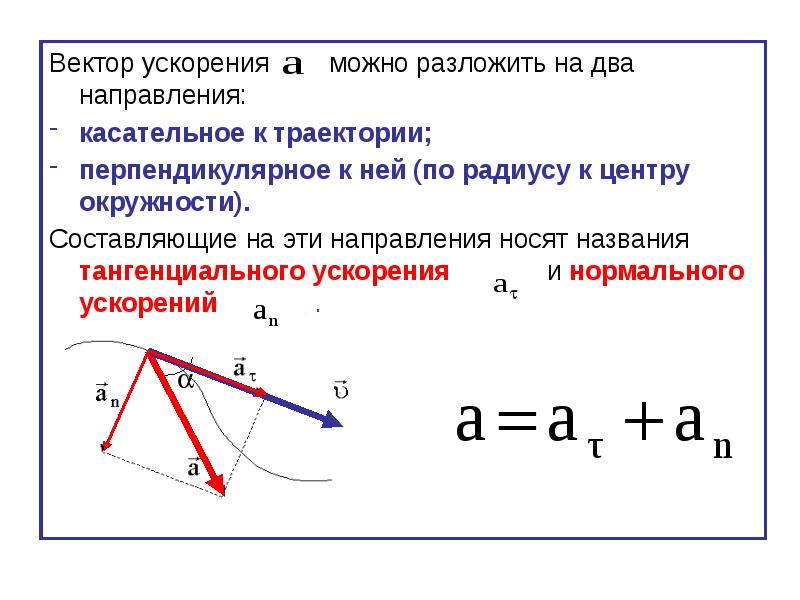
При движении по криволинейной траектории изменяется не только модуль скорости,
но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих
(см. следующий раздел).
В этом случае вектор ускорение представляют в виде двух составляющих
(см. следующий раздел).
Тангенциальное ускорение
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения,
направленная вдоль нормали к траектории движения в данной точке на траектории движения тела.
То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см.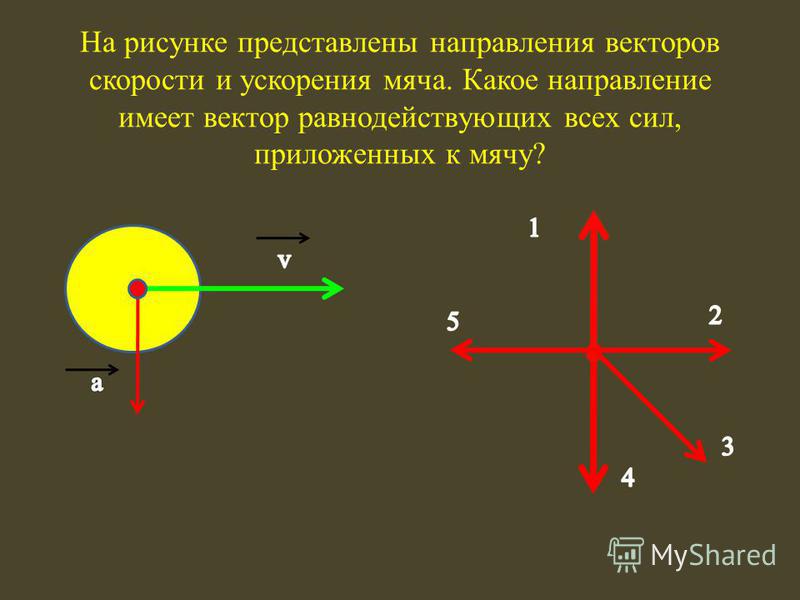 рис. 1.10).
Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n.
Вектор нормального ускорения направлен по радиусу кривизны траектории.
рис. 1.10).
Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n.
Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
= τ + n
8.3. Вектор скорости точки
Одной из кинематических характеристик движения точки является векторная величина, называемая скоростью точки.
Скорость точки — это векторная величина,
характеризующая быстроту и направление
движения точки в данной системе отсчета.
Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент временив положении(рис. 1.3), определяемом радиус-вектором, а в моментприходит в положение, определяемое вектором. Тогда перемещение точки за промежуток времениопределяется вектором, который будем называтьвектором перемещения точки.Этот вектор направлен по хорде, если точка движется криволинейно (рис. 1.3,а), и вдоль самой траектории, когда движение является прямолинейным (рис. 1.3,б).
Рисунок 1.3
Из треугольника , видно, что, следовательно,
.
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени :
. | (7) |
Направлен вектор так же, как и вектор, т.е. при криволинейном движении вдоль хорды, в сторону движения точки, а при прямолинейном движении – вдоль самой траектории.
Очевидно, что чем меньше промежуток времени , тем величинабудет точнее характеризовать движение точки.
Поэтому скоростью точки в данный момент времениназывается векторная величина, к которой стремится скоростьпри стремлении промежутка временик нулю.
.
Предел отношения припредставляет собой первую производную от векторапо аргументу и обозначается, тогда
. | (8) |
Итак, вектор скорости точки в данный
момент времени равен первой производной
от радиус-вектора точки по времени.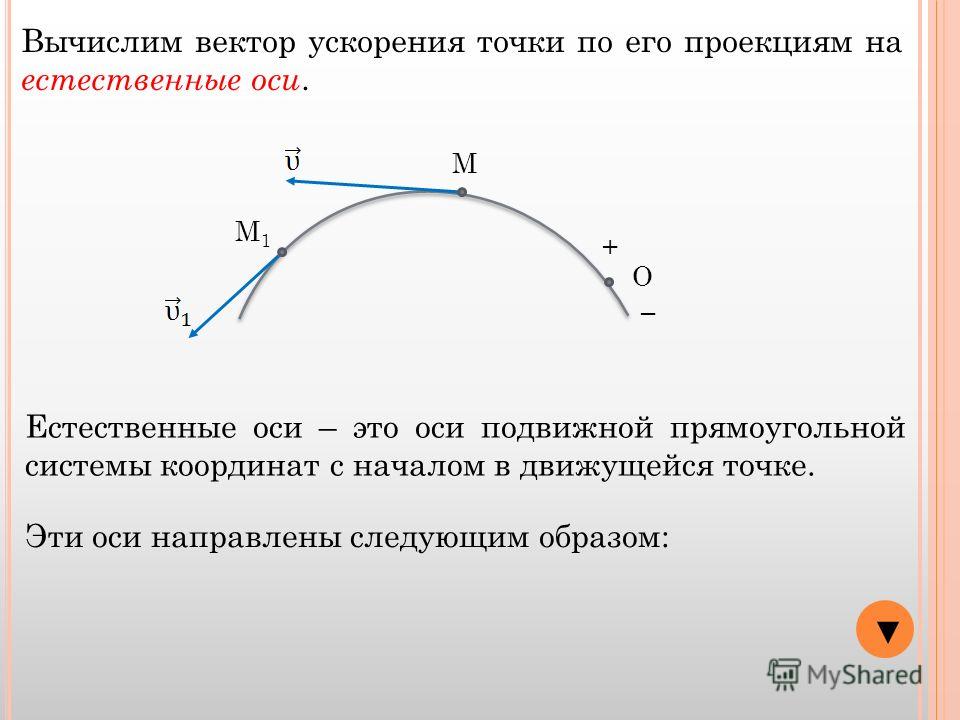 Так
как предельным направлением секущейявляется
касательная, то вектор скорости в данный
момент времени направлен по касательной
к траектории точки в сторону движения.
Так
как предельным направлением секущейявляется
касательная, то вектор скорости в данный
момент времени направлен по касательной
к траектории точки в сторону движения.
Размерность скорости , т.е.. Единицы измерения.
8.4. Вектор ускорения точки
Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости.
Пусть в некоторый момент времени движущаяся точка находится в положениии имеет скорость(рис.1.4), а в момент времениприходит в точкуи имеет
Рисунок 1.4
скорость . Тогда за промежуток временискорость изменится на. Для построения вектораотложим от точкивектор, равный, и построим параллелограмм, в котором диагональю будет, а одной из сторон. Тогда, очевидно,
вторая сторона и будет изображением
вектора
.
Заметим, что векторвсегда
направлен в сторону вогнутости траектории.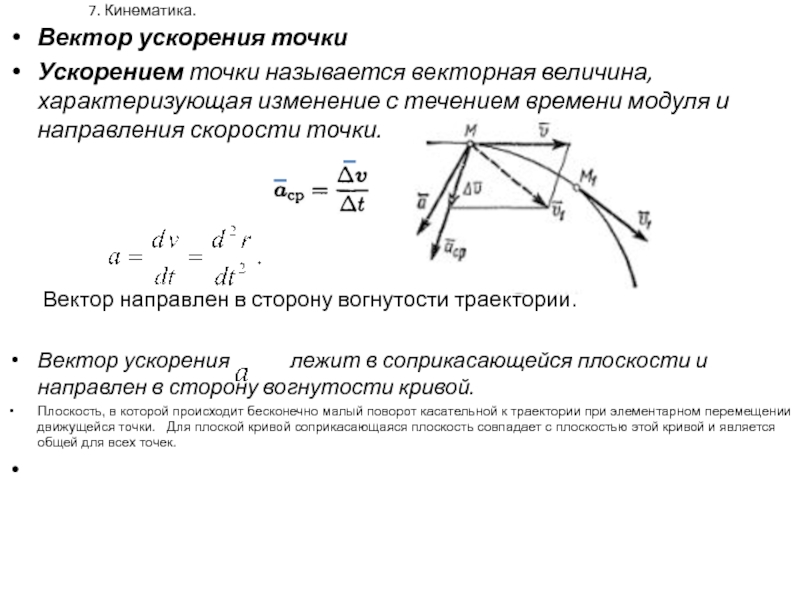
Отношение копределяет вектор среднего ускорения точки за промежуток времени.
. | (9) |
Вектор среднего ускорения имеет то же направление, что и вектор , т.е. направлен в сторону вогнутости траектории. Тогда
или с учетом равенства (8),
. | (10) |
Следовательно, вектор ускорения точки
в данный момент времени равен первой
производной от вектора скорости или
второй производной от радиус-вектора
точки по времени.
Размерность , т.е.. Единица измерения.
Вектор направлен, также как и вектор, лежит в плоскости этой кривой и направлен в сторону её вогнутости.
Вектор скорости в криволинейном движении
Вектор скорости в криволинейном движении. Пусть М и 7 1 — положения движущейся точки в моменты t и 7-1-ДГ. Отложим на хорде ММ (рис. 32) в направлении ММ отрезок MW, [c.59]Докажите, как направлен вектор скорости в криволинейном движении. [c.73]
Скорость в криволинейном движении. Пусть в некоторый момент времени t положение точки М. (рис. 51) определяется радиусом-вектором г, а в момент f — радиусом-вектором г = г-1-Аг. Тогда перемещение точки М за промежуток времени Ы = И — t будет [c.62]
При криволинейном движении скорость точки по направлению меняется. Для того чтобы установить направление вектора скорости при криволинейном движении, разобьем траекторию на бесконечно малые участки пути, которые можно считать, вследствие их малости, прямолинейными.
 Тогда на каждом участке условная скорость Оп такого прямолинейного движения будет направлена по хорде. В пределе при Дз, стремящемся к нулю, хорда совпадает с касательной, следовательно, скорость в каждый момент времени направлена по касательной к траектории (рис. 9.5, б).
[c.89]
Тогда на каждом участке условная скорость Оп такого прямолинейного движения будет направлена по хорде. В пределе при Дз, стремящемся к нулю, хорда совпадает с касательной, следовательно, скорость в каждый момент времени направлена по касательной к траектории (рис. 9.5, б).
[c.89]При изучении переменного прямолинейного движения точки под термином ускорение мы понимали только изменение скорости по величине. Однако в криволинейном движении меняется и направление скорости, так как криволинейное движение иначе не может возникнуть. Скорость является векторной величиной вектор скорости, обозначаемый V (в отличие от его модуля у), направлен по касательной к той же точке траектории, в которой в данный момент времени находится движущаяся точка . [c.118]
При равномерном криволинейном движении точки модуль скорости остается постоянным, но скорость, рассматриваемая как векторная величина, переменна, и поэтому на рис. 140 для вектора скорости в разных положениях точки обозначения неодинаковы. [c.118]
[c.118]
Из определения тангенциального ускорения, кроме того, следует, что в криволинейном движении вектор тангенциального ускорения, так же как вектор скорости, направлен по касательной к траектории. [c.71]
Рассматривая положения точки через бесконечно малые отрезки времени, можно считать, что вектор скорости совпадает с направлением движения. Но так как направление в криволинейном движении непрерывно меняется, то и вектор скорости точки при переходе ее в каждое [c.71]
Таким образом, вектор скорости точки в криволинейном движении непрерывно изменяет свое направление соответственно форме траектории, оставаясь все время касательным к ней. [c.71]
В кинематике часто приходится встречаться с переменными векторными величинами, изменяющимися с течением времени как по модулю, так и по направлению. Такими переменными векторами являются, например, радиус-вектор г движущейся точки, а также, как увидим далее, скорость и ускорение точки в криволинейном движении. Поэтому, прежде чем переходить к дальнейшему изучению криволинейного движения точки, рассмотрим операцию векторного дифференцирования
[c.249]
Поэтому, прежде чем переходить к дальнейшему изучению криволинейного движения точки, рассмотрим операцию векторного дифференцирования
[c.249]
Ускорение точки в криволинейном движении выражается векторной производной от скорости по времени. Это есть вектор, который согласно сказанному в 65 строится следующим образом [c.255]
При прямолинейном движении вектор скорости v все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь численно при криволинейном движении кроме числового значения все время изменяется и направление вектора скорости точки. Размерность скорости LIT, т. е. длина/время в качестве единиц измерения применяют обычно м/с или км/ч. Вопрос об определении модуля скорости будет рассмотрен в 40 и 42. [c.100]
Вектор ускорения. При равномерном прямолинейном движении точки скорость сохраняет свою величину и свое направление. При неравномерном и криволинейном движении скорость изменяется по величине и по направлению.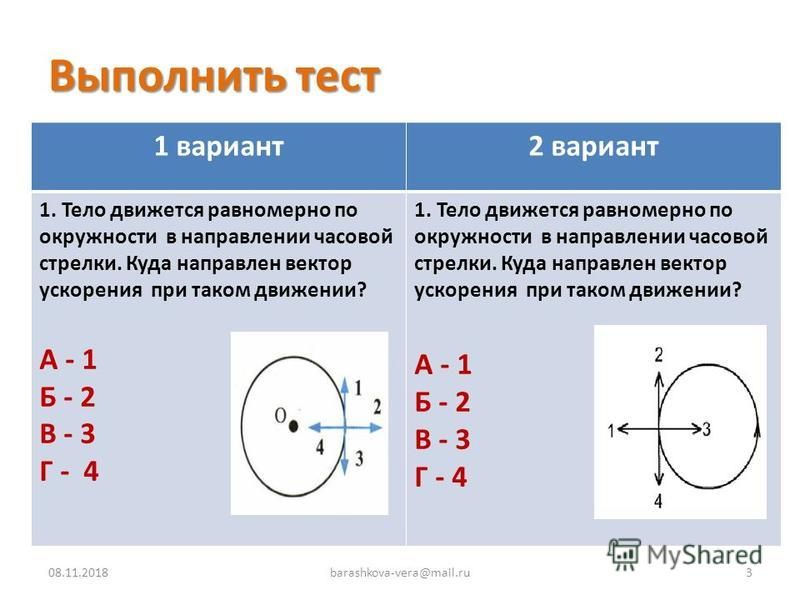 Изменение величины и направления скорости происходит с течением времени. Пространственно-временной мерой изменения скорости точки в данное мгновение и в данной системе отсчета, является ускорение точки Пусть скорость точки в некоторое мгновение изображается вектором II (рис. 82, а), а через промежуток времени М она изменилась
[c.128]
Изменение величины и направления скорости происходит с течением времени. Пространственно-временной мерой изменения скорости точки в данное мгновение и в данной системе отсчета, является ускорение точки Пусть скорость точки в некоторое мгновение изображается вектором II (рис. 82, а), а через промежуток времени М она изменилась
[c.128]
Итак, в этой плоскости расположен вектор скорости точки в данное мгновение и в мгновение бесконечно близкое, когда точка Ml сколь угодно близка к точке М. Ускорение характеризует изменение скорости точки в данное мгновение, следовательно, вектор ускорения лежит в соприкасающейся плоскости. Нормальная составляющая ускорения направлена перпендикулярно скорости 3 этой плоскости по так называемой главной нормали к траектории S сторону вогнутости, и при всяком криволинейном движении по модулю равна квадрату скорости, деленному на радиус кривизны траектории. [c.38]
Разложение вектора скорости по единичным векторам осей криволинейных координат 199, 200 ——-ускорения по осям натурального триэдра 188 Размах колебаний 147 Распределение скоростей в движущейся плоской фигуре 243 и д.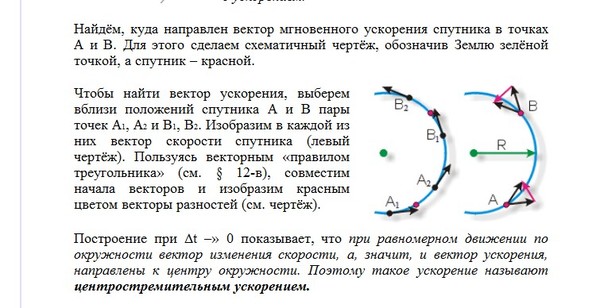 ——-твердом теле в общем случае его движения 284
[c.349]
——-твердом теле в общем случае его движения 284
[c.349]
В самом общем случае криволинейного движения точки ее вектор скорости характеризует изменение с течением времени модуля и направления радиуса-вектора этой точки. [c.224]
Годограф вектора скорости. Отнесем движение точки М к прямоугольной системе осей координат Оху г (рис. 154, а). В самом общем случае криволинейного движения вектор скорости и точки [c.225]
Модуль вектора ускорения пил также не меняется с течением времени. Таким образом, несмотря на постоянство модуля вектора скорости VA ТОЧКИ А, вектор ускорения WA этой точки не обращается в нуль. Это объясняется тем, что движение точки А происходит по криволинейной траектории и вектор скорости ол все время изменяет свое направление. [c.246]
Давая в выражениях (4) различные значения произвольным постоянным, можно сделать несколько неожиданный на первый взгляд вывод одна и та же сила может сообщить материальной точке не строго определенное движение, а целый класс разнообразных движений. По-видимому, присутствие шести произвольных постоянных интегрирования в общем решении (4) объясняется тем, что, зная массу движущейся точки и действующую на эту точку силу Р, мы не указали, из какого положения началось движение точки и какова была ее скорость в начальном положении, или, как говорят, в начальный момент времени 0. Таким образом, чтобы с помощью уравнений (6, 88) получить конкретное решение второй задачи динамики точки, надо, кроме массы точки и действующей на эту точку силы, знать еще, в каком положении находится точка в начальный момент (начальное положение) и какую она в этот момент имеет скорость (начальная скорость). Величины, определяющие значения начального момента радиуса-вектора Го начального положения точки и начальной скорости Vo, называются начальными условиями движения точки. В декартовых осях координат начальные условия в случае криволинейного движения точки задаются в виде
[c.458]
По-видимому, присутствие шести произвольных постоянных интегрирования в общем решении (4) объясняется тем, что, зная массу движущейся точки и действующую на эту точку силу Р, мы не указали, из какого положения началось движение точки и какова была ее скорость в начальном положении, или, как говорят, в начальный момент времени 0. Таким образом, чтобы с помощью уравнений (6, 88) получить конкретное решение второй задачи динамики точки, надо, кроме массы точки и действующей на эту точку силы, знать еще, в каком положении находится точка в начальный момент (начальное положение) и какую она в этот момент имеет скорость (начальная скорость). Величины, определяющие значения начального момента радиуса-вектора Го начального положения точки и начальной скорости Vo, называются начальными условиями движения точки. В декартовых осях координат начальные условия в случае криволинейного движения точки задаются в виде
[c.458]
При прямолинейном движении вектор скорости направлен вдоль траектории в сторону движения.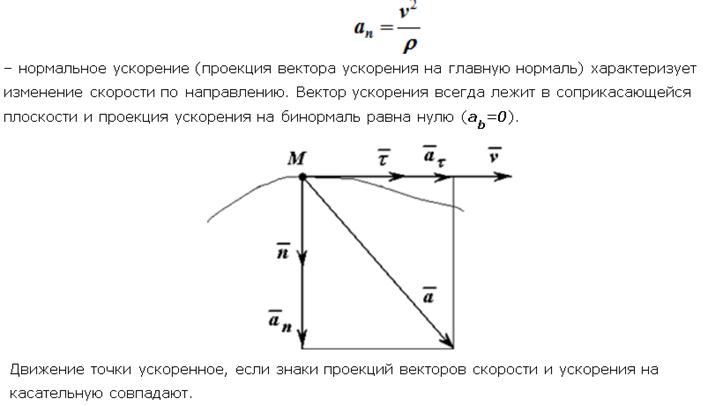 При криволинейном движении вектор скорости для каждого момента времени направлен по касательной к траектории в сторону движения (рис. 11).
[c.15]
При криволинейном движении вектор скорости для каждого момента времени направлен по касательной к траектории в сторону движения (рис. 11).
[c.15]
При любом криволинейном движении ускорение всегда направлено в сторону вогнутости траектории, т. е. в ту же сторону, что и вектор изменения скорости Ау (рис. 13). [c.16]
При криволинейном движении тела, принимаемого за материальную точку, вектор его ускорения и вектор действующей на тело силы можно разложить на составляющие в направлении вектора скорости и перпендикулярном ему направлении, т. е. на нормальную и тангенциальную составляющие (см. 4) [c.35]
Вышеизложенное дает основание сделать вывод, что существуют такие граничные точки внутренней и периферийной зон полостей, в которых осевые составляющие 1 вектора скорости движения частиц жидкости обращаются в нуль. Совокупность таких точек образует криволинейную поверхность С, пересечение которой с плоскостью Р торцов полумуфт представляет кривую г . [c.86]
[c.86]
Отложим ее на механизме (рис. 175) в некотором масштабе -в виде вектора У , перпендикулярного к радиусу вращения О А. В отношении скорости точки В наперед можно утверждать, что она будет перпендикулярна к ВО Уь ВО ), так как точка В совершает криволинейное движение по дуге окружности р с центром О2, поэтому проводим через шарнир В линию действия этой скорости в виде прямой, перпендикулярной к ВОз (на рис. 175 она обозначена л. д. рассматривая движение точки В как простое круговое движение по дуге р с центром Оз. Учтем теперь, что шарнир В движется в зависимости от шарнира А, и его скорость определенным образом будет связана с У . Для выяснения этой связи обратим внимание на то, что точка В является общей осью вращения пары 2—3 и что ее скорость будет одной и той же. Будем ли мы ее считать принадлежащей поводку 3 или шатуну 2. Рассмотрим точку В как принадлежащую звену 2. [c.122]
Криволинейные пазы фрезеруют за один рабочий ход на полную их глубину.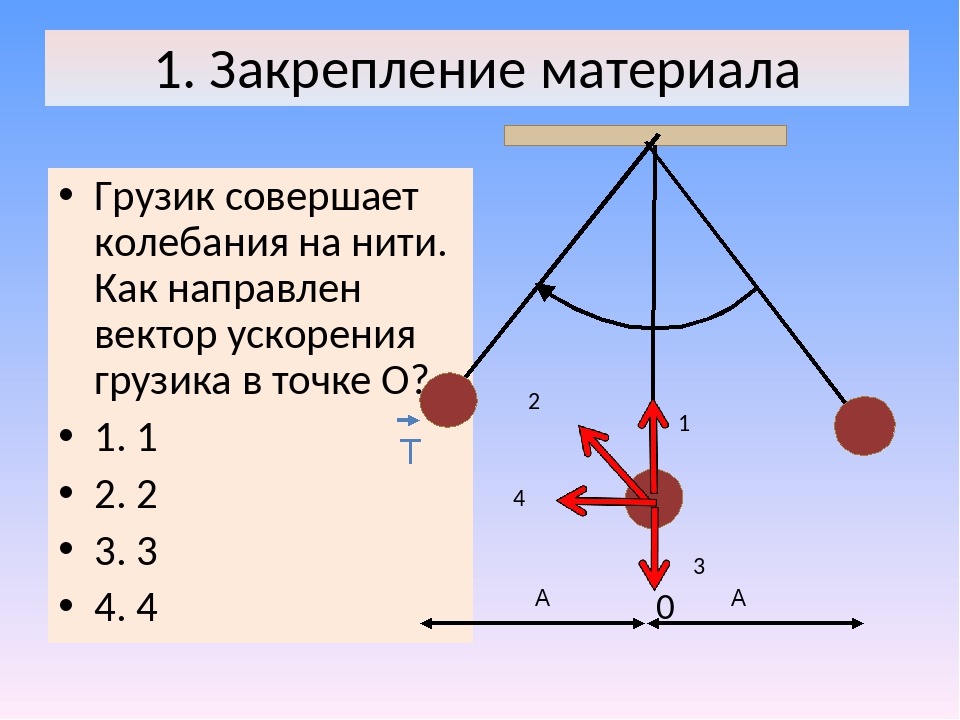 Соответственно этому условию назначают результирующее движение подачи, равное сумме векторов поперечного и продольного движения подач. Для уменьшения врезания в местах изменений направлений пазов необходимо вести обработку фрезами с минимальными вылетами и уменьшать скорости подачи.
[c.203]
Соответственно этому условию назначают результирующее движение подачи, равное сумме векторов поперечного и продольного движения подач. Для уменьшения врезания в местах изменений направлений пазов необходимо вести обработку фрезами с минимальными вылетами и уменьшать скорости подачи.
[c.203]
Напомним, что характерными чертами прямолинейных сдвиговых течений являются существование семейства параллельных материальных плоскостей, сохраняющих при движении неизменными относительные удаления друг от друга поток имеет постоянный объем и стационарен, если градиент скорости поперек сдвигающих плоскостей не зависит от времени и линии сдвига являются материальными линиями, т. е. если вектор скорости любых из двух сдвигающих плоскостей всегда параллелен одной и той же материальной линии, расположенной в одной из плоскостей сдвига. Эти свойства нетрудно обобщить на все криволинейные течения с ие-плоскими поверхностями сдвига, представляющие практический интерес. Введем следующие определения,
[c. 240]
240]
Во-вторых, покажем, что добавляющееся в случае криволинейных ударных волн условие Гюгонио о равенстве нулю тангенциальной составляющей вектора скорости на волне для случая движения по покою (выполнение условия Гюгонио для нормальной составляющей вектора скорости обеспечивается соотношением (1.1)) также будет приближенно выполняться для малых R с порядком o R) по крайней мере для некоторого класса движений. [c.324]
Далее в работах [4 — 8] была рассмотрена общая (без предположения о вырожденности движения) задача о примыкании произвольных потенциальных течений политропного газа через слабый разрыв к области покоя. Решение задачи было представлено в виде специальных рядов в пространстве временного годографа по степеням модуля вектора скорости г. Значение г = О соответствовало поверхности слабого разрыва, разделяющей область возмущенного движения и область покоя. В этих же работах исследовались некоторые приложения построенных решений, в частности, к задаче о движении выпуклого поршня и к задаче о распространении слабых криволинейных ударных волн. Сходимость в малом полученных рядов была доказана в [9]. Однако попытка построить ряды по степеням г, использованным в [4-8] для представления решений уравнений двойных волн в окрестности области покоя, к успеху не привела.
[c.338]
Сходимость в малом полученных рядов была доказана в [9]. Однако попытка построить ряды по степеням г, использованным в [4-8] для представления решений уравнений двойных волн в окрестности области покоя, к успеху не привела.
[c.338]
Суммарная поперечная сила/ л искривляет траекторию самолета в сторону своего действия (рис. 5.06). Вектор скорости направлен по касательной к траектории, а сила Ra, перпендикулярная к нему, направлена вдоль радиуса, т. е. к центру кривизны. Поэтому ее называют также центростремительной силой. Как видим, плоскость, в которой лежат векторы V и Rn, является плоскостью криволинейного движения. Она может быть горизонтальной, вертикальной и наклонной. Если в процессе движения вектор Rn поворачивается вокруг оси скорости, то траектория самолета не лежит [c.119]
В криволинейно.м движении вектор скорости движущейся точки всегда направлен по касательной к траектории. Нетрудно доказать справедливость этого положения.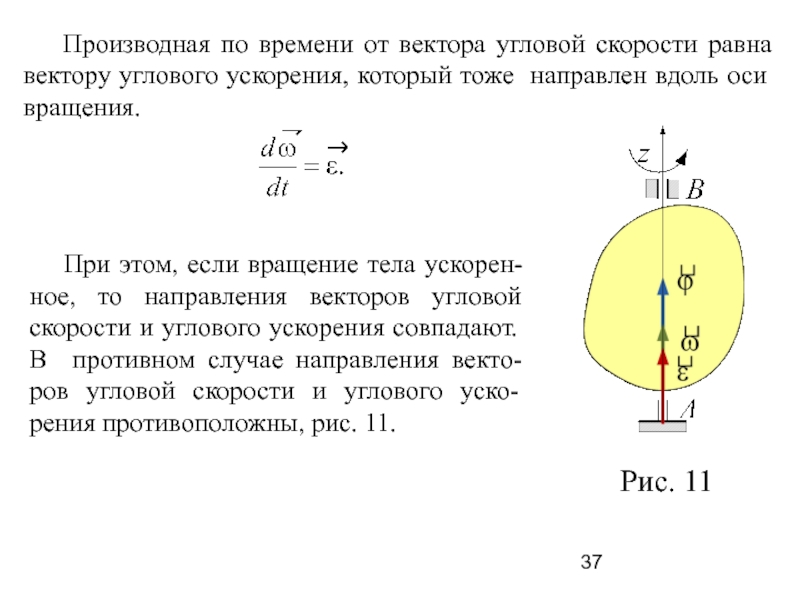 [c.82]
[c.82]
Отсюда следует, что вектор скорости точки, движущейся по криволинейной траектории, всегда направлен по касательной к этой траектории и всегда в сторону движения. [c.82]
Представим себе, что в момент времени, когда движущаяся точка находилась в положении Mi (рис. 117), была устранена причина, которая заставляла ее отклоняться от прямолинейного направления движения. Очевидно, что точка продолжала бы далее двигаться прямолинейно, а именно — по прямой, касательной к траектории в точке Mj. Отсюда следует, что и скорость будет направлена по этой касательной в сторону движения и вы ражаться в определенном масштабе вектором Vj. Точно так же скорость точки в положении Мг выражается вектором ггз направленным по касательной к траектории в этой точке. Итак, скорость криволинейно движущейся точки направлена по касательной к траектории в точке, соответствующей рассматриваемому моменту времени, в сторону движения. [c.116]
Обратим внимание на то, что согласно изложенному выше скорость криволинейного движения представляет собой вектор, т.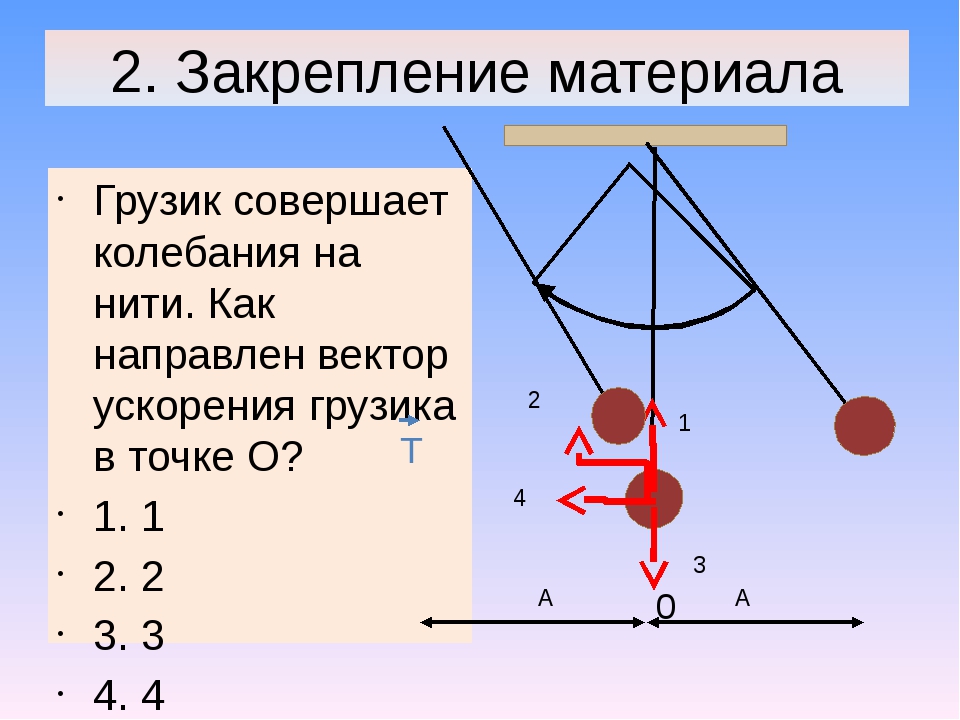 е. выражается направленным отрезком. Начало этого отрезка—движущаяся точка, направление — по касательной к траектории в сторону движения, длина—величина скорости в выбранном масштабе.
[c.139]
е. выражается направленным отрезком. Начало этого отрезка—движущаяся точка, направление — по касательной к траектории в сторону движения, длина—величина скорости в выбранном масштабе.
[c.139]
В рассмотренных примерах исследуемая точка двигалась прямолинейно. Для точек, имеющих криволинейное движение, удобнее строить кинематические диаграммы, дающие не только абсолютные значения скоростей и ускорений исследуемых точек, но и направления векторов полных скоростей и ускорений. Для этого откладываем векторы скоростей и ускорений, полученные на планах скоростей и ускорений, из общих полюсов / и я в их истинном наиравлеиин. Если после этого соединить концы всех векторов плавной кривой, то полученная диаграмма будет называться годографом скорости или соответствегию годографом ускорения. [c.105]
При движении тела по криволинейной траектории направление вектора С1сорости изменяется в процессе движения, вектор ускорения а при этом может оказаться направлен под любым углом к вектору скорости v-j (рис. 9).
[c.8]
9).
[c.8]
Вектор скорости точки в данный момент времени. Пусть некоторая точка соверщает какое-либо движение по криволинейной траектории АВ (рис. 153). Пусть в момент времени t эта точка занимает на траектории положение М, определяемое радиусом-вектором г [c.222]
Поскольку в относительном движении скорость тела в направлении силы P[j не изменяется, то должна присутствовать уравнове-щивающая сила R, равная по значению Р и противоположная ей по направлению (рис. 1.2). Сила R — реальная сила взаимодействия между телом т и стержнем — реакция стержня. С другой стороны, по третьему закону Ньютона на стержень действует точно такая же, но противоположно направленная сила реакции тела. Таким образом, в результате движения тела вдоль вращающегося стержня к центру вращения, на стержень действует сила реакции тела Ri, направленная в сторону вращения и численно равная кориолисовой силе инерции 2т o>Xw. Сила Ri является реальной силой взаимодействия, поэтому она существует независимо от выбора системы координат и в абсолютном движении может совершать работу. В относительном движении ни кориолисова сила Р , ни сила реакции R работы совершить не могут, так как они всегда перпендикулярны к вектору w. Это справедливо также и для криволинейного движения тела т в относительной системе координат.
[c.11]
В относительном движении ни кориолисова сила Р , ни сила реакции R работы совершить не могут, так как они всегда перпендикулярны к вектору w. Это справедливо также и для криволинейного движения тела т в относительной системе координат.
[c.11]
В общем случае (рассматриваем установившееся движение газа) величина и направление скорости различны для различных точек в [ютоке, а линии тока криволинейны. Скорость звука зависит от скорости потока и, следовательно, тоже меняется от точки к точке. В таком потоке характеристики будут криволинейны. Через каждую точку можно провести две характеристики АА, ВВ (рис. 5.2), которые наклонены к вектору скорости под углом а, определяемым местным числом М. Если провести через точку О линию тока, то характеристики будут составлять с ней также углы а, так как вектор скорости направлен по касательной к линии тока. [c.101]
Вектор скорости точки. Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки.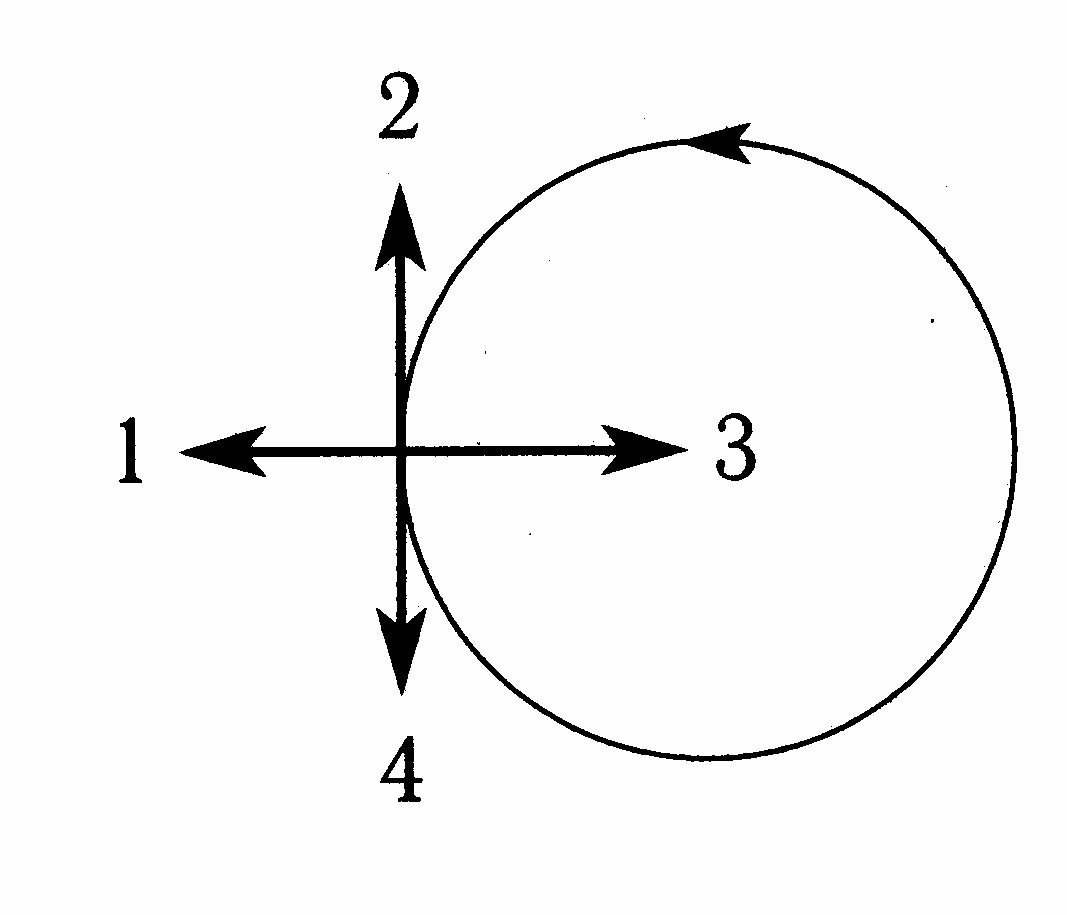 Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-вектором г, а в момент приходит в положение Мх, определяемое вектором г% (рис. 141). Тогда перемещение точки за промежуток времени — определ.чется вектором М.Мх, который ны будем называть вектором перемещения точки. Этот вектор направлен по хорде, если точка движется криволинейно (рис. 141, а), и вдоль самой траектории АВ, когда движение является прямолинейным (рис. 141, б).
[c.144]
Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-вектором г, а в момент приходит в положение Мх, определяемое вектором г% (рис. 141). Тогда перемещение точки за промежуток времени — определ.чется вектором М.Мх, который ны будем называть вектором перемещения точки. Этот вектор направлен по хорде, если точка движется криволинейно (рис. 141, а), и вдоль самой траектории АВ, когда движение является прямолинейным (рис. 141, б).
[c.144]
Пусть точка движется по кривой М[М (рис. 79). Эту кривую разделим на произвольные части, и точки деления соединим хордами М1М2, МгЛи, М3М4. Предположим, что точка движется не по кривой, а по звеньям вписанной ломаной М1Л 12МзМ4. Таким образом мы заменили криволинейное движение движением прямолинейным. Скорость и движения по хорде 171 2 направлена по этой хорде. Если мы будем увеличивать число звеньев ломаной, укорачивая длину каждой хорды, то точка Мг будет приближаться к точке М Вектор и будет вращаться вокруг точки М и в пределе, когда точка М2 совпадет с точкой Ми он окажется направленным по касательной. Но тогда и вписанная ломаная совпадет с кривой, так что мы получим опять действительное движение точки по кривой M M .
[c.82]
Но тогда и вписанная ломаная совпадет с кривой, так что мы получим опять действительное движение точки по кривой M M .
[c.82]
Тест по физике Кинематика периодического движения для 10 класса
Тест по физике Кинематика периодического движения для 10 класса с ответами. Тест включает в себя 2 варианта. В каждом варианте по 5 заданий.
1 вариант
1. Тело движется равномерно по окружности против часовой стрелки (рис. 15). Как направлен вектор ускорения при таком движении?
А. 1
Б. 2
В. 3
2. Тело движется по окружности радиусом 4 м со скоростью 10π м/с. Определите период вращения тела.
А. 0,8 с
Б. 1 с
В. 2 с
3. Мотоциклист совершает поворот по круговой траектории радиусом 50 м с постоянной по модулю скоростью 10 м/с. Каково ускорение мотоциклиста?
А. 1 м/с2
Б. 3 м/с2
В. 2 м/с2
4. Частица совершает гармонические колебания по закону х = 10 cos πt/10 см. Определите координату частицы в момент времени t = 10 с.
Частица совершает гармонические колебания по закону х = 10 cos πt/10 см. Определите координату частицы в момент времени t = 10 с.
А. 10 см
Б. -10 см
В. 0
5. По условию предыдущей задачи определите скорость частицы в момент времени t = 10 с.
А. 1 м/с
Б. 0
В. 2 м/с
2 вариант
1. Тело движется равномерно по окружности по часовой стрелке (рис. 16). Как направлен вектор ускорения при таком движении?
А. 1
Б. 2
В. 3
2. Какова частота вращения тела, движущегося по окружности радиусом 5 м со скоростью 5π м/с?
А. 2 Гц
Б. 0,5 Гц
В. 4 Гц
3. Трамвайный вагон движется на повороте по закруглению радиусом 40 м. Рассчитайте скорость трамвая, если центростремительное ускорение равно 0,4 м/с2.
А. 2 м/с
Б. 1 м/с
В. 4 м/с
4. Тело совершает гармонические колебания по закону х = 5 cos πt/6 см. Определите координату тела в момент времени t = 2 с.
Определите координату тела в момент времени t = 2 с.
А. 2,5 см
Б. 2 см
В. 0,4 см
5. По условию предыдущей задачи определите скорость частицы в момент времени t = 6 с.
А. 0
Б. 1 м/с
В. 0,5 м/с
Ответы на тест по физике Кинематика периодического движения для 10 класса
1 вариант
1-Б
2-А
3-В
4-Б
5-Б
2 вариант
1-В
2-Б
3-В
4-А
5-А
Ответы | Лаб. 2. Определение ускорения при равноускоренном движении тела — Физика, 9 класс
5. Найдите и занесите в таблицу средние значения $\langle l \rangle$ и $\langle t\rangle$.
$\langle t\rangle=\frac{1,43+1,8+1,38+1,71+1,72}{5}=\frac{8,04}{5}=1,61$
$\langle l\rangle=\frac{65+65+65+65+65}{5}=\frac{325}{5}=65$
6.
 2}=\dfrac{2·65}{2,59}=50,19$
2}=\dfrac{2·65}{2,59}=50,19$$\Delta t_{случ}=|65-65|=0$
$\Delta t_{случ_1}=|65-65|=0$
$\Delta t_{случ_2}=|65-65|=0$
$\Delta t_{случ_3}=|65-65|=0$
$\Delta t_{случ_4}=|65-65|=0$
7. Рассчитайте и занесите в таблицу значение абсолютной погрешности $Δl$.
$\Delta l_{случ}=\frac{0+0+0+0+0}{5}=0$ см;
$\Delta l=0,1$ с.
8.
 Вычислите максимальное значение абсолютной случайной погрешности измерений времени $t$.
Вычислите максимальное значение абсолютной случайной погрешности измерений времени $t$.
$\Delta t_{случ_1}=|1,43-1,61|=0,18$
$\Delta t_{случ_2}=|1,8-1,61|=0,19$
$\Delta t_{случ_3}=|1,38-1,61|=0,23$
$\Delta t_{случ_4}=|1,71-1,61|=0,1$
$\Delta t_{случ_5}=|1,72-1,61|=0,11$
$\langle\Delta t\rangle=\frac{0,18+0,19+0,23+0,1+0,11}{5}=0,16$
$\langle\Delta t\rangle=3·0,16=0,48$
9.
 Определите абсолютную систематическую погрешность измерений времени $t$.
Определите абсолютную систематическую погрешность измерений времени $t$.
$$\Delta t_{случ}=0,05+0,05=0,1$$
10. Вычислите и занесите в таблицу значение абсолютной погрешности прямых измерений времени $t$.
11.
 Вычислите и занесите в таблицу значения относительной погрешности измерений длины и времени.
Вычислите и занесите в таблицу значения относительной погрешности измерений длины и времени.
$ε_l=\dfrac{0,1}{65}·100\%=0,15$
$ε_t=\dfrac{0,48}{1,61}·100\%=29,81$
13. Ответьте письменно на контрольные вопросы
1. Что представляет модуль перемещения при данном движении шарика? Как направлен вектор перемещения?
Что представляет модуль перемещения при данном движении шарика? Как направлен вектор перемещения?
Представляет вектор, который соединяет две точки траектории движения — начальную и конечную. Вектор в данном случае это желоб.
2. Будут ли равными средние скорости шарика при его движении на первой и второй половинах пути? Почему?
Средние скорости будут различны, т. к. во время движения на шарик действую силы тяготения и трения, которые способны замедлять его.
Выводы: научился вычислять ускорение скатывающегося шарика и погрешности измерений времени движения шарика по желобу.
Разгон
Разгон Разгон : Ускорение — это скорость, с которой изменяется скорость.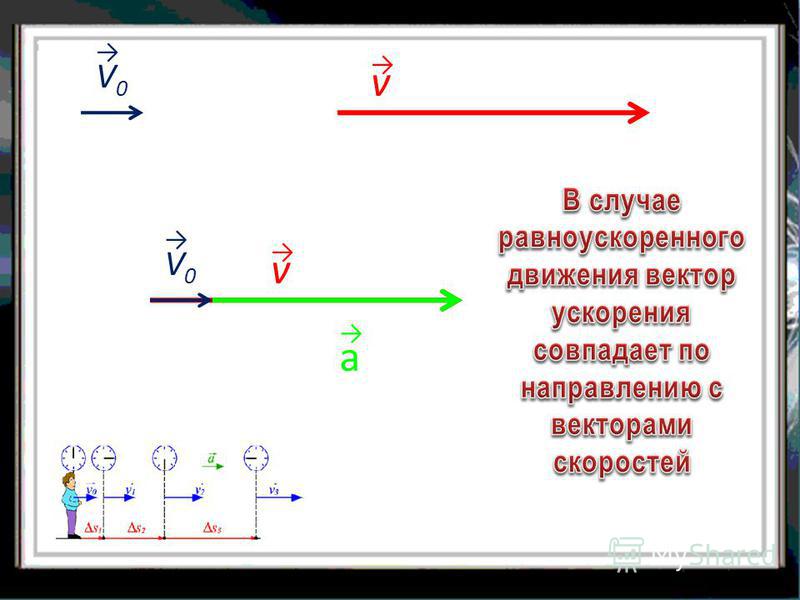 Поскольку скорость имеет как величину, так и направление, она называется
векторная величина; ускорение также является векторной величиной и должно
учитывать изменения как величины, так и направления
скорость. Скорость точки или объекта, движущегося по прямой.
путь может изменяться только по величине; на изогнутом пути это может или может
не меняется по величине, но всегда будет меняться по направлению.Этот
условие означает, что ускорение точки, движущейся по криволинейной
путь никогда не может быть нулевым.
Поскольку скорость имеет как величину, так и направление, она называется
векторная величина; ускорение также является векторной величиной и должно
учитывать изменения как величины, так и направления
скорость. Скорость точки или объекта, движущегося по прямой.
путь может изменяться только по величине; на изогнутом пути это может или может
не меняется по величине, но всегда будет меняться по направлению.Этот
условие означает, что ускорение точки, движущейся по криволинейной
путь никогда не может быть нулевым.
Если скорость точки, движущейся по прямому пути, увеличивается
(т.е. если скорость, которая является величиной скорости, равна
возрастает), вектор ускорения будет иметь то же направление, что и
вектор скорости. Если скорость уменьшается (т. Е.
точка или объект замедляется), вектор ускорения будет указывать
в обратном направлении. Среднее ускорение за время
интервал равен полному изменению скорости за время
интервал, деленный на временной интервал.Ускорение при любом
момент равен пределу отношения изменения скорости к
длина временного интервала, по мере приближения временного интервала
нуль.
Когда точка движется по изогнутой траектории, компонент ускорение, возникающее в результате изменения направления движения Вектор скорости перпендикулярен вектору скорости и равен направлен внутрь, на вогнутую сторону дорожки; его величина дается квадратом скорости, деленной на радиус кривизна r пути: v 2 / r.Изменение величины of v может быть представлен другим вектором (то есть вторым компонента ускорения) коллинеарны v и в том же направление, если v увеличивается, и противоположное направление, если v равно уменьшается. Если скорость указана в метрах в секунду, ускорение будут указаны в метрах в секунду в секунду.
Выдержка из Британской энциклопедии без разрешения.
Выдержка из Британской энциклопедии без разрешения.
Кинематика в двух измерениях
Представьте себе шарик, катящийся по горизонтальной поверхности, освещенный стробоскопическим светом.На рисунке (а) показано положение шара через равные промежутки времени по пунктирной траектории.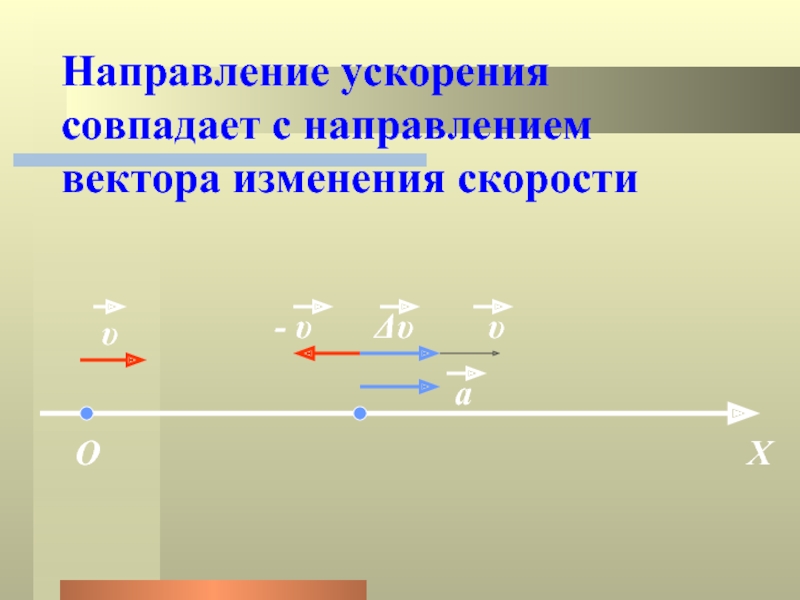 Случай 1 проиллюстрирован позициями с 1 по 3; величина и направление скорости не меняются (изображения расположены равномерно и по прямой линии), следовательно, ускорение отсутствует. Случай 2 указан для позиций с 3 по 5; мяч имеет постоянную скорость, но меняет направление, и, следовательно, существует ускорение. На рисунке (b) показано вычитание v 3 и v 4 и результирующее ускорение к центру дуги.Случай 3 встречается с позиций с 5 по 7; направление скорости постоянно, но величина меняется. Ускорение на этом участке пути происходит по направлению движения. Мяч изгибается из положения 7 в положение 9, показывая случай 4; скорость меняет направление и величину. В этом случае ускорение направлено почти вверх между 7 и 8 и имеет компонент по направлению к центру дуги из-за изменения направления скорости и компонент вдоль пути из-за изменения величины скорости.
Случай 1 проиллюстрирован позициями с 1 по 3; величина и направление скорости не меняются (изображения расположены равномерно и по прямой линии), следовательно, ускорение отсутствует. Случай 2 указан для позиций с 3 по 5; мяч имеет постоянную скорость, но меняет направление, и, следовательно, существует ускорение. На рисунке (b) показано вычитание v 3 и v 4 и результирующее ускорение к центру дуги.Случай 3 встречается с позиций с 5 по 7; направление скорости постоянно, но величина меняется. Ускорение на этом участке пути происходит по направлению движения. Мяч изгибается из положения 7 в положение 9, показывая случай 4; скорость меняет направление и величину. В этом случае ускорение направлено почти вверх между 7 и 8 и имеет компонент по направлению к центру дуги из-за изменения направления скорости и компонент вдоль пути из-за изменения величины скорости.
Рисунок 7
(а) Путь шара по столу. (b) Ускорение между точками 3 и 4.
Любой, кто наблюдал подброшенный объект — например, бейсбольный мяч в полете, — заметил движение снаряда . Для анализа этого распространенного типа движения делаются три основных допущения: (1) ускорение свободного падения постоянно и направлено вниз, (2) влияние сопротивления воздуха незначительно и (3) поверхность земли неподвижна. плоскости (то есть кривизна земной поверхности и вращение земли незначительны).
Для анализа движения разделите двумерное движение на вертикальные и горизонтальные составляющие. Вертикально объект испытывает постоянное ускорение силы тяжести. По горизонтали объект не испытывает ускорения и, следовательно, поддерживает постоянную скорость. Эта скорость проиллюстрирована на рисунке, где компоненты скорости изменяются в направлении y ; однако все они имеют одинаковую длину в направлении x (постоянное значение). Обратите внимание, что вектор скорости изменяется со временем из-за того, что изменяется вертикальная составляющая.
Рисунок 8
Движение снаряда.
В этом примере частица покидает начало координат с начальной скоростью ( v o ) вверх под углом θ o . Исходные компоненты скорости x и y задаются формулами v x0 = v o и v y0 = v o sin θ o .
Когда движения разделены на компоненты, величины в направлениях x и y могут быть проанализированы с помощью одномерных уравнений движения, обозначенных индексами для каждого направления: для горизонтального направления v x = v x0 и x = v x0 t ; для вертикального направления v y = v y0 — gt и y = v y0 — (1/2) gt 2 , где x и y представляют собой расстояния в горизонтальном и вертикальном направлениях соответственно, а ускорение свободного падения ( g ) равно 9.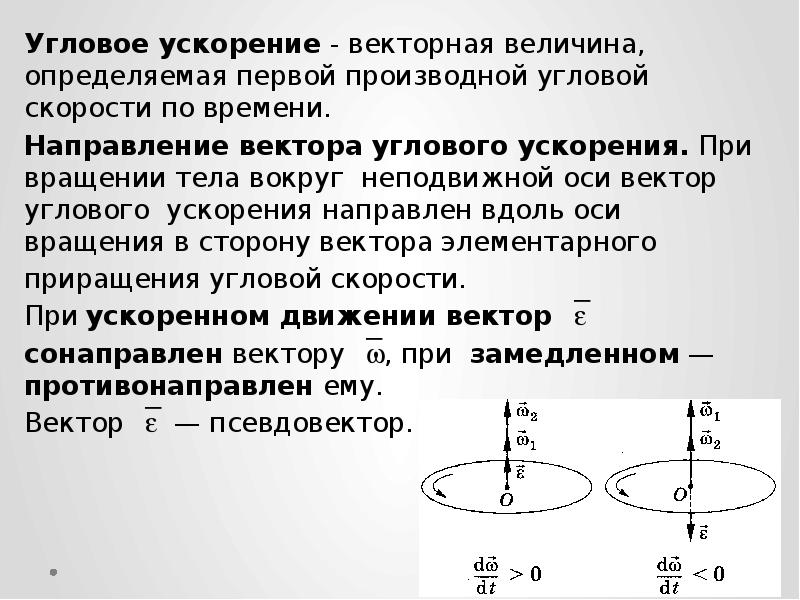 8 м / с 2 . (Отрицательный знак уже включен в уравнения.) Если объект стреляет под углом, составляющая y начальной скорости будет отрицательной. Скорость снаряда в любой момент времени может быть вычислена по компонентам в то время по теореме Пифагора, а направление может быть определено по обратной тангенсе соотношений компонентов:
8 м / с 2 . (Отрицательный знак уже включен в уравнения.) Если объект стреляет под углом, составляющая y начальной скорости будет отрицательной. Скорость снаряда в любой момент времени может быть вычислена по компонентам в то время по теореме Пифагора, а направление может быть определено по обратной тангенсе соотношений компонентов:
Другая информация полезна при решении проблем со снарядами. Рассмотрим пример, показанный на рисунке, где снаряд выстреливается под углом от уровня земли и возвращается на тот же уровень.Время, за которое снаряд достигнет земли из своей наивысшей точки, равно времени падения свободно падающего объекта, который падает прямо с той же высоты. Это равенство времени обусловлено тем, что горизонтальная составляющая начальной скорости снаряда влияет на то, как далеко снаряд летит по горизонтали, но не на время полета. Пути полета снаряда параболические и, следовательно, симметричные. Также в этом случае объект достигает вершины своего подъема за половину общего времени (T) полета.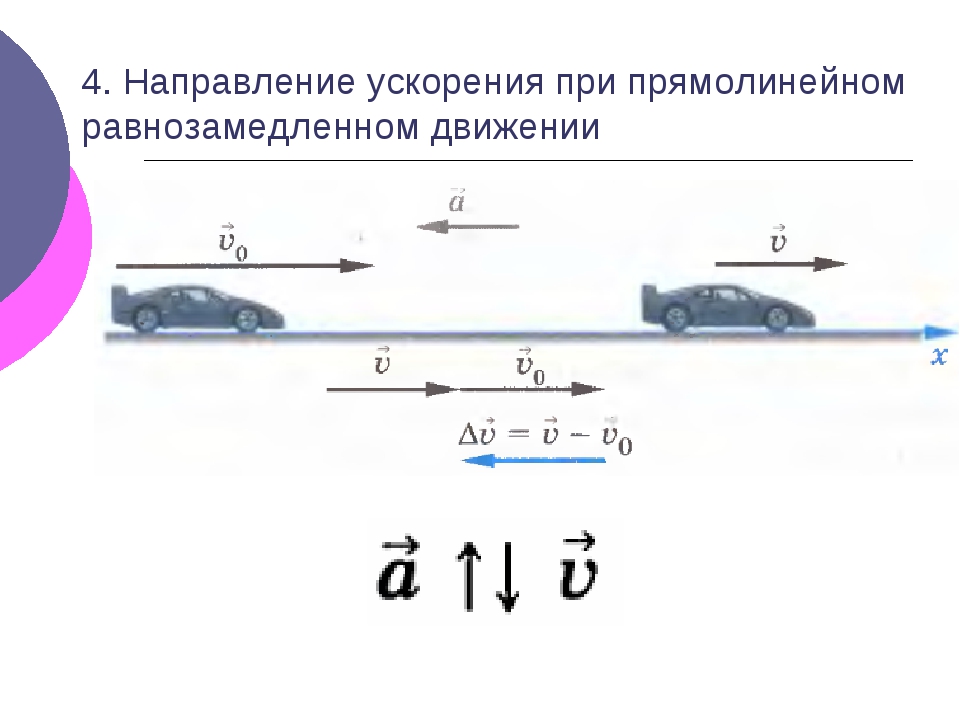 В верхней части подъема вертикальная скорость равна нулю. (Ускорение всегда составляет g , даже на пике полета.) Эти факты можно использовать для получения дальности снаряда или расстояния, пройденного по горизонтали. На максимальной высоте v y = 0 и t = T /2; следовательно, уравнение скорости в вертикальном направлении принимает вид 0 = v o sin θ — g T /2 или решение для T , T = (2 v 0 sin θ) / г .
В верхней части подъема вертикальная скорость равна нулю. (Ускорение всегда составляет g , даже на пике полета.) Эти факты можно использовать для получения дальности снаряда или расстояния, пройденного по горизонтали. На максимальной высоте v y = 0 и t = T /2; следовательно, уравнение скорости в вертикальном направлении принимает вид 0 = v o sin θ — g T /2 или решение для T , T = (2 v 0 sin θ) / г .
Подстановка в уравнение горизонтального расстояния дает R = ( v o cos θ) T . Подставьте T в уравнение диапазона и используйте тождество тригонометрии sin 2θ = 2 sin θ cos θ, чтобы получить выражение для диапазона в терминах начальной скорости и угла движения, R = ( v o 2 / г ) sin 2θ.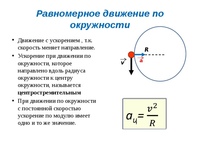 Как указано в этом выражении, максимальный диапазон возникает при θ = 45 градусов, потому что при этом значении θ sin 2θ имеет максимальное значение 1.На рисунке показаны траектории снарядов, выпущенных с одинаковой начальной скоростью под разными углами наклона.
Как указано в этом выражении, максимальный диапазон возникает при θ = 45 градусов, потому что при этом значении θ sin 2θ имеет максимальное значение 1.На рисунке показаны траектории снарядов, выпущенных с одинаковой начальной скоростью под разными углами наклона.
Рисунок 9
Дальность выстрела снарядов под разными углами.
Для равномерного движения объекта по горизонтальному кругу радиусом (R) , постоянная скорость определяется как v = 2π R / T , что представляет собой расстояние одного оборота, деленное на время для одна революция.Время на один оборот (T) определяется как период . За один оборот головка вектора скорости за один период описывает окружность 2π v ; таким образом, величина ускорения составляет a = 2π v / T . Объедините эти два уравнения, чтобы получить два дополнительных соотношения в других переменных: a = v 2 / R и a = (4π 2 / T 2 ) R .
Вектор смещения направлен из центра круга движения. Вектор скорости касается пути. Вектор ускорения, направленный к центру круга, называется центростремительным ускорением . На рисунке показаны векторы смещения, скорости и ускорения в различных положениях, когда масса движется по кругу в горизонтальной плоскости без трения.
Рисунок 10
Равномерное круговое движение.
Центростремительное ускорение
Центростремительное ускорениеСледующая: Конический маятник Up: Круговое движение Предыдущий: Равномерное круговое движение Объект, совершающий круговую орбиту радиуса с равномерным тангенциальным скорость обладает вектором скорости, величина которого постоянна, но чье направление постоянно меняется. Отсюда следует, что объект должен быть ускоряясь , поскольку (векторное) ускорение — это скорость изменения (вектора) скорость, а (векторная) скорость действительно меняется во времени.

Предположим, что объект перемещается от точки к точке между временами и, как
показано на рис. 58. Предположим, далее, что объект вращается
через радианы в этом временном интервале. Вектор
,
показанный на схеме, идентичен
к вектору
. Кроме того, угол между векторами и просто. Вектор
представляет
изменение векторной скорости между моментами и.Это можно увидеть
что этот вектор направлен к центру окружности . Из стандартной тригонометрии,
длина вектора
является
| (256) |
Однако для малых углов , при условии, что измеряется в радианах . Следовательно,
| (257) |
Следует, что
| (258) |
куда — угловая скорость объекта, измеренная в радианах в секунду .
 Таким образом, объект, совершающий круговую орбиту радиуса с равномерной тангенциальной
скорость и равномерная угловая скорость обладают ускорением
направленное к центру круга — , то есть , центростремительное ускорение — от
величина
Таким образом, объект, совершающий круговую орбиту радиуса с равномерной тангенциальной
скорость и равномерная угловая скорость обладают ускорением
направленное к центру круга — , то есть , центростремительное ускорение — от
величина | (259) |
Предположим, что к концу кабеля из
длины, и повернулся так, что вес совершает горизонтальный круг,
радиус, с равномерной тангенциальной скоростью.Как мы только что узнали,
груз подвержен центростремительному ускорению величины. Следовательно,
вес испытывает центростремительную силу
| (260) |
Что дает эта сила? Что ж, в данном примере сила обеспечивается натяжение в тросе.
 Следовательно, .
Следовательно, . Предположим, что трос таков, что он рвется всякий раз, когда в нем
превышает определенное критическое значение.Отсюда следует, что существует
максимальная скорость, с которой груз может вращаться: а именно,
| (261) |
Если превышает, то кабель порвется. Как только трос оборвется, груз перестанет подвергаться центростремительной силе, поэтому он улетит — с скорость — по прямой что на касательно к круговой орбите, которую он выполнял ранее.
Следующая: Конический маятник Up: Круговое движение Предыдущий: Равномерное круговое движение Ричард Фицпатрик 2006-02-02
Равномерное круговое движение
Центростремительное ускорение
youtube.com/embed/EX5DZ2MHlV4?rel=0″ frameborder=»0″ allowfullscreen=»»>
Движение объекта по круговой траектории с постоянной скоростью известно как равномерное круговое движение (UCM).Объект в UCM постоянно меняет направление, и поскольку скорость является вектором и имеет направление, можно сказать, что объект, подвергающийся UCM, имеет постоянно меняющуюся скорость, даже если его скорость остается постоянной. И если скорость объекта меняется, он должен ускоряться. Следовательно, объект, подвергающийся UCM, постоянно ускоряется. Этот тип ускорения известен как центростремительное ускорение .
Вопрос : Если автомобиль ускоряется, увеличивается ли его скорость?
Ответ : Это зависит от обстоятельств.Его скорость может увеличиваться, или он может ускоряться в направлении, противоположном его скорости (замедление). Или его скорость может оставаться постоянной, но при этом ускоряться, если он движется равномерно по кругу.
Не менее важно, что нам нужно выяснить направление ускорения объекта, поскольку ускорение является вектором. Для этого нарисуем объект, движущийся против часовой стрелки по круговой траектории, и покажем его вектор скорости в двух разных точках времени.Поскольку мы знаем, что ускорение — это скорость изменения скорости объекта во времени, мы можем определить направление ускорения объекта, найдя направление его изменения скорости Δv.
Чтобы найти его изменение скорости Δv, мы должны вспомнить это.
Следовательно, нам нужно графически найти разность векторов v f и v i , которую можно переписать как.
Напомним, что для графического сложения векторов мы выстраиваем их кончик к хвосту, а затем рисуем результирующий вектор от начальной точки (хвоста) нашего первого вектора до конечной точки (кончика) нашего последнего вектора.
Итак, вектор ускорения должен указывать в указанном выше направлении. Если я снова покажу этот вектор на нашем исходном круге, выстроив его прямо между нашим начальным и конечным векторами скорости, легко увидеть, что вектор ускорения указывает на центр круга.
Вы можете повторить эту процедуру из любой точки круга … куда бы вы ни пошли, вектор ускорения всегда направлен к центру круга. Фактически, слово центростремительный в центростремительном ускорении означает «центростремительный»!
Итак, теперь мы знаем направление ускорения объекта (к центру круга), но как насчет его величины? Величина центростремительного ускорения объекта может быть найдена в справочной таблице и определяется по формуле:
Круговая скорость
Итак, как определить скорость объекта, движущегося по круговой траектории? Формула скорости, которую мы изучили в кинематике, все еще применима.
Однако мы должны быть осторожны при использовании этого уравнения, чтобы понять, что объект, движущийся по круговой траектории, движется по окружности круга. Следовательно, если объект совершит один полный оборот по кругу, расстояние, которое он пройдет, будет равно длине окружности круга.
Давайте посмотрим на пример задачи:
Вопрос : Миранда едет на своей машине по часовой стрелке по круговой колее радиусом 30 метров.Она делает 10 кругов по трассе за 2 минуты. Найдите общее пройденное расстояние Миранды, среднюю скорость и центростремительное ускорение.
Ответ :
Центростремительная сила
youtube.com/embed/ldQWTNDBSSE?rel=0″ frameborder=»0″ allowfullscreen=»»>
Если объект, движущийся по круговой траектории, имеет внутреннее ускорение, 2-й закон Ньютона говорит нам, что чистая сила также должна быть направлена к центру круга.Этот тип силы, известный как центростремительная сила, может быть гравитационной силой, натяжением, приложенной силой или даже силой трения.
ПРИМЕЧАНИЕ: Имея дело с проблемами кругового движения, важно понимать, что центростремительная сила на самом деле не новая сила, центростремительная сила — это просто ярлык или группировка, которые мы применяем к силе, чтобы указать ее направление к центру круг. Это означает, что вы никогда не захотите обозначать силу на диаграмме свободного тела как центростремительную силу, F c .Вместо этого обозначьте силу, направленную к центру, как можно точнее. Если усилие вызывает натяжение, обозначьте его F T . Если сила трения вызывает направленную к центру силу, обозначьте ее F f и так далее.
Мы можем объединить уравнение центростремительного ускорения со 2-м законом Ньютона, чтобы получить 2-й закон Ньютона для кругового движения. Напомним, что 2-й закон Ньютона гласит:
Для объекта, движущегося по круговой траектории, должна существовать чистая (центростремительная) сила, направленная к центру круговой траектории, чтобы вызвать (центростремительное) ускорение, направленное к центру круговой траектории.В таком случае мы можем пересмотреть 2-й закон Ньютона для этого конкретного случая следующим образом:
Затем, вспоминая нашу формулу центростремительного ускорения как:
Мы можем сложить их вместе, заменив c в нашем уравнении, чтобы получить комбинированную форму 2-го закона Ньютона для равномерного кругового движения:
Конечно, если объект движется по круговой траектории и центростремительная сила устранена, объект будет продолжать движение по прямой в том направлении, в котором он двигался в момент снятия силы.
Вопрос : Бегущий назад 800N поворачивает угол по круговой траектории r = 1 м со скоростью 8 м / с. Найдите массу бегущего спина, центростремительное ускорение и центростремительную силу.
Ответ : Дано mg = 800N, r = 1m, v = 8m / s; Найдите m, ac, Fc
Попробуем еще:
Еще одна примерная задача, на этот раз включающая только алгебраические манипуляции:
Частота и период
Для объектов, движущихся по круговой траектории, мы можем охарактеризовать их движение по окружности с помощью терминов частота (f) и период (T).Частота объекта — это количество оборотов, которые объект совершает за полную секунду. Он измеряется в единицах [1 / с] или герцах (Гц). Точно так же период объекта — это время, необходимое для совершения одного полного оборота. Поскольку период — это временной интервал, он измеряется в секундах. Мы можем связать период и частоту, используя уравнения:
Поскольку период — это временной интервал, он измеряется в секундах. Мы можем связать период и частоту, используя уравнения:
Вопрос : Игрушечный поезд весом 500 г проходит 10 кругов по круговой колее за 1 мин 40 сек.Если диаметр пути составляет 1 м, найдите центростремительное ускорение поезда (a c ), центростремительную силу (F c ), период (T) и частоту (f).
Ответ :
Давайте посмотрим на другой пример:
Вертикальное круговое движение
Объекты движутся по кругу как по вертикали, так и по горизонтали.Поскольку скорость этих объектов обычно не является постоянной, технически это не равномерное круговое движение , но наши навыки анализа UCM по-прежнему применимы.
Представьте американские горки, движущиеся по вертикальной петле радиусом 10 м. Вы путешествуете по петле вверх ногами, но не падаете с американских горок. Как это возможно? Мы можем использовать наше понимание UCM и динамики, чтобы выяснить это!
Конец круга
Для начала давайте сначала посмотрим на каботажное судно, когда машина находится в нижней части петли.Рисуя диаграмму свободного тела, сила тяжести на подставке, также известная как его вес, тянет его вниз, поэтому мы рисуем направленный вниз вектор с надписью «mg». Этой силе противодействует нормальная сила, с которой рельсы подстаканника поднимаются вверх, которую мы обозначили как F N .
Поскольку каботажное судно движется по круговой траектории, мы можем проанализировать его с помощью инструментов, которые мы разработали для равномерного кругового движения. 2-й закон Ньютона все еще применяется, поэтому мы можем написать:
Обратите внимание: поскольку мы говорим о круговом движении, мы примем соглашение, согласно которому силы, направленные к центру круга, положительны, а силы, направленные от центра круга, отрицательны. На этом этапе вспомните, что сила, которую вы «чувствуете», когда вы в движении, на самом деле является нормальной силой. Итак, решая нормальную силу, когда вы начинаете двигаться по кругу, мы находим, что
На этом этапе вспомните, что сила, которую вы «чувствуете», когда вы в движении, на самом деле является нормальной силой. Итак, решая нормальную силу, когда вы начинаете двигаться по кругу, мы находим, что
Поскольку мы знаем, что чистая сила всегда равна массе, умноженной на ускорение, поэтому чистая центростремительная сила равна массе, умноженной на центростремительное ускорение, мы можем заменить F NET c следующим образом:
Из полученного уравнения видно, что нормальная сила теперь равна весу плюс дополнительный член центростремительной силы кругового движения.Когда мы движемся по круговой траектории в нижней части петли, мы чувствуем себя тяжелее своего веса. В общем, мы ощущаем дополнительные «перегрузки». Сколько g, по нашему мнению, можно получить, приложив немного больше усилий. Если мы перепишем наше уравнение для нормальной силы, вытягивая массу, применяя распределительное свойство умножения, мы получим:
Обратите внимание, что внутри круглых скобок у нас есть стандартное ускорение свободного падения, g, плюс член центростремительного ускорения ().
Этот дополнительный термин — дополнительная сила тяжести, которую ощущает человек. Например, если c было равно g (9,81 м / с 2 ), можно сказать, что человек в тележке испытывал две g (1 g от центростремительного ускорения и 1 g от гравитационного поля Земли). Если бы c было равно 3 * g (29,4 м / с 2 ), человек испытал бы в общей сложности четыре g.
Расширяя этот анализ до аналогичной ситуации в другом контексте, попробуйте представить вместо американских горок массу, вращающуюся по вертикальному кругу на веревке.В нашем анализе вы можете заменить нормальную силу натяжением струны. Поскольку сила больше в нижней части круга, вероятность разрыва струны наиболее высока, когда масса находится в нижней части круга!
Вершина круга
В верхней части цикла мы видим существенно другую картину. Теперь нормальная сила от рельсов подстаканника должна давить вниз на тележку, хотя все еще в положительном направлении, так как теперь вниз направлено к центру круговой траектории. В этом случае, однако, вес объекта также указывает на центр круга, так как гравитационное поле Земли всегда тянется к центру Земли. Наша диаграмма свободного тела выглядит значительно иначе, и поэтому наше приложение ко 2-му закону Ньютона для кругового движения также значительно отличается.
В этом случае, однако, вес объекта также указывает на центр круга, так как гравитационное поле Земли всегда тянется к центру Земли. Наша диаграмма свободного тела выглядит значительно иначе, и поэтому наше приложение ко 2-му закону Ньютона для кругового движения также значительно отличается.
Поскольку сила, которую вы чувствуете, на самом деле является нормальной силой, мы можем найти нормальную силу и расширить чистую центростремительную силу, как показано:
Из уравнения видно, что нормальная сила теперь равна центростремительной силе за вычетом вашего веса.Если бы центростремительная сила была равна вашему весу, вы бы почувствовали себя невесомым. Обратите внимание, что это также точка, в которой нормальная сила в точности равна 0. Это означает, что рельсы гусеницы больше не давят на тележку американских горок … если бы центростремительная сила была хоть чуть-чуть меньше (скорость автомобиля было немного меньше), нормальная сила FN будет меньше 0. Поскольку рельсы не могут физически тянуть тележку в отрицательном направлении (от центра круга), это означает, что вагон падает с рельса и у пассажира телеги вот-вот будет очень, очень плохой день. Только поддерживая высокую скорость, тележка может успешно преодолеть петлю … идти слишком медленно, и тележка падает.
Только поддерживая высокую скорость, тележка может успешно преодолеть петлю … идти слишком медленно, и тележка падает.
В целях безопасности настоящие американские горки на самом деле имеют колеса по обеим сторонам рельсов, чтобы тележка не упала, если она когда-либо замедлялась на вершине петли, хотя горки спроектированы так, что на самом деле такая ситуация никогда не возникает.
Центростремительное ускорение постоянно? — Обмен физическими стеками
Когда мы говорим о кинематике точечной частицы, в основном о векторах скорости и ускорения, было бы разумно использовать дифференциальную геометрию, чтобы понять, что происходит.Движение точечной частицы полностью описывается, если ей задан вектор положения $ \: \ mathbf {r} (t) \: $ как функция времени $ \: t \: $.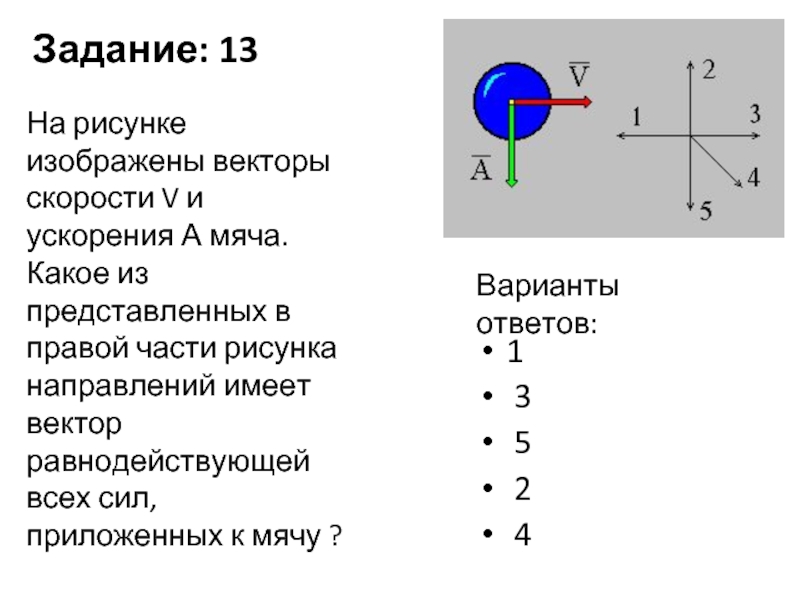 2} {16 \ pi}
\ tag {04}
\ end {Equation}
2} {16 \ pi}
\ tag {04}
\ end {Equation}
Вектор ускорения анализируется на две составляющие:
- Орбитальная составляющая $ \: \ mathbf {a} _ {\ Vert} \: $, касательная к кривой, параллельная вектору скорости $ \: \ mathbf {v} \: $ и отвечающая только за изменения величины этого вектора.
- Центростремительная составляющая $ \: \ mathbf {a} _ {\ perp} \: $ нормальная к кривой, нормальная к вектору скорости $ \: \ mathbf {v} \: $ и ответственная только за изменения направление этого вектора.
В этом примере и даны векторные диаграммы скорости и ускорения для каждого случая:
В левом полукруге частица совершает равномерное круговое движение. Вектор скорости имеет постоянную величину (скорость), вектор ускорения имеет постоянную величину и всегда перпендикулярен скорости.Компонента орбитального ускорения отсутствует.
На средних полуэллипсах вектор скорости непрерывно изменяется как по направлению, так и по величине из-за центростремительной и орбитальной составляющих ускорения соответственно.
 Вектор ускорения также непрерывно изменяется как по направлению, так и по величине.
Вектор ускорения также непрерывно изменяется как по направлению, так и по величине.В правом полукруге частица совершает неравномерное круговое движение. Оба вектора непрерывно изменяются как по направлению, так и по величине.2} {\ rho} \ tag {05} \ end {уравнение} справедливо не только для кругового движения, но и для любого криволинейного регулярного движения, где $ \: \ rho \: $ радиус кривизны . На рисунке ниже см. Подробности вокруг точки F рисунка выше.
Центростремительное ускорение | Школы онлайн
Центростремительное ускорение — это, по сути, ускорение объекта при равномерном круговом движении или скорость изменения тангенциальной скорости, при которой вектор ускорения всегда направлен к центру образованной окружности.По сути, тангенциальная скорость постоянна; однако направление вектора тангенциальной скорости изменяется по мере вращения объекта.
Пытаясь представить себе центростремительное ускорение в действии, представьте себе американские горки.
 Когда американские горки движутся по трассе, центростремительные и центробежные силы добавляются. Центростремительная сила толкает к центру объекта, чтобы каботажное судно оставалось на пути. Центростремительная сила (необходимая чистая сила) также гарантирует, что американские горки остаются на трассе, сочетая центростремительную силу и регулярное ускорение для создания центростремительного ускорения.Американские горки склонны двигаться по прямой линии, они также вдавливаются в колею, создавая эффект ускорения. Центробежная сила выталкивает за пределы рельсов, противодействуя своей противоположной центростремительной силе, таким образом позволяя каботажному кораблю двигаться круговыми движениями. В американских горках, путешествующих по петле или кругу, ваше тело привязано к ним, чтобы двигаться вместе с ним по круговой траектории, чтобы не продолжать движение прямо… Центробежная сила не существует. Нет ничего, что «толкает» наружу, пока объект движется по кривой.Единственными силами, действующими на американские горки, являются вес и сила, с которой рельсы толкают поезд.
Когда американские горки движутся по трассе, центростремительные и центробежные силы добавляются. Центростремительная сила толкает к центру объекта, чтобы каботажное судно оставалось на пути. Центростремительная сила (необходимая чистая сила) также гарантирует, что американские горки остаются на трассе, сочетая центростремительную силу и регулярное ускорение для создания центростремительного ускорения.Американские горки склонны двигаться по прямой линии, они также вдавливаются в колею, создавая эффект ускорения. Центробежная сила выталкивает за пределы рельсов, противодействуя своей противоположной центростремительной силе, таким образом позволяя каботажному кораблю двигаться круговыми движениями. В американских горках, путешествующих по петле или кругу, ваше тело привязано к ним, чтобы двигаться вместе с ним по круговой траектории, чтобы не продолжать движение прямо… Центробежная сила не существует. Нет ничего, что «толкает» наружу, пока объект движется по кривой.Единственными силами, действующими на американские горки, являются вес и сила, с которой рельсы толкают поезд. Затем, используя «сумму сил», вы можете определить ускорение поезда.
Затем, используя «сумму сил», вы можете определить ускорение поезда.Объекты, движущиеся в равномерном круговом движении, имеют центростремительное ускорение, направленное к центру кривизны траектории, имеют величину, пропорциональную квадрату скорости, и величину, обратно пропорциональную радиусу траектории.
Следующие уравнения могут использоваться для определения центростремительного ускорения и его связи с другими переменными.
- ac = v2 / r
- ac = 4∏2 r / T2
- ac = (2∏r / T) 2 / r
Чтобы еще раз проверить центростремительное ускорение, выполните следующие простые шаги процедуры.
Использование скрепки, веревки и небольшого, но тяжелого предмета, например, более крупного мрамора. Откройте скрепку, привяжите шнур к концу и надежно привяжите предмет к концу веревки. Держа пустой конец скрепки в одной руке, набирайте обороты и вращайте предмет вокруг головы по кругу.
Что такое угловое ускорение (ускорение вращения)?
КУгловое ускорение, также называемое ускорением вращения, является количественным выражением изменения угловой скорости, которой вращающийся объект претерпевает в единицу времени.
 Это векторная величина, состоящая из компонента величины и одного из двух определенных направлений или значений.
Это векторная величина, состоящая из компонента величины и одного из двух определенных направлений или значений.Величина или длина вектора углового ускорения прямо пропорциональна скорости изменения угловой скорости и измеряется в радианах с в секунду в квадрате (рад / с 2 или рад · с -2 ).В качестве альтернативы, величина углового ускорения может быть выражена в градусах в секунду в квадрате (град / с 2 или град · с -2 ). Направление вектора углового ускорения перпендикулярно плоскости, в которой происходит вращение. Если увеличение угловой скорости происходит по часовой стрелке относительно наблюдателя, то вектор углового ускорения направлен в сторону от наблюдателя. Если увеличение угловой скорости происходит против часовой стрелки, то вектор углового ускорения направлен в сторону наблюдателя.
Вектор углового ускорения не обязательно указывает в том же направлении, что и вектор угловой скорости. Представьте, что автомобиль катится по шоссе с увеличивающейся скоростью.




 Вектор ускорения также непрерывно изменяется как по направлению, так и по величине.
Вектор ускорения также непрерывно изменяется как по направлению, так и по величине. Когда американские горки движутся по трассе, центростремительные и центробежные силы добавляются. Центростремительная сила толкает к центру объекта, чтобы каботажное судно оставалось на пути. Центростремительная сила (необходимая чистая сила) также гарантирует, что американские горки остаются на трассе, сочетая центростремительную силу и регулярное ускорение для создания центростремительного ускорения.Американские горки склонны двигаться по прямой линии, они также вдавливаются в колею, создавая эффект ускорения. Центробежная сила выталкивает за пределы рельсов, противодействуя своей противоположной центростремительной силе, таким образом позволяя каботажному кораблю двигаться круговыми движениями. В американских горках, путешествующих по петле или кругу, ваше тело привязано к ним, чтобы двигаться вместе с ним по круговой траектории, чтобы не продолжать движение прямо… Центробежная сила не существует. Нет ничего, что «толкает» наружу, пока объект движется по кривой.Единственными силами, действующими на американские горки, являются вес и сила, с которой рельсы толкают поезд.
Когда американские горки движутся по трассе, центростремительные и центробежные силы добавляются. Центростремительная сила толкает к центру объекта, чтобы каботажное судно оставалось на пути. Центростремительная сила (необходимая чистая сила) также гарантирует, что американские горки остаются на трассе, сочетая центростремительную силу и регулярное ускорение для создания центростремительного ускорения.Американские горки склонны двигаться по прямой линии, они также вдавливаются в колею, создавая эффект ускорения. Центробежная сила выталкивает за пределы рельсов, противодействуя своей противоположной центростремительной силе, таким образом позволяя каботажному кораблю двигаться круговыми движениями. В американских горках, путешествующих по петле или кругу, ваше тело привязано к ним, чтобы двигаться вместе с ним по круговой траектории, чтобы не продолжать движение прямо… Центробежная сила не существует. Нет ничего, что «толкает» наружу, пока объект движется по кривой.Единственными силами, действующими на американские горки, являются вес и сила, с которой рельсы толкают поезд. Затем, используя «сумму сил», вы можете определить ускорение поезда.
Затем, используя «сумму сил», вы можете определить ускорение поезда. Это векторная величина, состоящая из компонента величины и одного из двух определенных направлений или значений.
Это векторная величина, состоящая из компонента величины и одного из двух определенных направлений или значений.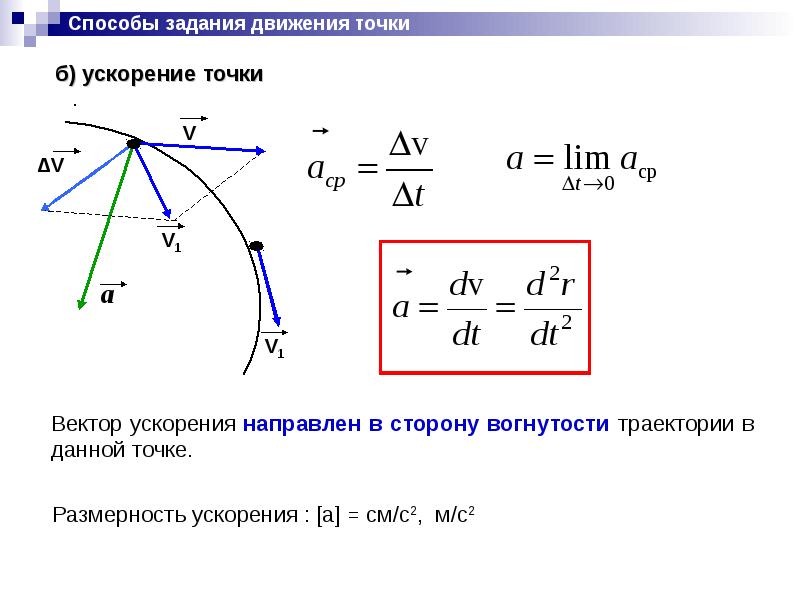
Leave A Comment