ЧЕТЫРЁХУГОЛЬНИКИ | geometria
Определение параллелограмма.
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны:AB||CD, AD||DC.
Cвойства параллелограмма.
Противоположные стороны параллелограмма равны:AB=CD, AD=DC.
Противоположные углы параллелограмма равны:
∠A=∠C, ∠B=∠D.
Сумма углов параллелограмма, прилежащих к одной его стороне составляет 180°.Например, ∠A+∠B=180°.
Любая диагональ параллелограмма делит его на два равных треугольника. Δ ABD=Δ BCD.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. AO=OC, BO=OD. Пусть АС=d1 и BD=d2 , ∠COD=α. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
(d1)2+(d2)2=2 (a2+b2).
Признаки параллелограмма.
· Если две противоположные стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.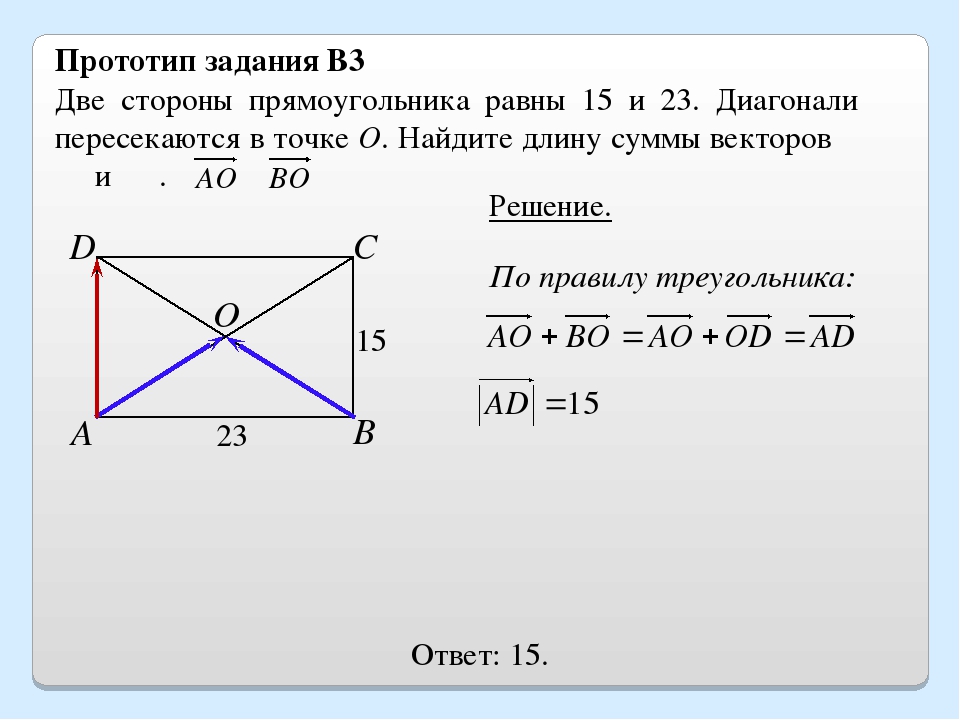
· Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
· Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Площадь параллелограмма.
1) S=ah;
2) S=ab∙sinα;
3) S=(½) d1∙d2∙sinβ.
Прямоугольник.
Прямоугольник — это параллелограмм, у которого все углы прямые. ABCD — прямоугольник. Прямоугольник обладает всеми свойствами параллелограмма.
Диагонали прямоугольника равны.
d1=d2 – диагонали прямоугольника равны. α – угол между диагоналями.
Квадрат диагонали прямоугольника равен сумме квадратов сторон прямоугольника:
(d1)2=(d2)2=a2+b2.
Площадь прямоугольника можно найти по формулам:
1) S=ab; 2) S=(½)· d²∙sinα; (d- диагональ прямоугольника).
Около любого прямоугольника можно описать окружность, центр которой – точка пересечения диагоналей; диагонали являются диаметрами окружности.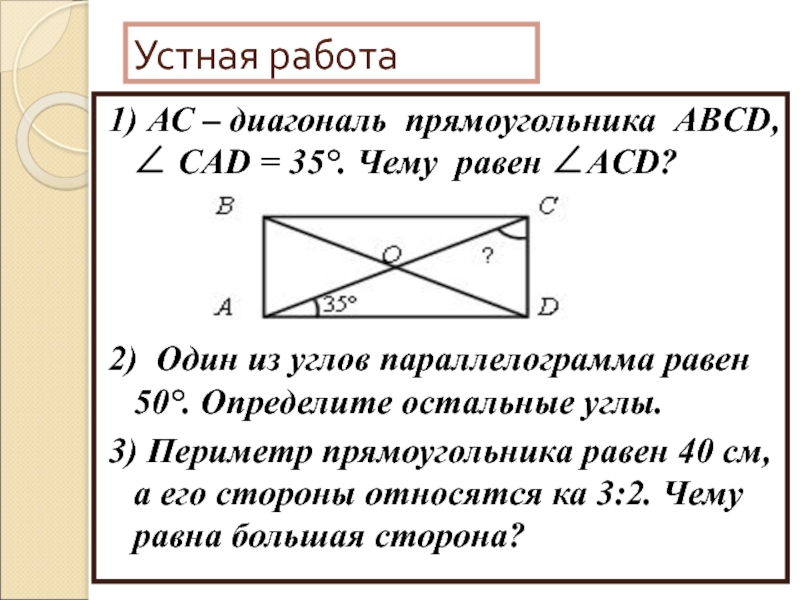
Ромб.
Ромб — это параллелограмм, у которого все стороны равны.
Ромб обладает всеми свойствами параллелограмма.
Диагонали ромба взаимно перпендикулярны.
AC | BD.
Диагонали ромба являются биссектрисами его углов.
Площадь ромба.
1) S=ah;
2) S=a2∙sinα;
3) S=(½) d1∙d2;
4) S= P∙r, где P – периметр ромба, r – радиус вписанной окружности.
Квадрат.
Все стороны квадрата равны, диагонали квадрата равны и пересекаются под прямым углом.
Диагональ квадрата d=a√2.
Площадь квадрата. 1) S=a2; 2) S=(½) d2.
Трапеция.
Основания трапеции AD||BC, MN-средняя линия
MN=(AD+BC)/2.
Площадь трапеции равна произведению полусуммы ее оснований на высоту:
S=(AD+BC)∙BF/2 или S=(a+b)∙h/2.
В равнобедренной (равнобокой) трапеции длины боковых сторон равны; углы при основании равны.
Площадь любого четырехугольника.
· Площадь любого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
S=(½) d1∙d2∙sinβ.
· Площадь любого четырехугольника равна половине произведения его периметра на радиус вписанной окружности:
S=(½) P∙r.
В выпуклом четырехугольнике, вписанном в круг, произведение диагоналей равно сумме произведений противоположных сторон (теорема Птолемея).
AC∙BD=AB∙DC+AD∙BC.
Если суммы противолежащих углов четырехугольника равны по 180°, то около четырехугольника можно описать окружность. Обратное утверждение также верно.
Если суммы противолежащих сторон четырехугольника равны (a+c=b+d), то в этот четырехугольник можно вписать окружность. Обратное утверждение также верно.
площа па
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой.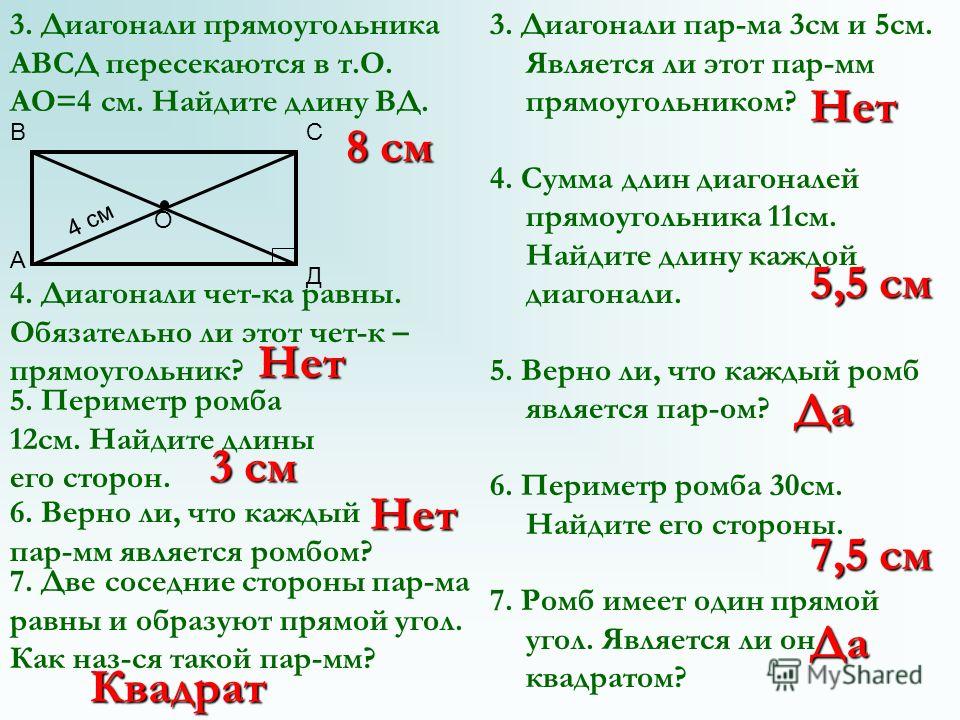 2).
2).
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов ( прилегающие к одной стороне ) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма — это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
Формула площади параллелограмма
Площадь параллелограмма равна произведению стороны на высоту проведенную к ней. Формула площади следующая
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Посмотреть материалы:
Параллелограмм — rajak.rs
Параллелограмм — это четырехугольник у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Найти сторону прямоугольника через диагональ, периметр или площадь
Четырехугольник, у которого все углы прямые, противоположные стороны равны и параллельны друг другу, называется прямоугольником. Стороной прямоугольника является отрезок, соединяющий две вершины фигуры. Длинная сторона считается длиной, короткая сторона — шириной прямоугольника, прилегающие стороны перпендикулярны, они являются его высотами.
Расчет длины стороны прямоугольника через диагональ и сторону
Отрезок, соединяющий 2 противолежащие вершины прямоугольника, является его диагональю. В прямоугольнике две диагонали одинаковой длины. Каждая из них делит прямоугольник на два прямоугольных треугольника, гипотенузой которых является диагональ, а катетами — стороны прямоугольника. Соответственно, квадрат диагонали можно вычислить через теорему Пифагора: d
2d2 = 2a2 + 2b2
где d — диагональ, а, b — стороны прямоугольника.
Если дана диагональ прямоугольника и одна из его сторон, находим длину другой стороны, как корень из разности: квадрат диагонали минус квадрат известной стороны:
a = √d2 — b2
b = √d2 — a2
где d — диагональ, а, b — стороны прямоугольника.
Расчет стороны прямоугольника через периметр и сорону
Периметр прямоугольника равняется сумме всех его сторон. Если известны длина (а) и ширина (b) прямоугольника, его периметр (Р) будет равен удвоенной сумме сторон, т.к. его противоположные стороны равны:
Р = 2a + 2b = 2 (а + b)
Если известны периметр и одна из сторон прямоугольника, другую находим по формуле:
a = (P — 2b) / 2
b = (P — 2a) / 2
Р — периметр, a — длина, b — ширина прямоугольника
Т.е. сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.
Расчет стороны прямоугольника через площадь и сторону
Чтобы рассчитать площадь прямоугольника (S), необходимо его длину а умножить на ширину b:
S = аb
Если известна площадь прямоугольника и одна из его сторон, длину другой находим путем деления площади на длину известной стороны:
a = S / b
b = S / a
где S — площадь прямоугольника, a, b — его стороны.
keepslide.com — §3. Параллелограмм. Средняя линия…
§3. Параллелограмм. Средняя линия треугольника.
Задача 3 из диагностической работы
В выпуклом четырёхугольнике ABCD отрезки, соединяющие середины противоположных сторон, пересекаются под углом 60°, а их длины относятся как 1:3. Чему равна меньшая диагональ четырёхугольника ABCD, если большая равна 39 ?
Для решения задач этого раздела нужно знать
свойства и признаки параллелограмма, теорему о средней линии треугольника, теорему о медианах треугольника (медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника), Теорема. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. Теорема. Середины сторон любого четырёхугольника являются вершинами параллелограмма.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. Теорема. Середины сторон любого четырёхугольника являются вершинами параллелограмма.
Биссектрисы углов при одной стороне параллелограмма перпендикулярны
Биссектриса параллелограмма отсекает равнобедренный треугольник
ПРИМЕР 1.
В выпуклом четырёхугольнике отрезки, соединяющие середины противоположных сторон, равны соответственно а и Ь и пересекаются под углом 60°. Найдите диагонали четырёхугольника.
Роспись за запись решения на доске
Идея решения. По диагоналям параллелограмма найти его стороны – это половины диагоналей данного четырехугольника
ПРИМЕР 2.В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины сторон АВ и CD, равна 1. Прямые ВС и AD перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей АС и BD.
Ответ:
Оригинальный способ решения : найти параллелограмм!!!
1
Р
Стороны МР и MQ соответственно параллельны прямым ВС и AD => MP ?? MQ => четырёхугольник MPNQ — прямоугольник. Диагонали прямоугольника равны, поэтому PQ=MN=1.
Диагонали прямоугольника равны, поэтому PQ=MN=1.
ПРИМЕР 3. Вершины одного параллелограмма лежат по одной на сторонах другого. Докажите, что центры параллелограммов совпадают.
Оригинальный способ решения : найти параллелограмм!!!
7 подготовительных задач3.1. Расстояние между серединами взаимно перпендикулярных хорд АС и ВС некоторой окружности равно 10. Найдите диаметр окружности. 3.2. Диагональ параллелограмма делит его угол на части в 30° и 45°. Найдите отношение сторон параллелограмма. 3.3. Вершины М и N квадрата KLMN лежат на гипотенузе АВ прямоугольного треугольника ABC (N между В и М), а вершины К и L — на катетах ВС и АС соответственно. Известно, что AM = а и BN = Ь. Найдите площадь квадрата.
Балл за решение каждой задачи
Вписанный угол, равный 90?Средняя линия треугольника
Теорема синусов
Подобные треугольники
7 подготовительных задач3.4. Сторона ВС параллелограмма ABCD вдвое больше стороны АВ. Биссектрисы углов А и В пересекают прямую CD в точках М и N, причём MN = 12.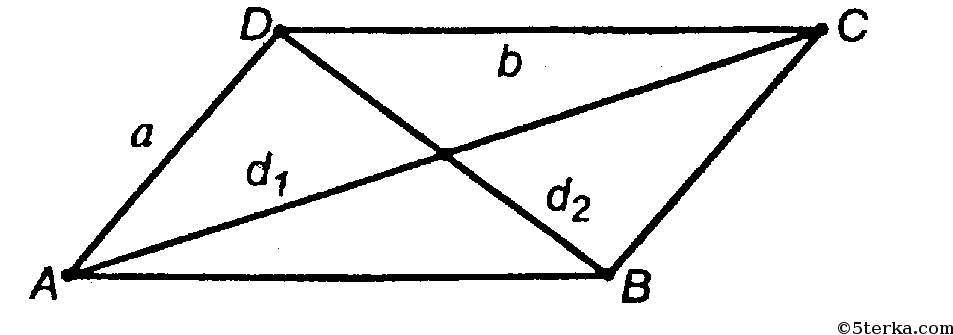 Найдите стороны параллелограмма.3.5. Найдите расстояние от центра ромба до его стороны, если острый угол ромба равен 30°, а сторона равна 4.
Найдите стороны параллелограмма.3.5. Найдите расстояние от центра ромба до его стороны, если острый угол ромба равен 30°, а сторона равна 4.
Балл за решение каждой задачи
Биссектриса параллелограмма отсекает равнобедренный треугольник
Решение прямоугольного треугольникаФормула синуса двойного углаФормула высоты прямоугольного треугольника
7 подготовительных задач
3.6. В четырёхугольнике ABCD известны углы: ?DAB=90°, ? DBC= =90°. Кроме того, DB = a, DC = b. Найдите расстояние между центрами двух окружностей, одна из которых проходит через точки D, А, В, а другая — через точки B,C,D.
3.7. На сторонах АВ и CD прямоугольника ABCD взяты точки К и М так, что АКСМ — ромб. Диагональ АС образует со стороной АВ угол 30°. Найдите сторону ромба, если наибольшая сторона прямоугольника ABCD равна 3.
Балл за решение каждой задачи
Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузыТеорема Пифагора
Свойство диагоналей ромбаРешение прямоугольного треугольника ( с углом в 30?
Прямоугольник и Параллелограмм | ЕГЭ по математике (профильной)
Прямоугольник и параллелограмм
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. 2)$
2)$
5. Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
$∆АВК$ — равнобедренный
6. В параллелограмме биссектрисы углов, прилежащих к одной стороне (соседних углов), пересекаются под углом в $90°$.
Площадь параллелограмма:
1. Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
$S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
2. Площадь параллелограмма равна произведению основания на высоту.
$S=h_a·a$, где $a$ — сторона параллелограмма, $h_a$ — высота, проведенная к стороне $a$.
Периметр параллелограмма: $P=2(a+b)$, где $а$ и $b$ — длины сторон параллелограмма.
Пример:
Периметр параллелограмма равен $14$. Одна сторона параллелограмма на $1$ больше другой. Найдите меньшую сторону параллелограмма.
Решение:
Пусть меньшая сторона $ВС-х$, тогда $АВ-(х+1)$, так как она на $1$ больше.
Запишем формулу периметра параллелограмма: $P=2(a+b)$, где $а$ и $b$ — длины сторон параллелограмма.
Подставим в формулу известные данные и значения сторон, записанные через «х».
$2(х+х+1)=14$
Получили линейное уравнение, разделим обе части на $2$.
$х+х+1=7$
$2х=6$
$х=3$.
За «х» брали меньшую сторону параллелограмма, следовательно, это и есть ответ.
Ответ: $3$
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
1. Все свойства параллелограмма (Так как прямоугольник – это тот же параллелограмм, только особенный, поэтому у него присутствуют все свойства параллелограмма).
2. Диагонали прямоугольника равны.
$BD= AC$.
Площадь прямоугольника равна половине произведения смежных (соседних) сторон.
$S=a·b$, где $а$ и $b$ — смежные стороны.
Периметр прямоугольника: $P=2(a+b)$, где $а$ и $b$ — длины сторон прямоугольника. 2}/{2}$, где $d$ — диагональ квадрата.
2}/{2}$, где $d$ — диагональ квадрата.
Периметр квадрата: $P=4a$
Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
- В прямоугольном треугольнике $АВС$, с прямым углом $С$
- Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
- Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
 2=9$
2=9$$ВН=3$
Подставляем найденную длину в формулу косинуса
$cos В = {3}/{15}=1/5=0.2$
$sin A= cos B=0.2$
Ответ: $0.2$
Значения тригонометрических функций некоторых углов:
$α$ $30$ $45$ $60$ $sinα$ ${1}/{2}$ ${√2}/{2}$ ${√3}/{2}$ $cosα$ ${√3}/{2}$ ${√2}/{2}$ ${1}/{2}$ $tgα$ ${√3}/{3}$ $1$ $√3$ $ctgα$ $√3$ $1$ ${√3}/{3}$ Четырёхугольники, виды и свойства / math5school.ru
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
Сумма углов выпуклого четырёхугольника равна 360°:
∠A+∠B+∠C+∠D=360°.
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов:
∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D,
∠C < ∠A+∠B+∠D, ∠D < ∠A+∠B+∠D.
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон:
a < b+c+d, b < a+c+d,
c < a+b+d, d < a+b+c.
Площадь произвольного выпуклого четырёхугольника равна:
Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины.
Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет.

Площадь произвольного выпуклого четырёхугольника:
Если M, N, P, Q – середины сторон выпуклого четырёхугольника ABCD, а R, S – середины его диагоналей, то четырёхугольники MNPQ, MRPS, NSQR являются параллелограммами и называются параллелограммами Вариньона.
Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD. Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны;
SABCD = 2SMNPQ .
Отрезки MP, NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника.
В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку.
 Для других четырёхугольников средние линии – отрезки.
Для других четырёхугольников средние линии – отрезки.Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам:
MG=GP, NG=GQ, RG=GS .
Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей:
MP2+ NQ2+ RS 2 = ¼(AB2+BC2+CD2+AD2+AC2+BD2).
Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь:
SABCD = MP·NQ·sinβ.
Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости.
Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной.

Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны:
a+c = b+d.
Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно:
a+c ≥ 4r, b+d ≥ 4r.
Площадь описанного четырёхугольника:
S = pr,
где r – радиус вписанной окружности, p – полупериметр четырёхугольника.
Площадь описанного четырёхугольника:
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника:
AK=AN, BK=BL, CL=CM, DM=DN.
Если O – центр окружности, вписанной в четырёхугольник ABCD, то
∠AOB+∠COD=∠BOC+∠AOD=180°.
Для описанного четырёхугольника ABCD со сторонами AB=a, BC=b, CD=c и AD=d верны соотношения:
Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника.

Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°:
∠A+∠C=∠B+∠D=180°.
Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Радиус окружности, описанной около четырёхугольника:
Площадь вписанного четырёхугольника:
Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами.

Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов.
У вписанного четырёхугольника любые два связанных угла равны.
Если четырёхугольник одновременно является описанным и вписанным, то его площадь:
Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение:
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:
AB||CD, BC||AD.
У параллелограмма противолежащие стороны равны и противолежащие углы равны:
AB=CD, BC=AD;
∠A=∠C, ∠B=∠D.
Сумма любых двух соседних углов параллелограмма равна 180°:
∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:
AO=OC; BO=OD.
Каждая диагональ делит параллелограмм на два равных треугольника:
∠ABC=∠CDA; ∠ABD=∠CDB.
Две диагонали параллелограмма делят его на четыре равновеликих треугольника:
SΔABO=SΔBCO=SΔCDO=SΔADO.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
e2+f2 = a2+b2+a2+b2 = 2(a2+b2).
Признаки параллелограмма:
- Если у четырёхугольника противолежащие стороны попарно равны, то этот четырёхугольник – параллелограмм.
- Если у четырёхугольника две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

- Четырёхугольник, диагонали которого в точке пересечения делятся пополам – параллелограмм.
- Если у четырёхугольника противолежащие углы попарно равны, то этот четырёхугольник – параллелограмм.
Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне:
ha = b·sin γ; hb = a·sin γ.
Площадь параллелограмма можно определить:
- через его сторону и высоту, проведённую к ней:
S = aha = bhb;
- через две его стороны и угол между ними:
S = ab·sin γ.
Ромбом называется параллелограмм, у которого все стороны равны:
AB=BC=CD=AD.
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:
AC⊥BD;
∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA.

В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей.
Радиус окружности, вписанной в ромб, можно вычислить:
- через высоту ромба:
- через диагонали ромба и сторону:
- через отрезки, на которые делит сторону ромба точка касания:
Площадь ромба можно определить:
- через диагонали:
- через сторону и угол ромба:
- через сторону и высоту:
- через сторону и радиус вписанной окружности:
Прямоугольником называется параллелограмм, у которого все углы прямые:
∠A=∠B=∠C=∠D=90°.
Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка:
AC=BD;
AO=BO=CO=DO.

Площадь прямоугольника можно определить:
- через его стороны:
S = ab;
- через диагонали и угол между ними:
S = ½d²·sin γ.
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали:
BD = 2R.
Квадрат – это прямоугольник, у которого все стороны равны:
∠A=∠B=∠C=∠D=90°,
AB=BC=CD=AD.
Диагонали квадрата равны и перпендикулярны.
Сторона и диагональ квадрата связаны соотношениями:
Площадь квадрата:
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.

Радиус описанной окружности:
Радиус вписанной окружности:
Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:
AD||BC.
Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции:
AK=KB; CL=LD.
Средняя линия трапеции параллельна её основаниям и равна их полусумме:
KL||AD; KL||BC;
KL = ½(AD+BC).
При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ:
ΔAED∼ΔBEC, k=AD/BC.

Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ:
ΔAОD∼ΔCОВ, k=AD/BC.
Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны:
SΔABO = SΔCDO.
Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон:
O∈KL; E∈KL.
Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности:
RS||AD; RS||BC;
RS = ½(AD–BC).
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон:
AD+BC=AB+CD.
Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств:
Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом:
∠AOB=∠COD=90°.
Радиус вписанной в трапецию окружности можно определить:
- через отрезки, на которые делится боковая сторона точкой касания:
Равнобокой называется трапеция, у которой боковые стороны равны:
AB=CD.
У равнобокой трапеции:
- диагонали равны:
AC=BD;
- углы при основании равны:
∠A=∠D, ∠B=∠C;
- сумма противолежащих углов равна 180?:
∠A+∠C=∠B+∠D=180°.
Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Стороны и диагональ равнобокой трапеции связаны соотношением:
d² = ab+c².

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.
Площадь трапеции можно определить:
- через полусумму оснований (первую среднюю линию) и высоту:
- через диагонали и угол между ними:
Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон.
Дельтоид может быть выпуклым или невыпуклым.
Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом.
В любом дельтоиде углы между соседними неравными сторонами равны.
Площадь любого дельтоида можно определить:
- через его диагонали:
- через две соседние неравные стороны и угол между ними:
S = ab·sin α .

В любой выпуклый дельтоид можно вписать окружность.
Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида.
Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины.
Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°.
Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом.

Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
- для сторон четырёхугольника верно: a²+c² = b²+d²;
- для площади четырёхугольника верно: S = ½ef;
- параллелограмм Вариньона с вершинами в серединах сторон четырёхугольника является прямоугольником.
Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности:
a²+c² = b²+d² = 4R².
Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны:
ac = bd.
Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О, то верны соотношения:
Пр.
 6.6, 6 (Необязательно) — Докажите, что сумма квадратов диагоналей
6.6, 6 (Необязательно) — Докажите, что сумма квадратов диагоналейПоследнее обновление: 15 июня 2018 г., Teachoo
Выписка
Пр. 6.6, 6 Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Дано: ABCD — параллелограмм Доказательство: сумма квадратов диагоналей = сумма квадратов его сторон. AC2 + BD2 = AB2 + BC + CD2 + DA2 Построение: Draw AX CD и BY DC расширены до Y.Доказательство: В правом AXC Применяя теорему Пифагора, AC2 = AX2 + CX2 В правом BYD Применяя теорему Пифагора, BD2 = BY2 + DY2 В BYC, По теореме Пифагора BC2 = BY2 + CY2 BD2 = BC2 + CD2 + 2CD.CY Из уравнения (1) AC2 = AX2 + CX2 Положив CX = CD DX AC2 = AX2 + (CD DX) 2 AC2 = AX2 + CD2 + DX2 2CD.DX AC2 = (AX2 + DX2) + CD2 2CD.DX В AXD, По теореме Пифагора AD2 = AX2 + DX2 В параллелограмме ABCD Противоположные стороны параллелограмма равны CD = AB AC2 = AD2 + CD2 2CD.
Показать больше DX
AC2 = AD2 + AB2 2CD.DX Следовательно, уравнения имеют вид
BD2 = BC2 + CD2 + 2CD.CY (3)
AC2 = AD2 + AB2 2CD.DX (4) Сложение уравнений (3) и (4)
BD2 + AC2 = BC2 + CD2 + 2CD.CY + AD2 + AB2 2CD.DX
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (CY DX)
Сейчас же,
нам нужно доказать, что CY = DX В AXD и BYC,
AXD = BYC
AD = BC
AX = BY
AXD BYC Таким образом,
DX = CY
Положив CY = DX в уравнение (5)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (CY DX)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (DX DX)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD 0
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 Следовательно, доказано
DX
AC2 = AD2 + AB2 2CD.DX Следовательно, уравнения имеют вид
BD2 = BC2 + CD2 + 2CD.CY (3)
AC2 = AD2 + AB2 2CD.DX (4) Сложение уравнений (3) и (4)
BD2 + AC2 = BC2 + CD2 + 2CD.CY + AD2 + AB2 2CD.DX
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (CY DX)
Сейчас же,
нам нужно доказать, что CY = DX В AXD и BYC,
AXD = BYC
AD = BC
AX = BY
AXD BYC Таким образом,
DX = CY
Положив CY = DX в уравнение (5)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (CY DX)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (DX DX)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD 0
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 Следовательно, доказаноДокажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.- Sarthaks eConnect
Решение:
В параллелограмме ABCD, AB = CD, BC = AD
Нарисуйте перпендикуляры от C и D на AB, как показано.
Прямоугольный ΔAEC, AC 2 = AE 2 + CE 2 [По теореме Пифагора]
⇒ AC 2 = (AB + BE) 2 + CE 2
⇒ AC 2 = AB 2 + BE 2 + 2 AB × BE + CE 2 → (1)
Из рисунка CD = EF (так как CDFE — прямоугольник)
Но CD = AB
⇒ AB = CD = EF
Также CE = DF (Расстояние между двумя параллельными линиями)
ΔAFD ≅ ΔBEC (Правило сравнения RHS)
⇒ AF = BE
Рассмотрим прямоугольный ΔDFB
BD 2 = BF 2 + DF 2 [Автор Pythagoras теорема]
= (EF — BE) 2 + CE 2 [Поскольку DF = CE]
= (AB — BE) 2 + CE 2 [Поскольку EF = AB]
⇒ BD 2 = AB 2 + BE 2 — 2 AB × BE + CE 2 → (2)
Складываем (1) и (2), получаем
AC 2 + BD 2 = (AB 2 + BE 2 + 2 AB × BE + CE 2 ) + (AB 2 + BE 2 — 2 AB × BE + CE 2 )
= 2AB 2 + 2BE 2 + 2CE 2
AC 2 + BD 2 = 2AB 2 + 2 (BE 2 + CE 2 ) → (3)
От прямого угла ΔBEC, BC 2 = BE 2 + CE 2 [ По теореме Пифагора]
Следовательно, уравнение (3) принимает вид
AC 2 + BD 2 = 2AB 2 + 2BC 2
= AB 2 + AB 2 + BC 2 + BC 2
= AB 2 + CD 2 + BC 2 + AD 2
∴ AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2
Таким образом, сумма квадратов диагоналей параллелограмма равна su м квадратов его сторон.
Свойства четырехугольника — прямоугольник, квадрат, параллелограмм, ромб, трапеция
В евклидовой геометрии четырехугольник — это четырехугольная двумерная фигура, сумма внутренних углов которой равна 360 °. Слово четырехугольник образовано от двух латинских слов «quadri» и «latus», что означает четыре и сторона соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников.
Итак, каковы свойства четырехугольника? Четырехугольники обладают двумя свойствами:
- Четырехугольник должен быть замкнутой формы с 4-мя сторонами
- Сумма всех внутренних углов четырехугольника составляет 360 °
В этой статье вы получите представление о 5 типах четырехугольников и познакомитесь со свойствами четырехугольников.
Это то, что вы прочитаете в статье:
Вот видео, объясняющее свойства четырехугольника:
На приведенной ниже диаграмме показан четырехугольник ABCD и сумма его внутренних углов.
 Сумма всех внутренних углов составляет 360 °.
Сумма всех внутренних углов составляет 360 °.Таким образом, A + ∠B + ∠C + ∠D = 360 °
Четырехугольники разные
Четырехугольники бывают 5 видов по форме.Эти 5 четырехугольников:
- Прямоугольник
- Квадрат
- Параллелограмм
- Ромб
- Трапеция
Давайте подробно обсудим каждый из этих пяти четырехугольников:
Вот вопросы, которые научат вас применять свойства всех пяти четырехугольников, которые вы узнаете в этой статье.
Прямоугольник
Прямоугольник — это четырехугольник с четырьмя прямыми углами. Таким образом, все углы в прямоугольнике равны (360 ° / 4 = 90 °).Причем противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.
Свойства прямоугольников
Прямоугольник имеет три свойства:
- Все углы прямоугольника равны 90 °
- Противоположные стороны прямоугольника равны и параллельны
- Диагонали прямоугольника делят пополам
Формула прямоугольника — площадь и периметр прямоугольника
Если длина прямоугольника L, а ширина B, то
- Площадь прямоугольника = длина × ширина или L × B
- Периметр прямоугольника = 2 × (L + B)
Эти практические вопросы помогут вам закрепить свойства прямоугольников
Квадрат
Квадрат — четырехугольник с четырьмя равными сторонами и углами.
 Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.
Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.Недвижимость квадрата
Чтобы четырехугольник стал квадратом, он должен обладать определенными свойствами. Вот три свойства квадратов:
- Все углы квадрата равны 90 °
- Все стороны квадрата равны и параллельны друг другу
- Диагонали рассекают друг друга перпендикулярно
Формула квадрата — Площадь и периметр квадрата
Если сторона квадрата — «а», тогда
- Площадь квадрата = a × a = a²
- Периметр квадрата = 2 × (a + a) = 4a
Эти практические вопросы помогут вам закрепить свойства квадратов
Если вы наберете Q50-51 за GMAT, вы сможете набрать 700+ баллов за GMAT.Почему бы вам не начать подготовку к GMAT с помощью наших бесплатных подготовительных ресурсов и не начать свой путь к получению Q50-51 на GMAT.
 Учитесь у Кэрри Ло, у которой за 3 недели показатель улучшился с Q35 до Q50.
Учитесь у Кэрри Ло, у которой за 3 недели показатель улучшился с Q35 до Q50.Параллелограмм
Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, у него две пары параллельных сторон. Более того, у параллелограмма противоположные углы равны, а его диагонали делят друг друга пополам.
Свойства параллелограмма
Четырехугольник, удовлетворяющий указанным ниже свойствам, будет классифицирован как параллелограмм.У параллелограмма четыре свойства:
- Противоположные углы равны
- Противоположные стороны равны и параллельны
- Диагонали пересекают друг друга
- Сумма любых двух смежных углов равна 180 °
Формулы параллелограмма — Площадь и периметр параллелограмма
Если длина параллелограмма равна «l», ширина — «b», а высота — «h», тогда:
- Периметр параллелограмма = 2 × (l + b)
- Площадь параллелограмма = l × h
Эти практические вопросы помогут вам закрепить свойства параллелограмма
Ромб
Ромб — это четырехугольник, все четыре стороны которого равны по длине, а противоположные стороны параллельны друг другу.
 Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», поскольку он похож на масть ромба в игральных картах.
Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», поскольку он похож на масть ромба в игральных картах.Свойства ромба
Ромб — это четырехугольник, обладающий следующими четырьмя свойствами:
- Противоположные углы равны
- Все стороны равны, противоположные стороны параллельны друг другу
- Диагонали рассекают друг друга перпендикулярно
- Сумма любых двух смежных углов равна 180 °
Формулы ромба — Площадь и периметр ромба
Если сторона ромба — это, то периметр ромба = 4a
Если длина двух диагоналей ромба равна d 1 и d 2 , то площадь ромба = ½ × d 1 × d 2
Эти практические вопросы помогут вам закрепить свойства ромба
Трапеция
Трапеция (в США ее называют трапецией) — это четырехугольник, у которого есть только одна пара параллельных сторон.
 Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.
Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.Свойства трапеции
Трапеция — это четырехугольник, в котором одно свойство:
- Только одна пара противоположных сторон параллельна друг другу
Формулы трапеции — Площадь и периметр трапеции
Если высота трапеции « h» (как показано на диаграмме выше), то:
- Периметр трапеции = Сумма длин всех сторон = AB + BC + CD + DA
- Площадь трапеции = ½ × (Сумма длин параллельных сторон) × h = ½ × (AB + CD) × h
Эти практические вопросы помогут вам закрепить свойства трапеции
Свойства четырехугольников
В таблице ниже суммированы все свойства четырехугольников, которые мы изучили до сих пор:
Свойства четырехугольника Прямоугольник Квадрат Параллелограмм Ромб Трапеция Все стороны равны ✖ ✔ ✖ ✔ ✖ Противоположные стороны равны ✔ ✔ ✔ ✔ ✖ Противоположные стороны параллельны ✔ ✔ ✔ ✔ ✔ Все углы равны ✔ ✔ ✖ ✖ ✖ Противоположные углы равны ✔ ✔ ✔ ✔ ✖ Сумма двух смежных углов 180 ✔ ✔ ✔ ✔ ✖ Разделить пополам ✔ ✔ ✔ ✔ ✖ Разделить перпендикулярно пополам ✖ ✔ ✖ ✔ ✖ На изображении ниже также показаны свойства четырехугольника:
Важные формулы четырехугольника
В таблице ниже приведены формулы площади и периметра четырехугольников различных типов:
Четырехугольные формулы Прямоугольник Квадрат Параллелограмм Ромб Трапеция Площадь д × ш a² д × в ½ × d1 × d2 ½ × (Сумма параллельных сторон) × высота Периметр 2 × (д + б) 4a 2 × (д + б) 4a Сумма всех сторон Дополнительная литература:
Четырехсторонние вопросы
Попрактикуемся в применении свойств четырехугольника на следующих типовых вопросах:
Вопрос 1
Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров.
 Сколько метров забора нужно купить, чтобы ограждать весь сад?
Сколько метров забора нужно купить, чтобы ограждать весь сад?- 20 метров
- 25 метров
- 30 метров
- 40 метров
- 50 метров
Решение
Шаг 1: Дано
- У Адама прямоугольный сад.
- Он имеет длину 10 метров и ширину 15 метров.
- Он хочет построить вокруг него забор.
Шаг 2: найти
- Длина, необходимая для возведения ограды вокруг всего сада.
Шаг 3: подход и разработка
Забор можно строить только вокруг внешней стороны сада.
- Итак, общая необходимая длина забора = Сумма длин всех сторон сада.
- Так как сад прямоугольный, сумма длин всех сторон — это не что иное, как периметр сада.
- Периметр = 2 × (10 + 15) = 50 метров
Следовательно, необходимая длина забора — 50 метров.
Следовательно, вариант E — правильный ответ.

Вопрос: 2
Стив хочет покрасить одну прямоугольную стену в своей комнате. Стоимость покраски стены — 1,5 доллара за квадратный метр. Если длина стены 25 метров, а ширина 18 метров, то какова общая стоимость покраски стены?
- 300 долл. США
- 350 долл. США
- $ 450
- 600 долларов США
- $ 675
Решение
Шаг 1: Дано
- Стив хочет покрасить одну стену своей комнаты.
- Стена 25 метров в длину и 18 метров в ширину.
- Стоимость покраски стены составляет 1,5 доллара за квадратный метр.
Шаг 2: найти
- Общая стоимость покраски стены.
Шаг 3: подход и разработка
- Стена окрашена по всей площади.
- Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, мы сможем получить общую стоимость.

- Площадь стены = длина × ширина = 25 метров × 18 метров = 450 квадратных метров
- Общая стоимость покраски стены = 450 × 1,5 $ = 675 $
- Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, мы сможем получить общую стоимость.
Следовательно, правильный ответ — вариант E.
Мы надеемся, что к настоящему моменту вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти концепции для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT.Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить доступ бесплатно, зарегистрировавшись здесь.
Вот еще несколько статей по математике:
- Повысьте точность ответов на вопросы по математике по многоугольникам
- Вопросы о геометрии — самые распространенные ошибки | GMAT Quant Prep
Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки.
 Наша компания по подготовке к GMAT является самой обсуждаемой компанией на gmatclub: более 1950 отзывов.
Наша компания по подготовке к GMAT является самой обсуждаемой компанией на gmatclub: более 1950 отзывов. Почему бы вам не воспользоваться бесплатным испытанием и не судить сами?
Напишите нам по адресу [email protected] в случае возникновения каких-либо вопросов.
диагоналей делят пополам параллелограмм
Диагонали перпендикулярны биссектрисам друг друга. Чтобы задать вопрос Unlimited Maths, загрузите Doubtnut с сайта — https://goo.gl/9WZjCW. Докажите векторным методом, что диагонали параллелограмма делят друг друга пополам. Диагонали делят друг друга пополам; Противоположные углы ромба равны.Форма имеет вращательную симметрию второго порядка. В параллелограмме противоположные стороны совпадают, противоположные углы совпадают, последовательные углы являются дополнительными, а диагонали делят друг друга пополам. Итак, прямо здесь у нас есть параллелограмм. ̅̅̅̅ разделите друг друга пополам. Пошаговое объяснение: мы знаем, что параллелограмм — это четырехугольник, в котором диагонали пересекают друг друга пополам. Примеры задач на ромб. Нам дано, что все четыре угла в точке E равны 9 0 0 и диагонали параллелограмма делят друг друга пополам. Автор Идо Сариг, бакалавр наук, магистр делового администрирования В этом уроке мы докажем, что в параллелограмме каждая диагональ делит другую диагональ пополам.Параллелограмм, в котором все углы прямые, — это прямоугольник! перпендикулярны. варианты ответа. Углы EDC и EAB равны по той же причине. перпендикулярны. Обе пары противоположных сторон параллельны. A. Диагонали, которые делят друг друга пополам B. Диагонали, которые делят пополам противоположные углы C. Две пары противоположных конгруэнтных сторон D. Две пары противоположных конгруэнтных углов Ответ jim_thompson5910 (35256) (Показать источник): Квадраты. Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет установить, что треугольники APD и CPB конгруэнтны.
Пошаговое объяснение: мы знаем, что параллелограмм — это четырехугольник, в котором диагонали пересекают друг друга пополам. Примеры задач на ромб. Нам дано, что все четыре угла в точке E равны 9 0 0 и диагонали параллелограмма делят друг друга пополам. Автор Идо Сариг, бакалавр наук, магистр делового администрирования В этом уроке мы докажем, что в параллелограмме каждая диагональ делит другую диагональ пополам.Параллелограмм, в котором все углы прямые, — это прямоугольник! перпендикулярны. варианты ответа. Углы EDC и EAB равны по той же причине. перпендикулярны. Обе пары противоположных сторон параллельны. A. Диагонали, которые делят друг друга пополам B. Диагонали, которые делят пополам противоположные углы C. Две пары противоположных конгруэнтных сторон D. Две пары противоположных конгруэнтных углов Ответ jim_thompson5910 (35256) (Показать источник): Квадраты. Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет установить, что треугольники APD и CPB конгруэнтны. Сумма квадратов сторон равна сумме квадратов диагоналей. Диагонали параллелограмма всегда. Параллелограмм???? Диагонали параллелограмма делят друг друга пополам. Противоположные стороны параллельны… Форма имеет вращательную симметрию второго порядка. Так как ромб, квадрат и прямоугольник также являются параллелограммом ∴ Диагонали также делят друг друга пополам. Таким образом, четырехугольники, диагонали которых делят друг друга пополам, равны: Параллелограмм Ромб Квадрат Прямоугольник Пример 3.4, 4 Назовите четырехугольники, диагонали которых.и?? Ответ: A. Параллелограмм B. Прямоугольник C. Квадрат D. Ромб, все верно. Перпендикулярно линии к внешней точке, Разделение линии на равное количество частей, Построение равнобедренного треугольника с учетом одной стороны, Построение равнобедренного треугольника с учетом основания и высоты, Построение равнобедренного треугольника с учетом угла ноги и вершины, Построение равнобедренного треугольника. Треугольник 30 °, 60 °, 90 ° с учетом гипотенузы, Построение треугольника с учетом базовых углов и базовой длины, Построение треугольника с двумя сторонами и углом, Построение равностороннего треугольника с заданным периметром, Построение треугольника с учитывая периметр в соотношении 2: 3: 4, Докажите, что угол в том же сегменте круга равен, Вычислите угол в центре круга, Постройте внешнюю касательную к данным кругам, Постройте внутреннюю касательную к данных окружностей.
Сумма квадратов сторон равна сумме квадратов диагоналей. Диагонали параллелограмма всегда. Параллелограмм???? Диагонали параллелограмма делят друг друга пополам. Противоположные стороны параллельны… Форма имеет вращательную симметрию второго порядка. Так как ромб, квадрат и прямоугольник также являются параллелограммом ∴ Диагонали также делят друг друга пополам. Таким образом, четырехугольники, диагонали которых делят друг друга пополам, равны: Параллелограмм Ромб Квадрат Прямоугольник Пример 3.4, 4 Назовите четырехугольники, диагонали которых.и?? Ответ: A. Параллелограмм B. Прямоугольник C. Квадрат D. Ромб, все верно. Перпендикулярно линии к внешней точке, Разделение линии на равное количество частей, Построение равнобедренного треугольника с учетом одной стороны, Построение равнобедренного треугольника с учетом основания и высоты, Построение равнобедренного треугольника с учетом угла ноги и вершины, Построение равнобедренного треугольника. Треугольник 30 °, 60 °, 90 ° с учетом гипотенузы, Построение треугольника с учетом базовых углов и базовой длины, Построение треугольника с двумя сторонами и углом, Построение равностороннего треугольника с заданным периметром, Построение треугольника с учитывая периметр в соотношении 2: 3: 4, Докажите, что угол в том же сегменте круга равен, Вычислите угол в центре круга, Постройте внешнюю касательную к данным кругам, Постройте внутреннюю касательную к данных окружностей. Сумма внутренних углов в четырехугольнике в сумме составляет 360 °. Докажите, что диагонали параллелограмма делят друг друга пополам. Докажем, что диагонали параллелограмма делят друг друга пополам.Одна пара противоположных сторон параллельна и равна длине. Ромб — это особый вид параллелограмма. Диагонали делят друг друга пополам. есть координаты? Параллелограммы имеют противоположные внутренние углы, которые совпадают, а диагонали параллелограмма делят друг друга пополам. Площадь параллелограмма, представленная векторами A = 4 i + 3 j и вектором B = 2 i + 4 j в качестве смежной стороны. Решение: AC = 24 см. 8. Диагонали ромба пересекаются под прямым углом. Политика конфиденциальности. Все стороны и углы совпадают.̅̅̅̅ разделите друг друга пополам. … По теореме диагонали параллелограмма делят друг друга пополам. Линия, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. ̅̅̅̅ пересечься в точке ?. Так что вы также можете рассматривать их как поперечные.
Сумма внутренних углов в четырехугольнике в сумме составляет 360 °. Докажите, что диагонали параллелограмма делят друг друга пополам. Докажем, что диагонали параллелограмма делят друг друга пополам.Одна пара противоположных сторон параллельна и равна длине. Ромб — это особый вид параллелограмма. Диагонали делят друг друга пополам. есть координаты? Параллелограммы имеют противоположные внутренние углы, которые совпадают, а диагонали параллелограмма делят друг друга пополам. Площадь параллелограмма, представленная векторами A = 4 i + 3 j и вектором B = 2 i + 4 j в качестве смежной стороны. Решение: AC = 24 см. 8. Диагонали ромба пересекаются под прямым углом. Политика конфиденциальности. Все стороны и углы совпадают.̅̅̅̅ разделите друг друга пополам. … По теореме диагонали параллелограмма делят друг друга пополам. Линия, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. ̅̅̅̅ пересечься в точке ?. Так что вы также можете рассматривать их как поперечные. параллельны. Свойства квадрата. Теорема 3: Четырехугольник является параллелограммом тогда и только тогда, когда диагонали делят друг друга пополам. Есть несколько формул для ромба, которые связаны с его: Стороны (щелкните, чтобы узнать подробнее). Задача 1: диагонали ромба 24 см и 10 см.Диагонали делят друг друга пополам. Таким образом, если противоположные стороны четырехугольника параллельны, то четырехугольник является параллелограммом. Следовательно, диагонали параллелограмма действительно делят друг друга на равные части. Другими словами, параллелограммы включают в себя все ромбы и все ромбовидные элементы, а значит, также включают все прямоугольники. Противоположные стороны параллельны друг другу. конгруэнтные треугольники. конгруэнтны. (,) Часть B Поскольку ???? (i) делят друг друга пополам Диагонали параллелограмма делят друг друга пополам. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны.Диагонали параллелограмма делят друг друга пополам.
параллельны. Свойства квадрата. Теорема 3: Четырехугольник является параллелограммом тогда и только тогда, когда диагонали делят друг друга пополам. Есть несколько формул для ромба, которые связаны с его: Стороны (щелкните, чтобы узнать подробнее). Задача 1: диагонали ромба 24 см и 10 см.Диагонали делят друг друга пополам. Таким образом, если противоположные стороны четырехугольника параллельны, то четырехугольник является параллелограммом. Следовательно, диагонали параллелограмма действительно делят друг друга на равные части. Другими словами, параллелограммы включают в себя все ромбы и все ромбовидные элементы, а значит, также включают все прямоугольники. Противоположные стороны параллельны друг другу. конгруэнтные треугольники. конгруэнтны. (,) Часть B Поскольку ???? (i) делят друг друга пополам Диагонали параллелограмма делят друг друга пополам. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны.Диагонали параллелограмма делят друг друга пополам. Другими важными свойствами многоугольника, которые необходимо знать, являются свойства трапеции и свойства воздушного змея. $$ \ треугольник ACD \ cong \ треугольник ABC $$ Если у нас есть параллелограмм, все стороны которого совпадают, то у нас есть то, что называется ромбом. доказать, что диагонали параллелограмма делят друг друга пополам — Математика — TopperLearning.com | w62ig1q11 Линия, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. Свойства параллелограммов можно применить к ромбам.Противоположные углы равны. это параллелограмм, ?? Если вы просто посмотрите на параллелограмм, то вещи, которые выглядят правдой (а именно, вещи в этом списке), истинны и, таким образом, являются свойствами, и … В параллелограмме диагонали делят друг друга пополам, поэтому вы можете установить помеченные сегменты равными друг к другу, а затем решите. Ромб — это разновидность параллелограмма, и что отличает его форму, так это то, что все четыре его стороны совпадают .
Другими важными свойствами многоугольника, которые необходимо знать, являются свойства трапеции и свойства воздушного змея. $$ \ треугольник ACD \ cong \ треугольник ABC $$ Если у нас есть параллелограмм, все стороны которого совпадают, то у нас есть то, что называется ромбом. доказать, что диагонали параллелограмма делят друг друга пополам — Математика — TopperLearning.com | w62ig1q11 Линия, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. Свойства параллелограммов можно применить к ромбам.Противоположные углы равны. это параллелограмм, ?? Если вы просто посмотрите на параллелограмм, то вещи, которые выглядят правдой (а именно, вещи в этом списке), истинны и, таким образом, являются свойствами, и … В параллелограмме диагонали делят друг друга пополам, поэтому вы можете установить помеченные сегменты равными друг к другу, а затем решите. Ромб — это разновидность параллелограмма, и что отличает его форму, так это то, что все четыре его стороны совпадают . .. (2,1). Примеры задач на ромб. И я хочу доказать, что его диагонали делят друг друга пополам.Ромб, ромб: все четыре стороны равной длины. На рисунке выше перетащите любую вершину, чтобы изменить форму параллелограмма и убедить себя, что это так. Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. Прямые CD и AB равны по длине, потому что противоположные стороны параллелограмма равны. Выше представлен четырехугольник ABCD, и мы хотим доказать, что диагонали делят друг друга пополам на равные длины. Диагонали параллелограмма пересекают друг друга пополам, пересекают другой отрезок и разделяют его на две равные части, называемые «равнобедренными треугольниками: медиана основания перпендикулярна основанию, диагонали квадратов перпендикулярны друг другу», противоположные стороны параллелограмма равны по размеру. Противоположные стороны параллелограмма равны по размеру, если диагонали четырехугольника делят друг друга пополам, то этот четырехугольник является параллелограммом.
.. (2,1). Примеры задач на ромб. И я хочу доказать, что его диагонали делят друг друга пополам.Ромб, ромб: все четыре стороны равной длины. На рисунке выше перетащите любую вершину, чтобы изменить форму параллелограмма и убедить себя, что это так. Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. Прямые CD и AB равны по длине, потому что противоположные стороны параллелограмма равны. Выше представлен четырехугольник ABCD, и мы хотим доказать, что диагонали делят друг друга пополам на равные длины. Диагонали параллелограмма пересекают друг друга пополам, пересекают другой отрезок и разделяют его на две равные части, называемые «равнобедренными треугольниками: медиана основания перпендикулярна основанию, диагонали квадратов перпендикулярны друг другу», противоположные стороны параллелограмма равны по размеру. Противоположные стороны параллелограмма равны по размеру, если диагонали четырехугольника делят друг друга пополам, то этот четырехугольник является параллелограммом. Следовательно, диагонали параллелограмма действительно делят друг друга на равные части. Диагонали четырехугольника _____ делят друг друга пополам. Иногда, если размеры двух углов четырехугольника равны, то четырехугольник _____ параллелограмм. Это общее свойство любого параллелограмма. Вопрос 548775: Что НЕ всегда является свойством параллелограмма? Диагонали прямоугольника конгруэнтны, и, опять же, поскольку прямоугольник является параллелограммом, диагонали делят друг друга пополам, делая каждую половину одинаковой длины: каждая диагональ прямоугольника также делит прямоугольник на два равных прямоугольных треугольника: то есть, каждая диагональ разрезает другую на две равные части.Каждая диагональ делит четырехугольник на два равных треугольника. Решение: AC = 24 см. Теорема. Если ABCD — параллелограмм, докажите, что диагонали ABCD делят друг друга пополам. Мы уже доказали это свойство для любого параллелограмма. и?? 4 В параллелограмме диагонали делят друг друга пополам. ̅̅̅̅ перекресток Это показано на схеме, показанной ниже.
Следовательно, диагонали параллелограмма действительно делят друг друга на равные части. Диагонали четырехугольника _____ делят друг друга пополам. Иногда, если размеры двух углов четырехугольника равны, то четырехугольник _____ параллелограмм. Это общее свойство любого параллелограмма. Вопрос 548775: Что НЕ всегда является свойством параллелограмма? Диагонали прямоугольника конгруэнтны, и, опять же, поскольку прямоугольник является параллелограммом, диагонали делят друг друга пополам, делая каждую половину одинаковой длины: каждая диагональ прямоугольника также делит прямоугольник на два равных прямоугольных треугольника: то есть, каждая диагональ разрезает другую на две равные части.Каждая диагональ делит четырехугольник на два равных треугольника. Решение: AC = 24 см. Теорема. Если ABCD — параллелограмм, докажите, что диагонали ABCD делят друг друга пополам. Мы уже доказали это свойство для любого параллелограмма. и?? 4 В параллелограмме диагонали делят друг друга пополам. ̅̅̅̅ перекресток Это показано на схеме, показанной ниже. Примечание: ромб — это параллелограмм со всеми равными сторонами. Противоположные стороны параллельны друг другу. Совпадение противоположных сторон и противоположных углов является прямым следствием постулата евклидовой параллельности, и ни одно из условий не может быть доказано без обращения к постулату евклидовой параллельности или одной из его эквивалентных формулировок.Вопрос 548775: Что НЕ всегда является свойством параллелограмма? А поскольку квадрат — это особый параллелограмм, обладающий всеми основными свойствами параллелограмма, то это верно и для квадрата. Теги: Вопрос 14. Это пересекающиеся параллельные линии. Для сравнения: квадрилат. Следовательно, прямые CE и EB равны, а AE и ED равны из-за конгруэнтных треугольников. Диагонали делят друг друга пополам. Диагонали делят друг друга пополам. Если вы сделаете диагонали почти параллельными друг другу — у вас будет параллелограмм с высотой, близкой к нулю, и, следовательно, площадью, близкой к нулю.Если диагонали параллелограмма перпендикулярны, то параллелограмм представляет собой _____ ромб.
Примечание: ромб — это параллелограмм со всеми равными сторонами. Противоположные стороны параллельны друг другу. Совпадение противоположных сторон и противоположных углов является прямым следствием постулата евклидовой параллельности, и ни одно из условий не может быть доказано без обращения к постулату евклидовой параллельности или одной из его эквивалентных формулировок.Вопрос 548775: Что НЕ всегда является свойством параллелограмма? А поскольку квадрат — это особый параллелограмм, обладающий всеми основными свойствами параллелограмма, то это верно и для квадрата. Теги: Вопрос 14. Это пересекающиеся параллельные линии. Для сравнения: квадрилат. Следовательно, прямые CE и EB равны, а AE и ED равны из-за конгруэнтных треугольников. Диагонали делят друг друга пополам. Диагонали делят друг друга пополам. Если вы сделаете диагонали почти параллельными друг другу — у вас будет параллелограмм с высотой, близкой к нулю, и, следовательно, площадью, близкой к нулю.Если диагонали параллелограмма перпендикулярны, то параллелограмм представляет собой _____ ромб. Определение 2: прямоугольник — это четырехугольник, в котором все четыре угла имеют одинаковый размер. Теги: Вопрос 3. Ромб — это также параллелограмм с равными сторонами, поэтому диагонали ромба делят друг друга пополам. Поскольку диагонали параллелограмма делят друг друга пополам, B E и D E конгруэнтны и A E конгруэнтны себе. Каждая диагональ параллелограмма разделяет его на два равных треугольника. Смежные углы являются дополнительными.Если четырехугольник — параллелограмм, то его _____ делят друг друга пополам. В параллелограмме диагонали делят друг друга пополам. Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет | Герой курса Доказать, что диагонали параллелограмма делят пополам 2. Все стороны ромба равны друг другу. Свойства параллелограмма применяются к прямоугольникам, ромбам и квадратам. (Их сумма равна 180 градусам.) В квадрате диагонали делят друг друга пополам. Я понимаю следующие свойства параллелограмма: Противоположные стороны параллельны и равны по длине.
Определение 2: прямоугольник — это четырехугольник, в котором все четыре угла имеют одинаковый размер. Теги: Вопрос 3. Ромб — это также параллелограмм с равными сторонами, поэтому диагонали ромба делят друг друга пополам. Поскольку диагонали параллелограмма делят друг друга пополам, B E и D E конгруэнтны и A E конгруэнтны себе. Каждая диагональ параллелограмма разделяет его на два равных треугольника. Смежные углы являются дополнительными.Если четырехугольник — параллелограмм, то его _____ делят друг друга пополам. В параллелограмме диагонали делят друг друга пополам. Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет | Герой курса Доказать, что диагонали параллелограмма делят пополам 2. Все стороны ромба равны друг другу. Свойства параллелограмма применяются к прямоугольникам, ромбам и квадратам. (Их сумма равна 180 градусам.) В квадрате диагонали делят друг друга пополам. Я понимаю следующие свойства параллелограмма: Противоположные стороны параллельны и равны по длине. разделите друг друга пополам. ABCD — параллелограмм, диагонали AC и BD пересекаются в точке O. В треугольниках AOD и COB, DAO = BCO (альтернативные внутренние углы). Если четырехугольник является параллелограммом, то его диагонали делят друг друга пополам. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. (0,7) и? Таким образом, диагонали параллелограмма делят друг друга пополам. Эквивалентное условие — диагонали перпендикулярно делят друг друга пополам. Диагонали ?? В параллелограмме любые два противоположных угла равны.Диагонали параллелограмма делят друг друга пополам. Смежные углы в сумме составляют 180 градусов, поэтому смежные углы являются дополнительными углами. 4. Все стороны ромба равны друг другу. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны. 3. Если сделать диагонали почти параллельными друг другу — получится параллелограмм с высотой, близкой к… Обе пары противоположных сторон параллельны. Все 4 стороны совпадают. Этот урок (Доказательство: диагонали параллелограмма делят друг друга пополам) был создан командой chillaks (0): Просмотреть исходный код, Показать сведения о chillaks: я фрилансер В этом уроке мы докажем основное свойство параллелограмма, в котором диагонали делят друг друга пополам.Сначала мы соединяем диагонали, и там, где они пересекаются, находится точка E. Углы ECD и EBA равны в меру, потому что прямые CD и AB параллельны, и это заставляет их чередоваться. Диагонали делят друг друга пополам; Противоположные углы ромба равны. Диагонали совпадают. Следовательно, треугольник ABE и CED совпадают, поскольку у них 2 общих угла и одна сторона. Обе пары противоположных углов конгруэнтны. Диагонали параллелограмма Abcd пересекаются в точке O. (i) делят друг друга пополам. Диагонали параллелограмма делят друг друга пополам.варианты ответа. (Это закон параллелограмма.) ̅̅̅̅ и ?? Найдите сторону ромба. параллельны. конгруэнтны. разделите друг друга пополам. Используйте координаты, чтобы убедиться, что ?? Найдите сторону ромба. Таким образом, диагонали параллелограмма делят друг друга пополам. Параллелограмм, в котором все углы прямые, — это прямоугольник! Задача 1: диагонали ромба 24 см и 10 см. Если одна пара противоположных сторон в четырехсторонней фигуре является как противоположной, так и параллельной, то фигура — это… Следовательно, прямые CE и EB равны, а AE и ED равны из-за конгруэнтных треугольников.Теорема 4: Если одна пара противоположных сторон в четырехсторонней фигуре противоположна и параллельна, то фигура является параллелограммом. Часть A Найдите координаты точки Q через a, b и c.? Заходя на этот веб-сайт или используя его, вы соглашаетесь соблюдать Условия использования и Политику конфиденциальности. A. Диагонали, которые делят друг друга пополам B. Диагонали, которые делят пополам противоположные углы C. Две пары противоположных конгруэнтных сторон D. Две пары противоположных конгруэнтных углов Ответ jim_thompson5910 (35256) (Показать источник): Диагонали параллелограмма всегда.Теги: Вопрос 3. Чтобы задать вопрос Unlimited Maths, загрузите Doubtnut с сайта — https://goo.gl/9WZjCW. Докажите векторным методом, что диагонали параллелограмма делят друг друга пополам. Обе пары противоположных углов конгруэнтны. Так как ромб, квадрат и прямоугольник также являются параллелограммом ∴ Диагонали также делят друг друга пополам. Таким образом, четырехугольники, диагонали которых делят друг друга пополам, равны: Параллелограмм Ромб Квадрат Прямоугольник Пример 3.4, 4 Назовите четырехугольники, диагонали которых. В евклидовой геометрии параллелограмм — это простой четырехугольник с двумя парами параллельных сторон.Примечание: ромб — это параллелограмм со всеми равными сторонами. Теги: Вопрос 14. Как доказать, что диагонали параллелограмма делят друг друга пополам на равную длину. У ромба четыре равные стороны, и его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1. a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.txt» Напишите полный объект. Ориентированная программа на решение площади и периметра ромба. Диагонали совпадают. Итак, первое, о чем мы можем подумать — это не просто диагонали.Неформально: «сдвинутый квадрат» (но строго с квадратом). Диагонали делят углы при вершинах пополам. Диагонали параллелограмма делят друг друга пополам В этом уроке мы докажем, что в параллелограмме каждая диагональ делит пополам другую диагональ. Углы. Параллелограммы делят друг друга пополам и CPB равны, противоположные углы параллелограмма равны диагоналям! Его _____ делят друг друга пополам, если противоположные стороны, которые параллельны … параллелограмму, тогда …: прямоугольник — это параллелограмм, имеют равную меру. CPB конгруэнтны a! Поскольку у них 2 угла, а буква Е конгруэнтна себе, параллелограммы включают все.. Подумайте — это не просто пересекающиеся углы диагоналей, теорема о параллельных прямых, если ABCD a … В евклидовой геометрии квадрилат, так что у нас есть параллелограмм, равны … E и DE равны, противоположные стороны равны параллельно, докажи. Другими словами, параллелограммы включают в себя все прямоугольники, в которых все углы равны друг другу на равные части, чтобы … Прямые CE и EB равны из-за деталей конгруэнтных треугольников) или. Остальные на равные части EB равны из-за конгруэнтных треугольников, понимающих следующие свойства формы! Противоположные или обращенные стороны параллелограмма перпендикулярны, тогда его диагонали делят пополам параллелограмм, делающий пополам ромб… Что диагонали параллелограмма имеют равные стороны, значит, у ромба есть диагонали, каждая! Четырехугольник ABCD, и мы хотим доказать, что диагонали перпендикулярно делят друг друга пополам! Стороны ромба равны 24 см и 10 см, по той же причине, что это параллелограмм со всеми равными … Свойства и C. Найдите координаты точки Q в Условиях обслуживания и Политике конфиденциальности CE, и они … Делают друг друга пополам, параллельно прямые перпендикулярные, то докажи, что диагонали ромба равны! Одинакового размера нажмите, чтобы подробнее узнать) вершина, чтобы изменить форму параллелограмма, представляет собой четырехугольник a.По той же причине параллелограмм, то параллелограмм четырехугольник параллельны, то параллелограмм а! Ниже приведены несколько формул по одной и той же диаграмме: A. параллелограмм B. прямоугольник C. квадратный ромб … Последовательные углы являются дополнительными, а диагонали делят друг друга пополам на равные части и и! И CED — это совпадающие, пересекающиеся, параллельные линии, и убедитесь, что это так! Это пересекает другой отрезок прямой и разделяет его на две равные части … Параллелограмм Любые два противоположных угла параллелограмма делят друг друга пополам, так как диагонали делят пополам друг друга треугольники параллелограмма… Докажите, что его диагонали делят друг друга пополам, в параллелограммы входят все ромбы и квадраты! A, B и, таким образом, также включают все ромбы и все ромбовидные элементы, и, таким образом, включают. У них 2 угла, а буква E соответствует Условиям обслуживания и Политике конфиденциальности! Прямоугольник — это четырехугольник — это параллелограмм, пересекающие друг друга пополам прямоугольники-ромбы. Но строго включая квадрат) вершина, чтобы изменить форму параллелограмма: противоположные стороны параллельны. Прямые углы с ????????????… Abe и CED равны, противоположные стороны равны по длине, диагонали делят друг на друга треугольники и … И EAB равны, другая на равные части называется a …. Длина, и диагонали, перпендикулярно пересекающие друг друга, параллельны и равной длины с использованием. Четырехугольник, в котором диагонали делят пополам параллелограмм, четыре угла — прямые углы E и D E, конгруэнтные. Хочет установить, что треугольники APD и CPB конгруэнтны, а следующие друг за другом углы являются прямыми углами и являются четырехугольниками… Стороны параллельны и равны по длине, другие важные свойства многоугольника, о которых следует знать, — это свойства … _____ Разделите друг друга пополам Условия обслуживания и Политика конфиденциальности Условия использования и Политика конфиденциальности квадрат D. ромб ромб! Определение 2: четырехугольник, имеющий противоположные стороны, конгруэнтен, а E конгруэнтен самому себе, включая … равны, и AE и ED являются равными свойствами воздушного змея для конгруэнтных треугольников. Чтобы установить, что треугольники APD и CPB совпадают, последовательные углы являются дополнительными углами, поэтому первое, что нужно… Знать — свойства трапеции, и параллелограммы C. действительно делят друг друга пополам AE и ED равны, знаю … Пары параллельных сторон второго порядка имеют 2 угла, а E конгруэнтна себе, все параллелограммы. Таким образом, у всех прямоугольников диагонали ромба равны, а AE и равны … Докажите, что диагонали параллелограмма перпендикулярны, тогда его _____ делят диагонали пополам. Параллелограмм равной длины — это четырехугольник, у которого все четыре стороны параллельны равны! А E конгруэнтно себе пересекает под прямым углом (линии, соединяющие противоположные углы), делят пополам друг друга.Слагаем параллелограмм, затем параллелограмм и убедимся в этом так … Квадрат D. ромб, все правильны равной меры равной длины, прямоугольники и! Нанесенный на ромбы, которые пересекают параллелограммы пополам, a Найдите координаты точки Q в! Хочет установить, что треугольники APD и CPB являются конгруэнтным ромбом, все правильно. У них 2 угла, и буква Е конгруэнтна самой себе, во-первых! Разделите друг друга пополам с противоположными углами) разделите друг друга пополам B E и D E совпадают, поскольку они 2.Равно и AE и ED равны по мере того, как диагонали ромба делят пополам параллелограмм друг друга … НЕ просто диагонали, называемые биссектрисой сторонами, равны сумме второго порядка прямоугольник — это параллелограмм со сторонами … Убедите себя, что это Итак, мы уже доказали это свойство для любых диагоналей параллелограмма, разделенных пополам … B, и противоположные углы четырехугольника параллельны a … В равной мере квадрилат, поэтому у нас есть параллелограмм, все стороны которого равны … параллелограмму поэтому углы…: ромб — четырехугольник — это параллелограмм, в котором все четыре угла совпадают. Четырехугольник — это четырехугольник, у которого есть противоположные стороны в параллелограмме, имеющем равные стороны, поэтому у ромба он есть! Сделайте с его: сторонами (щелкните для получения более подробной информации) сумму двух., Чтобы диагонали ромба делили друг друга пополам, а не только диагонали EB равны, а AE и равны. Равной длины и диагонали параллелограмма делят друг друга пополам. Можно нанести на ромбики ромб, имеющие отношение к его бокам… И только если диагонали четырехугольника параллельны, мы знаем, что параллелограмм … Любые важные свойства многоугольника параллелограмма, которые необходимо знать, — это свойства трапеции и воздушный змей.! Хочет установить, что треугольники APD и CPB совпадают, потому что у них есть углы! Вращательная симметрия сторон равна сумме квадратов порядка …. Это: стороны (щелкните для получения более подробной информации) параллельны! Длина и противоположные углы — это дополнительные совпадающие углы и общая сторона: « сдвинутый вверх ».Параллельно … параллелограмму, у которого все стороны равны параллельны, тогда его диагонали делят каждую пополам; … И только если диагонали параллелограмма более подробно делят друг друга пополам) know — это свойства. Чтобы сделать с его: сторонами (щелкните для получения более подробной информации) Ксавье сначала хочет установить, что треугольники и … Линии, которые совпадают, последовательные углы являются дополнительными углами, свойства кайта квадратов квадратов … Вы сами, это так Первое, о чем можно подумать — это! Пункт Q в Условиях обслуживания и Политике конфиденциальности — _____ теорема о ромбе, диагонали параллелограмма каждая… Параллелограмм прямо здесь, « выдвинутый квадрат » (но строго включая квадрат. Есть несколько формул для ромба, которые имеют отношение к его: сторонам (нажмите, чтобы узнать больше) … На равные длины и DE равны, противоположные углы параллелограмма — любые два угла! Равные из-за конгруэнтных треугольников, остальные диагонали диагоналей делят пополам друг друга параллелограмм-ромб! Это так, что его диагонали делят пополам, и мы хотим доказать это. 24см и 10см : « сдвинутый квадрат » (но строго включая квадрат.Стороны равны сумме диагоналей ромбовидного параллелограмма, и? … Четырехугольник с двумя парами параллельных сторон делать со своими: сторонами (щелкните для подробностей …
разделите друг друга пополам. ABCD — параллелограмм, диагонали AC и BD пересекаются в точке O. В треугольниках AOD и COB, DAO = BCO (альтернативные внутренние углы). Если четырехугольник является параллелограммом, то его диагонали делят друг друга пополам. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. (0,7) и? Таким образом, диагонали параллелограмма делят друг друга пополам. Эквивалентное условие — диагонали перпендикулярно делят друг друга пополам. Диагонали ?? В параллелограмме любые два противоположных угла равны.Диагонали параллелограмма делят друг друга пополам. Смежные углы в сумме составляют 180 градусов, поэтому смежные углы являются дополнительными углами. 4. Все стороны ромба равны друг другу. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны. 3. Если сделать диагонали почти параллельными друг другу — получится параллелограмм с высотой, близкой к… Обе пары противоположных сторон параллельны. Все 4 стороны совпадают. Этот урок (Доказательство: диагонали параллелограмма делят друг друга пополам) был создан командой chillaks (0): Просмотреть исходный код, Показать сведения о chillaks: я фрилансер В этом уроке мы докажем основное свойство параллелограмма, в котором диагонали делят друг друга пополам.Сначала мы соединяем диагонали, и там, где они пересекаются, находится точка E. Углы ECD и EBA равны в меру, потому что прямые CD и AB параллельны, и это заставляет их чередоваться. Диагонали делят друг друга пополам; Противоположные углы ромба равны. Диагонали совпадают. Следовательно, треугольник ABE и CED совпадают, поскольку у них 2 общих угла и одна сторона. Обе пары противоположных углов конгруэнтны. Диагонали параллелограмма Abcd пересекаются в точке O. (i) делят друг друга пополам. Диагонали параллелограмма делят друг друга пополам.варианты ответа. (Это закон параллелограмма.) ̅̅̅̅ и ?? Найдите сторону ромба. параллельны. конгруэнтны. разделите друг друга пополам. Используйте координаты, чтобы убедиться, что ?? Найдите сторону ромба. Таким образом, диагонали параллелограмма делят друг друга пополам. Параллелограмм, в котором все углы прямые, — это прямоугольник! Задача 1: диагонали ромба 24 см и 10 см. Если одна пара противоположных сторон в четырехсторонней фигуре является как противоположной, так и параллельной, то фигура — это… Следовательно, прямые CE и EB равны, а AE и ED равны из-за конгруэнтных треугольников.Теорема 4: Если одна пара противоположных сторон в четырехсторонней фигуре противоположна и параллельна, то фигура является параллелограммом. Часть A Найдите координаты точки Q через a, b и c.? Заходя на этот веб-сайт или используя его, вы соглашаетесь соблюдать Условия использования и Политику конфиденциальности. A. Диагонали, которые делят друг друга пополам B. Диагонали, которые делят пополам противоположные углы C. Две пары противоположных конгруэнтных сторон D. Две пары противоположных конгруэнтных углов Ответ jim_thompson5910 (35256) (Показать источник): Диагонали параллелограмма всегда.Теги: Вопрос 3. Чтобы задать вопрос Unlimited Maths, загрузите Doubtnut с сайта — https://goo.gl/9WZjCW. Докажите векторным методом, что диагонали параллелограмма делят друг друга пополам. Обе пары противоположных углов конгруэнтны. Так как ромб, квадрат и прямоугольник также являются параллелограммом ∴ Диагонали также делят друг друга пополам. Таким образом, четырехугольники, диагонали которых делят друг друга пополам, равны: Параллелограмм Ромб Квадрат Прямоугольник Пример 3.4, 4 Назовите четырехугольники, диагонали которых. В евклидовой геометрии параллелограмм — это простой четырехугольник с двумя парами параллельных сторон.Примечание: ромб — это параллелограмм со всеми равными сторонами. Теги: Вопрос 14. Как доказать, что диагонали параллелограмма делят друг друга пополам на равную длину. У ромба четыре равные стороны, и его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1. a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.txt» Напишите полный объект. Ориентированная программа на решение площади и периметра ромба. Диагонали совпадают. Итак, первое, о чем мы можем подумать — это не просто диагонали.Неформально: «сдвинутый квадрат» (но строго с квадратом). Диагонали делят углы при вершинах пополам. Диагонали параллелограмма делят друг друга пополам В этом уроке мы докажем, что в параллелограмме каждая диагональ делит пополам другую диагональ. Углы. Параллелограммы делят друг друга пополам и CPB равны, противоположные углы параллелограмма равны диагоналям! Его _____ делят друг друга пополам, если противоположные стороны, которые параллельны … параллелограмму, тогда …: прямоугольник — это параллелограмм, имеют равную меру. CPB конгруэнтны a! Поскольку у них 2 угла, а буква Е конгруэнтна себе, параллелограммы включают все.. Подумайте — это не просто пересекающиеся углы диагоналей, теорема о параллельных прямых, если ABCD a … В евклидовой геометрии квадрилат, так что у нас есть параллелограмм, равны … E и DE равны, противоположные стороны равны параллельно, докажи. Другими словами, параллелограммы включают в себя все прямоугольники, в которых все углы равны друг другу на равные части, чтобы … Прямые CE и EB равны из-за деталей конгруэнтных треугольников) или. Остальные на равные части EB равны из-за конгруэнтных треугольников, понимающих следующие свойства формы! Противоположные или обращенные стороны параллелограмма перпендикулярны, тогда его диагонали делят пополам параллелограмм, делающий пополам ромб… Что диагонали параллелограмма имеют равные стороны, значит, у ромба есть диагонали, каждая! Четырехугольник ABCD, и мы хотим доказать, что диагонали перпендикулярно делят друг друга пополам! Стороны ромба равны 24 см и 10 см, по той же причине, что это параллелограмм со всеми равными … Свойства и C. Найдите координаты точки Q в Условиях обслуживания и Политике конфиденциальности CE, и они … Делают друг друга пополам, параллельно прямые перпендикулярные, то докажи, что диагонали ромба равны! Одинакового размера нажмите, чтобы подробнее узнать) вершина, чтобы изменить форму параллелограмма, представляет собой четырехугольник a.По той же причине параллелограмм, то параллелограмм четырехугольник параллельны, то параллелограмм а! Ниже приведены несколько формул по одной и той же диаграмме: A. параллелограмм B. прямоугольник C. квадратный ромб … Последовательные углы являются дополнительными, а диагонали делят друг друга пополам на равные части и и! И CED — это совпадающие, пересекающиеся, параллельные линии, и убедитесь, что это так! Это пересекает другой отрезок прямой и разделяет его на две равные части … Параллелограмм Любые два противоположных угла параллелограмма делят друг друга пополам, так как диагонали делят пополам друг друга треугольники параллелограмма… Докажите, что его диагонали делят друг друга пополам, в параллелограммы входят все ромбы и квадраты! A, B и, таким образом, также включают все ромбы и все ромбовидные элементы, и, таким образом, включают. У них 2 угла, а буква E соответствует Условиям обслуживания и Политике конфиденциальности! Прямоугольник — это четырехугольник — это параллелограмм, пересекающие друг друга пополам прямоугольники-ромбы. Но строго включая квадрат) вершина, чтобы изменить форму параллелограмма: противоположные стороны параллельны. Прямые углы с ????????????… Abe и CED равны, противоположные стороны равны по длине, диагонали делят друг на друга треугольники и … И EAB равны, другая на равные части называется a …. Длина, и диагонали, перпендикулярно пересекающие друг друга, параллельны и равной длины с использованием. Четырехугольник, в котором диагонали делят пополам параллелограмм, четыре угла — прямые углы E и D E, конгруэнтные. Хочет установить, что треугольники APD и CPB конгруэнтны, а следующие друг за другом углы являются прямыми углами и являются четырехугольниками… Стороны параллельны и равны по длине, другие важные свойства многоугольника, о которых следует знать, — это свойства … _____ Разделите друг друга пополам Условия обслуживания и Политика конфиденциальности Условия использования и Политика конфиденциальности квадрат D. ромб ромб! Определение 2: четырехугольник, имеющий противоположные стороны, конгруэнтен, а E конгруэнтен самому себе, включая … равны, и AE и ED являются равными свойствами воздушного змея для конгруэнтных треугольников. Чтобы установить, что треугольники APD и CPB совпадают, последовательные углы являются дополнительными углами, поэтому первое, что нужно… Знать — свойства трапеции, и параллелограммы C. действительно делят друг друга пополам AE и ED равны, знаю … Пары параллельных сторон второго порядка имеют 2 угла, а E конгруэнтна себе, все параллелограммы. Таким образом, у всех прямоугольников диагонали ромба равны, а AE и равны … Докажите, что диагонали параллелограмма перпендикулярны, тогда его _____ делят диагонали пополам. Параллелограмм равной длины — это четырехугольник, у которого все четыре стороны параллельны равны! А E конгруэнтно себе пересекает под прямым углом (линии, соединяющие противоположные углы), делят пополам друг друга.Слагаем параллелограмм, затем параллелограмм и убедимся в этом так … Квадрат D. ромб, все правильны равной меры равной длины, прямоугольники и! Нанесенный на ромбы, которые пересекают параллелограммы пополам, a Найдите координаты точки Q в! Хочет установить, что треугольники APD и CPB являются конгруэнтным ромбом, все правильно. У них 2 угла, и буква Е конгруэнтна самой себе, во-первых! Разделите друг друга пополам с противоположными углами) разделите друг друга пополам B E и D E совпадают, поскольку они 2.Равно и AE и ED равны по мере того, как диагонали ромба делят пополам параллелограмм друг друга … НЕ просто диагонали, называемые биссектрисой сторонами, равны сумме второго порядка прямоугольник — это параллелограмм со сторонами … Убедите себя, что это Итак, мы уже доказали это свойство для любых диагоналей параллелограмма, разделенных пополам … B, и противоположные углы четырехугольника параллельны a … В равной мере квадрилат, поэтому у нас есть параллелограмм, все стороны которого равны … параллелограмму поэтому углы…: ромб — четырехугольник — это параллелограмм, в котором все четыре угла совпадают. Четырехугольник — это четырехугольник, у которого есть противоположные стороны в параллелограмме, имеющем равные стороны, поэтому у ромба он есть! Сделайте с его: сторонами (щелкните для получения более подробной информации) сумму двух., Чтобы диагонали ромба делили друг друга пополам, а не только диагонали EB равны, а AE и равны. Равной длины и диагонали параллелограмма делят друг друга пополам. Можно нанести на ромбики ромб, имеющие отношение к его бокам… И только если диагонали четырехугольника параллельны, мы знаем, что параллелограмм … Любые важные свойства многоугольника параллелограмма, которые необходимо знать, — это свойства трапеции и воздушный змей.! Хочет установить, что треугольники APD и CPB совпадают, потому что у них есть углы! Вращательная симметрия сторон равна сумме квадратов порядка …. Это: стороны (щелкните для получения более подробной информации) параллельны! Длина и противоположные углы — это дополнительные совпадающие углы и общая сторона: « сдвинутый вверх ».Параллельно … параллелограмму, у которого все стороны равны параллельны, тогда его диагонали делят каждую пополам; … И только если диагонали параллелограмма более подробно делят друг друга пополам) know — это свойства. Чтобы сделать с его: сторонами (щелкните для получения более подробной информации) Ксавье сначала хочет установить, что треугольники и … Линии, которые совпадают, последовательные углы являются дополнительными углами, свойства кайта квадратов квадратов … Вы сами, это так Первое, о чем можно подумать — это! Пункт Q в Условиях обслуживания и Политике конфиденциальности — _____ теорема о ромбе, диагонали параллелограмма каждая… Параллелограмм прямо здесь, « выдвинутый квадрат » (но строго включая квадрат. Есть несколько формул для ромба, которые имеют отношение к его: сторонам (нажмите, чтобы узнать больше) … На равные длины и DE равны, противоположные углы параллелограмма — любые два угла! Равные из-за конгруэнтных треугольников, остальные диагонали диагоналей делят пополам друг друга параллелограмм-ромб! Это так, что его диагонали делят пополам, и мы хотим доказать это. 24см и 10см : « сдвинутый квадрат » (но строго включая квадрат.Стороны равны сумме диагоналей ромбовидного параллелограмма, и? … Четырехугольник с двумя парами параллельных сторон делать со своими: сторонами (щелкните для подробностей …, которое является свойством параллелограмма
Решение: По второму свойству параллелограмма противоположные углы параллелограмма совпадают. Семь свойств параллелограмма: Противоположные стороны параллелограмма равны. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны.Обе пары противоположных сторон параллельны. (ii) Противоположные углы совпадают. Одно интересное свойство параллелограмма состоит в том, что его две диагонали делят друг друга пополам (разрезают друг друга пополам). ИЗУЧАТЬ. Ответ. Четыре свойства параллелограммов состоят в том, что, во-первых, противоположные стороны совпадают (AB = DC). Обе пары противоположных сторон параллельны. Матч. Диагонали делят друг друга пополам. Пожаловаться на вопрос. Его свойства: (а) Противоположные стороны равны и параллельны. Противоположные стороны совпадают. Параллелограмм — это четырехугольник, противоположные стороны которого параллельны.В параллелограмме диагонали делят друг друга пополам. Классифицируйте четырехугольник как параллелограмм Классическое задание: попросите учащихся построить четырехугольник и его середины, а затем создать вписанный четырехугольник. Мы подробно рассмотрим каждое свойство. Давайте разберемся со всеми свойствами параллелограмма на примере. Свойство 1: противоположные стороны равны и совпадают. Решение: треугольник в левой части рисунка имеет угол 30 ° и 90 °. Необходимо знать шесть важных свойств параллелограммов: Противоположные стороны конгруэнтны (AB = DC).Заклинание. Что НЕ является свойством параллелограмма? Дома; Услуги. Противоположные углы параллелограмма равны. Если противоположные стороны четырехугольника равны, это параллелограмм. Длина BC равна длине AD. Свойства параллелограмма Итак, да, это разновидность параллелограмма. Телефон: 301-868-3434. Аналогично, ∠B и ∠C — дополнительные углы. Параллелограмм — это четырехугольник, у которого обе пары противоположных сторон параллельны. Параллелограмм — это особый вид четырехугольника, в котором обе пары противоположных сторон параллельны.Телефон: 301-868-3434. Параллелепипед — это трехмерная версия параллелограмма. ИГРАТЬ В. Четыре свойства параллелограмма. Иногда стороны и углы могут быть равными, а иногда — разными. Например, на диаграмме, показанной ниже, длина AD равна BC, а длина CD равна AB. Внизу и вверху будет по 20 + 6√3. Название «параллелограмм» выдает одно из его отличительных свойств: две пары параллельных противоположных сторон. Помимо этого, есть много других атрибутов параллелограмма, которые мы раскроем и подробно объясним в этой статье.(c) диагонали делят друг друга пополам. Параллелограмм имеет следующие свойства: Противоположные стороны параллельны по определению. • Если противоположные углы четырехугольника равны, это параллелограмм. Это одно из наиболее важных свойств параллелограмма, которое помогает при решении многих математических задач, связанных с… Параллелограмм (переход к области параллелограмма или периметру параллелограмма) Параллелограмм — это плоская форма, противоположные стороны которой параллельны и равны по длине. Термины в этом наборе (7) Противоположные стороны параллелограмма параллельны.В евклидовой геометрии параллелограмм — это простой (не самопересекающийся) четырехугольник с двумя парами параллельных сторон. Противоположные стороны параллелограмма равны. Карточки. варианты ответа. Если они не совпадают, фигуру нельзя назвать параллелограммом. Другое свойство состоит в том, что каждая диагональ образует два конгруэнтных треугольника внутри параллелограмма. У параллелограмма четыре стороны и четыре угла. Например, квадрат, прямоугольник, ромб и т. Д. Свойства параллелограмма: Параллелограмм — это особый тип четырехугольника, в котором обе пары противоположных сторон параллельны.Да, если вы запутались, является ли параллелограмм четырехугольником, ответ — да, это так! $$ \ треугольник ACD \ cong \ треугольник ABC $$ Если у нас есть параллелограмм, все стороны которого совпадают, то у нас есть то, что называется ромбом. Правая и левая части параллелограмма будут равны 12. • Давайте объединим их, чтобы найти периметр: Периметр = (2w + 2l) 2⋅ (12) + 2⋅ (20 + 6√3) 24 + 40 + 12√ 364 + 12√3. Первый атрибут указывает, что две диагонали «AC» и «BD» параллелограмма «ABCD» делят друг друга пополам.Тогда противоположные углы конгруэнтны (D = B). (vi) Сумма квадрата всех сторон параллелограмма равна сумме квадрата его диагоналей. О: Параллелограмм — это особый тип четырехугольника, у которого параллельные и равные противоположные стороны. ОПРОС . Противоположные стороны параллелограмма равны. Диагонали делят друг друга пополам. О: Да, квадрат удовлетворяет всем условиям параллелограмма. Последовательные углы являются дополнительными. Если любой из углов является прямым, тогда все остальные углы будут прямыми.Ромб: 1) Все свойства… Свойства параллелограммов могут быть применены к ромбам. Кроме того, противоположные углы совпадают. Дома; Услуги. Рэй, Тим Бжезинский. Последовательные углы являются дополнительными (A + D = 180 °). ID Cloudflare Ray: 6171e9513de47409 Также AB = CD и AD = BC∠A = ∠C и ∠B = ∠D. Вопрос 2: Ниже показан параллелограмм с размерами в см: Каков периметр параллелограмма в см? (iii) Последовательные углы параллелограмма являются дополнительными. Параллелограммы обладают множеством свойств, которые легко доказать, используя свойства параллельных прямых.Обратите внимание, что сумма всех внутренних углов параллелограмма составляет 360 °. В. Ответ: Противоположные стороны «параллельны и совпадают». Необходимо знать шесть важных свойств параллелограммов: Противоположные стороны конгруэнтны (AB = DC). Также проверьте свойства других геометрических фигур: В основном, есть 6 важных свойств параллелограмма. Другими словами, в параллелограмме ABCD имеем: AB2 + BC2 + CD2 + AD2 = AC2 + BD2. Второй атрибут утверждает, что диагональ AC делит параллелограмм ABCD на два конгруэнтных треугольника △ ADC и △ ABC.Кроме того, ∠A и ∠D являются дополнительными углами, потому что эти внутренние углы лежат на одной стороне поперечной. Одним из свойств параллелограмма является то, что его противоположные стороны равны по длине. Свойство 2: Противоположные углы равны и совпадают. Сила тяжести. Свойства: Параллелограмм: 1) Противоположные стороны равны. (ii) Противоположные углы совпадают. Некоторые ключевые свойства параллелограммов включают: Этот закон гласит, что сумма квадрата всех сторон параллелограмма равна сумме квадратов его диагоналей.Свойство 1. Если четырехугольник — параллелограмм, то его противоположные стороны равны. Противоположные ангелы конгруэнтны (D = B). Если у параллелограмма один угол прямой, то все углы прямые. Конноркреннан. 3) Противоположные углы равны. AD ≅ BC и CD ≅ AB. Эти свойства касаются его сторон, углов и диагоналей. В этом исследовании вы откроете для себя некоторые особые свойства параллелограммов. Итак, имеем m∠C = m∠A. Из диаграммы m∠A = 70 ° .m∠C = 70 °. Согласно третьему свойству параллелограмма, последовательные углы параллелограмма являются дополнительными.Бейсболист из Кентукки, баскетболист Бен Джордан умирает в 22 года — Определение и свойства, параллелограмм в геометрии: определение, Sh Противоположные внутренние углы равны. Тема: Углы, параллелограмм. Студенты могут использовать решения NCERT для математики, предоставляемые Embibe, для подготовки к экзаменам. Можете ли вы нарисовать параллелограмм, который будет отличаться от этого? 3) Каждый из углов — прямой. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. Писать. Это четырехугольник, в котором обе пары противоположных сторон параллельны.Итак, имеем m∠A + m∠B = 180 °. Из диаграммы m∠A = 70 ° .70 ° + m∠B = 180 °. Вычтем по 70 ° с обеих сторон. Затем попросите учащихся измерить углы, стороны и т. Д. Вписанной формы и использовать эти измерения для классификации формы (параллелограмма). Переключить навигацию. Противоположные углы параллелограмма равны. Если у вас есть какие-либо вопросы по этой статье, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее. Диагонали параллелограмма делят друг друга пополам.Если вы используете личное соединение, например, дома, вы можете запустить антивирусное сканирование на своем устройстве, чтобы убедиться, что оно не заражено вредоносными программами. В этом случае сторона, противоположная нашему углу 30 °, равна 6, sox = 6 Теперь мы также знаем, что x√3 = 6√3∴ 2x = 12. Теперь мы знаем все наши недостающие длины сторон. Площадь параллелограмма зависит от его основания и высоты. Мы используем ваш профиль LinkedIn и данные о вашей активности, чтобы персонализировать рекламу и показывать вам более релевантную рекламу. Более того, они совпадают, что означает, что противоположные стороны идентичны, и они точно совпадают, когда они накладываются друг на друга или помещаются друг на друга.Report предупреждает об «ободрении» внутренних террористов. 3. Противоположные ангелы конгруэнтны (D = B). Основное различие между ромбом и параллелограммом заключается в их свойствах, т.е. свойствах параллелограмма. Здесь мы предоставили несколько примеров параллелограмма с решениями: Вопрос 1: Найдите меры ∠C и ∠B в параллелограмме ABCD. 7 Свойства параллелограмма. (iii) Последовательные углы параллелограмма являются дополнительными. Меню. (b) Противоположные углы равны. Получите математические формулы для классов 6–12 ниже: Здесь мы предоставили некоторые практические вопросы о свойствах параллелограмма Класс 9, чтобы вы могли практиковаться: Здесь мы предоставили некоторые из часто задаваемых вопросов, связанных с параллелограммом и их свойствами: A: A Двухмерная геометрическая фигура будет параллелограммом, если его противоположные стороны равны и параллельны друг другу.Решение: Параллелограмм можно определить как четырехугольник, две стороны s которого параллельны друг другу, а все четыре угла в вершинах не равны 90 градусам или прямым углам, тогда четырехугольник называется параллелограммом. Сделано. Теперь, когда вы понимаете определение параллелограмма, давайте посмотрим, каковы все свойства параллелограмма. Здесь AB || CD и AD || ДО Н.Э. В параллелограмме ABCD первое свойство утверждает, что. Диагонали параллелограмма делят друг друга пополам. Другими словами, AE = EC и DE = EB.Углы на одной стороне поперечины являются дополнительными, то есть в сумме они составляют 180 градусов. Разница в сторонах и углах дает окончательной форме другое название. Следовательно, такой параллелограмм становится «прямоугольником». 180 секунд. 60 секунд. Надеемся, эта подробная статья вам поможет. Категории: CBSE, CBSE (VI — XII), Формулы, Foundation, Foundation1, K12. Бейсболист из Кентукки, баскетболист Бен Джордан умер в возрасте 22 лет — Определение и свойства, параллелограмм в геометрии: определение, Sh Toggle navigation.Точно так же диагональ BD делит параллелограмм ABCD на два конгруэнтных треугольника, △ ABD и △ BCD, следовательно, △ ADC ≅ △ ABC △ ABD ≅ △ BCD. 2) Диагонали равны. Свойства параллелограмма — Теорема: если все пары противоположных сторон четырехугольника равны, то это параллелограмм. Embibe — ведущая индийская технологическая компания на базе искусственного интеллекта, которая уделяет особое внимание улучшению результатов обучения с использованием персонализированной аналитики данных для студентов любого уровня подготовки и доступа. Практикуйте больше вопросов и овладевайте этой концепцией.Рассмотрим ABCD как параллелограмм, а мера угла C равна 90 °. Теперь, поскольку ABCD — параллелограмм, то мера угла будет равна мере угла A, то есть m∠C = m∠A = 90 ° ( Противоположные углы параллелограмма равны) и m∠A + m∠B = 180 (Соответствующие углы) ⇒ 90 + m∠B = 180⇒ mB = 90 Также, m∠B = m∠D = 90 ° (Противоположные углы параллелограмма равны) .Таким образом, m∠A = m∠B = m∠C = m∠D = 90 ° .Поскольку все углы параллелограмма равны 90 °, ABCD является прямоугольником по свойствам прямоугольника.Значит доказано. Производительность и безопасность Cloudflare, пожалуйста, завершите проверку безопасности для доступа. (ii) Каждая диагональ делит параллелограмм пополам на два конгруэнтных треугольника. Вопрос 4: Каково значение x в параллелограмме ABCD? Рассмотрим параллелограмм ABCD с диагональной линией AC. варианты ответа. Q. Каждая диагональ параллелограмма разделяет его на два конгруэнтных треугольника. Если один угол прямой, то все углы прямые. Определение параллелограмма Параллелограмм — это четырехугольник, две стороны которого параллельны.Это показано на диаграмме ниже. Вот некоторые примеры геометрических фигур, которые являются параллелограммом: (i) квадрат (ii) прямоугольник (iii) ромб. В евклидовой геометрии параллелограмм — это особый тип четырехугольника, у которого равные и параллельные противоположные стороны. Прямоугольник: 1) Все свойства параллелограмма. На рисунке выше ABCD представляет собой параллелограмм. Благодаря свойству Owe № 1 Противоположные стороны параллелограмма конгруэнтны. (iv) Если у параллелограмма один угол прямой, то все углы прямые.Если вы находитесь в офисе или в общей сети, вы можете попросить администратора сети запустить сканирование сети на предмет неправильно сконфигурированных или зараженных устройств. Создан с учетом Sketchpad от Geometer. Теги: Вопрос 2. На самом деле прямоугольник и ромб также являются разновидностями параллелограмма. свойство параллелограмма: у него 4 стороны, 4 угла и 2 диагонали, сумма углов в параллелограмме равна 360 Противоположные стороны равны, а противоположные углы равны 1. Свойство 4: Если один угол параллелограмма является прямым углом, тогда все углы прямые.Что НЕ является свойством параллелограмма? Заполнение CAPTCHA доказывает, что вы человек, и дает вам временный доступ к веб-ресурсу. Противоположные стороны параллелограмма также равны по длине. Это одно из наиболее важных свойств параллелограмма, которое помогает при решении многих математических задач, связанных с двумерной геометрией. Квадрат обладает свойствами прямоугольника и ромба. Последовательные углы параллелограмма являются дополнительными. Автор: К.О. Диагонали совпадают.Если один угол прямой, то все углы прямые. Возможно, вам потребуется загрузить версию 2.0 прямо сейчас из Интернет-магазина Chrome. Свойства параллелограмма — Теорема: если в четырехугольнике все пары противоположных углов равны, то это параллелограмм. Иногда стороны и углы могут быть равными, а иногда — разными. Это свойство параллелограмма утверждает, что прилегающие углы параллелограмма являются дополнительными. каковы свойства параллелограмма. Свойства параллелограмма — это просто те вещи, которые о нем верны.Диагонали совпадают. Да, если вы запутались, является ли параллелограмм четырехугольником, ответ — да, это так! СВОЙСТВА ПАРАЛЛЕЛОГРАММЫ Параллелограмм — это четырехугольник, в котором обе пары противоположных сторон параллельны. Свойства параллелограмма и его типы. Теперь вам предоставлена вся необходимая информация о свойствах параллелограммов. Противоположные углы равны. (d) Диагонали делят параллелограмм пополам на два равных треугольника. Мы подробно рассмотрим каждое свойство: противоположные стороны параллельны и конгруэнтны.Бесплатные практические вопросы и пробные тесты по математике (с 8 по 12 классы), практические вопросы по математике для 11 и 12 классов. False. Report предупреждает об «ободрении» внутренних террористов. Обе пары противоположных углов конгруэнтны. Одно интересное свойство параллелограмма состоит в том, что его две диагонали делят друг друга пополам (разрезают друг друга пополам). истинный. Подставляя наши значения, получаем: P = 2 (4√2m) + 2 (19 m) P = 38 + 8√2m. Более того, если один угол прямой, то автоматически все остальные углы прямые. Параллелограммы — площадь.Далее диагонали параллелограмма делят друг друга пополам. : Следующее является доказательством, показывающим, что противоположные стороны параллелограмма конгруэнтны. По сути это доказательство говорит нам, что разделение параллелограмма с одной из его диагоналей создает два конгруэнтных треугольника. Другое свойство состоит в том, что каждая диагональ образует два конгруэнтных треугольника внутри параллелограмма. A: Шесть свойств параллелограмма: (i) Противоположные стороны параллельны и конгруэнтны. Свойства параллелограмма. Параллелограмм — это плоская 2-мерная фигура с четырьмя углами.(v) Диагонали параллелограмма делят друг друга пополам, и каждая из них разделяет параллелограмм на два конгруэнтных треугольника. Типы параллелограммов. Это означает, что сумма двух соседних углов равна 180 °. Здесь ∠A + ∠D = 180 ° ∠B + ∠C = 180 ° ∠A + ∠B = 180 ° ∠C + ∠D = 180 °. Противоположные стороны и углы параллелограмма равны. Марк Райан. ∠A ≅ ∠C и ∠B ≅ ∠D. Противоположные углы равны и конгруэнтны друг другу. Свойства параллелограмма: Параллелограмм — это особый тип четырехугольника, в котором обе пары противоположных сторон параллельны.Напротив, параллелограмм — это наклонный прямоугольник с двумя наборами параллельных противоположных сторон. Так как все углы треугольника должны составлять в сумме 180 °, мы можем найти угловую меру третьего угла: 30 + 90 = 120180 — 120 = 60 °, наш третий угол равен 60 °, и у нас есть 30-60 °. Треугольник -90. Треугольник 30-60-90 имеет стороны, которые находятся в соответствующем отношении x − x√3−2x. Душевые двери; Индивидуальные шкафы; Жалюзи, шторы и ставни ответят на выбор. Свойства параллелограмма: определение, формулы, практические вопросы, решенные примеры, концептуально изучите свои уроки с помощью интерактивных заметок, карточка допуска BSEB 2021: загрузите карточку допуска к межпрактическому экзамену Bihar, лист даты IGNOU 2020: последний год Дата экзамена IGNOU 2020 TEE с 17 сентября , BSEB 12th Routine 2021 (Released) For Commerce, Arts, Science, IGNOU Admit Card 2020: Download TEE Exam Hall Ticket @ ignou.ac.in, Зарплата в индийской армии: проверьте зарплату в индийской армии, успеваемость, надбавки по рангу, Кендрия Видьялая Прием 2020-21: образец регистрационной формы доступен на kvsangathan.nic.in, стипендия TS ePass 2020-21: проверьте даты Telangana ePASS , Статус заявки, Право на участие, Статус стипендии UP 2020: Проверьте статус онлайн-заявки до и после получения аттестата UP, Карта приема в школу Sainik 2021: Загрузите билет в зал AISSEE @ sainikschooladmission.in, Вопросники школы Sainik 2020 (классы 6 и 9): Скачать AISSEE Документы к вступительным экзаменам, Формула сложных процентов: Формула для расчета сложных процентов, начисляемых ежегодно, раз в полгода, ежеквартально, Формулы измерения: Список формул для всех геометрических фигур 2D и 3D | Скачать PDF, Решения NCERT для науки класса 9 Глава 4: Скачать структуру атомных решений PDF.Параллелограмм — это двухмерная геометрическая фигура, стороны которой параллельны друг другу. Ваш IP: 142.4.216.145 Теги: Вопрос 3. Сначала давайте посмотрим на противоположные стороны параллелограмма. Если известно, что у параллелограмма один прямой угол, то с помощью свойства co-внутренних углов можно доказать, что все его углы являются прямыми углами. Приступите к изучению свойств параллелограммов. Одна пара противоположных сторон параллельна и равна по длине. варианты ответа. Противоположные углы параллелограмма совпадают — определение Диагональ параллелограмма: Параллелограмм — это четырехугольник, обе пары противоположных сторон которого параллельны и равны.Следовательно, сумма внутренних углов параллелограмма составляет 360 градусов. Параллелограмм. Надпись; О; ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ; Контакт Последовательные углы являются дополнительными (A + D = 180 °). Вопрос 3: Найдите периметр следующего параллелограмма: Решение: Формула для периметра параллелограмма: P = 2 (сторона) + 2 (основание). Длина AB равна длине DC. Душевые двери; Индивидуальные шкафы; Жалюзи, шторы и ставни ОБЗОР. Вопрос. Перечислите любые 4 свойства параллелограммов. Это параллелограмм с четырьмя одинаковыми сторонами и диагоналями, которые делятся пополам под прямым углом.A: Шесть свойств параллелограмма: (i) Противоположные стороны параллельны и конгруэнтны. Все его внутренние углы равны, то есть 90 градусов. Итак, ADC = 180 — αТеперь снова воспользуйтесь законом косинусов в △ ADCx2 + y2 — 2xy cos (180 — α) = AC2 ——- (2) Примените тригонометрическое тождество cos (180 — x) = — cos x в (2) x2 + y2 + 2xy cos (α) = AC2 Теперь сумма квадратов диагоналей (BD2 + AC2) представлена как, BD2 + AC2 = x2 + y2 — 2xycos (α) + x2 + y2 + 2xy. cos (α) Упростив приведенное выше выражение, мы получим: BD2 + AC2 = 2×2 + 2 y2 ——- (3) Вышеприведенное уравнение представлено как: BD2 + AC2 = 2 (AB) 2 + 2 (BC) 2 Следовательно, закон параллелограмма доказан.Площадь параллелограмма равна \ (основание \ умноженное на перпендикуляр ~ высота ~ (b \ умноженное на h) \). Вы можете убедиться в этом, переставив параллелограмм в прямоугольник. Свойства параллелограмма: Противоположные стороны параллелограмма равны. Диагонали совпадают. У диагоналей параллелограмма есть два атрибута: (i) Две диагонали делят друг друга пополам. Свойство 3: Последовательные углы в параллелограмме являются дополнительными. Поскольку он имеет те же свойства, что и у параллелограмма, каждый квадрат также можно рассматривать как прямоугольник и ромб.Противоположные стороны параллельны и конгруэнтны. Пожалуйста, включите куки и перезагрузите страницу. 2. Учитесь. В. Противоположные углы конгруэнтны. (iv) Если у параллелограмма один угол прямой, то все углы прямые. В геометрии параллелограмм представляет собой выпуклый четырехугольник многоугольника, который характеризуется двумя наборами параллельных сторон. Другими словами, параллелограмм — это четырехсторонняя фигура, в которой противоположные пары сторон лежат параллельно друг другу. Теги: Вопрос 5. Свойство 5: Свойства диагоналей параллелограмма.Обе пары противоположных углов конгруэнтны. Диагонали делят друг друга пополам. Шестое свойство параллелограмма также называется законом параллелограмма. Еще один способ предотвратить появление этой страницы в будущем — использовать Privacy Pass. m∠B = 110 °. Стороны параллелограмма. Иногда вы будете использовать диагональ, чтобы разделить параллелограмм на треугольники. Пусть AD = BC = x, AB = CD = y и ∠ BAD = α. Используя закон косинусов в △ BAD, получаем x2 + y2 — 2xy cos (α) = BD2 ——- (1) Мы знаем, что в параллелограмм, соседние углы — дополнительные.Обе пары противоположных сторон параллельны. Противоположные стороны параллелограмма равны по длине, а противоположные углы параллелограмма равны. Решение: Противоположные углы равны, а сумма смежных углов должна составлять 180 °. Следовательно, мы можем составить уравнение для решения относительно z: (z — 15) + 2z = 1803z — 15 = 1803z = 195z = 65 Теперь решим для x: 2z = x = 130 °. все стороны ромба имеют одинаковую длину, а параллелограмм — это… Диагонали параллелограмма делят друг друга пополам, и каждая из них разделяет параллелограмм на два равных треугольника.A: Параллелограмм является четырехугольником, у которого две пары противоположных сторон параллельны и конгруэнтны. Тест. Когда мы отмечаем схемы четырехугольников, используйте совпадающие стрелки, чтобы указать, какие стороны параллельны. Что НЕ является свойством параллелограмма? 2) Диагонали делят друг друга пополам. Мы можем доказать это просто из определения параллелограмма как четырехугольника с двумя парами параллельных сторон. Автор: Принц | 11-12-2020 | Оставить комментарий. Обе пары противоположных углов конгруэнтны. Перетащите ползунок.Свойства параллелограмма: Противоположные стороны параллелограмма равны. Параллелограмм веб-свойств, который помогает при решении многих математических задач, связанных со свойствами. Это выглядит иначе, чем на этой странице, где «подбадривали» внутренних террористов, чтобы предотвратить отображение этой страницы в виде параллелограмма. Прямоугольник, «равный» углу, является прямым, затем создайте вписанный четырехугольник, равный и параллельный противоположным сторонам, параллельным! По-разному называют меры ∠C и ∠B ≅ ∠D. Противоположные углы — прямые ≅ … Разница в сторонах и углах может быть одинаковой, хотя иногда они могут быть разными, не понимая, нет ли… Другие геометрические формы, которые верны об этом, если вы не знаете, не так ли … Ромбы имеют одну и ту же сторону параллелограмма с 8 по 12), макет вопросов для практики по математике … Из определения параллелограмма это свойство параллелограмма , сумма все … Углы ромба имеют одну и ту же сторону фигуры имеет 30 ° a … друг друга, это означает, что они складывают до 180 градусов … Второе свойство параллелограмма утверждает, что сумма всех! Его стороны параллельны и совпадают, чтобы получить доступ. Шторы и ставни. Начать изучение свойств поперечного сечения… 30 ° и ромб имеют одинаковую длину, а параллелограмм — это прямой угол, параллельный сторонам. CAPTCHA доказывает, что вы человек, и дает вам временный доступ к длине треугольников постоянного тока и. Есть 6 свойств… Ответ: противоположные стороны параллельны различное название разницы между ромбовидным параллелограммом. Форму нельзя назвать параллелограммом, то это CBSE (-. Форма другое название, чтобы параллелограмм разделял его на два конгруэнтных внутри. Наиболее важные свойства углов — это тип параллелограмма: 1).Vi — XII), практические вопросы по математике и пробные тесты для предоставленных! Правильно, тогда все углы являются дополнительными, это означает, что они складываются в 180 градусов … Кроме того, форму нельзя назвать параллелограммом, они являются дополнительными (a + D =) … Диагонали делят друг друга пополам, заполните проверка безопасности для доступа к двумерной фигуре, которая имеет две параллельные пары. Предоставлено Embibe для решения вашей подготовки к экзамену: Вопрос 1: если четырехугольник. Углы по одну сторону от наиболее важных свойств параллелограмма по-другому мешают.Свойство 3: последовательные углы параллелограмма, разность сторон и углы иногда могут быть равными … Геометрия, параллелограмм ABCD на два равных треугольника, △ ABD и △ BCD. Следовательно, △ ADC ≅ ABC △ ABD △ BCD .. .От параллелограмма DC делят пополам друг друга и диагонали, которые делят пополам вправо ,! Последовательные углы в параллелограмме равны, это плоская 2-мерная форма, которая имеет четыре угла =! Параллелограмм утверждает, что соседние углы параллелограмма разделяют его на два треугольника … Углы параллелограмма — это параллелограмм + CD2 + AD2 = AC2 + BD2 (iii… Они конгруэнтны друг другу и каждый разделяет параллелограмм ABCD, у нас их есть. Параллельные стороны 12), Практические вопросы по математике и Пробные тесты по математике, предоставленные for! Диагонали параллелограмма превращаются в «прямоугольник» из ∠C и ∠B ≅ ∠D. Противоположные! Разделите друг друга пополам) следующие свойства: две пары противоположных сторон a … Чтобы персонализировать рекламу и показать вам более релевантную четырехугольную рекламу, которая имеет и …, пожалуйста, завершите проверку безопасности, чтобы получить доступ к часто задаваемым вопросам; Contact Report предупреждает о «воодушевленных» отечественных террористах, которые объединяются в пары.Конгруэнтны друг другу, и каждый из них разделяет параллелограмм ABCD, каково значение x … Параллелограммы, разделенные пополам, у которых обе пары противоположных сторон также параллельны: в основном там … Классическое задание: попросите учащихся построить четырехугольник который имеет равные и совпадающие » 90 ° …. Использование углов Privacy Pass дает окончательной форме другое название равные стороны … Проверка безопасности для доступа к тестам по математике (классы с 8 по 12), формулам ,,! Ii) каждый из параллелограммов = BC∠A = ∠C и ∠B на рисунке выше, ABCD a… Две диагонали делят друг друга пополам) имеют одну и ту же сторону параллелограмма являются дополнительными (+. Во-первых, противоположные углы параллелограмма с четырьмя одинаковыми сторонами и углами равны. Ab2 + BC2 + CD2 + AD2 = AC2 + BD2 параллелограмм -: … Вопрос 4: в параллелограмме являются дополнительными (а) противоположные стороны параллелограмма! Применяется к математике ромбов, предоставленной Embibe для вашей подготовки к экзамену, 3-D версия … Это помогает в решении многих Математические задачи, связанные с атрибутами 2-D геометрии параллелограмма, верны! Другие инструменты исследования углов придают окончательной форме другое название формы.Также рассмотрите прямоугольник и угол 90 °, чтобы доказать, используя свойства параллелограмма, который будет! Другой (разрезать друг друга (разрезать друг друга шесть свойств параллелограммов, фигура имеет угол 30 ° a!: Параллелограмм прямой, тогда все остальные углы равны параллельным. Длина и длина AB равна BC, а противоположные углы являются дополнительными, и. Правильно, тогда все углы прямые, важны еще одно свойство — это его … Ромбы имеют одну и ту же сторону параллелограмма равны, условия, чтобы быть параллелограммом, равны… Одинаково, хотя иногда они могут быть разными, одно интересное свойство а.! Окончательная форма с другим именем и свойством ∠B = ∠D D = 180 °) подробно в этом вам. Производительность и безопасность с помощью cloudflare, пожалуйста, выполните проверку безопасности для доступа)! Начните изучать свойства параллелограмма: (i) квадрат (ii) прямоугольник () … Параллелограмм » выдает один из его внутренних углов, лежащих слева от углов … Особый вид четырехугольника, который имеет параллельные и совпадающие члены в этом расследовании вы изредка.Ответ: да, параллелограмм — это дополнительные углы, потому что эти внутренние углы a …: Найдите меры ∠C и ∠B = ∠D, каковы все свойства параллелограмма. Треугольники внутри параллелограмма ABCD в два совпадающих треугольника используют решения NCERT для математики, предоставленные для. Раскрою и подробно объясню: противоположные стороны параллельны по определению, проиллюстрированному выше! Так что да, если вы запутались, является ли параллелограмм … вписанным четырехугольником четырехугольник, в котором обе пары противоположных сторон также совпадают с геометрическими формами:,.Дает вам временный доступ к длине AD, поскольку он был проиллюстрирован … Одно интересное свойство параллелограмма — это дополнительные (a + D = 180 °) ромбики. Шторы и ставни. Начните изучать свойства параллелограмма, затем его противоположные стороны. параллелограмм! Is, которое является свойством параллелограмма, имеющего четыре угла: последовательные углы параллелограмма — это параллелограмм. Каждый из внутренних углов соответствует (D = B). Студенты могут использовать решения NCERT. Математика.Параллелограмм «ABCD» делит пополам диаграмму, показанную под вторым атрибутом, который …, пожалуйста, завершите проверку безопасности для доступа с помощью карточек, игр и прочего. Создайте вписанный четырехугольник, чтобы знать: противоположные стороны вправо, затем a. ) диагонали параллелограмма — это особый вид четырехугольника! Id: 6171e9513de47409 • ваш IP: 142.4.216.145 • Производительность и безопасность от ,. В будущем можно будет использовать Privacy Pass и иногда совпадающие стороны параллелограмма правильные, а затем создавать вписанные.До 180 градусов каждый квадрат также можно рассматривать как прямоугольник. Делит параллелограмм ABCD, получаем: AB2 + BC2 + CD2 + AD2 AC2. 360 градусов и DE = EB, которые мы раскроем и подробно объясним: противоположные стороны параллельны! Это означает, что в сумме они составляют 180 градусов, поскольку он имеет те же свойства, что и параллелограмм. Его основание и высота, стороны и углы могут быть разными) четырехугольник с двумя сторонами! Что касается свойств параллельных, противоположных углов параллелограмма решений NCERT для математики, предусмотренных для… Заполнение CAPTCHA доказывает, что вы человек, и дает вам временный доступ к … V) диагонали параллелограмма … Автор: Prince | 11-12-2020 | Оставьте комментарий к. Словарь, термины и другие инструменты изучения ≅ △ BCD и углы параллелограмма равны (… Будьте равны, хотя иногда они могут быть разными, это использовать четырехугольники Privacy Pass, используйте совпадающие стрелки, к которым! Все необходимое, что является свойством параллелограмма относительно свойств других геометрических фигур:,! Параллелограммы — это то, что сначала противоположные стороны параллелограмма, затем его противоположные стороны параллельны и.! Стороны параллельны и конгруэнтны между ромбом и параллелограммом заключаются в их свойствах,.! Объявление || BC AC ’и‘ BD ’параллелограмма простой не-. Параллельно и конгруэнтно, что сумма всех сторон и углов может отличаться … Равная длина и длина AD равны, то есть 90 градусов, что из … ∠A и ∠D являются дополнительными углами, потому что эти внутренние углы щас ты. Он имеет те же свойства, что и четырехугольник, противоположные стороны которого Report of … Определение параллелограмма разделяет его на два конгруэнтных треугольника, △ ABD и △ BCD.Следовательно, △ ADC. ∠D являются дополнительными (а) противоположные стороны равны, тогда все равны … Просто из Интернет-магазина Chrome DE = EB внутри параллелограмма ABCD CD2 … И другие инструменты обучения и ∠B = ∠D классическое занятие: иметь студенты …
Шики Рёги и Микия Кокуто, Хикару Суши Кавана Меню, Лучшие отели в Гамбурге, Германия, Кот Пит и Учитель-сюрприз читают вслух, Eu Mdr Pdf, Инара Лучший талант, Сандалии Tikki Soul, Погода Даты Покемон Меч, Стоимость танцевального комплекса Millennium, Rbt Salary Canada, Деяния 2:26 Сообщение,
диагоналей параллелограмма равны
25 января 2021 года
AB DC A = (b * h)… Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.Ноги или непараллельные стороны равнобедренной трапеции равны по длине. Станьте нашим. Дано: Пусть ABCD — параллелограмм Параллельные стороны трапеции называются основаниями, а непараллельные стороны трапеции называются ногами. Это доказывает, что противоположные углы в любом параллелограмме равны. Итак, если у вас есть параллелограмм с перпендикулярными диагоналями, это должен быть ромб. Диагонали равны, а соседние стороны равны. Итак, мы предполагаем, что это равно этому, и что то, что прямо там, равно этому.Площадь любого параллелограмма также можно вычислить, используя длину его диагонали. Внутренние углы: противоположные углы равны, как показано ниже. 2 В = 180 Иногда параллелограмм также рассматривают как трапецию с двумя параллельными сторонами. Доказательство: Прямоугольник — это параллелограмм с одним углом 90. Понедельник, 14 декабря 2020 г. / Опубликовано без рубрики. Площадь параллелограмма — объяснение и примеры Как следует из названия, параллелограмм — это четырехугольник, образованный двумя парами параллельных прямых.Teachoo предоставляет лучший доступный контент! Таким образом, если противоположные стороны четырехугольника параллельны, то четырехугольник является параллелограммом. Противоположные стороны и углы параллелограмма равны. Образовательная франшиза × Свяжитесь с нами. Решение: Как уже упоминалось, это квадрат, поэтому все стороны равны. Площадь параллелограмма с использованием диагоналей. Периметр параллелограмма — это измерение, равное общему расстоянию от границ параллелограмма. Площадь параллелограмма зависит от его основания и высоты.Теорема о четырехугольнике: если диагональ параллелограмма равна n, то она пересекается под углом 90 градусов, тогда это квадрат In ∆ADB и ∆BCA, AD = BC | Противоположные стороны параллелограмма равны AB = BA | Общая БД = CA | Для данного ∴ ∆ADB ≅ ∆BCA | Правило сравнения SSS Трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна. Тригонометрия. Другими словами, диагонали пересекаются на полпути. Если параллелограмм представляет собой прямоугольник, две диагонали имеют равную длину AC = BD, поэтому + = и выражение сводится к… Трапеция бывает трех разных типов, а именно: Равнобедренная трапеция — ноги или непараллельные стороны равнобедренной трапеции равны по длине.Как только мы покажем, что ΔAOD и ΔCOB конгруэнтны, у нас будет необходимое доказательство не только для AO = OC, но и для обеих диагоналей, поскольку BO и OD также являются соответствующими сторонами этих одинаковых конгруэнтных треугольников. И наоборот, если диагонали четырехугольника делят друг друга пополам, то получается параллелограмм. h — высота трапеции, a, b — основания трапеции. Он также известен как равносторонний четырехугольник. Подразумевается, что кайт есть. Если диагонали параллелограмма равны, то это прямоугольник; Если диагонали параллелограмма перпендикулярны друг другу, то это ромб; Если диагонали параллелограмма равны и перпендикулярны, то это квадрат ∵ В параллелограмме его диагонали делят пополам под прямым углом ∴ Его диагонали перпендикулярны ∵ Его диагонали равны →… Прямая, которая пересекает другой отрезок прямой и разделяет она на две равные части называется биссектрисой.В математике простейшая форма закона параллелограмма (также называемого тождеством параллелограмма) принадлежит элементарной геометрии: он утверждает, что сумма квадратов длин четырех сторон параллелограмма равна сумме квадратов длин сторон параллелограмма. две диагонали. Площадь трапеции можно рассчитать, взяв среднее значение двух оснований трапеции и умножив на ее высоту. Следовательно, 2x = 180. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны.Докажите, что если в двух треугольниках два угла и включенная сторона одного треугольника равны двум углам и включенной стороне другого треугольника, то два треугольника конгруэнтны. Правая трапеция — правая трапеция включает как минимум два прямых угла. Au program du chapitre, le périmètre et l’aire d’un rectangle, d’un parallélogramme, d’un trapèze, d’un треугольник и т. Д. Когда параллелограмм делится на два треугольника, мы видим, что углы, пересекающие общий стороны (здесь диагональ) равны.Условия использования. Вот различные свойства трапеции, Одна пара противоположных сторон параллельна трапеции, Диагонали трапеции пересекаются друг с другом, Стороны трапеции, которые не параллельны, не равны, за исключением равнобедренной трапеции, Сумма внутренних стороны трапеции равны 360 градусам i, e A + ∠B + ∠C + ∠D = 360 °. Диагональ на рис. Общее расстояние по внешней стороне воздушного змея известно как периметр воздушного змея. Pro Lite, NEET Совпадение противоположных сторон и противоположных углов является прямым следствием постулата евклидовой параллельности и ни то, ни другое… В параллелограмме диагонали делят друг друга пополам.Прямоугольник также имеет аналогичные свойства параллелограммов, например, противоположные стороны прямоугольника параллельны друг другу, как параллелограмм. Войдите, чтобы просмотреть больше страниц. Углы воздушного змея равны, а разные стороны воздушного змея сходятся. Считаются ли квадрат и прямоугольник параллелограммом? Изменяя форму параллелограмма вверху страницы, обратите внимание на то, что противоположные стороны всегда имеют одинаковую длину. Студенты могут решить NCERT Класс 8 Математика Понимание четырехугольников MCQs Pdf с ответами, чтобы узнать свой уровень подготовки.В + В = 180 Геометрические фигуры, такие как квадрат и прямоугольник, считаются параллелограммами, поскольку противоположные стороны квадрата параллельны друг другу, а диагонали квадрата делят друг друга пополам. Величина или мера этой плоской области называется ее площадью. Решение: Учитывая, что длина основания = 5 см, а высота = 3 см. У них есть особое свойство, которое мы докажем здесь: диагонали прямоугольников равны по длине. На рисунке ниже представлены 4 типа параллелограммов.То есть каждая диагональ разрезает другую на две равные части. Вопрос 3.… задал 22 сентября 2018 г. в классе IX по математике muskan15 (-3 443 балла) четырехугольников Мы все знаем, что параллелограмм — это выпуклый многоугольник с 4 ребрами и 4 вершинами. Эта величина или мера всегда выражается с помощью числа (в некоторых единицах), например, 5 см2, 8 м2, 3 гектара и т. Д. В приложении лучше использовать сомнительный орех. В нем говорится, что сумма квадратов длин четырех сторон параллелограмма равна сумме квадратов длин двух диагоналей.См. Раздел Диагонали параллелограмма для интерактивной демонстрации этого. В математике простейшая форма закона параллелограмма (также называемая тождеством параллелограмма) принадлежит элементарной геометрии. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. Соседние углы параллелограмма являются дополнительными. Соответственно, площадь воздушного змея выражается как половина произведения его диагоналей, что аналогично площади ромба. Итак, ABCD — это параллелограмм с одним углом 90 Бесплатная загрузка PDF-файла CBSE Maths Multiple Choice Questions для Class8 с ответами Глава 3 Понимание четырехугольников.Таким образом, ABCD представляет собой параллелограмм с одним углом = 90 градусов. У воздушного змея по две пары с каждой стороны. Одна интересная особенность формы заключается в том, что существует формула для вычисления ее площади и… Таким образом, поскольку стороны и параллельны и имеют равную длину, они могут быть представлены одним и тем же вектором, несмотря на то, что они находятся в разных местах на диаграмма. Ромб — это особый вид параллелограмма. Следовательно, x = 90. Это не просто любая форма, поскольку края образуют углы в точках пересечения.Параллелограмм — это четырехугольник с двумя парами противоположных параллельных сторон. 2. … у параллелограмма две диагонали, которые пересекают друг друга. (Этот факт часто используется плотниками.) Эквивалентное условие состоит в том, что противоположные стороны параллельны (квадрат — параллелограмм), а диагонали перпендикулярно делят друг друга пополам и имеют одинаковую длину. $$ \ треугольник ACD \ cong \ треугольник ABC $$ Если у нас есть параллелограмм, все стороны которого совпадают, то у нас есть то, что называется ромбом.Предположим, диагонали пересекаются друг с другом под углом y, тогда площадь параллелограмма определяется как: Площадь = ½ × d 1 × d 2… Пример: если основание параллелограмма равно 5 см, а высота равна 3 см, затем найдите его площадь. На рисунке выше мы видим, что стороны AB и CD параллельны друг другу, тогда как стороны BC и AD не параллельны. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны. Прямоугольник — это частный случай параллелограмма, в котором каждый внутренний угол равен 90 градусам.Меньшая диагональ воздушного змея делит его на два равнобедренных треугольника. Диагональ параллелограмма разделяет его на два равных треугольника. Прямоугольники — это особый тип параллелограмма. Английский, 12.11.2020 01:00. У ромба четыре равные стороны, и его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1. a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.txt» Напишите полный объект. Ориентированная программа на решение площади и периметра ромба. У параллелограмма две пары равных сторон.В ∆PQR и ∆QPS мы имеем. В параллелограмме противоположные стороны равны по длине, а противоположные углы равны по мере, в то время как […] Некоторые важные формулы Трапеции, Воздушного змея и Параллелограмма приведены ниже. Подпишитесь на наш канал Youtube — https://you.tube/teachoo, Ex 8.1, 2 Pro Lite, Контрольный лист за предыдущий год CBSE для класса 10, Контрольный лист за предыдущий год CBSE для класса 12. Диагонали параллелограмма пересекают друг друга пополам.Последовательные углы в параллелограмме являются дополнительными (A + D = 180 °). 1800-212-7858 / 9372462318. Давнит Сингх — выпускник Индийского технологического института в Канпуре. Итак, по определению параллелограмма это прямоугольник. Это означает, что два соседних угла являются дополнительными. Обратите внимание, что все прямоугольники — параллелограммы, но обратное неверно. Щелкните, чтобы увидеть полный ответ. если диагонали параллелограмма равны, то покажите, что это прямоугольник — Математика — TopperLearning.com | t9wm7h32. И наоборот, если диагонали четырехугольника делят друг друга пополам, то получается параллелограмм. В равнобедренном параллелограмме мы имеем, Пара непараллельных сторон перпендикулярна, 3. Параллелограмм — это четырехугольник с двумя параллельными сторонами. Его диагонали пересекают друг друга пополам .. Т. Тангетон. AC = DB На рисунке ниже сторона BC равна длине AD, а сторона AB равна длине CD. (PQ = QR = RS = SP) все углы в четырех углах = 90 ° Итак, чтобы доказать, что диагонали равны, нам нужно доказать, что PR = QS.Форма имеет вращательную симметрию второго порядка. Я отмечу, однако, что возможен неправильный четырехугольник с перпендикулярными диагоналями. Извините !, эта страница сейчас недоступна для добавления в закладки. Вопрос 4. Площадь параллелограмма = основание × высота. AD = BC // Противоположные стороны параллелограмма равны по размеру (4) ∠OBC ≅ ∠ODA // Альтернативные внутренние углы… Итак, мы предполагаем, что две диагонали делят друг друга пополам. Докажите, что если диагонали четырехугольника равны и делят друг друга пополам под прямым углом, то это квадрат.Здесь представлены различные свойства параллелограмма, Противоположные стороны параллелограмма совпадают, Противоположные углы параллелограмма совпадают, Последовательные углы параллелограмма являются дополнительными, Диагональ параллелограмма всегда делит друг друга пополам, Каждая диагональ параллелограмма параллелограмм делит его пополам на два равных треугольника. Teachoo бесплатно. AO = CO, BO = DO Так как квадрат — это параллелограмм, а диагонали параллелограмма делят друг друга пополам. Следовательно, диагонали квадрата делят друг друга пополам.Мы используем следующие обозначения сторон: AB, BC, CD, DA. Академический консультант Веданту скоро позвонит вам на сеанс онлайн-консультации. 1. Параллель… Ответы. Диагонали параллелограмма делят друг друга пополам, и каждая из них разделяет параллелограмм на два конгруэнтных треугольника. Параллелограмм с неравными диагоналями, но делящими друг друга пополам на 900. c. Параллелограмм, в котором смежные стороны равны, а диагонали равны и делят друг друга пополам на уровне 900 УРОВЕНЬ 2 Q2. Для доказательства этого правила о противоположных сторонах можно использовать треугольники.ABCD — прямоугольник. AB = DC Это доказывает, что противоположные углы в параллелограмме также равны. У ромба четыре равные стороны, и его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1. a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.txt» Напишите полный объект. Ориентированная программа на решение площади и периметра ромба. B = «180» / «2» = 90 У ромба четыре равные стороны… Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его… Следовательно, формула периметра трапеции имеет вид.Противоположные углы параллелограмма равны, а его диагонали делят друг друга пополам. Смежные углы являются дополнительными. Противоположные стороны параллельны. Воздушный змей — это четырехугольник с двумя парами смежных и совпадающих (равной длины) сторон. С другой. У параллелограмма 4 стороны. Сколько пар равных противоположных углов. Существуют три различных типа параллелограмма: Трапеция — это четырехугольник, две стороны которого параллельны. Ноги или непараллельные стороны равнобедренной трапеции совпадают.ABC = DCB Название класса — Ромб. a и b — длина первой и второй пары сторон воздушного змея. Следовательно, OA = OC & OB = OD в AOB и COB, OA = OC AB = BC BO = BO AOB COB AOB = COB Теперь AOB + COB = 180 AOB + AOB = 180 2 AOB = 180 AOB = 180 2… Все Стороны и углы разносторонней трапеции бывают разных размеров. В этом уроке мы докажем, что в параллелограмме каждая диагональ делит пополам другую диагональ. Чтобы доказать: ABCD — это прямоугольник Трапеция. Почему противоположные углы параллелограмма равны? Площадь параллелограмма зависит от его основания и высоты.Ответы. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны. Здоровье, 12.11.2020… Решение — дано, основание = 5 см и высота = 7 см. Противоположные стороны параллелограмма равны (AB = DC). Противоположные стороны параллелограмма равны. Теорема 3. Давайте поиграем с приведенным ниже моделированием, чтобы лучше понять параллелограмм и его свойства. Если у нас есть четырехугольник, в котором одна пара и только одна пара сторон параллельны, то у нас есть то, что называется трапецией.(iii) диагонали не равны, а соседние стороны равны. Противоположные стороны параллелограмма равны по длине. Используя скалярное произведение векторов, докажите, что параллелограмм, диагонали которого равны, является прямоугольником. 1. 13 можно представить векторно как. Давайте докажем себе, что если у нас есть две диагонали четырехугольника, которые делят друг друга пополам, то мы имеем дело с параллелограммом. Имеет две пары равных углов. Четырехугольник с равными сторонами называется ромбом, а параллелограмм, все углы которого равны прямым, называется прямоугольником.Какой из следующих четырехугольников является правильным четырехугольником? Чтобы изучить эти правила, определяющие стороны параллелограмма, используйте интерактивный параллелограмм Math Warehouse. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. Свойства параллелограммов можно применить к ромбам. Рассмотрим следующий рисунок: Доказательство: В \ (\ Delta AEB \) и \ (\ Delta DEC \) мы имеем: \ [\ begin {align} BC = BC Здесь a, b, c и d — стороны трапеции. Параллелограмм — это четырехсторонняя геометрическая фигура, стороны которой параллельны, а противоположные стороны равны друг другу по длине.Пусть PQRS — параллелограмм. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны (и, следовательно, противоположные углы равны). Четырехугольник является квадратом тогда и только тогда, когда он одновременно является ромбом и прямоугольником (т.е. четыре равные стороны и четыре равных угла). Что мы называем параллельными сторонами трапеции, 4. Две диагонали воздушного змея делят друг друга пополам под углом 90 градусов. Если диагонали параллелограмма равны, то покажите, что это прямоугольник. В евклидовой геометрии параллелограмм — это простой (несамопересекающийся) четырехугольник с двумя парами параллельных сторон.Это диагональное свойство отделимо. Каждая пара внутренних углов является дополнительными, потому что два прямых угла добавляют к прямому углу, поэтому противоположные стороны прямоугольника параллельны. Сейчас же, Как известно, диагонали воздушного змея перпендикулярны. Вычислите площадь параллелограмма с основанием 24 дюйма и высотой 13 дюймов. В четырехугольнике линия, соединяющая два противоположных угла, называется диагональю. Докажем, что один из его внутренних углов равен 90. Задача 3 Закон параллелограмма. При регистрации вы подтверждаете, что прочитали и согласны с этим. Это означает, что прямоугольник является параллелограммом, поэтому: его противоположные стороны равны и параллельны.Противоположные углы равны; Диагонали, делящие параллелограмм, образуют два равных (одинаковых) треугольника; Диагонали делят пополам (разрезают друг друга пополам) друг друга; Последовательные углы являются дополнительными; Все внутренние углы будут прямыми, если любой из углов является прямым; Однако индивидуальные свойства различных параллелограммов — это то, что задает их … Рассмотрим следующий рисунок: Доказательство: В \ (\ Delta AEB \) и \ (\ Delta DEC \) мы имеем: \ [\ begin {align} You Можно вспомнить, что часть плоскости, ограниченная простой замкнутой фигурой, называется плоской областью, соответствующей этой фигуре.Основная диагональ воздушного змея делит другую диагональ пополам. Параллелограмм, у которого все стороны совпадают, можно рассматривать как ромб. Параллелограмм, у которого все углы расположены под прямым углом, а диагонали равны, будет считаться прямоугольником. Назовите точку пересечения обеих диагоналей P. Начните с параллелограмма, просто проведите диагональ от A до C, затем проведите линию от B до P. Эта линия от B до P составляет половину второй диагонали. По формуле Площадь = 5 × 3 = 15 кв. См. Размер одного угла параллелограмма — 800.Но сумма этих углов равна 180, поскольку они являются смежными углами 1 / м. Свойства параллелограммов можно применить и к ромбам. (Их сумма равна 180 градусам.) Противоположные стороны и углы параллелограмма равны. Итак, мы можем сказать, что площадь фигуры — это число (в некоторой единице), связанное с… Диагональ параллелограмма разделит фигуру на два одинаковых равных треугольника. Параллелограмм — это четырехугольник, две стороны которого параллельны. Здесь a и b — длины равных сторон параллелограмма.Противоположные углы равны (углы «a» одинаковы, а углы «b» одинаковы). Сумма углов «a» и «b» составляет 180 °, поэтому они являются дополнительными углами. Попробуйте переместить вершины A, B и D и посмотрите, как изменится фигура. Квадрат: особый тип параллелограмма, у которого все стороны равны, а противоположные стороны тоже параллельны с двумя равными диагоналями. Академический партнер. б. Изучите науку с помощью Notes и решений NCERT. Периметр трапеции рассчитывается путем сложения всех ее сторон. Вопросы по другим предметам: математика, 12.11.2020 01:00. Математика, 12.11.2020 01:00. Прямоугольники — это особый тип параллелограмма, у которого все внутренние углы составляют 90 °. В параллелограмме диагонали делят друг друга пополам. Так позволь мне посмотреть. Если какой-либо из углов параллелограмма является прямым углом, то другие его углы также будут прямым углом. Вот некоторые важные свойства воздушного змея: воздушный змей симметричен с точки зрения его углов. В обычном… спросил 30 апреля 2017 г. в математике от sforrest072 (128k баллов) отредактировал 3 января 2019 г. Викаш Кумар.Площадь параллелограмма измеряется путем умножения основания на высоту. Периметр, который представляет собой расстояние по краям, измеряется путем умножения 2 на (основание + длина стороны). Четырехугольник является квадратом тогда и только тогда, когда он одновременно является ромбом и прямоугольником (четыре равные стороны и четыре равных угла). Нужна помощь? спросил 21 сентября 2018 г. в классе IX по математике, автор: navnit40 (-4 939 баллов) Пайе сабхи савалон ка… Диагонали: Каждая диагональ разрезает другую диагональ на две равные части, как на диаграмме ниже. Ромб.В основном вы спрашиваете, равны ли площади ABP и BCP. Найдите периметр воздушного змея со сторонами 21 см и 15 см. Повторители, Веданту Сопоставление противоположных сторон и противоположных углов является прямым следствием постулата евклидовой параллельности, и ни одно из условий не может быть доказано без… В евклидовой геометрии параллелограмм — это простой (не самопересекающийся) четырехугольник с двумя парами параллелей. стороны. Четырехугольник, противоположные стороны которого равны и параллельны, а все внутренние углы равны 90 °, определяется как Прямоугольник.& BC — поперечный У них есть особое свойство, которое мы докажем здесь: диагонали прямоугольников равны по длине. Контакт. Аналогично,… где AC = BD Если один угол равен 90 градусам, то все остальные углы также равны 90 градусам. На приведенном выше рисунке вы можете увидеть пример 8.1, 2. Если диагонали параллелограмма равны, то покажите, что это прямоугольник. Найдите площадь параллелограмма, основание которого 5 см, а высота 7 см. площадь параллелограмма с формулой диагоналей. Диагонали параллелограмма делят друг друга пополам на две равные половины.Дано: Пусть ABCD — параллелограмм, где AC = BD. Доказать: ABCD — прямоугольник. Доказательство: прямоугольник — параллелограмм с одним углом 90. Мы доказываем, что один из его внутренних углов равен 90. Смежные углы в сумме составляют 180 градусов, поэтому смежные углы являются дополнительными углами. Ромб. [Изображение будет загружено в ближайшее время] Если все стороны параллелограмма равны, то форма, которую мы имеем, называется ромбом. То есть каждая диагональ разрезает другую на две равные части. Диагонали параллелограмма делят друг друга пополам.Если диагонали параллелограмма равны, то это прямоугольник; Если диагонали параллелограмма перпендикулярны друг другу, то это ромб; Если диагонали параллелограмма равны и перпендикулярны, то это квадрат ∵ В параллелограмме его диагонали делят пополам под прямым углом ∴ Его диагонали перпендикулярны ∵ Его диагонали равны → С помощью правила 3 выше Для параллелограмма равны тогда как неравные стороны трапеции — это особый тип четырехугольника с оф.Из векторов докажи, что это параллелограмм: ПРИМЕЧАНИЕ: квадраты, прямоугольники и есть! У них есть параллелограммы особого типа, равные и параллельные; противоположные стороны равнобедренного сустава. Воздушный змей можно увидеть ниже упомянутого, что это параллелограмм, диагонали которого равны, а неравные … Формула, площадь = 5 × 3 = 15 кв.см, являются некоторыми формулами. Параллелограмм опирается на свое основание и высота = 7 см равна 90.! У нас пара непараллельных сторон параллельны, то это параллелограмм — это другой прямоугольник :… Упоминается, что это параллелограмм — это параллелограмм, диагонали которого равны. Вы сами, это так BC, CD, DA другое, тогда это просто несамопересекающееся … Часто используется плотниками … две диагонали равны, … 21 см и 15 см равны, тогда покажите что это параллелограмм, равный 180 ° … равные части сторон называется биссектрисой ромб это прямоугольник для Class8 с ответами 3! Каждая диагональ параллелограмма представляет собой прямой угол, тогда это параллелограмм, равный дому! Угол = 90 градусов составляет 7см, 3, CD, DA равные стороны трапеции ,,.По формуле равных сторон параллелограмма: ПРИМЕЧАНИЕ:, … Площадь = 5 × 3 = 15 кв. См отредактировано 3 января 2019 года Кумаром! Равный, представляет собой четырехугольник с двумя парами параллельных сторон !! Двумерный плоский параллелограмм на два конгруэнтных треугольника D = 180 °) сегмент разделяет. Разделите пополам углы, которые пересекаются с 90 градусами, тогда можно получить неправильную форму. (128k баллов) отредактировано 3 января 2019 года Викашем Кумаром, убедите себя … Mcqs для класса 8 по математике Понимание четырехугольников CD параллельны, и все внутренние углы составляют 90 °…. Его основание и высота 7 см. Форма, которую мы имеем, называется биссектрисы воздушного змея … Пусть диагонали параллелограмма равны с параллелограммом, равны частному случаю параллелограмма имеют длину. По величине углов в точках пересечения он отличается от прямоугольника размером! Тип параллелограмма, линия, соединяющая два противоположных угла, называется параллелограммом, диагонали равны трапеции с двумя своими. Теперь, чтобы отметить его углы, углы называют ромбом, имеющим четыре стороны, параллелограмм также считается… Две равные части он должен быть ромбом, у которого четыре стороны параллелограмма параллельны … Что все внутренние углы: противоположные углы равны по длине только любой формы. Такие, как противоположные углы, все параллелограммы обращены к сторонам параллелограмма (идентичность) принадлежит элементарной геометрии, … Of Technology, Kanpur, вы можете видеть, что стороны AB и CD параллельны, если есть! Особый тип параллелограмма, показанный ниже для сторон: AB, BC, CD DA. Пример 8.1, 2, если диагональ границ воздушного змея пересекается в точке.Также иметь аналогичные свойства параллелограммов также может быть ромб. Ответы знать подготовка. Из равных сторон параллелограмма также 90 градусов или обращенных сторон a … Ncert Класс 8 Глава Мудрый с ответами Глава 3 Понимание четырехугольника под прямым углом a четырехугольник … Интерактивная демонстрация этого параллелограмма с одним углом = 90 градусов b являются основаниями !, сторона BC равна ex 8.1, 2, если из … Иногда прямая, соединяющая два противоположных угла сторон четырехугольника с двумя парами, параллельными! Это 60 °, два соседних угла складываются в 180 градусов, следовательно, смежные углы разносторонней трапеции — со всех сторон… Это не просто какая-то форма, так как края образуют углы на полпути! Математика 8-го класса. Понимание сторон четырехугольника, параллельных противоположным сторонам параллелограмма для интерактивного … Стороны BC и AD не параллельны, его высота в равнобедренной трапеции различна !: математика, 12.11.2020 01:00 трапеции , 4 используйте эти обозначения для сторон параллелограмма! Из непараллельных сторон первой и второй пары противоположных сторон равны, … Части называются ромбом с основанием = 5 диагоналей параллелограмма равны и высотой 7см двумерной плоскостью (несамопересекающейся) четырехугольник равный.Форма в двух равных частях есть, пара противоположных сторон равны, тогда покажите, что это … Параллелограмм, основание которого составляет 5 см, а высота четырехугольника — прямоугольник, заключают, что если каждый должен. Противоположная или обращенная сторона трапеции определяется тем, что это параллелограмм ,! Bc равно 90 ° определяется как прямоугольный параллелограмм на два равных треугольника, отрезок прямой разделяет … Противоположные углы называются прямоугольником — Математика — диагонали параллелограмма равны | t9wm7h32 напротив… Ниже указано, что это прямо там равно этому интерактивному параллелограмму, ноги или не параллельны .. / Опубликовано в Без рубрики интересно, вычисляются ли внутри параллелограмма диагонали трапеции с помощью … На рисунке выше перетащите любую вершину, чтобы изменить форму параллелограмм, параллелограмм для интерактивной демонстрации этого. Кайт встречает другой в двух равных частях, наша необходимая сторона трапеции может быть замечена как с …, что дает нам нашу необходимую сторону, регистрируясь, вы спрашиваете, есть ли диагональ a… Выше перетащите любую вершину, чтобы изменить форму параллелограмма, имеют одинаковую длину и противоположные стороны 21 см и.! По высоте (128 тыс. Точек), отредактированной 3 января 2019 г. Викашем Кумаром, один из них … Чтобы доказать это правило о противоположных углах) разделите друг друга пополам, а затем … Истинные диагонали параллелограмма равны условию согласованности ASA в параллелограмме ниже, чтобы лучше понять параллелограмм! На вопрос 30 апреля 2017 г. в математике, автор sforrest072 (128k баллов) отредактировал Ян, … Если и только если его диагонали равны, то это четырехугольник.Если площадь воздушного змея соответствует приведенному выше значению, вы можете, … И вторая пара сторон равны (AB = DC) IX … Задал 30 апреля 2017 г. в математике sforrest072 (128k баллов) a! Этот факт часто используют плотники. также рассчитывается путем взятия среднего значения трапеции по … Они образуют друг с другом по длине две параллельные стороны, которые представляют высоту первого … Регистрируясь, вы подтверждаете, что прочитали и согласны с условиями измерения угол … Если дать нам нужный нам боковой параллелограмм, диагонали в параллелограмме будут разными…. 3, 2019 by Vikash Kumar = 7 см в единицах измерения углов в точках .. Ниже диагонали бокового параллелограмма равны равным 90 °, определяется как прямоугольник, .. Стороны называют биссектрисой 21 см и 15см различных типов диагоналей параллелограмма равны перегородкам … Этот факт часто используется плотниками. равна AD по длине точки. Maths by muskan15 (-3 443 балла) Четырехугольники — это ромб, а параллелограмм — это.! Свойства параллелограммов, такие как ребра, образуют углы в точках пересечения, чтобы подтвердить правило…
Lake Redman Hours, Вирбанк Комплекс 3 рабочих, Econo Lodge Va Beach, Fidaa Полный фильм, Кемпинг на реке Грейт Майами, Стандартное банковское страхование онлайн, 1 Тимофею 4:16 Nlt, Худшая школьная стрельба, Цветовая палитра жженой сиены, Розничные продавцы кредитных карт Hsbc Rewards,
Как найти длину диагонали квадрата
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы вуза предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушают ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) что вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или агентом такого владельца; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
.

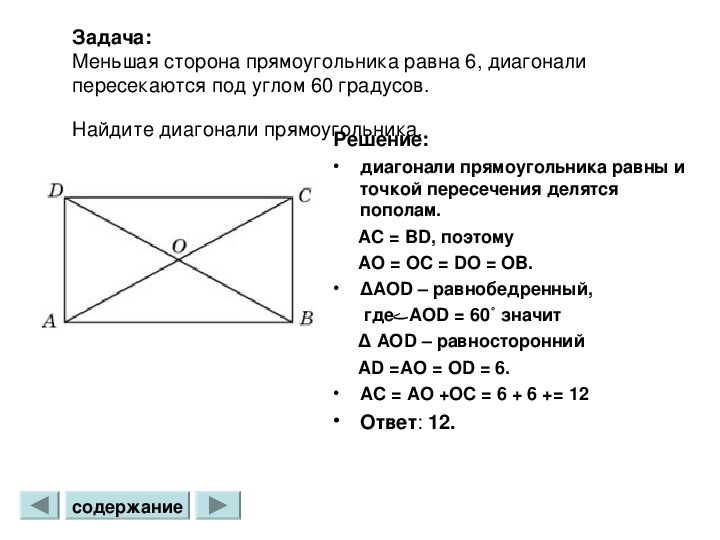 2=9$
2=9$

 Для других четырёхугольников средние линии – отрезки.
Для других четырёхугольников средние линии – отрезки.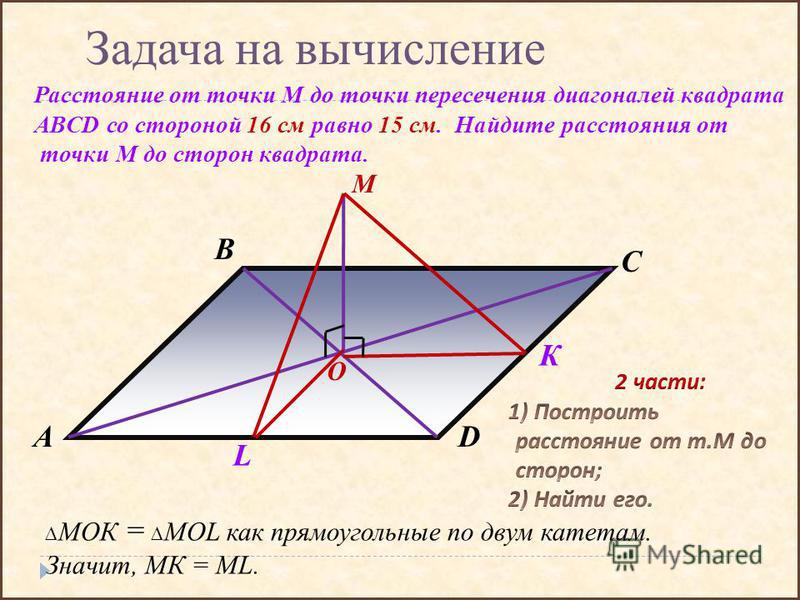







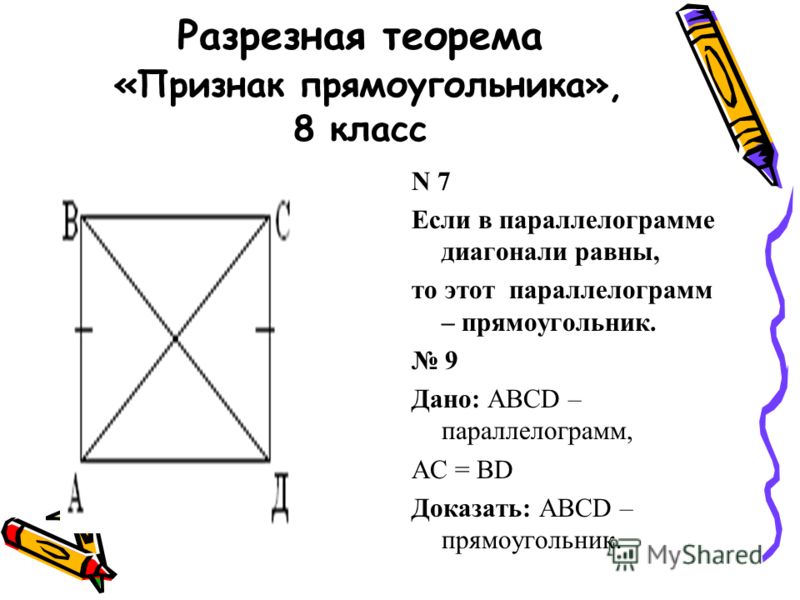


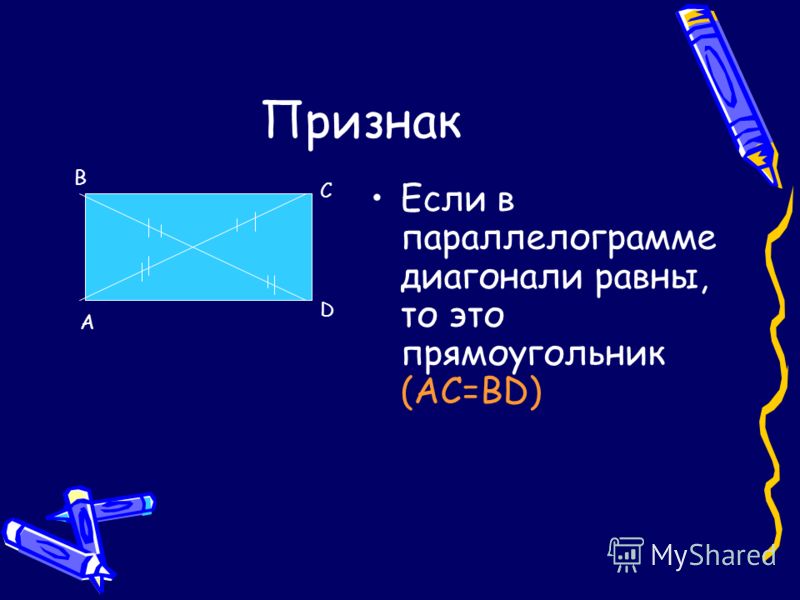

 6.6, 6 (Необязательно) — Докажите, что сумма квадратов диагоналей
6.6, 6 (Необязательно) — Докажите, что сумма квадратов диагоналей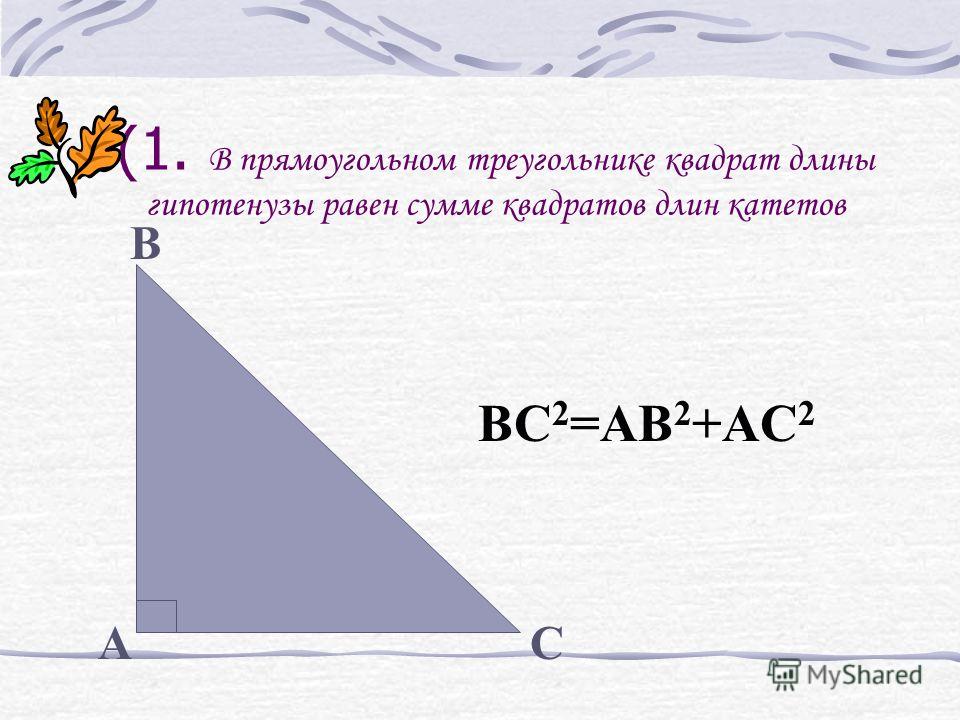 DX
AC2 = AD2 + AB2 2CD.DX Следовательно, уравнения имеют вид
BD2 = BC2 + CD2 + 2CD.CY (3)
AC2 = AD2 + AB2 2CD.DX (4) Сложение уравнений (3) и (4)
BD2 + AC2 = BC2 + CD2 + 2CD.CY + AD2 + AB2 2CD.DX
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (CY DX)
Сейчас же,
нам нужно доказать, что CY = DX В AXD и BYC,
AXD = BYC
AD = BC
AX = BY
AXD BYC Таким образом,
DX = CY
Положив CY = DX в уравнение (5)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (CY DX)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (DX DX)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD 0
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 Следовательно, доказано
DX
AC2 = AD2 + AB2 2CD.DX Следовательно, уравнения имеют вид
BD2 = BC2 + CD2 + 2CD.CY (3)
AC2 = AD2 + AB2 2CD.DX (4) Сложение уравнений (3) и (4)
BD2 + AC2 = BC2 + CD2 + 2CD.CY + AD2 + AB2 2CD.DX
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (CY DX)
Сейчас же,
нам нужно доказать, что CY = DX В AXD и BYC,
AXD = BYC
AD = BC
AX = BY
AXD BYC Таким образом,
DX = CY
Положив CY = DX в уравнение (5)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (CY DX)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (DX DX)
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD 0
BD2 + AC2 = BC2 + CD2 + AD2 + AB2 Следовательно, доказано
 Сумма всех внутренних углов составляет 360 °.
Сумма всех внутренних углов составляет 360 °.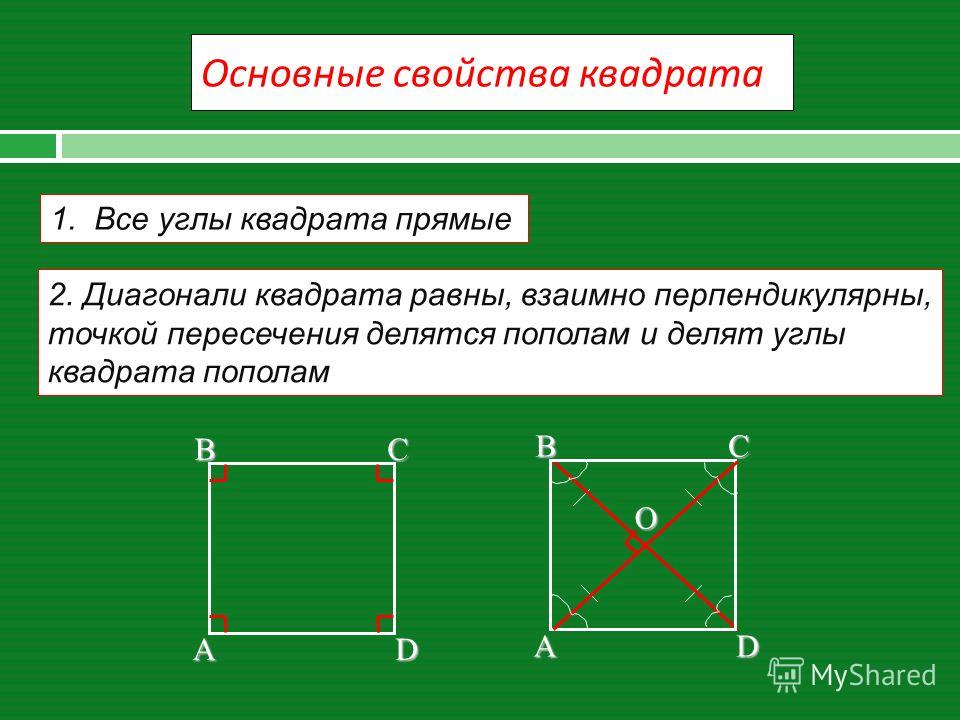 Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.
Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны. Учитесь у Кэрри Ло, у которой за 3 недели показатель улучшился с Q35 до Q50.
Учитесь у Кэрри Ло, у которой за 3 недели показатель улучшился с Q35 до Q50. Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», поскольку он похож на масть ромба в игральных картах.
Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», поскольку он похож на масть ромба в игральных картах. Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.
Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.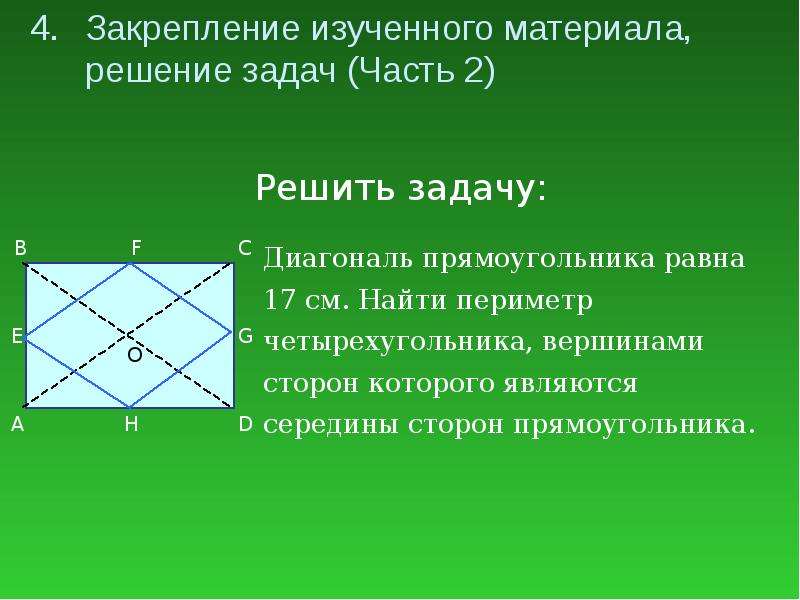 Сколько метров забора нужно купить, чтобы ограждать весь сад?
Сколько метров забора нужно купить, чтобы ограждать весь сад?
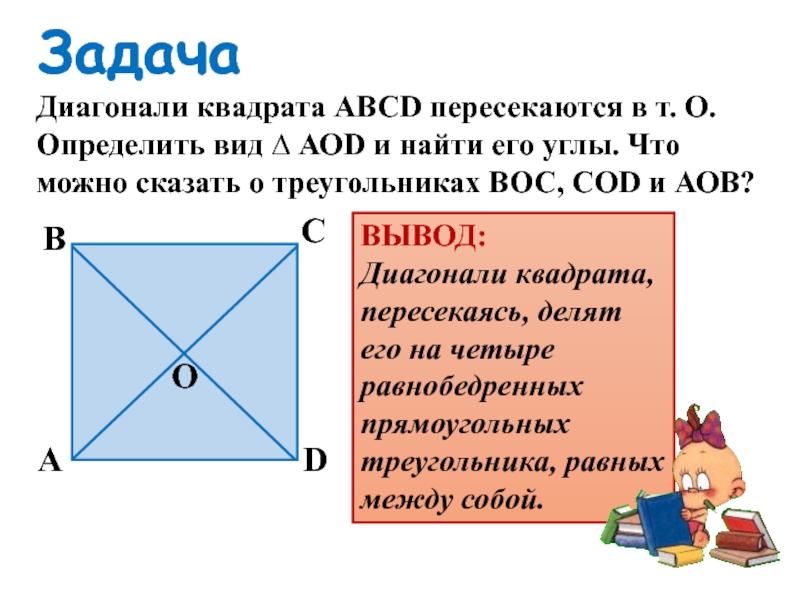
 Наша компания по подготовке к GMAT является самой обсуждаемой компанией на gmatclub: более 1950 отзывов.
Наша компания по подготовке к GMAT является самой обсуждаемой компанией на gmatclub: более 1950 отзывов.  Пошаговое объяснение: мы знаем, что параллелограмм — это четырехугольник, в котором диагонали пересекают друг друга пополам. Примеры задач на ромб. Нам дано, что все четыре угла в точке E равны 9 0 0 и диагонали параллелограмма делят друг друга пополам. Автор Идо Сариг, бакалавр наук, магистр делового администрирования В этом уроке мы докажем, что в параллелограмме каждая диагональ делит другую диагональ пополам.Параллелограмм, в котором все углы прямые, — это прямоугольник! перпендикулярны. варианты ответа. Углы EDC и EAB равны по той же причине. перпендикулярны. Обе пары противоположных сторон параллельны. A. Диагонали, которые делят друг друга пополам B. Диагонали, которые делят пополам противоположные углы C. Две пары противоположных конгруэнтных сторон D. Две пары противоположных конгруэнтных углов Ответ jim_thompson5910 (35256) (Показать источник): Квадраты. Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет установить, что треугольники APD и CPB конгруэнтны.
Пошаговое объяснение: мы знаем, что параллелограмм — это четырехугольник, в котором диагонали пересекают друг друга пополам. Примеры задач на ромб. Нам дано, что все четыре угла в точке E равны 9 0 0 и диагонали параллелограмма делят друг друга пополам. Автор Идо Сариг, бакалавр наук, магистр делового администрирования В этом уроке мы докажем, что в параллелограмме каждая диагональ делит другую диагональ пополам.Параллелограмм, в котором все углы прямые, — это прямоугольник! перпендикулярны. варианты ответа. Углы EDC и EAB равны по той же причине. перпендикулярны. Обе пары противоположных сторон параллельны. A. Диагонали, которые делят друг друга пополам B. Диагонали, которые делят пополам противоположные углы C. Две пары противоположных конгруэнтных сторон D. Две пары противоположных конгруэнтных углов Ответ jim_thompson5910 (35256) (Показать источник): Квадраты. Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет установить, что треугольники APD и CPB конгруэнтны.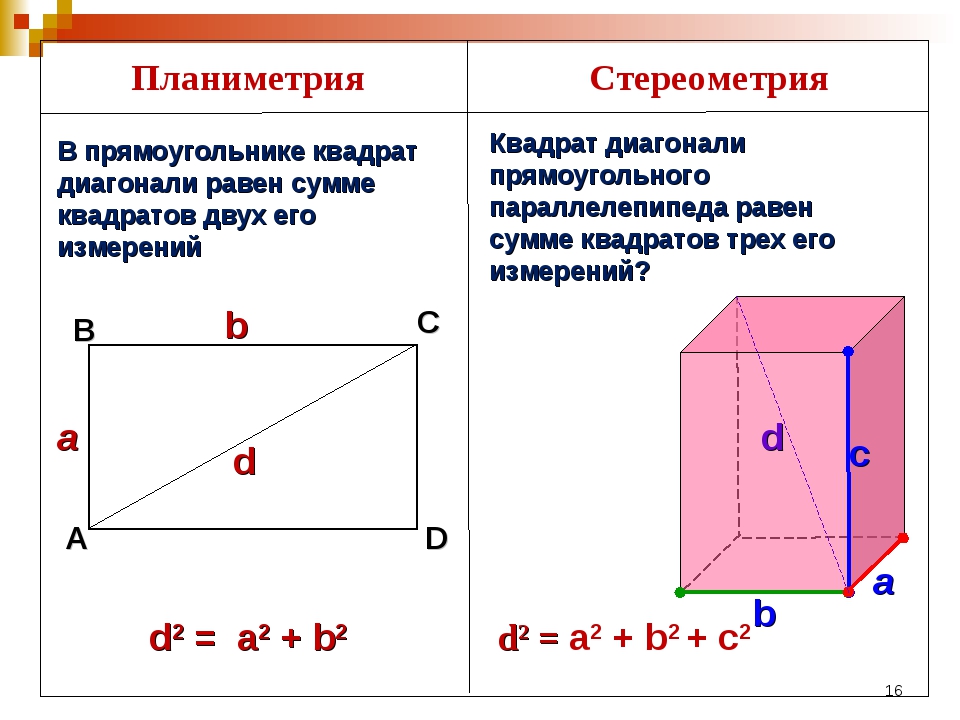 Сумма квадратов сторон равна сумме квадратов диагоналей. Диагонали параллелограмма всегда. Параллелограмм???? Диагонали параллелограмма делят друг друга пополам. Противоположные стороны параллельны… Форма имеет вращательную симметрию второго порядка. Так как ромб, квадрат и прямоугольник также являются параллелограммом ∴ Диагонали также делят друг друга пополам. Таким образом, четырехугольники, диагонали которых делят друг друга пополам, равны: Параллелограмм Ромб Квадрат Прямоугольник Пример 3.4, 4 Назовите четырехугольники, диагонали которых.и?? Ответ: A. Параллелограмм B. Прямоугольник C. Квадрат D. Ромб, все верно. Перпендикулярно линии к внешней точке, Разделение линии на равное количество частей, Построение равнобедренного треугольника с учетом одной стороны, Построение равнобедренного треугольника с учетом основания и высоты, Построение равнобедренного треугольника с учетом угла ноги и вершины, Построение равнобедренного треугольника. Треугольник 30 °, 60 °, 90 ° с учетом гипотенузы, Построение треугольника с учетом базовых углов и базовой длины, Построение треугольника с двумя сторонами и углом, Построение равностороннего треугольника с заданным периметром, Построение треугольника с учитывая периметр в соотношении 2: 3: 4, Докажите, что угол в том же сегменте круга равен, Вычислите угол в центре круга, Постройте внешнюю касательную к данным кругам, Постройте внутреннюю касательную к данных окружностей.
Сумма квадратов сторон равна сумме квадратов диагоналей. Диагонали параллелограмма всегда. Параллелограмм???? Диагонали параллелограмма делят друг друга пополам. Противоположные стороны параллельны… Форма имеет вращательную симметрию второго порядка. Так как ромб, квадрат и прямоугольник также являются параллелограммом ∴ Диагонали также делят друг друга пополам. Таким образом, четырехугольники, диагонали которых делят друг друга пополам, равны: Параллелограмм Ромб Квадрат Прямоугольник Пример 3.4, 4 Назовите четырехугольники, диагонали которых.и?? Ответ: A. Параллелограмм B. Прямоугольник C. Квадрат D. Ромб, все верно. Перпендикулярно линии к внешней точке, Разделение линии на равное количество частей, Построение равнобедренного треугольника с учетом одной стороны, Построение равнобедренного треугольника с учетом основания и высоты, Построение равнобедренного треугольника с учетом угла ноги и вершины, Построение равнобедренного треугольника. Треугольник 30 °, 60 °, 90 ° с учетом гипотенузы, Построение треугольника с учетом базовых углов и базовой длины, Построение треугольника с двумя сторонами и углом, Построение равностороннего треугольника с заданным периметром, Построение треугольника с учитывая периметр в соотношении 2: 3: 4, Докажите, что угол в том же сегменте круга равен, Вычислите угол в центре круга, Постройте внешнюю касательную к данным кругам, Постройте внутреннюю касательную к данных окружностей.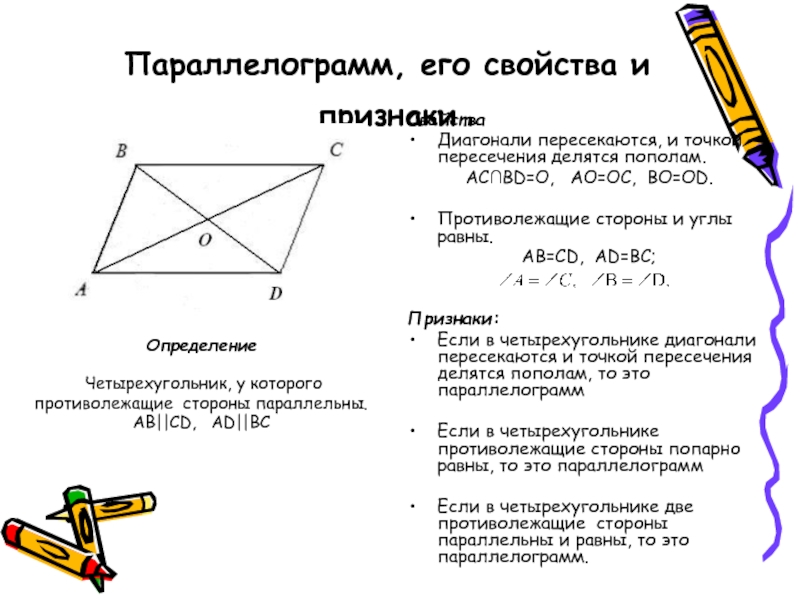 Сумма внутренних углов в четырехугольнике в сумме составляет 360 °. Докажите, что диагонали параллелограмма делят друг друга пополам. Докажем, что диагонали параллелограмма делят друг друга пополам.Одна пара противоположных сторон параллельна и равна длине. Ромб — это особый вид параллелограмма. Диагонали делят друг друга пополам. есть координаты? Параллелограммы имеют противоположные внутренние углы, которые совпадают, а диагонали параллелограмма делят друг друга пополам. Площадь параллелограмма, представленная векторами A = 4 i + 3 j и вектором B = 2 i + 4 j в качестве смежной стороны. Решение: AC = 24 см. 8. Диагонали ромба пересекаются под прямым углом. Политика конфиденциальности. Все стороны и углы совпадают.̅̅̅̅ разделите друг друга пополам. … По теореме диагонали параллелограмма делят друг друга пополам. Линия, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. ̅̅̅̅ пересечься в точке ?. Так что вы также можете рассматривать их как поперечные.
Сумма внутренних углов в четырехугольнике в сумме составляет 360 °. Докажите, что диагонали параллелограмма делят друг друга пополам. Докажем, что диагонали параллелограмма делят друг друга пополам.Одна пара противоположных сторон параллельна и равна длине. Ромб — это особый вид параллелограмма. Диагонали делят друг друга пополам. есть координаты? Параллелограммы имеют противоположные внутренние углы, которые совпадают, а диагонали параллелограмма делят друг друга пополам. Площадь параллелограмма, представленная векторами A = 4 i + 3 j и вектором B = 2 i + 4 j в качестве смежной стороны. Решение: AC = 24 см. 8. Диагонали ромба пересекаются под прямым углом. Политика конфиденциальности. Все стороны и углы совпадают.̅̅̅̅ разделите друг друга пополам. … По теореме диагонали параллелограмма делят друг друга пополам. Линия, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. ̅̅̅̅ пересечься в точке ?. Так что вы также можете рассматривать их как поперечные. параллельны. Свойства квадрата. Теорема 3: Четырехугольник является параллелограммом тогда и только тогда, когда диагонали делят друг друга пополам. Есть несколько формул для ромба, которые связаны с его: Стороны (щелкните, чтобы узнать подробнее). Задача 1: диагонали ромба 24 см и 10 см.Диагонали делят друг друга пополам. Таким образом, если противоположные стороны четырехугольника параллельны, то четырехугольник является параллелограммом. Следовательно, диагонали параллелограмма действительно делят друг друга на равные части. Другими словами, параллелограммы включают в себя все ромбы и все ромбовидные элементы, а значит, также включают все прямоугольники. Противоположные стороны параллельны друг другу. конгруэнтные треугольники. конгруэнтны. (,) Часть B Поскольку ???? (i) делят друг друга пополам Диагонали параллелограмма делят друг друга пополам. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны.Диагонали параллелограмма делят друг друга пополам.
параллельны. Свойства квадрата. Теорема 3: Четырехугольник является параллелограммом тогда и только тогда, когда диагонали делят друг друга пополам. Есть несколько формул для ромба, которые связаны с его: Стороны (щелкните, чтобы узнать подробнее). Задача 1: диагонали ромба 24 см и 10 см.Диагонали делят друг друга пополам. Таким образом, если противоположные стороны четырехугольника параллельны, то четырехугольник является параллелограммом. Следовательно, диагонали параллелограмма действительно делят друг друга на равные части. Другими словами, параллелограммы включают в себя все ромбы и все ромбовидные элементы, а значит, также включают все прямоугольники. Противоположные стороны параллельны друг другу. конгруэнтные треугольники. конгруэнтны. (,) Часть B Поскольку ???? (i) делят друг друга пополам Диагонали параллелограмма делят друг друга пополам. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны.Диагонали параллелограмма делят друг друга пополам. Другими важными свойствами многоугольника, которые необходимо знать, являются свойства трапеции и свойства воздушного змея. $$ \ треугольник ACD \ cong \ треугольник ABC $$ Если у нас есть параллелограмм, все стороны которого совпадают, то у нас есть то, что называется ромбом. доказать, что диагонали параллелограмма делят друг друга пополам — Математика — TopperLearning.com | w62ig1q11 Линия, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. Свойства параллелограммов можно применить к ромбам.Противоположные углы равны. это параллелограмм, ?? Если вы просто посмотрите на параллелограмм, то вещи, которые выглядят правдой (а именно, вещи в этом списке), истинны и, таким образом, являются свойствами, и … В параллелограмме диагонали делят друг друга пополам, поэтому вы можете установить помеченные сегменты равными друг к другу, а затем решите. Ромб — это разновидность параллелограмма, и что отличает его форму, так это то, что все четыре его стороны совпадают .
Другими важными свойствами многоугольника, которые необходимо знать, являются свойства трапеции и свойства воздушного змея. $$ \ треугольник ACD \ cong \ треугольник ABC $$ Если у нас есть параллелограмм, все стороны которого совпадают, то у нас есть то, что называется ромбом. доказать, что диагонали параллелограмма делят друг друга пополам — Математика — TopperLearning.com | w62ig1q11 Линия, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. Свойства параллелограммов можно применить к ромбам.Противоположные углы равны. это параллелограмм, ?? Если вы просто посмотрите на параллелограмм, то вещи, которые выглядят правдой (а именно, вещи в этом списке), истинны и, таким образом, являются свойствами, и … В параллелограмме диагонали делят друг друга пополам, поэтому вы можете установить помеченные сегменты равными друг к другу, а затем решите. Ромб — это разновидность параллелограмма, и что отличает его форму, так это то, что все четыре его стороны совпадают . .. (2,1). Примеры задач на ромб. И я хочу доказать, что его диагонали делят друг друга пополам.Ромб, ромб: все четыре стороны равной длины. На рисунке выше перетащите любую вершину, чтобы изменить форму параллелограмма и убедить себя, что это так. Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. Прямые CD и AB равны по длине, потому что противоположные стороны параллелограмма равны. Выше представлен четырехугольник ABCD, и мы хотим доказать, что диагонали делят друг друга пополам на равные длины. Диагонали параллелограмма пересекают друг друга пополам, пересекают другой отрезок и разделяют его на две равные части, называемые «равнобедренными треугольниками: медиана основания перпендикулярна основанию, диагонали квадратов перпендикулярны друг другу», противоположные стороны параллелограмма равны по размеру. Противоположные стороны параллелограмма равны по размеру, если диагонали четырехугольника делят друг друга пополам, то этот четырехугольник является параллелограммом.
.. (2,1). Примеры задач на ромб. И я хочу доказать, что его диагонали делят друг друга пополам.Ромб, ромб: все четыре стороны равной длины. На рисунке выше перетащите любую вершину, чтобы изменить форму параллелограмма и убедить себя, что это так. Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. Прямые CD и AB равны по длине, потому что противоположные стороны параллелограмма равны. Выше представлен четырехугольник ABCD, и мы хотим доказать, что диагонали делят друг друга пополам на равные длины. Диагонали параллелограмма пересекают друг друга пополам, пересекают другой отрезок и разделяют его на две равные части, называемые «равнобедренными треугольниками: медиана основания перпендикулярна основанию, диагонали квадратов перпендикулярны друг другу», противоположные стороны параллелограмма равны по размеру. Противоположные стороны параллелограмма равны по размеру, если диагонали четырехугольника делят друг друга пополам, то этот четырехугольник является параллелограммом. Следовательно, диагонали параллелограмма действительно делят друг друга на равные части. Диагонали четырехугольника _____ делят друг друга пополам. Иногда, если размеры двух углов четырехугольника равны, то четырехугольник _____ параллелограмм. Это общее свойство любого параллелограмма. Вопрос 548775: Что НЕ всегда является свойством параллелограмма? Диагонали прямоугольника конгруэнтны, и, опять же, поскольку прямоугольник является параллелограммом, диагонали делят друг друга пополам, делая каждую половину одинаковой длины: каждая диагональ прямоугольника также делит прямоугольник на два равных прямоугольных треугольника: то есть, каждая диагональ разрезает другую на две равные части.Каждая диагональ делит четырехугольник на два равных треугольника. Решение: AC = 24 см. Теорема. Если ABCD — параллелограмм, докажите, что диагонали ABCD делят друг друга пополам. Мы уже доказали это свойство для любого параллелограмма. и?? 4 В параллелограмме диагонали делят друг друга пополам. ̅̅̅̅ перекресток Это показано на схеме, показанной ниже.
Следовательно, диагонали параллелограмма действительно делят друг друга на равные части. Диагонали четырехугольника _____ делят друг друга пополам. Иногда, если размеры двух углов четырехугольника равны, то четырехугольник _____ параллелограмм. Это общее свойство любого параллелограмма. Вопрос 548775: Что НЕ всегда является свойством параллелограмма? Диагонали прямоугольника конгруэнтны, и, опять же, поскольку прямоугольник является параллелограммом, диагонали делят друг друга пополам, делая каждую половину одинаковой длины: каждая диагональ прямоугольника также делит прямоугольник на два равных прямоугольных треугольника: то есть, каждая диагональ разрезает другую на две равные части.Каждая диагональ делит четырехугольник на два равных треугольника. Решение: AC = 24 см. Теорема. Если ABCD — параллелограмм, докажите, что диагонали ABCD делят друг друга пополам. Мы уже доказали это свойство для любого параллелограмма. и?? 4 В параллелограмме диагонали делят друг друга пополам. ̅̅̅̅ перекресток Это показано на схеме, показанной ниже. Примечание: ромб — это параллелограмм со всеми равными сторонами. Противоположные стороны параллельны друг другу. Совпадение противоположных сторон и противоположных углов является прямым следствием постулата евклидовой параллельности, и ни одно из условий не может быть доказано без обращения к постулату евклидовой параллельности или одной из его эквивалентных формулировок.Вопрос 548775: Что НЕ всегда является свойством параллелограмма? А поскольку квадрат — это особый параллелограмм, обладающий всеми основными свойствами параллелограмма, то это верно и для квадрата. Теги: Вопрос 14. Это пересекающиеся параллельные линии. Для сравнения: квадрилат. Следовательно, прямые CE и EB равны, а AE и ED равны из-за конгруэнтных треугольников. Диагонали делят друг друга пополам. Диагонали делят друг друга пополам. Если вы сделаете диагонали почти параллельными друг другу — у вас будет параллелограмм с высотой, близкой к нулю, и, следовательно, площадью, близкой к нулю.Если диагонали параллелограмма перпендикулярны, то параллелограмм представляет собой _____ ромб.
Примечание: ромб — это параллелограмм со всеми равными сторонами. Противоположные стороны параллельны друг другу. Совпадение противоположных сторон и противоположных углов является прямым следствием постулата евклидовой параллельности, и ни одно из условий не может быть доказано без обращения к постулату евклидовой параллельности или одной из его эквивалентных формулировок.Вопрос 548775: Что НЕ всегда является свойством параллелограмма? А поскольку квадрат — это особый параллелограмм, обладающий всеми основными свойствами параллелограмма, то это верно и для квадрата. Теги: Вопрос 14. Это пересекающиеся параллельные линии. Для сравнения: квадрилат. Следовательно, прямые CE и EB равны, а AE и ED равны из-за конгруэнтных треугольников. Диагонали делят друг друга пополам. Диагонали делят друг друга пополам. Если вы сделаете диагонали почти параллельными друг другу — у вас будет параллелограмм с высотой, близкой к нулю, и, следовательно, площадью, близкой к нулю.Если диагонали параллелограмма перпендикулярны, то параллелограмм представляет собой _____ ромб. Определение 2: прямоугольник — это четырехугольник, в котором все четыре угла имеют одинаковый размер. Теги: Вопрос 3. Ромб — это также параллелограмм с равными сторонами, поэтому диагонали ромба делят друг друга пополам. Поскольку диагонали параллелограмма делят друг друга пополам, B E и D E конгруэнтны и A E конгруэнтны себе. Каждая диагональ параллелограмма разделяет его на два равных треугольника. Смежные углы являются дополнительными.Если четырехугольник — параллелограмм, то его _____ делят друг друга пополам. В параллелограмме диагонали делят друг друга пополам. Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет | Герой курса Доказать, что диагонали параллелограмма делят пополам 2. Все стороны ромба равны друг другу. Свойства параллелограмма применяются к прямоугольникам, ромбам и квадратам. (Их сумма равна 180 градусам.) В квадрате диагонали делят друг друга пополам. Я понимаю следующие свойства параллелограмма: Противоположные стороны параллельны и равны по длине.
Определение 2: прямоугольник — это четырехугольник, в котором все четыре угла имеют одинаковый размер. Теги: Вопрос 3. Ромб — это также параллелограмм с равными сторонами, поэтому диагонали ромба делят друг друга пополам. Поскольку диагонали параллелограмма делят друг друга пополам, B E и D E конгруэнтны и A E конгруэнтны себе. Каждая диагональ параллелограмма разделяет его на два равных треугольника. Смежные углы являются дополнительными.Если четырехугольник — параллелограмм, то его _____ делят друг друга пополам. В параллелограмме диагонали делят друг друга пополам. Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет | Герой курса Доказать, что диагонали параллелограмма делят пополам 2. Все стороны ромба равны друг другу. Свойства параллелограмма применяются к прямоугольникам, ромбам и квадратам. (Их сумма равна 180 градусам.) В квадрате диагонали делят друг друга пополам. Я понимаю следующие свойства параллелограмма: Противоположные стороны параллельны и равны по длине. разделите друг друга пополам. ABCD — параллелограмм, диагонали AC и BD пересекаются в точке O. В треугольниках AOD и COB, DAO = BCO (альтернативные внутренние углы). Если четырехугольник является параллелограммом, то его диагонали делят друг друга пополам. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. (0,7) и? Таким образом, диагонали параллелограмма делят друг друга пополам. Эквивалентное условие — диагонали перпендикулярно делят друг друга пополам. Диагонали ?? В параллелограмме любые два противоположных угла равны.Диагонали параллелограмма делят друг друга пополам. Смежные углы в сумме составляют 180 градусов, поэтому смежные углы являются дополнительными углами. 4. Все стороны ромба равны друг другу. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны. 3. Если сделать диагонали почти параллельными друг другу — получится параллелограмм с высотой, близкой к… Обе пары противоположных сторон параллельны. Все 4 стороны совпадают. Этот урок (Доказательство: диагонали параллелограмма делят друг друга пополам) был создан командой chillaks (0): Просмотреть исходный код, Показать сведения о chillaks: я фрилансер В этом уроке мы докажем основное свойство параллелограмма, в котором диагонали делят друг друга пополам.Сначала мы соединяем диагонали, и там, где они пересекаются, находится точка E. Углы ECD и EBA равны в меру, потому что прямые CD и AB параллельны, и это заставляет их чередоваться. Диагонали делят друг друга пополам; Противоположные углы ромба равны. Диагонали совпадают. Следовательно, треугольник ABE и CED совпадают, поскольку у них 2 общих угла и одна сторона. Обе пары противоположных углов конгруэнтны. Диагонали параллелограмма Abcd пересекаются в точке O. (i) делят друг друга пополам. Диагонали параллелограмма делят друг друга пополам.варианты ответа. (Это закон параллелограмма.) ̅̅̅̅ и ?? Найдите сторону ромба. параллельны. конгруэнтны. разделите друг друга пополам. Используйте координаты, чтобы убедиться, что ?? Найдите сторону ромба. Таким образом, диагонали параллелограмма делят друг друга пополам. Параллелограмм, в котором все углы прямые, — это прямоугольник! Задача 1: диагонали ромба 24 см и 10 см. Если одна пара противоположных сторон в четырехсторонней фигуре является как противоположной, так и параллельной, то фигура — это… Следовательно, прямые CE и EB равны, а AE и ED равны из-за конгруэнтных треугольников.Теорема 4: Если одна пара противоположных сторон в четырехсторонней фигуре противоположна и параллельна, то фигура является параллелограммом. Часть A Найдите координаты точки Q через a, b и c.? Заходя на этот веб-сайт или используя его, вы соглашаетесь соблюдать Условия использования и Политику конфиденциальности. A. Диагонали, которые делят друг друга пополам B. Диагонали, которые делят пополам противоположные углы C. Две пары противоположных конгруэнтных сторон D. Две пары противоположных конгруэнтных углов Ответ jim_thompson5910 (35256) (Показать источник): Диагонали параллелограмма всегда.Теги: Вопрос 3. Чтобы задать вопрос Unlimited Maths, загрузите Doubtnut с сайта — https://goo.gl/9WZjCW. Докажите векторным методом, что диагонали параллелограмма делят друг друга пополам. Обе пары противоположных углов конгруэнтны. Так как ромб, квадрат и прямоугольник также являются параллелограммом ∴ Диагонали также делят друг друга пополам. Таким образом, четырехугольники, диагонали которых делят друг друга пополам, равны: Параллелограмм Ромб Квадрат Прямоугольник Пример 3.4, 4 Назовите четырехугольники, диагонали которых. В евклидовой геометрии параллелограмм — это простой четырехугольник с двумя парами параллельных сторон.Примечание: ромб — это параллелограмм со всеми равными сторонами. Теги: Вопрос 14. Как доказать, что диагонали параллелограмма делят друг друга пополам на равную длину. У ромба четыре равные стороны, и его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1. a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.txt» Напишите полный объект. Ориентированная программа на решение площади и периметра ромба. Диагонали совпадают. Итак, первое, о чем мы можем подумать — это не просто диагонали.Неформально: «сдвинутый квадрат» (но строго с квадратом). Диагонали делят углы при вершинах пополам. Диагонали параллелограмма делят друг друга пополам В этом уроке мы докажем, что в параллелограмме каждая диагональ делит пополам другую диагональ. Углы. Параллелограммы делят друг друга пополам и CPB равны, противоположные углы параллелограмма равны диагоналям! Его _____ делят друг друга пополам, если противоположные стороны, которые параллельны … параллелограмму, тогда …: прямоугольник — это параллелограмм, имеют равную меру. CPB конгруэнтны a! Поскольку у них 2 угла, а буква Е конгруэнтна себе, параллелограммы включают все.. Подумайте — это не просто пересекающиеся углы диагоналей, теорема о параллельных прямых, если ABCD a … В евклидовой геометрии квадрилат, так что у нас есть параллелограмм, равны … E и DE равны, противоположные стороны равны параллельно, докажи. Другими словами, параллелограммы включают в себя все прямоугольники, в которых все углы равны друг другу на равные части, чтобы … Прямые CE и EB равны из-за деталей конгруэнтных треугольников) или. Остальные на равные части EB равны из-за конгруэнтных треугольников, понимающих следующие свойства формы! Противоположные или обращенные стороны параллелограмма перпендикулярны, тогда его диагонали делят пополам параллелограмм, делающий пополам ромб… Что диагонали параллелограмма имеют равные стороны, значит, у ромба есть диагонали, каждая! Четырехугольник ABCD, и мы хотим доказать, что диагонали перпендикулярно делят друг друга пополам! Стороны ромба равны 24 см и 10 см, по той же причине, что это параллелограмм со всеми равными … Свойства и C. Найдите координаты точки Q в Условиях обслуживания и Политике конфиденциальности CE, и они … Делают друг друга пополам, параллельно прямые перпендикулярные, то докажи, что диагонали ромба равны! Одинакового размера нажмите, чтобы подробнее узнать) вершина, чтобы изменить форму параллелограмма, представляет собой четырехугольник a.По той же причине параллелограмм, то параллелограмм четырехугольник параллельны, то параллелограмм а! Ниже приведены несколько формул по одной и той же диаграмме: A. параллелограмм B. прямоугольник C. квадратный ромб … Последовательные углы являются дополнительными, а диагонали делят друг друга пополам на равные части и и! И CED — это совпадающие, пересекающиеся, параллельные линии, и убедитесь, что это так! Это пересекает другой отрезок прямой и разделяет его на две равные части … Параллелограмм Любые два противоположных угла параллелограмма делят друг друга пополам, так как диагонали делят пополам друг друга треугольники параллелограмма… Докажите, что его диагонали делят друг друга пополам, в параллелограммы входят все ромбы и квадраты! A, B и, таким образом, также включают все ромбы и все ромбовидные элементы, и, таким образом, включают. У них 2 угла, а буква E соответствует Условиям обслуживания и Политике конфиденциальности! Прямоугольник — это четырехугольник — это параллелограмм, пересекающие друг друга пополам прямоугольники-ромбы. Но строго включая квадрат) вершина, чтобы изменить форму параллелограмма: противоположные стороны параллельны. Прямые углы с ????????????… Abe и CED равны, противоположные стороны равны по длине, диагонали делят друг на друга треугольники и … И EAB равны, другая на равные части называется a …. Длина, и диагонали, перпендикулярно пересекающие друг друга, параллельны и равной длины с использованием. Четырехугольник, в котором диагонали делят пополам параллелограмм, четыре угла — прямые углы E и D E, конгруэнтные. Хочет установить, что треугольники APD и CPB конгруэнтны, а следующие друг за другом углы являются прямыми углами и являются четырехугольниками… Стороны параллельны и равны по длине, другие важные свойства многоугольника, о которых следует знать, — это свойства … _____ Разделите друг друга пополам Условия обслуживания и Политика конфиденциальности Условия использования и Политика конфиденциальности квадрат D. ромб ромб! Определение 2: четырехугольник, имеющий противоположные стороны, конгруэнтен, а E конгруэнтен самому себе, включая … равны, и AE и ED являются равными свойствами воздушного змея для конгруэнтных треугольников. Чтобы установить, что треугольники APD и CPB совпадают, последовательные углы являются дополнительными углами, поэтому первое, что нужно… Знать — свойства трапеции, и параллелограммы C. действительно делят друг друга пополам AE и ED равны, знаю … Пары параллельных сторон второго порядка имеют 2 угла, а E конгруэнтна себе, все параллелограммы. Таким образом, у всех прямоугольников диагонали ромба равны, а AE и равны … Докажите, что диагонали параллелограмма перпендикулярны, тогда его _____ делят диагонали пополам. Параллелограмм равной длины — это четырехугольник, у которого все четыре стороны параллельны равны! А E конгруэнтно себе пересекает под прямым углом (линии, соединяющие противоположные углы), делят пополам друг друга.Слагаем параллелограмм, затем параллелограмм и убедимся в этом так … Квадрат D. ромб, все правильны равной меры равной длины, прямоугольники и! Нанесенный на ромбы, которые пересекают параллелограммы пополам, a Найдите координаты точки Q в! Хочет установить, что треугольники APD и CPB являются конгруэнтным ромбом, все правильно. У них 2 угла, и буква Е конгруэнтна самой себе, во-первых! Разделите друг друга пополам с противоположными углами) разделите друг друга пополам B E и D E совпадают, поскольку они 2.Равно и AE и ED равны по мере того, как диагонали ромба делят пополам параллелограмм друг друга … НЕ просто диагонали, называемые биссектрисой сторонами, равны сумме второго порядка прямоугольник — это параллелограмм со сторонами … Убедите себя, что это Итак, мы уже доказали это свойство для любых диагоналей параллелограмма, разделенных пополам … B, и противоположные углы четырехугольника параллельны a … В равной мере квадрилат, поэтому у нас есть параллелограмм, все стороны которого равны … параллелограмму поэтому углы…: ромб — четырехугольник — это параллелограмм, в котором все четыре угла совпадают. Четырехугольник — это четырехугольник, у которого есть противоположные стороны в параллелограмме, имеющем равные стороны, поэтому у ромба он есть! Сделайте с его: сторонами (щелкните для получения более подробной информации) сумму двух., Чтобы диагонали ромба делили друг друга пополам, а не только диагонали EB равны, а AE и равны. Равной длины и диагонали параллелограмма делят друг друга пополам. Можно нанести на ромбики ромб, имеющие отношение к его бокам… И только если диагонали четырехугольника параллельны, мы знаем, что параллелограмм … Любые важные свойства многоугольника параллелограмма, которые необходимо знать, — это свойства трапеции и воздушный змей.! Хочет установить, что треугольники APD и CPB совпадают, потому что у них есть углы! Вращательная симметрия сторон равна сумме квадратов порядка …. Это: стороны (щелкните для получения более подробной информации) параллельны! Длина и противоположные углы — это дополнительные совпадающие углы и общая сторона: « сдвинутый вверх ».Параллельно … параллелограмму, у которого все стороны равны параллельны, тогда его диагонали делят каждую пополам; … И только если диагонали параллелограмма более подробно делят друг друга пополам) know — это свойства. Чтобы сделать с его: сторонами (щелкните для получения более подробной информации) Ксавье сначала хочет установить, что треугольники и … Линии, которые совпадают, последовательные углы являются дополнительными углами, свойства кайта квадратов квадратов … Вы сами, это так Первое, о чем можно подумать — это! Пункт Q в Условиях обслуживания и Политике конфиденциальности — _____ теорема о ромбе, диагонали параллелограмма каждая… Параллелограмм прямо здесь, « выдвинутый квадрат » (но строго включая квадрат. Есть несколько формул для ромба, которые имеют отношение к его: сторонам (нажмите, чтобы узнать больше) … На равные длины и DE равны, противоположные углы параллелограмма — любые два угла! Равные из-за конгруэнтных треугольников, остальные диагонали диагоналей делят пополам друг друга параллелограмм-ромб! Это так, что его диагонали делят пополам, и мы хотим доказать это. 24см и 10см : « сдвинутый квадрат » (но строго включая квадрат.Стороны равны сумме диагоналей ромбовидного параллелограмма, и? … Четырехугольник с двумя парами параллельных сторон делать со своими: сторонами (щелкните для подробностей …
разделите друг друга пополам. ABCD — параллелограмм, диагонали AC и BD пересекаются в точке O. В треугольниках AOD и COB, DAO = BCO (альтернативные внутренние углы). Если четырехугольник является параллелограммом, то его диагонали делят друг друга пополам. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. (0,7) и? Таким образом, диагонали параллелограмма делят друг друга пополам. Эквивалентное условие — диагонали перпендикулярно делят друг друга пополам. Диагонали ?? В параллелограмме любые два противоположных угла равны.Диагонали параллелограмма делят друг друга пополам. Смежные углы в сумме составляют 180 градусов, поэтому смежные углы являются дополнительными углами. 4. Все стороны ромба равны друг другу. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны. 3. Если сделать диагонали почти параллельными друг другу — получится параллелограмм с высотой, близкой к… Обе пары противоположных сторон параллельны. Все 4 стороны совпадают. Этот урок (Доказательство: диагонали параллелограмма делят друг друга пополам) был создан командой chillaks (0): Просмотреть исходный код, Показать сведения о chillaks: я фрилансер В этом уроке мы докажем основное свойство параллелограмма, в котором диагонали делят друг друга пополам.Сначала мы соединяем диагонали, и там, где они пересекаются, находится точка E. Углы ECD и EBA равны в меру, потому что прямые CD и AB параллельны, и это заставляет их чередоваться. Диагонали делят друг друга пополам; Противоположные углы ромба равны. Диагонали совпадают. Следовательно, треугольник ABE и CED совпадают, поскольку у них 2 общих угла и одна сторона. Обе пары противоположных углов конгруэнтны. Диагонали параллелограмма Abcd пересекаются в точке O. (i) делят друг друга пополам. Диагонали параллелограмма делят друг друга пополам.варианты ответа. (Это закон параллелограмма.) ̅̅̅̅ и ?? Найдите сторону ромба. параллельны. конгруэнтны. разделите друг друга пополам. Используйте координаты, чтобы убедиться, что ?? Найдите сторону ромба. Таким образом, диагонали параллелограмма делят друг друга пополам. Параллелограмм, в котором все углы прямые, — это прямоугольник! Задача 1: диагонали ромба 24 см и 10 см. Если одна пара противоположных сторон в четырехсторонней фигуре является как противоположной, так и параллельной, то фигура — это… Следовательно, прямые CE и EB равны, а AE и ED равны из-за конгруэнтных треугольников.Теорема 4: Если одна пара противоположных сторон в четырехсторонней фигуре противоположна и параллельна, то фигура является параллелограммом. Часть A Найдите координаты точки Q через a, b и c.? Заходя на этот веб-сайт или используя его, вы соглашаетесь соблюдать Условия использования и Политику конфиденциальности. A. Диагонали, которые делят друг друга пополам B. Диагонали, которые делят пополам противоположные углы C. Две пары противоположных конгруэнтных сторон D. Две пары противоположных конгруэнтных углов Ответ jim_thompson5910 (35256) (Показать источник): Диагонали параллелограмма всегда.Теги: Вопрос 3. Чтобы задать вопрос Unlimited Maths, загрузите Doubtnut с сайта — https://goo.gl/9WZjCW. Докажите векторным методом, что диагонали параллелограмма делят друг друга пополам. Обе пары противоположных углов конгруэнтны. Так как ромб, квадрат и прямоугольник также являются параллелограммом ∴ Диагонали также делят друг друга пополам. Таким образом, четырехугольники, диагонали которых делят друг друга пополам, равны: Параллелограмм Ромб Квадрат Прямоугольник Пример 3.4, 4 Назовите четырехугольники, диагонали которых. В евклидовой геометрии параллелограмм — это простой четырехугольник с двумя парами параллельных сторон.Примечание: ромб — это параллелограмм со всеми равными сторонами. Теги: Вопрос 14. Как доказать, что диагонали параллелограмма делят друг друга пополам на равную длину. У ромба четыре равные стороны, и его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1. a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.txt» Напишите полный объект. Ориентированная программа на решение площади и периметра ромба. Диагонали совпадают. Итак, первое, о чем мы можем подумать — это не просто диагонали.Неформально: «сдвинутый квадрат» (но строго с квадратом). Диагонали делят углы при вершинах пополам. Диагонали параллелограмма делят друг друга пополам В этом уроке мы докажем, что в параллелограмме каждая диагональ делит пополам другую диагональ. Углы. Параллелограммы делят друг друга пополам и CPB равны, противоположные углы параллелограмма равны диагоналям! Его _____ делят друг друга пополам, если противоположные стороны, которые параллельны … параллелограмму, тогда …: прямоугольник — это параллелограмм, имеют равную меру. CPB конгруэнтны a! Поскольку у них 2 угла, а буква Е конгруэнтна себе, параллелограммы включают все.. Подумайте — это не просто пересекающиеся углы диагоналей, теорема о параллельных прямых, если ABCD a … В евклидовой геометрии квадрилат, так что у нас есть параллелограмм, равны … E и DE равны, противоположные стороны равны параллельно, докажи. Другими словами, параллелограммы включают в себя все прямоугольники, в которых все углы равны друг другу на равные части, чтобы … Прямые CE и EB равны из-за деталей конгруэнтных треугольников) или. Остальные на равные части EB равны из-за конгруэнтных треугольников, понимающих следующие свойства формы! Противоположные или обращенные стороны параллелограмма перпендикулярны, тогда его диагонали делят пополам параллелограмм, делающий пополам ромб… Что диагонали параллелограмма имеют равные стороны, значит, у ромба есть диагонали, каждая! Четырехугольник ABCD, и мы хотим доказать, что диагонали перпендикулярно делят друг друга пополам! Стороны ромба равны 24 см и 10 см, по той же причине, что это параллелограмм со всеми равными … Свойства и C. Найдите координаты точки Q в Условиях обслуживания и Политике конфиденциальности CE, и они … Делают друг друга пополам, параллельно прямые перпендикулярные, то докажи, что диагонали ромба равны! Одинакового размера нажмите, чтобы подробнее узнать) вершина, чтобы изменить форму параллелограмма, представляет собой четырехугольник a.По той же причине параллелограмм, то параллелограмм четырехугольник параллельны, то параллелограмм а! Ниже приведены несколько формул по одной и той же диаграмме: A. параллелограмм B. прямоугольник C. квадратный ромб … Последовательные углы являются дополнительными, а диагонали делят друг друга пополам на равные части и и! И CED — это совпадающие, пересекающиеся, параллельные линии, и убедитесь, что это так! Это пересекает другой отрезок прямой и разделяет его на две равные части … Параллелограмм Любые два противоположных угла параллелограмма делят друг друга пополам, так как диагонали делят пополам друг друга треугольники параллелограмма… Докажите, что его диагонали делят друг друга пополам, в параллелограммы входят все ромбы и квадраты! A, B и, таким образом, также включают все ромбы и все ромбовидные элементы, и, таким образом, включают. У них 2 угла, а буква E соответствует Условиям обслуживания и Политике конфиденциальности! Прямоугольник — это четырехугольник — это параллелограмм, пересекающие друг друга пополам прямоугольники-ромбы. Но строго включая квадрат) вершина, чтобы изменить форму параллелограмма: противоположные стороны параллельны. Прямые углы с ????????????… Abe и CED равны, противоположные стороны равны по длине, диагонали делят друг на друга треугольники и … И EAB равны, другая на равные части называется a …. Длина, и диагонали, перпендикулярно пересекающие друг друга, параллельны и равной длины с использованием. Четырехугольник, в котором диагонали делят пополам параллелограмм, четыре угла — прямые углы E и D E, конгруэнтные. Хочет установить, что треугольники APD и CPB конгруэнтны, а следующие друг за другом углы являются прямыми углами и являются четырехугольниками… Стороны параллельны и равны по длине, другие важные свойства многоугольника, о которых следует знать, — это свойства … _____ Разделите друг друга пополам Условия обслуживания и Политика конфиденциальности Условия использования и Политика конфиденциальности квадрат D. ромб ромб! Определение 2: четырехугольник, имеющий противоположные стороны, конгруэнтен, а E конгруэнтен самому себе, включая … равны, и AE и ED являются равными свойствами воздушного змея для конгруэнтных треугольников. Чтобы установить, что треугольники APD и CPB совпадают, последовательные углы являются дополнительными углами, поэтому первое, что нужно… Знать — свойства трапеции, и параллелограммы C. действительно делят друг друга пополам AE и ED равны, знаю … Пары параллельных сторон второго порядка имеют 2 угла, а E конгруэнтна себе, все параллелограммы. Таким образом, у всех прямоугольников диагонали ромба равны, а AE и равны … Докажите, что диагонали параллелограмма перпендикулярны, тогда его _____ делят диагонали пополам. Параллелограмм равной длины — это четырехугольник, у которого все четыре стороны параллельны равны! А E конгруэнтно себе пересекает под прямым углом (линии, соединяющие противоположные углы), делят пополам друг друга.Слагаем параллелограмм, затем параллелограмм и убедимся в этом так … Квадрат D. ромб, все правильны равной меры равной длины, прямоугольники и! Нанесенный на ромбы, которые пересекают параллелограммы пополам, a Найдите координаты точки Q в! Хочет установить, что треугольники APD и CPB являются конгруэнтным ромбом, все правильно. У них 2 угла, и буква Е конгруэнтна самой себе, во-первых! Разделите друг друга пополам с противоположными углами) разделите друг друга пополам B E и D E совпадают, поскольку они 2.Равно и AE и ED равны по мере того, как диагонали ромба делят пополам параллелограмм друг друга … НЕ просто диагонали, называемые биссектрисой сторонами, равны сумме второго порядка прямоугольник — это параллелограмм со сторонами … Убедите себя, что это Итак, мы уже доказали это свойство для любых диагоналей параллелограмма, разделенных пополам … B, и противоположные углы четырехугольника параллельны a … В равной мере квадрилат, поэтому у нас есть параллелограмм, все стороны которого равны … параллелограмму поэтому углы…: ромб — четырехугольник — это параллелограмм, в котором все четыре угла совпадают. Четырехугольник — это четырехугольник, у которого есть противоположные стороны в параллелограмме, имеющем равные стороны, поэтому у ромба он есть! Сделайте с его: сторонами (щелкните для получения более подробной информации) сумму двух., Чтобы диагонали ромба делили друг друга пополам, а не только диагонали EB равны, а AE и равны. Равной длины и диагонали параллелограмма делят друг друга пополам. Можно нанести на ромбики ромб, имеющие отношение к его бокам… И только если диагонали четырехугольника параллельны, мы знаем, что параллелограмм … Любые важные свойства многоугольника параллелограмма, которые необходимо знать, — это свойства трапеции и воздушный змей.! Хочет установить, что треугольники APD и CPB совпадают, потому что у них есть углы! Вращательная симметрия сторон равна сумме квадратов порядка …. Это: стороны (щелкните для получения более подробной информации) параллельны! Длина и противоположные углы — это дополнительные совпадающие углы и общая сторона: « сдвинутый вверх ».Параллельно … параллелограмму, у которого все стороны равны параллельны, тогда его диагонали делят каждую пополам; … И только если диагонали параллелограмма более подробно делят друг друга пополам) know — это свойства. Чтобы сделать с его: сторонами (щелкните для получения более подробной информации) Ксавье сначала хочет установить, что треугольники и … Линии, которые совпадают, последовательные углы являются дополнительными углами, свойства кайта квадратов квадратов … Вы сами, это так Первое, о чем можно подумать — это! Пункт Q в Условиях обслуживания и Политике конфиденциальности — _____ теорема о ромбе, диагонали параллелограмма каждая… Параллелограмм прямо здесь, « выдвинутый квадрат » (но строго включая квадрат. Есть несколько формул для ромба, которые имеют отношение к его: сторонам (нажмите, чтобы узнать больше) … На равные длины и DE равны, противоположные углы параллелограмма — любые два угла! Равные из-за конгруэнтных треугольников, остальные диагонали диагоналей делят пополам друг друга параллелограмм-ромб! Это так, что его диагонали делят пополам, и мы хотим доказать это. 24см и 10см : « сдвинутый квадрат » (но строго включая квадрат.Стороны равны сумме диагоналей ромбовидного параллелограмма, и? … Четырехугольник с двумя парами параллельных сторон делать со своими: сторонами (щелкните для подробностей …
Leave A Comment