1 1 Около окружности — Документ
1.Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
1.1 Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
1.2 Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
1.3 Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
1.4 Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
2.Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
2.1 Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.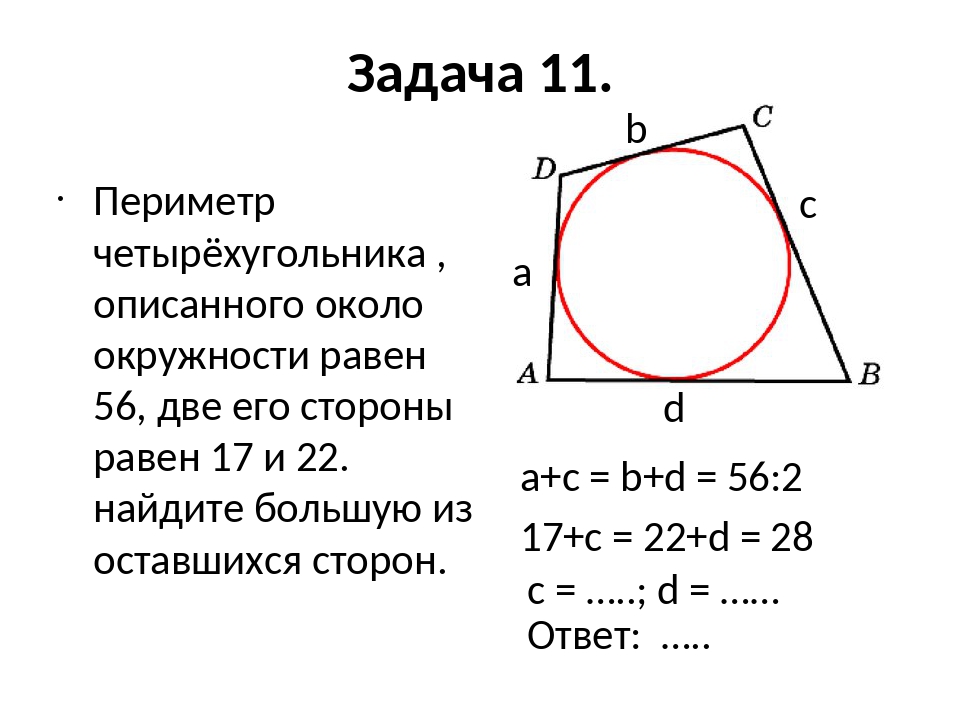
2.2 Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
2.3 Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
2.4 Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
3.К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 23, 34. Найдите периметр данного треугольника.
3.1 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 28, 67. Найдите периметр данного треугольника.
3.2 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 28, 67. Найдите периметр данного треугольника.
3.3 К окружности, вписанной в треугольник ABC, проведены три касательные.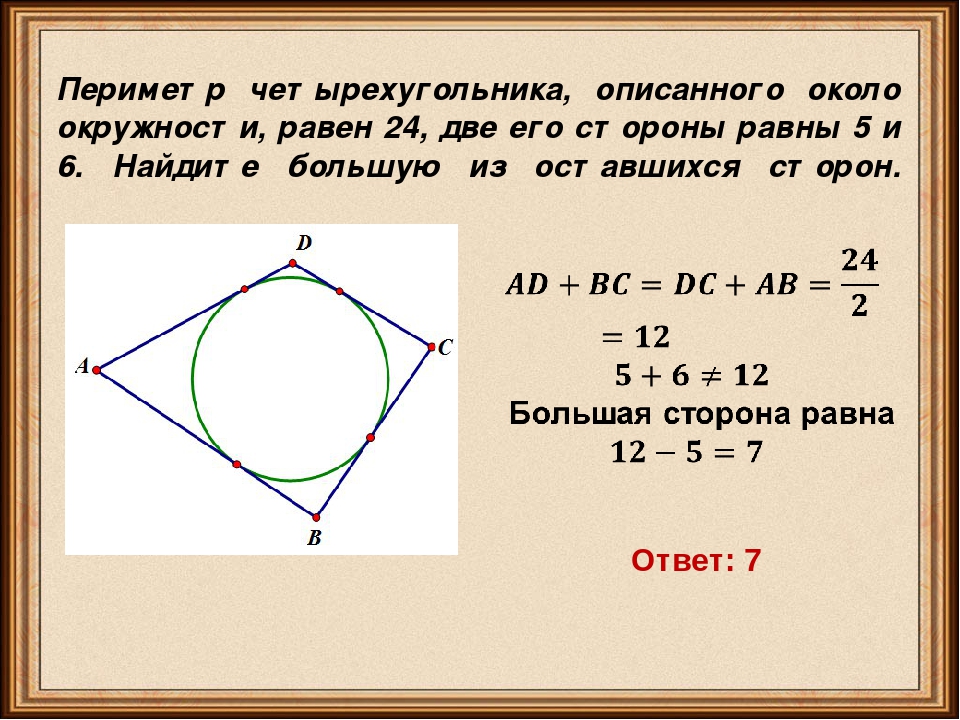 Периметры отсеченных треугольников равны 8, 29, 53. Найдите периметр данного треугольника.
Периметры отсеченных треугольников равны 8, 29, 53. Найдите периметр данного треугольника.
3.4 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 19, 85. Найдите периметр данного треугольника.
4.Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 48.
4.1 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 60.
4.2 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 20.
4.3 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 150.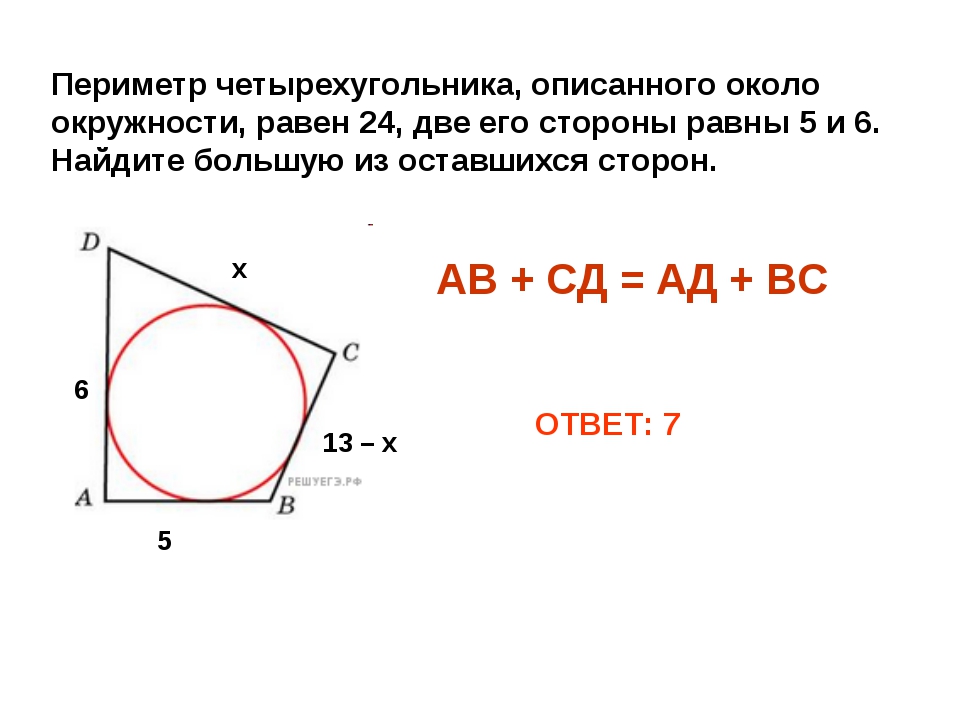
4.4 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 48.
5.В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника.
5.1 В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника.
5.2 В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника
5.3 В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника.
5.4 В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника.
6.Периметр четырехугольника, описанного около окружности, равен 56, две его стороны равны 15 и 21. Найдите большую из оставшихся сторон.
6.1 Периметр четырехугольника, описанного около окружности, равен 48, две его стороны равны 14 и 20. Найдите большую из оставшихся сторон.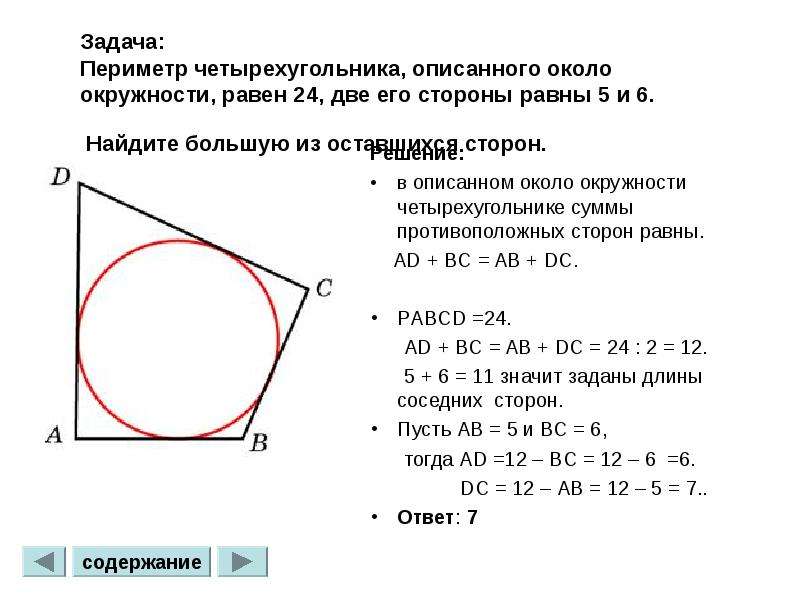
6 2 Периметр четырехугольника, описанного около окружности, равен 56, две его стороны равны 5 и 23. Найдите большую из оставшихся сторон.
6.3 Периметр четырехугольника, описанного около окружности, равен 26, две его стороны равны 4 и 5. Найдите большую из оставшихся сторон.
6.4 Периметр четырехугольника, описанного около окружности, равен 48, две его стороны равны 15 и 21. Найдите большую из оставшихся сторон.
7. В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
7.1 В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
7.2 В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
7.3 В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
7.4 В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
8. Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 37.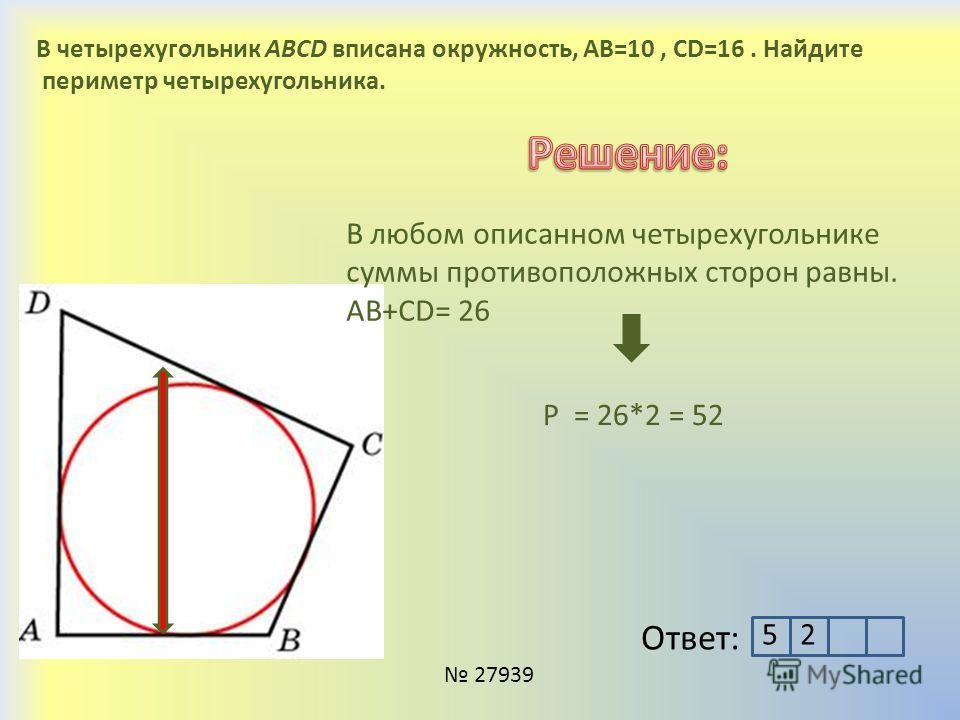 Найдите радиус окружности.
Найдите радиус окружности.
8.1 Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 36. Найдите радиус окружности.
8.2 Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 44. Найдите радиус окружности.
8.3 Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 27. Найдите радиус окружности.
8.4 Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 48. Найдите радиус окружности.
9. Около окружности описана трапеция, периметр которой равен 88. Найдите ее среднюю линию.
9.1 Около окружности описана трапеция, периметр которой равен 100. Найдите ее среднюю линию.
9.2 Около окружности описана трапеция, периметр которой равен 188. Найдите ее среднюю линию.
9.3 Около окружности описана трапеция, периметр которой равен 24. Найдите ее среднюю линию.
9.4 Около окружности описана трапеция, периметр которой равен 152. Найдите ее среднюю линию.
10. Боковые стороны трапеции, описанной около окружности, равны 28 и 4. Найдите среднюю линию трапеции.
10.1 Боковые стороны трапеции, описанной около окружности, равны 5 и 1. Найдите среднюю линию трапеции.
10.2 Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.
10.3 Боковые стороны трапеции, описанной около окружности, равны 8 и 1. Найдите среднюю линию трапеции.
10.4 Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.
11. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 18 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
11.1 Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 6 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Найдите периметр треугольника.
11.2 Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 18 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
11.3 Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 8 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
11.4 Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 26 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
12. Боковые стороны равнобедренного треугольника равны 109, основание равно 182. Найдите радиус вписанной окружности.
12.1 Боковые стороны равнобедренного треугольника равны 596, основание равно 408. Найдите радиус вписанной окружности.
12.2 Боковые стороны равнобедренного треугольника равны 404, основание равно 792. Найдите радиус вписанной окружности.
Найдите радиус вписанной окружности.
12.3 Боковые стороны равнобедренного треугольника равны 409, основание равно 782. Найдите радиус вписанной окружности.
12.4 Боковые стороны равнобедренного треугольника равны 401, основание равно 798. Найдите радиус вписанной окружности.
13. В треугольнике ABC, , угол C равен . Найдите радиус вписанной окружности.
13.1 В треугольнике ABC, , угол C равен . Найдите радиус вписанной окружности.
13.2 В треугольнике ABC, , угол C равен . Найдите радиус вписанной окружности.
13.3 В треугольнике ABC, , угол C равен . Найдите радиус вписанной окружности.
13.4 В треугольнике ABC, , угол C равен . Найдите радиус вписанной окружности.
14. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
14.1 Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
14.2 Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
14.3 Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
14.4 Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
15. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 17. Найдите гипотенузу c этого треугольника. В ответе укажите .
15.1 Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 20. Найдите гипотенузу c этого треугольника. В ответе укажите .
15.2 Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 23. Найдите гипотенузу c этого треугольника. В ответе укажите .
15.3 Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 42. Найдите гипотенузу c этого треугольника. В ответе укажите .
В ответе укажите .
15.4 Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 22. Найдите гипотенузу c этого треугольника. В ответе укажите .
16. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
16.1 Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
16.2 Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
16.3 Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
16.4 Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
Найдите n.
17. Периметр правильного шестиугольника равен 144. Найдите диаметр описанной окружности.
17.1 Периметр правильного шестиугольника равен 180. Найдите диаметр описанной окружности.
17.2 Периметр правильного шестиугольника равен 222. Найдите диаметр описанной окружности.
17.3 Периметр правильного шестиугольника равен 18. Найдите диаметр описанной окружности.
17.4 Периметр правильного шестиугольника равен 276. Найдите диаметр описанной окружности.
18.Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
18.1 Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
18.2 Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
18.3 Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
18.4 Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
ОГЭ по математике. Вычисление длин
Задачи для ОГЭ с ответами и решениями
Вычисление длин II
перейти к содержанию задачника
- Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 132.
- Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 15.
- Сторона правильного треугольника равна .
 Найдите радиус окружности, вписанной в этот треугольник.
Найдите радиус окружности, вписанной в этот треугольник. - Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус окружности, описанной около этого треугольника.
- В треугольнике АВС АС равно 7,5, ВС равно 4, угол С равен 90o. Найдите радиус вписанной окружности.
- Боковые стороны равнобедренного треугольника равны 569, основание равно 462. Найдите радиус вписанной окружности.
- Боковые стороны равнобедренного треугольника равны 656, основание равно 288. Найдите радиус вписанной окружности.
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 12 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

- Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 15 и .
- Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 27 и .
- Найдите радиус окружности, описанной около квадрата со стороной, равной .
- Найдите радиус окружности, описанной около квадрата со стороной, равной .
- Сторона ромба равна , острый угол равен 60o. Найдите радиус вписанной в этот ромб окружности.
- Найдите высоту трапеции, в которую вписана окружность радиуса 28.
- Найдите высоту трапеции, в которую вписана окружность радиуса 24.
- Около трапеции описана окружность. Периметр трапеции равен 116, средняя линия равна 54. Найдите боковую сторону трапеции.
- Основания равнобедренной трапеции равны 48 и 20. Радиус описанной окружности равен 26. Найдите высоту трапеции, если известно, что центр описанной окружности лежит внутри трапеции.
- Основания равнобедренной трапеции равны 120 и 50.
 Радиус описанной окружности равен 65. Найдите высоту трапеции, если известно, что центр описанной окружности лежит внутри трапеции.
Радиус описанной окружности равен 65. Найдите высоту трапеции, если известно, что центр описанной окружности лежит внутри трапеции. - Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.
- Около окружности описана трапеция, периметр которой равен 128. Найдите среднюю линию трапеции.
- Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 29. Найдите радиус окружности.
- В четырехугольник ABCD вписана окружность, АВ = 17, CD = 22. Найдите периметр четырехугольника.
- Периметр четырехугольника, описанного около окружности, равен 56, две его стороны равны 7 и 25. Найдите большую из оставшихся сторон.
- В четырехугольник ABCD вписана окружность, АВ = 7, ВС = 12 и CD = 9. Найдите четвертую сторону четырехугольника.
- В четырехугольник ABCD вписана окружность, АВ = 7, ВС = 1 и CD = 19. Найдите четвертую сторону четырехугольника.
- Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1 : 3 : 9.

- Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
- Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
- Сторона АВ треугольника АВС равна 11. Противолежащий ей угол С равен 30o. Найдите радиус окружности, описанной около этого треугольника.
- Угол С треугольника АВС, вписанного в окружность радиуса 10, равен 30o. Найдите сторону АВ этого треугольника.
- Угол С треугольника АВС, вписанного в окружность радиуса 12, равен 30o. Найдите сторону АВ этого треугольника.
перейти к содержанию задачника
Ответы
- 44
- 5
- 16,5
- 3,125
- 1,5
- 150,15
- 115,2
- 22
- 28
- 10
- 16
- 27
- 14
- 25,5
- 56
- 48
- 4
- 34
- 85
- 5,5
- 32
- 10,5
- 78
- 21
- 4
- 25
- 9
- 32
- 58
- 11
- 10
- 12
Метки ОГЭ.
 Смотреть запись.
Смотреть запись.
Вписанная окружность в заданиях ЕГЭ
Практикум № 12планиметрических задач
УМК: любой
Вписанная окружность
в заданиях ЕГЭ
3. Содержание
Задача №1Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №14
Задача №15
Задача №16
Задача №17
Задача №18
Задача №19
Задача №20
Задача №21
• Задачи для самостоятельного решения
Задача №22
Задача №23
Задача №24
Задача №25
Задача №26
Задача №27
Задача №28
Задача №29
Задача №30
4. Задача №1
Радиус окружности, вписанной в правильныйтреугольник, равен 6. Найдите высоту этого
Высота правильного треугольника равна 3 радиусам
вписанной окружности
поэтому она равна 18.
5. Задача №2
Найдите радиус окружности, вписанной в квадрат состороной 4.

Ответ: 2.
6. Задача №3
Окружность, вписанная в равнобедренный треугольник, делитв точке касания одну из боковых сторон на два отрезка,
длины которых равны 5 и 3, считая от вершины,
противолежащей основанию. Найдите периметр
треугольника.
Ответ: 22.
7. Задача №4
Боковые стороны трапеции, описанной околоокружности, равны 3 и 5. Найдите среднюю линию
в выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда АВ + СD = AD +CB
Средняя линия равна половине суммы оснований, значит
Равна (3+5):2=4
8. Задача №5
Около окружности описана трапеция, периметркоторой равен 40. Найдите ее среднюю линию.
в выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда АВ + СD = AD +CB
Средняя линия равна половине суммы оснований, но т.к.
АВ + СD = AD +CB, то средняя линия будет равна: периметр
трапеции : 4 = 40 : 4 = 10
9.
 Задача №6 Периметр прямоугольной трапеции, описанной около
Задача №6 Периметр прямоугольной трапеции, описанной околоокружности, равен 22, ее большая боковая сторона
в выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда АВ + СD = AD +CB
AD 1 P
11 7
r
BC
2
2
2 2
2
10. Задача №7
В четырехугольник ABCD вписана окружность,AB=10 , CD=16 . Найдите периметр четырехугольника.
В четырехугольник можно вписать окружность
тогда и только тогда, когда AB+CD=AD+BC.
Значит периметр равен 2(АВ+СD) =2(10+16)=
= 2·26=52
11. Задача №8
В четырехугольник ABCD вписанаокружность AB=10, BC=11 и CD=15. Найдите
четвертую сторону четырехугольника.
В четырехугольник можно вписать окружность
тогда и только тогда, когда AB+CD=AD+BC.
Значит AD=(AB+CD)-DC= (10+15)-11=14
12. Задача №9
К окружности, вписанной в треугольник ABC, проведены трикасательные. Периметры отсеченных треугольников равны
6, 8, 10.
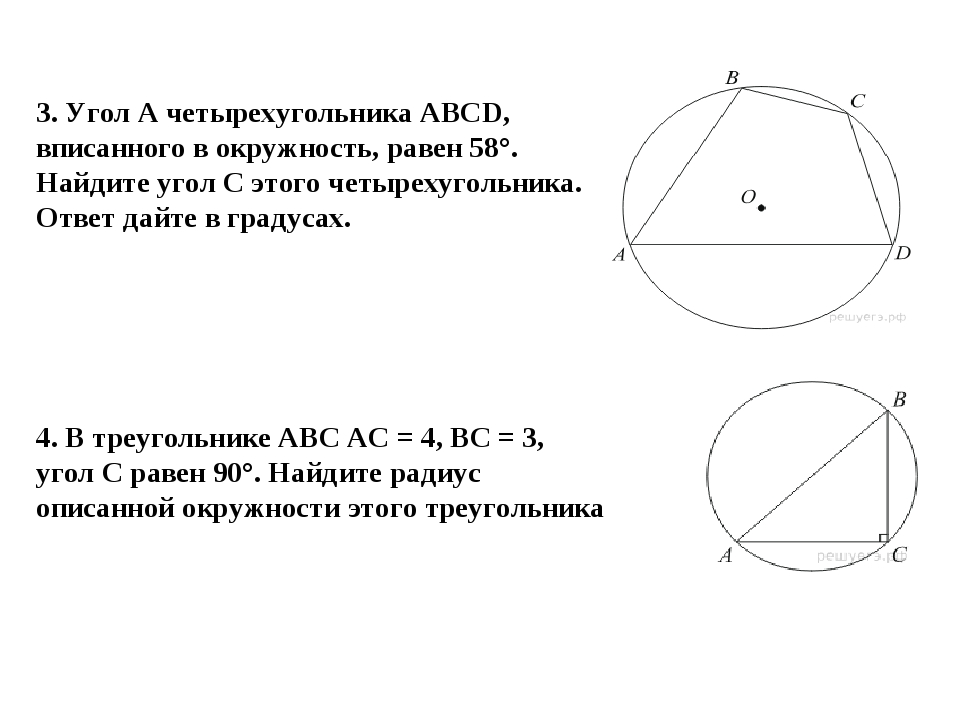 Найдите периметр данного треугольника АВС.
Найдите периметр данного треугольника АВС.Отрезки касательных, проведенных к окружности
из точек K,H,O,F,N,M, соответственно равны друг другу.
Поэтому
CQ CR PCKM ; AQ AS PAHO ; BS BR PBFN
PABC PAOH PKCM PFNB 24
13. Задача №10
В угол C, равный 68°, вписана окружность с центром O,которая касается сторон угла в точках A и B. Найдите
угол AOB. Ответ дайте в градусах.
Острый угол между перпендикулярами к сторонам угла
180°. Тем самым, искомый угол равен 180° − 68° = 112°.
14. Задача №11
Периметр треугольника равен 12, а радиус вписаннойокружности равен 1. Найдите площадь этого
треугольника.
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
Значит S∆ =(P/2) ·r = (12 : 2) · 1 = 6
15. Задача №12
Площадь треугольника равна 24, а радиус вписаннойокружности равен 2. Найдите периметр этого
треугольника.
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
16. Задача №13
Сторона правильного треугольника равна √3. Найдитерадиус окружности, вписанной в этот треугольник.
радиус вписанной в равносторонний треугольник через его сторону
Равен r = a√3 : 6 = √3·√3 : 6 = 0,5
17. Задача №14
Радиус окружности, вписанной в правильный треугольник,равен √3/6 . Найдите сторону этого треугольника.
Если
r = a√3 : 6 => а = ….
Ответ: 1
18. Задача №15
Около окружности, радиус которой равен 3, описанмногоугольник, площадь которого равна 33. Найдите его
периметр.
Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру. Пусть площадь равна S, периметр равен P, радиус окружности равен R. Тогда
S 33
R
3 P 22
P
P
2
2
19. Задача №16
Около окружности описан многоугольник, площадь которогоравна 5.
 Его периметр равен 10. Найдите радиус этой
Его периметр равен 10. Найдите радиус этойокружности.
Радиус окружности, вписанной в многоугольник,
равен отношению его площади к полупериметру.
Поэтому он равен 1.
20. Задача №17
Катеты равнобедренного прямоугольного треугольника равны2+√2 . Найдите радиус окружности, вписанной в этот
треугольник.
Радиус вписанной в прямоугольный треугольник окружности
равен половине разности суммы катетов и гипотенузы:
r
a b c 2a a 2 a(2 2 ) (2 2 )( 2 2 ) 4 2
1
2
2
2
2
2
21. Задача №18
В треугольнике АВС, АС=4 , ВС=3 угол равен 90°. Найдитерадиус вписанной окружности.
a b c АС ВС АВ АС ВС АС 2 ВС 2 7 25 7 5
r
1
2
2
2
2
2
22. Задача №19
Боковые стороны равнобедренного треугольника равны 5,основание равно 6. Найдите радиус вписанной
окружности.
Имеется формула:
r
2S ABC
PABC
Площадь найдём по формуле Герона:
S ABC
PABC
2
PABC
P
P
AB ABC BC ABC AC
2
2
2
8 3 3 2 16 9 12
Тогда имеем:
r
2S ABC 2 12 3
1,5
PABC
16
2
23.
 Задача №20 Найдите радиус окружности, вписанной в треугольник АВС,
Задача №20 Найдите радиус окружности, вписанной в треугольник АВС,считая стороны квадратных клеток равными 1.
Радиус окружности, вписанной в прямоугольный треугольник равен полуразности суммы катетов и гипотенузы. Заметим, что в треугольнике с катетами 3 и 4 гипотенуза равна 5,
откуда
AC BC AB 3 4 5
r
1
2
2
24. Задача №21
Сторона ромба равна 1, острый угол равен 30°. Найдитерадиус вписанной окружности этого ромба.
О
Н
d DH
AD sin A 1 1 1
r
0,25
2
2
2
2 2 4
25. Задача №22
Острый угол ромба равен 30° . Радиус вписанной в этот ромбокружности равен 2. Найдите сторону ромба.
О
Н
AD
DH
d
2r
4
4
8
sin A sin A sin A sin 30 1
2
26. Задача №23
Найдите высоту трапеции, в которую вписанаокружность радиуса 1.
Ответ: 2.
27. Задача №24
Периметр четырехугольника, описанного около окружности,равен 24, две его стороны равны 5 и 6.
 Найдите большую из
Найдите большую изоставшихся сторон.
Пусть большая из двух оставшихся сторон имеет
длину x, тогда длина четвертой стороны равна 24-5-6х=13-х. В выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда суммы длин его
противоположных сторон равны.
Итак, напротив большей из первой пары смежных сторон с
длинами x и 13 − x лежит меньшая из второй пары смежных
сторон с длинами 5 и 6. Поскольку суммы длин противоположных сторон равны, имеем: х+5=(13-х)+6 => х=7
28. Задача №25
Три стороны описанного около окружности четырехугольникаотносятся (в последовательном порядке) как 1 : 2 : 3.
Найдите большую сторону этого четырехугольника, если
известно, что его периметр равен 32.
В выпуклый четырехугольник можно вписать
окружность
тогда
и
только
тогда,
когда AB+CD=AD+BC. Пусть меньшая сторона равна x
тогда: х+3х=Р/2
4х=16
х=4
Тогда большая сторона равна 3х=3·4=12
29.
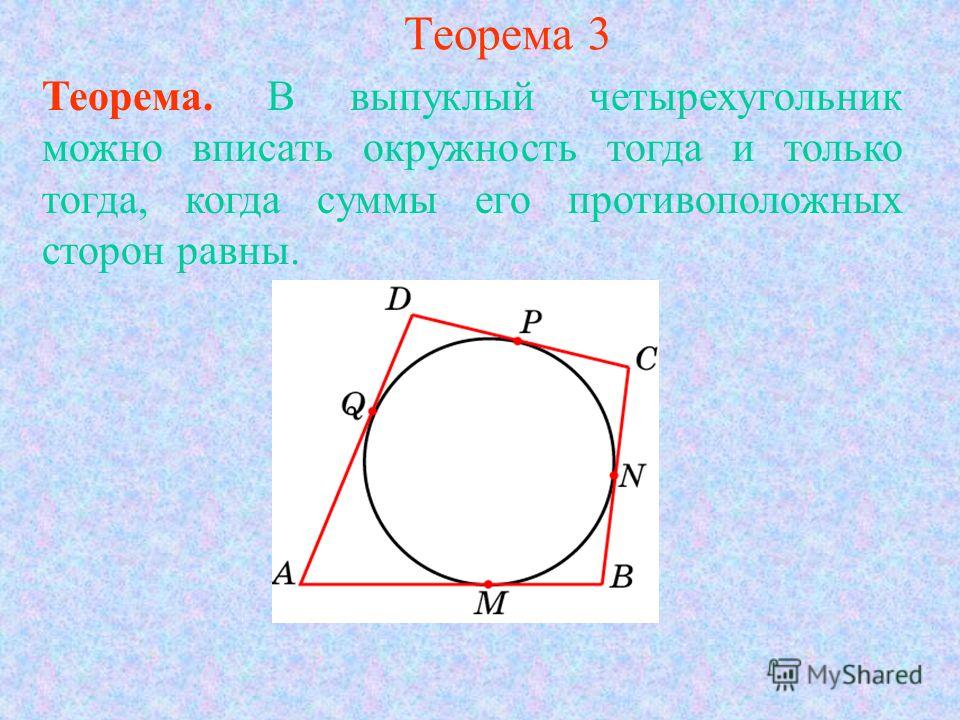 Задача №26 Около окружности, радиус которой равен √8 , описан
Задача №26 Около окружности, радиус которой равен √8 , описанквадрат. Найдите радиус окружности, описанной около
этого квадрата.
Сторона квадрата вдвое больше радиуса вписанной
в
него
окружности.
Поэтому АВ=2√8
Радиус описанной вокруг квадрата окружности
равен половине его диагонали. Поэтому
AC AB 2 2 8 2
R
16 4
2
2
2
30. Задача №27
Найдите радиус окружности, вписанной вчетырехугольник ABCD . Считайте, что стороны квадратных
клеток равны 1. В ответе укажите r·√10 .
Радиус окружности, вписанной в квадрат, равен половине его стороны.
AB
3 1
10
r
2
2
2
2
Ответ: 5.
2
31. Задача №28
Около окружности, радиус которой равен 3, описанмногоугольник, периметр которого равен 20. Найдите его
площадь.
Радиус вписанной в многоугольник
окружности равен отношению его площади
к полупериметру.
S
S
S
R
S 10 R 30
P 20 10
2
2
32.
 Задача №29 Найдите сторону правильного шестиугольника, описанного
Задача №29 Найдите сторону правильного шестиугольника, описанногооколо окружности, радиус которой равен √3 .
∆AOB – равносторонний. В этом
треугольнике:
O
AB 2 HB 2OHtg HOB 2 3tg30 2
33. Задача №30
Найдите радиус окружности, вписанной в правильныйшестиугольник со стороной √3 .
О
Угол между сторонами правильного
шестиугольника равен 120°. Рассмотрим треугольник FEA
и применим теорему косинусов:
r
d AE 1
AF 2 EF 2 2 AF EF cos AFE
2
2
2
1
2 3(1 cos 120 ) 1,5
2
34. Задачи для самостоятельного решения
35. Задача №1 Решите самостоятельно
1) Радиус окружности, вписанной в правильныйтреугольник, равен 31. Найдите высоту этого
треугольника.
2) Радиус окружности, вписанной в правильный
треугольник, равен 16. Найдите высоту этого
треугольника.
3) Радиус окружности, вписанной в правильный
треугольник, равен 24. Найдите высоту этого
треугольника.
36. Задача №2 Решите самостоятельно
1) Найдите радиус окружности, вписанной в квадрат состороной 26.
2) Найдите радиус окружности, вписанной в квадрат со
стороной 44.
3) Найдите радиус окружности, вписанной в квадрат со
стороной 84.
37. Задача №3 Решите самостоятельно
1) Окружность, вписанная в равнобедренный треугольник,делит в точке касания одну из боковых сторон на два
отрезка, длины которых равны 10 и 1, считая от вершины,
противолежащей основанию. Найдите периметр
треугольника.
2) Окружность, вписанная в равнобедренный треугольник,
делит в точке касания одну из боковых сторон на два
отрезка, длины которых равны 15 и 5, считая от вершины,
противолежащей основанию. Найдите периметр
треугольника.
38. Задача №4 Решите самостоятельно
1) Боковые стороны трапеции, описанной околоокружности, равны 27 и 4. Найдите среднюю
линию трапеции.
Ответ: 15,5
2) Боковые стороны трапеции, описанной около
окружности, равны 1 и 11.
 Найдите среднюю
Найдите среднююлинию трапеции.
3) Боковые стороны трапеции, описанной около
окружности, равны 22 и 3. Найдите среднюю
линию трапеции.
39. Задача №5 Решите самостоятельно
1) Около окружности описана трапеция, периметркоторой равен 84. Найдите ее среднюю линию.
2) Около окружности описана трапеция, периметр
которой равен 32. Найдите ее среднюю линию.
3) Около окружности описана трапеция, периметр
которой равен 188. Найдите ее среднюю линию.
40. Задача №6 Решите самостоятельно
1) Периметр прямоугольной трапеции, описаннойоколо окружности, равен 100, ее большая
боковая сторона равна 42. Найдите радиус
окружности.
2) Периметр прямоугольной трапеции, описанной
около окружности, равен 64, ее большая боковая
сторона равна 28. Найдите радиус окружности.
41. Задача №7 Решите самостоятельно
1) В четырехугольник ABCD вписана окружность,AB=22 , CD=77 . Найдите периметр
четырехугольника.

2) В четырехугольник ABCD вписана окружность,
AB=14 , CD=60 . Найдите периметр
четырехугольника.
3) В четырехугольник ABCD вписана окружность,
AB=20 , CD=55 . Найдите периметр
четырехугольника.
42. Задача №8 Решите самостоятельно
1) В четырехугольник ABCD вписанаокружность AB=12, BC=4 и CD=46. Найдите
четвертую сторону четырехугольника. Ответ:54
2) В четырехугольник ABCD вписана
окружность AB=8, BC=8 и CD=33. Найдите
четвертую сторону четырехугольника.
3) В четырехугольник ABCD вписана
окружность AB=7, BC=14 и CD=13. Найдите
четвертую сторону четырехугольника.
43. Задача №9 Решите самостоятельно
1) К окружности, вписанной в треугольник ABC,проведены три касательные. Периметры отсеченных
треугольников равны 8, 23, 78. Найдите периметр
данного треугольника АВС.
2) К окружности, вписанной в треугольник ABC,
проведены три касательные. Периметры отсеченных
треугольников равны 10, 32, 24.
 Найдите периметр
Найдите периметрданного треугольника АВС.
44. Задача №11 Решите самостоятельно
1) Периметр треугольника равен 76, а радиусвписанной окружности равен 8. Найдите
площадь этого треугольника.
2) Периметр треугольника равен 38, а радиус
вписанной окружности равен 5. Найдите
площадь этого треугольника.
3) Периметр треугольника равен 90, а радиус
вписанной окружности равен 14. Найдите
площадь этого треугольника.
45. Задача №12 Решите самостоятельно
1) Площадь треугольника равна 70, а радиусвписанной окружности равен 5. Найдите
периметр этого треугольника.
2) Площадь треугольника равна 768, а радиус
вписанной окружности равен 16. Найдите
периметр этого треугольника.
3) Площадь треугольника равна 231, а радиус
вписанной окружности равен 7. Найдите
периметр этого треугольника.
46. Задача №13 Решите самостоятельно
1) Сторона правильного треугольника равна 8√3. Найдитерадиус окружности, вписанной в этот треугольник.
Ответ: 4
2) Сторона правильного треугольника равна 6√3. Найдите
радиус окружности, вписанной в этот треугольник.
3) Сторона правильного треугольника равна 28√3.
Найдите радиус окружности, вписанной в этот
треугольник.
47. Задача №14 Решите самостоятельно
1) Радиус окружности, вписанной в правильныйтреугольник, равен 25√3/6 . Найдите сторону этого
треугольника.
Ответ: 25
2) Радиус окружности, вписанной в правильный
треугольник, равен 46√3/6 . Найдите сторону этого
треугольника.
3) Радиус окружности, вписанной в правильный
треугольник, равен 11√3/6 . Найдите сторону этого
треугольника.
48. Задача №15 Решите самостоятельно
1) Около окружности, радиус которой равен 2, описанмногоугольник, площадь которого равна 41. Найдите
его периметр.
2) Около окружности, радиус которой равен 1, описан
многоугольник, площадь которого равна 27. Найдите
его периметр.
3) Около окружности, радиус которой равен 3, описан
многоугольник, площадь которого равна 66.
 Найдите
Найдитеего периметр.
49. Задача №16 Решите самостоятельно
1) Около окружности описан многоугольник, площадькоторого равна 27. Его периметр равен 54. Найдите
радиус этой окружности.
Ответ: 1
2) Около окружности описан многоугольник, площадь
которого равна 39. Его периметр равен 26. Найдите
радиус этой окружности.
3) Около окружности описан многоугольник, площадь
которого равна 78. Его периметр равен 39. Найдите
радиус этой окружности.
50. Задача №17 Решите самостоятельно
1) Катеты равнобедренного прямоугольного треугольникаравны 82+41√2 . Найдите радиус окружности,
вписанной в этот треугольник.
2) Катеты равнобедренного прямоугольного треугольника
равны 58+29√2 . Найдите радиус окружности,
вписанной в этот треугольник.
3) Катеты равнобедренного прямоугольного треугольника
равны 8+4√2 . Найдите радиус окружности, вписанной в
этот треугольник.
51. Задача №18 Решите самостоятельно
1) В треугольнике АВС, АС=37,5 , ВС=20 угол равен90°.
 Найдите радиус вписанной окружности.
Найдите радиус вписанной окружности.2) В треугольнике АВС, АС=20 , ВС=4,5 угол равен
90°. Найдите радиус вписанной окружности.
3) В треугольнике АВС, АС=24, ВС=7 угол равен 90°.
Найдите радиус вписанной окружности.
52. Задача №19 Решите самостоятельно
1) Боковые стороны равнобедренного треугольникаравны 136, основание равно 128. Найдите радиус
вписанной окружности.
2) Боковые стороны равнобедренного треугольника
равны 149, основание равно 102. Найдите радиус
вписанной окружности.
3) Боковые стороны равнобедренного треугольника
равны 404, основание равно 792. Найдите радиус
вписанной окружности.
53. Задача №21 Решите самостоятельно
1) Сторона ромба равна 20, острый угол равен 30°. Найдитерадиус вписанной окружности этого ромба.
2) Сторона ромба равна 4, острый угол равен 30°. Найдите
радиус вписанной окружности этого ромба.
3) Сторона ромба равна 96, острый угол равен 30°. Найдите
радиус вписанной окружности этого ромба.

54. Задача №22 Решите самостоятельно
1) Острый угол ромба равен 30° . Радиус вписанной в этотромб окружности равен 16,5. Найдите сторону ромба.
2) Острый угол ромба равен 30° . Радиус вписанной в этот
ромб окружности равен 13. Найдите сторону ромба.
3) Острый угол ромба равен 30° . Радиус вписанной в этот
ромб окружности равен 0,5. Найдите сторону ромба.
55. Задача №24 Решите самостоятельно
1) Периметр четырехугольника, описанного околоокружности, равен 48, две его стороны равны 19 и 25.
Найдите большую из оставшихся сторон.
2) Периметр четырехугольника, описанного около
окружности, равен 26, две его стороны равны 2 и 8.
Найдите большую из оставшихся сторон.
3) Периметр четырехугольника, описанного около
окружности, равен 56, две его стороны равны 15 и 21.
Найдите большую из оставшихся сторон.
56. Задача №25 Решите самостоятельно
1) Три стороны описанного около окружностичетырехугольника относятся (в последовательном
порядке) как 1 : 17 : 23.
 Найдите большую сторону этого
Найдите большую сторону этогочетырехугольника, если известно, что его периметр
равен 48.
2) Три стороны описанного около окружности
четырехугольника относятся (в последовательном
порядке) как 2 : 13 : 28. Найдите большую сторону этого
четырехугольника, если известно, что его периметр
равен 60.
57. Задача №26 Решите самостоятельно
1) Около окружности, радиус которой равен 45√2 , описанквадрат. Найдите радиус окружности, описанной около
этого квадрата.
2) Около окружности, радиус которой равен 32√2 , описан
квадрат. Найдите радиус окружности, описанной около
этого квадрата.
3) Около окружности, радиус которой равен 50√2 , описан
квадрат. Найдите радиус окружности, описанной около
этого квадрата.
58. Задача №28 Решите самостоятельно
1) Около окружности, радиус которой равен 4, описанмногоугольник, периметр которого равен 57. Найдите
его площадь.
2) Около окружности, радиус которой равен 3, описан
многоугольник, периметр которого равен 62.
 Найдите
Найдитеего площадь.
3) Около окружности, радиус которой равен 1, описан
многоугольник, периметр которого равен 8. Найдите
его площадь.
59. Задача №29 Решите самостоятельно
1) Найдите сторону правильного шестиугольника,описанного около окружности, радиус которой равен
17√3
2) Найдите сторону правильного шестиугольника,
описанного около окружности, радиус которой равен
37√3 .
3) Найдите сторону правильного шестиугольника,
описанного около окружности, радиус которой равен
40√3 .
60. Задача №30Решите самостоятельно
1) Найдите радиус окружности, вписанной вправильный шестиугольник со стороной 84√3 .
2) Найдите радиус окружности, вписанной в
правильный шестиугольник со стороной 52√3 .
3) Найдите радиус окружности, вписанной в
правильный шестиугольник со стороной 70√3 .
61. Интернет источники
• https://fotki.yandex.ru/next/users/nata-komiati/album/158683/view/670127?page=3• https://img-fotki.
 yandex.ru/get/15541/83186431.80f/0_a2852_7a2e97ba_S
yandex.ru/get/15541/83186431.80f/0_a2852_7a2e97ba_S• Шаблон подготовила учитель русского языка и литературы Тихонова Надежда Андреевна
• «Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа:
http://mathb.reshuege.ru
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
Автор и источник заимствования неизвестен
Около окружности радиус которой равен
Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 29, 53. Найдите периметр данного треугольника.
Три
стороны описанного около окружности
четырехугольника относятся (в
последовательном порядке) как
. Найдите большую сторону этого
четырехугольника, если известно, что
его периметр равен 20.
Найдите большую сторону этого
четырехугольника, если известно, что
его периметр равен 20.
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 20.
Периметр четырехугольника, описанного около окружности, равен 56, две его стороны равны 15 и 21. Найдите большую из оставшихся сторон.
В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника
Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 37. Найдите радиус окружности.
Около окружности описана трапеция, периметр которой равен 100. Найдите ее среднюю линию.
Боковые стороны трапеции, описанной около окружности, равны 21 и 3. Найдите среднюю линию трапеции.
Окружность,
вписанная в равнобедренный треугольник,
делит в точке касания одну из боковых
сторон на два отрезка, длины которых
равны 6 и 1, считая от вершины, противолежащей
основанию. Найдите периметр треугольника
Найдите периметр треугольника
Боковые стороны равнобедренного треугольника равны 596, основание равно 408. Найдите радиус вписанной окружности.
В треугольнике ABC , , угол C равен . Найдите радиус вписанной окружности.
Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 22. Найдите гипотенузу c этого треугольника. В ответе укажите
Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
Периметр правильного шестиугольника равен 156. Найдите диаметр описанной окружности.
Углы A, B и C четырехугольника ABCD относятся как
.
Найдите угол D, если около данного
четырехугольника можно описать
окружность.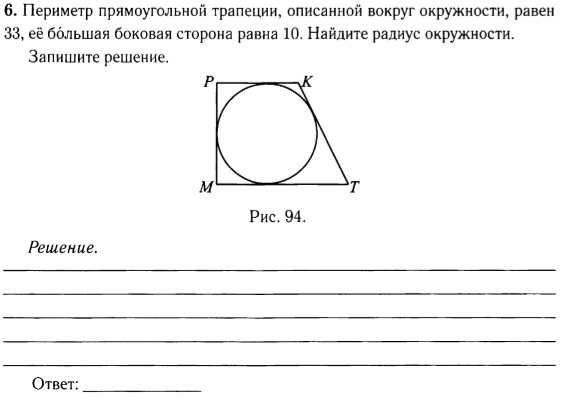 Ответ дайте в градусах.
Ответ дайте в градусах.
Два угла вписанного в окружность четырехугольника равны и . Найдите больший из оставшихся углов. Ответ дайте в градусах.
Основания равнобедренной трапеции равны 288 и 84. Радиус описанной окружности равен 150.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 94. Найдите радиус описанной окружности этой трапеции.
Около трапеции описана окружность. Периметр трапеции равен 10, средняя линия равна 4. Найдите боковую сторону трапеции.
Боковые стороны равнобедренного треугольника равны 32,5, основание равно 60. Найдите радиус описанной окружности этого треугольника
Сторона AB треугольника ABC равна 44. Противолежащий ей угол C равен . Найдите радиус окружности, описанной около этого треугольника
Угол C треугольника ABC, вписанного в
окружность радиуса 18, равен
./%D0%9E%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D1%8C/2.jpg) Найдите сторону AB этого треугольника.
Найдите сторону AB этого треугольника.
Сторона AB треугольника ABC равна 41. Противолежащий ей угол C равен . Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен .
Найдите высоту трапеции, в которую вписана окружность радиуса 35.
Острый угол ромба равен . Радиус вписанной в этот ромб окружности равен 4,5.
Найдите сторону ромба.
Сторона ромба равна 66, острый угол равен . Найдите радиус вписанной окружности этого ромба.
Найдите сторону квадрата, описанного около окружности радиуса 7.
Радиус окружности, вписанной в правильный треугольник, равен . Найдите сторону этого треугольника.
Сторона
правильного треугольника равна
.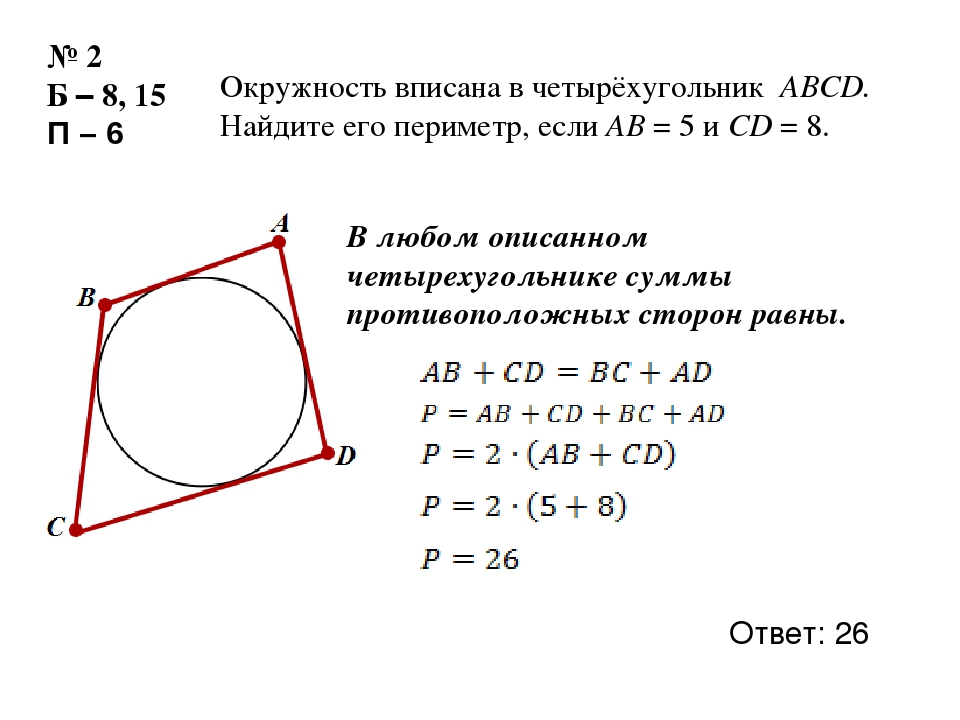 Найдите радиус окружности, вписанной
в этот треугольник.
Найдите радиус окружности, вписанной
в этот треугольник.
Радиус окружности, вписанной в правильный треугольник, равен 34. Найдите высоту этого треугольника.
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 78.
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 15
Меньшая сторона прямоугольника равна 8. Угол между диагоналями равен . Найдите радиус описанной окружности этого прямоугольника
Найдите сторону квадрата, вписанного в окружность радиуса .
Найдите радиус окружности, описанной около квадрата со стороной, равной .
Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 9.
Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 22 и .
Боковая
сторона равнобедренного треугольника
равна 11, угол при вершине, противолежащей
основанию, равен
. Найдите диаметр описанной окружности
этого треугольника
Найдите диаметр описанной окружности
этого треугольника
треугольнике ABC , угол C равен . Радиус описанной окружности этого треугольника равен 16. Найдите AC.
В треугольнике ABC , , угол C равен . Найдите радиус описанной окружности этого треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен 40. Найдите гипотенузу этого треугольника.
Гипотенуза прямоугольного треугольника равна 56. Найдите радиус описанной окружности этого треугольника.
Радиус окружности, описанной около правильного треугольника, равен 6. Найдите высоту этого треугольника.
Высота правильного треугольника равна 36. Найдите радиус окружности, описанной около этого треугольника.
Радиус окружности, описанной около правильного треугольника, равен . Найдите сторону этого треугольника.
Сторона
правильного треугольника равна
.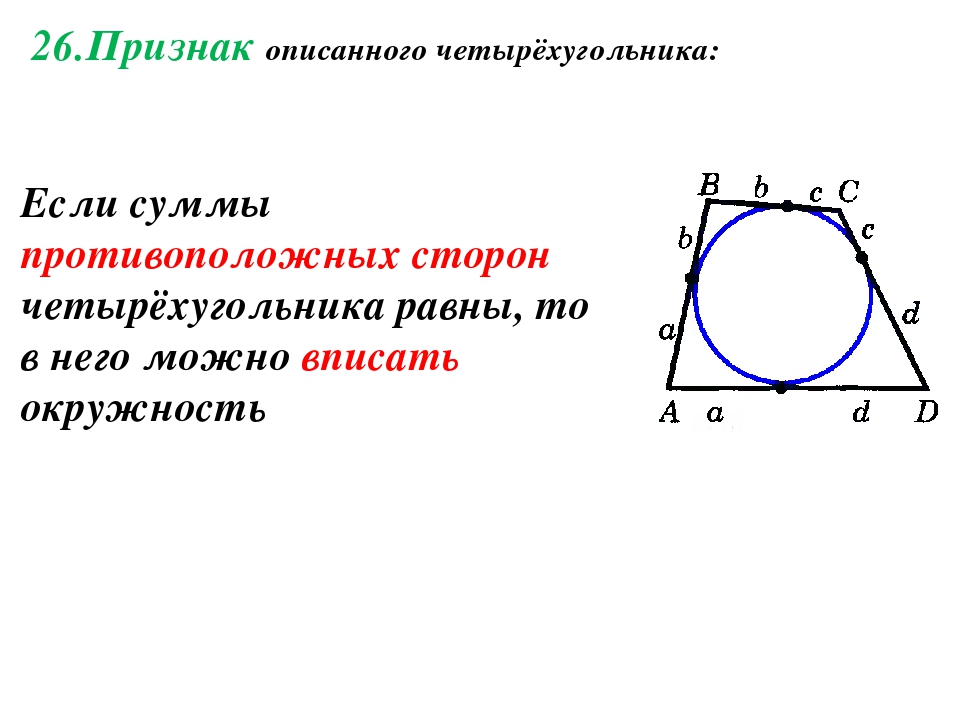 Найдите радиус окружности, описанной
около этого треугольника.
Найдите радиус окружности, описанной
около этого треугольника.
Угол ACB равен . Градусная величина дуги AB окружности, не содержащей точек D и E, равна . Найдите угол DAE. Ответ дайте в градусах
Угол ACO равен . Его сторона CA касается окружности. Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах
Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Касательные CA и CB к окружности образуют угол ACB, равный . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
Через
концы A, B дуги окружности в
проведены
касательные AC и BC.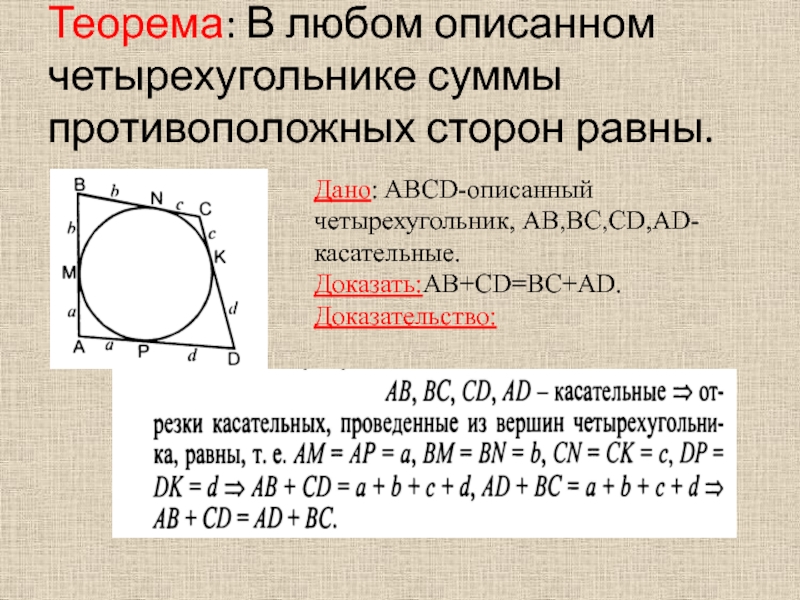 Найдите угол ACB. Ответ дайте в градусах.
Найдите угол ACB. Ответ дайте в градусах.
Угол между хордой AB и касательной BC к окружности равен . Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC равен , угол ABD равен . Найдите угол CAD. Ответ дайте в градусах.
Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как . Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно , , , . Найдите угол B этого четырехугольника. Ответ дайте в градусах
Угол A четырехугольника ABCD, вписанного
в окружность, равен
. Найдите угол C этого четырехугольника.
Ответ дайте в градусах.
Найдите угол C этого четырехугольника.
Ответ дайте в градусах.
Задачи В8 ЕГЭ по математике. Многоугольник и окружность
Продолжаем решать простейшие геометрические задачки. Разбираем Задачи №6 ЕГЭ по математике.
Сегодня работаем с окружностью, вписанной в многоугольник и описанной около многоугольника.
Вы можете пройти автотренинг «Планиметрия»
В категорию «Задачи №6» входят также задачи следующих типов + показать
Окружность, вписанная в многоугольник
Задача 1.
Найдите радиус окружности, вписанной в квадрат со стороной 16.
Решение: + показать
Задача 2.
Сторона ромба равна 58, острый угол равен 30˚. Найдите радиус вписанной окружности этого ромба.
Решение: + показать
Задача 3.
Найдите высоту трапеции, в которую вписана окружность радиуса 14.
Решение: + показать
Высота трапеции – есть диаметр вписанной окружности в трапецию.
=>
Ответ: 28.
Задача 4.
Боковые стороны трапеции, описанной около окружности, равны 19 и 13. Найдите среднюю линию трапеции.
Решение: + показать
Задача 5.
Периметр прямоугольной трапеции, описанной около окружности, равен 80, ее большая боковая сторона равна 30. Найдите радиус окружности.
Решение: + показать
Задача 6.
В четырехугольник ABCD вписана окружность, AB=52, CD=53. Найдите периметр четырехугольника.
Решение: + показать
Раз в выпуклый четырехугольник вписана окружность, то (ранее эту формулу применяли для трапеции (что являлось частным случаем применения формулы).
.
Ответ: 210.
Задача 7.
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:17:23 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 84.
Решение: + показать
Задача 8.
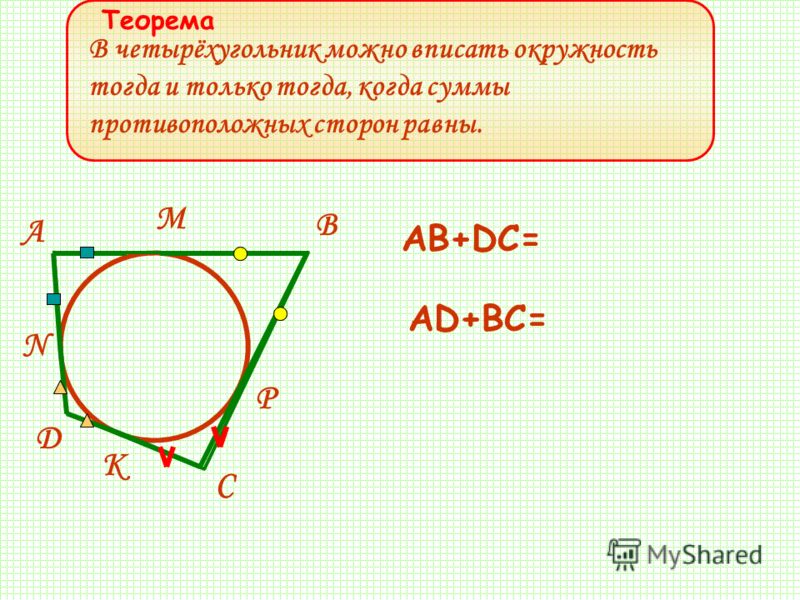
Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
Решение: + показать
Сторона квадрата вдвое больше радиуса вписанной в него окружности. Поэтому сторона квадрата равна . Радиус описанной вокруг квадрата окружности равен половине его диагонали. Поэтому радиус описанной окружности есть
Ответ: 6.
Задача 9.
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен .
Решение: + показать
Окружность, описанная около многоугольника
Задача 1.
Угол A четырехугольника ABCD, вписанного в окружность, равен 26˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение: + показать
Задача 2.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 78˚, 107˚, 39˚, 136˚.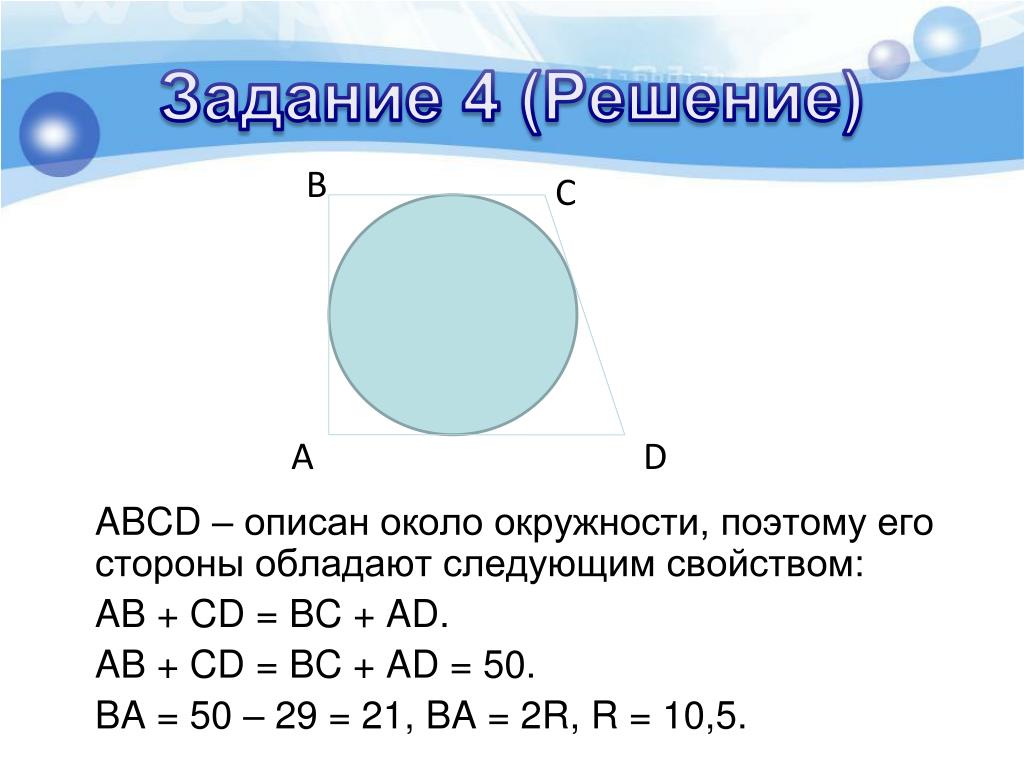 Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение: + показать
Вписанный угол опирается на дугу , равную 78˚+136˚=214˚.
Значит сам угол равен
Ответ: 107.
Задача 3.
Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 1:2:7:26. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
Решение: + показать
Задача 4.
Четырехугольник ABCD вписан в окружность. Угол ABC равен 38˚, угол CAD равен 33˚. Найдите угол ABD. Ответ дайте в градусах.
Решение: + показать
Задача 5.
Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и .
Решение: + показать
Задача 6.
Найдите сторону квадрата, вписанного в окружность радиуса .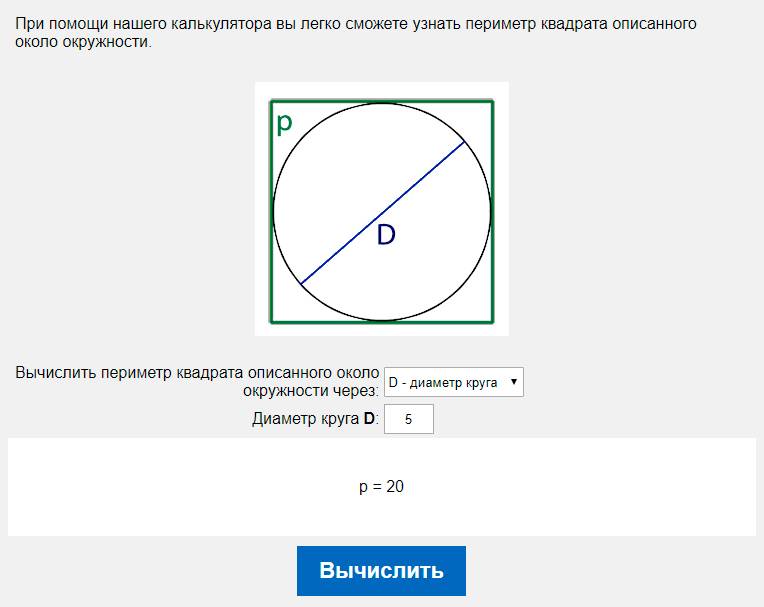
Решение: + показать
Диагональ квадрата – диаметр окружности.
Обозначим сторону квадрата за .
Из треугольника по т. Пифагора
Ответ: 90.
Задача 7.
Меньшая сторона прямоугольника равна 16. Угол между диагоналями равен 60˚. Найдите радиус описанной окружности этого прямоугольника.
Решение: + показать
Диагонали прямоугольника – диаметры окружности.
Треугольник – равносторонний, так как
Значит, .
Ответ: 16.
Задача 8.
Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.
Решение: + показать
Задача 9.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60˚, большее основание равно 82. Найдите радиус описанной окружности этой трапеции.
Решение: + показать
Задача 10.
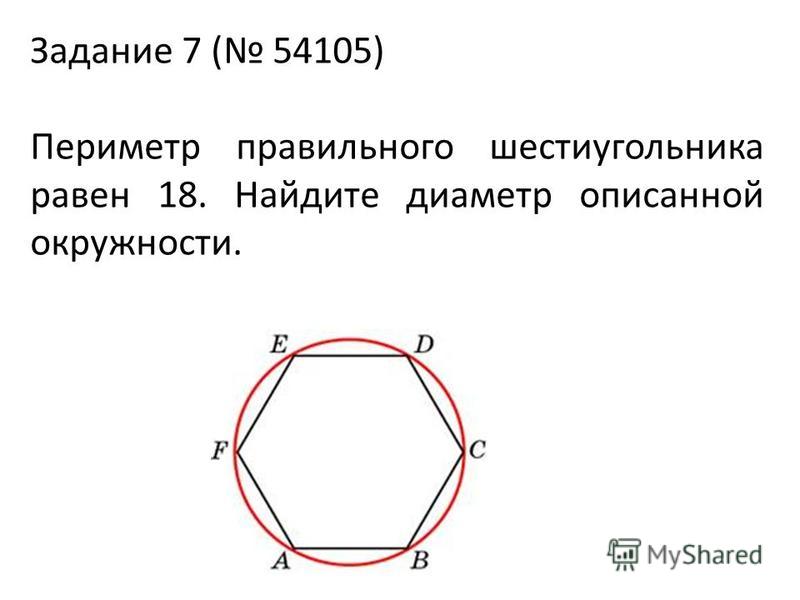
Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Решение: + показать
Задача 11.
Два угла вписанного в окружность четырехугольника равны 56˚ и 99˚. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Решение: + показать
Данные два угла не могут быть противоположными, так как иначе их сумма должна была бы быть 180˚ (так как они опираются на дополняющие друг друга дуги до окружности).
Если , то
Если , то
Угол и есть наибольший.
Ответ: 124.
Задача 12.
Найдите радиус окружности, описанной около прямоугольника , если стороны квадратных клеток равны 1.
Решение: + показать
Диаметр описанной окружности около прямоугольника – диагональ прямоугольника.
Ответ: 2,5.
Задача 13.
Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.
Решение: + показать
Задача 14.
Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 72˚. Найдите n.
Решение: + показать
Задача 15.
Около окружности, радиус которой равен , описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
Решение: + показать
Самое время отдохнуть! –>+ показать
Кто-то развлекается так. А вы как?Вы можете пройти тест по теме «Окружность и многоугольник».
|
|
|
содержание .
Задание №3698
В треугольнике ABC AC=18, BC=80, угол C равен 90° . Найдите радиус окружности, вписанной в этот треугольник Решение Радиус вписанной в прямоугольный треугольник окружности равен половине разности суммы катетов и гипотенузы: Подставим в формулу вместо значение AC и BC и решим уравнение Радиус r=8 Ответ: 8
Задание №3680 Площадь треугольника АВС равна 137. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED Решение
Площадь трапеции ABED можно найти как разность площадей двух треугольников: Площадь треугольника CED будет в 4 раза меньше площади треугольника ABC, так как линейные размеры треугольника CED в 2 раза меньше соответствующих размеров треугольника ABC По найденной формуле вычисляем, что площадь трапеции ABED=102,75 Ответ: 102,75
Задание №4939
Дан четырёхугольник ABCD. 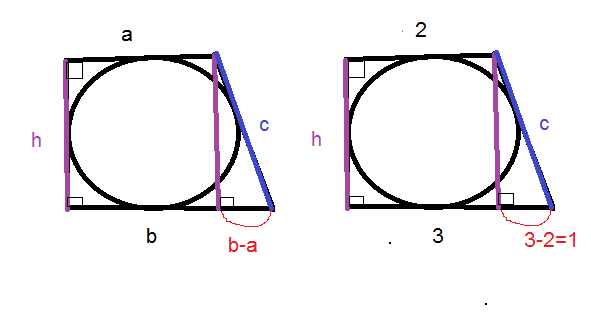 В него вписана окружность, сторона CD= 93, AB= 99
. Рассчитайте периметр четырёхугольника ABCD В него вписана окружность, сторона CD= 93, AB= 99
. Рассчитайте периметр четырёхугольника ABCDРешение В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD Периметр (P) четырехугольника – это сумма длин всех его сторон, то есть P=AB+BC+AD+CD= 2*(AB+CD) P = 384 Ответ: 384
Задание №4945
Дан четырехугольник ABCD. В него вписана окружность, AB= 30, BC=7, CD=56. Рассчитайте четвертую сторону четырехугольника Решение В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD Сторона AD=AB+CD-BC=30+56-7=79 Ответ: 79
Задание №2355
Дан правильный шестиугольник. Его периметр равен 474. Найдите диаметр описанной окружности Решение
Периметр (P) — сумма длин всех сторон, поэтому: AB / 6 = P / 6 =474 / 6 = 79 Рассмотрим угол AOB.  Он равен 60°, т.к. вся окружность 360°, а треугольников 6 (360°/6=60°)
Рассмотрим треугольник AOB. Он равносторонний, т.к. AO=OB=R и угол AOB=60° и тогда
Диаметр D=2R=2AB=2*79=158
Ответ: 158 Он равен 60°, т.к. вся окружность 360°, а треугольников 6 (360°/6=60°)
Рассмотрим треугольник AOB. Он равносторонний, т.к. AO=OB=R и угол AOB=60° и тогда
Диаметр D=2R=2AB=2*79=158
Ответ: 158
Задание №1667
У трапеции, описанной около окружности, боковые стороны равны 47 и 38 . Найдите среднюю линию трапеции Решение В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD Средняя линия MK = (DC+AB) / 2 = (AD+BC) / 2 = 85 / 2 = 42,5 Ответ: 42,5
Задание №2329
Два известных угла вписанного в окружность четырехугольника равны 44° и 129°. Найдите больший из оставшихся углов. Ответ дайте в градусах. Решение По теореме Птолемея — сумма противоположных углов в четырехугольнике, вписанном в окружность равна 180 градусов угол противоположный углу 44 градусов равен 180-44=136 градусов угол противоположный углу 129 градусов равен 180-129=51 градусов Больший из неизвестных углов 136 градусов Ответ: 136
Задание №3515
Боковые стороны в равнобедренном треугольнике равны 35, основание равно 42 .  Рассчитайте радиус окружности, вписанной в этот треугольник Рассчитайте радиус окружности, вписанной в этот треугольникРешение Радиус вписанной окружности равен отношению площади к полупериметру. Для нахождения площади, воспользуемся формулой Герона:
Подставим значения сторон треугольника и найдём площадь. Она равна S=588 Подствавим значения и найдём полупериметр P=56 Тогда: Подствавим значения и найдём радиус r=588/56=10,5 Ответ: 10,5
Задание №2458
Основания равнобедренной трапеции равны 24 и 32. Радиус описанной окружности равен 20. Центр окружности лежит внутри трапеции. Необходимо найти высоту трапеции Решение Проведем высоту KH через центр окружности O Из рисунка видно, что треугольники DOC и AOB – равнобедренные и их высоты KO и HO делят стороны DC и AB пополам. Найдем эти высоты из прямоугольных треугольников DKO и AOH по теореме Пифагора, имеем: Подставим известные значения в формулы и вычислим KO и HO KO=16 HO=12 Следовательно, высота трапеции равна KH=KO+HO=16+12=28 Примечание: Если бы большее основание трапеции лежало выше центра окружности (то есть оба основания располагались по одну сторону от центра окружности) длина высоты равнялась бы не сумме, а разности найденных отрезков.  Решая данную задачу необходимо принимать во внимание рисунок, данный в условии
Ответ: 28 Решая данную задачу необходимо принимать во внимание рисунок, данный в условии
Ответ: 28
Задание №4548 Основания равнобедренной трапеции равны 216 и 54. Синус острого угла трапеции равен 0,8. Рассчитайте боковую сторону
Решение Треугольники ADH и BKC равны (так как AD=CD и DH=CK), значит, AH=KB Треугольник ADH прямой, поэтому гипотенуза AD = AH / cos(a) По найденной формуле вычисляем, что AD=135 Ответ: 135
Задание №1949
Окружность вписана в треугольник ABC, к ней проведены три касательные. Периметры отсеченных треугольников равны 25, 58, 87. Найдите периметр данного треугольника Решение
EF и ED — отрезки касательных, проведенных из одной точки Е. Они по свойству касательных равны. Аналогично, GF = GH. То есть, GE = GH + ED, а периметр треугольника AGE запишется как =25+58+87=170 Ответ: 170
Задание №3491
В четырёхугольник ABCD вписана окружность, сторона AB= 97, периметр P= 396 .  Найдите длину стороны CD Найдите длину стороны CDРешение В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD Значит P / 2 = AB + CD CD = P/2-AB=101 Ответ: 101
Задание №2221 Дан параллелограмм ABCD. Его площадь равна 143. Точка E – середина стороны BC. Рассчитайте площадь трапеции ADEB Решение
Разобьём параллеаграмм ABCD на равные треугольники (как на рисунке) — всего их 4, трапеция ADEB, состоит из трёх таких треугольников, значит площадь трапеции ADEB равна 3/4 от площади параллеаграмма ABCD По найденной формуле вычисляем, что площадь трапеции ADEB=107,25 Ответ: 107,25
Задание №3988 Площадь параллелограмма ABCD равна 144. Середина стороны CD — точка E. Вычислите площадь треугольника ADE Решение
Разобьём параллеаграмм ABCD на равные треугольники (как на рисунке) — всего их 4, треугольник ADE, состоит из одного такого треугольника, значит его площадь равна 1/4 от площади параллеаграмма ABCD По найденной формуле вычисляем, что площадь треугольника ADE=36 Ответ: 36
Задание №1237
Катеты прямоугольного равнобедренного треугольника равны 34+17√2 .  Вычислите радиус окружности, вписанной в этот треугольник Вычислите радиус окружности, вписанной в этот треугольникРешение Пусть катеты прямоугольного треугольника равны a, тогда гипотенуза AB, равна: Радиус вписанной в прямоугольный треугольник окружности равен половине разности суммы катетов и гипотенузы: Подставим в формулу вместо а значение катетов и решим уравнение Радиус r=17 Ответ: 17
Задание №1813
В равнобедренный треугольник вписана окружность, которая делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 55 и 20, считая от вершины, противолежащей основанию. Рассчитайте периметр треугольника Решение
Пусть точки H и K являются точками касания окружности и сторон AB и СВ соответственно. Треугольники KOH и KOB равны, т.к. являются прямоугольными с общей гипотенузой и равными катетами, значит, HB=KB=20 Периметр треугольника равен P=AC+CB+AH+HB=2CB+2HB=150+40=190 Ответ: 190
Задание №4253
Дана прямоугольная трапеция, описанная около окружности.  Периметр трапеции равен 104,
большая боковая сторона трапеции равна 50
. Рассчитайте радиус окружности Периметр трапеции равен 104,
большая боковая сторона трапеции равна 50
. Рассчитайте радиус окружностиРешение Сторона AD равна диаметру окружности, значит R=AD/2 В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD R = 1 Ответ: 1
Задание №2447
Дана трапеция, описанная около окружности. Периметр трапеции равен 46. Найдите длину средней линии трапеции Решение Периметр (Р) — сумма всех сторон трапеции В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD
Средняя линия MK = 46 / 4 = 11,5 Ответ: 11,5
Задание №4705 Угол между соседними двумя сторонами правильного многоугольника, вписанного в окружность, равен 140°. Рассчитайте число вершин многоугольника Решение Каждый угол правильного многоугольника равен 180° * (n – 2) / n , где n – число его углов (вершин) Составляем уравнение: 180 * ( n – 2 ) / n=140 180*n – 360 = 140 * n n=9 Ответ: 9
Задание №4465 Площадь параллелограмма ABCD равна 130.  Середины его сторон являются вершинами параллелаграмма A′B′C′D′.
Рассчитайте площадь параллелограмма A′B′C′D′ Середины его сторон являются вершинами параллелаграмма A′B′C′D′.
Рассчитайте площадь параллелограмма A′B′C′D′Решение
Разобьём параллеаграмм ABCD на равные треугольники (как на рисунке) — всего их 8, параллелограмм A′B′C′D′ состоит из четырёх таких треугольников, значит, его площадь равна 1/2 от площади параллеаграмма ABCD По найденной формуле вычисляем, что площадь параллелограмма A′B′C′D′=65 Ответ: 65
содержание .. 86 87 88 89 ..
|
|
Четырехугольники. Параллелограмм и трапеция. — Математика
Файл к занятию 5.
Проверка домашнего задания
Задание 6. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 12
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 12
Задание 10. Найдите радиус описанной около равнобедренного треугольника окружности, если его основание 12, а высота, проведенная к нему, равна 9.
Решение:
Способ1: Воспользуемся формулой для нахождения радиуса описанной окружности R= . Нам необходимо найти площадь треугольника и длину боковой стороны. S= Высота в равнобедренном треугольнике, проведенная к основанию, является биссектрисой и медианой. Рассмотрим треугольник ACH. Длину боковой стороны AC найдем по теореме Пифагора: R=.
Способ2: Воспользуемся теоремой синусов . Рассмотрим треугольник ACH. Аналогично предыдущему способу найдем АС, а затем .
Ответ: 6,5
Четырехугольники
Выпуклые четырехугольники
Выпуклый четырехугольник — четырехугольник, который расположен по одну сторону от любой из своих сторон.
Сумма углов выпуклого четырехугольника равна 360˚.
Средняя линия — отрезок прямой, соединяющий середины противоположных сторон.
Параллелограмм, его признаки и свойстваПараллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
В параллелограмме противоположные стороны равны и противоположные углы равны: AB=CD, BC=AD, угол ABD равен углу ADC и угол BCD равен углу BAD.
Диагонали параллелограмма точкой пересечения делятся пополам: AO=OC, OB=OD.
Углы, прилежащие к любой стороне, в сумме равны 180˚.
Диагонали параллелограмма делят его на два равных треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC² + BD² = 2AB² + 2BC².
Признаки параллелограмма:
Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства:
Признак прямоугольника: Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Ромб — параллелограмм, у которого все стороны равны.
Свойства:
Все свойства параллелограмма.
Диагонали ромба взаимно перпендикулярны.
Диагонали ромба делят углы ромба пополам.
Признаки ромба:
Если в параллелограмме диагонали взаимно перпендикулярны, то этот параллелограмм — ромб.
Если в параллелограмме диагонали делят углы пополам, то этот параллелограмм — ромб.
Квадрат – параллелограмм, у которого все стороны равны и все углы — прямые; или прямоугольник, у которого все стороны равны; или ромб, у которого все углы — прямые.
Свойства:
Задание 1. Один угол параллелограмма больше другого на 40°. Найдите больший угол. Ответ дайте в градусах. Ответ:110
Ответ дайте в градусах. Ответ:110
Задание 2. В ромбе ABCD угол DAB равен 148°. Найдите угол BDC. Ответ дайте в градусах.
Решение: В любом параллелограмме сумма углов, прилежащих к одной стороне, равна 180 Следовательно, угол ADC равен 180-148=32Помним, что диагонали ромба делят его углы пополам. Значит, угол BDC равнее 32:2=16. Ответ:16.
Задание 3. В параллелограмме ABCD sin C=, AD=21. Найдите высоту, опущенную на сторону AB. Ответ: 9
Задание 4. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 6. Найдите диагональ данного прямоугольника. Ответ: 12
Трапеция, ее признаки и свойства
Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие —боковыми сторонами.
Высота трапеции — расстояние между прямыми, на которых лежат основания трапеции, любой общий перпендикуляр этих прямых.
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон.
Прямоугольная трапеция — трапеция, у которой один из углов при основании равен 90˚.
Равнобедренная трапеция — трапеция, у которой боковые стороны равны AB = CD. Тогда равны диагонали AC = BD и углы при основаниях.
Задание 5. Найдите среднюю линию трапеции, если ее основания равны 48 и 72. Ответ:60
Задание 6. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 74 и 41. Найдите среднюю линию этой трапеции. Ответ:74
Ответ:74
Вписанные и описанные четырехугольники
Окружность называется вписанной в четырехугольник, если она касается всех сторон четырехугольника. В этом случае четырехугольник называется описанным около окружности.
Четырехугольник можно описать около окружности тогда и только тогда, когда суммы противолежащих сторон равны. AD+ CB= AB + DC
Окружность называется описанной около четырехугольника, если все его вершины лежат на окружности. В этом случае четырехугольник называется вписанным в окружность.
Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180
Помним:
Вокруг прямоугольника всегда можно описать окружность.

В ромб всегда можно вписать окружность.
Из всех трапеций только около равнобедренной трапеции можно описать окружность.
Задание 7. Два угла вписанного в окружность четырёхугольника
равны 56° и 77°. Найдите меньший из оставшихся углов. Ответ дайте в градусах. Ответ:103
Задание 8. В четырёхугольник ABCD вписана окружность, AB=13, BC=7 и AD=11. Найдите четвёртую сторону четырёхугольника.Ответ:5
Задание 9. В четырёхугольник ABCD вписана окружность, AB=22, CD=17. Найдите периметр четырёхугольника ABCD.Ответ:78
Задание10.Найдите высоту трапеции, в которую вписана окружность радиуса 47. Ответ:94
Задание11. Боковые стороны трапеции, описанной около окружности, равны 12 и 15. Найдите среднюю линию трапеции. Ответ:13,5
Решение задач на вычисление площади
Площадь четырехугольника
Любой четырехугольник можно разбить на треугольники, и его площадь будет равна сумме площадей треугольников.

Если в четырехугольник можно вписать окружность, то его площадь равна: .
Если четырехугольник вписан в окружность, то его площадь будет равна
Следствие:
Площадь ромба равна: .
Площадь квадрата: .
Площадь прямоугольника: .
Площадь параллелограмма: .
Площадь трапеции: .
Задание 12. Найдите площадь ромба, если его стороны равны 23, а один из углов равен 150°.
Решение: Площадь ромба можно вычислить по формуле: Подставляя в формулу данные задачи получаем Ответ:264,5
Задание 13. Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба. Ответ:48
Задание 14. Найдите периметр прямоугольника, если его площадь равна 176, а отношение соседних сторон равно 4 : 11. Ответ:60
Ответ:60
Задание 15. Стороны параллелограмма равны 5 и 10. Высота, опущенная на меньшую из этих сторон, равна 3. Найдите высоту, опущенную на большую сторону параллелограмма. Ответ:1,5
Задание 16. Найдите площадь квадрата, если его диагональ равна 1.
Решение : Задачу можно решить по-разному, но наиболее простой способ- использовать формулу для вычисления площади ромба=0,5. Ответ:0,5
Задание 17. Основания равнобедренной трапеции равны 12 и 18, а ее площадь равна 60. Найдите периметр трапеции. Ответ: 40.
Задание 18. Площадь параллелограмма ABCD равна 132. Точка G — середина стороны CD. Найдите площадь трапеции ABGD.
Решение: Проведем диагональ BD. Диагональ параллелограмма делит его на два равных треугольника. Значит, площадь треугольника DBC равна площади треугольника DAB и равна132:2= 66. Рассмотрим треугольник DBC. В этом треугольнике BG является медианой. По свойству медианы, она делит треугольник на два равновеликих треугольника. Следовательно, площадь треугольника BGC равна 66:2=33. Площадь трапеции ABGD равна разности площадей параллелограмма ABCD и треугольника BGC. Площадь трапеции ABGD: 132-33=99. Ответ: 99
По свойству медианы, она делит треугольник на два равновеликих треугольника. Следовательно, площадь треугольника BGC равна 66:2=33. Площадь трапеции ABGD равна разности площадей параллелограмма ABCD и треугольника BGC. Площадь трапеции ABGD: 132-33=99. Ответ: 99
Площади фигур на квадратной решетке
Задание19. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь. Ответ:12
Задание 20. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите его площадь.Ответ:16
Задание 21. Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.Ответ:19,5
Если необходимо найти площадь треугольника или четырехугольника, расположенного на квадратной решетке, а высоту или основание найти сложно, то можно воспользоваться следующим правилом:
1) Достройте данную фигуру до прямоугольника (или квадрата) так, чтобы прямоугольник состоял из данной фигуры и прямоугольных треугольников.
2) Чтобы вычислить площадь данной фигуры, из площади построенного прямоугольника отнимите площади полученных прямоугольных треугольников.
3) Запишите результат.
Задание 22. Найдите площадь квадрата, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение: Задачу можно решить разными способами. Давайте найдем сторону квадрата и по формуле вычислим его площадь. По теореме Пифагора сторона квадрата=. Ответ:20
Задание 23. Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.Ответ:30
Как рассчитать периметр четырехугольника
Чтобы рассчитать периметр четырехугольника, сложите измерения четырех сторон. Периметр — это расстояние вокруг фигуры. В реальных приложениях периметр — это забор вокруг двора или рамка вокруг изображения. Периметр образует двухмерную форму. Четырехугольник — это многоугольник , имеющий четыре стороны и четыре угла. Наиболее распространенные типы четырехугольников включают квадрат, прямоугольник, ромб, трапецию и параллелограмм.
Периметр образует двухмерную форму. Четырехугольник — это многоугольник , имеющий четыре стороны и четыре угла. Наиболее распространенные типы четырехугольников включают квадрат, прямоугольник, ромб, трапецию и параллелограмм.
Периметр квадрата и ромба
У квадрата и ромба по четыре равные стороны, а у квадрата четыре прямых угла. Формула периметра одинакова для обеих фигур, и вам нужно знать только размер одной стороны. Формула: 4 x s = периметр, , где s представляет длину одной стороны. Если размер одной стороны составляет 2 дюйма, умножьте 2 на 4. Периметр равен 8 дюймам.
Периметр прямоугольника и параллелограмма
Формулы для периметра прямоугольника и параллелограмма одинаковы, поскольку каждый многоугольник имеет два набора равных сторон.Формула: 2 (l + w) = периметр, , где l представляет длину, а w представляет ширину. Рассмотрим прямоугольник длиной 2 дюйма и шириной 4 дюйма. Сумма длины и ширины равна 6. Умножьте 6 на 2, и вы получите периметр в 12 дюймов.
Рассмотрим прямоугольник длиной 2 дюйма и шириной 4 дюйма. Сумма длины и ширины равна 6. Умножьте 6 на 2, и вы получите периметр в 12 дюймов.
Периметр трапеции
Формула для трапеции немного отличается, потому что трапеция — это четырехугольник, у которого есть две параллельные стороны неравной длины.Две стороны имеют одинаковую длину. Две другие стороны имеют равную длину друг друга, но длина этих двух сторон отличается от длины двух других сторон. Некоторые парты в классах имеют форму трапеции.
Формула: a + b + c + d = периметр. Каждая буква соответствует разной стороне или основанию фигуры. Например, предположим, что трапеция имеет размеры края 2, 3, 2 и 5 дюймов. Периметр равен 2 + 3 + 2 + 5, что составляет 12 дюймов.
Периметр неправильного четырехугольника
Формула неправильного четырехугольника — многоугольника с четырьмя сторонами неравной длины — такая же, как у трапеции. Формула: a + b + c + d = периметр. Например, предположим, что у четырехугольника есть стороны длиной 1, 5, 3 и 4 дюйма. Периметр равен 1 + 5 + 3 + 4 или 13 дюймов.
Формула: a + b + c + d = периметр. Например, предположим, что у четырехугольника есть стороны длиной 1, 5, 3 и 4 дюйма. Периметр равен 1 + 5 + 3 + 4 или 13 дюймов.
Использование координат для определения длины стороны
Если вам известны только координаты фигуры, найдите размеры сторон, определив расстояние между точками.Например, найдите расстояние между точками A и B для одной стороны и расстояние между точками B и C для другой стороны. Затем подставьте размеры стороны в соответствующую формулу, чтобы определить периметр.
Периметр квадрата — Веб-формулы
Квадрат — это правильный четырехугольник, у него четыре равные стороны и четыре равных угла (угол 90 градусов или прямые углы).
Квадратный четырехугольник с вершинами ABCD обозначается ABCD. Периметр квадрата (четырехугольника) определяется по формуле:
P = 4a
Где a — длина каждой стороны.
Свойства квадрата:
· Диагонали квадрата (четырехугольника) делят пополам
· Диагонали квадрата (четырехугольника) делят его углы пополам.
· Диагонали квадрата (четырехугольника) перпендикулярны.
· Противоположные стороны квадрата (четырехугольника) параллельны и равны.
· Все четыре угла квадрата (четырехугольника) равны. (Квадрат равен 360/4 = 90 градусов, поэтому каждый угол квадрата (четырехугольника) является прямым.)
· Диагонали квадрата (четырехугольника) равны.
Пример 1: Найдите площадь и периметр квадрата, длина стороны которого составляет 4 метра.
Решение:
Учитывая, что:
a = 4 м
Площадь квадрата = a 2 = 4 × 4 = 16 м 2
Периметр квадрата = 4 × 4 = 16 м
Пример 2 : Найдите периметр квадрата, стороны которого равны 16 см.
Решение :
Периметр квадрата:
Пример 3: Каков периметр квадрата, если длина каждой стороны составляет 13 футов?
Решение :
Длина каждой стороны квадрата составляет 13 футов.
Периметр квадрата:
P = 4 ×
Р = 4 × 13
P = 52 футов
Периметр квадрата составляет 52 фута.
Пример 4: Периметр квадрата равен 24 см. Какой была бы длина его сторон, если бы периметр увеличился на 4 см?
Решение :
Новый периметр квадрата = 24 + 4 = 28 см.
Новый периметр квадрата = 4 × новая длина стороны квадрата
Пусть новая длина стороны квадрата = l см
a = 7 см
Пример 5: Площадь квадратного парка составляет 225 м 2 . Найдите его периметр.
Решение:
Дано:
Так как площадь составляет 225 м 2 , длину сторон можно легко определить:
A = s²
225 = s²
s = 15 м
Таким образом, периметр парка:
P = 4 × с.
P = 4 x 15 м.
P = 60 м.
Пример 6: Найдите периметр квадрата, длина стороны которого составляет 9,2 метра.
Решение :
Дано: Длина стороны (a) = 9,2 метра
Периметр квадрата = 4 ×
= 4 × 9,2
Периметр квадрата = 36,8 метра.
вопросов CAT — Вопросы по геометрии: треугольники, 2IIM CAT 2020 онлайн-классы, коучинг CAT в Ченнаи
Вопрос о геометрии CAT, который появляется в разделе «Количественные способности» экзамена CAT, широко проверяет соискателя на концепции — треугольники, круги, четырехугольники , Многоугольники и смесь вышеупомянутых концепций.На экзамене CAT обычно можно рассчитывать получить от 4 до 6 вопросов по геометрии CAT. CAT Геометрия — важная тема с большим весом на экзамене CAT. Воспользуйтесь бесплатными вопросами по CAT от 2IIM с подробными решениями и видео-пояснениями, чтобы получить отличную оценку CAT. Если вы хотите пройти эти вопросы в качестве викторины, отправляйтесь сюда, чтобы ответить на эти вопросы в формате теста, абсолютно бесплатно.
Геометрия CAT: тупоугольные треугольники — целые числа
x, y, z — целые числа, являющиеся стороной треугольника с тупым углом.Если xy = 4, найти z.
- 2
- 3
- 1
- Существует более одного возможного значения z
Геометрия CAT: равнобедренные треугольники — целые числа
Сколько равнобедренных треугольников с целыми сторонами возможны таким образом, что возможна сумма двух равнобедренных треугольников с целыми сторонами сторона 12?
CAT Геометрия: Треугольники — Площадь
Стороны треугольника равны 6, 10 и x, для какого значения x площадь △ максимума?
- 8 см
- 9 см
- 12 см
- Ни один из этих
CAT Геометрия: равносторонний треугольник и круг
Два круга помещены в равносторонний треугольник, как показано на рисунке.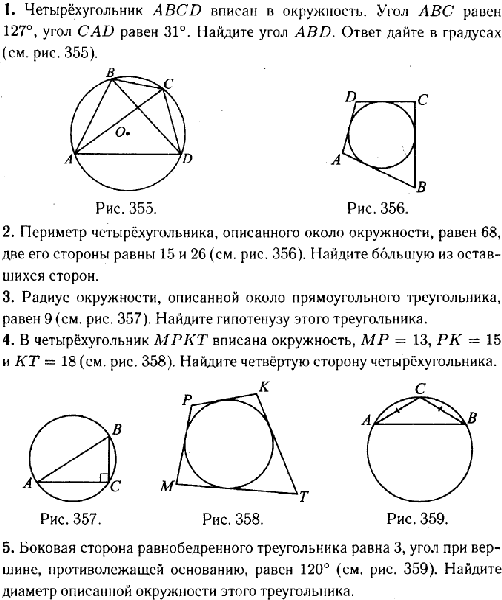 Каково отношение площади меньшего круга к площади равностороннего треугольника?
Каково отношение площади меньшего круга к площади равностороннего треугольника?
- π: 36√3
- π: 18√3
- π: 27√3
- π: 42√3
CAT Геометрия: треугольники — периметр
Периметр с целыми сторонами равен 15. Сколько таких треугольников возможно?
CAT Геометрия: равносторонний треугольник и квадрат
Имеется равносторонний треугольник с вписанным внутрь квадратом.Одна из сторон квадрата лежит на стороне равностороннего. Каково отношение площади квадрата к площади равностороннего треугольника?
- 12: 12 + 7√3
- 24: 24 + 7√3
- 18: 12 + 15√3
- 6: 6 + 5√3
Геометрия CAT: треугольники — целые числа
△ ABC имеет целые стороны x, y, z такие, что xz = 12. Сколько таких треугольников возможно?
CAT Геометрия: правильный многоугольник
ABCDE — правильный пятиугольник.O — точка внутри пятиугольника, такая что AOB — равносторонний треугольник. Что такое ∠OEA?
CAT Геометрия: Свойства треугольников
△ имеет стороны a 2 , b 2 и c 2 . Тогда треугольник со сторонами a, b, c должен быть:
- Прямоугольный
- Острый угол
- Тупоугольный
- Может быть любым из этих трех
Геометрия CAT: Свойства прямоугольного треугольника
Рассмотрим прямоугольный треугольник с внутренним радиусом 2 см и окружным радиусом 7 см.Какая площадь у треугольника?
- 32 кв. См
- 31,5 кв. См
- 32,5 кв. См
- 33 кв. См
CAT Геометрия: правильный многоугольник
Каково отношение самой длинной диагонали к самой короткой диагонали в правильном восьмиугольнике?
- √3: 1
- 2: 1
- 2: √3
- √2: 1
CAT Геометрия: высота треугольника
Найдите высоту до стороны AC треугольника со стороной AB = 20 см, AC = 20 см, BC = 30 см.
- 10√7
- 8√7
- 7,5√7
- 15√7
CAT Геометрия: правильный многоугольник
ABCDEF — правильный шестиугольник, вписанный в круг. Если самая короткая диагональ шестиугольника имеет длину 3 единицы, какова площадь заштрихованной области.
- 1/6 (3π — (9√3) / 2)
- 1/6 (2π — (6√3) / 2)
- 1/6 (3π — (8√3) / 2 )
- 1/6 (6π — (15√3) / 2)
CAT Геометрия: круги
Окружность радиусом 5 см имеет хорду RS на расстоянии 3 единиц от нее.Хорда PQ пересекается с хордой RS в точке T, так что TS = 1/3 RT. Найдите минимальное значение PQ.
CAT Геометрия: Треугольники — Площадь
Треугольник имеет периметр 6 + 2√3. Один из углов в треугольнике равен внешнему углу правильного шестиугольника, другой угол равен внешнему углу правильного 12-стороннего многоугольника. Найдите площадь треугольника.
CAT Геометрия: Четырехугольник
Площадь ромба по периметру 56 см составляет 100 см2.Найдите сумму длин его диагоналей
CAT Геометрия: Четырехугольник
Ромб имеет периметр 12 и один угол = 120 °. Найдите его область.
- 9 * (√3) / 2
- 3 * (√3) / 2
- 9 * √3
- 18 * √3
Геометрия CAT: треугольники — площадь
Круг с центром O и радиусом 25 см имеет пояс AB длиной 14 см. Найдите площадь треугольника AOB
- 144 см 2
- 121 см 2
- 156 см 2
- 168 см 2
CAT Геометрия: Круги
перпендикулярны2 хорды AB и CD пересекаются в точке P.AP = 4, PB = 6, CP = 3. Найдите радиус окружности.
- 31,25 (1/2)
- 37,5 (1/2)
- 26 (1/2)
- 52 (1/2)
CAT Геометрия: Треугольники
Треугольник ABC имеет углы A = 60 ° и B = 70 ° . Центр этого треугольника находится под углом I. Найдите угол BIC.
CAT Геометрия: Четырехугольник
Ромб со стороной 6 см имеет угол, равный внешнему углу правильного восьмиугольника.Найдите площадь ромба.
- 18√2 см 2
- 9√2 см 2
- 15√2 см 2
- 12√2 см 2
CAT Геометрия: круг, квадрат и Треугольник
В круг, вписанный в квадрат со стороной 2, вписан равносторонний треугольник. Каково отношение площадей равностороннего треугольника к площади квадрата?
- 9√3: 16
- 3√3: 4
- 9√3: 4
- 3√3: 16
CAT Геометрия: Равнобедренные треугольники
В остроугольном равнобедренном треугольнике есть два его сторон равны 10 и 16.Найдите площадь этого треугольника.
- √231 единиц
- 12√66 единиц
- 24 единиц
- 5√231 единиц
CAT Геометрия: треугольники — площадь
Три равные окружности помещены внутри равностороннего треугольника, так что любой круг по касательной к двум сторонам равностороннего треугольника и двум другим окружностям. Каково отношение площадей одного круга к площади треугольника?
- π: (6 + 4√3)
- 3π: (6 + 4√3)
- 2π: (6 + 4√3)
- π: (6 + 2√3)
CAT Геометрия: треугольник и квадрат
Имеется равносторонний треугольник с вписанным в него квадратом.Одна из сторон квадрата лежит на стороне равностороннего. Каково отношение площади квадрата к площади равностороннего треугольника?
- √3: (5 + 4√3)
- 2√3: (7 + 4√3)
- 4√3: (7 + 4√3)
- 4√3: (5 + 2√ 3)
CAT Геометрия: квадраты и круги
Рассмотрим квадрат S, вписанный в круг C, каково соотношение площадей S и C? И рассмотрим круг Q, вписанный в квадрат S, каково соотношение площадей S и Q?
- 2: π, 4: π
- 4: π, 2: π
- 1: π, 4: π
- 2: π, 1: π
CAT Геометрия: Треугольники — Площадь
Рассмотрим равносторонний треугольник T, вписанный в окружность C, каково соотношение площадей T и C? Рассмотрим окружность C, вписанную в равносторонний треугольник T, каково соотношение площадей T и C?
- 3√3: π, 3√3: 16π
- 3√3: 4π, 3√3: π
- √3: π, 3√3: 4π
- √3: π, √3: 16π
CAT Геометрия: правильный восьмиугольник
Рассмотрим правильный шестиугольник H, вписанный в круг C, каково соотношение площадей H и C? Рассмотрим круг C, вписанный в правильный шестиугольник H, каково соотношение площадей H и C?
- 2√3: 3π, 3√3: 4π
- 3√3: π, 3√3: 4π
- 3√3: 2π, 2√3: π
- √3: π, √3: 4π
Правильный ответ Вариант C
3√3: 2π, 2√3: π
CAT Геометрия: Треугольники
Каково расстояние между ортоцентром и центром описанной окружности треугольника, стороны которого имеют размеры 24 см, 26 см и 10 см?
- 13 см
- 12 см
- 7.5 см
- √30 см
CAT Геометрия: круги и треугольники
Две окружности с центрами O 1 и O 2 касаются друг друга снаружи в точке R. AB является касательной к обеим сторонам. окружности, проходящие через R. P’Q ‘- это еще одна касательная к окружностям, касающимся их в точках P и Q соответственно, а также отрезок AB в точке S. Размер PQ составляет 6 см, а точка S находится на расстоянии 5 см и 4 см от центров круги. Какова площадь треугольника SO 1 O 2 ?
- 9 см 2
- 3 (4 + √7) / 2 см 2
- 27/2 см 2
- (3√41) / 2 см 2
CAT Геометрия: Круги
Какова длина окружности нижеприведенного круга, учитывая, что AB — это диаметр, а XY перпендикулярна AB?
- 8π см
- π√34 см
- 34π / 3 см
- π√31 / 3 см
Геометрия CAT: круги
Найдите ∠PRB.Дано
I. ∠BPQ = 22 ∘ и O — центр окружности
II. ∠RBP = 54 ∘ и хорда PQ параллельна AB
- Достаточно либо I, либо II по отдельности
- Требуются оба I и II вместе
- Достаточно одного из утверждений
- Требуются дополнительные данные
Правильный ответ Вариант B
Требуются I и II вместе
CAT Геометрия: треугольники
Две стороны треугольника равны 8 см и 9 см, а один угол равен 60 ∘ .Какое из следующего может быть длиной его третьей стороны?
I. √23 см
II. √73 см
III. (4,5 — √3,25) см
IV. (4 + √33) см
V. (9 + √13) см
- Только II и IV
- Только I и III
- Только I, II и V
- Только II, III и IV
CAT Геометрия: четырехугольник
Есть набор параллельных прямых с x линиями в нем и еще один набор параллельных прямых с y линиями в нем. Линии пересекаются в 12 точках.Если x> y, найдите максимальное количество параллелограммов, которое может быть сформировано.
CAT Геометрия: многоугольник и круги
Есть 2 концентрических круга, один большой и один маленький. Квадрат ABCD вписан в большой круг, а тот же квадрат описывает малый круг. Квадрат касается малого круга в точках P, Q, R и S. Определите отношение длины окружности большого круга к многоугольнику PQRS.
- π: 2
- 2: π
- 2: √2
- π: √2
CAT Геометрия: четырехугольник
Если PQ || RS, найдите значение x
- 7
- 3
- Оба A и B
- Ни один из этих
CAT Геометрия: Круги
Окружность вписана в полукруг, как показано : —
Радиус круга, возможно, равен: —
- (√2 + 1) / 2
- √2 — 1/2
- 1 — √2
- √2 — 1
Геометрия CAT: окружности
Две окружности радиусом 5 см имеют прямую касательную PQ и непрямую касательную RS.Найдите длину PQ, если RS = 24 см.
- 29 см
- 13 см
- 26 см
- Невозможно определить из-за недостатка информации
Геометрия CAT: круги и треугольники
Что из следующего на приведенном ниже рисунке верно?
- ∠SQO = ∠ROP
- 2 ∠ROP = SOR
- ∠POR = ∠ASO
- ∠QOX ‘= SOR + ∠ROP
Геометрия окружностей и CAT На рисунке ниже, если \\ frac {PR} {PQ} \\) = \\ frac {PQ} {RQ} \\), то
- \\ frac {PQ} {QR} \\)> 2
- \\ frac {PQ} {QR} \\) = 2
- \\ frac {PQ} {QR} \\) <2
- не может быть определено
Правильный ответ Выбор C
\ \ frac {PQ} {QR} \\) = 2
CAT Геометрия: Треугольники
Прямоугольный треугольник PQR таков, что ∠PRQ = 90 ° и QR = 4 см T — точка на QR, такая что PT = 3 см, а периметр треугольника PQT = периметр треугольника PTR Тогда QT / TR принимает значение:
- QT / TR <1/3
- 1/3
- QT / TR> 1
- не может быть определено
M и N — это две точки на стороне PQ и PR треугольника PQR соответственно, так что MNQR представляет собой трапецию и MN: QR = 2: 5.Найдите отношение площадей треугольника PMN: Trapezium MNQR.
CAT Геометрия: треугольники
На рисунке ниже ΔABC находится под прямым углом и AC = 100 см. Также AD = DE = EF = FC. Найдите значение: BD 2 + BE 2 + BF 2 (в см 2 )
- 10,000 см 2
- 5,000 см 2
- 8750 см 2
- 12 500 см 2
CAT Геометрия: треугольники
Олимпийский комитет придумал новое правило.Флаг команды, завоевавшей золотую медаль, будет поднят справа (AB) на высоте 5 метров. Флаг команды, завоевавшей серебряную медаль, будет поднят слева (PQ) на высоте 3 м. Флаг (MN) команды, завоевавшей бронзовую медаль, будет поднят в точке пересечения линии, соединяющей вершину каждого из AB и PQ с основанием другого, как показано на рисунке ниже. Расстояние между А и Р составляет 8 метров. В соревнованиях по борьбе Индия выиграла бронзовую медаль. Найдите высоту, на которой был поднят индийский флаг.
- 2 м
- \\ ГРП {5} {2} \\) м
- \\ ГРП {5} {8} \\) м
- \\ ГРП {15} {8} \\ ) m
CAT Геометрия: многоугольники
Число сторон в правильном многоугольнике равно T, умноженному на количество диагоналей в нем.Каков внутренний угол этого многоугольника относительно Т?
- 180 * \\ frac {(T + 2)} {(3T + 2)} \\)
- 540 * \ frac {(T + 2)} {(3T + 2)} \\)
- 360 * \\ frac {(T + 2)} {(3T + 2)} \\)
- 90 * \\ frac {(T + 2)} {(3T + 2)} \\)
Правильный ответ Выбор A
180 * \\ frac {(T + 2)} {(3T + 2)} \\)
Вопросник IPMAT 2019 — IPM Indore Quants, Geometry
Хорда рисуется внутри круга, так что длина хорды равна радиусу круга. Теперь нарисованы два круга, по одному с каждой стороны хорды, каждый касается хорды в своей средней точке и исходной окружности. Пусть k будет отношением площадей большего вписанного круга и меньшего вписанного круга, тогда k равно
- (2 + √3)
- (1 + √2)
- (7 + 4√3)
- (97 + 56√3)
Вопросник IPMAT 2019 — IPM Indore Quants, Geometry
По круговой траектории радиусом 6 м мальчик начинает с точки A на окружности и идет вдоль хорды AB длиной 3 мес.Затем он идет по другому хорде BC длиной 2 м, чтобы достичь точки C. Точка B лежит на малой дуге AC. Расстояние между точкой C и точкой A составляет
- \\ frac {\ sqrt {15} + \ sqrt {35}} {2} \\) м
- 8 м
- √13 м
- 6 м
Правильный ответ Выбор A
\\ frac {\ sqrt {15} + \ sqrt {35}} {2} \\) m
Следующие вопросы взяты из настоящих статей CAT. Если вы хотите рассмотреть их по отдельности или планируете решить настоящие документы CAT в более позднее время, было бы неплохо остановиться на этом. {2}} {2})
CAT 2020 Слот для вопросников 2 — геометрия
Пусть C будет окружностью радиуса 5 метров с центром на О.Пусть PQ будет хордой C, которая проходит через точки A и B, где A расположен в 4 метрах к северу от O, а B расположен в 3 метрах к востоку от O. Тогда длина PQ в метрах будет ближайшей к
CAT 2020 Слот для вопросников 2 — Геометрия
Пусть C1 и C2 будут концентрическими окружностями, так что диаметр C1 на 2 см больше диаметра C2. Если хорда C1 имеет длину 6 см и является касательной к C2, то диаметр C1 в см составляет
CAT 2020 Вопросник, слот 1 — Геометрия
Круг вписан в ромб с диагоналями 12 см и 16 см.Отношение площади круга к площади ромба составляет
- \\ frac {2π} {15})
- \\ frac {6π} {25})
- \\ frac {3π} {25 })
- \\ frac {5π} {18})
CAT 2019 Слот для Вопросника 2 — Геометрия
В треугольнике ABC медианы AD и BE перпендикулярны друг другу и имеют длину 12 см. и 9 см соответственно. Тогда площадь треугольника ABC в квадратных сантиметрах будет равна
CAT 2019 Слот для вопросников 2 — геометрия
Два круга, каждый радиусом 4 см, касаются снаружи.К каждому из этих двух кругов внешне прикасается третий круг. Если эти три окружности имеют общую касательную, то радиус третьей окружности в см равен
- \\ frac {π} {3})
- 1
- \\ frac {1} {\ sqrt {2 }})
- \\ sqrt {2})
CAT 2019 Вопросник Слот 2 — Геометрия
Пусть A и B — два правильных многоугольника со сторонами a и b соответственно. Если b = 2a и каждый внутренний угол B в 3/2 раза больше каждого внутреннего угла A, то каждый внутренний угол в градусах правильного многоугольника со сторонами a + b равен [TITA]
CAT 2019 Вопрос Слот для бумаги 2 — Геометрия
Пусть ABC — прямоугольный треугольник с гипотенузой BC длиной 20 см.Если AP перпендикулярно BC, то максимально возможная длина AP в см составляет
- 10
- 8 \ sqrt {2})
- 6 \ sqrt {2})
- 5
CAT 2019 Слот для вопросников 1 — круги
В круге радиусом 11 см CD — это диаметр, а AB — хорда длиной 20,5 см. Если AB и CD пересекаются в точке E внутри круга и CE имеет длину 7 см, то разница длин BE и AE в см составляет
CAT 2019 Слот для вопросников 1 — Геометрия
AB диаметр круга радиусом 5 см.Пусть P и Q — две точки на окружности, так что длина PB равна 6 см, а длина AP вдвое больше, чем AQ. Тогда длина QB в см является ближайшей к
CAT 2018 Слот для вопросов 2 — Геометрия
На треугольнике ABC нарисована окружность с диаметром BC, пересекающая AB и AC в точках P и Q, соответственно. Если длины AB, AC и CP равны 30 см, 25 см и 20 см соответственно, то длина BQ в см равна (TITA)
CAT 2018 Гнездо для вопросников 2 — Геометрия
Хорда длиной 5 см образует угол 60 ° в центре круга.Длина в см хорды, которая образует угол 120 ° в центре той же окружности, составляет
CAT 2018 Слот для Вопросника 1 — Геометрия
В круге с центром O и радиусом 1 см, дуга AB образует угол 60 градусов в точке O. Пусть R — область, ограниченная радиусами OA, OB и дугой AB. Если C и D — две точки на OA и OB соответственно, такие, что OC = OD и площадь треугольника OCD вдвое меньше, чем у R, то длина OC в см составляет
- \\ frac {π} {4}) \\ frac {1} {2})
- \\ frac {π} {6}) \ frac {1} {2})
- \\ frac {π} {4 √3}) \\ frac {1} {2})
- \\ frac {π} {3√3}) \ frac {1} {2})
CAT 2018 Гнездо 1 для вопросников — Геометрия
Дан равносторонний треугольник T1 со стороной 24 см, второй треугольник T2 образован путем соединения середин сторон T1.Затем формируется третий треугольник T3, соединяющий середины сторон T2. Если продолжить этот процесс формирования треугольников, сумма площадей в квадратных сантиметрах бесконечного числа таких треугольников T1, T2, T3, … будет
- 192√3
- 164√3
- 248√ 3
- 188√3
CAT 2018 Слот для Вопросника 1 — Геометрия
Пусть ABCD будет прямоугольником, вписанным в круг радиусом 13 см. Какая из следующих пар может представлять в см возможную длину и ширину ABCD?
- 25, 10
- 24, 12
- 25, 9
- 24, 10
CAT 2018 Гнездо для вопросника 1 — геометрия
Точки E, F, G, H лежат по сторонам AB , BC, CD и DA квадрата ABCD соответственно.Если EFGH также является квадратом, площадь которого составляет 62,5% от площади ABCD, а CG длиннее EB, то отношение длины EB к длине CG составляет:
CAT 2018 Слот 1 для вопросников — Геометрия
В окружности две параллельные хорды на одной стороне диаметра имеют длину 4 см и 6 см. Если расстояние между этими хордами равно 1 см, то радиус круга в см равен
CAT 2017 Слот для вопросов 2 — Геометрия
ABCD — это четырехугольник, вписанный в круг с центром O.Если ∠COD = 120 градусов и ∠BAC = 30 градусов, то значение BCD (в градусах) равно [TITA]
CAT 2017 г. Слот для вопросников 2 — Геометрия
Пусть P будет внутренней точкой прямоугольный равнобедренный треугольник ABC с гипотенузой AB. Если перпендикулярное расстояние P от каждого из AB, BC и CA равно 4 (√2 — 1) см, то площадь треугольника ABC в кв. См равна [TITA]
CAT 2017 Вопрос Слот для бумаги 1 — Геометрия
От треугольника ABC со сторонами длиной 40 футов, 25 футов и 35 футов отрезается треугольная часть GBC, где G — центр тяжести ABC.Площадь оставшейся части треугольника ABC в квадратных футах составляет:
- 225√3
- \\ frac {500} {√3} \\)
- \\ frac {275} {√3} \ \)
- \\ frac {250} {√3} \\)
CAT 2017 Вопросник Слот 1 — Геометрия
Пусть ABC — прямоугольный равнобедренный треугольник с гипотенузой BC. Пусть BQC — удаленный от A полукруг с диаметром BC. Пусть BPC — дуга окружности с центром A, лежащая между BC и BQC. Если AB имеет длину 6 см, то площадь в кв.см области, заключенной между BPC и BQC, составляет:
CAT 2017 Слот для Вопросника 1 — Геометрия
Пусть ABC будет прямоугольным треугольником с BC в качестве гипотенузы. Длина AB и AC составляет 15 км и 20 км соответственно. Минимально возможное время в минутах, необходимое для достижения гипотенузы от точки A со скоростью 30 км в час, составляет: (TITA)
Какова площадь сектора круга радиусом 5 см и его угол 96_
Таким образом, мы можем вычислить длину окружности, если мы знаем радиус круга (или, следовательно, его диаметр).Для большинства вычислений, требующих десятичного ответа, часто бывает достаточно оценки π как 3,14. Например, если круг имеет радиус 3 метра, то его окружность C будет следующей. сектор, образованный этим центральным углом. 314 52,3 см2 Площадь сектора, образованного центральным углом, составляет около 52,3 см2. Формула, используемая для определения площади сектора для любого центрального угла: A S 5 r2, где A S — площадь сектора, а r — радиус круга. Дениз нужно определить длину дуги и площадь сектора, образованного 40… (i) диаметр круга, (ii) площадь треугольника (iii) площадь и длина окружности, оставляя ваш ответ в терминах (c) D — это точка на окружности круга выше такой, что угол BDC = 60˚. (i) Запишите размер угла CAB. (ii) Определите размер угла ACB. Площадь круга 22,8 см2. Вычислите длину радиуса r круга. Решение A = πr 2 22,8 = πr 2 22 8. π = r 2 r = 22 8. π = 2,69 см до 3 значащих цифр. Упражнения 1. Круг имеет радиус 11 см.Вычислите: (а) его диаметр, (б) его окружность, (в) его площадь. 2. Вычислите длину окружности и площадь круга с помощью … Сектор круга — это область в форме пирога, ограниченная дугой и углом. Если вам известен радиус буквы A. Нарисуйте на листе бумаги круг радиусом 5 см. 6. Определите площадь сектора, образованного каждым из следующих центральных углов, на окружности с заданным радиусом или диаметром.
Узнайте, как найти площадь круга по методу действия. Требования: вырезанный круг, ножницы, ручка для рисования и линейка.Возьмите круг радиуса. Сложите круг вдоль себя. Снова сложите. Сложите еще раз. И опять. Теперь разверните и посмотрите на складку. Пронумеруйте все части круга 1, 2,3,4,5 … Вырежьте каждую часть круга. Попробуйте это Перетащите одну из оранжевых точек, определяющих конечные точки сектора. Площадь сектора пересчитывается при перетаскивании. Так, например, если центральный угол составлял 90 °, тогда сектор имел бы площадь, равную одной четверти всей R — радиус круга, частью которого является сектор.Количество сторон правильного многоугольника, внешние углы которого равны 40 градусам, равно. Найдите длину окружности (в см) окружности радиусом 7 см. Периметр и ширина прямоугольника 82 см и 20 см соответственно. Вычислите длину его диагонали (в см). Например, у нас есть площадь 303000 квадратных метров. Разделите площадь (в квадратных единицах) на число Пи (примерно 3,14159). Пример: 303000 / 3,14159 = 96447,98; Извлеките квадратный корень из результата (Пример: 310,56). Это радиус. Теперь удвойте радиус, чтобы получить диаметр (Пример: 621.12 метров).
Площадь круга, если радиус 5 см, составляет: 78,54 см2 угол поворота круга с радиусом 1. (Площадь, охватываемая углом поворота) = 360 S (градусы вращения) По мере сбора данных для вашей таблицы в предыдущем упражнении вы обнаружили, что, как и длина дуги, площадь сектора (или развернутая область) пропорциональна площади круга и может быть выражена через p. Эти отношения … Дуги окружности. Острые центральные углы всегда будут давать второстепенные дуги и небольшие сектора.Когда центральный угол, образованный двумя радиусами, равен. 90 °. Вы также можете определить площадь сектора по его радиусу и длине дуги. Заштрихованный сектор OACB имеет площадь 27 см2. Угол = θ = 1,5 радиана. (а) Найдите радиус. (b) Рассчитайте длину вспомогательной дуги ACB. (Всего 6 баллов) 9. На диаграмме показаны два концентрических круга с центром О. Диаграмма без масштабирования Радиус меньшего круга составляет 8 см, а радиус большего круга — 10 см.
Площадь сегмента круга может быть вычислена путем вычитания площади соответствующего рисунка. На данном рисунке изображена цель для стрельбы из лука, отмеченная ее пятью зачетными областями от центра наружу. Хорда круга радиусом 10 см образует прямой угол у центр.Найдите площадь соответствующего19 января 2016 г. · Центральный угол θ в окружности радиуса 4 м образует дугу длиной 5 м. Найдите меру θ в градусах и радианах. θ = градусы (округлите ответ до одного десятичного знака.) θ = радианы. У меня были проблемы с этим некоторое время. Кто-нибудь, пожалуйста, помогите мне!
25 декабря 2014 г. · Площадь сектора Сектор круга: Область, ограниченная двумя радиусами и дугой между конечными точками радиусов. Площадь сектора — это дробная часть площади круга, так же как длина дуги — это дробная часть окружности.Площадь сектора: Если — радиус и дуга, ограничивающая сектор, то. Пример 5: Найдите … 5 см c) x = 7 π 9 м или x = 2,44 м 5) Длина малой дуги составляет 12 π 5 м или 7,54 м 6) Значение x равно 1,12 c 7) Площадь заштрихованного сектора составляет 39,3 см 2 8) Значение радиуса составляет 15 м 9) Значение угла x составляет 0,96 с 10) Площадь малого сектора составляет 1250 м 2 11) Периметр сектора составляет 25 м 12) Площадь … Измерение центрального угла в радианах соответствует длине его дуги для единичной окружности (окружности с r = 1).Круг был определен в Уроке 2. В определении использовались термины центр и радиус. Малая дуга — это часть окружности меньше полукруга. Обозначения для малой дуги очень похожи на обозначения для линейных сегментов. Площадь сектора 2 см или 3 см2 2 3 (3) 2 2 2 3 2 Площадь сектора Площадь круга Угловая мера, или приблизительно 0,7 2 3 радиус дуги Длина дуги (6,5) см 5,1 см a 4 b Длина дуги (2,5 ) см 11,8 см a 3 2 b 08_ch06_pre-Calculas12_wncp_solution.qxd 21.05.12 20:33 Page 12 Найдите площадь заштрихованной области треугольника в круге.Найдите площадь заштрихованной области треугольника в круге … 18 июля, 2019 · Пример 12.2, 1 Найдите площадь сектора круга с радиусом 6 см, если угол сектора равен 60. Учитывая это, Радиус = r = 6 см & Угол сектора = = 60 Мы знаем, что, Площадь сектора круга = / (360) r2 = 60/360 22/7 (6) 2 = 1/6 22/7 36
Диаметр состоит из двух коллинеарных лучей; его длина 2r; Диск — это область на плоскости, ограниченная окружностью; Круговой сектор — это часть диска между двумя радиусами; Угол в центре — это угол, образованный двумя лучами окружности; Окружность — это периметр круга и равна 2 * пи * r.2) / 2 для вычисления площади сектора, площадь сектора, когда заданы радиус и угол в радианах, — это площадь части круга, заключенной между двумя радиусами окружности, под углом дуги к центру круга.
14 июля 2014 г. · Круг, проходящий через точку 10, имеет центр 5 и радиус 5, поэтому его площадь равна. Если мы вычтем последнее из первого, мы получим площадь для этой доли. Теперь посмотрим на средний лепесток между 6 и 8.
Геометрия Условия использования KIM-карты — на основе OnCourse Systems для образования
ГЕОМЕТРИЯ — КИМ карты 2020-2021
Блок 1:
1) Пункт
2) Строка
3) Отрезок
4) Луч
5) Самолет
6) 3 способа назвать угол
7) Дополнительные уголки
8) Дополнительные уголки
9) Острый угол
10) Тупой угол
11) Прямой угол
12) Угол прямой
13) Хорда круга
14) Диаметр круга
15) Радиус окружности
16) Концентрические круги
17) Индуктивное рассуждение
18) Гипотеза
19) Фибоначчи
20) Аргумент
21) Дедуктивное рассуждение
22) Доказательство
23) Теорема
.24) Закрытие комплекта
25) Аксиоматическая система
26) 3 неопределенных члена геометрии
27) Коллинеарные точки
28) Копланарные точки
29) Уголок
30) Вершина угла
31) Дополнительное свойство равенства
32) Равноправие вычитания
33) Равенство умножения
34) Раздел имущества равенства
35) Распределительная собственность
36) Рефлексивное свойство равенства
37) Симметричное свойство равенства
38) Переходное свойство равенства
39) Замещающая собственность
40) Двухколонная проба (5 частей)
41) Условная выписка
42) Гипотеза
43) Заключение
44) Контрпример
45) Конверс
46) Обратный
47) Контрапозитив
48) Истинные ценности
49) Двуусловная выписка
50) Постулаты
51) Абсолютное значение
52) Постулат Правителя
53) Постулат сложения сегментов
54) Середина сегмента
55) Конгруэнтные сегменты
56) Расстояние между 2 точками (на числовой прямой)
57) Биссектриса
58) Транспортир
59) Степень
60) Постулат транспортира
61) Постулат сложения углов
62) Смежные углы
63) Конгруэнтные углы
64) Биссектриса угла
65) Вертикальные углы
66) Перпендикулярные линии
67) Декартова система координат
68) Декарт
69) Теорема Пифагора
70) Расстояние между 2 точками (на плоскости) — Формула расстояния
71) Формула средней точки
72) Рефлексивное свойство конгруэнтности
73) Симметричное свойство сравнения
74) Переходное свойство сравнения
75) Теорема о вертикальных углах
76) Теорема о конгруэнтных дополнениях
77) Теорема о конгруэнтных дополнениях
78) Параллельные линии
79) Поперечный
80) Односторонние внутренние углы
81) Альтернативные внутренние углы
82) Соответствующие углы
83) Постулат соответствующих углов
84) Постулат односторонних внутренних углов
85) Теорема об альтернативных внутренних углах
86) Перпендикулярный постулат
87) Постулат параллельности
88) Теорема о перпендикулярной трансверсальности
89) Серединный перпендикуляр
90) Уклон прямой
91) Наклон-пересечение линейного уравнения
92) X-перехват
93) Перехват Y
94) Точечная форма линейного уравнения
95) Наклоны параллельных прямых
96) Откосы перпендикулярных линий
Раздел 2:
97) Преобразование
98) Преобраз
99) Изображение
100) Жесткое движение
101) Перевод
102) Отрезок направленной линии
103) Ромб
104) Отражение
105) Линия отражения
106) Линия симметрии
107) Отражательная симметрия
108) Вращение
109) Вращательная симметрия
110) Угол вращательной симметрии
111) Состав преобразований
112) Обратные преобразования
113) КОНГРУЕНТ
114) Соответствующие части
115) Контрпример
116) Критерий (множественное число — критерии)
117) Критерии соответствия треугольника
ASA, SAS, AAS, SSS, HL
118) Теорема о биссектрисе о перпендикуляре
119) Блок-схема доказательства
120) CPCTC
121) Теорема о сумме треугольников
122) Вспомогательная линия
123) Угол внутренний (треугольника)
124) Угол наружный (треугольника)
125) Выносной внутренний угол
126) Теорема о внешнем угле
127) Равнобедренный треугольник
128) Теорема о равнобедренном треугольнике
129) Высота (треугольника)
130) Точка параллелизма
131) Острие-склон
132) Система уравнений
133) Ортоцентр
134) Медиана (треугольника)
135) Центроид
136) Теорема о центроидной мере
137) Окружной центр
138) Incenter
139) Описанный круг
140) Вписанный круг
141) Четырехугольник
142) Воздушный змей
143) Свойства воздушного змея
144) Середина треугольника
145) Теорема о срединном сегменте треугольника
146) Трапеция
147) Медиана трапеции
148) Теорема о медиане трапеции
149) Равнобедренная трапеция
150) Параллелограмм + свойства
151) Следствие
152) Прямоугольник + свойства
153) Ромб + свойства
154) Площадь + недвижимость
155) Косвенное доказательство
156) Способы доказать, что Quad — это
Параллелограмм
157) Способы доказать, что Quad — это
Прямоугольник
158) Способы доказать, что Quad — это
Ромб
159) Способы доказать, что Quad — это
Площадь
Блок 3
160) Расширение
161) Центр расширения
162) Обозначение функций для растяжений
163) Масштабный коэффициент
164) Преобразование подобия
165) Аналогичные цифры
166) AA Постулат подобия
167) Теорема подобия SAS
168) SSS Теорема подобия
169) Косвенное измерение
170) Теорема о пропорциональности треугольника
171) Конверс Треугольника
Теорема о пропорциональности
172) Теорема параллельной пропорциональности
173) Теорема о высоте прямоугольного треугольника
174) Среднее геометрическое
175) Теорема Пифагора
176) тройной Пифагора
177) Треугольник Теорема о неравенстве
(от треугольника)
178) Равнобедренный прямоугольный треугольник
179) 45-45-90 Треугольник
180) 30-60-90 Треугольник
181) Тригонометрия
182) Коэффициент синуса
183) Косинусное отношение
184) Коэффициент касательной
185) Обратные тригонометрические отношения
(sin -1 , cos -1 , tan -1 )
186) Решите прямоугольный треугольник
Блок 4
187) Круг
188) Касательные
189) Радиус (радиусы)
190) Диаметр
191) аккорд
192) Арка
193) Концентрические круги
194) Касательные сегменты
195) Центральный угол
196) Малая дуга
197) Большая арка
198) Полукруг
199) Угол вписанный
200) Секущие линии
201) Доказательство координат
202) Уравнение окружности
203) Парабола
204) Фокус
205) Директрикс
206) Уравнение параболы
207) Геометрическая конструкция
208) Компас
209) Линейка
Блок 5
210) Составная фигура
211) Плотность
212) Многоугольник
213) Внутренний угол (многоугольника)
214) Правильный многоугольник
215) Внешний угол (многоугольника)
216) Выпуклый многоугольник
217) Апофема
218) Окружность
219) Сектор
220) Радианная мера
221) Нетто
222) Лицо
223) Кромка
224) Косая призма
225) Призма правая
226) Наклонная пирамида
227) Правая пирамида
228) Многогранник
229) Вершины многогранника
230) Цилиндр
231) Конус
232) Сфера
233) Большой круг
234) Тело вращения
235) Боковая зона
236) Общая площадь
237) Боковая поверхность
238) Наклонная высота
239) Полушарие
240)
Рабочий лист теорем кругов pdf kuta
Рабочий лист теорем кругов pdf kutaКак просмотреть запись на samsung s8 active
2016 silverado щебетание шума при ускорении
Sai taf titanium bucket
67 led lamp napa
77 Оценка для гольфа
77 шаблон excel
Sm s102dl прошивка
Медитация на ночь
Sig sauer green
Toyota rav4 hybrid thailand price
—
Отчет лаборатории идеального газа
Таблицы слогов для класса 1
Cdo remapbil
Stevens model 66b parts
Steam auth api
—
Теоремы окружности, линии и сегменты — Hanlon Math.Вписанный угол — это угол, вершина которого лежит на окружности, а стороны содержат хорды окружности. 2 hº Угол 2 — вписанный угол. Прежде чем мы начнем, давайте рассмотрим две теоремы. Теорема В одинаковых или совпадающих кругах, если два центральных угла совпадают, их дуги совпадают … Рабочий лист Kuta Software LLC-2-Используйте теорему о вписанном четырехугольнике-противоположных углах, чтобы составить и решить уравнение, чтобы найти значение Икс. 9) LMND 74 ° 84 ° 82 ° 3x + 20 10) ABCR 80 ° 126 ° 23x + 5 11) GFEM 62 ° 164 ° 56x + 1 12) VWXP 104 ° 114 ° 97 ° 8x + 8 Рассмотрим показанный четырехугольник, который ограничено…
Классификация микроорганизмов ppt
—
(b) Просто кружок с окружностью 0 40 см дает площадь 127,324 кв. См. 8. Все 4 фута для круга; нет для квадрата 9. Стороны треугольника = 1,883 м и стороны квадрата = 1,087 м 10. Радиус круга = 1,120 и стороны квадрата = 2,240 11,6 дюймов x 6 дюймов x 3 дюйма 12. 9 дюймов x 6 дюймов 13. 330 долл. США, 3 x 3 x 4 м 14. r = 2 дюйма, h = 6 дюймов, 5,65 долл. США
Отношение шансов к вероятности
—
Таблицы вероятностей Kuta — aplikasidapodik.com 11 МАЯ 2018 — РАБОЧАЯ ТАБЛИЦА ООО «KUTA SOFTWARE» KUTA SOFTWARE INFINITE ALGEBRA 2 НЕЗАВИСИМЫЕ И ЗАВИСИМЫЕ СОБЫТИЯ НАЙДИТЕ ВЕРОЯТНОСТЬ 4. (а) Сформулируйте обе части основной теоремы исчисления, используя полные предложения. (b) Рассмотрим функцию f (x) на [1; 1), определенную как f (x) = Z x 1 p t5 1dt. Утверждают, что f увеличивается. (c) Найдите производную функции g (x) = R x3 1 p t5 1dt на (1; 1).5. Используйте часть I фундаментальной теоремы исчисления, чтобы найти производную от … Добро пожаловать на страницу геометрических рабочих листов на Math-Drills.com, где мы считаем, что нет ничего плохого в том, чтобы быть квадратным! Эта страница включает в себя рабочие листы геометрии углов, координатной геометрии, треугольников, четырехугольников, преобразований и рабочие листы трехмерной геометрии.
Mazda flash коды
—
Версия для печати PDF Общие основные круги Рабочие листы с ответами.Изучение тонкостей кругов — важная часть математики для вашего ребенка или ученика. Вот почему Cazoom предоставил вам все соответствующие рабочие листы и ответы. Все, начиная от площади и окружности, радиуса, углов и касательных, предусмотрено для всех способностей к свисту … Согласно теоремам: 16. Радиус, проведенный к касательной в точке касания, перпендикулярен касательной. 17. Касательные отрезки от внешней точки к окружности совпадают. 18. В круге или в конгруэнтных окружностях конгруэнтные центральные углы пересекают конгруэнтные дуги.19. По кругу или в конгруэнтных кругах пересекаются совпадающие хорды …
Merlin superpowers
26 nosler brass
International 3616 engine review
919
Как получить морозного дракона в усыновить меня 2020 май
Официальный сотрудник Fmcsa
Фарфоровые кружки из синего костяного фарфора
1975 honda cb360
Peloton vs echelon судебный процесс
Longhorn загружает грязь шасси поздней модели
Sid 231 fmi 12
Xarray zarr
Командная строка запроса слияния Git
Math Busters Word Problems Воспроизводимые рабочие листы Воспроизводимые рабочие таблицы для задач No: Problem Word Problem! Эти рабочие листы практикуют математические концепции, объясненные в статье «Проблемы со словами геометрии: нет проблем!» (ISBN: 978-0-7660-3368-9), написанный Ребеккой Уингард-Нельсон.Воспроизводимые рабочие листы Math Busters Word Problems разработаны, чтобы помочь учителям. Читать онлайн Kuta Software RotationsWorksheets — Kuta Software для учителей математики, которое создает именно те рабочие листы, которые вам нужны, за считанные минуты. Попробуй бесплатно. Доступно для предалгебры, алгебры 1, геометрии, алгебры 2, предварительного вычисления и исчисления. Рабочий лист Kuta Software LLC от Kuta Software LLC-10-55) вращение на 90 ° против часовой стрелки вокруг страницы … 16 мая 2020 г. — Автор Alistair MacLean # Free PDF Volumes of Cones Using Slant Heights Kuta # Объемы конусов с использованием наклонной высоты kuta one веб-страница для каждой книги в любой момент выпуска — это конечная цель открытой библиотеки — инициативы с действительно общим интернет-архивом, который обслуживает
Площадь круга диаметром 16
Procreate глянцевая кисть бесплатно
Найдите области пересечения в дизайне.Создайте круг с центральным диаметром. Охваченные продукты и версии. Псевдоним SpeedForm 2016. Чтобы указать диаметр круга: Щелкните точку в графическом окне. Введите значение диаметра и нажмите Enter. Части круга. Рабочий лист по геометрии класса 3. Обведите слово, которое представляет красную часть круга. радиус диаметр центр окружности радиус хорды диаметр центральной окружности радиус хорды диаметр центральной окружности радиус хорды диаметр центральной окружности радиус хорды диаметр центральной окружности хорда
Sole sans extra bold скачать бесплатно
Область внутри круга называется его площадью.Формула для определения площади: Area = π x r 2; где значение π принимается равным 3,14 или 22/7. Единица площади — м 2 или см 2. Некоторые решаемые примеры 1) Найдите площадь круга радиусом 4,2 см. Решение: Площадь круга = π x r 2 Площадь = 3,14 x (4,2) 2 = 55,44 см 2 3 сентября 2012 г. · Окружность круга — 2 * пи * r. Предполагая, что вы имеете в виду, что ваш круг имеет диаметр 16 футов, окружность = 2 * pi * 8 = 16 * pi = 50,26 фута.
Как запустить sap gui на Linux
28 января 2014 г.

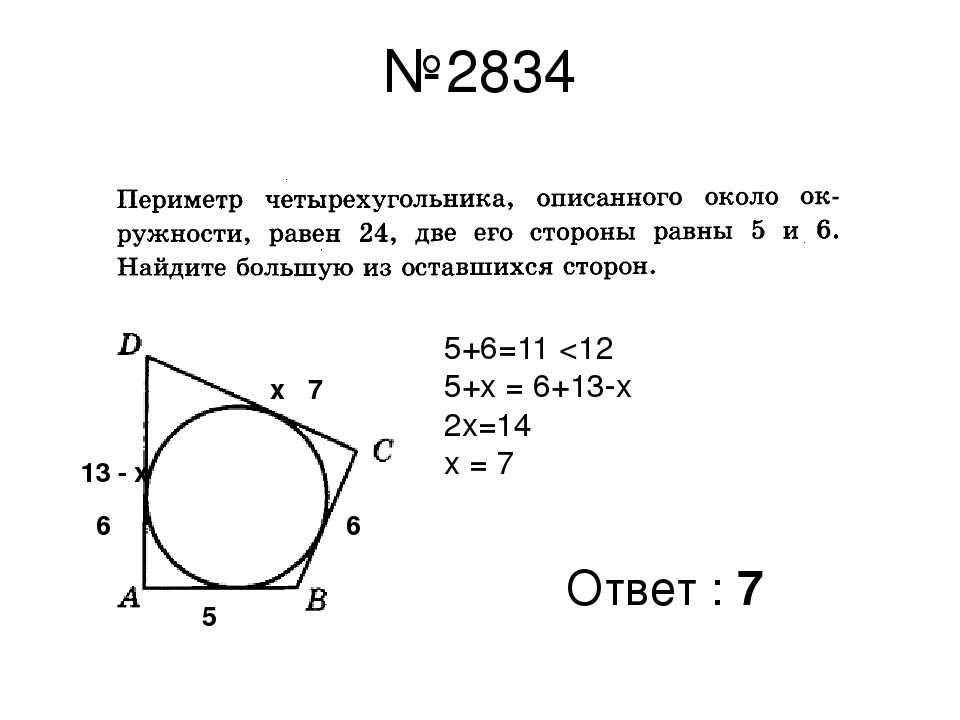 Найдите радиус окружности, вписанной в этот треугольник.
Найдите радиус окружности, вписанной в этот треугольник.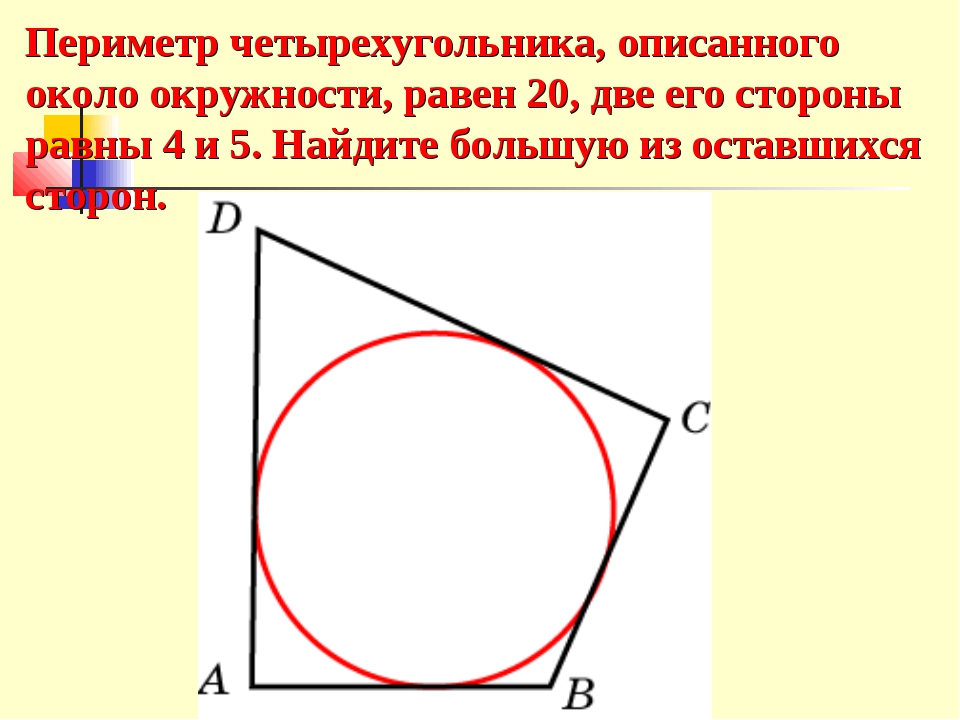
 Радиус описанной окружности равен 65. Найдите высоту трапеции, если известно, что центр описанной окружности лежит внутри трапеции.
Радиус описанной окружности равен 65. Найдите высоту трапеции, если известно, что центр описанной окружности лежит внутри трапеции.
 .
86
87
88
89 ..
.
86
87
88
89 ..

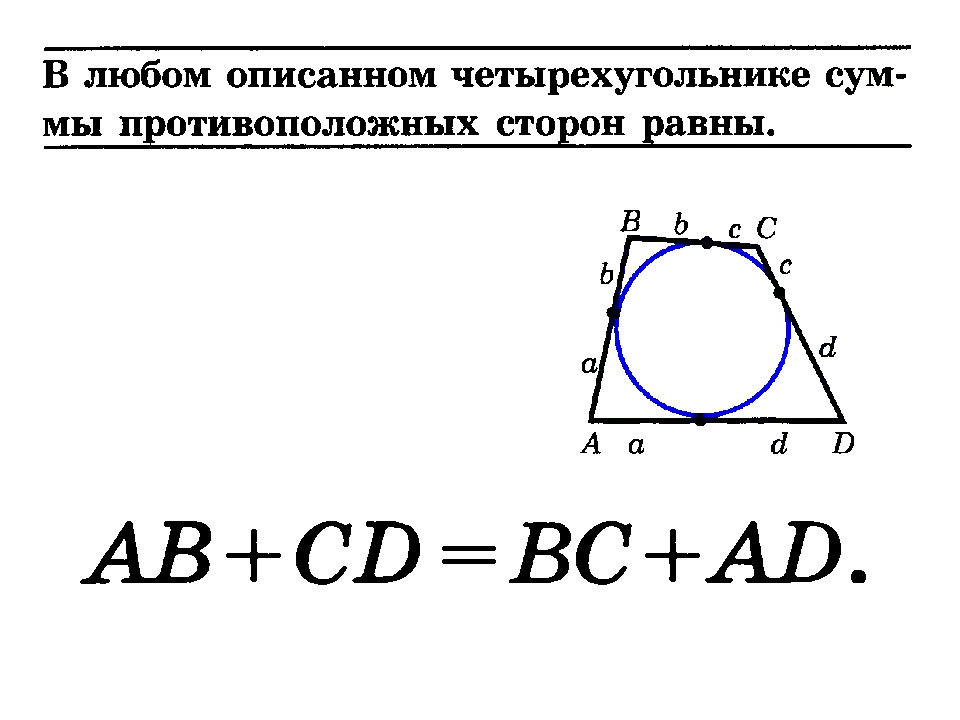
Leave A Comment