Модуль вектора равен: Как найти модуль вектора? Ответ на webmath.ru

модуль вектора на украинский — Русский-Украинский

Полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы коллинеарны.

Корисний для «вимірювання» перпендикулярності векторів — модуль векторного добутку двох векторів дорівнює добутку їхніх модулів, якщо вони перпендикулярні, і зменшується до нуля, якщо вектори колінеарні.

WikiMatrix

В физической оптике интенсивность поля электромагнитного излучения определяется квадратом модуля вектора напряженности электромагнитного поля E, (который является основной рассчитываемой величиной в физической оптике), и характеризуется плотностью поля (нем.

У фізичній оптиці інтенсивність поля електромагнітного випромінювання визначається квадратом модуля вектора напруженості електромагнітного поля E,(який є основною розрахунковою величиною у фізичній оптиці), і характеризуеться щільністю поля (нім.

WikiMatrix

В оптическом диапазоне спектра частоты электромагнитных колебаний настолько высоки, что непосредственное измерение модуля этого вектора (в отличие от радиотехники) невозможно.

В оптичному діапазоні спектру частоти електромагнітних коливань настільки високі, що безпосереднє вимірювання модуля цього вектора (на відміну від радіотехніки) неможливе.

WikiMatrix

Расстоянием Чебышёва между n-мерными числовыми

векторами называется максимум модуля разности компонент этих векторов.

Відстанню Чебишова між n-вимірними числовими векторами називається максимум модуля різниці компонент цих векторів.

WikiMatrix

Энергия и импульс тела являются компонентами 4-вектора энергии-импульса (четырёхимпульса) (энергия — временной, импульс — пространственными) и соответствующим образом преобразуются при переходе из одной системы отсчёта в другую, а масса тела является лоренц-инвариантом, оставаясь при переходе в другие системы отсчёта постоянной, и имея смысл модуля вектора четырёхимпульса.

Енергія та імпульс тіла є компонентами 4-вектора енергії-імпульсу (4-імпульсу) (енергія — часовий, імпульс — просторові компоненти), і відповідним чином перетворюються при переході з однієї системи відліку в іншу, а маса тіла є лоренц-інваріантом, залишаючись при переході в інші системи відліку сталою, і маючи сенс модуля вектора чотирихімпульсу.

WikiMatrix

Иначе: их векторная сумма есть вектор с модулем, равным нулю.

Іншими словами: їх векторна сума є вектор з модулем

, рівним нулю.

WikiMatrix

Блок из n букв рассматривается как n-мерный вектор и умножается на n × n матрицу по модулю 26.

Блок з n букв розглядається як n-мірний вектор і множиться на n × n матрицю по модулю 26.

WikiMatrix

Схема «Вектора» изначально предусматривала подключение внешнего модуля расширения памяти объёмом 64 или 256 Кбайт, который назывался «квазидиском», потому что предназначался для использования в качестве дискового накопителя.

Схема «

Вектора» спочатку передбачала підключення зовнішнього модуля розширення пам’яті об’ємом 64 або 256 Кбайт, який називався «квазидиском», тому що призначався для використання як дисковий накопичувач.

WikiMatrix

Обычно под вращающимся магнитным полем понимается магнитное поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается с постоянной угловой скоростью.

Обертальне магнітне поле — магнітне поле, вектор магнітної індукції якого, не змінюючись за модулем, обертається з постійною кутовою швидкістю.

WikiMatrix

В квантовой механике состояние системы (частицы) характеризуется волновой функцией (вообще говоря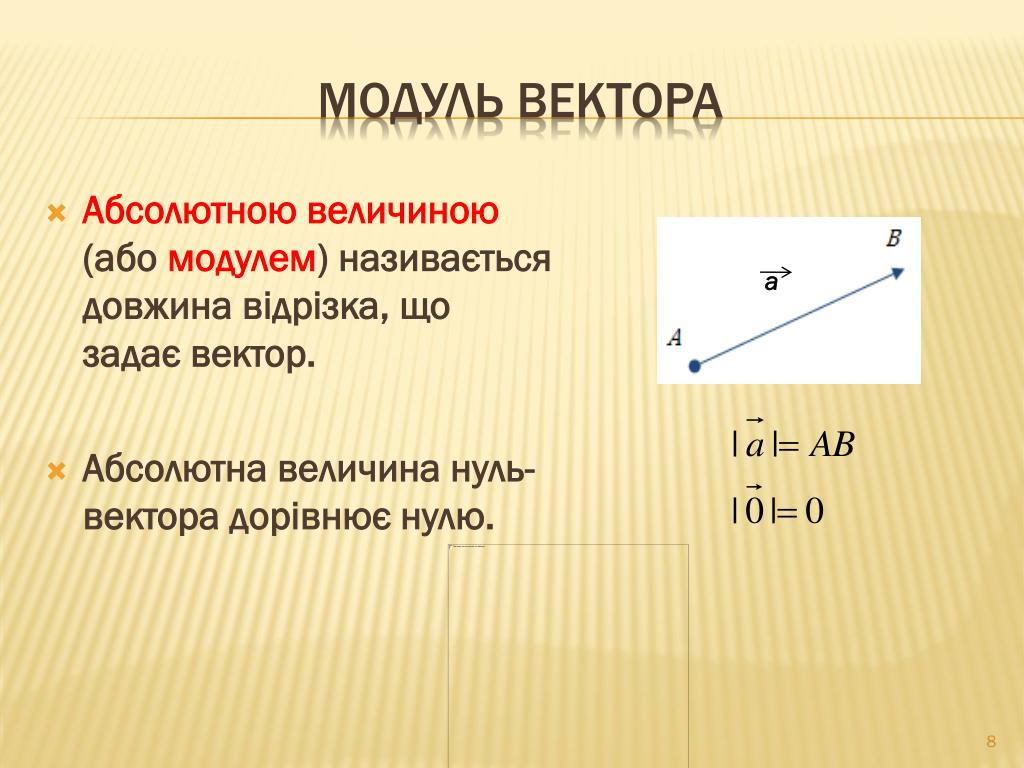

вектором состояния) — комплекснозначной функцией «координат», квадрат модуля которого интерпретируется как плотность вероятности получения заданных значений «координат».

У квантовій механіці стан системи (частинки) характеризується хвильовою функцією (загалом кажучи вектором стану) — комплекснозначною функцією «координат», квадрат модуля якої інтерпретується як густина імовірності отримання заданих значень «координат».

WikiMatrix

Квадрат — модуль — вектор

Cтраница 1

Квадрат модуля вектора равен сумме квадратов его компонент. [1]

Но квадрат модуля вектора равен скалярному квадрату этого вектора. [2]

Равенство Парсеваля означает, что квадрат модуля вектора равен сумме квадратов всех его координат ( в ортонормированием базисе), а неравенство Бесселя — что квадрат модуля вектора не меньше суммы квадратов некоторых из его координат. [3]

Кинетическая энергия системы материальных точек равна половине квадрата модуля вектора скорости v изображающей точки.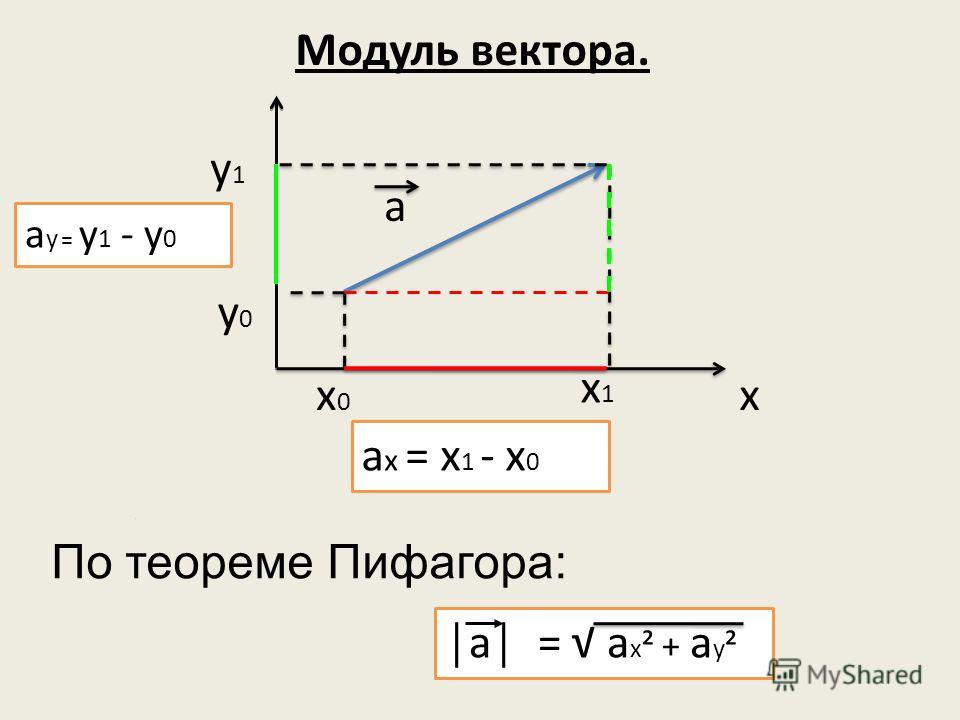

[4]

Формула эта по своей конструкции аналогична известной формуле квадрата модуля вектора. [5]

Следовательно, У2 const или У2 — У02, т.е. квадрат модуля вектора скорости постоянен. [6]

Из формул (8.111), (8.112) видно, что ослабление правильных отражений, связанное с наличием в кристалле дислокационных диполей, не зависит от направления вектора х, причем L пропорциональна квадрату модуля вектора q1; величине / 2 и линейно зависит от плотности диполей Пдд Численное значение L может быть как больше, так и много меньше единицы.

Значения L при увеличении ngg и / на порядок могут оказаться гораздо больше единицы. В зависимости от значения L можно говорить о сильно — и слабоискаженных кристаллах, картина распределения интенсивности рассеяния которых качественно отличается. [8]

При прохождении тока через электролиты электрическая мощность, затрачиваемая на преодоление омического сопротивления электролита и необратимых процессов при электролизе, расходуется на выделение джоулева тепла. При этом удельная мощность, а следовательно, и количество тепла, выделяемое в единице объема в единицу времени ( dw / dq), пропорциональные квадрату модуля вектора плотности тока, в различных точках электролита будут различны и вызовут неоднородность электролита в отношении распределения температуры. Поэтому удельное сопротивление среды, зависящее от температуры, не будет постоянным. [9]

Если в физических приложениях каждой точке некоторой пространственной области О отнесено определенное значение величины и, например плотность вещества в этой точке, так что в О задана одна-единственная функция uf ( x y, z) F ( r), причем тт.

Говгрят также, что в области О задано скалярное поле. Так, например, во всяком векторном поле и и ( г) величина и 2 иf — — и — j — г / является скалярной функцией точки: сна ведь равна квадрату модуля вектора поля, а стало быть, не зависит от выбора системы координат. [10]

Страницы: 1

Вектор, модуль вектора. Коллинеарные векторы. Компланарные векторы. Координаты вектора

Напомним, что вектором называется направленный отрезок, то есть отрезок, имеющий длину и определённое направление. Если начало вектора находится в точке , а конец в точке , то такой вектор обозначается: . Часто векторы обозначаются и вот таким образом: .

Модулем, или длиной вектора, называется длина отрезка, который изображает вектор (, ).

Нулевым вектором называется вектор, начало и конец которого совпадают ().

Направления нулевой вектор не имеет, а его длина равна нулю ().

Два отличных от нуля вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. При этом два коллинеарных вектора могут быть сонаправленными () или противоположно направленными (, ).

Векторы называются равными, если они одинаково направлены и их длины равны.

Сумму двух векторов можно найти по правилу треугольника:

А также по правилу параллелограмма:

Отметим, что для любого вектора справедливо равенство .

Также напомним, что для любых векторов , и справедливы:

1. (переместительный закон).

2. (сочетательный закон).

Разностью векторов и называется такой вектор, сумма которого с вектором даст вектор .

Для любых векторов и справедливо следующее равенство .

Произведением ненулевого вектора на число называется такой вектор , длина которого равна произведению .

При этом векторы и сонаправлены при и противоположно направлены при .

Основные свойства умножения вектора на число.

Для любых чисел , и любых векторов , справедливы:

1. (сочетательный закон).

2. (первый распределительный закон).

3. (второй распределительный закон).

Теорема. На плоскости любой вектор можно разложить по двум неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.

, – неколлинеарные векторы,

, – коэффициенты разложения.

Векторы, лежащие в параллельных плоскостях (или в одной плоскости), называются компланарными.

При этом, если вектор можно разложить по векторам и , то есть представить в виде

где и – некоторые числа, то векторы , и компланарны.

Для сложения трёх некомпланарных векторов можно использовать правило параллелепипеда:

Теорема. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

, , – некомпланарные векторы,

, , – коэффициенты разложения.

Коэффициенты разложения вектора по координатным векторам называются координатами вектора в данной системе координат.

, .

Также напомним, что координатами вектора с началом в точке и концом в точке называются числа , .

В пространстве координатами вектора с началом в точке и концом в точке называются числа , , .

Теперь вспомним следующие правила.

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

, ,

вектор имеет координаты .

, ,

вектор имеет координаты .

Каждая координата разности равна разности соответствующих координат этих векторов.

, ,

вектор имеет координаты .

, ,

вектор имеет координаты .

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

, – произвольное число,

вектор имеет координаты .

, – произвольное число,

вектор имеет координаты .

Также напомним, что длина вектора вычисляется .

В пространстве длина вектора по его координатам вычисляется аналогично.

, .

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Скалярный квадрат вектора (то есть скалярное произведение вектора на себя) равен квадрату его длины.

Скалярное произведение двух векторов можно вычислить, зная координаты этих векторов. Скалярное произведение векторов и выражается следующей формулой:

В пространстве скалярное произведение векторов определяется аналогичным образом.

, , .

И напомним свойства скалярного произведения векторов.

Для любых векторов , , и любого числа справедливы соотношения:

1. , причём при .

2. (переместительный закон).

3. (распределительный закон).

4. (сочетательный закон).

Отметим, что распределительный закон имеет место для любого числа слагаемых.

Мы с вами повторили основные моменты, а теперь давайте перейдём к практической части занятия.

Задание первое. Стороны равностороннего треугольника равны . Найдите длину вектора, равного сумме векторов и .

Решение.

Задание второе. Найдите координаты вектора и его модуль, если , .

Решение.

Задание третье. Даны векторы и . Найдите координаты вектора и его модуль.

Решение.

Задание четвёртое. При каких значениях векторы и взаимно перпендикулярны?

Решение.

Задание пятое. Найдите модуль суммы и модуль разности векторов и .

Решение.

Задание шестое. Найдите косинус угла треугольника , если , и .

Решение.

Вектор его модуль — Энциклопедия по машиностроению XXL

Так как эти векторы взаимно перпендикулярны, то абсолютное ускорение изображается диагональю прямоугольного параллелепипеда, построенного на этих векторах. Его модуль [c.305]

Мы можем рассматривать только величину вектора без учёта направления этого вектора выраженная в каких-нибудь единицах измерения, она представится арифметическим числом и будет скалярной величиной мы назовём величину вектора его модулем и будем обозначать модуль вектора тою же буквою, как и сам вектор но изо-И [c. 26]

Это означает, что в каждой точке пространства вращение жидких частиц может быть охарактеризовано этим вектором. Его модуль [c.36]

Решение этой задачи мы начнем с геометрической интерпретации вопроса о двух решениях системы уравнений (1). Вектор р мы определяем по его модулю (он равен единице) и известным проекциям на направления [c.633]

Здесь и далее две черты под вектором показывают, что известны его модуль и направление, а одна черта — только направление вектора или линия его действия. [c.35]

Зная проекции этого вектора на координатные оси, находим его модуль [c.97]

Из определения скалярного произведения двух векторов следует, что os 0°=v т. e. скалярный квадрат вектора равен квадрату его модуля. Этот результат здесь использован мы будем пользоваться нм без оговорок н в дальнейшем. [c. 303]

Направление этого вектора совпадает с направлением силы, а его модуль равен произведению модуля силы на время ее действия [c.126]

Выберем масштаб построения векторов. Выбор масштаба построения производим на основе очевидной зависимости длина отрезка /, изображающего вектор Р, прямо пропорциональна его модулю Р [c.6]

Задать вектор — это значит задать его модуль и направление. [c.11]

Задача 4-2. Вектор F, модуль которого F= 12 направлен под углом 35° к горизонтальной прямой разложить его на два составляющих, направленных вертикально и горизонтально (рис. 10). [c.12]

Задача 7-2. Вектор F направлен под углом 55° к горизонту (вправо и вверх) и имеет модуль 15 единиц один из его составляющих Fx имеет модуль 20 единиц и направлен по горизонтали влево. Найти второй вектор (определить его модуль и направление относительно данного вектора) (рис. 12). [c. 14]

Таким образом, главный вектор V=Fi- -2Fj- -Fk, а его модуль [c.193]

Если дан вектор а, т. е. даны его модуль а и его направление, которое определяется направляющими косинусами, то известны и проекции вектора на оси координат в самом деле, на основании равенства (5) эти проекции будут (рис. 9) [c.23]

По существу, алгебраические величины v v. w представляют собой проекции векторов v и w на ось х, т. г. v = v . и w = Wx- Однако здесь и всюду далее проекцию любого вектора и, коллинеарного оси /, на эту ось мы будем (как и модуль) обозначать символом и(иг = и) и называть, в отличие от модуля, численной или алгебраической величиной вектора и. Так как численная величина вектора может отличаться от его модуля только знаком, то это совпадение обозначений обычно несущественно. В случаях же, когда могут возникнуть недоразумения, модуль вектора будет обозначаться символом ) и . [c.56]

При изучении курса физики установлены основные понятия кинематики точки и твердых тел. При движении точки по траектории скорость и ускорение точки рассматриваются как векторные величины. При этом вектор скорости V направлен по касательной к траектории, и его модуль (числовое значение) равен первой производной от пути по времени v = ds первой производной от вектора скорости по времени а = с1 и/с1/. Он может быть разложен на две составляющие вектор касательного ускорения а , направленный по касательной к траектории и равный по модулю а = dv di и вектор нормального ускорения направленный по главной нормали к траектории в данной точке в сторону вогнутости кривой и имеющий модуль а, == у-/р, где р — радиус кривизны траектории. Модуль вектора ускорения а = ] а + я- [c.28]

Для получения проекции мы умножали на os а не вектор, а его модуль, его абсолютную величину. Проекция силы на ось не является вектором, поскольку она не имеет собственного направления, а вполне определяется направлением оси, величиной проекции [c. 38]

Для определения проекции скорости на ось мы умножали на направляющий косинус не вектор, а его модуль, его абсолютную величину. Проекция скорости на ось (как и алгебраическая скорость точки) не является вектором, так как не имеет собственного направления, а вполне определяется величиной проекции, направлением оси и знаком + или — . Проекция на ось вектора скорости (как и всякого другого вектора) АВ положительна (рис. 9, а) (+ аЬ), если угол между положительным направлением оси и направлением вектора АВ острый, и отрицательна (рис. 9, б) [c.30]

Для вывода формул тангенциального и нормального ускорений представим вектор скорости (11) как произведение его модуля на единичный вектор [c.35]

Если из этого положения вектор г, сохраняя его модуль, вращать против хода часовой стрелки с угловой скоростью ш, то его проекция на действительную ось дает в любой момент времени значение действительной координаты X, соответствующее гармоническому колебанию. [c.214]

Если имеем любой другой вектор Ь с постоянным модулем, то для него остается справедливым все, что было получено для единичного вектора, только радиус годографа следует заменить его модулем Ь. Получим [c.112]

Ускорение Кориолиса а, определяем по правилу Жуковского. Для его модуля имеем 1 = 2(1)1 где п — проекция относительной скорости на плоскость, перпендикулярную оси переносного вращения Ог. В рассматриваемом случае н = Vr, поэтому Оц = 2(0Уг = 16,8 см/с . Направление кориолисова ускорения а, получаем поворотом на 90° вектора и по направлению дуговой стрелки (I) вокруг оси, проходящей через точку М параллельно оси вращения стержня Ог. [c.195]

Тензоры первого ранга (N=1) имеют в трехмерном пространстве компоненты п=3 =3, оии называются векторами и представляют величины, которые характеризуются как числовым значением, так и направлением. При мерами векторов могут служить сила, скорость, ускорение и т.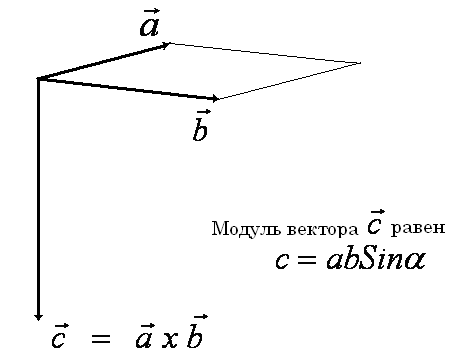 д. Графически вектор изображается направленным прямолинейным отрезком, длина которого в масштабе соответствует значению вектора или его модулю. Векторы обозначаются строчными буквами с черточкой вверху, например а, Б и т. д. Модули векторов означаются, как скаляры, т. е. а =а, 151=6 и т. д. Отрицательным по отношению к данному называется вектор с тем же модулем, но противоположно направленный. Единичным вектором (ортом) называется вектор, длина которого равна единице. Единичные векторы обозначим крышечкой над буквой, например й, S, д. [c.7]

Гипотеза локальной определенности (В. С. Ленский) . В соответствии с этой гипотезой приращение da вектора напряжений а определяется его модулем а и ориентацией в текущем репере Френе (т. е. величинами локальных углов в /,), внутренней геометрией последующего участка траектории деформаций (текущими кривизнами Хй), т. е. [c.265]

Векторы Ei и / 2 направлены противоположно, по модулю вектор Е больше вектора Ег. Поэтому вектор Е направлен от. В к. А и модуль его равен [c.202]

Вектор Вд называется единичным (ортом), так как его модуль равен единице. [c.28]

Зная проекции вектора на оси, мы можем найти его модуль и направляющие косинусы. Модуль вектора а определяется так [c.39]

Здесь А — амплитуда, Ф — полная фаза В., m угл. частота, к — волновой вектор его модуль /с =А наз. волновым числом Фо ноет, сдвиг фазы (часто именуемый просто фазой). Ф-ция г з(г, длиной В.) (рис. 1). Поверхности постоянных Ф — волновые фронты представляют собой плоскости, перпендикулярные вектору /с и перемещающиеся вдоль /с с фазовой ско11остью г, ф=сй/А . В любом другом направлении, отклонённом от /е на угол а, скорость перемещения фазовых фронтов равна ф/со8а> ф это означает, что, в отличие от /с, гф не является вектором (иначе скорость вдоль направления а равнялась бы г фсоаа, т. е, проекции соответствующего вектора). [c. 317]

Тякой случай имеет, например, место для самолета, иа котором установлен воздушно-реактивный двигатель, засасывающий воздух из атмосферы и выбрасывающий его вместе с продуктами горения топлива. Так как доля этих продуктов в отбрасываемом воздухе очень мала (не превышает 2—3%), то здесь практически можно считать Gi =G2 =G . Кроме того, очевидно, что относительная скорость присоединяемой массы воздуха —v, где v — скорость самолета. Тогда, полагая и =и, получим соответственно для вектора Ф и его модуля Ф значения [c.289]

Можно при помотци тригонометрических функций сначала найти направление вектора, а зате.м его модуль (задача 17-4, пункты 1 и 8 ). [c.21]

XiM являются проекциями вектора напряжения Sv, то конец этого вектора всегда находится на поверхности эллипсоида с полуосями ai 02 03. Полученный эллипсоид дает геометрический образ напряженного состояния (тензора напряжений) в точке тела и носит название эллипсоида напряжений Ламе (рис. 2.7). Он показывает, что главное напряжение Oi есть одновременно наибольшее значение полного напряжения l v ma) = amax. Ес-ли а = (Т2=(Гз = ао, то эллипсоид превращается в шар. Тензор напряжений в этом частном случае называют шаровым, а среднее напряжение ао — его модулем. [c.50]

Учтем также, что поворот вектора на тс/2 эквивалентен умножению его модуля на г. Следовательно, наличие комплексного отношения составляющих Еу/Ех у волны свидетельствует об эллиптической поляризации излучения. Преобразуя систему четырех уравнений (1.17), в которую входят проекции Е и И, в систему (1.18), получающуюся при закреплении направления колебаний этих векторов, мы переходим от эллиптической поляризации к линейной Е =- Н -= Ну. Соответствующая экспериментальная процедура с использованием пластинки к/4 описана в гл. 3. [c.26]

Симметричность величин относительно индексов /г следует из правой части равенства (а). Теперь рассмотрим закон преобразования величин Первый член в правой части преобразуется как компонента смешанного тензора второго ранга, так как величины 6, совпадают со смешанными компонентами метрического тензора, а является абсолютным скаляром. Что касается второго члена, то следует отметить, что радиус-вектор в криволинейной системе координат нужно считать определенным своими компонентарли в местном координатном базисе начало местной координатной системы должно совпадать с началом радиуса-вектора. Зная модуль радиуса-вектора и его направление относительно упомянутой местной координатной системы, можно найти его компоненты, как это отмечалось в первом томе. [c.78]

«Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.»

Министерство образования, науки и молодежной политики Краснодарского края государственное бюджетное профессиональное образовательное учреждение Краснодарского края

«Лабинский социально-технический техникум»

Методическая разработка

урока математики

по теме:

«Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.»

Подготовила:

преподаватель математики

Пятакова З.В.

Лабинск, 2015

Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.

Цели урока:

Образовательные:Изучить, что такое “вектор в пространстве», как определяются координаты, вектора, если известны координаты его начала и конца, научится решать задачи, связанные с векторами.

Развивающие: расширение кругозора учащихся, формирование умений применять приёмы сравнивания, обобщения, выделения главного, переноса знаний в новую ситуацию, развитие мышления, речи, умение комментировать, развитие учебно-познавательных компетенций учащихся

Воспитательные: воспитывать трудолюбие, чувство товарищества и взаимопомощи, привитие навыков самооценки, умения работать в коллективе, умения правильно оценивать работуодногруппников,прививать интерес к предмету.

План урока:

Организационный момент.
Актуализация знаний.
Изучение нового материала.
Закрепление знаний.
Итоги урока.
Самостоятельная подготовка.

Оборудование: Интерактивная доска

Тип урока: Комбинированный.

Ход урока:

1. Организационный момент.

Приветствие учащихся, проверка готовности класса к уроку, организация внимания учащихся, раскрытие общих целей урока и плана его проведения.

2. Актуализация знаний

3. Изучение нового материала

Рассказ преподавателя:

ВЕКТОР. КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ

В пространстве, как и на плоскости, вектором называется величина, которая задается своей длиной и направлением. Вектор изображатеся направленным отрезком, длина которого равна длине вектора.

(Слайд 2)

Буквально так же, как и на плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов.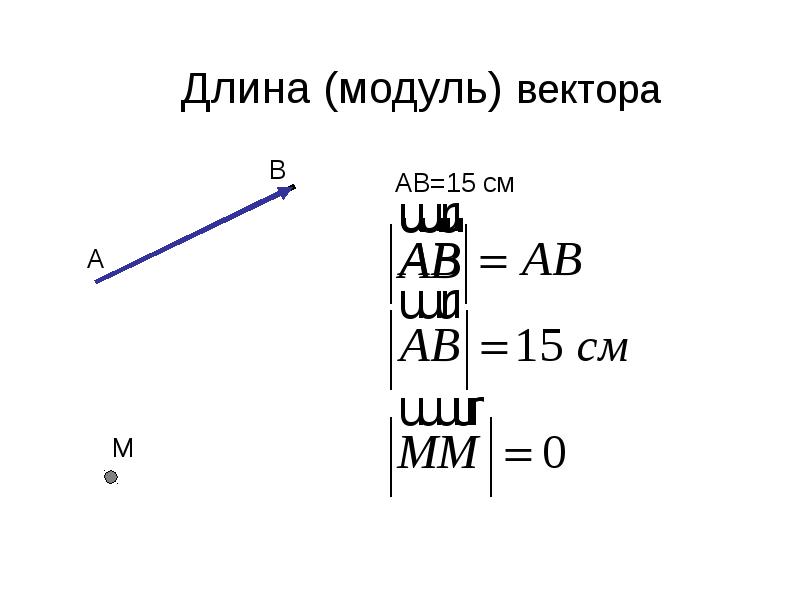

Но это не простое повторение, а обобщение, распространение свойств двумерной геометрии на трехмерную. Если в планиметрии для задания вектора достаточно указать две его координаты, то в стереометрии — три координаты.

Определение. Координатами вектора , начало которого точка A(x₁,y₁,z₁), а конец — точкаВ(х₂, у₂, z₂), называются числа a₁= х_2- x_1,a₂=y₂-y_1,a₃=z₂-z₁.

Записывают такой вектор, указывая его координаты: (a₁ а₂, а₃) или (a₁ а₂, а₃).

(Слайд 3)

Например, если точки А(4; 0; 3) и B(0; 6; 4) — начало и конец направленного отрезка , тогда

а₁ = 0 — 4 = -4, а₂ = 6 — 0 = 6, а₃ = 4 — 3 = 1.

Значит, направленному отрезку соответствует вектор (-4; 6; 1) (рис. 67).

(Слайд 4)

Так же, как и на плоскости, равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны. Это дает основание говорить о том, что любой вектор можно отложить от любой точки пространства.

(слайд 5)

Длину вектора (a₁ а₂, а₃) можно выразить через его координаты. Отложим вектор от начала координат (рис. 68). Тогда четырехугольник OPAN — прямоугольник. Его стороны равны а₁и а₂, поэтому ОА_z² = а₁² + а₂². В прямоугольном треугольнике ОА₂А второй катет А_z А = а₃ и ОА² = ОА²_г + а₃² = а₁² + а₂²+ а₃². Отсюда | | =

Длина любого ненулевого вектора — число положительное. Длина нулевого вектора равна нулю.

Вспомним, что два вектора, лежащих на одной прямой или параллельных прямых, называютколлинеарными. Коллинеарные векторы бывают сонаправлены (а b) или противоположно направлены (а b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.

ДЕЙСТВИЯ НАД ВЕКТОРАМИ В КООРДИНАТАХ

Действия над векторами в пространстве осуществляются аналогично тому, как они определялись для векторов на плоскости.

Определение. Суммой векторов a (a₁ а₂, а₃) и b(b₁ b₂, b₃) называется вектор а + b с координатами (а₁ + b₁; а₂ + b₂ ; а₃ + b₃)

Для любых векторов а , b и с справедливы равенства:

а+b=b+а — переместительный закон сложения;
а + (b + с) = (а+ b) + с — сочетательный закон сложения.

Чтобы доказать эти свойства, достаточно сравнить соответствующие

координаты левой и правой частей каждого векторного равенства.

Для любых трех точек А, В, С в пространстве имеет место векторное равенство + = .

Действительно, для любых трех точек A(a₁ а₂, а₃), B(b₁ b₂, b₃), C(c₁, с₂, с₃) (b₁ – а₁; b₂ — а₂;b₃ — а₃) и (с₁ — b_г; с₂ — b₂, с₃ — b₃).

Отсюда + = (с₁ – а₁; с₂ — а₂; с₃ — а₃).

Геометрически сумму двух векторов пространства можно находить, пользуясь правилам треугольника(рис. 69).

Также применяется и правило параллелограмма. Оно часто используется в физике.

Если ABCD — параллелограмм (рис. 70), то + = .

Чтобы найти сумму нескольких векторов, используем правило многоугольника. Например, если в пространстве даны точки А, В, С, D, Е, F, то всегда

АВ + ВС +CD + DE + EF = AF.

(слайд 6)

Определение. Два вектора, сумма которых равна нулевому вектору, называютсяпротивоположными.

Из определения следует, что у противоположных векторов соответствующие координаты имеют противоположные знаки.

Определение. Разностью векторов а и b называется такой вектор с , который в сумме с вектором bдает вектор а .

Если а (а₁; а₂; а₃) и b( b₁; b₂; b₃), то — = (а₁ –b₁; а₂ — b₂; а₃ – b₃).

Закрепление знаний

Работа студентов по слайдам. Решение задач у доски по желанию.

(слайд7)

(слайд 8)

(слайд9)

(слайд10)

5.Итоги урока.

Комментирование ответов и решений задач. Выставление отметок.

Самостоятельная подготовка.

Составить краткий опорный конспект.

Глава 29. Понятие вектора. Проекция вектора

Глава 29. Понятие вектора. Проекции вектора

Направленные отрезки принято называто также геометрическими векторами или просто векторами. Вектор как направленный отрезок мы будем по-прежнему записывать в тексте двумя большими латинскими буквами с общей чертовй наверху при условии, что первая из них обозначает начало, вторая — конец вектора. Наряду с этим мы будем также обозначать вектор одной малой латинской буквой полужирного шрифта, которая на чертежах ставится у конца стрелки, изображающей вектор (рис. 1, где изображен вектор а с началом А и концом В). Начало вектора часто будет называться таже его точкой приложения.

Векторы называются равными, если они имеют одинаковые длины, лежат на параллельных прямых или на одной прямой и направлены в одну сторону.

Число, равное длине вктора (при заданном масштабе), называется его модулем. Модуль вектора a обозначается символом или а. Если , то вектор называется единичным.

Единичный вектор, имеющий одинаковое направление с данным вектором , называется ортом вектора и обозначается обычно символом .

Проекцией вектора на ось u называется число, равное величине отрезка оси u, где точка является проекцией точки А на ось u, а — проекцией точки В на эту ось.

Проекция вектора на ось u обозначается символом . Если вектор обозначен символом , то его проекцию на ось u принято обозначать: .

Проекция вектора на ось u выражается через его модуль и угол наклона к оси u формулой

Проекции произвольного вектора на оси некоторой заданной системы координат в дальнейшем обозначаются буквами X, Y, Z. Равенство ={X, Y, Z} означает, что числа X, Y, Z являются проекциями вектора на координатные оси. Вектор, для которого X=Y=Z=0, называется нулевым и обозначается .

Проекции вектора на координатные оси называются также его (декартовыми) координатами. Если даны две точки (, , ) и (, , ), являющиеся соответственно началом и концом вектора , то его координаты X, Y, Z определяются по формулам , , .

Формула

(2)

позволяет по координатам вектора определить его модуль.

Если , , — углы, которые составляет вектор с координатными осями (см. рис. 2), то , , называются направляющими косинусами вектора .

Вследствие формулы (1)

, , .

Отсюда, и из формулы (2) следует, что

Последнее равенство позволяет определить один из углов , , , если известны два других.

748		Вычислить модуль вектора ={6; 3; -2}.
749		Даны две координаты вектора X=4, Y=-12. Определить его третью координату Z при условии, что =13.
750		Даны точки A(3; -1; 2), B(-1; 2; 1). Найти координаты векторов и .
751		Определить точку N, с которой совпадает конец вектора ={3; -1; 4}, если его начало совпадает с точкой М(1; 2; -3).
752		Определить начало вектора ={2; -3; -1}, если его конец совпадает с точкой (1; -1; 2).
753		Дан модуль вектора =2 и углы =45⁰, =60⁰, =120⁰. Вычислить проекции вектора на координатные оси.
754		Вычислить направляющие косинусы вектора ={12; -15; -16}.
755		Вычислить направляющие косинусы вектора ={3/13; 4/13; 12/13}.
756		Может ли вектор составлять с координатными осями следующие углы:
	756.1	=45⁰, =60⁰, =120⁰;
	756.2	=45⁰, =135⁰, =60⁰;
	756.3	=90⁰, =150⁰, =60⁰.
757		Может ли вектор составлять с двумя координатными осями следующие углы:
	757. 1	=30⁰, =45⁰;
	757.2	=60⁰, =60⁰:
	757.3	=150⁰, =30⁰.
758		Вектор составляет с осями Ox и Oz углы =120⁰и =45⁰. Какой угол он составляет с осью Oy?
759		Вектор составляет с координатными осями Ox и Oy углы =60⁰, =120⁰. Вычислить его координаты при условии, что =2.
760		Определить координаты точки М, если ее радиус-вектор составляет с координатными осями одинаковые углы и его модуль равен 3.

Решение: 1 Длиной стороны ав является модуль вектора. Его координаты

Вариант №8.

Задание №1 Даны вершины треугольник АВС. Найти:

1) Длину стороны АВ;

2) Уравнение сторон АВ и АС и их угловые коэффициент;

3) Внутренний угол А в радианах с точностью 0,01;

4) Уравнение высоты CD и ее длину;

5) Уравнение окружности, для которой высота CD есть диаметр;

6) Систему линейных неравенств, определяющих треугольник АВС.

Решение:

1) Длиной стороны АВ является модуль вектора . Его координаты:

Его модуль:

Получили:

2) Прямая АВ проходит через точку А и вектор является направляющим для него, следовательно:

Коэффициент наклона прямой АВ найдем из его уравнения:

Прямая АС проходит через точку А и С, следовательно:

Коэффициент наклона прямой АС найдем из его уравнения:

3) Внутренний угол А найдем воспользовавшись скалярным произведением векторов и .

Координаты вектора АС:

Его модуль:

В свою очередь:

Отсюда:

4) Уравнение стороны CD запишем через коэффициент наклона:

Высота CD перпедикулярна стороне АВ, следовательно:

Отсюда:

Так как высота CD проходит через точку , следовательно, его уравнение должно удовлетворят условию:

Получили:

Длину высоты CD найдем как расстояние от точки C до прямой АВ:

5) Уравнение окружности в каноническом виде записывается уравнением:

где – координаты центра окружности, – диаметр окружности.

Так как высота CD является диаметром искомой окружности, его радиус равен половине длины этой высоты, а центр находится в его середине. Следовательно:

Для нахождения координат середины высоты CD найдем координаты точки D. Так как точка D является точкой пересечения прямых AB и CD, его координаты находятся как решение системы уравнений:

Согласно формулам Крамера:

Следовательно, координаты середины высоты CD:

Отсюда искомое уравнение окружности:

6) Найдем уравнение стороны ВC, как прямой, проходящей через точки В и С:

Таким образом, стороны треугольника задаются уравнениями:

Схематично изобразим данный треугольник и его высоту:

Согласно рисунку для треугольника можем записать систему уравнений:

Ответ:

Задание 2: Составить уравнение линии, для каждой точки которой ее расстояние до точки равно расстоянию и до прямой . Полученное уравнение привести к простейшему виду и построить кривую.

Решение:

Для любой точки на кривой расстояние от точки А определяется как:

Для любой точки на кривой расстояние до прямой определится как :

Согласно заданию:

_{— уравнение параболы, с вершиной в
точке
.}

Задание 3: Даны координаты точек Требуется:

Записать векторы и в системе орт и найти модули этих векторов
Найти угол между векторами и
Составить уравнение плоскости, проходящей через точку перпендикулярно вектору .

Решение:

Угол между векторами найдем и воспользовавшись свойствами их скалярного произведения:

В свою очередь:

Отсюда:

Вектор является нормалью для искомой плоскости, следовательно, искомое уравнение плоскости можем записать в виде:

Ответ:

Задание 4: Даны вектора Показать что векторы образуют базис трехмерного пространства, и найти координаты вектора в этом базисе.

Решение:

Вычислим смешанное произведение векторов :

Смешанное произведение векторов не равно нулю, следовательно, они не компланарны и образуют базис. Найдем коэффициенты разложения x, y, z вектора в этом базисе, решив систему:

Искомое разложение:

Ответ:

Задание 5: Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы.

Решение.

Ответ:

Задание 6: Найти указанные пределы.

а) б) в) г)

Векторов

Это вектор:

Вектор имеет величину , (размер) и направление :

Длина линии показывает ее величину, а стрелка указывает направление.

Мы можем сложить два вектора, соединив их голова к хвосту:

И неважно, в каком порядке мы их добавляем, результат будет тот же:

Пример: самолет летит на север, но дует ветер с северо-запада.

Два вектора (скорость, создаваемая гребным винтом, и скорость ветра) приводят к немного более низкой путевой скорости при движении немного к востоку от севера.

Если бы вы смотрели на самолет с земли, казалось бы, он немного поскользнулся.

Вы когда-нибудь видели это? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают это объяснить.

Скорость, ускорение, сила и многое другое — векторы.

Вычитание

Мы также можем вычесть один вектор из другого:

сначала мы меняем направление вектора, который хотим вычесть,
, затем добавьте их как обычно:

а — б

Обозначение

Вектор часто пишется полужирным шрифтом , например a или b .

Вектор также можно записать как буквы
в его голове и хвосте со стрелкой над ним, например:

Расчеты

Сейчас. .. как мы делаем расчеты?

Самый распространенный способ — сначала разбить векторы на части x и y, например:

Вектор a разбит на
, два вектора a _x и a _y

(Позже мы увидим, как это сделать.)

Добавление векторов

Затем мы можем сложить векторы на , добавив части x и , добавив части y :

Сумма вектора (8, 13) и вектора (26, 7) дает вектор (34, 20)

Пример: складываем векторы

a = (8, 13) и b = (26, 7)

c = a + b

c = (8, 13) + (26, 7) = (8 + 26, 13 + 7) = (34, 20)

Когда мы разбиваем такой вектор, каждая часть называется компонентом :

Вычитание векторов

Для вычитания сначала переверните вектор, который мы хотим вычесть, а затем сложите.

Пример: вычесть

k = (4, 5) из v = (12, 2)

a = v + — k

a = (12, 2) + — (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)

Величина вектора

Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:

| a |

ИЛИ можно записать с двойной вертикальной чертой (чтобы не путать с абсолютным значением):

|| a ||

Мы используем теорему Пифагора для его вычисления:

| a | = √ (х ² + у ²)

Пример: какова величина вектора

b = (6, 8)?

| b | = √ (6 ² + 8 ²) = √ (36 + 64) = √100 = 10

Вектор с величиной 1 называется единичным вектором.

Вектор против скалярного

Скаляр имеет величину (размер) только .

Скаляр: просто число (например, 7 или -0,32) … определенно не вектор.

Вектор имеет величину и направление и часто выделяется полужирным шрифтом , поэтому мы знаем, что это не скаляр:

, поэтому c — вектор, его величина и направление
, но c — это просто значение, например 3 или 12.4

Пример: k

b на самом деле является скаляром k, умноженным на вектор b .

Умножение вектора на скаляр

Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы изменяем размер вектора.

Пример: умножить вектор

m = (7, 3) на скаляр 3

a = 3 м = (3 × 7, 3 × 3) = (21, 9)

По-прежнему указывает в том же направлении, но в 3 раза длиннее

(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз. )

Умножение вектора на вектор (скалярное произведение и перекрестное произведение)

Как умножить два вектора вместе? Есть несколько способов!

(Подробности см. На этих страницах.)

Более двух размеров

Векторы также отлично работают в трех или более измерениях:

Вектор (1, 4, 5)

Пример: складываем векторы

a = (3, 7, 4) и b = (2, 9, 11)

c = a + b

c = (3, 7, 4) + (2, 9, 11) = (3 + 2, 7 + 9, 4 + 11) = (5, 16, 15)

Пример: какова величина вектора

w = (1, −2, 3)?

| w | = √ (1 ² + (−2) ² + 3 ²) = √ (1 + 4 + 9) = √14

Вот пример с 4-мя измерениями (но его сложно нарисовать!):

Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)

(3, 3, 3, 3) + — (1, 2, 3, 4)
= (3, 3, 3, 3) + (−1, −2, −3, −4)
= (3 −1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)

Звездная величина и направление

Мы можем знать величину и направление вектора, но нам нужны его длины x и y (или наоборот):

	<=>
Вектор a в полярных координатах Координаты		Вектор a в декартовых координатах

Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткое описание:

От полярных координат (r, θ ) до декартовых координат (x, y)		От декартовых координат (x, y) до полярных координат (r, θ)
x = r × cos ( θ ) y = r × sin ( θ )		r = √ (x ² + y ²) θ = загар ^-1 (y / x)

Пример

Сэм и Алекс тянут ящик.

Сэм тянет с силой 200 Ньютонов при 60 °
Алекс тянет с силой 120 Ньютонов под углом 45 °, как показано на рисунке

Что такое общая сила и ее направление?

Давайте сложим два вектора голова к хвосту:

Первое преобразование из полярной в декартову (до 2 десятичных знаков):

Вектор Сэма:

x = r × cos ( θ ) = 200 × cos (60 °) = 200 × 0,5 = 100
y = r × sin ( θ ) = 200 × sin (60 °) = 200 × 0.8660 = 173,21

Вектор Алекса:

x = r × cos ( θ ) = 120 × cos (-45 °) = 120 × 0,7071 = 84,85
y = r × sin ( θ ) = 120 × sin (-45 °) = 120 × -0,7071 = -84,85

Теперь у нас:

Добавьте их:

(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)

Этот ответ верен, но давайте вернемся к полярному, поскольку вопрос был в полярном:

r = √ (x ² + y ²) = √ (184. 85 ² + 88,36 ²) = 204,88
θ = tan ^-1 (y / x) = tan ^-1 (88,36 / 184,85) = 25,5 °

И у нас есть результат (округленный):

А для Сэма и Алекса это выглядит так:

Они могли бы получить лучший результат, если бы стояли плечом к плечу!

32.3: Векторы — Chemistry LibreTexts

Скалярное произведение векторов \ (\ mathbf {u} \) и \ (\ mathbf {v} \), также известное как скалярное произведение или внутреннее произведение, определяется как (обратите внимание на точка между символами, представляющими векторы)

\ [\ mathbf {u} \ cdot \ mathbf {v} = | \ mathbf {u} || \ mathbf {v} | \ cos \ theta \ nonumber \]

где \ (\ theta \) — угол между векторами.Обратите внимание, что скалярное произведение равно нулю, если два вектора перпендикулярны друг другу, и равно произведению их абсолютных значений, если они параллельны. Несложно доказать, что

\ [\ mathbf {u} \ cdot \ mathbf {v} = u_xv_x + u_yv_y + u_zv_z \ nonumber \]

Пример \ (\ PageIndex {1} \)

Покажите, что векторы

\ [\ begin {align *} \ mathbf {u_1} & = \ dfrac {1} {\ sqrt {3}} \ hat {\ mathbf {i}} + \ dfrac {1} {\ sqrt {3}} \ hat {\ mathbf {j}} + \ dfrac {1} {\ sqrt {3}} \ hat {\ mathbf {k}} \\ [4pt] \ mathbf {u_2} & = \ dfrac {1} {\ sqrt {6}} \ hat {\ mathbf {i}} — \ dfrac {2} {\ sqrt {6}} \ hat {\ mathbf {j}} + \ dfrac {1} {\ sqrt {6}} \ шляпа {\ mathbf {k}} \\ [4pt] \ mathbf {u_3} & = — \ dfrac {1} {\ sqrt {2}} \ hat {\ mathbf {i}} + \ dfrac {1} {\ sqrt {2}} \ hat {\ mathbf {k}} \ end {align *} \ nonumber \]

имеют единичную длину и взаимно перпендикулярны.{1/2} = 1 \ end {align *} \ nonumber \]

Чтобы проверить, перпендикулярны ли два вектора, мы выполняем скалярное произведение:

\ [\ begin {align *} \ mathbf {u_1} \ cdot \ mathbf {u_2} & = \ left (\ dfrac {1} {\ sqrt {3}} \ dfrac {1} {\ sqrt {6}} — \ dfrac {1} {\ sqrt {3}} \ dfrac {2} {\ sqrt {6}} + \ dfrac {1} {\ sqrt {3}} \ dfrac {1} {\ sqrt {6}} \ right) = 0 \\ [4pt] \ mathbf {u_1} \ cdot \ mathbf {u_3} & = \ left (- \ dfrac {1} {\ sqrt {3}} \ dfrac {1} {\ sqrt {2 }} + \ dfrac {1} {\ sqrt {3}} \ dfrac {1} {\ sqrt {2}} \ right) = 0 \\ [4pt] \ mathbf {u_2} \ cdot \ mathbf {u_3} & = \ left (- \ dfrac {1} {\ sqrt {6}} \ dfrac {1} {\ sqrt {2}} + \ dfrac {1} {\ sqrt {6}} \ dfrac {1} {\ sqrt {2}} \ right) = 0 \ end {align *} \ nonumber \]

Таким образом, мы только что доказали, что три пары взаимно перпендикулярны, а три вектора имеют единичную длину. 2.* \ cdot \ mathbf {v} = (\ hat {\ mathbf {i}} + (1 + i) \ hat {\ mathbf {j}}) ((1 + i) \ hat {\ mathbf {i}} + \ hat {\ mathbf {j}}) = (1) (1 + i) + (1 + i) (1) = 2 + 2i \ neq 0 \ nonumber \]

Следовательно, векторы не ортогональны.

Векторная алгебра:

ВЕКТОРНЫЕ МЕТОДЫ

Приоритетные направления:

Векторы и векторное сложение
Единичные векторы
Базовые векторы и компоненты вектора
прямоугольный координаты в 2-D
прямоугольный координаты в 3-D
Вектор соединение двух точек
Точечный продукт
Перекрестное произведение
Трехместный товар
Трехместный векторное произведение

Векторы и сложение вектора:

Скаляр — это величина, такая как масса или температура, которая имеет только величину. » на жирном символе (т.е.е.,). Следовательно,

Любой вектор можно превратить в единичный вектор, разделив его на длину.

Любой вектор можно полностью представить, указав его величину и единицу. вектор вдоль его направления.

Базовые векторы и компоненты вектора:

Базовые векторы — это набор векторов, выбранных в качестве базовых для представления всех остальных векторов.Идея состоит в том, чтобы построить каждый вектор из сложения векторов по базовым направлениям. Например, вектор на рисунке можно записать как сумму трех векторов u ₁, u ₂, и u ₃, каждый по направлению одного из базовых векторов e ₁, e ₂ и e ₃, так что

Каждый из векторов u ₁, u ₂ и u ₃ параллельно одному из базовых векторов и может быть записано как скалярное кратное эта база. Пусть u ₁, u ₂ и u ₃ обозначим эти скалярные множители так, чтобы получилось

Оригинальный вектор u банка теперь записывается как

Скалярные множители u ₁, u ₂ и u ₃ известны как компоненты и в базе, описываемой базой векторы e ₁, e ₂ и e ₃.Если базовые векторы являются единичными векторами, то компоненты представляют собой длины соответственно трех векторов u ₁, u ₂, и u ₃. Если базовые векторы являются единичными векторами и взаимно ортогонально, то основание известно как ортонормированное, евклидово или декартово основание.

Вектор может быть разрешен по любым двум направлениям в плоскости, содержащей его. На рисунке показано, как правило параллелограмма используется для построения векторов и . и b , что в сумме дает c .

В трех измерениях вектор может быть разрешен вдоль любых трех некомпланарных линий. На рисунке показано, как можно разрешить вектор по трем направлениям. сначала найдя вектор в плоскости двух направлений, а затем разрешая этот новый вектор по двум направлениям в плоскости.

Когда векторы представлены в терминах базовых векторов и компонентов, сложение двух векторов приводит к сложению компонентов векторов.Следовательно, если два вектора A и B представлены как

тогда,

прямоугольный компоненты в 2-D:

Базовые векторы прямоугольной системы координат x-y задаются формулой единичные векторы и вдоль x и y направления соответственно.

Используя базовые векторы, можно представить любой вектор F как

Из-за ортогональности оснований имеются следующие соотношения.

прямоугольный координаты в 3-D:

Базовые векторы прямоугольной системы координат задаются набором три взаимно ортогональных единичных вектора, обозначенные,, и что расположены вдоль координатных направлений x , y и z , соответственно, как показано на рисунке.

Показанная система является системой для правшей, поскольку большой палец правой руки указывает в направлении z , если пальцы таковы, что представляют вращение вокруг оси z от x до y . Эта система может превратиться в левостороннюю систему, изменив направление любого из координатные линии и связанный с ними базовый вектор.

В прямоугольной системе координат компонентами вектора являются проекции вектора на x , y и z направления. Например, на рисунке проекции вектора A вдоль направлений x, y, и z задаются как A _x, A _y, и A _z соответственно.

В результате теоремы Пифагора и ортогональности базы векторов, величина вектора в прямоугольной системе координат может быть рассчитано по

Направляющий косинус:

Направляющие косинусы определены как

где углы, и — углы показаны на рисунке.Как показано на рисунке, направляющие косинусы представляют собой косинусы углов между вектором и тремя координаты направления.

Направляющие косинусы могут быть вычислены из компоненты вектора и его величина через соотношения

Три направляющих косинуса не являются независимыми и должно удовлетворять соотношению

Эти результаты формируют тот факт, что

Единичный вектор может быть построен вдоль вектора используя направляющие косинусы в качестве компонентов вдоль x , y и z направление. Например, единичный вектор вдоль вектора A получается из

Следовательно,

Вектор соединение двух точек:

Вектор, соединяющий точку A с точкой B дается

Единичный вектор вдоль линии A-B может быть получен из

Вектор F вдоль линии A-B и величиной F может таким образом получается из соотношения

Точечный продукт:

Скалярное произведение обозначается «» между двумя векторами.В скалярное произведение векторов A и B приводит к скаляру, заданному отношение

где — угол между двумя векторами. Порядок не важен в скалярное произведение, как видно из определения скалярных произведений. В результате один получает

Скалярное произведение имеет следующие свойства.

Поскольку косинус 90 ^o равен нулю, скалярное произведение двух ортогональные векторы приведут к нулю.

Поскольку угол между вектором и самим собой равен нулю, а косинус нуля единица, величина вектора может быть записана через скалярное произведение используя правило

Прямоугольные координаты:

При работе с векторами, представленными в прямоугольная система координат по компонентам

, то скалярное произведение может быть оценено из отношение

Это можно проверить прямым умножением векторы и отмечая, что из-за ортогональности базовых векторов прямоугольная система

Проекция вектора на линию:

Ортогональная проекция вектора вдоль прямой получается перемещением одного конца вектора на линию и опусканием перпендикулярно линии от другого конца вектора. Результирующий отрезок на прямой — это ортогональная проекция вектора или просто его проекция.

Скалярная проекция вектора A вдоль направления единичный вектор — длина ортогональной проекции A вдоль линии, параллельной, и может быть оценен с помощью скалярного произведения. В отношение для проекции

Векторная проекция А вдоль агрегата. вектор просто умножает скалярную проекцию на единичный вектор, чтобы получить вектор вместе.Это дает соотношение

Крест товар:

Перекрестное произведение векторов a и b — это вектор, перпендикулярный как a , так и b и имеет величину, равную площади параллелограмм, созданный из a и b . Направление креста продукт определяется правилом правой руки.Перекрестное произведение обозначается «» между векторами

Порядок важен в перекрестном произведении. Если порядок операций изменится в перекрестном произведении направление результирующего вектора меняется на противоположное. То есть

Перекрестное произведение имеет следующие свойства.

Прямоугольные координаты:

При работе в прямоугольных системах координат, перекрестное произведение векторов a и b , заданное

можно оценить с помощью правила

Можно также использовать прямое умножение основания векторов с использованием соотношений

Тройной товар:

Тройное произведение векторов a , b и c равно

Стоимость тройного произведения равна объему параллелепипеда. построенный из векторов. Это видно из рисунка с

Тройной продукт имеет следующие свойства

Прямоугольные координаты:

Рассмотрим векторы, описанные в прямоугольной система координат как

Тройное произведение можно оценить с помощью отношение

Тройной вектор товар:

Произведение тройного вектора имеет свойства

7.Векторы в трехмерном пространстве

Ранее мы видели, как представить двумерные векторы на плоскости x — y .

Теперь мы расширяем идею представления трехмерных векторов с помощью осей x — y — z . (См. «Трехмерную систему координат» для справки по этому поводу).

Пример

Вектор OP имеет начальную точку в начале координат O (0, 0, 0) и конечную точку в P (2, 3, 5). 2) = 6.16 \ «единиц» `

Добавление трехмерных векторов

Ранее мы видели, как складывать двумерные векторы. Теперь мы расширим идею для трехмерных векторов.

Мы просто складываем компоненты i вместе, затем компоненты j и, наконец, компоненты k .

Пример 1

Два якоря удерживают корабль на месте, и их силы, действующие на корабль, представлены векторами A и B следующим образом:

A = 2 i + 5 j — 4 k и B = −2 i — 3 j — 5 k

Если бы мы заменили 2 якоря на 1 якорь, какой вектор представляет этот единственный вектор?

Ответ

Задача просто требует, чтобы мы сложили векторы, чтобы получить единственный результирующий вектор.

A + B
= (2 + −2) i + (5 — 3) j + (−4 — 5) k
= 0 i + 2 j — 9 k
= 2 j — 9 k

Точечное произведение трехмерных векторов

Чтобы найти скалярное произведение (или скалярное произведение) трехмерных векторов, мы просто расширяем идеи скалярного произведения в двух измерениях, с которыми мы встречались ранее.

Пример 2 — Точечное произведение с использованием величины и угла

Найдите скалярное произведение векторов P и Q , учитывая, что угол между двумя векторами составляет 35 ° и

| P | = 25 ед. с и | Q | = 4 шт.

Ответ

Используя нашу формулу для скалярного произведения:

P • Q = | P | | Q | cos θ

имеем:

P • Q
= | P | | Q | cos θ
= 25 × 4 × cos 35 °
= 81.92

Пример 3 — Точечное произведение, если векторы являются кратными единичным векторам

Найдите скалярное произведение векторов A и B (они взяты из нашего примера привязки выше):

A = 2 i + 5 j — 4 k и B = −2 i — 3 j — 5 k

Ответ

A • B
= (2 i + 5 j — 4 k ) • (−2 i — 3 j — 5 k )
= (2 × −2) + (5 × −3) + (−4 × −5)
= −4 + −15 + 20
= 1

Направление косинусов

Предположим, у нас есть вектор OA с начальной точкой в начале координат и конечной точкой в A.

Предположим также, что у нас есть единичный вектор в том же направлении, что и OA . (См. Напоминание об единичных векторах).

Пусть наш единичный вектор будет:

u = u ₁ i + u ₂ j + u ₃ k

На графике u — это единичный вектор (черный), указывающий в том же направлении, что и вектор OA и i , j и k (единичные векторы в x-, y- и z- соответственно) отмечены зеленым.

Теперь мы увеличиваем вектор и и немного меняем ориентацию, как показано ниже:

Теперь, если на диаграмме выше,

α — это угол между u и осью x (темно-красным),
β — угол между u и осью y (зеленый), а
γ — угол между u и z — ось (розовая),

, то мы можем использовать скалярное произведение и написать:

u ₁
= u • i
= 1 × 1 × cos α
= cos α

u ₂
= u • j
= 1 × 1 × cos β
= cos β

u ₃
= u • k
= 1 × 1 × cos γ
= cos γ

Итак, мы можем записать единичный вектор и как:

u = cos α i + cos β j + cos γ k

Эти 3 косинуса называются направляющими косинусами .

Угол между трехмерными векторами

Ранее мы видели, как найти угол между двумерными векторами. Мы используем ту же формулу для трехмерных векторов:

`theta = arccos ((P * Q) / (| P || Q |))`

Пример 4

Найдите угол между векторами P = 4 i + 0 j + 7 k и Q = -2 i + j + 3 k .

Ответ

Векторы P и Q следующие.Вектор P находится на плоскости x — z (обратите внимание, что значение y для вектора P равно «0»), а Q находится «позади» y — z самолет.

По формуле

`theta = arccos ((P * Q) / (| P || Q |))`

имеем:

P • Q
= (4 i + 0 j + 7 j ) • (−2 i + j + 3 k)
= (4 × −2) + (0 × 1) + (7 × 3)
= 13

А теперь знаменатель:

`| P || Q | = sqrt (4 ^ 2 + (0) ^ 2 + 7 ^ 2)` `xxsqrt ((- 2) ^ 2 + 1 ^ 2 + 3 ^ 2)`

`= sqrt (65) sqrt (14)`
`= 30. 166 \ «единиц» `

Так

θ = arccos (13 ÷ 30,166)

Следовательно, угол между векторами P и Q равен

.
θ = 64,47 °
Упражнение
Найдите угол между векторами P = 3 i + 4 j -7 k и Q = -2 i + j + 3 k .
Ответ
По формуле
`theta = arccos ((P * Q) / (| P || Q |))`
сначала находим скалярное произведение:
P • Q
= (3 i + 4 j — 7 j ) • (−2 i + j + 3 k)
= (3 × −2) + (4 × 1) + (−7 × 3)
= −23
А теперь знаменатель:
| P | | Q |
= √ (3 ² + 4 ² + (−7) ²) × √ ((- 2) ² + 1 ² + 3 ²)
= 32. 187
Так
θ = arccos (−23 ÷ 32,187)
Следовательно, угол между векторами P и Q равен
.
θ = 135,6 °
Приложение
У нас есть куб ABCO PQRS, у которого есть нить по диагонали куба от B до S, а другая по другой диагонали от C до P
Какой угол между двумя струнами?
Ответ

Для удобства предположим, что у нас есть куб единиц (каждая сторона имеет длину 1 единицу), и мы разместим его так, чтобы один угол куба находился в начале координат.

Единичные векторы i , j и k действуют в направлениях x -, y — и z — соответственно. Итак, на нашей диаграмме, поскольку у нас есть единичный куб,

OA = i
OC = j
OS = k

Из диаграммы мы видим, что для перехода от B к S нам нужно пройти −1 единицу в направлении x , −1 единицу в направлении y и вверх на 1 единицу в направлении z . .Поскольку у нас есть единичный куб, мы можем написать:

BS = −i — j + k

и аналогично:

CP = i — j + k

Скалярное произведение векторов BS и CP :

BS • CP = | BS | | CP | cos θ
, где θ — угол между BS и CP .

Таким образом, угол θ равен

.
θ = arccos [( BS • CP ) ÷ ( | BS | | CP | )]
Сейчас,
BS • CP
= ( −i — j + k ) • ( i — j + k )
= – 1 + 1 + 1
= 1
и
| BS | | CP |
`= sqrt ((- 1) ^ 2 + (-1) ^ 2 + 1 ^ 2)` `× sqrt (1 ^ 2 + (-1) ^ 2 + 1 ^ 2)`
`= (sqrt3) (sqrt3)`
= 3
Так
`θ = arccos (1/3)`
θ = 70. 5 °
Итак, угол между струнами равен «70,5 °». (В этой ситуации мы предполагаем, что «угол» относится к острому углу между струнами.)
Величина и направление векторов
Величина вектора
Величина вектора п Q → это расстояние между начальной точкой п и конечная точка Q . В символах величина п Q → записывается как | п Q → | .
Если заданы координаты начальной и конечной точек вектора, Формула расстояния можно использовать для определения его величины.
| п Q → | знак равно ( Икс 2 — Икс 1 ) 2 + ( y 2 — y 1 ) 2
Пример 1:
Найдите величину вектора п Q → чья начальная точка п я сидела ( 1 , 1 ) и конечная точка находится в Q я сидела ( 5 , 3 ) .
Решение:
Используйте формулу расстояния.
Подставьте значения Икс 1 , y 1 , Икс 2 , и y 2 .
| п Q → | знак равно ( 5 — 1 ) 2 + ( 3 — 1 ) 2 знак равно 4 2 + 2 2 знак равно 16 + 4 знак равно 20 ≈ 4. 5
Величина п Q → около 4.5 .
Направление вектора
Направление вектора — это мера угла, который он образует с горизонтальная линия .
Для определения направления вектора можно использовать одну из следующих формул:
загар θ знак равно y Икс , куда Икс горизонтальное изменение и y это вертикальное изменение
или же
загар θ знак равно y 2 — y 1 Икс 2 — Икс 1 , куда ( Икс 1 , y 1 ) начальная точка и ( Икс 2 , y 2 ) это конечная точка.
Пример 2:
Найдите направление вектора п Q → чья начальная точка п я сидела ( 2 , 3 ) и конечная точка находится в Q я сидела ( 5 , 8 ) .
Приведены координаты начальной и конечной точек.Подставьте их в формулу загар θ знак равно y 2 — y 1 Икс 2 — Икс 1 .
загар θ знак равно 8 — 3 5 — 2 знак равно 5 3
Найдите обратный загар и воспользуйтесь калькулятором.
θ знак равно загар — 1 ( 5 3 ) ≈ 59 °
Вектор п Q → имеет направление около 59 ° .
Умножение векторов — Гипертекст по физике
Обсуждение
скалярно-векторное умножение
Умножение вектора на скаляр изменяет величину вектора, но оставляет его направление неизменным.Скаляр изменяет размер вектора. Скаляр «масштабирует» вектор. Например, вектор полярной формы…
r = r r̂ + θ θ̂
умноженное на скаляр , а равно…
a r = ar r̂ + θ θ̂
Умножение вектора на скаляр дистрибутивно.
a ( A + B ) = a A + a B
Следовательно, вектор прямоугольной формы…
r = x î + y ĵ
умноженное на скаляр , а равно…
a r = ax до + ay ĵ
точечный продукт
Геометрически скалярное произведение двух векторов — это величина, умноженная на проекцию второго на первый.
Символ, используемый для представления этой операции, представляет собой маленькую точку на средней высоте (·), отсюда и произошло название «скалярный продукт». Поскольку это произведение имеет только величину, оно также известно как скалярное произведение .
A · B = AB cos θ
Скалярное произведение распределительное…
A · ( B + C ) = A · B + A · C
и коммутативный…
A · B = B · A
Поскольку проекция вектора на сам себя оставляет его величину неизменной, скалярное произведение любого вектора с самим собой является квадратом величины этого вектора.
A · A = AA cos 0 ° = A ²
Применение этого следствия к единичным векторам означает, что скалярное произведение любого единичного вектора на себя равно единице. Кроме того, поскольку вектор не имеет проекции, перпендикулярной самому себе, скалярное произведение любого единичного вектора на любой другой равно нулю.
î · î = · ĵ = k̂ · k = (1) (1) (cos 0 °) = 1
î · = · k̂ = k̂ · î = (1) (1) (cos 90 °) = 0
Используя эти знания, мы можем вывести формулу для скалярного произведения любых двух векторов в прямоугольной форме.Полученный продукт выглядит ужасно беспорядочно, но состоит в основном из членов, равных нулю.
9036 B _{y + B _z )}
A · B = ( A _x î + A _y ĵ + A _z k̂ ) · ( B _x î +
A · B = A _x или · B _x или + A _x или · B _y ĵ + A _x или · B _z k̂
+ A _y ĵ · B _x или + A _y ĵ · B _y ĵ + A _y ĵ · B _z k̂
+ A _z k̂ · B _x или + A _z k̂ · B _y ĵ + A _z k̂ · B _z k̂
A · B = A _x B _x + A _y B _y + A _z B _z
Скалярное произведение двух векторов, таким образом, является суммой произведений их параллельных компонентов. Отсюда мы можем вывести теорему Пифагора в трех измерениях.
A · A = AA cos 0 ° = A _x A _x + A _y A _y + A _z A _z
A ² = A _x ² + A _y ² + A _z ²
крестообразное произведение
Геометрически скрещенное произведение двух векторов — это площадь параллелограмма между ними.
Символ, используемый для представления этой операции, представляет собой большой диагональный крест (×), отсюда и произошло название «перекрестное произведение». Поскольку этот продукт имеет величину и направление, он также известен как векторное произведение .
A × B = AB sin θ n̂
Вектор n̂ (n шляпа) — это единичный вектор, перпендикулярный плоскости, образованной двумя векторами. Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим.
Перекрестное произведение распределительное…
A × ( B + C ) = ( A × B ) + ( A × C )
, но не , а , коммутативный…
A × B = — B × A
Изменение порядка перекрестного умножения меняет направление произведения на противоположное.
Поскольку два идентичных вектора образуют вырожденный параллелограмм без площади, векторное произведение любого вектора на себя равно нулю…
A × A = 0
Применение этого следствия к единичным векторам означает, что перекрестное произведение любого единичного вектора на себя равно нулю.
î × î = ĵ × ĵ = k̂ × k̂ = (1) (1) (sin 0 °) = 0
Следует отметить, что произведение любого единичного вектора на любой другой будет иметь величину, равную единице. (В конце концов, синус 90 ° равен единице.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение , а не коммутативно, порядок операций важен.
Держите правую руку ровно, держа большой палец перпендикулярно пальцам. Никогда не сгибайте большой палец.
Укажите пальцами в направлении первого вектора.
Сориентируйте ладонь так, чтобы при сгибании пальцев они указывали в направлении второго вектора.
Ваш большой палец теперь указывает в направлении перекрестного произведения.
Правая система координат , которая является обычной системой координат, используемой в физике и математике, — это система, в которой любое циклическое произведение трех осей координат положительно, а любое антициклическое произведение отрицательно.Представьте себе часы с тремя буквами x-y-z вместо обычных двенадцати цифр. Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно циклическим и положительным. Любой продукт, который движется в обратном направлении, — это антициклический и отрицательный.
Перекрестное произведение циклической пары
единичных векторов равно положительным . Перекрестное произведение антициклической пары
единичных векторов равно отрицательным .
Используя эти знания, мы можем вывести формулу для векторного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто это будет ужасный беспорядок, и это так!
A × B = ( A _x î + A _y ĵ + A _z k̂ ) × ( B _{x 9007 90 9036 + B _y ĵ + B _z k̂ )}
Произведение двух трехчленов состоит из девяти членов.
A × B = A _x или × B _x или + A _x или × B _y ĵ + A _x или × B _z k̂
+ A _y ĵ × B _x или + A _y ĵ × B _y ĵ + A _y ĵ × B _z k̂
+ A _z k̂ × B _x или + A _z k̂ × B _y ĵ + A _z k̂ × B _z k̂
Три из них равны нулю. Устраните их.
A × B = A _x B _y k̂ – A _x B _z ĵ
– A _y B _x k̂ + A _y B _z или
+ A _z B _x ĵ – A _z B _y или
Сгруппируйте термины по единичному вектору и коэффициенту.
A × B = ( A _y B _z — A _z B _y ) или + ( A _z B _x — A _x B _z ) ĵ + ( A _x B _y — A _y B _x ) k̂
Есть более простой способ написать это. Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов является определителем матрицы, первая строка которой является единичными векторами, вторая строка — первым вектором, а третья строка — вторым вектором.Условно…
A × B = – ĵ k̂
A _x A _y A _z
B _x B _y B _z
Расширение определителя 3 × 3 его первой строкой является первым шагом.Это дает нам три определителя 2 × 2.
A × B = A _y A _z – — A _x A _z ĵ + A _x A _y k̂
B _y B _z B _x B _z B _x B _y
Эти детерминанты 2 × 2 можно найти быстро. Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать термины и множители.
A × B = ( A _y B _z — A _z B _y ) или + ( A _z B _x — A _x B _z ) ĵ + ( A _x B _y — A _y B _x ) k̂
Что это такое и как рассчитать их составные части и модуль
Теперь я объясню вам, что такое векторы, и концепции, связанные с векторами, которые вам понадобятся для вычисления и работы с ними, например, компоненты вектора, модуль вектора, его направление и смысл.
Мы также рассмотрим типы существующих векторов и типы векторов, с которыми удобно работать в математике.
Что такое векторы?
Векторы — это ориентированные сегменты, которые начинаются в точке, соответствующей началу вектора, и заканчиваются в другой точке, которая является концом вектора:
Они определяются двумя компонентами: компонентом x и компонентом y, также называемыми векторными координатами. Это двумерные величины.
Чтобы выразить их аналитически, они обычно выражаются строчной буквой со стрелкой вверху с двумя ее компонентами в скобках (например, координатами):
Буквы u, v, w и z обычно используются, но не являются обязательными и могут использоваться в любой букве.
Вот несколько примеров векторов:
Это также можно выразить двумя заглавными буквами со стрелкой наверху, где первая буква — точка начала, а вторая буква — точка, где находится конец:
Таким образом, вектор AB будет иметь начало в точке A и конец в точке B:
В дополнение к компонентам вектора другими характеристиками, которые определяют векторы, являются модуль, направление и направление.
Мы увидим каждого из них.
Компоненты вектора
Каковы компоненты вектора?
Это элементы, которые определяют вектор, поскольку, зная его координаты, мы знаем о нем все: модуль (который нужно будет вычислить), направление и смысл.
Говорить о компонентах вектора и координатах вектора — это одно и то же.
Как вычислить компоненты вектора?
Чтобы вычислить компоненты вектора, нам нужно заранее знать координаты его начала и координаты его конца, так как они будут вычисляться по ним.
Если координаты начальной точки вектора:
И координаты конечной точки вектора:
Вычисляем координаты вектора, вычитая координаты конца минус координаты начала:
Чтобы вычислить компонент x вектора, мы вычитаем координату x конца за вычетом координаты x начала координат. Таким же образом, чтобы вычислить компонент «y» вектора, мы вычитаем координату «y» конца минус координату «y» начала координат.
Помните, всегда крайнее меньшее происхождение, и каждый компонент вычитается со своим собственным: x с x и y с 0 и.
Рассмотрим пример:
У нас есть пункт отправления:
И точка, соответствующая концу вектора:
Координаты вектора AB будут соответствовать x-координатам конца минус x-координата начала координат с одной стороны и y-координаты конца минус y-координату начала координат с другой стороны:
Теперь мы работаем с каждым компонентом, и он у нас есть:
Модуль вектора
Что такое векторный модуль?
Модуль вектора — это расстояние от начала до конца, поэтому он соответствует длине вектора.
Буква вектора (или букв) представлена заключенной между двумя полосами:
Модуль вектора, будучи длиной, всегда положителен.
Как рассчитывается модуль?
Модуль вектора вычисляется из координат вектора по следующей формуле:
Модуль вектора — это квадратный корень из квадрата координаты x плюс квадрат координаты y.
Звонит ли эта формула в колокол?
Это то же самое, что и для вычисления гипотенузы прямоугольного треугольника, поскольку для ее получения применяется теорема Пифагора в треугольнике, образованном между вектором и его компонентами, где вектор будет гипотенузой:
Вам не нужно знать, откуда вы взяли формулу, но это важно знать.
Давайте посмотрим на примере, как вычислить векторный модуль. У нас есть следующий вектор:
Какой у вас модуль?
Применяем формулу и она подходит:
Теперь действуем и решаем, получив значение модуля:
Оставляем в виде корня, так как корень 13 не точный.
Как вычислить модуль вектора с координатами его начала и конца
Как мы видели ранее, компоненты вектора вычисляются по координатам точек его начала и конца.
Следовательно, мы можем вычислить модуль вектора напрямую, если нам известны координаты точек его начала и конца, просто заменив в предыдущей расчетной формуле модуля компоненты x и «y» вычитанием координат конца минус координаты начала:
Давайте посмотрим на это на примере.
У нас есть вектор, начало которого находится в точке A, а его конец — в точке B:
Мы собираемся вычислить модуль вектора AB, который будет корнем из квадрата вычитания координат x, минус квадрат вычитания координат «y», всегда вычитая крайнее минус начало координат:
Будьте осторожны с отрицательными координатами.Убираем скобку -4 во втором члене внутренней части корня:
Теперь мы работаем внутри каждой скобки:
Возводим в квадрат и решаем:
Также можно проделать операцию в обратном порядке, то есть, зная модуль вектора, вычислить его компоненты.
Направление и направление вектора
Как мы говорили ранее, вектор — это сегмент, ориентированный, поэтому направление вектора — это линия, которой принадлежит этот вектор.
Все параллельные векторы имеют одинаковое направление.
Направление вектора — это то место, куда направляется этот вектор, куда указывает стрелка.
Направление вектора AB будет идти от точки A к точке B, а направление вектора BA будет идти от точки B к точке A:
Оба вектора имеют одинаковое направление, но противоположные направления
Давайте сравним вектор с прямой дорогой. Сама дорога будет направлением вектора, и внутри дороги вы можете двигаться в обоих направлениях, которые будут соответствовать направлениям вектора.
Типы векторов
Векторов можно фиксировать, когда их точка начала и конец не может перемещаться, и когда их исходная точка может находиться где угодно в пространстве.
Фиксированный вектор
Чтобы определить фиксированный вектор, вам необходимо знать координаты его начала и координаты его конца. Поскольку он зафиксирован, его никак нельзя перемещать.
Два параллельных вектора одного и того же модуля, но из разных исходных точек, являются разными векторами.
Векторы, которые имеют одинаковый модуль, направление и направление, но начинаются в разных точках, называются равноправными векторами.
Бесплатный вектор
Свободные векторы — это те векторы, начало которых может быть расположено в любой точке, и с которыми мы работаем в математике, поскольку они имеют особенность, которая делает их особенными.
А что делает бесплатный вектор таким особенным?
Поскольку мы можем переместить начало свободного вектора в нужную нам точку, мы всегда можем предположить, что его начало находится в начале координат (0.0), и поэтому вектор будет определен, только зная координаты конца.
Вам больше не нужно вычитать координаты начала координат из координат конечной точки для вычисления компонентов вектора.
Итак, когда мы говорим, что вектор:
Мы пытаемся сказать, что его происхождение (0,0), а его крайнее значение (1.