Параллелограмм и прямоугольник имеют одинаковые стороны найдите острый угол параллелограмма: № 9. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника.

Острый угол — параллелограмм — Большая Энциклопедия Нефти и Газа, статья, страница 1

Острый угол — параллелограмм

Cтраница 1

Острый угол параллелограмма, лежащего в основании призмы, равен а.  [1]

Острый угол параллелограмма равен 30, а высоты, проведенные из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.  [2]

Острый угол параллелограмма равен я / 3, длина одной стороны равна 1 см, а его площадь равна ] 3 сма.  [3]

Длина меньшей стороны параллелограмма равная, острый угол параллелограмма равен а, угол между меньшей диагональю и большей стороной равен р Найдите объем тела, полученного вращением параллелограмма вокруг его большей стороны.  [4]

Длина меньшей стороны параллелограмма равна а, острый угол параллелограмма равен а, угол между меньшей диагональю и большей стороной равен ( J.

 [5]

Параллелограмм и прямоугольник имеют одинаковые стороны. Найти острый угол параллелограмма, если площадь параллелограмма равна половине площади прямоугольника.  [6]

Параллелограмм и прямоугольник имеют одинаковые стороны. Найти острый угол параллелограмма, если площадь его равна половине площадв прямоугольника.  [7]

Параллелограмм и прямоугольник имеют одинаковые стороны. Найти острый угол параллелограмма

, если площадь его равна половине площади прямоугольника.  [8]

Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника.  [9]

В отличие от прямоугольного параллелепипеда, все грани которого — прямоугольники, в прямом параллелепипеде в основании находится параллелограмм, а прямоугольниками являются только четыре боковые грани. Поэтому чертеж прямого параллелепипеда по существу ничем не отличается от чертежа прямоугольного параллелепипеда, и это создает дополнительные трудности при пользовании чертежом: необходимо помнить, что

острый угол параллелограмма на чертеже является острым и в самом деле у изображенной фигуры.  [10]

Страницы:      1

Касательная, хорда, секущая

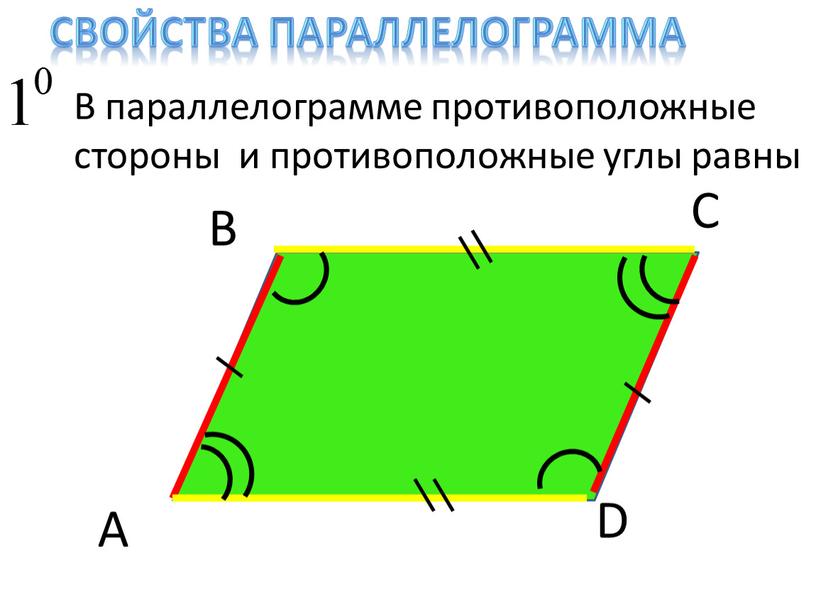
Параллелограмм

1. B 8 № 27433. В па­рал­ле­ло­грам­ме вы­со­та, опу­щен­ная на сто­ро­ну , равна 4, . Най­ди­те синус угла B.

Ответ: 0,5

2. B 8 № 27434. В па­рал­ле­ло­грам­ме вы­со­та, опу­щен­ная на сто­ро­ну , равна 4, . Най­ди­те .

Ответ: 6

3. B 8 № 27435. В па­рал­ле­ло­грам­ме . . Най­ди­те вы­со­ту, опу­щен­ную на сто­ро­ну .

Ответ: 9

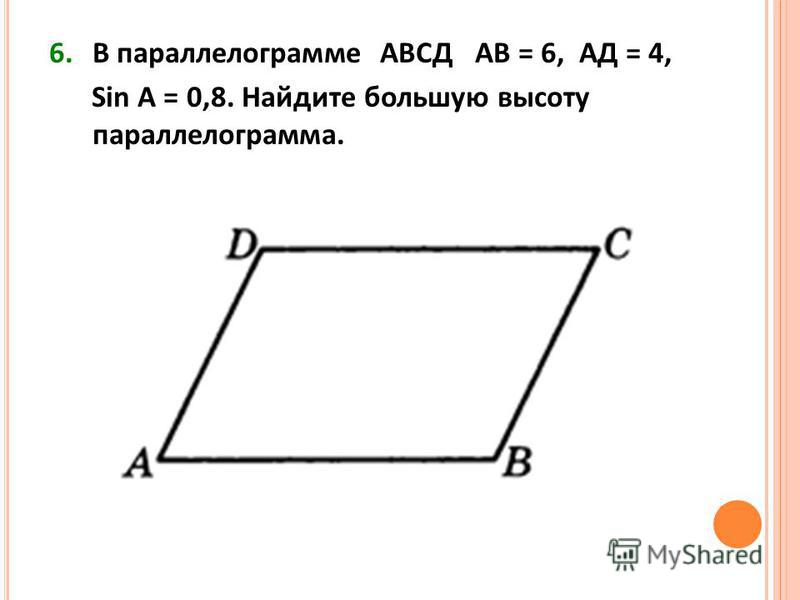
4. B 8 № 27436. В па­рал­ле­ло­грам­ме , , . Най­ди­те боль­шую вы­со­ту па­рал­ле­ло­грам­ма.

Ответ: 18

5. B 8 № 27437. В па­рал­ле­ло­грам­ме . Най­ди­те .

Ответ: -0,4

6. B 8 № 27438. В па­рал­ле­ло­грам­ме . Най­ди­те .

Ответ: 0,7

B 8 № 27610.

Па­рал­ле­ло­грамм и пря­мо­уголь­ник имеют оди­на­ко­вые сто­ро­ны. Най­ди­те ост­рый угол па­рал­ле­ло­грам­ма, если его пло­щадь равна по­ло­ви­не пло­ща­ди пря­мо­уголь­ни­ка. Ответ дайте в гра­ду­сах.

Ответ: 30

8. B 8 № 27611. Сто­ро­ны па­рал­ле­ло­грам­ма равны 9 и 15. Вы­со­та, опу­щен­ная на первую сто­ро­ну, равна 10. Най­ди­те вы­со­ту, опу­щен­ную на вто­рую сто­ро­ну па­рал­ле­ло­грам­ма.

Ответ: 6

9. B 8 № 27612. Пло­щадь па­рал­ле­ло­грам­ма равна 40, две его сто­ро­ны равны 5 и 10. Най­ди­те боль­шую вы­со­ту этого па­рал­ле­ло­грам­ма.

Ответ: 8

10. B 8 № 27805. Най­ди­те тупой угол па­рал­ле­ло­грам­ма, если его ост­рый угол равен . Ответ дайте в гра­ду­сах.

Ответ: 120

11. B 8 № 27806. Сумма двух углов па­рал­ле­ло­грам­ма равна . Най­ди­те один из остав­ших­ся углов. Ответ дайте в гра­ду­сах.

Ответ: 130

12. B 8 № 27807. Один угол па­рал­ле­ло­грам­ма боль­ше дру­го­го на . Най­ди­те боль­ший угол. Ответ дайте в гра­ду­сах.

Ответ: 125

13. B 8 № 27808. Диа­го­наль па­рал­ле­ло­грам­ма об­ра­зу­ет с двумя его сто­ро­на­ми углы и . Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма. Ответ дайте в гра­ду­сах.

Ответ: 120

14. B 8 № 27822. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма, если два его угла от­но­сят­ся как . Ответ дайте в гра­ду­сах.

Ответ: 126

15. B 8 № 27823. Най­ди­те угол между бис­сек­три­са­ми углов па­рал­ле­ло­грам­ма, при­ле­жа­щих к одной сто­ро­не. Ответ дайте в гра­ду­сах.

Ответ: 90

16. B 8 № 27826. Бис­сек­три­са ту­по­го угла па­рал­ле­ло­грам­ма делит про­ти­во­по­лож­ную сто­ро­ну в от­но­ше­нии 4 : 3, счи­тая от вер­ши­ны остро­го угла. Най­ди­те боль­шую сто­ро­ну па­рал­ле­ло­грам­ма, если его пе­ри­метр равен 88.

Ответ: 28

17. B 8 № 27827. Точка пе­ре­се­че­ния бис­сек­трис двух углов па­рал­ле­ло­грам­ма, при­ле­жа­щих к одной сто­ро­не, при­над­ле­жит про­ти­во­по­лож­ной сто­ро­не. Мень­шая сто­ро­на па­рал­ле­ло­грам­ма равна 5. Най­ди­те его боль­шую сто­ро­ну.

Ответ: 10

Прямоугольник

1. B 8 № 27810. Мень­шая сто­ро­на пря­мо­уголь­ни­ка равна 6, диа­го­на­ли пе­ре­се­ка­ют­ся под углом . Най­ди­те диа­го­на­ли пря­мо­уголь­ни­ка.

Ответ: 12

2. B 8 № 27812. Диа­го­наль пря­мо­уголь­ни­ка вдвое боль­ше одной из его сто­рон. Най­ди­те боль­ший из углов, ко­то­рый об­ра­зу­ет диа­го­наль со сто­ро­на­ми пря­мо­уголь­ни­ка? Ответ вы­ра­зи­те в гра­ду­сах.

Ответ: 60

3. B 8 № 27813. В пря­мо­уголь­ни­ке диа­го­наль делит угол в от­но­ше­нии , мень­шая его сто­ро­на равна 6. Най­ди­те диа­го­наль дан­но­го пря­мо­уголь­ни­ка.

Ответ: 12

Ромб

1. B 8 № 27613. Най­ди­те пло­щадь ромба, если его вы­со­та равна 2, а ост­рый угол 30°.

Ответ: 8

2. B 8 № 27614. Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 4 и 12.

Ответ: 24

3. B 8 № 27615. Пло­щадь ромба равна 18. Одна из его диа­го­на­лей равна 12. Най­ди­те дру­гую диа­го­наль.

Ответ: 3

4. B 8 № 27616. Пло­щадь ромба равна 6. Одна из его диа­го­на­лей в 3 раза боль­ше дру­гой. Най­ди­те мень­шую диа­го­наль.

Ответ: 2

5. B 8 № 27816. Най­ди­те мень­шую диа­го­наль ромба, сто­ро­ны ко­то­ро­го равны 2, а ост­рый угол равен .

Ответ: 2

6.

B 8 № 27817. Най­ди­те вы­со­ту ромба, сто­ро­на ко­то­ро­го равна , а ост­рый угол равен .

Ответ: 1,5

7. B 8 № 27828. Най­ди­те боль­шую диа­го­наль ромба, сто­ро­на ко­то­ро­го равна , а ост­рый угол равен .

Ответ: 3

8. B 8 № 27829. Диа­го­на­ли ромба от­но­сят­ся как 3:4. Пе­ри­метр ромба равен 200. Най­ди­те вы­со­ту ромба.

Ответ: 48

9. B 8 № 282851. В ромбе ABCD угол ABC равен 122°. Най­ди­те угол ACD. Ответ дайте в гра­ду­сах.

Ответ: 29

10. B 8 № 282852. В ромбе ABCD угол ACD равен 43°. Най­ди­те угол

ABC. Ответ дайте в гра­ду­сах.

Ответ: 94

Трапеция

1. B 8 № 27439. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 51 и 65. Бо­ко­вые сто­ро­ны равны 25. Най­ди­те синус остро­го угла тра­пе­ции.

Ответ: 0,96

2. B 8 № 27440. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 43 и 73. Ко­си­нус остро­го угла тра­пе­ции равен . Най­ди­те бо­ко­вую сто­ро­ну.

Ответ: 21

3. B 8 № 27441. Боль­шее ос­но­ва­ние рав­но­бед­рен­ной тра­пе­ции равно 34. Бо­ко­вая сто­ро­на равна 14. Синус остро­го угла равен . Най­ди­те мень­шее ос­но­ва­ние.

Ответ: 22

4. B 8 № 27442. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 7 и 51. Тан­генс остро­го угла равен . Най­ди­те вы­со­ту тра­пе­ции.

Ответ: 10

5. B 8 № 27443. Мень­шее ос­но­ва­ние рав­но­бед­рен­ной тра­пе­ции равно 23. Вы­со­та тра­пе­ции равна 39. Тан­генс остро­го угла равен . Най­ди­те боль­шее ос­но­ва­ние.

Ответ: 71

6. B 8 № 27444. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 17 и 87. Вы­со­та тра­пе­ции равна 14. Най­ди­те тан­генс остро­го угла.

Ответ: 0,4

7. B 8 № 27631.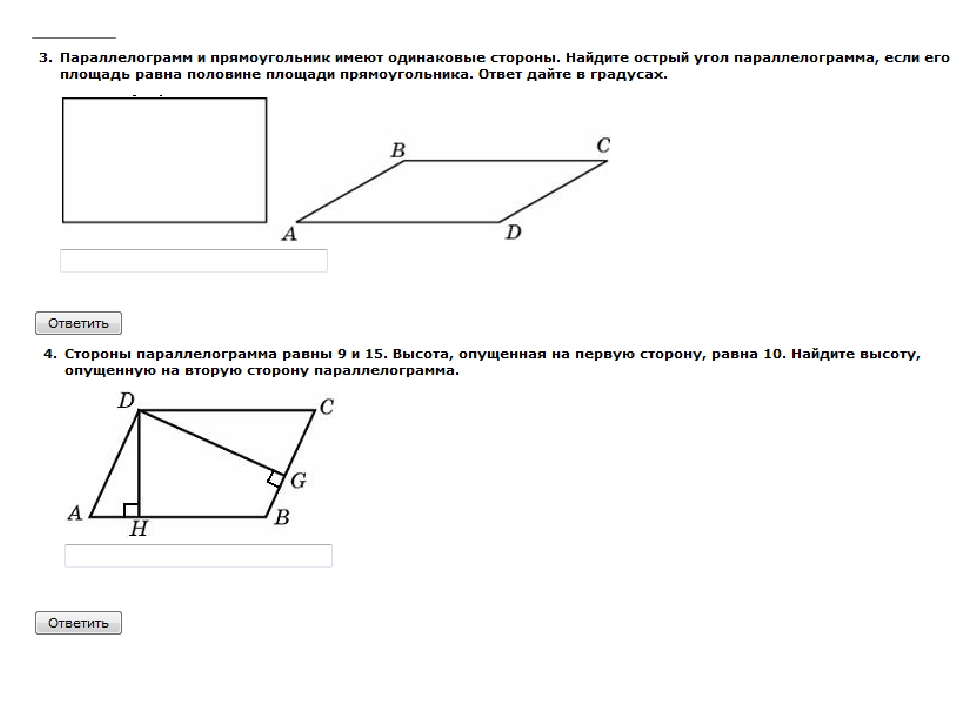 Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 14 и 26, а ее пе­ри­метр равен 60. Най­ди­те пло­щадь тра­пе­ции.

Ответ: 160

8. B 8 № 27632. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 7 и 13, а ее пло­щадь равна 40. Най­ди­те пе­ри­метр тра­пе­ции.

Ответ: 30

9. B 8 № 27633. Най­ди­те пло­щадь пря­мо­уголь­ной тра­пе­ции, ос­но­ва­ния ко­то­рой равны 6 и 2, боль­шая бо­ко­вая сто­ро­на со­став­ля­ет с ос­но­ва­ни­ем угол 45°.

Ответ: 16

10. B 8 № 27634. Ос­но­ва­ния пря­мо­уголь­ной тра­пе­ции равны 12 и 4. Ее пло­щадь равна 64. Най­ди­те ост­рый угол этой тра­пе­ции. Ответ дайте в гра­ду­сах.

Ответ: 45

11. B 8 № 27635. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 14 и 26, а ее бо­ко­вые сто­ро­ны равны 10. Най­ди­те пло­щадь тра­пе­ции.

Ответ: 160

12. B 8 № 27636. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 7 и 13, а ее пло­щадь равна 40. Най­ди­те бо­ко­вую сто­ро­ну тра­пе­ции.

Ответ: 5

13. B 8 № 27637. Ос­но­ва­ния тра­пе­ции равны 18 и 6, бо­ко­вая сто­ро­на, рав­ная 7, об­ра­зу­ет с одним из ос­но­ва­ний тра­пе­ции угол 150°. Най­ди­те пло­щадь тра­пе­ции.

Ответ: 42

14. B 8 № 27638. Ос­но­ва­ния тра­пе­ции равны 27 и 9, бо­ко­вая сто­ро­на равна 8. Пло­щадь тра­пе­ции равна 72. Най­ди­те ост­рый угол тра­пе­ции, при­ле­жа­щий к дан­ной бо­ко­вой сто­ро­не. Ответ вы­ра­зи­те в гра­ду­сах.

Ответ: 30

15. B 8 № 27818. Чему равен боль­ший угол рав­но­бед­рен­ной тра­пе­ции, если из­вест­но, что раз­ность про­ти­во­ле­жа­щих углов равна ? Ответ дайте в гра­ду­сах.

Ответ: 115

16. B 8 № 27819. Най­ди­те сред­нюю линию тра­пе­ции, если ее ос­но­ва­ния равны 30 и 16.

Ответ: 23

17. B 8 № 27820. Сред­няя линия тра­пе­ции равна 28, а мень­шее ос­но­ва­ние равно 18.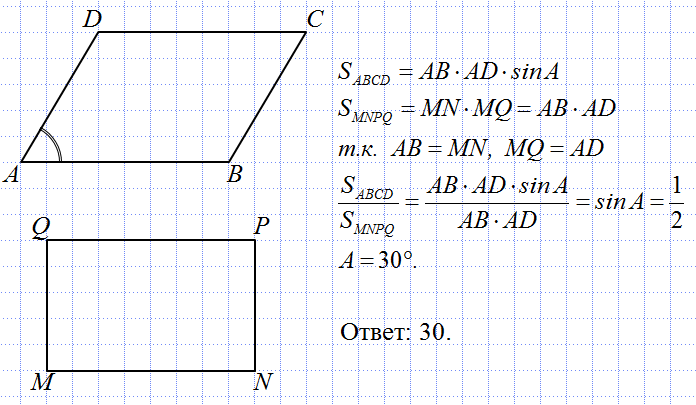 Най­ди­те боль­шее ос­но­ва­ние тра­пе­ции.

Ответ: 38

18. B 8 № 27833. В рав­но­бед­рен­ной тра­пе­ции боль­шее ос­но­ва­ние равно 25, бо­ко­вая сто­ро­на равна 10, угол между ними . Най­ди­те мень­шее ос­но­ва­ние.

Ответ: 15

19. B 8 № 27834. В рав­но­бед­рен­ной тра­пе­ции ос­но­ва­ния равны 12 и 27, ост­рый угол равен . Най­ди­те ее пе­ри­метр.

Ответ: 69

20. B 8 № 27837. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 15 и 9, один из углов равен . Най­ди­те вы­со­ту тра­пе­ции.

Ответ: 3

21. B 8 № 27838. Пе­ри­метр тра­пе­ции равен 50, а сумма не­па­рал­лель­ных сто­рон равна 20. Най­ди­те сред­нюю линию тра­пе­ции.

Ответ: 15

22. B 8 № 27839. Ос­но­ва­ния тра­пе­ции от­но­сят­ся как , а сред­няя линия равна 5. Най­ди­те мень­шее ос­но­ва­ние.

Ответ: 4

23. B 8 № 27840. Пе­ри­метр рав­но­бед­рен­ной тра­пе­ции равен 80, ее сред­няя линия равна бо­ко­вой сто­ро­не. Най­ди­те бо­ко­вую сто­ро­ну тра­пе­ции.

Ответ: 20

24. B 8 № 27841. Сред­няя линия тра­пе­ции равна 7, а одно из ее ос­но­ва­ний боль­ше дру­го­го на 4. Най­ди­те боль­шее ос­но­ва­ние тра­пе­ции.

Ответ: 9

25. B 8 № 27842. Сред­няя линия тра­пе­ции равна 12. Одна из диа­го­на­лей делит ее на два от­рез­ка, раз­ность ко­то­рых равна 2. Най­ди­те боль­шее ос­но­ва­ние тра­пе­ции.

Ответ: 14

26. B 8 № 27843. Ос­но­ва­ния тра­пе­ции равны 3 и 2. Най­ди­те от­ре­зок, со­еди­ня­ю­щий се­ре­ди­ны диа­го­на­лей тра­пе­ции.

Ответ: 0,5

Центральные и впи­сан­ные углы

1. B 8 № 27855. Чему равен впи­сан­ный угол, опи­ра­ю­щий­ся на диа­метр окруж­но­сти? Ответ дайте в гра­ду­сах.

Ответ: 90

2. B 8 № 27857. Чему равен ост­рый впи­сан­ный угол, опи­ра­ю­щий­ся на хорду, рав­ную ра­ди­у­су окруж­но­сти? Ответ дайте в гра­ду­сах.

Ответ: 30

3. B 8 № 27859. Чему равен тупой впи­сан­ный угол, опи­ра­ю­щий­ся на хорду, рав­ную ра­ди­у­су окруж­но­сти? Ответ дайте в гра­ду­сах.

Ответ: 150

4. B 8 № 27860. Ра­ди­ус окруж­но­сти равен 1. Най­ди­те ве­ли­чи­ну остро­го впи­сан­но­го угла, опи­ра­ю­ще­го­ся на хорду, рав­ную . Ответ дайте в гра­ду­сах.

Ответ: 45

5. B 8 № 27861. Ра­ди­ус окруж­но­сти равен 1. Най­ди­те ве­ли­чи­ну ту­по­го впи­сан­но­го угла, опи­ра­ю­ще­го­ся на хорду, рав­ную . Ответ дайте в гра­ду­сах.

Ответ: 135

6. B 8 № 27863. Цен­траль­ный угол на боль­ше остро­го впи­сан­но­го угла, опи­ра­ю­ще­го­ся на ту же дугу окруж­но­сти. Най­ди­те впи­сан­ный угол. Ответ дайте в гра­ду­сах.

Ответ: 36

7. B 8 № 27864. Най­ди­те впи­сан­ный угол, опи­ра­ю­щий­ся на дугу, ко­то­рая со­став­ля­ет окруж­но­сти. Ответ дайте в гра­ду­сах.

Ответ: 36

8. B 8 № 27865. Най­ди­те впи­сан­ный угол, опи­ра­ю­щий­ся на дугу, ко­то­рая со­став­ля­ет окруж­но­сти. Ответ дайте в гра­ду­сах.

Ответ: 36

9. B 8 № 27866. Дуга окруж­но­сти , не со­дер­жа­щая точки , со­став­ля­ет . А дуга окруж­но­сти , не со­дер­жа­щая точки , со­став­ля­ет . Най­ди­те впи­сан­ный угол . Ответ дайте в гра­ду­сах.

Ответ: 40

10. B 8 № 27869. В окруж­но­сти с цен­тром и – диа­мет­ры. Впи­сан­ный угол равен . Най­ди­те цен­траль­ный угол . Ответ дайте в гра­ду­сах.

Ответ: 104

11. B 8 № 27870. В окруж­но­сти с цен­тром и – диа­мет­ры. Цен­траль­ный угол равен . Най­ди­те впи­сан­ный угол . Ответ дайте в гра­ду­сах.

Ответ: 35

12. B 8 № 27885. Най­ди­те угол , если впи­сан­ные углы и опи­ра­ют­ся на дуги окруж­но­сти, гра­дус­ные ве­ли­чи­ны ко­то­рых равны со­от­вет­ствен­но и . Ответ дайте в гра­ду­сах.

Ответ: 40

13. B 8 № 27886. Угол равен . Гра­дус­ная ве­ли­чи­на дуги окруж­но­сти, не со­дер­жа­щей точек и , равна . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ответ: 20

14. B 8 № 27887. Най­ди­те ве­ли­чи­ну угла . Ответ дайте в гра­ду­сах.

Ответ: 45

15. B 8 № 27888. Най­ди­те ве­ли­чи­ну угла . Ответ дайте в гра­ду­сах.

Ответ: 135

16. B 8 № 27889. Най­ди­те ве­ли­чи­ну угла . Ответ дайте в гра­ду­сах.

Ответ: 45

17. B 8 № 27890. Най­ди­те гра­дус­ную ве­ли­чи­ну дуги окруж­но­сти, на ко­то­рую опи­ра­ет­ся угол . Ответ дайте в гра­ду­сах.

Ответ: 45

18. B 8 № 27891. Най­ди­те гра­дус­ную ве­ли­чи­ну дуги окруж­но­сти, на ко­то­рую опи­ра­ет­ся угол Ответ дайте в гра­ду­сах.

Ответ: 135

19. B 8 № 245385. Най­ди­те цен­траль­ный угол , если он на боль­ше впи­сан­но­го угла , опи­ра­ю­ще­го­ся на ту же дугу.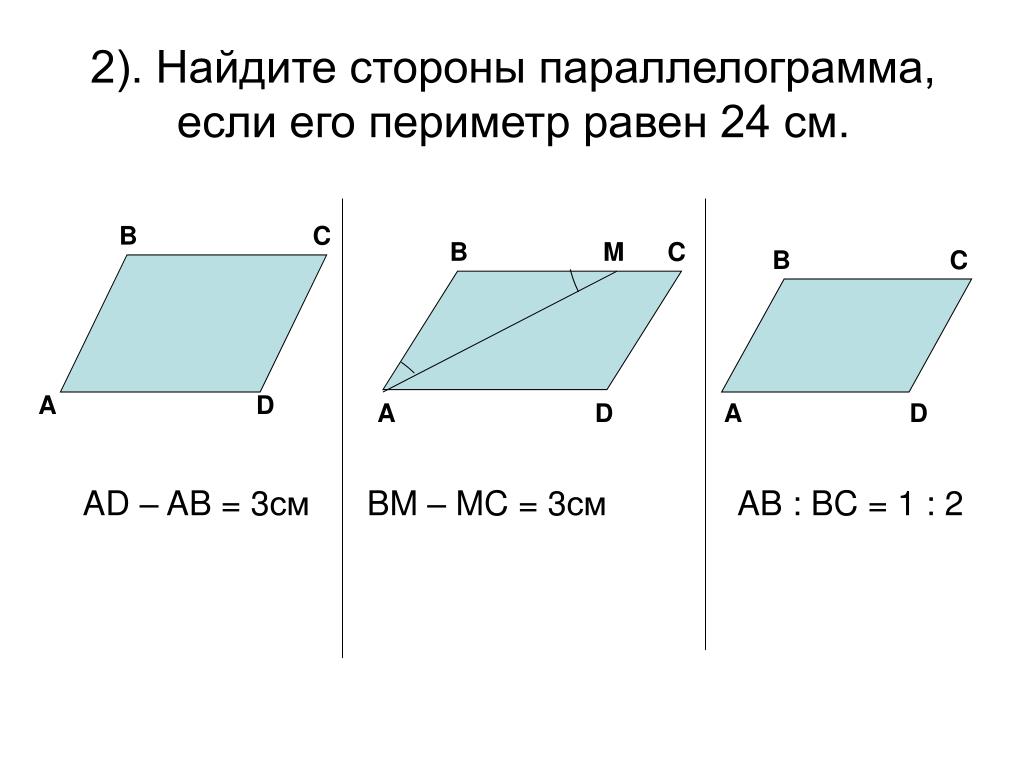 Ответ дайте в гра­ду­сах.

 

Ответ: 30

20. B 8 № 505378. Четырёхуголь­ник ABCD впи­сан в окруж­ность. Угол ABC равен 104°, угол CAD равен 66°. Най­ди­те угол ABD. Ответ дайте в гра­ду­сах.

Ответ: 38

21. B 8 № 505399. Четырёхуголь­ник ABCD впи­сан в окруж­ность. Угол ABC равен 100°, угол CAD равен 64°. Най­ди­те угол ABD. Ответ дайте в гра­ду­сах.

Ответ: 36

Касательная, хорда, секущая

1. B 8 № 27856. Най­ди­те хорду, на ко­то­рую опи­ра­ет­ся угол 90°, впи­сан­ный в окруж­ность ра­ди­у­са 1.

Ответ: 2

2. B 8 № 27862. Най­ди­те хорду, на ко­то­рую опи­ра­ет­ся угол , впи­сан­ный в окруж­ность ра­ди­у­са .

Ответ: 3

3. B 8 № 27867. Хорда делит окруж­ность на две части, гра­дус­ные ве­ли­чи­ны ко­то­рых от­но­сят­ся как 5:7.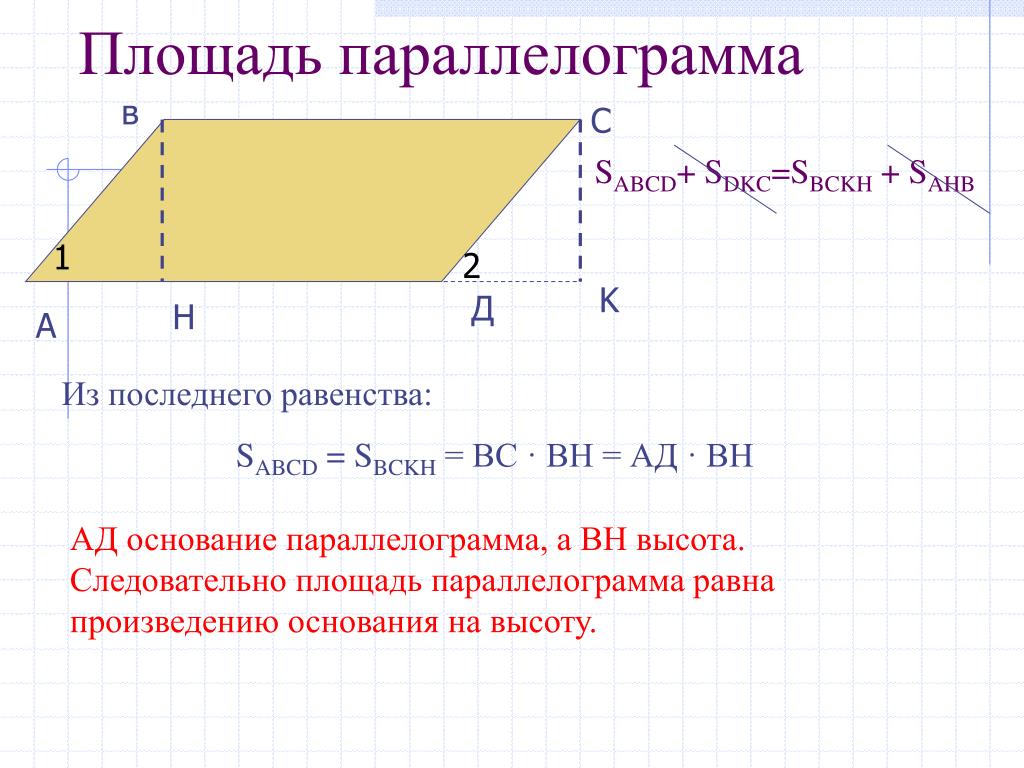 Под каким углом видна эта хорда из точки , при­над­ле­жа­щей мень­шей дуге окруж­но­сти? Ответ дайте в гра­ду­сах.

Ответ: 105

4. B 8 № 27877. Хорда стя­ги­ва­ет дугу окруж­но­сти в . Най­ди­те угол между этой хор­дой и ка­са­тель­ной к окруж­но­сти, про­ве­ден­ной через точку . Ответ дайте в гра­ду­сах.

Ответ: 46

5. B 8 № 27878. Угол между хор­дой и ка­са­тель­ной к окруж­но­сти равен . Най­ди­те ве­ли­чи­ну мень­шей дуги, стя­ги­ва­е­мой хор­дой . Ответ дайте в гра­ду­сах.

Ответ: 64

6. B 8 № 27879. Через концы , дуги окруж­но­сти в про­ве­де­ны ка­са­тель­ные и . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ответ: 118

7. B 8 № 27881. Най­ди­те угол , если его сто­ро­на ка­са­ет­ся окруж­но­сти, – центр окруж­но­сти, а дуга мень­шая дуга окруж­но­сти , за­клю­чен­ная внут­ри этого угла, равна . Ответ дайте в гра­ду­сах.

Ответ: 26

8. B 8 № 27882. Угол равен , где – центр окруж­но­сти. Его сто­ро­на ка­са­ет­ся окруж­но­сти. Най­ди­те ве­ли­чи­ну мень­шей дуги окруж­но­сти, за­клю­чен­ной внут­ри этого угла. Ответ дайте в гра­ду­сах.

Ответ: 62

9. B 8 № 27883. Най­ди­те угол , если его сто­ро­на ка­са­ет­ся окруж­но­сти, – центр окруж­но­сти, а боль­шая дуга окруж­но­сти, за­клю­чен­ная внут­ри этого угла, равна . Ответ дайте в гра­ду­сах.

Ответ: 26

Окружность, впи­сан­ная в треугольник

1. B 8 № 27624. Пе­ри­метр тре­уголь­ни­ка равен 12, а ра­ди­ус впи­сан­ной окруж­но­сти равен 1. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

Ответ: 6

2. B 8 № 27625. Пло­щадь тре­уголь­ни­ка равна 24, а ра­ди­ус впи­сан­ной окруж­но­сти равен 2. Най­ди­те пе­ри­метр этого тре­уголь­ни­ка.

Ответ: 24

3. B 8 № 27909. Сто­ро­на пра­виль­но­го тре­уголь­ни­ка равна . Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в этот тре­уголь­ник.

Ответ: 0,5

4. B 8 № 27910. Ра­ди­ус окруж­но­сти, впи­сан­ной в пра­виль­ный тре­уголь­ник, равен . Най­ди­те сто­ро­ну этого тре­уголь­ни­ка.

Ответ: 1

5. B 8 № 27931. Ра­ди­ус окруж­но­сти, впи­сан­ной в рав­но­бед­рен­ный пря­мо­уголь­ный тре­уголь­ник, равен 2. Най­ди­те ги­по­те­ну­зу этого тре­уголь­ни­ка. В от­ве­те ука­жи­те .

Ответ: 4

6. B 8 № 27932. Ка­те­ты рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка равны . Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в этот тре­уголь­ник.

Ответ: 1

7. B 8 № 27933. В тре­уголь­ни­ке , , угол равен 90°. Най­ди­те ра­ди­ус впи­сан­ной окруж­но­сти.

Ответ: 1

8. B 8 № 27934. Бо­ко­вые сто­ро­ны рав­но­бед­рен­но­го тре­уголь­ни­ка равны 5, ос­но­ва­ние равно 6. Най­ди­те ра­ди­ус впи­сан­ной окруж­но­сти.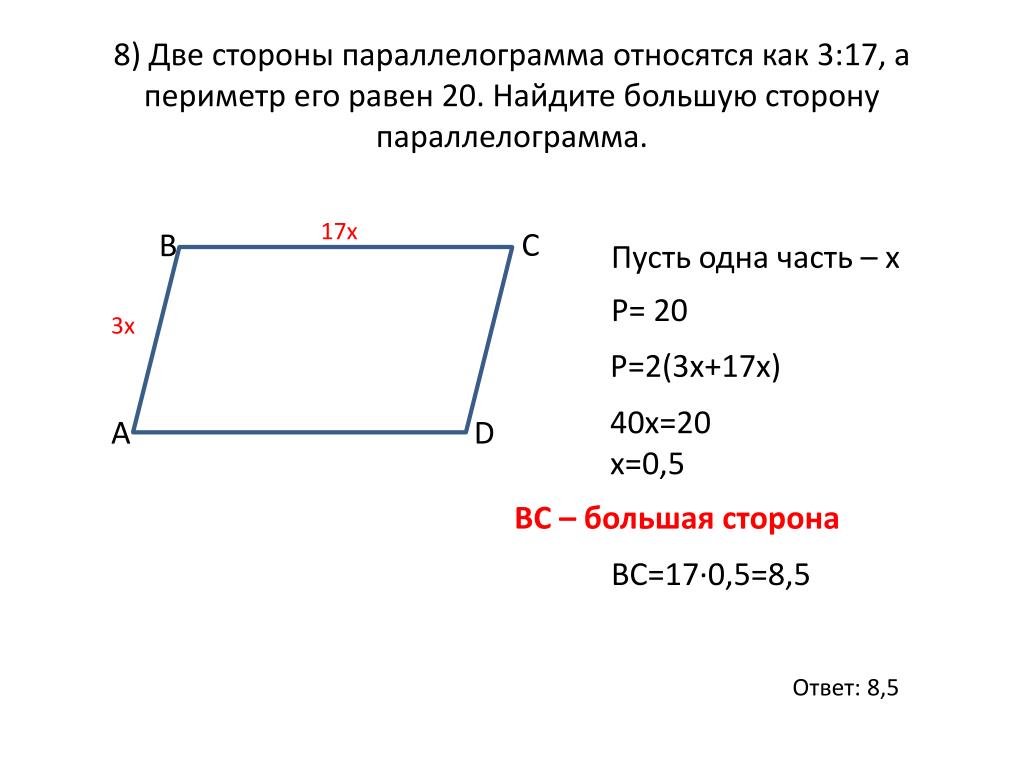

Ответ: 1,5

9. B 8 № 27951. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в тре­уголь­ник , счи­тая сто­ро­ны квад­рат­ных кле­ток рав­ны­ми 1.

Ответ: 1

 

10. B 8 № 27884. Угол равен . Его сто­ро­на ка­са­ет­ся окруж­но­сти. Най­ди­те гра­дус­ную ве­ли­чи­ну боль­шей дуги окруж­но­сти, за­клю­чен­ной внут­ри этого угла. Ответ дайте в гра­ду­сах.

Ответ: 114

Окружность, впи­сан­ная в четырехугольник

1. B 8 № 27911. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в квад­рат со сто­ро­ной 4.

Ответ: 2

2. B 8 № 27912. Най­ди­те сто­ро­ну квад­ра­та, опи­сан­но­го около окруж­но­сти ра­ди­у­са 4.

Ответ: 8

3. B 8 № 27913. Сто­ро­на ромба равна 1, ост­рый угол равен . Най­ди­те ра­ди­ус впи­сан­ной окруж­но­сти этого ромба.

Ответ: 0,25

4. B 8 № 27914. Ост­рый угол ромба равен . Ра­ди­ус впи­сан­ной в этот ромб окруж­но­сти равен 2. Най­ди­те сто­ро­ну ромба.

Ответ: 8

5. B 8 № 27915. Най­ди­те вы­со­ту тра­пе­ции, в ко­то­рую впи­са­на окруж­ность ра­ди­у­са 1.

Ответ: 2

6. B 8 № 27940. Пе­ри­метр че­ты­рех­уголь­ни­ка, опи­сан­но­го около окруж­но­сти, равен 24, две его сто­ро­ны равны 5 и 6. Най­ди­те боль­шую из остав­ших­ся сто­рон.

Ответ: 7

7. B 8 № 27942. Три сто­ро­ны опи­сан­но­го около окруж­но­сти че­ты­рех­уголь­ни­ка от­но­сят­ся (в по­сле­до­ва­тель­ном по­ряд­ке) как . Най­ди­те боль­шую сто­ро­ну этого че­ты­рех­уголь­ни­ка, если из­вест­но, что его пе­ри­метр равен 32.

Ответ: 12

8. B 8 № 27944. Около окруж­но­сти, ра­ди­ус ко­то­рой равен , опи­сан квад­рат. Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около этого квад­ра­та.

Ответ: 4

9. B 8 № 27952. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в че­ты­рех­уголь­ник .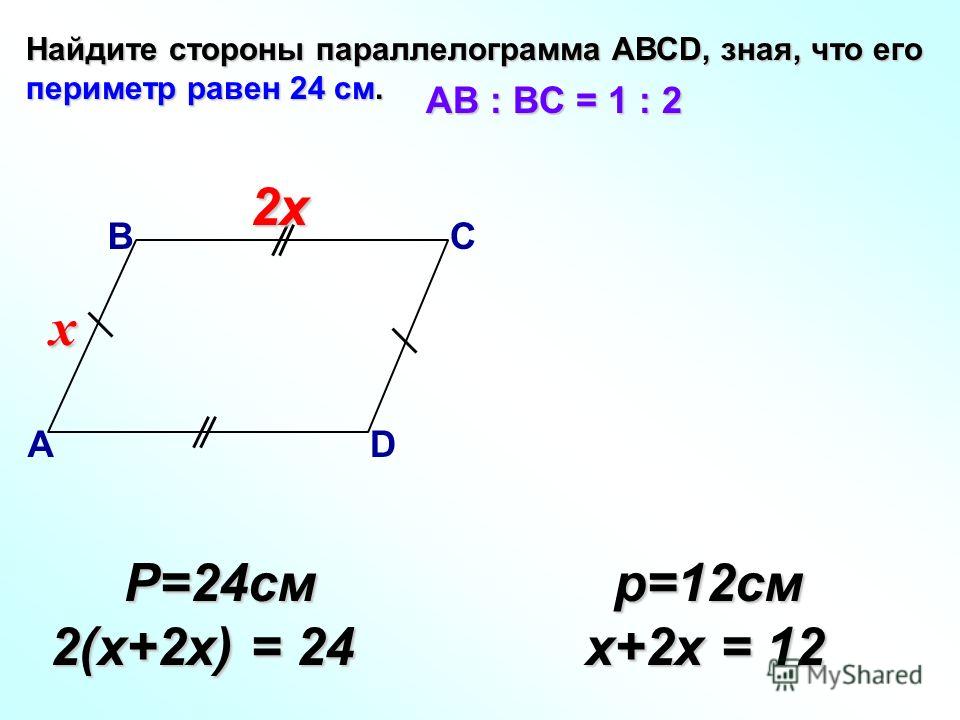 Счи­тай­те, что сто­ро­ны квад­рат­ных кле­ток равны 1. В от­ве­те ука­жи­те .

Ответ: 5

Окружность, впи­сан­ная в многоугольник

1. B 8 № 27640. Около окруж­но­сти, ра­ди­ус ко­то­рой равен 3, опи­сан мно­го­уголь­ник, пе­ри­метр ко­то­ро­го равен 20. Най­ди­те его пло­щадь.

Ответ: 30

2. B 8 № 27916. Най­ди­те сто­ро­ну пра­виль­но­го ше­сти­уголь­ни­ка, опи­сан­но­го около окруж­но­сти, ра­ди­ус ко­то­рой равен .

Ответ: 2

3. B 8 № 27917. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в пра­виль­ный ше­сти­уголь­ник со сто­ро­ной .

Ответ: 1,5

Окружность, опи­сан­ная вокруг треугольника

1. B 8 № 27868. Точки , , , рас­по­ло­жен­ные на окруж­но­сти, делят ее на три дуги, гра­дус­ные ве­ли­чи­ны ко­то­рых от­но­сят­ся как . Най­ди­те боль­ший угол тре­уголь­ни­ка . Ответ дайте в гра­ду­сах.

Ответ: 100

2. B 8 № 27892. Сто­ро­на пра­виль­но­го тре­уголь­ни­ка равна . Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

Ответ: 1

3. B 8 № 27893. Ра­ди­ус окруж­но­сти, опи­сан­ной около пра­виль­но­го тре­уголь­ни­ка, равен . Най­ди­те сто­ро­ну этого тре­уголь­ни­ка.

Ответ: 3

4. B 8 № 27898. В тре­уголь­ни­ке , , угол равен 90°. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка.

Ответ: 2,5

5. B 8 № 27899. В тре­уголь­ни­ке , угол равен 90°. Ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка равен 5. Най­ди­те .

Ответ: 8

6. B 8 № 27900. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 1, угол при вер­ши­не, про­ти­во­ле­жа­щей ос­но­ва­нию, равен . Най­ди­те диа­метр опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка.

Ответ: 2

7. B 8 № 27918. Сто­ро­на тре­уголь­ни­ка равна 1.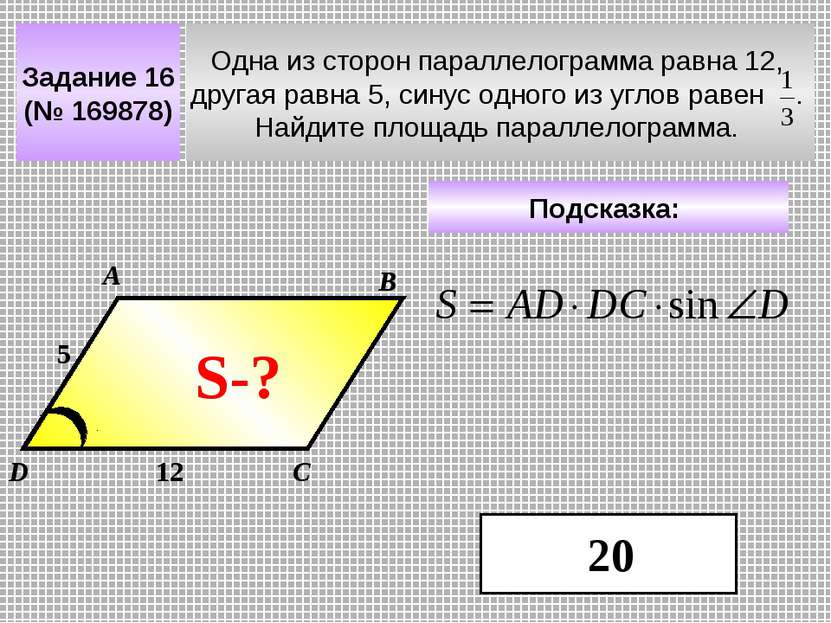 Про­ти­во­ле­жа­щий ей угол равен . Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

Ответ: 1

8. B 8 № 27919. Одна сто­ро­на тре­уголь­ни­ка равна ра­ди­у­су опи­сан­ной окруж­но­сти. Най­ди­те угол тре­уголь­ни­ка, про­ти­во­ле­жа­щий этой сто­ро­не. Ответ дайте в гра­ду­сах

Ответ: 30

9. B 8 № 27920. Угол тре­уголь­ни­ка , впи­сан­но­го в окруж­ность ра­ди­у­са 3, равен . Най­ди­те сто­ро­ну этого тре­уголь­ни­ка.

Ответ: 3

10. B 8 № 27921. Сто­ро­на тре­уголь­ни­ка равна 1. Про­ти­во­ле­жа­щий ей угол равен . Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

Ответ: 1

11. B 8 № 27922. Сто­ро­на ту­по­уголь­но­го тре­уголь­ни­ка равна ра­ди­у­су опи­сан­ной около него окруж­но­сти. Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ответ: 150

12. B 8 № 27923.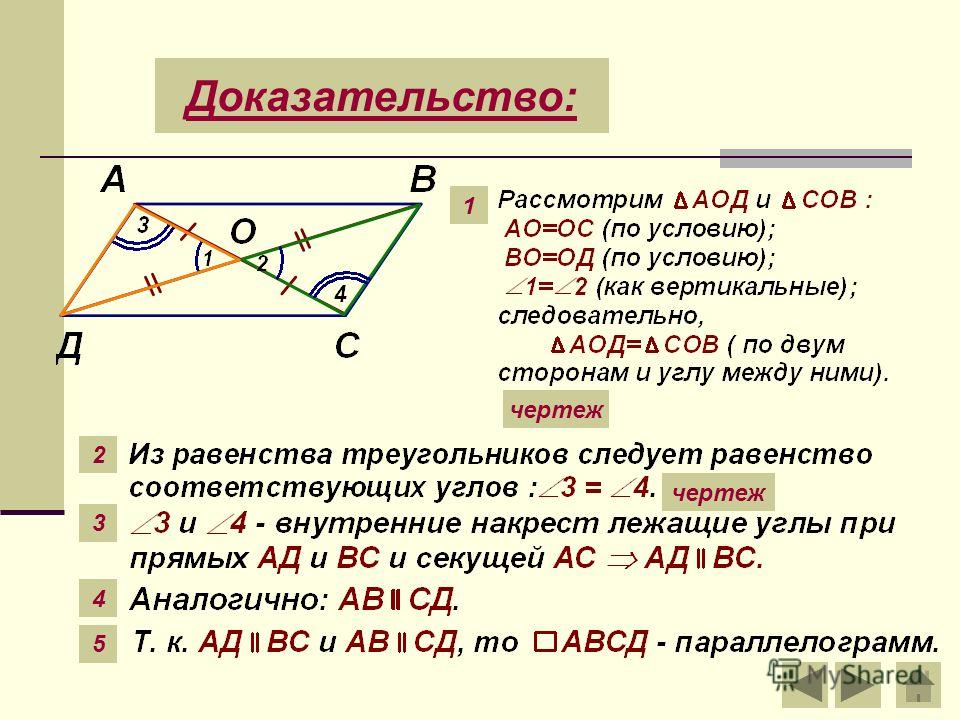 Бо­ко­вые сто­ро­ны рав­но­бед­рен­но­го тре­уголь­ни­ка равны 40, ос­но­ва­ние равно 48. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка.

Ответ: 25

Окружность, опи­сан­ная вокруг четырехугольника

1. B 8 № 27871. Угол че­ты­рех­уголь­ни­ка , впи­сан­но­го в окруж­ность, равен . Най­ди­те угол этого че­ты­рех­уголь­ни­ка. Ответ дайте в гра­ду­сах.

Ответ: 122

2. B 8 № 27872. Сто­ро­ны че­ты­рех­уголь­ни­ка , , и стя­ги­ва­ют дуги опи­сан­ной окруж­но­сти, гра­дус­ные ве­ли­чи­ны ко­то­рых равны со­от­вет­ствен­но , , , . Най­ди­те угол этого че­ты­рех­уголь­ни­ка. Ответ дайте в гра­ду­сах.

Ответ: 108

3. B 8 № 27873. Точки , , , , рас­по­ло­жен­ные на окруж­но­сти, делят эту окруж­ность на че­ты­ре дуги , , и , гра­дус­ные ве­ли­чи­ны ко­то­рых от­но­сят­ся со­от­вет­ствен­но как . Най­ди­те угол че­ты­рех­уголь­ни­ка .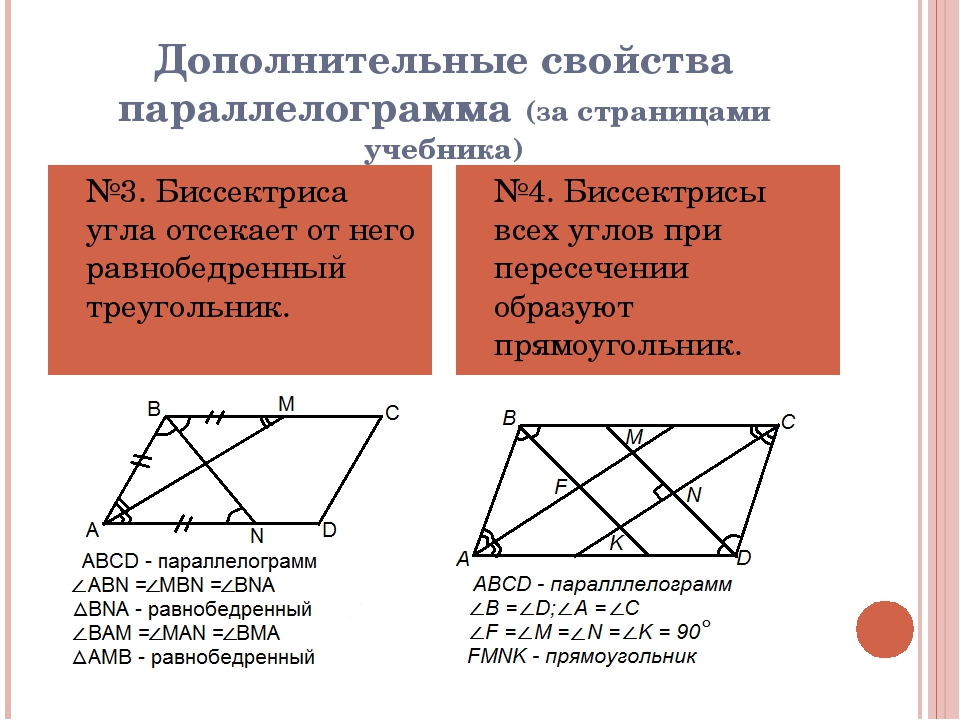 Ответ дайте в гра­ду­сах.

Ответ: 60

4. B 8 № 27874. Че­ты­рех­уголь­ник впи­сан в окруж­ность. Угол равен , угол равен . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ответ: 70

Читайте также:

Рекомендуемые страницы:

Поиск по сайту

Задачи по школьной математике. Параллелограмм

Сторона параллелограмма втрое больше другой его стороны. Найдите стороны параллелограмма, если его периметр равен 24.

Сторона ромба равна 5, а меньшая диагональ равна 6. Найдите большую диагональ.

Найдите сторону ромба, если его диагонали равны 6 и 8.

Сторона ромба равна 17, а одна из диагоналей равна 30. Найдите длину второй диагонали.

Найдите тупой угол (в градусах) ромба, если высота, проведенная из его вершины, делит противоположную сторону пополам.

Диагональ ромба образует с его стороной угол 25^о. Найдите больший угол ромба.

Диагональ ромба равна его стороне. Найдите больший угол ромба.

Периметр ромба равен 24. Высота равна 3. Найдите тупой угол ромба.

В ромбе диагонали равны 10 и 15. Найдите площадь ромба.

Найдите сторону ромба, если его острый угол 30^о, а площадь равна 18.

Найдите сторону ромба, если его диагонали относятся как 3:4, а площадь равна 384.

Найдите большую сторону прямоугольника, площадь которого равна 400, а стороны относятся как 4 : 1.

Периметр прямоугольника равен 60. Одна сторона больше другой на 10. Найдите меньшую сторону прямоугольника.

В параллелограмме сторона АВ равна 6, диагонали равны 9 и 5, О — точка пересечения диагоналей. Чему равен периметр треугольника АОВ?

Сумма двух противоположных углов параллелограмма равна 94^о. Найдите больший угол парал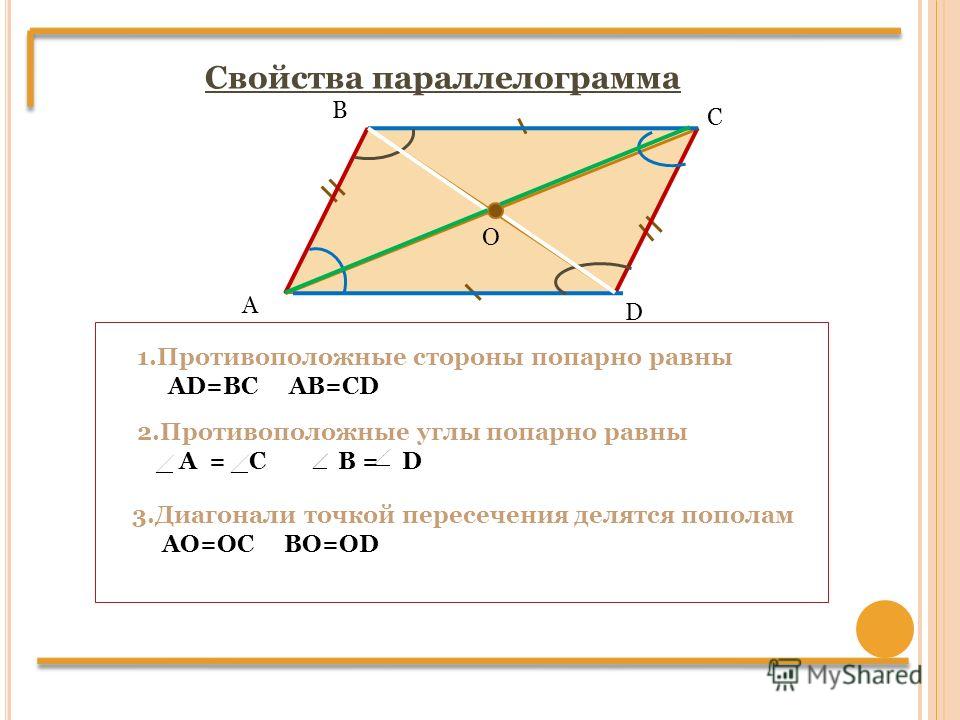лелограмма.

Периметр параллелограмма равен 60. Найдите площадь параллелограмма, если его стороны относятся как 2 : 3, а острый угол равен 30^о.

Найдите площадь параллелограмма ABCD, если угол BAD равен 150^о, АВ равно 3 и AD равно 8.

Параллелограмм и прямоугольник имеют соответственно одинаковые стороны. Площадь параллелограмма в два раза меньше площади прямоугольника. Найдите тупой угол параллелограмма.

Найдите периметр параллелограмма, если его площадь равна 144, а высоты равны 8 и 12.

Диагонали параллелограмма равны 6 и 8, а угол между ними равен 30^о. Найдите площадь параллелограмма.

Площадь параллелограмма равна 120, а его высоты равны 8 и 12. Найдите периметр параллелограмма.

Стороны параллелограмма равны и . Найдите сумму квадратов длин диагоналей параллелограмма.

Стороны параллелограмма равны соответственно 6 и 16, а его тупой угол равен 120^о. Найдите длину меньшей диагонали параллелограмма.

Во сколько раз увеличится площадь квадрата, если его диагональ увеличить в 2 раза?

Во сколько раз увеличится площадь ромба, если каждую диагональ увеличить в 2 раза?

Во сколько раз изменится площадь прямоугольника, если каждую сторону увеличить в 3 раза?

Найдите сторону квадрата, равновеликого прямоугольнику со сторонами, равными 4 и 9.

Середины сторон квадрата соединены отрезками. Найдите отношение площади фигуры, образованной этими отрезками к площади квадрата.

Стороны квадрата ABCD разделены точками E, F, L и N в отношении 1:2 каждая. Найдите отношение площадей квадрата и четырехугольника EFLN.

Периметр прямоугольника равен 24. Внутри прямоугольника выбрана точка. Найдите сумму расстояний от этой точки до всех сторон прямоугольника.

В параллелограмме ABCD высота BE делит сторону AD в точке E пополам. Найдите сторону AB, если периметр параллелограмма равен 7, а периметр треугольника ABD равен 5.

Диагонали параллелограмма равны 17 и 19. Одна сторона равна 10. Найдите другую сторону.

В параллелограмме ABCD проведена высота BK. Найдите углы и стороны параллелограмма, если AK = 5, KD = 8 и угол ABK равен 30^о.

В параллелограмме боковая сторона равна 8 и острый угол при основании равен 30^о. Найдите проекции высоты, опущенной на основание, на основание и на боковую сторону.

Точки M и N — середины противолежащих сторон BC и AD параллелограмма ABCD. Докажите, что четырехуголь­ник AMCN — параллелограмм.

Биссектриса угла параллелограмма делит сторону па­раллелограмма на отрезки, равные a и b. Найдите стороны па­раллелограмма.

Высота параллелограмма, проведенная из вершины ту­пого угла, равна 2 и делит сторону параллелограмма пополам. Острый угол параллелограмма равен 30◦. Найдите диагональ, проведенную из вершины тупого угла, и углы, которые она об­разует со сторонами.

Диагонали  параллелограмма  ABCD  пересекаются  в точке O. Периметр параллелограмма равен 12, а разность пери­метров треугольников BOC и COD равна 2. Найдите стороны параллелограмма.

Сторона BC параллелограмма ABCD вдвое больше стороны AB. Биссектрисы углов A и B пересекают прямую CD в точках M и N, причем MN = 12. Найдите стороны паралле­лограмма.

Угол при вершине A ромба ABCD равен 20◦. Точки M и N — основания перпендикуляров, опущенных из вершины B на стороны AD и CD. Найдите углы треугольника BMN.

Докажите, что точки попарного пересечения биссек­трис всех четырех углов параллелограмма являются вершинами прямоугольника.

Докажите, что отрезок, соединяющий середины про­тивоположных сторон параллелограмма, проходит через его центр.

Найдите расстояние от центра ромба до его стороны, если острый угол ромба равен 30◦, а сторона равна 4.

На сторонах AB и CD прямоугольника ABCD взя­ты точки K и M так, что AKCM является ромбом. Диаго­наль AC составляет со стороной AB угол 30◦. Найдите сторону ромба, если наибольшая сторона прямоугольника ABCD рав­на 3.

Прямая имеет с параллелограммом ABCD единствен­ную общую точку B. Вершины A и C удалены от этой прямой на расстояния a и b соответственно. На какое расстояние удалена от этой прямой вершина D?

Угол при вершине A ромба ABCD равен 60◦. На сторо­нах AB и BC взяты соответственно точки M и N, причем AM = BN. Докажите, что треугольник DMN равносторонний.

Точка внутри параллелограмма соединена со всеми его вершинами. Докажите, что суммы площадей треугольников, прилежащих к противоположным сторонам параллелограмма, равны между собой.

На сторонах AB и AD параллелограмма ABCD взя­ты точки M и N так, что прямые MC и NC делят параллело­грамм на три равновеликие части. Найдите MN, если BD = d.

Пусть E и F — середины сторон BC и AD параллелограмма ABCD. Найдите площадь четырехугольника, образованного прямыми AE, ED, BF и FC, если известно, что площадь ABCD равна S.

Докажите, что середины сторон произвольного четырехугольника — вершины параллелограмма. Для каких четырехугольников этот параллелограмм является прямоугольником, для каких — ромбом, для каких — квадратом?

Задания В5. Параллелограмм | Подготовка к ЕГЭ по математике

В этой статье работаем с Задачами №3 ЕГЭ по математике, которые связаны с параллелограммом.
Смотрите в других статьях разбор Задачи №3, в которых фигурирует:
– треугольник;
– прямоугольник;
– ромб;
– произвольный четырехугольник;
– трапеция;
– многоугольник;
– круг;
– векторы;
– координатная плоскость;

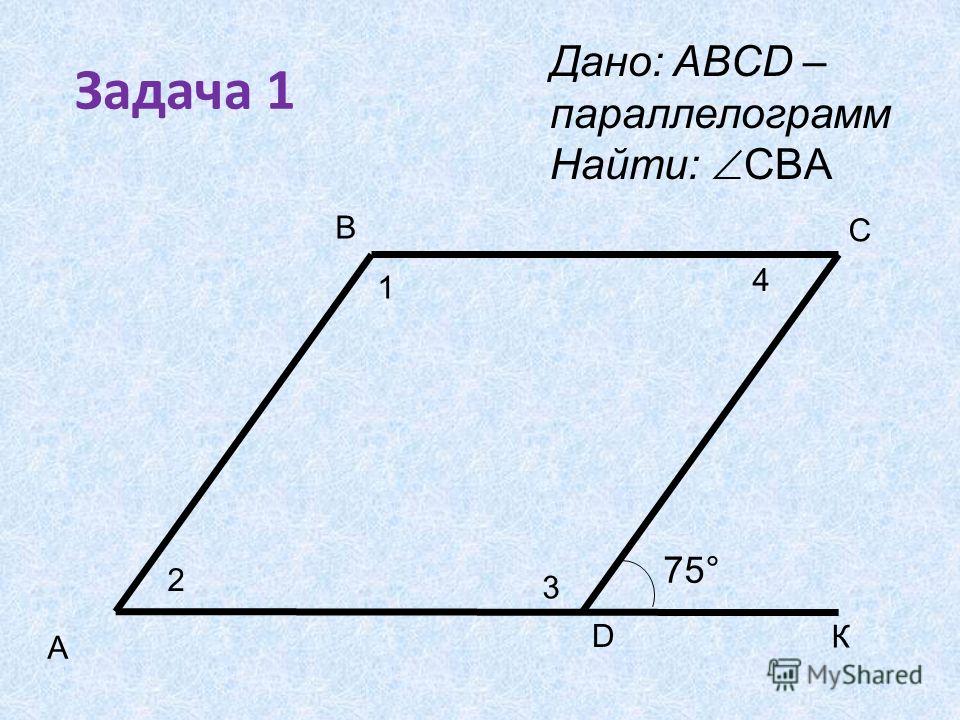
Задача 1.  Найдите площадь параллелограмма, изображенного на рисунке.

Решение: + показать

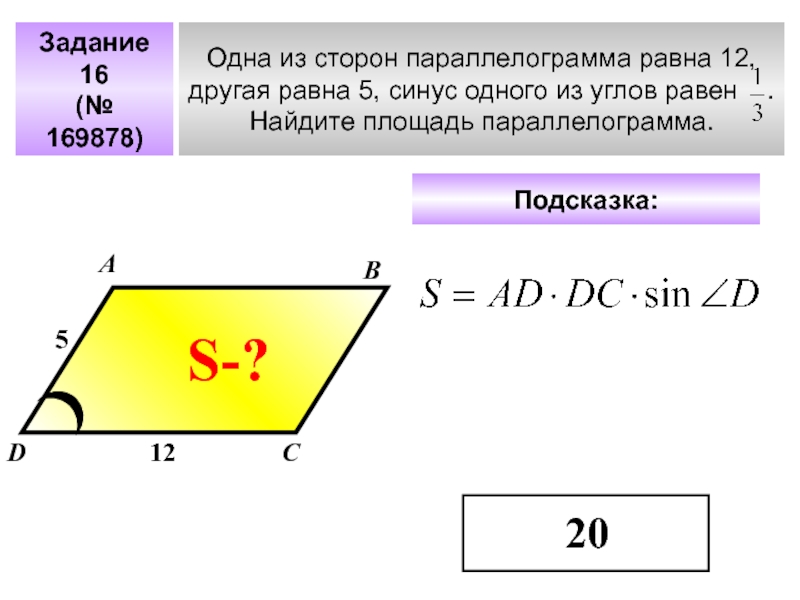
Задача 2. Найдите площадь параллелограмма, если две его стороны равны 25 и 20, а угол между ними равен 30˚.

Решение: + показать

Задача 3. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Решение: + показать

Задача 4. Стороны параллелограмма равны 8 и 16. Высота, опущенная на первую сторону, равна 12. Найдите высоту, опущенную на вторую сторону параллелограмма.

Решение: + показать

Так как согласно формуле площади параллелограмма , то

Откуда

Ответ: 6. 

Задача 5. Периметр параллелограмма равен 38. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.

Решение: + показать

Пусть меньшая сторона параллелограмма равна , тогда большая сторона равна согласно условию.

Периметр параллелограмма – сумма длин всех сторон, при этом противоположные стороны параллелограмма равны.

Поэтому

Ответ: 8. 

Задача 6. Боковая сторона равнобедренного треугольника равна 26.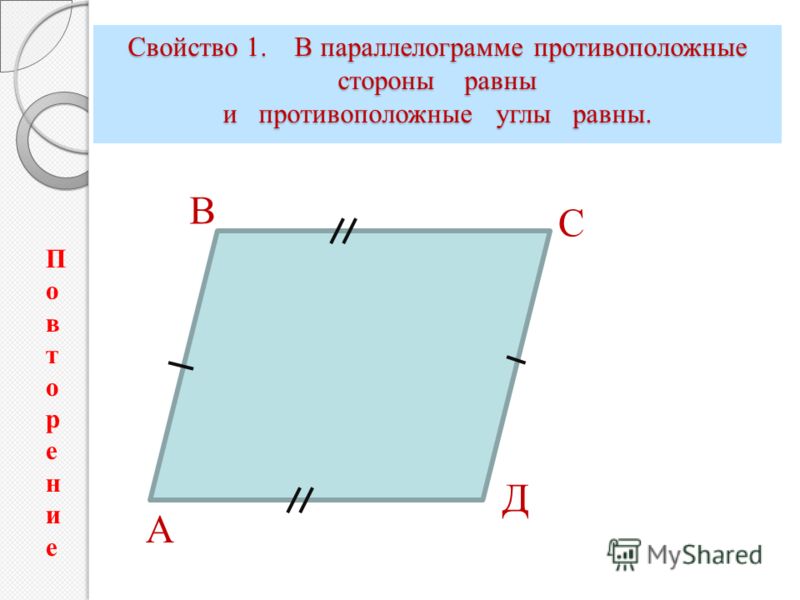 Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

Решение: + показать

Задача 7. Площадь параллелограмма   равна 116. Найдите площадь параллелограмма , вершинами которого являются середины сторон данного параллелограмма.

Решение: + показать

Задача 8. Площадь параллелограмма  равна 180. Точка   — середина стороны . Найдите площадь треугольника .

Решение: + показать

Вы можете пройти тест «Задачи №3. Параллелограмм»

Счастливый случай — Урок

Счастливый случай Геометрия 8

Российская Федерация Кемеровская область

Муниципальное образование Юргинский городской округ

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа № 10 г. Юрги»

Счастливый случай

Урок геометрии в 8 классе

Учитель математики:

Ивченко Анна Владимировна

Юрга 2008

Геометрия 8 класс(2 урока)

«;Счастливый случай»;

Цели урока:

1) обобщение и систематизация знаний учащихся по темам «;Четырехуголь­ники»; и «;Площади фигур»;;

2) подготовка учащихся к контрольной работе.

Организация урока

Разбиваем класс на 2 команды. Каждая коман­да выбирает 4—5 основных игроков. Остальные — болель­щики. За верный ответ на вопрос команда получает 2 бал­ла. Если на вопрос отвечают болельщики, команда получа­ет 1 балл. Если у команды нет правильного решения, то право на ответ переходит к команде соперников; за правиль­ный ответ она может получить 1 балл. Время на размышле­ние — 1 мин.

Болельщики получают заранее задание — подготовить­ся к доказательству теорем:

— площадь параллелограмма,

— площадь треугольника,

— площадь трапеции.

Оценка за доказательство теорем прибавляется к очкам, набранным командой.

Гейм 1. «;Гонка за лидером»; (20—25 мин).

Оборудование

Кубик, с помощью которого команды выбирают по­очередно номер и категорию вопроса.

Красный цвет — «;четырехугольники»;, зеленый цвет — «;площади»;, каждая команда отвечает на 5 вопросов.

Гейм 2. «;Спешите видеть»; (15 мин).

Каждая команда выбирает поочередно 3 чертежа. Не­обходимо найти ошибку на чертеже. Для болельщиков на доске вывешиваются большие чертежи.

Гейм 3. «;Семь раз отмерь — один отрежь»; (15 мин).

Команды выбирают задачи на разрезание фигур. Во время проведения этого гейма болельщики (по 3 человека от каждой команды) получают задание доказать теорему (пись­менно).

Гейм 4. «;Дальше, дальше, дальше…»; (10 мин).

Нужно быстро ответить на 20 вопросов. Если за 3 ми­нуты отведенного времени все ответы правильные, команда получает 10 премиальных очков.

После этого гейма подводятся итоги и проводится са­мостоятельная работа по 4 вариантам. Команда-победитель­ница получает дополнительный балл к оценке за самостоя­тельную работу.

Гейм 1. «;Гонка за лидером»;

1-я категория вопросов — «;четырехугольники»;

1.Верно ли, что если диагонали четырехугольника перпендикулярны, то это ромб? Почему?

2. Верно ли, что если в четырехугольнике противопо­ложные углы прямые, то это прямоугольник? Почему?

3. Существует ли четырехугольник с 3 тупыми углами? Доказать.

4. Существует ли такой параллелограмм, который диа­гональю разбивается на два равносторонних треугольника? Доказать.

5. Какие одинаковые свойства у прямоугольника и квад­рата?

6. Может ли больший угол четырехугольника быть ост­рым? Доказать.

7. Могут ли углы треугольника соответственно равняться трем углам параллелограмма? Почему?

8. Швея следующим образом убеждается в том, что кусок материи имеет форму квадрата: сгибает по каждой его диагонали. Если в обоих случаях края материи совпадают, то она считает, что кусок материи имеет форму квадрата. Правильный ли вывод делает швея и почему?

2-я категория вопросов — «;площади многоугольников»;

1.Параллелограмм и прямоугольник имеют одинако­вые стороны. Найти острый угол параллелограмма, если его площадь равна половине площади прямоугольника.

2. Диагональ квадрата равна а. Чему равна его пло­щадь?

3. Параллелограмм и прямоугольник имеют равные ос­нования и равные периметры. Площадь какой фигуры боль­ше и почему?

4. Как надо изменить сторону квадрата, если площадь его нужно увеличить в 4 раза?

5. В трапеции проведены диагонали. Найти 3 пары равновеликих треугольников. Доказать.

6. Что больше: площадь квадрата со стороной а или площадь равностороннего треугольника со стороной а? По­чему?

7. Можно ли, зная длины смежных сторон параллелог­рамма и длину одной из его диагоналей, найти его площадь? Если да, то как?

8. Правда ли, что, зная катеты прямоугольного треу­гольника, можно найти высоту, проведенную к гипотенузе? Если да, то как?

Гейм 2. «;Спешите видеть»;

Найдите ошибку на чертеже.

Гейм 3. «;Семь раз отмерь — один отрежь»;

1. Разрезать трапецию по одной линии так, чтобы из полупившихся частей можно было составить треугольник.

2. Треугольник разрезать на 2 треугольника так, чтобы площадь одного из них была вдвое больше площади другого.

3. Разрезать параллелограмм на 3 треугольника так, что­бы площадь одного из них была равна сумме площадей двух другие.

4. Разрезать трапецию на 2 равновеликие трапеции.

5. Разрезать параллелограмм по одной линии так, что­бы из получившихся частей можно было составить прямоу­гольник.

6. Отрезать от параллелограмма треугольник, площадь ко­торого в 4 раза меньше площади данного параллелограмма.

Гейм 4. «;Дальше, дальше, дальше…»;

1-я КОМАНДА

1. Равны ли диагонали прямоугольника?

2. Верно ли, что в параллелограмме сумма противопо­ложных углов 180⁰?

3. Формула площади прямоугольника.

4. В каком ромбе сторона равна его высоте?

5. Сколько вершин у четырехугольника?

6. Верно ли, что прямоугольник — это параллелограмм, у которого один угол прямой?

7. Формула площади ромба.

8. Какая трапеция называется равнобедренной?

9. Может ли высота трапеции быть ее диагональю?

10. Формула площади равностороннего треугольника со стороной а.

11. Существует ли параллелограмм, у которого диаго­нали перпендикулярны?

12. Сколько диагоналей можно провести в треугольнике?

13. Можно ли утверждать, что если в четырехугольни­ке две противоположные стороны равны, то это паралле­лограмм?

14. Сколько пар равных сторон у прямоугольника?

15. Может ли квадрат иметь диагонали разной длины?

16. Верно ли, что площадь квадрата равна произведе­нию его противоположных сторон?

17. Можно ли, зная длины смежных сторон паралле­лограмма, найти его площадь?

18. Могут ли фигуры быть равны и равновелики одно­временно?

19. Сколько высот разной длины можно провести в параллелограмме?

20. Что можно сказать о треугольнике, в котором квад­рат одной стороны равен сумме квадратов 2 других?

2-я КОМАНДА

1. Сколько пар параллельных сторон у трапеции?

2. У какого параллелограмма диагонали перпендику­лярны?

3. Что такое диагональ многоугольника?

4. Верно ли, что в параллелограмме противоположные углы равны?

5. Правда ли, что ромб — это параллелограмм, у кото­рого смежные стороны равны?

6. Формула Герона.

7. Сколько диагоналей можно провести в четырехуголь­нике?

8. Можно ли утверждать, что если в четырехугольнике 2 стороны параллельны, то это параллелограмм?

9. Может ли прямоугольная трапеция быть равнобед­ренной?

10. Формула площади параллелограмма.

11. Верно ли, что в ромбе противоположные стороны равны?

12. Может ли диагональ параллелограмма быть его вы­сотой?

13. Формула площади прямоугольного треугольника.

14. Верно ли, что если площади 2 треугольников рав­ны, то равны и сами треугольники?

15. Формула площади треугольника.

16. Определение ромба.

17. Верно ли, что диагонали прямоугольника равны?

18. Сколько высот разной длины можно провести в тра­пеции?

19. Можно ли, зная длину стороны ромба, найти его площадь?

20. Может ли диагональ ромба быть в 2 раза больше его стороны?

Дополнительно: САМОСТОЯТЕЛЬНАЯ РАБОТА

1-й вариант

1. Смежные стороны параллелограмма равны 52 и 30 см, а острый угол равен 30^е. Найти площадь параллелог­рамма.

2. Вычислить площадь трапеции ABCDс основаниями ADи ВС, если AD= 24 см, ВС = 16 см, ∟А= 45⁰, ∟D= 90⁰.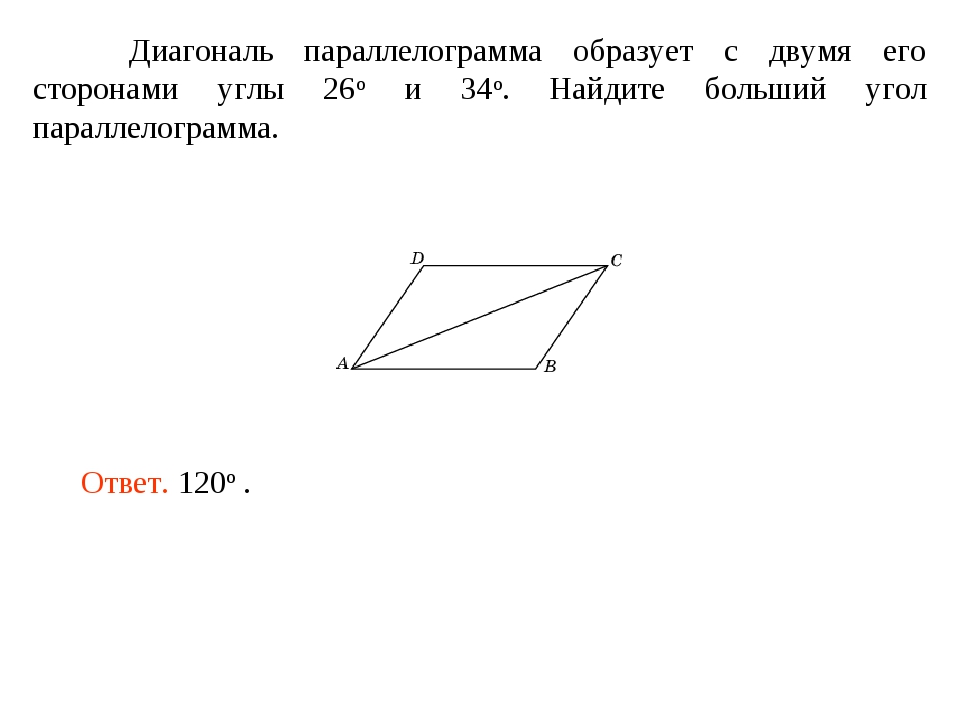

2-й вариант

1. Высота ВК, проведенная к стороне АDпараллелограмма ABCD, делит эту сторону на 2 отрезка АК = 7 см, KD= 15 см. Найти площадь параллелограмма, если ∟A= 45°

2. Вычислил площадь трапеции ABCDс основаниями ADи ВС, если ВС = 13 см, AD= 27 см, CD= 10 см, ∟D= 30⁰.

3-й вариант

1. В треугольнике ABCвысоты AA₁и ВВ₁равны соот­ветственно 5 и 7 см, ВС = 21 см. Найти АС

2. В трапеции ABCD ∟BADпрямой, АС = CD, AC_┴CD. Высота трапеции СК равна 6 см. Найти площадь трапе­ции.

4-й вариант

1. В треугольнике MPК MP= 14 см, РК = 21 см, вы­сота КК₁ равна 18 см. Найти высоту MM₁.

2. В трапеции ABCD ∟A= 90⁰. Высота СК составляет с диагональю АС и боковой стороной CDуглы, равные 45⁰, АК = 8 см. Найти площадь трапеции.

Итоги урока.

Вариант № 33006762 тренировочный ЕГЭ по математике профильный уровень с ответами

Сохраните:

Пробный тренировочный вариант №33006762 ЕГЭ по математике 11 класс профильный уровень, 19 тренировочных заданий с решением для проверки.

Ссылка для скачивания варианта (заданий): скачать

Ссылка для скачивания ответов (решений) к варианту: скачать

Решать пробный вариант ЕГЭ 33006762 по математике 11 класс онлайн:

Решения и ответы к варианту 33006762:

Задание 1 №504225) В доме, в котором живёт Женя, один подъезд. На каждом этаже по восемь квартир. Женя живёт в квартире 87. На каком этаже живёт Женя?

Ответ: 11

Задание 2 №27512) На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия.

Ответ: 20

Задание 3 №502041) На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 34. Найдите площадь закрашенной фигуры.

Ответ: 102

Задание 4 №282856) При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.

Ответ: 0,006

Задание 5 №26657) Найдите корень уравнения log4(x+3)=log4(4x-15).

Ответ: 6

Задание 6 №27610) Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Ответ: 30

Задание 7 №27505) На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

Ответ: -2

Задание 8 №27102) Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.

Ответ: 2

Задание 9 №26788) Найдите 3cosa-4sina/2sina-5cosa, если tg a=3.

Ответ:-9

Задание 10 №27962) Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: , где – время в минутах, К, К/мин, К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.

Ответ:2

Задание 11 №99593) Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.

Ответ: 45

Задание 12 №26712) Найдите точку минимума функции y=(3-x)e3-x.

Ответ: 4

Задание 13 №514623) а) Решите уравнение 6log 2/8x-5log8x+1=0. б) Найдите все корни этого уравнения, принадлежащие отрезку [2;2,5].

Задание 14 №520190) Прямоугольник ABCD и цилиндр расположены таким образом, что AB — диаметр верхнего основания цилиндра, а CD лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом 60 градусов.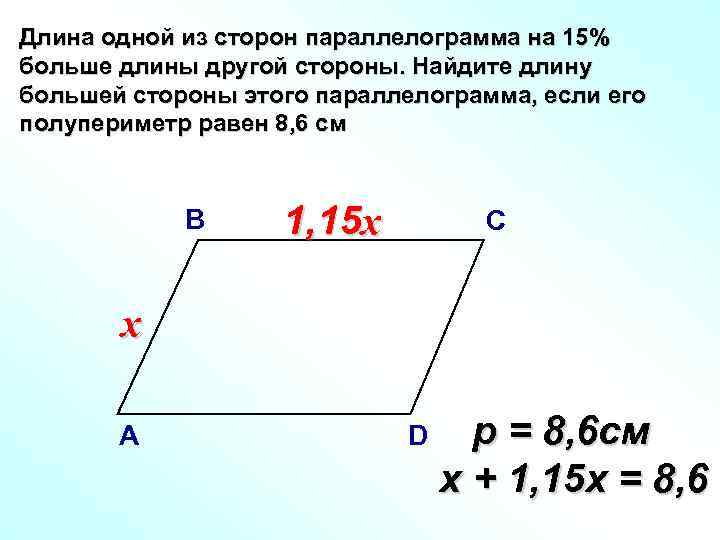 а) Докажите, что ABCD — квадрат. б) Найдите длину той части отрезка BD, которая находится снаружи цилиндра, если радиус цилиндра равен корень из 2

Ответ: 0,8

Задание 15 №508213) Решите неравенство: 1/x-1+1/2-x<5.

Задание 16 №517758) В трапецию ABCD с основаниями AD и BC вписана окружность с центром O. а) Докажите, что sin AOD=sin BOC. б) Найдите площадь трапеции, если BAD=90 градусов, а основания равны 5 и 7.

Ответ: 35

Задание 17 №508609) Семья Ивановых ежемесячно вносит плату за коммунальные услуги, телефон и электричество. Если бы коммунальные услуги подорожали на 50%, то общая сумма платежа увеличилась бы на 35%. Если бы электричество подорожало на 50%, то общая сумма платежа увеличилась бы на 10%. Какой процент от общей суммы платежа приходится на телефон?

Ответ: 10%

Задание 18 №514741) Найдите все значения a, при каждом из которых уравнение корень из x+ корень 2a-x=a имеет ровно два различных корня.

Задание 19 №514485) На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлённая до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8). а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел. б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7? в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?

Решайте также другие тренировочные варианты ЕГЭ:

Вариант № 33006761 тренировочный ЕГЭ по математике профильный уровень с ответами

Новые тренировочные варианты ЕГЭ 2020 с ответами по математике профильный уровень

Найдите площадь параллелограмма

Найдите площадь параллелограмма.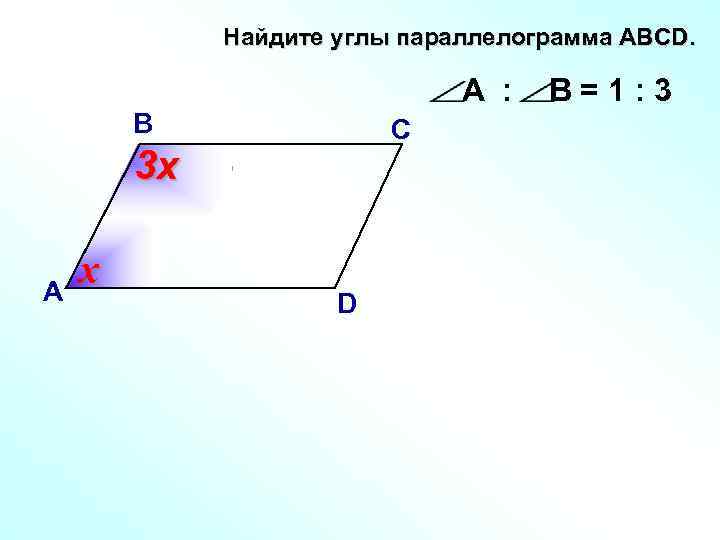 Здравствуйте! В этой статье представлена группа заданий решение которых связанно с площадью параллелограмма. Задачи входят в состав экзамена. Рекомендую посмотреть статью в которой о площади параллелограмма (и треугольника) всё подробно расписано. При решении пригодятся формулы:

*Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.

*Площадь параллелограмма равна произведению параллелограмма на высоту проведённую к этой стороне.

Также рассматриваются задачи с ромбами. Как известно, ромб является параллелограммом и обладает его свойствами, но есть ещё и дополнительные. Нам понадобится это:

— Диагонали ромба взаимно перпендикулярны.

Рассмотрим задачи:

27586. Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150⁰.

Используем формулу площади параллелограмма:

Стороны равны 1, а острый угол будет равен 30⁰:

Ответ: 0,5

27614.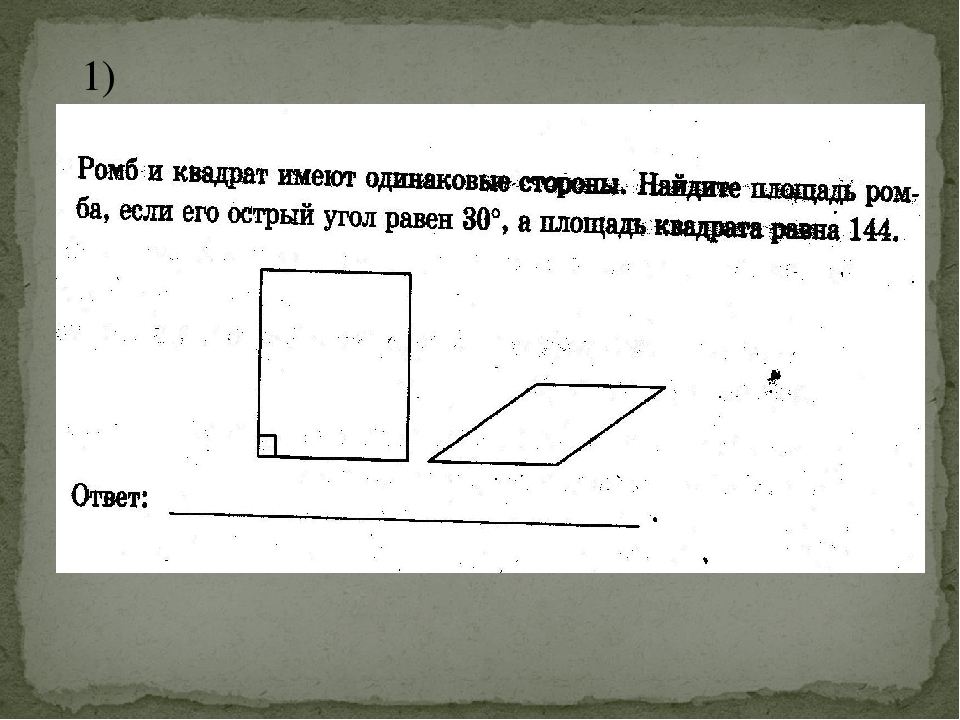 Найдите площадь ромба, если его диагонали равны 4 и 12.

Известно, что диагонали ромба пересекаются под прямым углом, также они точкой пересечения делятся пополам. Построим эскиз следующим образом и отметим на нём размеры половин диагоналей:

Получается, что ромб диагоналями разбивается на 4 равных прямоугольных треугольника с катетами 2 и 6. Можем вычислить площадь этого треугольника:

Так как все четыре треугольника образованные диагоналями равны, то

Ответ: 24

317338. Площадь параллелограмма ABCD равна 189. Точка Е середина стороны AD. Найдите площадь трапеции AECB.

Для того чтобы вычислить площадь трапеции достаточно понимать как определить площадь отсечённого треугольника EDC. *Далее мы из площади параллелограмма просто вычтем площадь треугольника.

Посмотрите! Сторона треугольника ED равна половине стороны параллелограмма, высота у них общая. Что это значит? А то что:

Получается, что площадь треугольника в четыре раза меньше площади параллелограмма:

Таким образом:

Ответ: 141,75

*Какую часть по площади занимает треугольник в параллелограмме можно увидеть разделив параллелограмм диагональю (он делится пополам):

Площадь треугольника ADC составляет ½ от площади параллелограмма, а площадь треугольника EDC равна половине площади ADC, то есть треугольник EDC по площади будет в 4 раза меньше.

319056. Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A′B′C′D′, вершинами которого являются середины сторон данного параллелограмма.

Построим эскиз:

Нетрудно заметить, что площади треугольников 1, 2, 3 и 4 равны, так как у них есть равные стороны и синусы углов между ними приобретают равные значения.

Вычислим площадь треугольника АA′D′:

Получается, что площадь треугольника будет в восемь раз меньше. Таким образом, искомая площадь равна:

Ответ: 76,5

*Конечно же, «опытный глаз» сразу увидит, что площадь параллелограмма A′B′C′D′ в два раза меньше площади данного параллелограмма, но понимать формальное соотношение площадей фигур необходимо и важно.

**Если вы построите отрезки соединяющие середины противоположных сторон, то сразу наглядно увидите каким образом параллелограмм разбивается на равные по площади треугольники и решение будет очевидно.

319057. Площадь параллелограмма ABCD равна 176. Точка E– середина стороны CD. Найдите площадь треугольника ADE.

Площадь треугольника ADE составляет четвёртую часть от площади параллелограмма, посмотрите вше задачу 317338. То есть S_ADE=176/4=44.

Ответ: 44

27585. Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30⁰.

Посмотреть решение

27610. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Посмотреть решение

27611. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

Посмотреть решение

27612. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Посмотреть решение

27613. Найдите площадь ромба, если его высота равна 2, а острый угол 30⁰.

Посмотреть решение

27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.

Посмотреть решение

27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

Посмотреть решение

На этом всё. Успеха вам!

С уважением, Александр

Делитесь информацией о сайте в социальных сетях.

Площадь параллелограмма — объяснение и примеры

Как следует из названия, параллелограмм — это четырехугольник, образованный двумя парами параллельных прямых . Он отличается от прямоугольника величиной углов при углах. В параллелограмме противоположные стороны равны по длине и противоположные углы равны по мере, в то время как в прямоугольнике все углы равны 90 градусам.

Из этой статьи вы узнаете , как вычислить площадь параллелограмма по формуле площади параллелограмма.

Чтобы узнать, чем его площадь отличается от других четырехугольников и многоугольников, посетите предыдущие статьи.

Как найти площадь параллелограмма?

Площадь параллелограмма — это пространство, ограниченное двумя парами параллельных линий. Прямоугольник и параллелограмм обладают схожими свойствами, поэтому площадь параллелограмма равна площади прямоугольника.

Площадь параллелограмма Формула

Рассмотрим параллелограмм ABCD , показанный ниже.Площадь параллелограмма — это пространство, ограниченное сторонами AD, DC, CB и AB.

Площадь состояний формулы параллелограмма;

Площадь параллелограмма = основание x высота

A = (b * h) Кв. единиц

Где b = основание параллелограмма и

h = высота или высота параллелограмма.

Высота или высота параллели — это перпендикулярная линия (обычно пунктирная) от вершины параллелограмма до любого из оснований.

Пример 1

Вычислите площадь параллелограмма, основание которого составляет 10 сантиметров, а высота — 8 сантиметров.

Раствор

A = (b * h) кв. единицы.

A = (10 * 8)

A = 80 см ²

Пример 2

Вычислить площадь параллелограмма с основанием 24 дюйма и высотой 13 дюймов

Решение

А = (б * в) кв.единицы.

= (24 * 13) квадратный дюйм.

= 312 квадратных дюймов.

Пример 3

Если основание параллелограмма в 4 раза больше высоты, а площадь равна 676 см², найдите основание и высоту параллелограмма.

Решение

Пусть высота параллелограмма = x

, а основание = 4x

Но площадь параллелограмма = b * h

676 см² = (4x * x) кв. единиц

676 = 4x ²

Разделим обе стороны на 4, чтобы получить,

169 = x ²

Найдя квадратный корень из обеих сторон, мы получим

x = 13.

Заменитель.

База = 4 * 13 = 52 см

Высота = 13 см.

Следовательно, основание и высота параллелограмма равны 52 см и 13 см соответственно.

Кроме формулы площади параллелограмма, существуют другие формулы для вычисления площади параллелограмма.

Давайте посмотрим.

Как найти площадь параллелограмма без высоты?

Если высота параллелограмма нам неизвестна, то мы можем использовать здесь понятие тригонометрии, чтобы найти его площадь.

Площадь = ab sine (α) = ab sine (β)

, где a и b — длина параллельных сторон, а β или α — угол между сторонами параллелограмма.

Пример 4

Найдите площадь параллелограмма, если его две параллельные стороны составляют 80 см и 40 см, а угол между ними составляет 56 градусов.

Решение

Пусть a = 80 см и b = 40 см.

Угол между a и b = 56 градусов.

Площадь = ab sine (α)

Заменитель.

A = 80 × 40 синус (56)

A = 3200 синус 56

A = 2652,9 кв. См.

Пример 5

Вычислите углы между двумя сторонами параллелограмма, если длина его сторон составляет 5 м и 9 м, а площадь параллелограмма равна 42,8 м ² .

Решение

Площадь параллелограмма = ab sine (α)

42,8 м ² = 9 * 5 sine (α)

42.8 = 45 синус (α)

Разделим обе части на 45.

0,95111 = sin (α)

α = синус ^-1 0,95111

α = 72 °

Но β + α = 180 °

β = 180 ° — 72 °

= 108 °

Следовательно, углы между двумя парами параллельных сторон параллели равны; 108 ° и 72 °.

Пример 6

Вычислите высоту параллелограмма, параллелограммы которого равны 30 см и 40 см, а угол между этими двумя сторонами равен 36 градусам.Примите основание параллелограмма равным 40 см.

Решение

Площадь = ab sine (α) = bh

30 * 40 синус (36) = 40 * h

1,200 синус (36) = 40 * h.

Разделите обе стороны на 40.

h = (1200/40) синус 36

= 30 синус 36

h = 17,63 см

Итак, высота параллелограмма составляет 17,63 см.

Как найти площадь параллелограмма по диагоналям?

Предположим, что d ₁ и d ₂ — это диагонали параллелограмма ABCD, , тогда площадь параллелограмма задается как,

A = ½ × d ₁ × d ₂ синус (β ) = ½ × d ₁ × d ₂ синус (α)

Где β или α — угол пересечения диагоналей d ₁ и d ₂ .

Пример 7

Вычислите площадь параллелограмма, диагонали которого составляют 18 см и 15 см, а угол пересечения диагоналей равен 43 °.

Решение

Пусть d ₁ = 18 см и d ₂ = 15 см.

β = 43 °.

A = ½ × d ₁ × d ₂ синус (β)

= ½ × 18 × 15 синус (43 °)

= 135 синус 43 °

= 92,07 см ²

Следовательно, площадь параллелограмма 92.07 см ² .

Практические вопросы

1. Флаг имеет основание 2,5 фута и высоту 4,5 фута. Если флаг имеет форму параллелограмма, найдите площадь флага.
2. Рассмотрим параллелограмм, площадь которого в два раза больше площади треугольника. Если обе эти формы имеют общее основание, какова связь между их высотой?

Ответы

1. 25 футов ²
2. Высоты параллелограмма и треугольника будут равны.

Предыдущий урок | Главная страница | Следующий урок

Многоугольники — четырехугольники — в глубину

Есть много разные виды четырехугольников, но все они имеют несколько общих черт: все они имеют четыре стороны, компланарны, имеют две диагонали, а сумма их четырех внутренних углов равняется 360 градусам. Вот в чем они похожи, но что их отличает?

Мы знаем многих четырехугольники по их особой форме и свойствам, как квадраты.Помните, если вы видите слово четырехугольник, это не обязательно означает фигуру с особые свойства, такие как квадрат или прямоугольник! В словесных задачах будьте осторожны не предполагать, что у четырехугольника есть параллельные или равные стороны, если только что заявлено.

Специальные четырехугольники

ср Можно использовать диаграмму Венна, чтобы сгруппировать типы четырехугольников.

Диаграмма Венна использует перекрывающиеся круги, чтобы показать отношения между группами объектов.Все «четырехугольники» можно разделить на три подгруппы: общие четырехугольники, параллелограммы и трапеции.

— это прямоугольник всегда ромб? Нет, потому что все четыре стороны прямоугольника не обязательно быть равным. Однако наборы прямоугольников и ромбов пересекаются, и их пересечение — это множество квадратов — все квадраты представляют собой прямоугольник и ромб.

Можем поставить квадраты на пересечении двух кругов.

Из этой диаграммы, вы можете видеть, что квадрат — это четырехугольник, параллелограмм, прямоугольник, и ромб!

— это трапеция параллелограмм? Нет, потому что у трапеции только одна пара параллельных сторон. Поэтому мы должны показать набор трапеций отдельным кружком на Диаграмма Венна.

А как насчет воздушных змеев? Воздушные змеи — это четырехугольники, которые могут быть параллелограммами . Если их две пары сторон равны, он становится ромбом, а если их углы равны, он становится квадратом.

Ссылки по теме: Формулы площади
Формулы периметра

назад наверх

фактов о параллелограммах | Sciencing

Параллелограмм — это двухмерный четырехугольник — форма, имеющая четыре стороны, пересекающиеся в четырех точках, также известных как вершины. Две противоположные стороны параллелограмма всегда параллельны и равны или равны по длине. Прямоугольники, квадраты и ромбы — все это примеры параллелограммов.

Противоположные стороны

Обе пары противоположных сторон параллелограмма всегда параллельны, и обе пары противоположных сторон параллелограмма всегда конгруэнтны.Вы можете найти расстояние вокруг параллелограмма, также известное как периметр, путем измерения и сложения длины четырех сторон вместе. Поскольку противоположные стороны параллелограмма параллельны, они никогда не пересекаются с .

Диагональные линии

Диагонали параллелограмма — линии, идущие от одного угла к противоположному — делят друг друга пополам. Другими словами, каждая диагональ разрезает свою противоположную диагональ на две равные части . Независимо от того, как вы измените форму параллелограмма, например, сделав стороны короче или длиннее или увеличив или уменьшив высоту, диагонали всегда будут делить друг друга пополам.

Площадь параллелограмма

Вычислите площадь параллелограмма, умножив основание на высоту , также известную как высота. Вы можете использовать любую сторону параллелограмма в качестве основы. Высота — это расстояние по перпендикуляру от основания до противоположной стороны. В некоторых случаях вам может потребоваться удлинить противоположную сторону параллелограмма, чтобы найти и измерить перпендикулярное расстояние.

Внутренние углы

Противоположные внутренние углы параллелограмма всегда равны .Например, если один внутренний угол составляет 36 градусов, противоположный внутренний угол также будет составлять 36 градусов. Последовательные внутренние углы в параллелограмме — углы, расположенные рядом — являются дополнительными. Это означает, что когда вы складываете два внутренних последовательных угла вместе, общая сумма всегда равна 180 градусам. Когда вы складываете все четыре внутренних угла вместе, общая сумма всегда равна 360 градусам.

Середины четырехугольника

Когда вы размещаете средние точки — середину отрезка прямой или среднюю точку — на каждой стороне четырехугольника и соединяете эти точки последовательными прямыми линиями, результат всегда будет параллелограммом .

Особые геометрические формы

Прямоугольники и квадраты являются примерами параллелограммов с углами 90 градусов, также известными как прямые углы. Ромбы и квадраты — это примеры параллелограммов со сторонами одинаковой длины.

Какие степени у четырехугольника?

Для решения многих геометрических задач важно понимать основы измерения углов и правила, которым следуют все многоугольники. Вычисляя сумму внутренних углов для конкретного многоугольника, можно найти недостающие измерения углов и использовать их для решения проблемы.

Углы и многоугольники

Угол образуется, когда две прямые (или отрезки) встречаются в одной точке. Углы подразделяются на отдельные группы на основе их измерения в градусах. Острые углы составляют от 0 ° до 90 °; тупые углы составляют от 90 ° до 180 °. Прямые углы составляют 90 °. «Прямые» углы, в которых стороны угла образуют прямую линию, составляют 180 °.

Многоугольник — это замкнутая фигура, состоящая из точек, соединенных отрезками прямых линий.В каждой точке или вершине образуется угол. Измерения этих углов подчиняются определенным правилам, которые зависят от типа многоугольника.

Что такое четырехугольник?

Многоугольник, образованный соединением четырех точек с четырьмя непересекающимися отрезками прямой, называется четырехугольником. Все четырехугольники имеют четыре стороны и, следовательно, четыре внутренних угла. Важно понимать, какие углы внутренние, если четырехугольник вогнутый. В выпуклом четырехугольнике линия, проведенная между любыми двумя углами, полностью попадет внутрь многоугольника; кроме того, каждый из внутренних углов составляет менее 180 °.Однако в вогнутом четырехугольнике линия может быть проведена между одной парой противоположных друг другу углов, выходящих за пределы многоугольника. У этих четырехугольников один угол больше 180 °; этот большой угол необходимо измерить, чтобы следующая формула была верной.

Формула для вычисления суммы внутренних углов многоугольника

Формула для нахождения суммы внутренних углов многоугольника: (n-2) _180 °, где n — количество сторон многоугольника. Применяя эту формулу к четырехугольникам, для которых n = 4, мы видим, что (4-2) _180 ° = 360 °.Следовательно, сумма внутренних углов любого четырехугольника равна 360 °; это измерение применяется к любому четырехугольнику независимо от его типа.

Специальные четырехугольники

Размеры каждого внутреннего угла фиксируются, если многоугольник является одним из следующих специальных типов четырехугольника. Прямоугольник — это четырехугольник, в каждой точке отрезки которого перпендикулярны друг другу; это означает, что каждый внутренний угол составляет 90 °. Квадрат, определяемый как прямоугольник с четырьмя равными сторонами и четырьмя равными углами, представляет собой прямоугольник определенного типа; поэтому каждый внутренний угол квадрата также составляет 90 °.

Иллюстративная математика

Задача

1. Посмотрите на каждую цифру. Прочтите каждое из описаний. Поместите X в рамку, если кажется, что она описывает изображенную фигуру.

   	А.	Б.	С.	Д.
   4 вершины
   Четыре стороны
   Противоположные стороны параллельны
   Перпендикулярные стороны
   Противоположные стороны имеют одинаковую длину
   Все стороны имеют одинаковую длину
   Содержит прямой угол (-а)
   Содержит острый (е) угол (ы)
   Содержит тупой угол (углы)

2. Что верно для всех цифр?

Все приведенные выше рисунки — прямоугольники.Обведите прямоугольники ниже. Используйте то, что вы знаете, что верно для всех прямоугольников, чтобы помочь вам.

Выберите цифру, по которой вы не звонили. Объясните, почему это не прямоугольник.

Посмотрите на каждую цифру. Прочтите каждый из атрибутов. Поместите X в рамку, если кажется, что это атрибут изображенной фигуры.

Что верно для всех цифр?

Все приведенные выше рисунки — параллелограммы. Обзвоните все параллелограммы ниже. Использование того, что вы знаете, что верно для всех параллелограммов, чтобы помочь вам.

Выберите цифру, по которой вы не звонили. Объясните, почему это не параллелограмм.

IM Комментарий

На ранних этапах понимания геометрических фигур учащиеся описывают формы, но еще не характеризуют формы по их свойствам. Одним из примеров заблуждения учащихся на этом этапе является то, что прямоугольник имеет две короткие стороны и две длинные стороны.

Цель этого задания — помочь учащимся определить определяющие атрибуты прямоугольников и параллелограммов.Это задание следует выполнить после того, как учащиеся получат большой опыт сортировки фигур по атрибутам. Понимание того, какие характеристики являются определяющими атрибутами, позволит учащимся использовать работу в 5-м классе 5.G.3 (Понимать, что атрибуты, принадлежащие к категории двумерных фигур, также принадлежат ко всем подкатегориям этой категории) и 5.G.4 (Классифицировать) двухмерные фигуры в иерархии на основе свойств.)

Эту задачу можно изменить, чтобы определить определяющие атрибуты треугольников и других четырехугольников.

Решение

Что верно для всех цифр?

У всех фигур 4 стороны и 4 вершины, причем противоположные стороны параллельны и совпадают. У них четыре прямых угла, поэтому они также имеют перпендикулярные отрезки прямых.

Все приведенные выше рисунки — прямоугольники. Оберните все прямоугольники внизу кольцом. Используйте то, что вы знаете, что верно для всех прямоугольников, чтобы помочь вам.

Выберите фигуру, которую вы не обвели.Объясните, почему это не прямоугольник.

Пример: у этой фигуры 4 стороны и 4 вершины. Только один набор противоположных сторон параллелен, и у него нет прямых углов, поэтому он не может быть прямоугольником.

Что верно для всех цифр?

У всех фигур 4 стороны и 4 вершины, причем противоположные стороны параллельны и совпадают.

Все приведенные выше рисунки — параллелограммы. Обведите в кольцо все параллелограммы ниже. Использование того, что вы знаете, что верно для всех параллелограммов, чтобы помочь вам.

Выберите цифру, по которой вы не звонили. Объясните, почему это не параллелограмм.

Пример: у правильного шестиугольника противоположные стороны параллельны и конгруэнтны, но он не четырехгранный.

Что такое ромб? (Определение, Форма, Свойства) // Tutors.com

Содержание

1. Ромб Определение
2. Как построить ромб
3. Как выглядит ромб?
4. Различные названия для ромба
5. Квадрат — это ромб?
6. Форма ромба
7. Свойства ромба
8. Уголки ромб
9. Диагонали ромба

Ромб Определение

Ромб — четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу.Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Все квадраты — ромбы, но не все ромбы квадраты. Противоположные внутренние углы ромбов совпадают. Диагонали ромба всегда пересекают друг друга под прямым углом.

Как построить ромб

Вы можете построить ромб прямо сейчас на любой плоской поверхности, если у вас есть четыре одинаковых линейных объекта. Зубочистки, карандаши, измерительные палочки — подойдут любые четыре одинаковых прямых отрезка.

Положите четыре прямых предмета на плоскую поверхность так, чтобы их восемь концов соприкасались только в четырех местах. Вы не можете потерпеть неудачу в этом! Положите два предмета параллельно друг другу, но на небольшом расстоянии друг от друга. Если вы используете два других объекта для соединения конечных точек, у вас есть ромб!

Как выглядит ромб?

Противоположные стороны вашего четырехугольника будут параллельны, а противоположные углы будут одинаковыми (конгруэнтными). Ваш четырехугольник по определению должен быть ромбом!

Это означает, что каждый ромб равен:

• Фигурка плоская (двухмерная)
• Закрытая форма (имеет внутреннюю и внешнюю)
• Четырехугольник (четырехсторонняя плоская фигура с прямыми сторонами)

Различные названия ромба

У ромба может быть три дополнительных имени:

1. Ромб
2. Пастилки
3. Бриллиант

Ромб — это особый случай параллелограмма, поскольку он удовлетворяет требованиям параллелограмма: четырехугольник с двумя парами параллельных сторон.У него есть четыре стороны равной длины, но это все еще разновидность параллелограмма.

Каждый увиденный вами ромб также будет параллелограммом, но не каждый встречный параллелограмм будет ромбом.

Квадрат — это ромб?

Если у вас есть ромб с четырьмя равными внутренними углами, у вас есть квадрат . Квадрат — это особый случай ромба, потому что у него четыре стороны равной длины, и он выходит за пределы и имеет четыре прямых угла.

Каждый квадрат, который вы видите, будет ромбом, но не каждый ромб, который вы встретите, будет квадратом.

Форма ромба

В большинстве случаев ромб, который вы видите, будет нарисован так, чтобы у него было основание — две противоположные стороны будут горизонтальными, а нижняя сторона будет служить основанием фигуры.

Но будьте осторожны, потому что ромб может появиться в любой ориентации. Когда он «встает» и выглядит симметричным (его диагонали горизонтальны и вертикальны), его обычно называют ромбом.

Если вам сложно вспомнить его название, представьте себе квадрат, в который врезался автобус, поэтому он перевернулся ( наезжает на на автобус … ромб).

Свойства ромба

Одной из двух характеристик, которые делают ромб уникальным, является то, что его четыре стороны равны по длине или совпадают. Другое отличительное свойство — параллельность противоположных сторон.

Если у вас есть четырехугольник с одной парой параллельных сторон, у вас определенно нет ромба (потому что две его стороны не могут быть одинаковой длины).У вас есть трапеция .

Если у вас есть четырехугольник с двумя парами параллельных сторон, у вас не обязательно есть ромб; у вас может быть параллелограмм или ромб, если все четыре стороны имеют одинаковую длину.

Уголки ромбические

В дополнение к этим четырем сторонам ромб имеет четыре внутренних угла. Также можно построить две диагонали внутри ромба, соединив противоположные вершины (углы).

Неважно, как вы расположите эти четыре линейных объекта на своей плоской поверхности, у вас всегда будет две пары равных противоположных углов.Начните сначала с двух ваших предметов и на этот раз сконцентрируйтесь на том, чтобы сделать из них острый (менее 90 °) угол. Используйте два других объекта, чтобы соединить два исходных объекта, вверх и вправо, чтобы сделать вашу четырехстороннюю (четырехугольную) плоскую фигуру — ромб.

Посмотрите на нижний левый угол и верхний правый угол. Они одинаковые. Они совпадают. Посмотрите на нижний правый угол и верхний левый угол: они совпадают. Противоположные внутренние углы ромба совпадают.

Четыре внутренних угла ромба в сумме всегда составляют 360 °.

Диагонали ромба

Замечательное и редкое свойство ромба в том, что его диагонали всегда перпендикулярны друг другу. Вы можете убедиться в этом сами, если сложите четыре прямых предмета так, чтобы получился ромб, а затем начертите диагонали. Независимо от того, под каким углом у вас четыре вершины ромба, диагонали ромба всегда расположены под прямым углом друг к другу.

Эти диагонали тоже разрезают друг друга ровно пополам. Геометристы говорят, что они делят пополам друг друга.Это означает, что две диагонали делят ромб на четыре прямоугольных треугольника.

Краткое содержание урока

Ромб — это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Все квадраты — ромбы, но не все ромбы квадраты. Противоположные внутренние углы ромбов совпадают. Диагонали ромба всегда пересекают друг друга под прямым углом.

Что вы узнали:

Посмотрев этот урок и прочитав о ромбе, вы узнаете, как эта плоская фигура вписывается во все семейство плоских фигур, какие свойства делают ромб уникальным и как распознать ромб по двум его особым идентифицирующим свойствам.

Следующий урок:

Как найти площадь ромба

GRE Math: прямоугольник и параллелограмм с одинаковой площадью

Сегодня мы быстро рассмотрим, как прямоугольник и параллелограмм могут иметь одинаковую площадь.

На схеме выше параллелограмм и прямоугольник имеют общую вершину (D), одна вершина прямоугольника (E) находится на стороне параллелограмма, а одна вершина параллелограмма (C) находится на стороне параллелограмма. прямоугольник. Этой информации достаточно, чтобы гарантировать, что прямоугольник и параллелограмм имеют одинаковую площадь.

Вот аргумент, почему. На диаграмме ниже обратите внимание, что я построил сегментный эквалайзер, который перпендикулярен CD. Этот сегмент равен высоте параллелограмма, так что, умноженная на длину CD, будет площадь параллелограмма.

Посмотрите на ΔDGC и ΔEQD. Эти два треугольника похожи. Почему?

Ну, во-первых, ∠QDG и ∠EDQ дополняют друг друга: они вместе составляют 90 ° угла EDG. Кроме того, ∠QDG и ∠QCG дополняют друг друга, потому что они являются острыми углами прямоугольного треугольника. Поскольку ∠EDQ и ∠QCG дополняют один и тот же угол (∠QDG), они совпадают: ∠EDQ: ∠QCG.

Поскольку мы знаем EDQ≅ ∠QCG и знаем EQD≅ ∠G (оба прямых угла), мы знаем, что два угла в ΔDGC конгруэнтны двум углам в ΔEQD.По теореме подобия AA они должны быть подобными треугольниками.

ΔDGC ~ ΔEQD

Подобные треугольники имеют пропорциональные стороны. В частности, мы можем установить пропорцию:

После перекрестного умножения получаем два равных произведения. (ED) * (DG) = площадь прямоугольника. (EQ) * (DC) = площадь параллелограмма. Следовательно, эти две области равны.

Это более основанный на уравнениях способ доказательства равенства площадей. Вот еще одна ОГРОМНАЯ идея, которая гораздо более привлекательна для мыслителей визуального образа.Представьте, что одна пара сторон параллелограмма протягивается, как железнодорожные рельсы:

Если мы сдвинем любую сторону вдоль его «рельса», форма параллелограмма изменится, но площадь останется прежней, потому что основание (длина рельса) не изменится, высота (расстояние между параллельные линии) не меняется.

Фиолетовый и оранжевый параллелограммы должны иметь одинаковую площадь. Это ОГРОМНАЯ геометрическая идея.

Теперь подумайте о нашей диаграмме с добавленными «рельсами».

Теперь, когда мы сдвигаем AB вверх так, чтобы A совпадала с E, это сделает AD и BC идеально вертикальными:

Теперь, если мы сдвинем BC вниз, чтобы он точно совпал с FG, то параллелограмм точно совпадет с прямоугольником, а это значит, что они должны иметь одинаковые площади.

Этот «метод скольжения» может быть очень удобным ярлыком с областями параллелограмма.

стр.S. Готовы улучшить свой GRE? Начни сегодня.

Самые популярные ресурсы

О Майке MᶜGarry

Майк создает уроки для экспертов и практические вопросы, чтобы помочь студентам GMAT добиться успеха. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах. Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидных черепных дефектов, он настаивает на том, чтобы болеть за Нью-Йорк Метс.

.