Квадратные уравнения задания для тренировки. Что такое квадратное уравнение? Решения различных типов квадратных уравнений
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Виды квадратных уравнений
Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.
Говоря математическим языком, квадратное уравнение — это уравнение вида:
Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:
Здесь а =1; b = 3; c = -4
Здесь а =2; b = -0,5; c = 2,2
Здесь а =-3; b = 6; c
Ну, вы поняли…
В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.
Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.
Такие квадратные уравнения называются полными.
А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:
5х 2 -25 = 0,
2х 2 -6х=0,
-х 2 +4х=0
И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:
2х 2 =0,
-0,3х 2 =0
Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.
Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…
Вот и все главные виды квадратных уравнений. Полные и неполные.
Полные и неполные.
Решение квадратных уравнений.
Решение полных квадратных уравнений.
Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:
Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .
Формула для нахождения корней квадратного уравнения выглядит так:
Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:
а =1; b = 3; c = -4. Вот и записываем:
Пример практически решён:
Это ответ.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !
Предположим, надо вот такой примерчик решить:
Здесь
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно?
Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:
Узнали?) Да! Это неполные квадратные уравнения .
Решение неполных квадратных уравнений.
Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .
Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b
Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку,
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:
Остаётся корень извлечь из 9, и всё. Получится:
Тоже два корня. х 1 = -3 , х 2 = 3 .
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
Дискриминант. Формула дискриминанта.
Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:
Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой
D = b 2 — 4ac
И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.
Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания
 Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)
Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…
Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:
Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
Вот так:
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:
А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.
Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.
Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…
Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.
Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:
Вот и всё! Решать – одно удовольствие!
Итак, подытожим тему.
Практические советы:
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.
3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.
4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!
Теперь можно и порешать.)
Решить уравнения:
8х 2 — 6x + 1 = 0
х 2 + 3x + 8 = 0
х 2 — 4x + 4 = 0
(х+1) 2 + x + 1 = (x+1)(x+2)
Ответы (в беспорядке):
х 1 = 0
х 2 = 5
х 1,2 = 2
х 1 = 2
х 2 = -0,5
х — любое число
х 1 = -3
х 2 = 3
решений нет
х 1 = 0,25
х 2 = 0,5
Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.
Прогуляйтесь по ссылке, это полезно.
Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Цель: Применение теоремы Виета и ей обратной теоремы при нахождении коэффициентов в квадратных уравнениях, при решении заданий из вариантов ЕГЭ.
Воспитательные задачи: Способствовать формированию умений, применять приемы сравнений, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию творческих способностей. Побуждать учащихся к самоконтролю и взаимоконтролю, самоанализу своей учебной деятельности.
Оборудование: плакаты, компьютер, экран, видеопроектор.
Ход урока
I. Вводная беседа. Устные упражнения (5 мин.)
Сегодня на уроке мы с вами вместе подведем итог, как важно применение теоремы Виета. В каких упражнениях применяется теорема и как важно ее знать и применять. (Учитель показывает презентацию, в которой сформулированы цели, задачи, структура урока).
Учащиеся формулируют теорему Виета и ей обратную теорему. У доски два ученика записывают формулы теоремы Виета для приведенного и полного квадратных уравнений:
– формулы для полного квадратного уравнения;
– формулы для приведенного квадратного уравнения;
Трое учащихся решают на дополнительных досках индивидуальные задания.
Решите уравнения и выполните проверку по теореме, обратной теореме Виета:
II. Устные упражнения (5 мин.)
Затем с учащимися решаем устные упражнения:
Найдите корни уравнения:
3. Если в квадратном уравнении сумма коэффициентов a + b + c = 0,
То Используя это свойство, решите уравнения:
4. Теорема Виета применяется при нахождении суммы и произведения корней. Покажите, как это выглядит. Перед вами уравнения:
У какого из данных уравнений:
III. Лабораторная работа (3 мин .)
Учащимся предлагается выполнить лабораторную работу.
Составьте квадратные уравнения, которые:
- не имеют корней;
- имеет один из корней, равный 0;
- имеет два корня, равных по модулю, но противоположных по знаку;
- имело бы один корень;
- сумма коэффициентов уравнения равна 0.
Учащиеся выполняют это задание по группам (4–5 учащихся в группе).
Пример лабораторной работы:
IV. Работа с таблицей (3 мин.)
Выполнив лабораторную работу, три группы озвучивают свою лабораторную работу, а остальные группы сдают лабораторные работы на плакатах на проверку (2 мин.).
Один из учащихся (Евсеев А.) заранее готовит презентацию об исследовании знаков в приведенных квадратных уравнениях.
Все учащиеся работают с таблицей и отвечают на вопросы о знаках в квадратных уравнениях:
- Когда корни квадратного уравнения имеют одинаковые знаки?
- Когда оба корня положительные, отрицательные?
- Когда корни имеют разные знаки?
- Когда больший по модулю корень отрицателен?
- Когда больший по модулю корень положителен?
Сформулируйте выводы о знаках корней квадратных уравнений.
V. Тренировочные упражнения. Работа у доски (23 мин.)
Следующий этап урока: двое учащихся решают у доски задания о нахождении неизвестных коэффициентов в квадратных уравнениях.
1. В уравнении один из корней равен 7. Найдите другой корень и коэффициент р . Ответ:
2. Один из корней уравнения равен 12,5. Найдите другой корень уравнения и коэффициент с . Ответ:
Такого вида уравнения часто встречаются на экзаменах. Поэтому сейчас Слинько В. предлагает просмотреть презентацию о нахождении коэффициентов в квадратных уравнениях.
А после просмотра презентации учащимся предлагается решить 2 уравнения самостоятельно с последующей проверкой.
1. Разность корней квадратного уравнения равна 2. Найдите с .
Ответ: c = 35.
2. Разность корней квадратного уравнения равна 6. Найдите с .
Ответ: c = –8,75.
Использование теоремы Виета дает возможность решать более сложные задания.
Трое учащихся решают задания у доски, комментируя и объясняя ход решения:
1. Один из корней уравнения равен 8. Найдите другой корень и коэффициент в .
Ответ: .
2. Один из корней уравнения равен 5,3. Найдите другой корень и коэффициент с .
Ответ: .
3. В уравнении квадратов корней равна . Найдите с . Ответ: с = 9.
VI. Заключение (6 мин.)
В заключение урока подводим итоги. Учащиеся формулируют применение теоремы Виета.
Теорема Виета применяется:
- при нахождении суммы и произведения корней квадратных уравнений;
- при составлении квадратных уравнений;
- при решении уравнений методом подбора;
- при нахождении коэффициентов в уравнении, свободного члена;
- при сравнении знаков коэффициентов в квадратном уравнении.
Один из учащихся рассказывает стихотворение.
По праву достойна в стихах быть воспета
О свойстве корней теорема Виета.
Что проще скажи постоянства такого?
Умножишь ты корни и дробь уж готова!
В числителе с , в знаменателе а ,
А сумма корней тоже дроби равна.2 + b*x + c = 0 ,где x — переменная, a,b,c – константы; a0 . Задача состоит в отыскании корней уравнения.
Геометрический смысл квадратного уравнения
Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х) . Из этого следует, что есть три возможных случая:
1) парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).2) парабола имеет одну точку пересечения с осью Ох . Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).
3) Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс.
2 и осуществим преобразование
Отсюда находим
Формула дискриминанта и корней квадратного уравнения
Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0 При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле
Теорема Виета
Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p , взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q . Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета.
2+x-6=0 .
Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения
С второго условия получаем, что произведение должно быть равно -6 . Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2} . С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равныЗадача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см 2 .
Решение: Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х – большую сторону, тогда 18-x меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
х 2 -18х+77=0.
Найдем дискриминант уравненияВычисляем корни уравнения
Если х=11 , то 18-х=7 , наоборот тоже справедливо (если х=7 , то 21-х=9 ).Задача 6. Разложить квадратное 10x 2 -11x+3=0 уравнения на множители.
Решение: Вычислим корни уравнения, для этого находим дискриминант
Подставляем найденное значение в формулу корней и вычисляем
Применяем формулу разложения квадратного уравнения по корнями
Раскрыв скобки получим тождество.2+(2а+6)х-3а-9=0 имеет более одного корня?
Решение: Рассмотрим сначала особые точки, ими будут значения а=0 и а=-3 . При а=0 уравнение упростится до вида 6х-9=0; х=3/2 и будет один корень. При а= -3 получим тождество 0=0 .
Вычислим дискриминант
и найдем значения а при котором оно положительно
С первого условия получим а>3 . Для второго находим дискриминант и корни уравнения
Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0 получим 3>0 . Итак, за пределами промежутка (-3;1/3) функция отрицательная. Не стоит забывать о точке а=0 , которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи
Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.Теорема Виета. Примеры и решение
Теорема Виета:
Сумма корней приведённого квадратного уравнения
x2 + px + q = 0
равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену
x1 + x2 = -p, x1 · x2 = q.
Доказательство:
Если приведённое квадратное уравнение имеет вид
x2 + px + q = 0,
то его корни равны:
,
где D = p2 — 4q. Чтобы доказать теорему, сначала найдём сумму корней:
,
а теперь найдём их произведение:
Равенства, показывающие зависимость между корнями и коэффициентами квадратного уравнения:
x1 + x2 = —p,
x1 · x2 = q
называются формулами Виета.
Примечание: если дискриминант равен нулю (D = 0), то подразумевается, что уравнение имеет не один корень, а два равных корня.
Обратная теорема
Теорема:
Если сумма двух чисел равна -p, а их произведение равно q, то эти числа являются корнями приведённого квадратного уравнения:
x2 + px + q = 0.
Доказательство:
Пусть дано x1 + x2 = —p, значит, x2 = —p — x1. Подставим это выражение в равенство x1 · x2 = q, получим:
x1(-p — x1) = q;
—px1 — x12 = q;
x12 + px1 + q = 0.
Это доказывает, что число x1 является корнем уравнения x2 + px + q = 0.
Точно так же можно доказать, что и число x2 является корнем для этого уравнения.
Решение примеров
Зависимость между корнями и коэффициентами квадратного уравнения позволяет в некоторых случаях находить корни уравнения устно, не используя формулу корней.
Пример 1. Найти корни уравнения:
x2 — 3x + 2 = 0.
Решение: Так как
x1 + x2 = -(-3) = 3;
x1 · x2 = 2;
очевидно, что корни равны 1 и 2:
1 + 2 = 3;
1 · 2 = 2.
Подставив числа 1 и 2 в уравнение, убедимся, что корни найдены правильно:
12 — 3 · 1 + 2 = 0
и
22 — 3 · 2 + 2 = 0.
Ответ: 1, 2.
Пример 2. Найти корни уравнения:
x2 + 8x + 15 = 0.
Решение:
x1 + x2 = -8;
x1 · x2 = 15.
Методом подбора находим, что корни равны -3 и -5:
-3 + -5 = -8;
-3 · -5 = 15.
Ответ: -3, -5.
С помощью теоремы, обратной теореме Виета, можно составлять квадратное уравнение по его корням.
Пример 1. Составить квадратное уравнение по его корням:
x1 = -3, x2 = 6.
Решение: Так как x1 = -3, x2 = 6 корни уравнения x2 + px + q = 0, то по теореме, обратной теореме Виета, составим уравнения:
p = -(x1 + x2) = -(-3 + 6) = -3;
q = x1 · x2 = -3 · 6 = -18.
Следовательно, искомое уравнение:
x2 — 3x — 18 = 0.
Ответ: x2 — 3x — 18 = 0.
Пример 2. Записать приведённое квадратное уравнение, имеющее корни:
x1 = 2, x2 = 3.
Решение:
p = -(x1 + x2) = -(2 + 3) = -5;
q = x1 · x2 = 2 · 3 = 6.
Ответ: x2 — 5x + 6 = 0.
Графическое решение квадратных уравнений — Математика — Педагогическая копилка — В помощь учителю
МБОУ « Выльгортская средняя общеобразовательная школа №1»
Пояснительная записка
Этап мотивации идет через личностные УУД, где дети защищают проект» Домашнее задание- парабола в жизни». При актуализации знаний используются самопроверка, взаимопроверка в паре. Поиск нового способа идет через математическое задание, учащиеся работают в группах.
Решение проблемы осуществляется через дискуссию, в группе. Обсуждение выводов выводит учащихся на личностные УУД. Применение новых знаний идет с использованием выработанного алгоритма учащими ся.
Урок « Графическое решение квадратных уравнений» в 8 классе
Учитель Блох Татьяна Ивановна
УМК Мордкович А.Г. Урок № 16 в теме «Квадратичная функция. Функция у = »
Цели урока:1.Овладение графическим способом решения квадратных уравнений на основе системно- деятельностного подхода.
2. Развитие УУД:
* Личностных — ученики понимают, что графики не оторваны от жизни и многие реальные объекты имеют форму параболы.
* Познавательных- происходит формирование пространственного мышления через соотнесение точек параболы с числами накоординатной прямой, формируется потребность найти решение проблемы, получить алгоритм решения задачи.
* Регулятивных- развиваются в ходе взаимопроверки и самопроверки.
* Коммуникативных — формируются через работу в паре и в группе.
Этапы урока.
Организационный момент- приветствие и настрой на работу(1 мин)
1этап – мотивация( 6 мин)
1. Какой математический объект мы изучаем на уроке?
2. Заслушаем защиту проекта « Парабола в жизни» (выступление 2 пар с защитой проекта)
3. Значение параболы в нашей жизни очевидно. Как она может быть полезна на уроке? (С помощью параболы мы можем читать свойства квадратичной функции).
2 этап- актуализация знаний( 5 мин)
В парах выполните такую работу. У вас на столах карточки. Каждый выбирает себе параболу и записывает ответ на вопросы:1) найти х, при которых у=0, у>0, у<0.
2) проверить ответы друга и записать оба ответа в каждую тетрадь. Проконтролируйте, чтобы записи были совершенно одинаковыми.
Карточки:
Сверьте ваши ответы и оцените работу своей пары. Ответы к карточкам проектируются на экран.
Зелёная: у=0 при х= -5; 1, у>0 при х (-5;1),
у<0 при х .
Оранжевая:у=0- не существует, у>0 прих ,
у<0 – не существует.
Красная:у=0 при х= -2;2,
у>0 при х
Синяя:у=0 при х= -4, у>0- не существует,
у< 0 при х
Какое задание надо прокомментировать?
Оцените свою работу.
3 этап-целеполагание и получение новых знаний(16 мин)
Постановка проблемы(1 мин)
По графику мы можем прочесть свойства функции. Какие другие математические задания можно выполнить с помощьюпараболы? Какое новое задание будем учиться выполнять на уроке? Приведите примеры таких заданий и попытайтесь решить хотя бы одно из них.Найдите ответы на эти вопросы в группе. Оцените работу каждого смайликом.
Работа в группах,решение проблемы и обсуждение итогов ( 15 мин)
Примеры математических заданий: 1. Решить уравнение.
2. Решить неравенство.
3. Решить систему уравнений.
4. Найти значения коэффициентов а,в,с .
Представители от групп выходят и по очереди, не повторяясь, зачитывают свои ответы. Сдают листы с ответами групп для оценивания. В результате обсуждения делают вывод, что на уроке научатся графически решать квадратное уравнение.
5 этап-применение новых знаний (4 мин)
Тема урока:Графическое решение уравнения ах2+вх +с =0.
Составление алгоритма графического решения уравнения ах2+вх+с+0.
Фронтально с помощью таблицы на доске, где изображена парабола, отвечают на вопрос: Какие шаги надо сделать, чтобы графически решить квадратное уравнение?
Алгоритм:
1. Построить параболу у = ах2+вх +с.
2.
Указать точки пересечения с осью ох.
3. Записать абсциссы точек пересечения.
Сколько ответов можем получить, решая квадратное уравнение?
6 этап-тренировка (8 мин)
Решение №23.4 а. Решите графически уравнение:х2+2х -3=0.Решают письменно, один ученик у доски. Сверяют полученные ответы и высказывают своё мнение о решении на доске.
Осуждение ответов: сколько корней может иметь квадратное уравнение. От чего зависит количество корней квадратного уравнения?
7 этап- рефлексия. ( 5 мин)
Какое новое назначение параболы вы открыли для себя?С помощью шкалы оцените себя, на каком уровне вы находитесь.
Итак, завершая урок,охарактеризуйте параболу. Я открыл для себя, что Парабола – это…
Урок составила и провела Блох Т.И., учитель математики МБОУ « Выльгортская СОШ №1»
1.Технологическая карта урока.
1. Ф.И.О. учителя: Блох Татьяна Ивановна
2.
Класс: 8 а Дата: 29.01.2016 Предмет математика № урока по расписанию: 4
3. Тема урока:Графический способ решения квадратного уравнения
4. Место и роль урока в изучаемой теме: Построение графика квадратичной функции. Обобщение знаний , умений строить параболу, использовать график для чтения свойств функции .
5. Цель урока: Овладение графическим способом решения квадратных уравнений на основе системно — деятельностного подхода
Характеристика этапов урока
Структура
урока
Деятельность
учителя
Деятельность
ученика
Задания для
учащихся
Предметные
результаты
УУД
Оргмомент
приветствие
Настроиться на урок
Регулятивные, личностные
Мотивация
Дает слово ученикам для защиты проекта «Парабола в жизни»
Слушать выступления одноклассников
Увидеть, что в окружающем мире многие предметы, траетории движения, явления природы имеют форму параболы.
Личностные (проявление любознательности, профессиональных пристрастий, смыслообразование)
Актуализация
Инструктаж работы в паре
Выполняет задание, взаимопроверка с соседом по парте, оценивание
По рисунку на карточке найти х, при которых у=0, у>0, у<0.
Читать свойство знакопостоянства функции по графику
Познавательные ( формирование пространственного мышления, критического мышления), коммуникативные ( работа в паре), регулятивные( самопроверка, взаимопроверка, контроль по образцу)
Целеполагание и получение новых знаний
Постановка проблемы
Работа в группе
Ищет ответ на вопрос«Какие новые математические задания можно выполнить с помощью параболы?»
Возможность использования параболы для решения уравнений, неравенств, систем уравнений
Познавательные, регулятивные, коммуникативные, личностные
Решение проблемы
Обсуждение выводов работы групп
Участие в дискуссии.
Обсуждение предложений по применению параболы
Использование графического способа решения квадратных уравнений
Познавательные, регулятивные, коммуникативные, личностные
Применение новых знаний
Фронтальная работа
Ответы на вопросы учителя, выдвижение предложений
Создание алгоритма решения квадратного уравнения графическим способом
алгоритм решения квадратного уравнения графическим способом
Познавательные, регулятивные, коммуникативные, личностные
Тренировка
Комментирование оформления решения квадратного уравнения графическим способом
Решают в тетради № 23.4 а, комментируют решение ученика у доски
Письменно № 23.4 а,23.8 а (для сильных)
Применение алгоритма решения квадратного уравнения графическим способом
Познавательные, регулятивные, коммуникативные, личностные
Рефлексия
Оценить свой уровень понимания темы.
Продолжить фразу «Парабола — это..»
Самооценивание. Завершают фразу
Предлагает свой вариант ответа
Познавательные, регулятивные, коммуникативные, личностные
Урок алгебры на тему «Квадратные уравнения» (9 класс)
Тема урока: «Квадратные уравнения»
Тип урока: урок изучения нового.
Цели урока:- организовать коллективный способ изучения нового материала;
— сформулировать определение квадратного уравнения;
-выбирать квадратные уравнения из предложенных;
-составлять квадратные уравнения по его коэффициентам.
В результате ученик знает:
-какие учебные задачи стоят перед ним
-определение квадратного уравнения
Умеет:
-из предложенных уравнений выбирать квадратные
-составлять квадратные уравнения
-приводить уравнения к виду ax2+bx+c=0
I.
Организационный момент.
II.Актуализация имеющихся знаний и умений учащихся.
Сформулировать определение корня уравнения.
Что значит решить уравнение?
Сформулировать определение линейного уравнения.
Уравнение какого вида вы умеете решать?
(x2=a, a>0
a=0
a<0)
Сколько корней имеет это уравнение?
При изучении каких предметов приходится составлять и решать уравнения?
-Решите уравнение
x2= — ; x2+144=0
3x2=0; x2-1=15
= ; (x+5)2=0
-При каком значении р можно представить в виде квадрата двучлена следующие выражения:
x2+6x+p;
y2+py+16;
px2-20x+25;
-Выделите квадрат двучлена и решите уравнение:
а)25x2+30x+9=0 б)x2-12x+20=0
-Такие уравнения являются квадратными.
III.Значит, тема урока: «Квадратные уравнения»
-Сегодня на уроках мы:
1) сформулируем определение квадратного уравнения,
2)будем выбирать квадратные уравнения из предложенных,
3)составлять квадратные уравнения.
-Сформулируем определение квадратного уравнения
Уравнение вида ax2+bx+c=0, где a,b,c–произвольные числа, причем a ≠ 0, называется квадратным уравнением.
—Найдите квадратные уравнения:
2x2-14x+7=0
x2-9=0
15x+24=0
x3-4x-81=0
-6×2-5x=0
x2-x+ =0
–x2+x=19
-Запишите квадратные уравнения в тетрадь
-Назовите коэффициенты a,b,c квадратного уравнения (заполните таблицу)
-В квадратных уравнениях x2-9=0 ; x2 – x+ =0 коэффициент а=1,
такие квадратные уравнения называютсяприведенными.
-Сформулируем определение приведённого квадратного уравнения.
-Всякое неприведённое квадратное уравнение можно преобразовать в приведённое, имеющие те же корни.
-Как это сделать?
-Преобразуйте квадратное уравнение в приведенное:
2x2-14x+7=0
-6x2-5x=0
-x2+x=19
IV.Закрепление
1.№141 (Рабочая тетрадь)
Составить квадратное уравнение с данными коэффициентами (самопроверка по образцу).
2.Приведите уравнения к виду ax2+bx+c=0
(2x-1)(x-3)=0
2x2-3x=5x-1
(x-1)2=2x+4
(x-2)(x+2)=3
3.№138a
Являются ли корнями уравнения x2-6x+5=0 числа -1;1?
4.Самостоятельная работа (на карточках)
1.Представьте уравнения в виде квадратного уравнения
x(1-2x)=4-5x2 5-3x2=x(2-x)
2.Какое из чисел является корнем уравнения?
3x2+4x-7=0 2x2+3x-2=0
-3;1 -2;1
V.Рефлексивно-оценочная часть
-Подведем итоги
-С какими уравнениями мы работали?
-Какой общий вид квадратных уравнений?
-Как называется уравнение, первый коэффициент которого равен 1?
-На следующих уроках продолжим работу с квадратными уравнениями; научимся их решать, исследуем вопрос о количестве корней квадратного уравнения.
VI.Домашнее задание: п.3.1 (знать определение квадратного уравнения)
№423, 425, 430а.
Решение задач с помощью квадратных и рациональных уравнений (PISA)
Тема: «Решение задач с помощью квадратных и рациональных уравнений».
Цель: Развитие у учащихся навыков к решению задач с помощью квадратных и рациональных уравнений через внедрение заданий PISA, тренировка способности к их практическому использованию.
Дидактическая:
Повторить определение квадратного уравнения, различные формулы для решения квадратных уравнений.
Рассмотреть различные типы задач, связанных с реальной жизнью (PISA), решаемые с помощью квадратных или рациональных уравнений, а также их систем.
Формировать навыки к практическому использованию данных задач.
Развивать критическое мышление, навыки групповой самоорганизации, умение вести диалог
Воспитательная:
Развивать интерес учащихся к предмету: алгебра.
Стимулировать ребят к поиску различных способов решения задач.
Воспитывать коллективизм, взаимопомощь.
Воспитывать в учениках средствами урока уверенность в своих силах;
Тип урока : Урок обобщения и практического применения
Оборудование: интерактивная доска, презентация, бумага А3, фломастеры, стикеры
Формы и методы работы: индивидуальная, групповая, парная, коллективная
ОЖИДАЕМЫЙ РЕЗУЛЬТАТ
Все учащиеся вспомнят определение квадратного уравнения и способы его решения, познакомятся и рассмотрят задачи практического содержания и задачи PISA;
Большинство смогут решить, а значит, и применить данные решения в жизни;
Некоторые смогут вывести формулы и применить их для решения данных задач.
План урока
Вызов
Психологический настрой — 1мин
Мотивационный этап стратегия «Собери картинку» /для создания коллаборативной среды/ — 2мин
Пригласительный билет в «Дом актера».Стратегия «Мозговой штурм» задание №1. Самооценка по критериям 4мин
Осмысление
Задача №1 (год создания группы), коллективная работа у доски — 3 мин
Задача №2 (Степень популярности), коллективная работа у доски- 3мин
Задача №3 (Поездка) Стратегия «Думай – объединяйся -делись». /работа в группах/ — 6 мин
Задача №4 (Увлечения) коллективная работа у доски — 3 мин
Задание №2 Входной билет на встречу со зрителями сериала «Ранетки» (стратегия «Мозговой штурм») 3 мин
Задача №5 (Путешествия), индивидуальная работа 4 мин
Задача №6 (Минута славы), коллективная работа 3 мин
Задача №7 (Я — поэт…), в парах 4 мин
Задача № 8 (Музыка, футбол, математика), в группах 4 мин
Рефлексия 5 мин
Выводы
Домашнее задание.
Ход урока
Стадия вызова.
Психологический настрой:
Здравствуйте, дорогие ребята!
Посмотрите, друг другу в глаза,
Улыбнитесь друг другу,
Пожелайте друг другу удачи.
Мотивационный этап.
Сегодня мы с вами — репортеры.
Наша задача – взять интервью у участников группы «Ранетки».
Сейчас мы с вами разобьемся на группы. Стратегия «Собери картинку». На столах у вас лежат кусочки от картинок. Выберите себе понравившийся кусочек. Ваша задача с помощью данных кусочков собрать 3 целых картинки./саморегуляция/
/картинки – это фото трех участниц группы «Ранетки»/
Мотивационный этап.
Нам необходимо попасть в «Дом актера», где сегодня праздничный вечер.
Для того, чтобы получить пригласительный билет, придется потрудиться и вспомнить ранее изученный материал.
Повторение /самостоятельная работа/
стратегия «Мозговой штурм»
1 группа
Сформулируйте определение квадратного уравнения.
Запишите пример неполного квадратного уравнения.
Запишите, чему равен второй коэффициент в уравнении: 2х2+х-3=0.
Запишите, чему равны: а, в и с в уравнении -3х2+5х=0.
Сколько корней имеет неполное квадратное уравнение вида
Сколько корней имеет квадратное уравнение, если дискриминант положительный?
В каком случае квадратное уравнение имеет два равных корня?
Напишите формулу дискриминанта квадратного уравнения.
Напишите формулу корней квадратного уравнения со вторым четным коэффициентом.
Сформулируйте теорему Виета.
Чему равна сумма корней квадратного уравнения
Приведите пример целого рационального уравнения.
группа
Какое уравнение называют неполным квадратным уравнением?
Запишите пример квадратного уравнения.
Запишите, чему равен первый коэффициент в уравнении: .
Запишите, чему равны: а, в, с в уравнении ?
Сколько корней может иметь неполное квадратное уравнение вида ?
Сколько корней имеет квадратное уравнение, если дискриминант отрицательный?
Какое уравнение называют приведенным квадратным уравнением?
Напишите формулу дискриминанта квадратного уравнения со вторым четным коэффициентом.
Напишите формулу корней квадратного уравнения.
Чему равно произведение корней квадратного уравнения ?
Сформулируйте теорему, обратную теореме Виета.
Приведите пример дробного рационального уравнения.
Ответы / высвечиваются на доске/
Вариант 1
Вариант 2
1.
Квадратным уравнением называется уравнение видагде х- переменная, а, в, с-некоторые числа, причем а≠0
1.Если в квадратном уравнении хотя бы один из коэффициентов в или с равен 0, то такое уравнение называют неполным квадратным уравнением.
2.-3х2+5х=0
2.Х2+4х-7=0
3.в=1
3.а=1
4.а=-3,в=5,с=0
4.а=5,в=0,с=-8
5.Два или ни одного корня.
5.Два корня
6.Два корня
6.Ни одного корня.
7.Если дискриминант равен 0
7.Если а=-1
8.
8.
9.
9.
10.Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
10.Если числа m , n таковы, что их сумма равна – р, а призведение равно q , то эти числа являются кор
Квадратные уравнения
Квадратное уравнение — это уравнение вида ах2 + bx + c = 0 (при а ≠ 0).
Рассмотрим несколько видов квадратных уравнений.
1. Неполные квадратные уравнения — это такие уравнения, в которых хотя бы один из коэффициентов b или c равен нулю.
Пусть с = 0, тогда уравнение примет вид ах2 + bx = 0.
Такое уравнение решается с помощью вынесения общего множителя x (возможно с числовых коэффициентом, если такой будет иметься) за скобку.
Пусть b = 0, тогда квадратное уравнение примет вид ах2 + c = 0.
Чтобы решить такое уравнение надо выразить x2 и извлечь корень.
Пусть b = 0 и с = 0. Тогда уравнение примет вид ax2 = 0.
Такое уравнение также решается через выражение х2.
2. Полные квадратные уравнения — уравнения, в которых числовые коэффициенты b и c отличны от 0 (Число а по умолчанию не равно нулю, помнишь? В противном случае, уравнение перестанет быть квадратным).
В основном их решают через дискриминант по формуле D = b2 — 4ac. Возможны три случая:
КОРОЧЕ! Квадратное уравнение всегда имеет два корня! Вот такие дела) К сожалению, школьная алгебра слишком поверхностна для таких чудес.
Примеры.
3. Приведенные квадратные уравнения — это уравнения, в которых a = 1. Прекрасно решаются через дискриминант.
Но я не могу пройти мимо теоремы Виета. Она, конечно, работает и для полных квадратных уравнений, чутка по-другому правда, но речь не об этом.
Чаще всего теорема Виета используется именно для приведенных квадратных уравнений, т.к. она доступна для всех умов. На ней я и остановлюсь.
Итак, дано уравнение х2 + bx + c = 0.
Если его корни равны х1 и х2, то должны выполнятся два равенства:
1) x1 · x2 = c;
2) x1 + x2 = -b.
В чем смысл? При решении приведенного квадратного уравнения мы должны подобрать корни таким образом, чтобы их произведение равнялось свободному члену с, а сумма равнялась коэффициенту b только с противоположным знаком. И этот подбор происходит в мозгу намного быстрее, чем расписывание дискриминанта и прилегающих к нему формул. Ты просто пишешь уравнение, а потом сразу к нему ответ. Клёво же?!
Конечно, без тренировок никуда; надо как следует потренироваться, чтобы в дальнейшем не возникало трудностей. А если корни подобрать невозможно, значит дискриминант отрицательный или корни дробные/иррациональные.
Решим по теореме Виета следующее приведенное квадратное уравнение:
Вот и всё!
Скажу по секрету, что решать уравнения с отрицательным дискриминантом ты тоже научишься, но это уже совсем другая история…)
Удачи!
Как научиться решать уравнения сложные
Два плюс два: Учимся решать сложные уравнения
Решение сложных уравнений очень непростая тема!
Для тренировки предлагаю поработать со сказочными героями — Незнайкой и Знайкой — повторить компоненты действий!
Чтобы найти уменьшаемое надо к разности прибавить вычитаемое.

Чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое.
Чтобы найти делитель надо делимое разделить на частное.
Чтобы найти неизвестный множитель надо произведение разделить на известный множитель.
Попробуйте решить сложные уравнения!
На страничке «Детям на заметку» опубликована памятка-алгоритм решения и оформления сложных уравнений.Решение уравнений со сложными решениями
- Образование
- Математика
- Алгебра
- Решение уравнений со сложными решениями
Автор Мэри Джейн Стерлинг
Часто встречаются уравнения, не имеющие реальных решений, или уравнения, которые имеют потенциал для гораздо большего количества реальных решений, чем они есть на самом деле. Например, уравнение x 2 + 1 = 0 не имеет реальных решений. Если вы запишете это как x 2 = –1 и попытаетесь извлечь квадратный корень из каждой стороны, вы столкнетесь с проблемами.
Только когда у вас есть мнимые числа, вы не сможете написать, что решение этого уравнения: x = +/– i . Уравнение имеет два комплексных решения.
Пример уравнения без достаточного количества реальных решений: x 4 — 81 = 0. Это уравнение множится в ( x 2 — 9) ( x 2 + 9) = 0. два действительных решения этого уравнения — 3 и –3. Два комплексных решения: 3 i и –3 i .
Чтобы найти комплексные решения уравнения, вы используете факторизацию, свойство квадратного корня для решения квадратичных уравнений и формулу корней квадратного уравнения.
Примеры вопросов
Найдите все корни, действительные и комплексные, уравнения x 3 — 2 x 2 + 25 x — 50 = 0.
x = 2, 5 i , –5 i . Сначала разложите уравнение на множители, чтобы получить x 2 ( x — 2) + 25 ( x — 2) = ( x — 2) ( x 2 + 25) = 0 .
Используя нулевое свойство умножения, вы определяете, что x — 2 = 0 и x = 2. Вы также получаете x 2 + 25 = 0 и x 2 = –25. Извлеките квадратный корень из каждой стороны и получим
Упростим радикал, используя эквивалент для i , и комплексные решения будут
Действительный корень равен 2, а мнимый корень равен 5 i и –5 i .
Найдите все корни, действительные и мнимые, уравнения 5 x 2 — 8 x + 5 = 0.
x = 0,4 + 0,6 i , 0,4 — 0,6 i . Квадратичный коэффициент не учитывается, поэтому вы используете квадратную формулу:
Сложны только два решения: 0,4 + 0,6 i и 0,4 — 0,6 i .
Практические вопросы
Найдите все корни, действительные и мнимые, из x 2 + 9 = 0.
Найдите все корни, действительные и мнимые, из x 2 + 4 x + 7 = 0.
Найдите все корни, действительные и мнимые, из 5 x 2 + 6 x + 3 = 0.
Найдите все корни, действительные и мнимые, для x 4 + 12 x 2 — 64 = 0.
Ниже приведены ответы на вопросы практики:
.
Ответ: x = 3 i , –3 i .
Добавьте –9 к каждой стороне, чтобы получить x 2 = –9.Извлеките квадратный корень из каждой стороны. Затем упростите выражение, используя i для отрицательного значения под корнем:
Ответ:
Используйте формулу корней квадратного уравнения, чтобы найти x . Упростите выражение, используя i для отрицательного значения под корнем:
Ответ:
Используйте формулу корней квадратного уравнения, чтобы найти x . Упростите выражение, используя i для отрицательного значения под корнем:
Ответ: x = 2, –2, 4 i , –4 i .
Фактор левой части: ( x 2 + 16) ( x 2 — 4) = ( x 2 + 16) ( x — 2) ( x + 2 ) = 0. Получите два действительных корня, установив x — 2 и x + 2 равными 0. Когда x 2 + 16 = 0, вы обнаружите, что x 2 = –16 . Извлечение квадратного корня из каждой стороны и использование i вместо –1 под корнем дает два мнимых корня.
math — Как решить сложные уравнения с двумя переменными в Python?
Переполнение стека
- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Загрузка…
.python — Как использовать SymPy для решения сложного уравнения с приближенным решением
Переполнение стека
- Около
- Товары
- Для команд
.
- Переполнение стека Общественные вопросы и ответы
повседневных ситуаций для применения квадратных уравнений
Квадратные уравнения фактически используются в повседневной жизни, например, при вычислении площадей, определении прибыли продукта или формулировании скорости движения объекта. Квадратные уравнения относятся к уравнениям по крайней мере с одной квадратной переменной, наиболее стандартной формой является ax² + bx + c = 0. Буква X представляет неизвестное, а ab и c являются коэффициентами, представляющими известные числа, а буква a не равна до нуля.
Расчет площадей комнат
Людям часто требуется рассчитать площадь комнат, ящиков или земельных участков. В качестве примера можно привести прямоугольную коробку, одна сторона которой должна быть вдвое длиннее другой.
2.Это уравнение должно быть меньше или равно четырем, чтобы успешно создать коробку с этими ограничениями.
Расчет прибыли
Иногда для расчета прибыли бизнеса требуется использование квадратичной функции. Если вы хотите что-то продать — даже такое простое, как лимонад — вам нужно решить, сколько товаров производить, чтобы получить прибыль. Допустим, вы продаете стаканы лимонада и хотите сделать 12 стаканов. Однако вы знаете, что продадите разное количество очков в зависимости от того, как вы установили цену.2. Используя любые затраты на производство лимонада, вы можете установить это уравнение равным этой сумме и выбрать оттуда цену.
Квадраты в легкой атлетике
В спортивных соревнованиях, которые включают метание таких предметов, как толкание ядра, мячи или копье, квадратные уравнения становятся очень полезными. Например, вы подбрасываете мяч в воздух, и ваша подруга ловит его, но вы хотите дать ей точное время, в течение которого мяч прибудет.
Используйте уравнение скорости, которое вычисляет высоту мяча на основе параболического или квадратного уравнения.2. Если руки вашей подруги тоже на высоте 3 метра, сколько секунд потребуется мячу, чтобы добраться до нее? Чтобы ответить на этот вопрос, задайте уравнение равным 3 = h и решите относительно t. Ответ составляет примерно 2,8 секунды.
Определение скорости
Квадратные уравнения также полезны при вычислении скорости. Например, заядлые каякеры используют квадратные уравнения для оценки своей скорости при движении вверх и вниз по реке. Предположим, каякер поднимается по реке, и река движется со скоростью 2 км в час.Если он идет вверх против течения на высоте 15 км, а поездка занимает 3 часа, чтобы добраться туда и вернуться, помните, что время = расстояние, разделенное на скорость, пусть v = скорость каяка относительно земли, а x = скорость каяка. в воде. При движении вверх по течению скорость каяка равна v = x — 2 — вычтите 2 для сопротивления от течения реки — а при движении вниз по течению скорость каяка будет v = x + 2.
Общее время равно 3 часам, который равен времени подъема вверх по течению плюс времени спуска вниз, и оба расстояния составляют 15 км.2 — 30x -12 = 0. Решая для x, мы знаем, что каякер двигал каяк со скоростью 10,39 км в час.
Квадратичные уравнения | Колледж алгебры
Результаты обучения
К концу этого раздела вы сможете:
- Разложите на множители квадратное уравнение для его решения.
- Используйте свойство квадратного корня для решения квадратного уравнения.
- Используйте теорему Пифагора и свойство квадратного корня, чтобы найти неизвестную длину стороны прямоугольного треугольника.
- Заполните квадрат, чтобы решить квадратное уравнение.
- Используйте формулу корней квадратного уравнения, чтобы решить квадратное уравнение.
- Используйте дискриминант, чтобы определить количество и тип решений квадратного уравнения.
Левый компьютерный монитор на изображении ниже — это 23,6-дюймовая модель, а правый — 27-дюймовая.
Пропорционально мониторы выглядят очень похожими. Если пространство ограничено, и нам нужен максимально большой монитор, как нам решить, какой из них выбрать? В этом разделе мы узнаем, как решать такие проблемы, используя четыре разных метода.{2} -4 = 0 [/ latex] — квадратные уравнения. Они используются бесчисленным количеством способов в области инженерии, архитектуры, финансов, биологии и, конечно же, математики.
Часто самый простой метод решения квадратного уравнения — это , разложив на множители . Факторинг означает поиск выражений, которые можно перемножить, чтобы получить выражение на одной стороне уравнения.
Если квадратное уравнение можно разложить на множители, оно записывается как произведение линейных членов. Решение путем факторизации зависит от свойства нулевого продукта, которое гласит, что если [latex] a \ cdot b = 0 [/ latex], то [latex] a = 0 [/ latex] или [latex] b = 0 [/ latex] , где a и b — действительные числа или алгебраические выражения.
Другими словами, если произведение двух чисел или двух выражений равно нулю, то одно из чисел или одно из выражений должно равняться нулю, потому что ноль, умноженный на что-либо, равен нулю.
При умножении на множители уравнение превращается в строку терминов, разделенных знаками плюс или минус. Таким образом, в этом смысле операция умножения отменяет операцию факторинга. Например, разверните факторизованное выражение [латекс] \ left (x — 2 \ right) \ left (x + 3 \ right) [/ latex], умножив два множителя вместе.{2} + x — 6 = 0 [/ latex] в стандартной форме.
Мы можем использовать свойство нулевого произведения для решения квадратных уравнений, в которых мы сначала должны вычесть наибольший общий множитель (GCF), и для уравнений, которые также имеют специальные формулы факторизации, такие как разность квадратов, оба из которых мы увидим позже в этом разделе.
Общее примечание: свойство нулевого произведения и квадратные уравнения
Свойство нулевого продукта указывает
[латекс] \ text {If} a \ cdot b = 0, \ text {then} a = 0 \ text {или} b = 0 [/ latex],
, где a и b — действительные числа или алгебраические выражения.
{2} [/ latex], равно 1. У нас есть один метод разложения квадратных уравнений на множители в этой форме.
Практическое руководство. Для квадратного уравнения со старшим коэффициентом 1 разложите его на множители
- Найдите два числа, произведение которых равно c , а сумма равна b .
- Используйте эти числа, чтобы записать два множителя в форме [латекс] \ left (x + k \ right) \ text {или} \ left (xk \ right) [/ latex], где k — одно из найденных чисел на шаге 1. Используйте числа в точности так, как они есть.{2} + x — 6 = 0 [/ latex], мы ищем два числа, произведение которых равно [latex] -6 [/ latex], а сумма равна 1. Начните с рассмотрения возможных множителей [latex] -6 [/латекс].
[латекс] \ begin {array} {l} 1 \ cdot \ left (-6 \ right) \ hfill \\ \ left (-6 \ right) \ cdot 1 \ hfill \\ 2 \ cdot \ left (-3 \ right) \ hfill \\ 3 \ cdot \ left (-2 \ right) \ hfill \ end {array} [/ latex]
Последняя пара, [латекс] 3 \ cdot \ left (-2 \ right) [/ latex] суммируется до 1, так что это числа.
Обратите внимание, что подойдет только одна пара чисел.Затем запишите факторы.
[латекс] \ left (x — 2 \ right) \ left (x + 3 \ right) = 0 [/ латекс]
Чтобы решить это уравнение, мы используем свойство нулевого произведения. Установите каждый коэффициент равным нулю и решите.
[латекс] \ begin {array} {l} \ left (x — 2 \ right) \ left (x + 3 \ right) = 0 \ hfill \\ \ left (x — 2 \ right) = 0 \ hfill \ \ x = 2 \ hfill \\ \ left (x + 3 \ right) = 0 \ hfill \\ x = -3 \ hfill \ end {array} [/ latex]
Два решения: [латекс] x = 2 [/ латекс] и [латекс] x = -3 [/ латекс]. Мы можем увидеть, как решения соотносятся с графиком ниже.\ circ [/ latex] угол, а [latex] c [/ latex] относится к гипотенузе. Он находит неизмеримое применение в архитектуре, инженерии, науках, геометрии, тригонометрии и алгебре, а также в повседневных приложениях.
Мы используем теорему Пифагора, чтобы найти длину одной стороны треугольника, когда у нас есть длины двух других. Поскольку каждый член в теореме возведен в квадрат, когда мы решаем сторону треугольника, мы получаем квадратное уравнение.
Мы можем использовать методы решения квадратных уравнений, которые мы узнали в этом разделе, чтобы найти недостающую сторону.{2} = 128 \ hfill \\ a = \ sqrt {128} \ hfill \\ a = 8 \ sqrt {2} \ hfill \ end {array} [/ latex]
Попробуй
Используйте теорему Пифагора для решения задачи о прямоугольном треугольнике: отрезок a имеет размер 4 единицы, отрезок b имеет размер 3 единицы. Найдите длину гипотенузы.
Завершение квадрата и квадратичной формулы
Не все квадратные уравнения могут быть разложены на множители или могут быть решены в их исходной форме с использованием свойства квадратного корня. В этих случаях мы можем использовать метод решения квадратного уравнения , известный как , завершающий квадрат .{2} -6x = 13 [/ латекс].
Показать решение[латекс] x = 3 \ pm \ sqrt {22} [/ латекс]
Использование квадратичной формулы
Четвертый метод решения квадратного уравнения заключается в использовании квадратной формулы , формулы, которая решает все квадратные уравнения.
Хотя квадратная формула работает с любым квадратным уравнением в стандартной форме, легко сделать ошибку, подставляя значения в формулу. Будьте внимательны при замене и используйте круглые скобки при вставке отрицательного числа.{2} — \ left (4 \ right) \ cdot \ left (1 \ right) \ cdot \ left (2 \ right)}} {2 \ cdot 1} \ hfill \\\ hfill & = \ frac {-1 \ pm \ sqrt {1–8}} {2} \ hfill \\ \ hfill & = \ frac {-1 \ pm \ sqrt {-7}} {2} \ hfill \\\ hfill & = \ frac {-1 \ pm я \ sqrt {7}} {2} \ hfill \ end {array} [/ latex]
Решение уравнения: [латекс] x = \ frac {-1} {2} + \ frac {i \ sqrt {7}} {2} [/ latex] и [латекс] x = \ frac {-1 } {2} — \ frac {i \ sqrt {7}} {2} [/ latex].
. Обратите внимание, что они записаны в стандартной форме комплексного числа. Если решение представляет собой комплексное число, необходимо отделить действительную часть от мнимой и записать ее в стандартной форме.{2} -4 \ left (3 \ right) \ left (15 \ right) = — 80 [/ латекс]. Будет два сложных решения.
Ключевые концепции
- Многие квадратные уравнения могут быть решены путем факторизации, когда уравнение имеет старший коэффициент, равный 1, или если уравнение представляет собой разность квадратов. Затем свойство нулевого фактора используется для поиска решений.
- Многие квадратные уравнения со старшим коэффициентом, отличным от 1, могут быть решены путем факторизации с использованием метода группировки.
- Другой метод решения квадратичных вычислений — это свойство извлечения квадратного корня.Переменная возведена в квадрат. Мы выделяем квадратный член и извлекаем квадратный корень из обеих частей уравнения. Решение даст положительное и отрицательное решение.
- Завершение квадрата — это метод решения квадратных уравнений, когда уравнение не может быть разложено на множители.
- Очень надежный метод решения квадратных уравнений — это квадратная формула, основанная на коэффициентах и постоянном члене в уравнении.
- Дискриминант используется, чтобы указать природу решений, которые даст квадратное уравнение: действительные или комплексные, рациональные или иррациональные, и сколько из них.
- Теорема Пифагора, одна из самых известных теорем в истории, используется для решения задач прямоугольного треугольника и имеет приложения во многих областях. Чтобы определить длину одной стороны прямоугольного треугольника, необходимо решить квадратное уравнение.
Глоссарий
- завершение квадрата
- процесс решения квадратных уравнений, в котором члены складываются или вычитаются из обеих сторон уравнения, чтобы сделать одну сторону идеальным квадратом.
- дискриминант
- выражение под корнем в формуле корней квадратного уравнения, указывающее на природу решений, действительные или комплексные, рациональные или иррациональные, одинарные или двойные корни.
- Теорема Пифагора
- теорема, устанавливающая соотношение между длинами сторон прямоугольного треугольника, используемая для решения задач прямоугольного треугольника. {2} [/ latex] изолирован, так что квадратный корень из обеих частей уравнения может использоваться для решения для x
- собственность нулевого продукта
- свойство, которое формально заявляет, что умножение на ноль равно нулю, так что каждый коэффициент квадратного уравнения может быть установлен равным нулю для решения уравнений
Раздел 4: Решение уравнений, квадратичных по форме | Общественный колледж Хьюстона
Квадратичное по форме уравнение — это уравнение, которое можно преобразовать в квадратичную форму, сделав замену.Например, уравнение x 4 — 14 x 2 + 49 = 0 может быть преобразовано в квадратное уравнение путем замены y = x ².
x 4 — 14 x 2 + 49 = 0 становится y ² — 14 y + 49 = 0
После преобразования уравнения в квадратичную форму уравнение можно решить путем факторизации, завершения квадрата или использования квадратичной формулы.
y ² — 14 y + 49 = 0 можно разложить на ( y — 7) ² = 0
Это дает решение для y : y = 7
Теперь мы можем выполнить обратную замену, чтобы получить решение (я) для x . Напомним, что y = x ².
y = 7 становится x ² = 7
Решите для x , применив свойство квадратного корня.
x = ± √ 7
Пример 1 . Решите уравнение ( x — 2) 2/3 + ( x — 2) 1/3 — 2 = 0.
Решение
Это уравнение можно преобразовать в квадратное уравнение, сделав замену y = ( x — 2) 1/3 .
[( x — 2) 1/3 ] 2 + ( x — 2) 1/3 — 2 = 0 становится y ² + y — 2 = 0
Это уравнение можно решить путем факторизации.
y ² + y — 2 = 0 можно разложить на ( y — 1) ( y + 2) = 0
Установите множители равными нулю и решите:
y — 1 = 0 или y + 2 = 0
y = 1 или y = −2
Обратный заменитель, чтобы получить решение (я) для x . Напомним, что y = ( x — 2) 1/3 .
y = 1 становится ( x — 2) 1/3 = 1 и y = −2 становится ( x — 2) 1/3 = −2
Решите относительно x , построив кубики каждой стороны каждого уравнения и затем прибавив 2.
( x — 2) 1/3 = 1
Куб с каждой стороны уравнения:
[( x — 2) 1/3 ] 3 = 1³ Упростить:
x — 2 = 1 Решить относительно x :
x = 3
( x — 2) 1/3 = −2
Кубы с каждой стороны уравнения:]
[( x — 2) 1/3 ] 3 = (−2) ³ Упростить:
x — 2 = −8 Решить относительно x :
х = −6
Для уравнений, которые включают корни, отличные от квадратного корня, вы хотите удалить корни путем (1) выделения корневого члена на одной стороне уравнения и (2) возведения обеих сторон уравнения в соответствующую степень .
Проверьте свои знания, открыв действие «Проверьте себя».
квадратов | G’Day Math
Моя работа над блоком квадратиков претерпевает изменения!Изучив различные учебные программы международных школ, я решил составить исчерпывающий набор материалов по этой теме.
Этот веб-сайт в уроках, которые вы видите ниже, содержит мои мысли и подходы к обучению всему этому содержанию.Вы также можете загрузить это содержимое здесь как единый документ PDF, если хотите.
ПОЛНОЕ ДОПОЛНИТЕЛЬНОЕ РУКОВОДСТВО ПО КВАДРАТИКЕ: свежие, доступные и понятные заметки для всех, кто чувствует, что никогда не «понял». Quadratics: подробное сопроводительное руководство
Если я предпочитаю преподавать, загрузите это следующее руководство. Большинство учебных программ сочли бы эти примечания «неполными»: Где факторинг? Почему вы преуменьшаете значение квадратной формулы? Почему бы не назвать ваши графики «параболами»? См. Подробные примечания выше, где это содержание и мои ответы на такие вопросы.
ГЛАВА О КВАДРАТИКАХ: Только заметки, которые я выбираю для преподавания Колледж, модуль алгебры 8 КВАДРАТИКА
И, конечно же, есть мой любимый дополнительный материал, которого нет в учебной программе:
ВСЕ ЛИ U-ОБРАЗНЫЕ ГРАФИКИ КВАДРАТИЧНЫЕ? U-образных графиков. См. Опыт 3 по этой ссылке.
ДРУГОЙ ВАРИАНТРаздел по квадратичности доступен как часть комплексного курса в каталоге Edfinity.Этот доступный по цене курс «самообслуживания», который также обеспечивает официальное признание преподавателям опыта профессионального развития в Интернете. Предлагаем сертификат, подтверждающий 12 часов онлайн-обучения. По завершении курса преподаватели могут также записать своих студентов на идентичный курс квадратичного обучения для обучения в классе. Мы взимаем умеренную плату за все эти курсы.
Вы можете увидеть примеры видео и задач на странице курса Edfinity здесь.
Присоединяйтесь к обсуждению в Facebook и Twitter и любезно поделитесь этой страницей с помощью кнопок ниже.Квадратичные уравнения | Решенные задачи и практические вопросы
В этой статье мы рассмотрим квадратные уравнения — определения, форматы, решенные задачи и примеры вопросов для практики.
Квадратное уравнение — это многочлен, максимальная степень которого равна квадрату переменной (x 2 , y 2 и т. Д.)
Определения
Моном — это алгебраическое выражение, содержащее только один член.
Пример: x 3 , 2x, y 2 , 3xyz и т. Д.
Многочлен — это алгебраическое выражение, содержащее более одного члена.
В качестве альтернативы можно указать —
Многочлен формируется путем сложения / вычитания нескольких одночленов.
Пример: x 3 + 2y 2 + 6x + 10, 3x 2 + 2x-1, 7y-2 и т. Д.
Многочлен, содержащий два члена, называется биномиальным выражением .
Многочлен, содержащий три члена, называется выражением трехчлена .
Стандартное квадратное уравнение выглядит так:
топор 2 + bx + c = 0
Где a, b, c — числа, а a≥1.
a, b называются коэффициентами x 2 и x соответственно, а c называется константой.
Ниже приведены примеры некоторых квадратных уравнений:
1) x 2 + 5x + 6 = 0, где a = 1, b = 5 и c = 6.
2) x 2 + 2x-3 = 0, где a = 1, b = 2 и c = -3
3) 3x 2 + 2x = 1
→ 3x 2 + 2x-1 = 0, где a = 3, b = 2 и c = -1
4) 9x 2 = 4
→ 9x 2 -4 = 0, где a = 9, b = 0 и c = -4
Для каждого квадратного уравнения может быть одно или несколько решений.Они называются корнями квадратного уравнения.
Для квадратного уравнения ax 2 + bx + c = 0,
сумма его корней = –b / a и произведение его корней = c / a.
Квадратное уравнение может быть выражено как произведение двух биномов.
Например, рассмотрим следующее уравнение
x 2 — (a + b) x + ab = 0
x 2 -ax-bx + ab = 0
х (х-а) -b (х-а) = 0
(х-а) (х-б) = 0
x-a = 0 или x-b = 0
x = a или x = bЗдесь a и b называются корнями данного квадратного уравнения.
Теперь давайте вычислим корни уравнения x 2 + 5x + 6 = 0.
Мы должны взять два числа, сложить которые мы получим 5 и умножить получим 6. Это 2 и 3.
Выразим средний член как сложение 2х и 3х.
→ x 2 + 2x + 3x + 6 = 0
→ х (х + 2) +3 (х + 2) = 0
→ (х + 2) (х + 3) = 0
→ x + 2 = 0 или x + 3 = 0
→ x = -2 или x = -3
Этот метод называется факторингом .
Ранее мы видели, что сумма корней равна –b / a, а произведение корней равно c / a. Давайте проверим это.
Сумма корней уравнения x 2 + 5x + 6 = 0 равна -5, а произведение корней равно 6.
Корни этого уравнения -2 и -3 при сложении дают -5, а при умножении дают 6.
Решенные примеры квадратных уравнений
Решим еще несколько примеров этим методом.
Задача 1: Решить для x: x 2 -3x-10 = 0
Решение :
Выразим -3x как сумму -5x и + 2x.
→ х 2 -5x + 2x-10 = 0
→ х (х-5) +2 (х-5) = 0
→ (х-5) (х + 2) = 0
→ x-5 = 0 или x + 2 = 0
→ x = 5 или x = -2
Задача 2: Решить относительно x: x 2 -18x + 45 = 0
Решение :
Числа, которые в сумме дают -18 и дают +45 при умножении: -15 и -3.
Переписывая уравнение,
→ х 2 -15x-3x + 45 = 0
→ х (х-15) -3 (х-15) = 0
→ (х-15) (х-3) = 0
→ x-15 = 0 или x-3 = 0
→ x = 15 или x = 3
До сих пор коэффициент x 2 был равен 1.Давайте посмотрим, как решить уравнения, в которых коэффициент при x 2 больше 1.
Задача 3: Решить относительно x: 3x 2 + 2x = 1
Решение :
Переписывая наше уравнение, получаем 3x 2 + 2x-1 = 0
Здесь коэффициент при x 2 равен 3. В этих случаях мы умножаем константу c на коэффициент x 2 . Следовательно, произведение выбранных нами чисел должно быть равно -3 (-1 * 3).
Выражение 2x как суммы + 3x и –x
→ 3x 2 + 3x-x-1 = 0
→ 3х (х + 1) -1 (х + 1) = 0
→ (3x-1) (x + 1) = 0
→ 3x-1 = 0 или x + 1 = 0
→ x = 1/3 или x = -1
Задача 4: Решите для x: 11x 2 + 18x + 7 = 0
Решение :
В этом случае сумма выбранных чисел должна быть равна 18, а произведение чисел должно быть равно 11 * 7 = 77.
Это можно сделать, представив 18x как сумму 11x и 7x.
→ 11x 2 + 11x + 7x + 7 = 0
→ 11x (x + 1) +7 (x + 1) = 0
→ (х + 1) (11x + 7) = 0
→ x + 1 = 0 или 11x + 7 = 0
→ x = -1 или x = -7/11.
Факторинг — это простой способ найти корни. Но этот метод применим только к уравнениям, которые можно разложить на множители.
Например, рассмотрим уравнение x 2 + 2x-6 = 0.
Если мы возьмем +3 и -2, их умножение даст -6, но их сложение не даст +2. Следовательно, это квадратное уравнение нельзя факторизовать.
Для этого типа уравнений мы применяем формулу корней квадратного уравнения, чтобы найти корни.
Квадратичная формула для нахождения корней,
x = [-b ± √ (b 2 -4ac)] / 2a
Теперь давайте найдем корни приведенного выше уравнения.
x 2 + 2x-6 = 0
Здесь a = 1, b = 2 и c = -6.
Подставляя эти значения в формулу,
x = [-2 ± √ (4 — (4 * 1 * -6))] / 2 * 1
→ x = [-2 ± √ (4 + 24)] / 2
→ x = [-2 ± √28] / 2
Когда мы получаем неполный квадрат в квадратном корне, мы обычно пытаемся выразить его как произведение двух чисел, одно из которых является точным квадратом. Это сделано для упрощения. Здесь 28 может быть выражено как произведение 4 и 7.
→ x = [-2 ± √ (4 * 7)] / 2
→ x = [-2 ± 2√7] / 2
→ x = 2 [-1 ± √7] / 2
→ х = -1 ± √7
Следовательно, √7-1 и -√7-1 являются корнями этого уравнения.
Рассмотрим другой пример.
Решите относительно x: x 2 = 24 — 10x
Решение :
Перепишите уравнение в стандартную квадратичную форму,
x 2 + 10x-24 = 0
Какие два числа при сложении дают +10, а при умножении — -24? 12 и -2.
Значит, это можно решить методом факторинга. Но давайте решим его новым методом, применив формулу корней квадратного уравнения.
Здесь a = 1, b = 10 и c = -24.
x = [-10 ± √ (100 — 4 * 1 * -24)] / 2 * 1
x = [-10 ± √ (100 — (- 96))] / 2
x = [-10 ± √196] / 2
x = [-10 ± 14] / 2
x = 2 или x = -12 — корни.
Дискриминант
Для уравнения ax 2 + bx + c = 0, b 2 -4ac называется дискриминантом и помогает в определении природы корней квадратного уравнения.
Если b 2 -4ac> 0, корни действительны и различны.
Если b 2 -4ac = 0, корни действительные и равны.
Если b 2 -4ac <0, корни не являются действительными (они комплексные).
Рассмотрим следующий пример:
Задача: Найдите характер корней уравнения x 2 + x + 12 = 0.
Решение :
b 2 -4ac = -47 для этого уравнения. Итак, у него сложные корни. Давайте проверим это.
→ [-1 ± √ (1-48)] / 2 (1)
→ [-1 ± √-47] / 2
√-47 обычно записывается как i √47, что означает, что это мнимое число.
Значит проверено.
Тест по квадратным уравнениям: решите следующие
Проблема 1
Решить относительно x: x 2 -15x + 56 = 0
A. x = 14 или x = 4
B. x = 8 или x = 7
C. x = 28 или x = 2
D. Все вышеперечисленноеОтвет 1
Б.
Пояснение
Только 8 и 7 удовлетворяют условиям сложения до 15 и получения произведения 56.
Проблема 2
Найти x, если 2x 2 + 7x + 4 = 0
A. -7 ± √17 / 4
B. -7 ± √7 / 4
C. [-7 ± √17] / 4
D. [-7 ± √17] / 2Ответ 2
C.
Пояснение :
Применяя формулу корней квадратного уравнения и подставляя a = 2, b = 7 и c = 4, мы получаем ответ как C.
Проблема 3
При каком значении k уравнение x 2 -12x + k = 0 имеет действительные и равные корни?
А.6
Б. 35
С. 12
Д. 36Ответ 3
Д.
Пояснение
b 2 -4ac = 0, чтобы уравнение имело действительные и равные корни.
144-4к = 0 → к = 36Пройдите этот доступный по цене онлайн-курс по квадратным уравнениям. Из решения, построения графиков и записи квадратного уравнения вы узнаете все шаг за шагом. Щелкните ниже. квадратные уравнения; Ваше полное руководство
квадратных уравнений | Блестящая вики по математике и науке
Основная статья: Факторинговые полиномы
Мы можем решать квадратичные уравнения, используя факторинг и свойство нулевого произведения.2 + 2x + 3x + 6 & = 0 \\ х (х + 2) +3 (х + 2) & = 0. \ end {align} x2 + 2x + 3x + 6x (x + 2) +3 (x + 2) = 0 = 0. Взяв (x + 2) (x + 2) (x + 2) в качестве общего множителя, мы имеем (x + 3) (x + 2) = 0x + 3 = 0 ⟹ x = −3x + 2 = 0 ⟹ x = −2. \ begin {align} (х + 3) (х + 2) & = 0 \\ x + 3 & = 0 \ подразумевает x = -3 \\ x + 2 & = 0 \ подразумевает x = -2. \ end {выровнены} (x + 3) (x + 2) x + 3x + 2 = 0 = 0⟹x = −3 = 0⟹x = −2. Следовательно, два корня данного уравнения равны −3-3−3 и −2-2−2. □ _ \ квадрат □
Метод решения квадратного уравнения путем факторизации:
Шаг 1.2 + 1 = (х + я) (х-я). Х2 + 1 = (х + я) (х-я). {2} + x-20 = 0x2 + x − 20 = 0.2 + bx + c} \) задается тремя числами, разумно предположить, что мы могли бы подогнать параболу к трем точкам на плоскости. Это действительно так, и это полезная идея. На этом этапе мы увидим, как алгебраически подогнать параболу к трем точкам на декартовой плоскости. Это включает в себя напоминание или обучение тому, как решить три уравнения с тремя неизвестными. Это полезный навык сам по себе.
Уникальный круг через три неколлинеарных точки
Линия определяется двумя точками.С другой стороны, окружность определяется тремя точками, если эти точки не лежат на одной прямой (все три точки не могут лежать на одной линии). Построение круга, проходящего через три точки, является стандартным упражнением в евклидовой геометрии: мы строим серединные перпендикуляры отрезков прямых, определяемых этими тремя точками, а затем эти три прямые пересекаются в центре описанной окружности треугольника \ (\ normalsize { ABC} \), а именно центр единственной окружности, проходящей через все три точки. 2 + 7x + 1} \).Вот график:Решение трех линейных уравнений с тремя неизвестными
Поскольку два линейных уравнения представляют две линии на плоскости, их общее решение соответствует геометрическому пересечению этих двух линий. Для трех линейных уравнений с тремя неизвестными ситуация на самом деле соответствует общей точке пересечения трех плоскостей в трехмерном пространстве! К счастью, древние китайцы смогли разработать общую технику решения таких систем уравнений. Здесь мы просто пытаемся найти простой практический метод.2 + bx + c} \), который проходит через точки \ (\ normalsize {[1,3], [2, -1]} \) и \ (\ normalsize {[4,1]} \). Это означает, что у нас есть три уравнения, по одному для каждой точки — поскольку мы знаем, что данные точки должны удовлетворять неизвестному уравнению. Три уравнения: \ [\ Large {3 = a + b + c} \ label {b1p} \ tag {1} \] \ [\ Large {-1 = 4a + 2b + c} \ label {b2p} \ tag {2} \] \ [\ Large {1 = 16a + 4b + c}. \ label {b3p} \ tag 3 \] Какая стратегия? Это просто: мы пытаемся исключить одну из переменных, оставляя нам два уравнения с двумя неизвестными.Мы знаем, как это решить. Чтобы получить два уравнения с двумя переменными, давайте исключим \ (\ normalsize {c} \) из первых двух уравнений. Мы делаем это, вычитая одно из другого, скажем, вычитая первое из второго: \ [\ Large {-4 = 3a + b} \ label {b4p} \ tag {4} \] Пожалуйста, убедитесь, что вы понимаете, как мы получили который. Теперь мы делаем то же самое с двумя последними уравнениями: берем третье уравнение и вычитаем из второго: \ [\ Large {2 = 12a + 2b} \] Мы можем сделать это немного проще, разделив все коэффициенты на \ (\ normalsize {2} \), чтобы получить \ [\ Large {1 = 6a + b}.\ label {b5p} \ tag {5} \] Теперь мы рассматриваем \ (\ normalsize {(\ ref {b5p})} \) и \ (\ normalsize {(\ ref {b4p})} \) как новые уравнения, и используйте их, чтобы найти \ (\ normalsize {a} \) и \ (\ normalsize {b} \). Если мы возьмем \ (\ normalsize {(\ ref {b5p})} \) — \ (\ normalsize {( \ ref {b4p})} \) мы получаем \ (\ normalsize {5 = 3a} \), так что \ (\ normalsize {a = 5/3} \), а затем снова подключаемся к \ (\ normalsize { (\ ref {b3p})} \) или \ (\ normalsize {(\ ref {b4p})} \) дает \ (\ normalsize {b = -9} \).




 2 + b*x + c = 0
,где x
—
переменная, a,b,c
– константы; a0
. Задача состоит в отыскании корней уравнения.
2 + b*x + c = 0
,где x
—
переменная, a,b,c
– константы; a0
. Задача состоит в отыскании корней уравнения.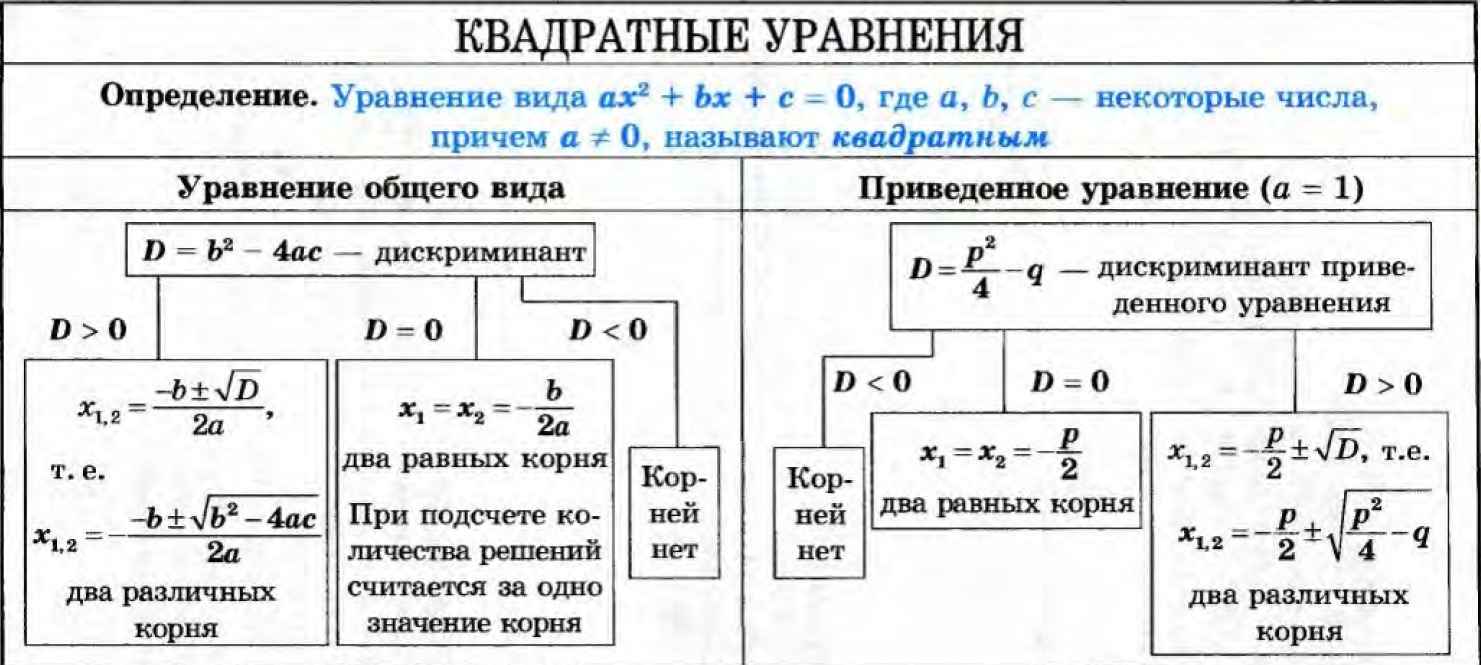 2
и осуществим преобразование
2
и осуществим преобразование 2+x-6=0
.
2+x-6=0
. 2+(2а+6)х-3а-9=0
имеет более одного корня?
2+(2а+6)х-3а-9=0
имеет более одного корня?

 Точно так же можно доказать, что и число x2 является корнем для этого уравнения.
Точно так же можно доказать, что и число x2 является корнем для этого уравнения.

 Решение проблемы осуществляется через дискуссию, в группе. Обсуждение выводов выводит учащихся на личностные УУД. Применение новых знаний идет с использованием выработанного алгоритма учащими ся.
Решение проблемы осуществляется через дискуссию, в группе. Обсуждение выводов выводит учащихся на личностные УУД. Применение новых знаний идет с использованием выработанного алгоритма учащими ся.


 Указать точки пересечения с осью ох.
Указать точки пересечения с осью ох. Класс: 8 а Дата: 29.01.2016 Предмет математика № урока по расписанию: 4
Класс: 8 а Дата: 29.01.2016 Предмет математика № урока по расписанию: 4

 Продолжить фразу «Парабола — это..»
Продолжить фразу «Парабола — это..» Организационный момент.
Организационный момент.

 Рефлексивно-оценочная часть
Рефлексивно-оценочная часть




 Квадратным уравнением называется уравнение видагде х- переменная, а, в, с-некоторые числа, причем а≠0
Квадратным уравнением называется уравнение видагде х- переменная, а, в, с-некоторые числа, причем а≠0




 Используя нулевое свойство умножения, вы определяете, что x — 2 = 0 и x = 2. Вы также получаете x 2 + 25 = 0 и x 2 = –25. Извлеките квадратный корень из каждой стороны и получим
Используя нулевое свойство умножения, вы определяете, что x — 2 = 0 и x = 2. Вы также получаете x 2 + 25 = 0 и x 2 = –25. Извлеките квадратный корень из каждой стороны и получим


 2.Это уравнение должно быть меньше или равно четырем, чтобы успешно создать коробку с этими ограничениями.
2.Это уравнение должно быть меньше или равно четырем, чтобы успешно создать коробку с этими ограничениями. Используйте уравнение скорости, которое вычисляет высоту мяча на основе параболического или квадратного уравнения.2. Если руки вашей подруги тоже на высоте 3 метра, сколько секунд потребуется мячу, чтобы добраться до нее? Чтобы ответить на этот вопрос, задайте уравнение равным 3 = h и решите относительно t. Ответ составляет примерно 2,8 секунды.
Используйте уравнение скорости, которое вычисляет высоту мяча на основе параболического или квадратного уравнения.2. Если руки вашей подруги тоже на высоте 3 метра, сколько секунд потребуется мячу, чтобы добраться до нее? Чтобы ответить на этот вопрос, задайте уравнение равным 3 = h и решите относительно t. Ответ составляет примерно 2,8 секунды. Общее время равно 3 часам, который равен времени подъема вверх по течению плюс времени спуска вниз, и оба расстояния составляют 15 км.2 — 30x -12 = 0. Решая для x, мы знаем, что каякер двигал каяк со скоростью 10,39 км в час.
Общее время равно 3 часам, который равен времени подъема вверх по течению плюс времени спуска вниз, и оба расстояния составляют 15 км.2 — 30x -12 = 0. Решая для x, мы знаем, что каякер двигал каяк со скоростью 10,39 км в час. Пропорционально мониторы выглядят очень похожими. Если пространство ограничено, и нам нужен максимально большой монитор, как нам решить, какой из них выбрать? В этом разделе мы узнаем, как решать такие проблемы, используя четыре разных метода.{2} -4 = 0 [/ latex] — квадратные уравнения. Они используются бесчисленным количеством способов в области инженерии, архитектуры, финансов, биологии и, конечно же, математики.
Пропорционально мониторы выглядят очень похожими. Если пространство ограничено, и нам нужен максимально большой монитор, как нам решить, какой из них выбрать? В этом разделе мы узнаем, как решать такие проблемы, используя четыре разных метода.{2} -4 = 0 [/ latex] — квадратные уравнения. Они используются бесчисленным количеством способов в области инженерии, архитектуры, финансов, биологии и, конечно же, математики. Другими словами, если произведение двух чисел или двух выражений равно нулю, то одно из чисел или одно из выражений должно равняться нулю, потому что ноль, умноженный на что-либо, равен нулю.
Другими словами, если произведение двух чисел или двух выражений равно нулю, то одно из чисел или одно из выражений должно равняться нулю, потому что ноль, умноженный на что-либо, равен нулю. {2} [/ latex], равно 1. У нас есть один метод разложения квадратных уравнений на множители в этой форме.
{2} [/ latex], равно 1. У нас есть один метод разложения квадратных уравнений на множители в этой форме. Обратите внимание, что подойдет только одна пара чисел.Затем запишите факторы.
Обратите внимание, что подойдет только одна пара чисел.Затем запишите факторы. Мы можем использовать методы решения квадратных уравнений, которые мы узнали в этом разделе, чтобы найти недостающую сторону.{2} = 128 \ hfill \\ a = \ sqrt {128} \ hfill \\ a = 8 \ sqrt {2} \ hfill \ end {array} [/ latex]
Мы можем использовать методы решения квадратных уравнений, которые мы узнали в этом разделе, чтобы найти недостающую сторону.{2} = 128 \ hfill \\ a = \ sqrt {128} \ hfill \\ a = 8 \ sqrt {2} \ hfill \ end {array} [/ latex] Хотя квадратная формула работает с любым квадратным уравнением в стандартной форме, легко сделать ошибку, подставляя значения в формулу. Будьте внимательны при замене и используйте круглые скобки при вставке отрицательного числа.{2} — \ left (4 \ right) \ cdot \ left (1 \ right) \ cdot \ left (2 \ right)}} {2 \ cdot 1} \ hfill \\\ hfill & = \ frac {-1 \ pm \ sqrt {1–8}} {2} \ hfill \\ \ hfill & = \ frac {-1 \ pm \ sqrt {-7}} {2} \ hfill \\\ hfill & = \ frac {-1 \ pm я \ sqrt {7}} {2} \ hfill \ end {array} [/ latex]
Хотя квадратная формула работает с любым квадратным уравнением в стандартной форме, легко сделать ошибку, подставляя значения в формулу. Будьте внимательны при замене и используйте круглые скобки при вставке отрицательного числа.{2} — \ left (4 \ right) \ cdot \ left (1 \ right) \ cdot \ left (2 \ right)}} {2 \ cdot 1} \ hfill \\\ hfill & = \ frac {-1 \ pm \ sqrt {1–8}} {2} \ hfill \\ \ hfill & = \ frac {-1 \ pm \ sqrt {-7}} {2} \ hfill \\\ hfill & = \ frac {-1 \ pm я \ sqrt {7}} {2} \ hfill \ end {array} [/ latex]
Leave A Comment