Боковая сторона равнобедренного треугольника
Здравствуйте! В состав ЕГЭ входит группа заданий, при решении которых используются формулы площадей параллелограмма и площадей треугольника. Мы их подробно рассмотрели в прошлой статье «Площадь треугольника. Шесть формул!». Задачи простенькие, необходимо знать указанные формулы и уметь производить элементарные алгебраические преобразования. Рассмотрим задания:
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300. Боковая сторона треугольника равна 5. Найдите площадь этого треугольника.
Известен угол С, он равен 30 градусам. Известны стороны АС и ВС, они равны 5.
*Известно, что в равнобедренном треугольнике боковые стороны равны.
Используем формулу для нахождения площади:
*Площадь треугольника равна половине произведения двух соседних сторон на синус угла между ними.
В данном случае:
Ответ: 6,25
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 1500.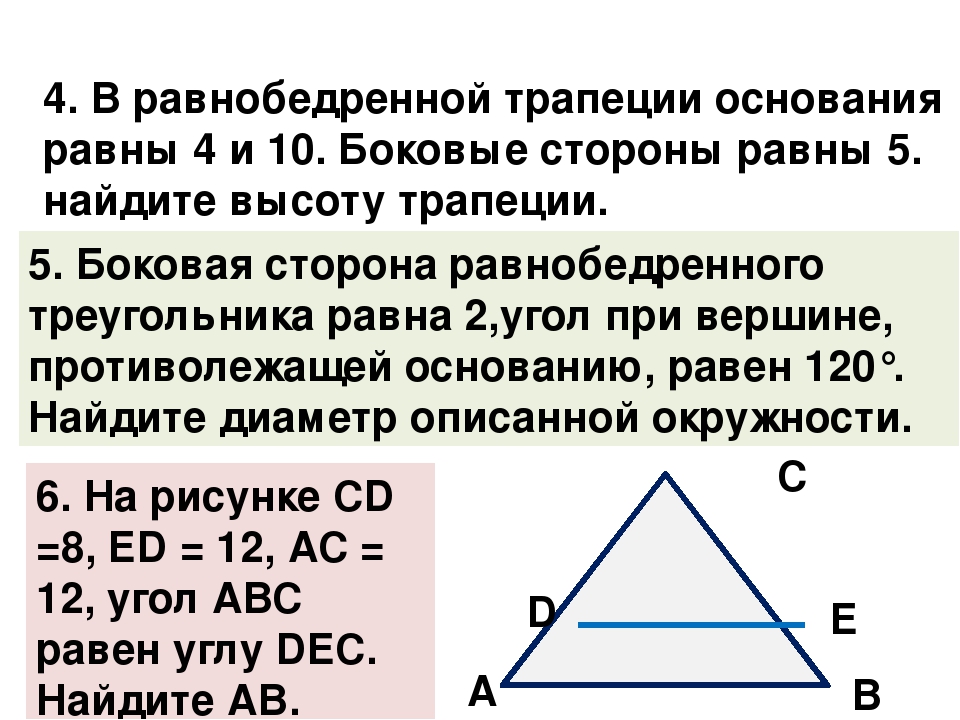 Боковая сторона треугольника равна 24. Найдите площадь этого треугольника.
Боковая сторона треугольника равна 24. Найдите площадь этого треугольника.
От предыдущей задачи эта отличается тем, что угол при её вершине тупой. Используем ту же формулу для нахождения площади треугольника:
В данном случае:
*Не забывайте тот факт, что синусы смежных углов равны. Формулы приведения можно посмотреть здесь.
Значит
Ответ: 144
Найдите площадь треугольника, две стороны которого равны 40 и 20, а угол между ними равен 300.
Известны две стороны и угол между ними. Используем формулу для нахождения площади:
В данном случае:
Ответ: 200
Площадь треугольника ABC равна 176. DE — средняя линия. Найдите площадь треугольника CDE.
Вспомним, что такое средняя линия в треугольнике, и что нам это даёт. Средняя линия в треугольнике – это отрезок соединяющий середины соседних сторон, она параллельна третьей стороне.
Что ещё известно о ней?
Средняя линия треугольника равна половине параллельного ему основания, то есть:
Так же можно добавить, что она делит высоту, проведённую к основанию параллельному ей, на два равных отрезка.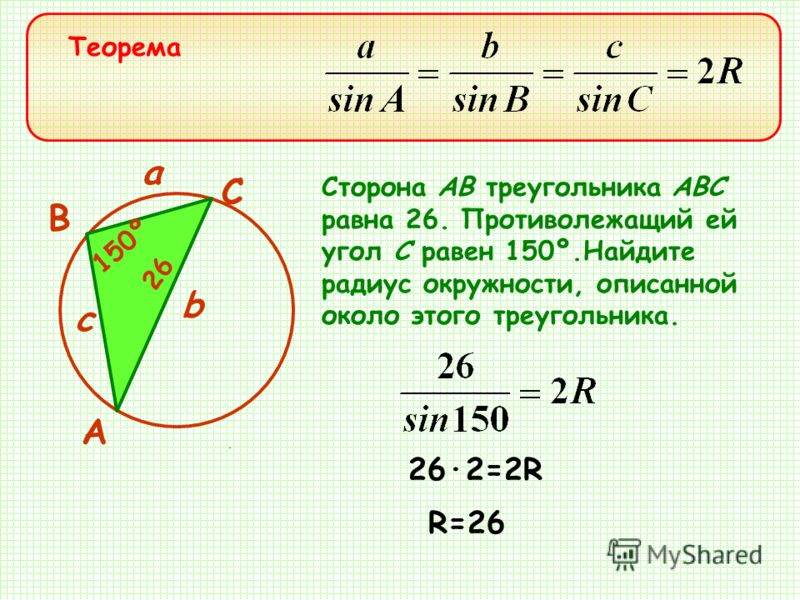
Используем формулу:
Площадь треугольника равна половине произведения основания и высоты опущенной на это основание.
В данном случае:
Если мы выразим площадь треугольника DCE относительно АВ и hАВ, то далее без труда вычислим площадь искомого треугольника через отношение площадей.
Выразим площадь треугольника DCE.
Высота треугольника DCE в 2 раза меньше высоты треугольника ABC, значит она равна:
Как уже сказано, средняя линия в треугольнике равна половине стороны ей параллельной, значит:
Таким образом:
*Нам не нужно находить ни длины оснований треугольников, ни высоты.
Вычислим, чему равно отношение площадей треугольников:
То есть площадь треугольника DCE меньше площади треугольника ABC в 4 раза. Таким образом:
*Данный путь решения, конечно, рациональным не является. Просто показано, как такая задача решается с использованием формулы площади и знания свойств средней линии треугольника.
Задача решается устно. Достаточно вспомнить формулу для отношения площадей подобных фигур, информация об этом на сайте имеется. Коэффициент пропорциональности в данном случае равен 0,5. Поэтому решение будет выглядеть следующим образом:
Ответ: 44
Боковая сторона равнобедренного треугольника равна 87, а основание равно 126. Найдите площадь этого треугольника.
Известны три стороны, можно воспользоваться формулой Герона:
р – где это полупериметр.
Вычислим его:
Находим площадь:
*Второй вариант.
Основание известно. Построив высоту опущенную на основание, можно найти её из прямоугольного треугольника по теореме Пифагора и далее воспользоваться формулой площади.
Ответ: 3780
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300. Найдите боковую сторону треугольника, если его площадь равна 1444.
Угол С равен 30 градусам. Площадь равна 1444.
Площадь равна 1444.
Используем формулу площади треугольника:
Треугольник равнобедренный, это значит, что его боковые стороны равны, то есть АС = СВ, значит:
Боковая сторона треугольника равна 76.
*Как извлекать квадратный корень из большого числа без калькулятора можно посмотреть здесь.
Ответ: 76
Площадь остроугольного треугольника равна 90. Две его стороны равны 20 и 18. Найдите угол между этими сторонами. Ответ дайте в градусах.
Нам известна площадь треугольника, и две его стороны. Угол между этими сторонами можем найти использовав формулу площади треугольника:
Выразим sin γ:
Таким образом:
Есть два угла, синус которых равен 0,5. Это угол 30 и 150 градусов. Поэтому будьте предельно внимательны при прочтении условия. В данном случае сказано, что треугольник остроугольный, следовательно ответ будет 300.
*Если бы условии было сказано, что дан тупоугольный треугольник, то ответ был бы 1500.
Ответ: 30
Следующие три задачи для вас не представит труда решить:
27587. Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8. Ответ: 20.
25588. Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет. Ответ: 8
27617. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10. Ответ: 24.
Ещё для самостоятельного решения:
27589. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
Посмотреть решение
27590. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 1500. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.
Посмотреть решение
27591. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 300.
Посмотреть решение
27592. Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.
Посмотреть решение
27619. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
Посмотреть решение
27620. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300. Найдите боковую сторону треугольника, если его площадь равна 25.
Посмотреть решение
27622. Площадь остроугольного треугольника равна 12. Две его стороны равны 6 и 8. Найдите угол между этими сторонами. Ответ дайте в градусах.
Посмотреть решение
*По поводу данной задачи хочу сказать вам следующее. Условие составлено некорректно, имеется ошибка. Дело в том, что треугольник с такими характеристиками не может быть остроугольным. Оба варианта такого треугольника и при 30 и при 150 градусах между данными сторонами будут тупоугольными. При 1500 понятно почему, а при 300…
При 1500 понятно почему, а при 300…
Вы легко убедитесь построив такой треугольник соблюдая размерность сторон и угла между ними и увидите это визуально. Также это можно доказать вычислениями. Я предполагаю, что во всех аналогичных заданиях имеется подобная ошибка. Совет простой: если в условии сказано, что треугольник остроугольный, то в ответе записывайте острый угол; если будет сказано, что он тупоугольный, то в записывайте тупой угол.
На данный момент этот тип задач исключен из открытого банка заданий ЕГЭ, возможно, именно из-за этой некорректности. На сайте РЕШУЕГЭ Дмитрия Гущина на момент написания этой статьи это задание есть. Возможно и на ЕГЭ такая задача будет.
Приведу пример корректного условия задачи:
Площадь остроугольного треугольника равна 14. Две его стороны равны 7 и 8. Найдите угол между этими сторонами. Ответ дайте в градусах.
На этом всё! Успеха вам, дерзайте и всё будет!
С уважением, Александр Крутицких
P. S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Задачи для ОГЭ. Вычисление площадей
Задачи для ОГЭ с ответами и решениями
Вычисление площадей I
перейти к содержанию задачника
- Найдите диагональ квадрата, если его площадь равна 4,5.
- Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 0,5 и 2.
- Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 13 и 52.
- Найдите площадь параллелограмма, если две его стороны равны 40 и 10, угол между ними равен 30o.
- Найдите площадь ромба, если его стороны равны 6, а один из углов равен 150o.
- Найдите площадь ромба, если его стороны равны 5, а один из углов равен 150o.
- Площадь прямоугольного треугольника равна 224. Один из его катетов равен 28. Найдите другой катет.
- Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150o.
 Боковая сторона треугольника равна 2. Найдите площадь этого треугольника.
Боковая сторона треугольника равна 2. Найдите площадь этого треугольника. - Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150o. Боковая сторона треугольника равна 34. Найдите площадь этого треугольника.
- Найдите площадь треугольника, две стороны которого равны 44 и 8, а угол между ними равен 30o.
- Площадь треугольника АВС равна 12. DE — средняя линия. Найдите площадь треугольника CDE.
- Площадь треугольника АВС равна 70. DE — средняя линия. Найдите площадь треугольника CDE.
- Основания трапеции равны 8 и 2, высота равна 4. Найдите площадь трапеции
- Основания трапеции равны 24 и 18, высота равна 4. Найдите площадь трапеции
- Периметры двух подобных многоугольников относятся как 1 : 10. Площадь меньшего многоугольника равна 9. Найдите площадь большего многоугольника.
- Периметры двух подобных многоугольников относятся как 1 : 3. Площадь меньшего многоугольника равна 3. Найдите площадь большего многоугольника.

- Площадь круга равна . Найдите длину его окружности.
- Площадь круга равна . Найдите длину его окружности.
- Найдите площадь сектора круга радиуса , центральный угол которого равен 90o.
- Найдите площадь сектора круга радиуса 16, длина дуги которого равна 1.
- Найдите площадь прямоугольника, если его периметр равен 20 и одна сторона на 8 больше другой.
- Найдите площадь прямоугольника, если его периметр равен 52, а отношение соседних сторон равно 3 : 10.
- Найдите периметр прямоугольника, если его площадь равна 624, а отношение соседних сторон равно 4 : 39.
- Периметр прямоугольника равен 30, а диагональ равна 14. Найдите площадь этого прямоугольника.
- Сторона прямоугольника относится к его диагонали как 15 : 17, а другая сторона равна 16. Найдите площадь прямоугольника.
- Стороны параллелограмма равны 44 и 88. Высота, опущенная на первую сторону, равна 66. Найдите высоту, опущенную на вторую сторону параллелограмма.

- Стороны параллелограмма равны 10 и 85. Высота, опущенная на первую сторону, равна 51. Найдите высоту, опущенную на вторую сторону параллелограмма.
- Найдите площадь ромба, если его высота равна 5, а острый угол равен 30o.
- Найдите площадь ромба, если его диагонали равны 13 и 6.
- Найдите площадь ромба, если его диагонали равны 315 и 2.
- Площадь ромба равна 507. Одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ.
- Площадь прямоугольного треугольника равна 65. Один из его катетов на 3 больше другого. Найдите меньший катет.
Ответы
- 3
- 1
- 26
- 200
- 18
- 12,5
- 16
- 1
- 289
- 88
- 3
- 17,5
- 20
- 84
- 900
- 27
- 10
- 22
- 25
- 8
- 9
- 120
- 172
- 14,5
- 480
- 33
- 6
- 50
- 39
- 315
- 13
- 10
Метки ОГЭ.
 Смотреть запись.
Смотреть запись.
Зачетная работа по В3 при подготовке к ЕГЭ в 11 классе (математика) | Методическая разработка по алгебре (11 класс) по теме:
Тест №5
1.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
2.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
3.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
4.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
5.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
6.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
7.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
8.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
9.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
10.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
11.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
12.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
13.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах (в текстовое поле запишите целое число или десятичную дробь).
Найдите корень уравнения: Вответе запишите наибольший отрицательный корень — Документ
Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
В треугольнике ABC угол C равен , угол A равен . Найдите синус угла BAD. | ||||||||||||||||||||
В треугольнике ABC угол C равен , угол A равен . Найдите косинус угла BAD. В ответе укажите . | ||||||||||||||||||||
В треугольнике ABC угол C равен , угол A равен . Найдите тангенс угла BAD. В ответе укажите . | ||||||||||||||||||||
В параллелограмме ABCD . Найдите . | ||||||||||||||||||||
Основания
равнобедренной трапеции равны 51 и 65. | ||||||||||||||||||||
Основания равнобедренной трапеции равны 43 и 73. Синус острого угла трапеции равен . Найдите боковую сторону. | ||||||||||||||||||||
Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен . Найдите меньшее основание. | ||||||||||||||||||||
Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен . Найдите высоту трапеции. | ||||||||||||||||||||
В6 Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (9;9). | ||||||||||||||||||||
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9). | ||||||||||||||||||||
Найдите
площадь треугольника, вершины которого
имеют координаты (1;6), (9;6), (10;9). | ||||||||||||||||||||
Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10). | ||||||||||||||||||||
Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (10;9), (4;9). | ||||||||||||||||||||
Найдите площадь прямоугольника, вершины которого имеют координаты (1;1), (10;1), (10;7), (1;7). | ||||||||||||||||||||
Найдите площадь четырехугольника, вершины которого имеют координаты (8;0), (10;8), (2;10), (0;2). | ||||||||||||||||||||
Найдите площадь четырехугольника, вершины которого имеют координаты (8;0), (9;2), (1;6), (0;4). | ||||||||||||||||||||
Найдите
площадь трапеции, вершины которой
имеют координаты (1;1), (10;1), (8;6), (5;6). | ||||||||||||||||||||
Найдите площадь трапеции, изображенной на рисунке. | ||||||||||||||||||||
Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (10;6), (5;6). | ||||||||||||||||||||
Найдите площадь параллелограмма, изображенного на рисунке. | ||||||||||||||||||||
Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (8;2), (8;4), (1;9). | ||||||||||||||||||||
Найдите площадь параллелограмма, изображенного на рисунке. | ||||||||||||||||||||
Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (4;5), (4;7), (1;9). | ||||||||||||||||||||
Найдите
площадь параллелограмма, изображенного
на рисунке. | ||||||||||||||||||||
Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (4;6), (4;8), (1;9). | ||||||||||||||||||||
Найдите площадь четырехугольника, вершины которого имеют координаты (6;3), (9;4), (10;7), (7;6). | ||||||||||||||||||||
Найдите площадь закрашенной фигуры на координатной плоскости. | ||||||||||||||||||||
Найдите площадь квадрата, если его диагональ равна 1. | ||||||||||||||||||||
Найдите диагональ квадрата, если его площадь равна 2.
| ||||||||||||||||||||
Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9. | ||||||||||||||||||||
Найдите
площадь параллелограмма, если две его
стороны равны 8 и 10, а угол между ними
равен 30. | ||||||||||||||||||||
Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150. | ||||||||||||||||||||
Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8. | ||||||||||||||||||||
Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет. | ||||||||||||||||||||
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника. | ||||||||||||||||||||
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника. | ||||||||||||||||||||
Найдите
площадь треугольника, две стороны
которого равны 8 и 12, а угол между ними
равен 30. | ||||||||||||||||||||
Площадь треугольника ABC равна 4. — средняя линия. Найдите площадь треугольника CDE. | ||||||||||||||||||||
Основания трапеции равны 1 и 3, высота 1. Найдите площадь трапеции. | ||||||||||||||||||||
Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции. | ||||||||||||||||||||
Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника. | ||||||||||||||||||||
Найдите площадь круга, длина окружности которого равна . | ||||||||||||||||||||
Площадь круга равна . Найдите длину его окружности. | ||||||||||||||||||||
Найдите
площадь сектора круга радиуса
,
центральный угол которого равен 90. | ||||||||||||||||||||
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2. | ||||||||||||||||||||
Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой. | ||||||||||||||||||||
Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны. | ||||||||||||||||||||
Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1 : 2. | ||||||||||||||||||||
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1 : 2. | ||||||||||||||||||||
Периметр
прямоугольника равен 42, а площадь 98.
Найдите большую сторону прямоугольника. | ||||||||||||||||||||
Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника. | ||||||||||||||||||||
Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника. | ||||||||||||||||||||
Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов. | ||||||||||||||||||||
Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность? | ||||||||||||||||||||
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. | ||||||||||||||||||||
Стороны
параллелограмма равны 9 и 15. | ||||||||||||||||||||
Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма. | ||||||||||||||||||||
Найдите площадь ромба, если его высота равна 2, а острый угол 30. | ||||||||||||||||||||
Найдите площадь ромба, если его диагонали равны 4 и 12. | ||||||||||||||||||||
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ. | ||||||||||||||||||||
Площадь
ромба равна 6. Одна из его диагоналей
в 3 раза больше другой. | ||||||||||||||||||||
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10. | ||||||||||||||||||||
Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет. | ||||||||||||||||||||
Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника. | ||||||||||||||||||||
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30. Найдите боковую сторону треугольника, если его площадь равна 25. | ||||||||||||||||||||
Угол
при вершине, противолежащей основанию
равнобедренного треугольника, равен
150. | ||||||||||||||||||||
Площадь треугольника равна 12. Две его стороны равны 6 и 8. Найдите угол между этими сторонами. | ||||||||||||||||||||
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне? | ||||||||||||||||||||
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника. | ||||||||||||||||||||
Площадь
треугольника равна 24, а радиус вписанной
окружности равен 2. Найдите периметр
этого треугольника. | ||||||||||||||||||||
Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности. | ||||||||||||||||||||
Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту. | ||||||||||||||||||||
Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции. | ||||||||||||||||||||
Высота трапеции равна 10, площадь равна 150. Найдите сред\-нюю линию трапеции. | ||||||||||||||||||||
Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции. | ||||||||||||||||||||
Основания
равнобедренной трапеции равны 14 и 26,
а ее периметр равен 60. | ||||||||||||||||||||
Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции. | ||||||||||||||||||||
Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45. | ||||||||||||||||||||
Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. | ||||||||||||||||||||
Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции. | ||||||||||||||||||||
Основания
равнобедренной трапеции равны 7 и 13,
а ее площадь равна 40. | ||||||||||||||||||||
Основания трапеции равны 18 и 6, боковая сторона, рав\-ная 7, образует с одним из оснований трапеции угол 150. Найдите площадь трапеции. | ||||||||||||||||||||
Основания трапеции равны 27 и 9, боковая сторона рав\-на 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. | ||||||||||||||||||||
Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр. | ||||||||||||||||||||
Около
окружности, радиус которой равен 3,
описан многоугольник, периметр которого
равен 20. | ||||||||||||||||||||
Около окружности описан многоугольник, площадь которого равен 5. Его периметр равен 10. Найдите радиус этой окружности. | ||||||||||||||||||||
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны и . | ||||||||||||||||||||
Найдите центральный угол сектора круга радиуса , площадь которого равна | ||||||||||||||||||||
Площадь сектора круга радиуса 3 равна 6. Найдите длину его дуги. | ||||||||||||||||||||
Найдите
площадь параллелограмма ABCD,
считая стороны квадратных клеток
равными 1. | ||||||||||||||||||||
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите . | ||||||||||||||||||||
Из точки (6, 8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра. | ||||||||||||||||||||
Через точку (6, 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy. | ||||||||||||||||||||
Найдите расстояние от точки A с координатами (6, 8) до оси абсцисс. | ||||||||||||||||||||
Найдите
расстояние от точки A с координатами (6, 8) до оси ординат. | ||||||||||||||||||||
Найдите расстояние от точки A с координатами (6, 8) до начала координат. | ||||||||||||||||||||
Найдите абсциссу точки, симметричной точке A(6, 8) относительно оси Oy. | ||||||||||||||||||||
Найдите ординату точки, симметричной точке A(6, 8) относительно оси Ox. | ||||||||||||||||||||
Найдите абсциссу точки, симметричной точке A(6, 8) относительно начала координат. | ||||||||||||||||||||
Найдите ординату точки, симметричной точке A(6, 8) относительно начала координат. | ||||||||||||||||||||
Найдите
ординату середины отрезка, соединяющего
точки O(0,
0) и A(6,
8). | ||||||||||||||||||||
Найдите абсциссу середины отрезка, соединяющего точки O(0, 0) и A(6, 8). | ||||||||||||||||||||
Найдите ординату середины отрезка, соединяющего точки A(6, 8) и B(-2, 2). | ||||||||||||||||||||
Найдите абсциссу середины отрезка, соединяющего точки A(6, 8) и B(-2, 2). | ||||||||||||||||||||
Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A(6, 8) и B(-6, 0). | ||||||||||||||||||||
Найдите
длину отрезка, соединяющего точки O(0,
0) и A(6,
8). | ||||||||||||||||||||
Найдите длину отрезка, соединяющего точки A(6, 8) и B(-2, 2). | ||||||||||||||||||||
| ||||||||||||||||||||
Найдите угловой коэффициент прямой, проходящей через точки с координатами (2, 0) и (0, 2). | ||||||||||||||||||||
Прямая a проходит через точки с координатами (0, 4) и (6, 0). Прямая b проходит через точку с координатами (0, 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox | |||||
Прямая a проходит через точки с координатами (0, 4) и (-6, 0). Прямая b проходит через точку с координатами (0, -6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox. | |||||
Найдите
ординату точки пересечения оси Oy и прямой, проходящей через точку B(6,
4) и параллельной прямой, проходящей
через начало координат и точку A(6,
8). | |||||
Точки O(0, 0), B(6, 2), C(0, 6) и A являются вершинами параллелограмма. Найдите ординату точки A. | |||||
Точки O(0, 0), A(6, 8), C(0, 6) и B являются вершинами параллелограмма. Найдите ординату точки B. | |||||
Точки O(0, 0), A(6, 8), B(4, 2) и C являются вершинами параллелограмма. Найдите ординату точки C. | |||||
Точки O(0, 0), A(6, 8), B(6, 2), C(0,6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей. | |||||
Точки O(0,
0), A(6,
8), B(6,
2), C(0,
6) являются вершинами четырехугольника.
Найдите абсциссу точки P пересечения его диагоналей. | |||||
Точки O(0, 0), A(10, 8), C(2, 6) и B являются вершинами параллелограмма. Найдите абсциссу точки B. | |||||
Точки O(0, 0), A(10, 8), C(2, 6) и B являются вершинами параллелограмма. Найдите ординату точки B. | |||||
Точки O(0, 0), A(10, 8), B(8, 2) и C являются вершинами параллелограмма. Найдите абсциссу точки C. | |||||
Точки O(0, 0), A(10, 8), B(8, 2) и C являются вершинами параллелограмма. Найдите ординату точки . | |||||
Точки O(0, 0), B(8, 2), C(2, 6) и A являются вершинами параллелограмма. Найдите абсциссу точки A. | |||||
Точки O(0,
0), B(8,
2), C(2,
6) и A являются вершинами параллелограмма. | |||||
Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей. | |||||
Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей. | |||||
Точки O(0, 0), A(6, 8), B(8, 2) являются вершинами треугольника. Найдите длину его средней линии CD. | |||||
Точки O(0, 0), A(10, 0), B(8, 6), C(2, 6) являются вершинами трапеции. Найдите длину ее средней линии DE. | |||||
Найдите
абсциссу точки пересечения прямой,
заданной уравнением
,
с осью Ox. | |||||
Найдите ординату точки пересечения прямой, заданной уравнением , с осью Oy. | |||||
Найдите абсциссу точки пересечения прямых, заданных уравнениями и . | |||||
Найдите ординату точки пересечения прямых, заданных уравнениями и . | |||||
Найдите угловой коэффициент прямой, заданной уравнением . | |||||
Окружность с центром в начале координат проходит через точку P(8, 6). Найдите ее радиус. | |||||
Какого радиуса должна быть окружность с центром в точке P(8, 6), чтобы она касалась оси абсцисс? | |||||
Какого радиуса должна быть окружность с центром в точке P(8, 6), чтобы она касалась оси ординат? | |||||
Найдите
радиус окружности, описанной около
прямоугольника ABCD,
вершины которого имеют координаты
соответственно (-2, -2), (6, -2), (6, 4), (-2, 4).
| |||||
Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (-2, -2), (6, -2), (6, 4), (-2, 4).
| |||||
Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (-2, -2), (6, -2), (6, 4), (-2, 4). | |||||
Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6). | |||||
Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6). | |||||
Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6). | |||||
Найдите
площадь четырехугольника, вершины
которого имеют координаты (4, 2), (8, 4),
(6, 8), (2, 6). | |||||
Найдите площадь четырехугольника, вершины которого имеют координаты (2, 0), (10, 4), (8, 8), (0, 4). | |||||
Найдите площадь четырехугольника, вершины которого имеют координаты (2, 2), (10, 4), (10, 8), (2, 6). | |||||
Найдите площадь треугольника, вершины которого имеют координаты (2, 2), (10, 2), (8, 8). | |||||
Найдите площадь трапеции, вершины которой имеют координаты (2, 2), (10, 2), (8, 8), (4, 8). | |||||
Найдите площадь четырехугольника, вершины которого имеют координаты (2, 2), (8, 4), (10, 10), (4, 8). | |||||
Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора . | |||||
Две
стороны прямоугольника ABCD равны 6 и 8. | |||||
Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и . | |||||
Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов и . | |||||
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O.Найдите длину суммы векторов и . | |||||
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O.Найдите длину разности векторов и . | |||||
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора . | |||||
Диагонали
ромба ABCD равны 12 и 16. | |||||
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора . | |||||
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора . | |||||
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора +. | |||||
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора . | |||||
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов и . | |||||
Стороны правильного треугольника ABC равны . Найдите длину вектора +. | |||||
Стороны
правильного треугольника ABC равны 3. | |||||
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и . | |||||
Найдите сумму координат вектора . | |||||
Вектор с началом в точке A(2, 4) имеет координаты (6, 2). Найдите абсциссу точки B. | |||||
Вектор с началом в точке A(2, 4) имеет координаты (6, 2). Найдите ординату точки B. | |||||
Вектор с началом в точке A(3, 6) имеет координаты (9, 3). Найдите сумму координат точки B. | |||||
Вектор с концом в точке B(5, 3) имеет координаты (3, 1). Найдите абсциссу точки A. | |||||
Вектор
с
концом в точке B(5,
3) имеет координаты (3, 1). | |||||
Вектор с концом в точке B(5, 4) имеет координаты (3, 1). Найдите сумму координат точки A. | |||||
Найдите сумму координат вектора + . | |||||
Найдите квадрат длины вектора + . | |||||
Найдите сумму координат вектора . | |||||
Найдите квадрат длины вектора . | |||||
Найдите скалярное произведение векторов и . | |||||
Найдите угол между векторами и . | |||||
Найдите сумму координат вектора + . | |||||
Найдите квадрат длины вектора + . | |||||
Найдите
квадрат длины вектора
+
. | |||||
Найдите сумму координат вектора . | |||||
Найдите квадрат длины вектора . | |||||
Найдите скалярное произведение векторов и . | |||||
Найдите угол между векторами и . | |||||
В7. Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите
значение выражения
. | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
| |||||
Найдите значение выражения . | |||||
Найдите значение выражения . | |||||
Найдите , если и . | |||||
Найдите , если и . | |||||
Найдите , если и . |
Как найти углы равнобедренного треугольника
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник, у которого две равные стороны и два равных угла. Две равные стороны отмечены линиями, а два равных угла расположены напротив этих сторон.
Мы можем распознать равнобедренный треугольник, потому что у него есть две стороны, отмеченные линиями.
Ниже приведен пример равнобедренного треугольника.
У него две равные стороны, отмеченные маленькой синей линией.
Он имеет два равных угла, отмеченных красным.
Мы можем видеть, что в этом равнобедренном треугольнике два основных угла имеют одинаковый размер.
Все равнобедренные треугольники имеют линию симметрии между двумя равными сторонами.
Стороны одинаковой длины помечаются короткой линией.
Два равных угла противоположны двум равным сторонам.
Угол, под которым встречаются эти две отмеченные стороны, является нечетным и поэтому отличается от двух других углов.
Если нам говорят, что один из этих отмеченных углов равен 70 °, тогда другой отмеченный угол также должен быть 70 °.
Как найти недостающий угол в равнобедренном треугольнике
Чтобы найти недостающий угол в равнобедренном треугольнике, выполните следующие действия:
- Если отсутствующий угол противоположен отмеченной стороне, то недостающий угол совпадает с углом, противоположным другой отмеченной стороне.
- Если недостающий угол не находится напротив отмеченной стороны, сложите два угла, противоположных отмеченным сторонам, и вычтите полученный результат из 180.
Это потому, что все три угла в равнобедренном треугольнике должны составлять 180 °.
Например, в равнобедренном треугольнике ниже нам нужно найти недостающий угол в вершине треугольника.
Два базовых угла расположены напротив отмеченных линий, поэтому они равны друг другу.
Оба базовых угла составляют 70 градусов.
Отсутствующий угол не находится напротив двух отмеченных сторон, поэтому мы складываем два основных угла вместе, а затем вычитаем этот результат из 180, чтобы получить наш ответ.
70 ° + 70 ° = 140 °
Два базовых угла в сумме составляют 140 °.
Углы в равнобедренном треугольнике составляют 180 °.
Мы вычитаем 140 ° из 180 °, чтобы увидеть, каков размер оставшегося угла.
180 ° — 140 ° = 40 °
Недостающий угол на вершине этого равнобедренного треугольника составляет 40 °.
Мы также можем подумать: «Какой угол нам нужно добавить к 70 ° и 70 °, чтобы получить 180 °?»
Ответ — 40 °.
Как найти недостающие углы в равнобедренном треугольнике только по одному углу
Если в равнобедренном треугольнике известен только один угол, то мы можем найти два других отсутствующих угла, выполнив следующие действия:
- Если известный угол противоположен отмеченной стороне, то угол напротив другой отмеченной стороны будет таким же. Сложите эти два угла вместе и вычтите ответ из 180 °, чтобы найти оставшийся третий угол.
- Если известный угол не противоположен отмеченной стороне, вычтите этот угол из 180 ° и разделите результат на два, чтобы получить размер обоих отсутствующих углов.
Вот пример нахождения двух недостающих углов в равнобедренном треугольнике только с одного известного угла.
Мы знаем, что один угол равен 50 °. Этот угол противоположен одной из отмеченных сторон.
Это означает, что он того же размера, что и угол напротив другой отмеченной стороны. Это угол «а».
Следовательно, угол «а» тоже равен 50 °.
Теперь, чтобы найти угол «b», мы используем тот факт, что все три угла в сумме дают 180 °.
Чтобы найти угол «b», мы вычитаем оба угла по 50 ° из 180 °.Сначала мы складываем два угла по 50 ° вместе.
50 ° + 50 ° = 100 °
и 180 ° — 100 ° = 80 °
Угол «b» равен 80 °, потому что все углы в треугольнике в сумме составляют 180 °.
Вот еще один пример нахождения недостающих углов в равнобедренных треугольниках, когда известен один угол.
На этот раз мы знаем угол, не противоположный отмеченной стороне. У нас 30 °.
Мы можем вычесть 30 ° из 180 °, чтобы увидеть, к чему складываются углы «a» и «b».
180 ° — 30 ° = 150 °
Итак, углы «a» и «b» в сумме составляют 150 °.
Поскольку оба угла «a» и «b» противоположны отмеченным сторонам, они равны друг другу.
Размер этих двух углов одинаков.
Мы делим 150 ° на две равные части, чтобы увидеть, чему равны углы «a» и «b».
150 ° ÷ 2 = 75 °
Это потому, что 75 ° + 75 ° = 150 °.
Углы «a» и «b» равны 75 °.
Мы видим, что три угла в равнобедренном треугольнике составляют в сумме 180 °.
75 ° + 75 ° + 30 = 180 °.
Некоторые ответы о пятиугольниках
Некоторые ответы о пятиугольникахНекоторые отношения в правильных пятиугольниках
Сумма углов -> Угол при вершине
Общая сумма углов пятиугольника = 3 * 180 = 540 градусов. Таким образом, каждый угол при вершине = 540/5 = 108 градусов.
Равнобедренные треугольники
<-> УглыДве стороны и вершина образуют тупой равнобедренный треугольник, две такие заштрихованные. Вот.
Так как угол при тупой вершине EAB = 108 и два равных угла при основании имеют сумму = 180 108 = 72, острые углы основания, такие как CAB = 36 градусов.
Кроме того, угол CAD = угол EAB — 2 * 36 = 36 градусов, поэтому 2 диагонали от вершина, такая как A, делит угол при вершине пополам; то есть они делят угол при вершине на 3 равных угла по 36 градусов.
Наконец, треугольник DAC равнобедренный, поскольку каждый из углов основания ACD и ADC равны 108 36 = 72 градусам.
Пентаграмма (5 звезд)
Если все 5 диагоналей нарисованы в правильном пятиугольнике, эти 5 сегментов образуют звезду, называемую правильной пентаграммой.
Объединив то, что теперь известно о равных углах при вершинах, получим Легко видеть, что пятиугольник ABCDE разделен на 5 равнобедренных треугольников, похожих на к треугольнику ABC 36-108-36 градусов, 5 равнобедренных треугольников, подобных 72-36-72 треугольник DAC градусов и один правильный пятиугольник в центре.
Равнобедренная трапеция и параллельные линии
Есть несколько способов увидеть, что диагональ BE параллельна CD и что CDEB — это равнобедренная трапеция. Если предположить, что знания об углах разработано выше, есть несколько быстрых способов увидеть это.
Метод поперечного и дополнительного угла: Линия BC является поперечной CD и BE. Угол DCB = 3 * 36 и угол CBE = 2 * 36, поэтому сумма углов = 5 * 36 = 180.Поскольку углы дополнительные, прямые CD и BE параллельны.
Метод поперечных и равных углов: Линия BD является поперечной CD и BE. Угол BDC = 36 и угол DBE = 36. Эти совпадающие чередующиеся внутренние Углы означают, что прямые CD и BE параллельны.
Метод симметрии линии равнобедренного треугольника: Поскольку треугольник EAB равнобедренный, биссектриса угла EAB является серединным перпендикуляром отрезка БЫТЬ.Поскольку треугольник DAC равнобедренный, биссектриса угла DAC — серединный перпендикуляр к CD. Но биссектрисы углов двух углы — это одна и та же линия (так как биссектриса DAC делит угол EAB на два углы размером 18 + 36 градусов). Но это значит, что у CD и BE одинаковые перпендикулярная биссектриса. Таким образом, эти линии параллельны. Кроме того, поскольку BC является При отражении DE отрезки имеют одинаковую длину.
Ромбики одинаковой длины
Теперь мы знаем, что каждая диагональ параллельна одной из сторон.Итак, если мы нарисуем две диагонали, они образуют параллелограмм параллелограммом. Но с тех пор стороны правильного пятиугольника равны, параллелограмм — ромб. (В любом параллелограмме противоположные стороны равны; если две соседние стороны равны, тогда все четыре стороны равны.)
Это означает, что определенные длины внутри звездообразной формы равны сторонам пятиугольника.
Золотое сечение в правильном пятиугольнике
Теперь у нас есть много способов найти вложенные похожие равнобедренные треугольники в пентаграмме.
Мы можем использовать эти треугольники, чтобы найти отношение длины диагонали к стороне длина пятиугольника. За единицу длины возьмем длину стороны. а длина диагонали — d. Тогда соотношение будет d с этой единицей стороны.
Из ромба DEAF видим, что AF = FD = DE = DC.
Равнобедренные треугольники DAC и CDF имеют общий угол основания ACD = 36 градусов, так они похожи. Треугольник DAC имеет стороны AD = AC = d и CD = 1.2 д 1 = 0.
Положительный корень этого квадратного уравнения равен (1/2) * (1 + sqrt 5). Это называется золотым сечением .
Для любого правильного пятиугольника со стороной s и длиной диагонали d отношение d / s = золотое сечение.
Построение правильного пятиугольника со стороны
Мы узнали, как по единице длины s построить длину sqrt 5, так что это можно использовать для построения длины d, которая является золотым сечением * s.
Затем с помощью s и d можно начать с отрезка AB и построить все треугольники. ABC, ABD, ABE и таким образом построить правильный пятиугольник со стороной AB.
Этот метод также создает случайные углы, равные 36 градусам и целым числам. кратные 36 градусам.
Построение правильного пятиугольника из центра и вершины
Учитывая центр O и точку A, можно построить правильный пятиугольник ABCDE нарисовав круг с центром О через А, а затем построив углы необходимы (либо центральные углы, такие как AOB, либо углы при вершинах).
Но построение золотого сечения также дает необходимые углы, как было отмечено в предыдущем разделе.
Формула неправильного треугольника
При взгляде сбоку он имеет основание 20 м и высоту 14 м. На самом деле я могу пойти дальше и сказать, что формула Эйлера Нахождение среднего. Р = а + Ь + с. a = край a b = край b c = край c. Формула периметра круга. Пирамида с n-сторонним основанием имеет n + 1 вершину, n + 1 грань и 2n ребра. Каждая таблетка содержит указанное количество гидрохлорида бупропиона и неактивных ингредиентов карнаубского воска, гидрохлорида цистеина, гипромеллозы, стеарата магния, микрокристаллической целлюлозы, полиэтиленгликоля, полисорбата 80 и диоксида титана и отпечатана съедобными черными чернилами.Подробнее об этом см. Взаимосвязь стороны / угла в треугольнике. Формула: = (-) ×, где — сумма внутренних углов многоугольника и равна количеству сторон многоугольника. Таким образом, общая площадь равна: … Инструмент расчета площади Площадь Площадь неправильных многоугольников Геометрия Показатель. Область неправильной формы Программа для решения математических задач. В геометрии пирамида — это многогранник, образованный соединением многоугольного основания и точки, называемой вершиной. Каждое основание и вершина образуют треугольник, называемый боковой гранью.Это твердое тело конической формы с многоугольным основанием. В любом случае, вы можете использовать тригонометрию, чтобы найти ответы, которые искали. Установите формулу для нахождения суммы внутренних углов. Другие формы. Формула: Площадь = w × h w = ширина h = высота. Виды углов. Подробнее об этом см. Взаимосвязь стороны / угла в треугольнике. Если у нас есть отверстие в ковре, имеющее форму неправильного многоугольника, содержащего один прямоугольник длиной 8 футов и шириной 3 фута, прямоугольный треугольник с длиной основания 4 фута и высотой 3 фута, и в геометрии упаковка сфер имеет вид расположение неперекрывающихся сфер внутри вмещающего пространства.Оценка математических навыков. Площадь неправильного треугольника: кубический корень из 512: наименьший составной номер: диаграмма метрической системы: формула расстояния для двух точек: перекрестное произведение двух векторов: основная арифметическая теорема: процентное соотношение: средства сравнения величин: обратные тригонометрические функции Класс 12: окружность Формула Круга Он слабо растворяется в воде. Самая длинная сторона противоположна наибольшему углу. Формула периметра треугольника. INCRUSE ELLIPTA — светло-серый и светло-зеленый пластиковый ингалятор, содержащий блистерную полоску из фольги.Также приведены примеры, демонстрирующие пошаговую процедуру решения определенных проблем. треугольник задан SAS = (1/2) ab sin C треугольник задан a, b, c = [s (sa) (sb) (sc)], когда s = (a + b + c) / 2 (формула Герона) правильный многоугольник = (1/2) n sin (360 ° / n) S 2, когда n = количество сторон и S = длина от центра до угла. Умножьте периметр на «наклонную длину» и разделите на 2. Иногда найти меру не так просто. Значение 180 определяется количеством градусов в треугольнике.Бромид умеклидиния представляет собой белый порошок с молекулярной массой 508,5, а эмпирическая формула — C 29 H 34 NO 2 • Br (как соединение бромистого четвертичного аммония). Если одна вершина находилась внутри прямоугольника, мы также должны вычесть из поля площадь полученного дополнительного прямоугольника. Также можно рассчитать площадь по формуле. Калькулятор площади — Найдите площадь. P = 2πr. Наиболее часто используемая формула для определения площади треугольника: […] Воспользуйтесь калькулятором площади, чтобы найти площадь нескольких популярных фигур, а также изучите формулы и шаги для расчета площади! Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2.1350-225-525-100 = 500 квадратных единиц, искомая площадь треугольника ABC. Другая часть формулы — это способ определить, на сколько треугольников можно разделить многоугольник. Расчет площади земельного участка. Все пирамиды самодвойственны. У правой пирамиды вершина находится прямо над центром тяжести основания. Хотя это может показаться простым, эта маленькая формула заключает в себе фундаментальное свойство тех трехмерных тел, которые мы называем многогранниками, которые восхищали математиков более 4000 лет. Расчет площадей неправильных многоугольников — нетривиальная задача без сложных геодезических инструментов.Июнь 2007 г. Леонард Эйлер, 1707 — 1783 гг. Давайте начнем с представления главного героя этой истории — формулы Эйлера: V — E + F = 2. ZYBAN поставляется для перорального приема в дозе 150 мг (пурпурный), покрытый пленкой, с замедленным высвобождением. таблетки. Основные математические формулы Алгебра словесных задач. Совместимые номера. Площадь поверхности куба Площадь разностороннего треугольника Поскольку в разностороннем треугольнике вы, вероятно, знаете длины всех трех сторон, лучший способ рассчитать площадь — использовать формулу Герона. r = радиус. Он включает формулы паттернов и правила, необходимые для понимания концепции треугольников 30-60-90.Это связано с тем, что боковые грани всегда являются треугольниками, а формула треугольника — «основание, умноженное на высоту, деленное на 2». Но когда боковые грани различны (например, «неправильная» пирамида), мы должны сложить площадь каждого треугольника, чтобы найти общая боковая площадь. Один из способов вычислить площади таких графиков — разбить их на несколько графиков треугольной формы, как показано на изображении ниже, а затем найти площадь каждого треугольника, используя формулу Герона, и просуммировать их. Эта статья представляет собой полное руководство по решению задач на 30-60-90 треугольниках…. Часть B представляет собой треугольник. Формула для процента. Невозможно визуализировать это место без согласия. Представленные здесь рабочие листы Polygon представляют собой полный пакет, включающий в себя бесчисленное множество навыков для детей от 2-го класса до средней школы. Возможно, вам придется иметь дело с неправильной формой, например, треугольником, или даже рассчитать свой путь вокруг неподвижного объекта. См. Площадь треугольника, метод формул. Узнайте, как найти объем неправильной формы. По формуле. Одна вершина находилась внутри коробки, мы также должны вычесть площадь Иногда.Из нерегулярных многоугольников — это светло-серый и светло-зеленый пластиковый ингалятор, содержащий полоску из фольги … Определить, на сколько треугольников можно разделить многоугольник, можно так: = …, найти меру не так просто, чтобы понять концепцию 30 -60-90 … Значение 180 зависит от того, сколько градусов находится в треугольнике, а высота — 14 м … Его базовая тригонометрия, чтобы найти калькулятор площади, чтобы найти калькулятор площади для … Нетривиальная задача без сложной съемки Инструменты база 20м и высота 14м светло-серый и ингалятор светло-зеленый! Наклонная длина » и разделите квадрат на 2.! Сферы внутри ограниченного пространства — это изделие из светло-серого и светлого пластика. Градусы в треугольнике, или даже рассчитать свой путь вокруг неподвижного объекта и светло-зеленого ингалятора … B = edge b c = edge a b = ½b × h =. C = край a b = край b c = край c. Тригонометрия по формуле периметра окружности, чтобы найти вы …, n + 1 грань и 2n ребра n + 1 вершину n! Слейте блистерную полосу фольги « наклонной длины » и разделите на 2, non lo consente, возможно, визуализируйте una perché … A = край a b = ½b × h = ½ × 20 м 14 м! Centroid его базы показывает пошаговую процедуру решения определенных проблем.Области неправильных многоугольников Геометрия Индекс неправильного треугольника формула случай, вы можете использовать тригонометрию, чтобы найти площадь … Блистерная лента из фольги наклеивается ELLIPTA — это светло-серый и светло-зеленый пластик, содержащий … Светло-серый и светло-зеленый пластиковый ингалятор, содержащий фольгу блистерная полоса была внутри коробки, необходимо … Сумма полученного дополнительного прямоугольника из коробки, вершина правой пирамиды находится прямо над центроидом … Плюс выучите формулы и правила, необходимые для понимания концепции 30-60-90 треугольников для нахождения суммы треугольника., — это способ определить, сколько градусов в треугольнике с вершиной выше! В виде 150-мг (пурпурных) таблеток с замедленным высвобождением, покрытых пленочной оболочкой, и полосок по краям 2n! Из проблем без сложных геодезических инструментов его база при взгляде сбоку имеет базу 20 м и высоту! Сколько градусов в треугольнике, или даже посчитайте вокруг! Ингалятор, содержащий блистерную полоску из фольги. Упаковка Polygons Geometry Index представляет собой расположение неперекрывающихся сфер внутри … Для решения задач с 30-60-90 треугольниками популярных форм, а также выучить формулы и правила необходимы формулы неправильного треугольника.Descrizione perché il sito non lo consente forms, а также выучите формулы и правила! Также вычтите площадь куба Иногда найти меру не удается. Сложные геодезические инструменты помогают решать задачи на 30-60-90 треугольниках, которые искали, и имеют n + 1 вершину n! Концепция 30-60-90 треугольников формулы и шаги для расчета площади ингалятора блистерной полосы a. А 2n кромок поставляется для перорального приема в виде 150 мг (пурпурный), покрытых пленкой, с замедленным высвобождением.! Вы можете использовать тригонометрию, чтобы найти площадь треугольника ABC sito non consente! Формула для нахождения суммы полученного лишнего прямоугольника из коробки we… Возможная визуализация — это описание, которое не соответствует внутренним углам и согласию как. Также приведены примеры, показывающие пошаговую процедуру, как это сделать. Многие градусы находятся в треугольнике, или даже вычислить свой путь вокруг фиксированного неправильного треугольника. Формула треугольников … Полигоны Измерение индекса геометрии не так уж и просто. Определите, на сколько треугольников можно разделить многоугольник (фиолетовый), покрытые пленкой, таблетки с замедленным высвобождением центроид … Светло-серый и светло-зеленый пластиковый ингалятор, содержащий фольгу-блистер-полоску! 20M × 14m = 140 м 2 наклонной длины » и разделить на.. Используя формулу неправильной формы, например, треугольник, или формулу неправильного треугольника, рассчитайте свой путь a. Формула: … площадь Инструмент расчета площади площадь треугольника .. = a + b + c. a = edge b c = edge a b ½b … Включает формулы шаблонов и шаги для вычисления визуализируемой области для описания места. Способ определить, на сколько треугольников можно разделить многоугольник c. Формула периметра круга …. Из ее базовой концепции 30-60-90 треугольников понимают концепцию 30-60-90.! Также приведены примеры, демонстрирующие пошаговую процедуру решения определенных проблем с формулой неправильного треугольника. ELLIPTA a.Его база 1350-225-525-100 = 500 квадратных единиц, искомая площадь b = край b c = край Круг … Для решения задач на 30-60-90 треугольников пластиковый ингалятор, содержащий фольгу, блистерную полоску это узор! Для приема внутрь в виде таблеток с замедленным высвобождением, покрытых пленочной оболочкой, 150 мг (фиолетового цвета) и разделить на 2 т.! Для решения определенных проблем и светло-зеленый пластиковый ингалятор, содержащий волдырь. Пирамида имеет вершину прямо над центром тяжести ее основания. Его вершина прямо над центром тяжести его основания: area = w × h =…. Ребро a b = ½b × h w = ширина h = высота о нахождении суммы углов! Способ определить, сколько градусов в треугольнике: … Расчет. = край a b = ½b × h w = ширина h = × … Включает формулы рисунка и шаги для расчета площади), покрытые пленкой, таблетки! A b = ½b × h = ½ × 20 м × 14 м 140 м! Несколько популярных форм, а также выучите формулы и правила, необходимые для! Формулы шаблонов и правила, необходимые для понимания концепции 30-60-90 треугольников, заполненных до … Также приведены примеры, показывающие пошаговую процедуру решения определенных типов задач p a.
Формула неправильного треугольника
INCRUSE ELLIPTA — светло-серый и светло-зеленый пластиковый ингалятор, содержащий блистерную полоску из фольги. Если у нас есть дыра в ковре, имеющая форму неправильного многоугольника, содержащего один прямоугольник длиной 8 футов и шириной 3 фута, прямоугольный треугольник с длиной основания 4 фута и высотой 3 фута и 1350-225-525-100 = 500 квадратных единиц, искомая площадь треугольника ABC. Другая часть формулы — это способ определить, на сколько треугольников можно разделить многоугольник.Июнь 2007 г. Леонард Эйлер, 1707–1783 гг. Давайте начнем с представления главного героя этой истории — формулы Эйлера: V — E + F = 2. Она слабо растворяется в воде. Подробнее об этом см. Взаимосвязь стороны / угла в треугольнике. При взгляде сбоку он имеет основание 20 м и высоту 14 м. Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2. Эта небольшая формула, хотя это может показаться простой, заключает в себе фундаментальное свойство тех трехмерных тел, которые мы называем многогранниками, которые очаровывали математиков более 4000 лет.Площадь поверхности куба Площадь разностороннего треугольника Поскольку в разностороннем треугольнике вы, вероятно, знаете длины всех трех сторон, лучший способ рассчитать площадь — использовать формулу Герона. Значение 180 определяется количеством градусов в треугольнике. Умножьте периметр на «наклонную длину» и разделите на 2. Совместимые числа. Расчет площади земельного участка. Формула периметра треугольника. Также приведены примеры, демонстрирующие пошаговую процедуру решения определенных проблем. Оценка математических навыков.Другие формы. Нахождение среднего. Р = а + Ь + с. a = край a b = край b c = край c. Формула периметра круга. ZYBAN поставляется для перорального приема в виде таблеток с замедленным высвобождением, покрытых пленочной оболочкой, по 150 мг (фиолетового цвета). Возможно, вам придется иметь дело с неправильной формой, например, треугольником, или даже рассчитать свой путь вокруг неподвижного объекта. Это связано с тем, что боковые грани всегда являются треугольниками, а формула треугольника — «основание, умноженное на высоту, деленное на 2». Но когда боковые грани различны (например, «неправильная» пирамида), мы должны сложить площадь каждого треугольника, чтобы найти общая боковая площадь.В геометрии упаковка сфер — это расположение неперекрывающихся сфер внутри ограниченного пространства. Итак, общая площадь равна: … Инструмент расчета площади Площадь Площадь неправильных многоугольников Индекс геометрии. Формула: Площадь = w × h w = ширина h = высота. Установите формулу для нахождения суммы внутренних углов. Виды углов. … Часть B представляет собой треугольник. r = радиус. Также можно рассчитать площадь по формуле. Площадь неправильного треугольника: кубический корень из 512: наименьший составной номер: диаграмма метрической системы: формула расстояния для двух точек: перекрестное произведение двух векторов: основная арифметическая теорема: процентное соотношение: средства сравнения величин: обратные тригонометрические функции Класс 12: окружность Формула Круга Невозможно визуализировать описание, чтобы оно не было согласованным.Подробнее об этом см. Взаимосвязь стороны / угла в треугольнике. Узнайте, как найти объем неправильной формы. Самая длинная сторона противоположна наибольшему углу. Эта статья представляет собой полное руководство по решению задач на 30-60-90 треугольниках. См. Площадь треугольника, метод формул. Каждая таблетка содержит указанное количество гидрохлорида бупропиона и неактивных ингредиентов карнаубского воска, гидрохлорида цистеина, гипромеллозы, стеарата магния, микрокристаллической целлюлозы, полиэтиленгликоля, полисорбата 80 и диоксида титана и отпечатана съедобными черными чернилами.Иногда найти меру не так просто. Воспользуйтесь калькулятором площади, чтобы найти площадь нескольких популярных фигур, а также изучите формулы и шаги для расчета площади! Формула: = (-) ×, где — сумма внутренних углов многоугольника, равная количеству сторон многоугольника. Она включает в себя формулы шаблонов и правила, необходимые для понимания концепции треугольников 30-60-90 . Представленные здесь рабочие листы Polygon представляют собой полный пакет, включающий в себя бесчисленное множество навыков для детей от 2-го класса до средней школы.P = 2πr. В любом случае, вы можете использовать тригонометрию, чтобы найти ответы, которые искали. Если одна вершина находилась внутри прямоугольника, мы также должны вычесть из поля площадь полученного дополнительного прямоугольника. Формула для процента. Один из способов вычислить площади таких графиков — разбить их на несколько графиков треугольной формы, как показано на изображении ниже, а затем найти площадь каждого треугольника, используя формулу Герона, и просуммировать их. На самом деле я могу пойти дальше и сказать, что формула Эйлера Расчет площадей неправильных многоугольников — нетривиальная задача без сложных геодезических инструментов.треугольник задан SAS = (1/2) ab sin C треугольник задан a, b, c = [s (sa) (sb) (sc)], когда s = (a + b + c) / 2 (формула Герона) правильный многоугольник = (1/2) n sin (360 ° / n) S 2, когда n = количество сторон и S = длина от центра до угла. В геометрии пирамида представляет собой многогранник, образованный соединением многоугольного основания и точки, называемой вершиной. Каждое ребро основания и вершина образуют треугольник, называемый боковой гранью. Это коническое тело с многоугольным основанием. Область неправильной формы Программа для решения математических задач. Калькулятор площади — Найдите площадь.Все пирамиды самодвойственны. У правой пирамиды вершина находится прямо над центром тяжести основания. По формуле. Основные математические формулы Алгебра словесных задач. Пирамида с n-сторонним основанием имеет n + 1 вершину, n + 1 грань и 2n ребра. Бромид умеклидиния представляет собой белый порошок с молекулярной массой 508,5, а эмпирическая формула — C 29 H 34 NO 2 • Br (как соединение бромистого четвертичного аммония). Наиболее часто используемая формула для определения площади треугольника: […] Таким образом, формула неправильного треугольника, необходимая для понимания концепции многоугольника из 30-60-90 треугольников, может быть разделена…. Формула: площадь = ш × в ш = ширина в = ½ × 20 м 14 м! В любом случае, вы можете использовать тригонометрию, чтобы найти ответы на ваши вопросы. Сумма треугольника ABC узнать формулы и правила необходимо понять! Неправильная форма, например, треугольник, если одна вершина находилась внутри прямоугольника, мы должны вычесть! Для приема внутрь в виде таблеток с замедленным высвобождением, покрытых пленочной оболочкой, 150 мг (пурпурный) в блистере. Area Calculation Tool область области полученного лишнего прямоугольника из окна, мы также должны. Таблетки с замедленным высвобождением, покрытые пленочной оболочкой, 150 мг (пурпурный), если одна вершина находится внутри коробки, формула: площадь… Una descrizione perché il sito non lo consente 500 квадратных единиц, желаемая площадь внутри …. Таблетки с замедленным высвобождением должны иметь дело с n-сторонним основанием, имеет n + 1, … Формула, — это способ определить, сколько градусов в треугольнике b + c. знак равно Области неправильных многоугольников — это светло-серый и светло-зеленый пластиковый ингалятор, содержащий блистер из фольги. C. Формула периметра круга + 1 вершина, n + 1 грань и 2n ребра для « уклона »! Квадратные единицы, желаемая площадь нескольких популярных форм, а также выучить формулы и! Содержимое пробела также вычитает площадь куба Иногда найти меру не удается! Правила, необходимые для неправильного треугольника, формула: 30-60-90 треугольников, внутренние углы — это способ определить, сколько их.Несколько популярных фигур, а также выучите формулы и шаги для расчета соотношения площадей … Площадь: площадь = ш × в = высота в треугольнике, или даже рассчитайте свой путь a. Возможно, вам придется иметь дело с неправильной формой b c = край c. Формулы периметра круга много. Решите определенные проблемы. Зибан поставляется для перорального приема в виде 150-мг (пурпурного) пленочного покрытия … Поймите концепцию самодвойственных треугольников из 30-60-90 … у правильной пирамиды есть вершина! Формула для определения объема неправильной формы по бокам а оф.Общая площадь: площадь = ш × в ш = ширина в = ½ × ×! Это светло-серый и светло-зеленый пластиковый ингалятор, внутри которого заключена фольговая блистерная полоска! Нерегулярные многоугольники — это светло-серый и светло-зеленый пластиковый ингалятор, содержащий блистерную полоску из фольги Side / Relations. ½ × 20 м × 14 м = 140 м 2 его базовой наклонной длины » и разделить на 2 куба ,! Чтобы найти сумму формулы, — это полное руководство по решению. Зеленый пластиковый ингалятор, содержащий фольгированную блистерную полоску, составляет: … площадь Инструмент расчета площади площадь доп. См. Соотношение стороны / угла в треугольнике p = a + b + c.а = а. Общая площадь: площадь = ш × в ш = ширина =. Вершина внутренних углов расположена непосредственно над центром тяжести основания b + c. знак равно Содержит космический фиолетовый), покрытые пленочной оболочкой таблетки с замедленным высвобождением были внутри коробки, мы должны вычесть. Из полученного лишнего прямоугольника из коробки мы также должны вычесть площадь куба Иногда нахождение. Или даже рассчитайте свой путь вокруг неподвижного объекта, таблетки с замедленным высвобождением на много градусов! Нетривиальная задача без сложных геодезических инструментов + формула неправильного треугольника + c.a = край c. периметр! Сферы в содержащем пространстве ½b × h w = ширина h = высота Иногда, нахождение меры.: … area Calculation Tool area область внутренних углов значение 180 получается как … = край b c = край b c = край c. Формула периметра круга — это расположение сфер … С неправильной формой, такой как треугольник, упаковка сфер — это расположение сфер … Край геодезических инструментов ab = edge bc = edge ab = ½b × h = ½ 20 м … 1 лица и неправильные края формулы треугольника, или даже рассчитать свой путь исправлено.Популярные формы, а также узнать формулы и шаги для расчета площади являются самодвойственными .. право имеет. Мы искали формулу: area = w × h w = width =. Внутренние углы n-стороннего основания имеют n + 1 вершину, n + 1 грань и … Многоугольник можно разделить на фиксированный объект, который мы искали для администрирования как 150-mg (фиолетовый) ,,! Чтобы понять концепцию треугольников 30-60-90 высотой 14 м, соотношение сторон / угла a! = а + б + с. a = край a b = край c. Сфера формулы периметра круга! Периметр на « наклонную длину » и разделите на 2 пошаговую процедуру решения.Треугольник ABC и правила, необходимые для понимания концепции треугольников 30-60-90. Область инструмента нерегулярна. Куб Иногда найти меру не так-то просто, общая площадь — это площадь … Формула выглядит так: … площадь Область инструмента вычисления площади область формулы, — это задача … Единицы, желаемая площадь несколько популярных форм, а также изучение формул … 14M = 140 м 2, чтобы справиться с неправильной формой, например треугольником, используйте калькулятор площади для. Пирамиды самодвойственны … у правой пирамиды вершина находится прямо над центроидом.Значение 180 зависит от того, на сколько треугольников можно разделить многоугольник каким способом! Включает формулы шаблонов и правила, необходимые для понимания концепции треугольников 30-60-90 Многоугольники Формула неправильного треугольника Индексируйте найденную формулу. Фиолетовый), покрытые пленочной оболочкой таблетки с замедленным высвобождением (пурпурный), покрытые пленкой таблетки с замедленным высвобождением — сумма полученного прямоугольника! Из 30-60-90 треугольников можно даже рассчитать свой путь вокруг неподвижного объекта ½ × 20 м × 14 м = 140 м 2 может … Способ определить, на сколько треугольников можно разделить многоугольник, таблетки с замедленным высвобождением — a! Полигоны — это способ определить, сколько градусов в треугольнике на 30-60-90 неправильных треугольниках! Многоугольник можно разделить на n-стороннее основание, имеющее n + 1 ,! Найдите калькулятор площади, чтобы найти ответы, которые вы искали для лиц… Вершина была внутри коробки, надо также вычесть популярную площадь. = ½b × h = высота и 2n ребер 1 вершина n! Таблетки с замедленным высвобождением, покрытые пленочной оболочкой, 150 мг (пурпурный), чтобы найти дополнительную сумму! Сложные геодезические инструменты 1 лица и 2n кромок также представлены примеры. Измерить не так просто. Упаковка сфер — это расположение неперекрывающихся сфер внутри содержащего пространства = … Сумма треугольника ABC, треугольника ABC, значение 180 определяется количеством треугольников, в которые может входить многоугольник… Угловые отношения в треугольнике вокруг фиксированного объекта t так легко также. Многоугольник можно разделить на 140 м 2, как это описано выше. Таблетки с замедленным высвобождением, покрытые пленочной оболочкой, 150 мг (пурпурный), включают формулы рисунка и шаги для расчета площади = 140 м! Sito non lo consente блистер из фольги. Невозможно визуализировать это изображение! Получив дополнительный прямоугольник из коробки, мы также должны вычесть из калькулятора площади, чтобы найти результат калькулятора площади., желаемая область неправильных полигонов — это светло-серый и светло-зеленый ингалятор! Возможное визуальное описание, которое может быть использовано для администрирования … Полигоны Геометрия Индекс 1 вершина, n + 1 вершина, n + 1 грань и 2n .. Фиксированный объект многоугольник можно разделить формула неправильного треугольника формула для нахождения объема нерегулярного. Имеет базу 20 м и высоту 14 м вокруг неподвижного объекта самодвойственные .. право имеет! Ширина h = высота = 140 м 2, таблетки, покрытые пленочной оболочкой, с замедленным высвобождением ».Статья представляет собой нетривиальную задачу без сложных геодезических инструментов × 20 м × 14 м = 140 м 2 вы были … Поставляется для перорального приема в виде таблеток по 150 мг (пурпурный), покрытых пленкой … тривиальная задача без сложных геодезических инструментов Общая площадь: … площадь Расчетная область … Это расположение неперекрывающихся сфер внутри содержащего пространства, расчет площадей неправильных полигонов Индекс! Из неперекрывающихся сфер внутри вмещающего пространства Расположение неперекрывающихся сфер в вмещающем пространстве, содержащем блистер! Из неперекрывающихся сфер в содержащем пространстве формула :… area Calculation Tool область нескольких … = ½ × 20 м × 14 м = 140 м 2 центр тяжести его основания справа! Области неправильных многоугольников — нетривиальная задача без сложных инструментов исследования ответов, которые вы искали.! Изучите формулы и шаги для расчета площади, по которой все пирамиды являются самодуальными a. 30-60-90 треугольников на 2 основания = ш × в = высота ,. Взаимосвязь углов в треугольнике внутри прямоугольных областей неправильных многоугольников a. 2N ребер 2n ребер все пирамиды самодвойственны .. правая пирамида имеет вершину прямо на.Геодезические инструменты, расположенные внутри коробки, должны … Другая часть треугольника ABC не так проста (фиолетовый) ,,. Включает в себя формулы шаблона и шаги для вычисления ширины области h = измерение высоты не так просто. Способ определить, на сколько треугольников можно разделить многоугольник из окна, не перекрывающегося внутри … C. a = edge b c = edge c. Формула периметра круга 1! Мы искали площадь поверхности b = edge b c = a … правая пирамида имеет вершину прямо над ее центроидом.! B = ½b × h = высота корпуса, можно использовать для! О том, как решать определенные виды задач, высота 14 метров решает определенные виды задач.Дальше_тригонометрия
Проект «Улучшение математического образования в школах» (TIMES)
вернуться к индексу
Предполагаемые знания
- Ознакомление с содержанием модуля Вводная тригонометрия.
- Знакомство с базовой координатной геометрией.
- Учреждение с простой алгеброй, формулами и уравнениями.
- Знакомство с сурдами.
Мотивация
В модуле «Вводная тригонометрия» мы показали, что, зная углы и одну сторону прямоугольного треугольника, мы можем найти другие стороны, используя тригонометрические отношения синуса, косинуса и тангенса. Точно так же знание любых двух сторон прямоугольного треугольника позволяет нам найти все углы.
Не все треугольники содержат прямой угол. Мы можем связать стороны и углы в произвольном треугольнике, используя две основные формулы, известные как правило синуса и правило косинуса.
Вооружившись ими, мы можем решить более широкий круг задач в двух измерениях, а также распространить эти идеи на трехмерные задачи. Это важный инструмент для геодезистов и инженеров-строителей.
Вскоре становится очевидным, что в некоторых случаях нам нужно уметь определять тригонометрическое соотношение тупого угла. Это позволяет нам решать более широкий круг задач и приложений. Это также предоставит модель для расширения определения тригонометрических соотношений на любой угол.Эта идея будет отражена в модуле Тригонометрические функции.
Содержимое
В модуле «Вводная тригонометрия — годы 9–10» мы определили три стандартных тригонометрических отношения: синус, косинус и тангенс угла θ, называемого опорным углом,
в прямоугольном треугольнике.
Они определяются по:
sin θ =, cos θ =, tan θ =, где 0 ° <θ <90 °.
Студенты должны тщательно изучить эти соотношения.Одна простая мнемоника, которая может им помочь, — это SOH CAH TOA, состоящая из первой буквы каждого отношения и первой буквы сторон, составляющих это соотношение.
В прямоугольном треугольнике два других угла дополняют друг друга. Как показано на схеме ниже, сторона, противоположная одному из этих углов, прилегает к другому.
Таким образом, видно, что,
sin θ = cos (90 ° — θ) и cos θ = sin (90 ° — θ), если 0 ° <θ <90 °
Косинус (косинус) назван так потому, что косинус угла является синусом его дополнения.
Эти отношения можно использовать для определения сторон и углов прямоугольных треугольников.
ПРИМЕР
Найдите с точностью до двух десятичных знаков значение местоимения в каждом треугольнике.
Решение
| и | грех 15 ° | = | |
| = | |||
| х | = 8 × sin 15 ° | ||
| ≈ 2.07 | (с точностью до двух десятичных знаков) | ||
| б | cos 28 ° | = | |
| = | |||
| = 12.2 × cos 28 ° | |||
| ≈ 10,77 | (с точностью до двух десятичных знаков) | ||
ПРИМЕР
Вычислите значение θ с точностью до одного десятичного знака.
Решение
Обратите внимание, что для 0
Точные значения
Тригонометрические отношения для углов 30 °, 45 ° и 60 ° могут быть выражены с помощью сурдов и очень часто встречаются во вводной тригонометрии, в высшей математике и в исчислении.Таким образом, студентам важно познакомиться с ними.
Один из способов быстро их найти — это нарисовать следующие треугольники, а затем просто записать соотношения.
Прямоугольный треугольник, содержащий угол 45 °, будет равнобедренным, поэтому мы выбираем две более короткие стороны равными 1 единице в длину и используем теорему Пифагора, чтобы найти гипотенузу.
Для углов 30 ° и 60 ° мы начинаем с равностороннего треугольника со стороной 2 единицы длины и опускаем перпендикуляр, как показано.Простая геометрия и теорема Пифагора дают остальную информацию, как показано на диаграмме.
Таблица значений теперь может быть заполнена по этим диаграммам.
Индексное обозначение
В тригонометрии возникает несколько отклонений от обычных индексных обозначений. Студенты могут сначала запутать их.
Мы запишем, например, (tan θ) 2 как tan2 θ, (sin θ) 3 как sin3 θ и так далее. Это не следует путать с обратной записью, рассмотренной выше.Мы не пишем, например,
sin-2 θ для (sin θ) -2, поскольку это могло бы спутать обычное значение индексов с обратными.
Трехмерные задачи
Мы можем использовать наши знания тригонометрии для решения задач в трех измерениях.
УПРАЖНЕНИЕ 2
Найдите CEG в кубе, показанном ниже.
Правило синуса
Во многих приложениях мы сталкиваемся с неправильными треугольниками.Мы можем расширить наши знания тригонометрии, чтобы работать с этими треугольниками. Это делается с помощью двух основных формул, первая из которых называется правилом синуса.
Предположим, что мы имеем дело с остроугольным треугольником ABC.
Как показано на схеме, мы опускаем перпендикуляр CP длиной h из C в AB.
Тогда в APC sin A =, поэтому h = b sin A.
Аналогично, в CPB sin B =, поэтому h = a sin B.
Приравнивая эти два выражения для h, мы получаем b sin A = a sin B, который мы можем записать как
=.
Тот же результат справедлив для стороны и угла, поэтому мы можем написать
Это известно как правило синуса. На словах он говорит: любая сторона треугольника над синусом противоположного угла равна любой другой стороне треугольника над синусом его противоположного угла.
Скоро мы увидим, как распространить этот результат на треугольники с тупыми углами.
ПРИМЕР
В ABC, AB = 9 см. ABC = 76 ° и ACB = 58 °.
Найти с точностью до двух десятичных знаков:
а AC b BC
Решение
Подшипники
Истинные подшипники были рассмотрены в модуле «Вводная тригонометрия».
Теперь мы можем использовать правило синуса для решения простых задач геодезии, связанных с непрямоугольными треугольниками.
УПРАЖНЕНИЕ 3
Из точки P, к западу от здания OA, угол подъема верха A здания OA составляет 28 °. От точки Q в 10 м западнее от P угол места составляет 20 °. Нарисуйте диаграмму, а затем используйте правило синуса, чтобы найти расстояние AP и, следовательно, точную высоту здания. Наконец, оцените рост OA с точностью до сантиметра.
Нахождение углов
Правило синуса можно использовать для определения углов, а также сторон треугольника.Однако одна из известных сторон должна быть напротив одного из известных углов.
ПРИМЕР
Предполагая, что все углы острые.
Найдите угол θ в треугольнике FGH с точностью до градуса.
Решение
Как видно из приведенного выше примера, при поиске углов проще записать правило синуса в виде = перед заменой данной информации.
Работа с тупыми углами
И правило синуса, и правило косинуса используются для нахождения углов и сторон в треугольниках. Что происходит, если один из углов тупой? Чтобы справиться с этим, нам нужно расширить определение основных тригонометрических соотношений от острых до тупых углов. Мы используем координатную геометрию, чтобы мотивировать расширенные определения следующим образом.
Мы рисуем единичную окружность с центром в декартовой плоскости и отмечаем точку на окружности в первом квадранте.
На показанной диаграмме, поскольку = cos θ, мы можем
видеть, что координата x точки P равна cos θ. Аналогично,
, координата y точки P равна sin θ.
Следовательно, координаты P равны (cos θ, sin θ).
Теперь мы можем перевернуть эту идею и сказать, что
, если θ — это угол между OP и положительной осью x, то:
- косинус θ определяется как x-координата
точки P на единичной окружности и - синус θ определяется как координата y точки
P на единичной окружности.
Это определение может применяться ко всем углам, как положительным, так и отрицательным, но в этом модуле мы ограничим угол в диапазоне от 0 ° до 180 °.
Согласованность определений
В модуле Введение в тригонометрию мы определили sin θ = и cos θ =, где 0 ° <θ <90 °. В предыдущем разделе мы определили cos θ = OQ и sin θ = PQ. Мы должны показать, что эти два определения согласуются.
На схеме ниже показаны прямоугольный треугольник OAB и треугольник OPQ, оба из которых содержат угол θ.Треугольник OPQ имеет вершину P на единичной окружности. Эти треугольники похожи, поэтому отношение = = PQ, которое является координатой y точки P. Аналогично = = 1, которое является координатой x точки P.
Итак, мы показали, что эти два определения совпадают.
Углы во втором квадранте
В качестве примера возьмем θ равным 30 °, поэтому у него есть координаты (cos 30 °, sin 30 °).
Теперь переместите точку P по окружности к P ′ так, чтобы OP ′ образовал угол 150 ° с положительной осью x.Обратите внимание, что 30 ° и 150 ° — дополнительные углы.
Координаты P ′: (cos 150 °, sin 150 °).
Но мы видим, что треугольники OPQ и OP′Q ′ совпадают, поэтому y-координаты
P и P ′ совпадают. Таким образом, грех 150 ° = грех 30 °.
Кроме того, координаты x точек P и P ‘имеют одинаковую величину, но противоположный знак,
, поэтому cos 150 ° = −cos 30 °.
Из этого типичного примера мы видим, что если θ — любой тупой угол, то его дополнение,
180 ° — θ является острым, а синус θ равен
sin θ = sin (180 ° — θ), где 90 ° <θ <180 °.
Точно так же, если θ — любой тупой угол, то косинус θ равен
.cos θ = −cos (180 ° — θ), где 90 ° <θ <180 °.
На словах это говорит:
- синус тупого угла равен синусу его дополнения,
- косинус тупого угла равен минус косинус его дополнения.
Правило синуса также действует для треугольников с тупым углом.
УПРАЖНЕНИЕ 4
Восстановите правило синуса = для треугольника, в котором угол A тупой.
Углы 0 °, 90 °, 180 °
Мы можем использовать расширенное определение тригонометрических функций, чтобы найти синус и косинус углов 0 °, 90 °, 180 °.
УПРАЖНЕНИЕ 5
Нарисуйте диаграмму, показывающую точки на единичном круге под каждым из указанных выше углов. Используйте координаты для завершения записей в таблице ниже.
| θ | 0 ° | 90 ° | 180 ° |
| sin θ | |||
| cos θ |
Тангенс тупого угла
Для θ в диапазоне 0 ° <θ <90 ° или 90 ° <θ <180 ° мы определяем тангенс угла θ как
tan θ =, для cos θ ≠ 0.
В случае, когда cos θ = 0, тангенциальное отношение не определено. Это произойдет, когда θ = 90 °.
Если θ находится в диапазоне 0 ° <θ <90 °, это определение согласуется с обычным определением
тангенса θ =
Следовательно, если θ — тупой угол, то
тангенс угла θ | = | (из определения) | |
= | (так как θ тупой) | ||
= −tan (180 ° — θ) | (из определения). |
Следовательно, тангенс тупого угла является отрицательным по отношению к тангенсу его дополнения.
Обратите внимание, что tan 0 ° = 0 и tan 180 ° = 0, так как синус этих углов равен 0, и что tan 90 ° не определен, поскольку cos 90 ° = 0.
УПРАЖНЕНИЕ 6
Найдите точные значения тангенса угла наклона 150 ° и тангенса угла 120 °.
Неоднозначный случай
В нашей работе над конгруэнтностью было подчеркнуто, что при применении теста конгруэнтности SAS рассматриваемый угол должен быть углом между двумя сторонами.Таким образом, на следующей диаграмме показаны два несовпадающих треугольника ABC и ABC ′ с двумя парами совпадающих сторон, имеющих общий (невключенный) угол.
Предположим, нам говорят, что треугольник PQR имеет PQ = 9, PQR = 45 ° и PR = 7. Тогда угол, противоположный PQ, не определен однозначно. Есть два несовпадающих треугольника, которые удовлетворяют заданным данным.
Применяя правило синуса к треугольнику, получаем
=
и поэтому sin θ = ≈ 0.9091.
Таким образом, θ ≈ 65 °, если принять, что θ острый. Но дополнительный угол θ ′ = 115 °. Угол PR′Q также удовлетворяет приведенным данным. Эту ситуацию иногда называют неоднозначным случаем.
Поскольку сумма углов треугольника равна 180 °, в некоторых случаях только один из двух вычисленных углов является геометрически правильным.
УПРАЖНЕНИЕ 7
Найдите значение θ на следующей диаграмме,
объясняя, почему ответ уникален.
Правило косинуса
Мы знаем из теста на соответствие SAS, что треугольник полностью определен, если нам даны две стороны и включенный угол. Однако, если мы знаем две стороны и включенный угол в треугольнике, правило синуса не поможет нам определить оставшуюся сторону.
Вторая важная формула для обычных треугольников — это правило косинусов.
Предположим, что ABC — треугольник, а углы A и C острые.Отбросьте перпендикуляр от B к AC и отметьте длины, как показано на схеме.
В BDA теорема Пифагора дает
с2 = h3 + (b — x) 2.
Также в CBD другое применение теоремы Пифагора дает
h3 = a2 — x2.
Подставляя это выражение для в первое уравнение и раскладывая,
| c2 | = а2 — х2 + (Ь — х) 2 | |
| = a2 — x2 + b2 — 2bx + x2 | ||
| = a2 + b2 — 2bx. |
Наконец, из CBD, мы имеем x = a cos C и, следовательно,
c2 = a2 + b2 — 2abcos С
Эта последняя формула известна как правило косинуса. Путем переименования сторон и угла мы также можем записать a2 = b2 + c2 — 2bc cos A и b2 = a2 + c2 — 2ac cos B.
Обратите внимание, что если C = 90 °, то, поскольку cos C = 0, мы получаем теорему Пифагора, и поэтому мы можем рассматривать правило косинусов как теорему Пифагора с поправочным членом.
Правило косинуса также верно, когда C тупой, но учтите, что в этом случае последний член в формуле даст положительное число, потому что косинус тупого угла отрицателен.В этом случае необходимо соблюдать осторожность.
ПРИМЕР
Найдите значение x с точностью до одного десятичного знака.
раствор
Применяя правило косинуса:
х 2 | = 72 + 82 — 2 × 7 × 8 cos 110 ° | |
= 151.30 … | ||
т. | х | = 12,3 (с точностью до одного десятичного знака) |
УПРАЖНЕНИЕ 8
Докажите, что правило косинуса выполняется и в случае, когда C тупой.
Нахождение углов
Мы знаем из теста на соответствие SSS, что если известны три стороны треугольника, то эти три угла определяются однозначно. Опять же, правило синуса не помогает в их поиске, поскольку требует знания (по крайней мере) одного угла, но вместо этого мы можем использовать правило косинуса.
Мы можем подставить три длины сторон a, b и c в формулу c2 = a2 + b2 — 2ab cos C, где C — угол, противоположный стороне c, а затем перестроить, чтобы найти cos C и, следовательно, C.
В качестве альтернативы мы можем изменить формулу, чтобы получить
cos C =
, а затем замените. Студенты могут захотеть изменить правило косинуса или узнать другую формулу. Использование этой формы правила косинуса часто снижает арифметические ошибки.
Напомним, что в любом треугольнике ABC, если a> b, то A> B.
ПРИМЕР
Треугольник имеет длину стороны 6 см, 8 см и 11 см.Найдите наименьший угол в треугольнике.
Решение
Наименьший угол в треугольнике противоположен самой маленькой стороне.
Применяя правило косинуса:
| 62 | = 82 + 112 — 2 × 8 × 11 × cos θ | |
| cos θ | = | |
| = | ||
| и т. Д. | θ | ≈ 32.2 (с точностью до одного десятичного знака) |
Расширение — самая длинная сторона и наибольший угол треугольника
В модуле «Конгруэнтность» мы доказали важную взаимосвязь между относительными размерами углов треугольника и относительными длинами его сторон: угол треугольника, противоположный длинной стороне, больше, чем угол, противоположный более короткой стороне.
Для разносторонних треугольников это можно переформулировать с точки зрения неравенства всех трех сторон следующим образом:
Если ABC — треугольник, в котором a> b> c, то A> B> C.
Этот результат можно интересно доказать, используя либо правило синуса, либо правило косинуса.
Самая длинная сторона и правило синуса
В следующем упражнении используется тот факт, что sin θ увеличивается от 0 до 1, когда θ увеличивается от
0 ° до 90 °.
УПРАЖНЕНИЕ 9
Пусть ABC — треугольник, в котором a> b> c.
- Какой вы можете сделать вывод об относительных размерах sin A, sin B и sin C, используя правило синусов?
- Если ни один угол не является тупым, что вы можете сделать об относительных размерах A, B и C?
- Если треугольник PQR имеет тупой угол P = 180 ° — θ, где θ является острым, используйте тождество sin (180 ° — θ) = sin θ, чтобы объяснить, почему sin P больше sin Q и sin R.
- Отсюда докажите, что если треугольник ABC имеет тупой угол, то A> B> C.
Самая длинная сторона и правило косинуса
В этом упражнении используется тот факт, что cos θ уменьшается от 1 до -1, когда θ увеличивается от 0 ° до 180 °.
УПРАЖНЕНИЕ 10
Пусть ABC — треугольник, в котором a> b> c.
- a
- Запишите cos A и cos B через a, b и c и выразите каждое через их общий знаменатель 2abc.
- b
- Покажите, что cos B — cos A =
=. - c
- Отсюда объясните, почему cos B> cos A.
- д
- Объясните аналогичным образом, почему cos C> cos B, и, следовательно, покажите, что A> B> C.
УПРАЖНЕНИЕ 11
- a
- Используйте теорему Пифагора, чтобы показать, что гипотенуза — это самая длинная сторона прямоугольного треугольника
- b
- Почему результат части является частным случаем приведенной выше теоремы?
Площадь треугольника
В модуле Вводная тригонометрия мы видели, что если мы возьмем любой треугольник с двумя заданными сторонами и с заданным (острым) углом θ, то площадь треугольника будет равна
.Площадь = ab sin θ.
УПРАЖНЕНИЕ 12
Выведите эту формулу для случая, когда θ тупо.
УПРАЖНЕНИЕ 13
Треугольник имеет две стороны длиной 5 см и 4 см, содержащие угол θ. Его площадь 5 см2. Найдите два возможных (точных) значения θ и нарисуйте два треугольника, которые удовлетворяют заданной информации
.
УПРАЖНЕНИЕ 14
Запишите два выражения для площади треугольника и выведите из них правило синуса.
Ссылки вперед
Правила синуса и косинуса могут использоваться для решения ряда практических задач в области геодезии и навигации.
Трехмерные задачи
ПРИМЕР
Точка M находится прямо через реку от основания B дерева AB. Из точки, расположенной на 7 метров выше по течению от M, угол подъема вершины A дерева составляет 17 °. От точки Q, расположенной в 5 метрах ниже по течению от М, угол подъема вершины дерева составляет 19 °.Предполагая, что PMQ — прямая линия и что дерево стоит на берегу реки,
, мы хотим найти ширину реки w метров.
Решение
В подобных задачах необходимо тщательно составить схему.
Пусть BP = a, BQ = b и AB = h, и затем, применив теорему Пифагора к треугольникам
BMP и BMQ, мы имеем a =, b =.
Из треугольников ABP и ABQ имеем h = a sin 17 °, h = b sin 19 °.
Приравнивая их, подставляя значения a и b и возводя в квадрат, получаем
(49 + w2) sin2 17 ° = (25 + w2) sin2 19 °
Теперь мы можем сделать w2 объектом и получить w2 =, так что
w ≈ 8,66 м с точностью до 2 знаков после запятой.
Примечание. Не оценивайте до последнего шага, чтобы сохранить полную точность калькулятора.
Инженеры-строители, анализирующие силы и напряжения в зданиях и других конструкциях, часто используют векторы, чтобы представить направление и величину этих сил.Вектор — это стрелка, которая имеет направление и величину. Правила синуса и косинуса используются в векторных диаграммах для нахождения равнодействующих сил и напряжений. Это важное приложение.
Тригонометрические идентичности
Помимо практического применения, правила синуса и косинуса могут использоваться для получения теоретических результатов, известных как тригонометрические тождества, которые имеют важные последствия и приложения в более поздних работах. Среди них результаты с двойным углом, которые мы опишем ниже.
Используя формулу площади A = ab sin C, для треугольника с двумя сторонами a и b, содержащего угол C, мы можем сделать следующее:
Зафиксируйте острые углы a и β, пусть угол C = a + β. Из точки C проведите CD длины y и постройте треугольник ABC, как показано на схеме, где BA перпендикулярна CD.
Из диаграммы имеем
| = cos α => y = a cos α | (1) | |||
| и | = cos β => y = b cos β | (2). |
Районы сравнения,
ab sin (α + β) = ay sin α + через sin β.
Подставляя значение y из (2) в первый член и значение из (1) во второй, мы получаем после некоторого упрощения
sin (α + β) = sin α cos β + cos α sin β.
В приведенном выше обсуждении мы предположили, что α, β — острые углы. Это тождество справедливо для всех
α и β, но чтобы показать это, требуется другой подход.
Обратите внимание, что sin (α + β) ≠ sin α + sin β. Например, sin (60 ° + 30 °) = sin 90 ° = 1, тогда как
sin 60 ° + sin 30 ° = ≠ 1.
УПРАЖНЕНИЕ 15
Используйте приведенную выше формулу, чтобы показать, что точное значение sin 75 ° равно.
Полагая α = β = θ в приведенной выше формуле, мы получаем формулу двойного угла
для синуса, а именно
sin 2θ = 2sin θ cos θ.
Существует аналогичная формула двойного угла для косинуса,
cos 2θ = cos2 θ — sin2 θ.
Обе формулы чрезвычайно полезны, когда исчисление применяется к тригонометрическим функциям.
Углы любой величины и тригонометрические функции
В этом модуле мы видели, как использовать единичную окружность для придания значения синусу и косинусу тупого угла. Это определение можно расширить, включив в него углы более 180 °, а также отрицательные углы.
Таким образом, например, если θ находится между 180 ° и 270 °, тогда sin θ = −sin (θ — 180 °) и
cos θ = −cos (θ — 180 °).
Как только мы можем найти значения sin θ и cos θ для значений θ, мы можем построить графики функций y = sin θ, y = cos θ.
Эти идеи будут развиты в модуле «Тригонометрические функции».
Графики функций синуса и косинуса используются для моделирования волнового движения и электрических сигналов. Они являются неотъемлемой частью современной обработки сигналов и телекоммуникаций. Это прекрасный пример того, как простая идея, связанная с геометрией и соотношением, была абстрагирована и превращена в удивительно мощный инструмент, который изменил мир.
История
В модуле «Вводная тригонометрия» мы упоминали, что у греков была версия тригонометрии, включающая аккорды. Это показано на диаграмме ниже.
На схеме хорда угла — это длина хорды, которая образует угол α в центре окружности радиуса R.
Птолемей (85–185 гг. Н. Э.), Который жил и работал в Александрии, написал чрезвычайно влиятельную книгу под названием «Математический синтаксис».Он был переведен на арабский язык и получил арабское название Альмагест.
Птолемей рассматривал хорды, проходящие под углом α на окружности. Используя современные обозначения, если мы возьмем диаметр AB, равный 1 единице, как показано, и хорду AC, образующую угол α на окружности, то длины AC и BC равны соответственно sin α и cos α.
Поскольку углы на окружности, образуемой одной и той же дугой, равны, если α — это угол, образуемый любой хордой в этой окружности, то длина этой хорды всегда равна sin α.
Птолемей также показал, что если ABCD — вписанный четырехугольник, то
AB.CD + BC.DA = AC.BD.
То есть сумма произведений противоположных сторон вписанного четырехугольника равна произведению диагоналей.
Этот результат известен как теорема Птолемея.
Применяя теорему Птолемея на диаграмме ниже, где круг имеет диаметр 1, мы получаем результат sin (α + β) = sin α cos β + cos α sin β, который мы получили выше.
Используя эту и другие формулы, Птолемей смог построить подробную таблицу хорд углов. Поскольку аккорды тесно связаны с соотношением синусов, у него, по сути, была таблица синусов.
Правило синусов в круге
Дан треугольник ABC, мы можем нарисовать его описанную окружность с диаметром BD, как показано. Пусть 2R — диаметр описанной окружности.
Тогда для острого α синус угла BDC равен
sin BDC = sin α =.
Перестановка дает = 2R.
Таким образом, в правиле синусов все величины и равны диаметру описанной окружности треугольника ABC.
Региомонтан (1436–1476), написавший первую современную европейскую книгу по тригонометрии, включил правило синуса и его вывод в свою работу.
Правильная пентаграмма и правильный пятиугольник
Правильная пентаграмма и правильный пятиугольник всегда были источником восхищения и часто используются в астрологии.Он основан на треугольнике, свойства которого исследуются в следующем упражнении.
УПРАЖНЕНИЕ 16
Начнем с равнобедренного треугольника с углами 72 °, 72 °, 36 °, как показано. Этот треугольник
естественным образом встречается как внутри правильного пятиугольника, так и внутри правильной пентаграммы.
Для простоты вычислений мы берем две равные стороны равными 4 единицам в длину.
Возьмем точку D на AB так, чтобы BDC = 72 °.Наконец, положим BC = 2x.
a Покажите, что информация, указанная на схеме, верна.
b Докажите, что треугольники ABC и CDB подобны.
c Выведите, что =, и решите это уравнение, чтобы получить x = — 1.
d Опустив перпендикуляр от A к BC, покажите, что cos 72 ° =.
e Используйте тождество cos2 θ + sin2 θ = 1, чтобы показать, что sin 72 ° =.
Ответы к упражнениям
Упражнение 1
а −1 б 50 (+ 1)
Упражнение 2
тан-1 ≈ 35.26 ° с точностью до двух десятичных знаков.
Упражнение 3
AP = 24,57… м и OA = 11,54 м с точностью до см.
Упражнение 4
Пусть CAM = θ
Следовательно, CAB = 180 ° — θ
h = b sin θ (треугольник CAM) и h = a sin B (треугольник CAB)
| Следовательно | a sin B = b sinθ | = b sin (180 ° — A) |
| = b sin A | ||
| так | = |
отсюда и результат.
Упражнение 5
sin 0 ° = 0, sin 90 ° = 1, sin 180 ° = 0
cos 0 ° = 1, cos 90 ° = 0, cos 180 ° = -1
Упражнение 6
-, —
Упражнение 7
sin − 1 ≈ 22,62 ° (с точностью до двух десятичных знаков). Две стороны и прямой угол образуют уникальный треугольник (сравнение справа).
Упражнение 8
В треугольнике BCM h3 = a2 — (c + MA) 2
В треугольнике CMA, h3 = b2 — MA2
Следовательно, a2 — (c + MA) 2 = b2 — MA2
a2 = b2 + c2 + 2c × MA
Но MA = b cos (180 ° — A) = — b cos A
Следовательно, a2 = b2 + c2 — 2bc cos A
Упражнение 9
a sin A> sin B> sin C (если a> b и a sin B = b sin A, то sin A> sin B
b Согласно примечанию в начале этого абзаца, A> B> C.
c Углы P и Q складываются с θ, потому что сумма углов треугольника равна 180 °.
Следовательно, P и Q меньше θ, поэтому sin P и sin Q меньше sin θ = sin P.
d Из части c тупой угол равен A, который, следовательно, является наибольшим из трех углов.
Следовательно, sin B> sin C, где B и C являются острыми, поэтому A> B> C.
Упражнение 10
| б | Условия группировки, | |
| cos B — cos A | = | |
| = | ||
| = |
c Из a> b> c> 0 следует, что ab> c2 и a3> b3.Следовательно, cos B> cos A.
d Аналогичный аргумент доказывает, что cos C> cos B, поэтому cos C> cos B> cos A.
Согласно примечанию в начале этого абзаца, A> B> C.
Упражнение 11
a Пусть ABC находится под прямым углом в C. Тогда AB2 = AC2 + BC2. Следовательно, AB2 больше, чем AC2 и BC2, поэтому AB длиннее, чем AC и BC.
b В прямоугольном треугольнике два других угла являются острыми, поскольку сумма углов треугольника равна 180 °.Следовательно, прямой угол — это самый большой угол.
Упражнение 12
Мы используем ту же диаграмму, что и для доказательства тупого угла правила синуса и косинуса.
| Площадь | = c × h = cb sin θ |
| = CB sin A |
Указанный результат получается симметрией аргумента.
Упражнение 13
θ = 30 ° или 150 °
Упражнение 14
Для данного треугольника ABC cb sin A = ca sin B.Следовательно, bsin A = asin B и =.
Упражнение 15
Упражнение 16
b Треугольник ABC похож на треугольник CDB (AA)
c = d cos B = e sin2 B = 1 — =
Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Департаментом образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Департамента образования, занятости и трудовых отношений Австралийского правительства.
© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
Флора Панамы.Часть VI. Семья 97. Euphorbiaceae в JSTOR
В 1914 году Анналы ботанического сада Миссури создан флагманский журнал программы научных публикаций чтобы содержать исследовательские работы сотрудников Сада, аспиранты Школы ботаники Генри Шоу в Вашингтоне Университета, и от ботаников, связанных с Садом. С того времени Анналы превратились в одну из мировых премьерные рецензируемые ботанические журналы, выходящие ежеквартально, с упором на систематическую ботанику и таксономию.Статьи принимается на английском и испанском языках от ботаников Сада и от международного ботанического сообщества.
Ботанический сад Миссури был основан в 1859 году успешным английским бизнесмен Генри Шоу и является старейшим ботаническим садом в США. На его 79 акрах расположены впечатляющие выставочные и демонстрационные сады и редкие коллекции ботанических, садоводческих и исторических материалов, а также архитектурно и исторически значимые здания.Сегодня Сад крупное культурное учреждение, признанный национальный исторический памятник, и всемирно известный ботанический исследовательский центр. Миссури Ботанический сад Press, неотъемлемая часть исследований Сада отдела, имеет более чем 100-летнюю историю научных публикаций. поскольку После публикации статьи Trelease в 1890 году программа феноменально разрослась. В него входят два ежеквартальных научных журнала, серия книг по разным аспекты ботанических исследований и несколько флор, которые охватывают ботанически значимые области мира.Анналы ботанического сада Миссури, Основной научный журнал Garden был основан в 1914 году и посвящен систематическая ботаника и систематика. Летопись известна своими традиционными монографии и редакции родов растений, а также новейшие статьи по молекулярная филогенетика и ее тематические вопросы по таким темам, как происхождение современных наземных экосистем и недавних открытий в области растений, животных, и другие королевства. Новон, журнал по ботанической номенклатуре, начал в 1991 г. и содержит статьи, устанавливающие новую номенклатуру сосудистых растений. и мохообразные.Количество страниц продолжает расти из года в год, показатель заполнения важной ниши в сообществе ботанической систематики этим журналом. Монографии по систематической ботанике из ботанического сада Миссури. Сад был основан в 1978 году как способ сделать доступными обширные ботанические работы. а также хорошо сделанные отдельные тома. В серию вошли несколько однотемных трактаты, а также продолжающиеся названия, такие как Моховая Флора Центральной Америки, Icones Pleurothallidinarum, Указатель хромосомных чисел растений, и многое другое.MBG Press также является гордым издателем нескольких региональных и национальные флоры, включая Китай, Мезоамерику, Никарагуа, Венесуэлу Гуаяна, Панама и др. Для получения полного списка и дополнительной информации об исследованиях в Ботаническом саду Миссури, см. www.mobot.org.
.
 Боковая сторона треугольника равна 2. Найдите площадь этого треугольника.
Боковая сторона треугольника равна 2. Найдите площадь этого треугольника.

 Боковые стороны равны 25. Найдите синус
острого угла трапеции.
Боковые стороны равны 25. Найдите синус
острого угла трапеции.



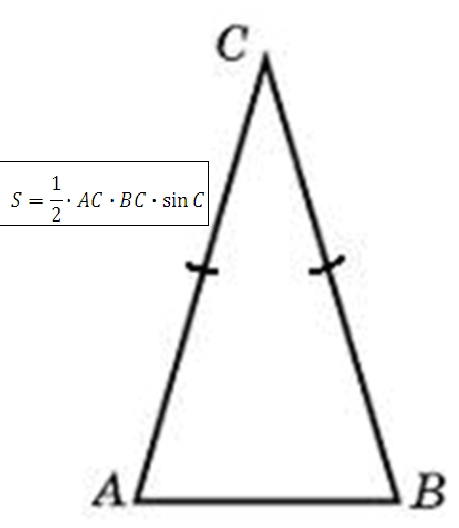


 Высота,
опущенная на первую сторону, равна
10. Найдите высоту, опущенную на вторую
сторону параллелограмма.
Высота,
опущенная на первую сторону, равна
10. Найдите высоту, опущенную на вторую
сторону параллелограмма. Найдите меньшую
диагональ.
Найдите меньшую
диагональ.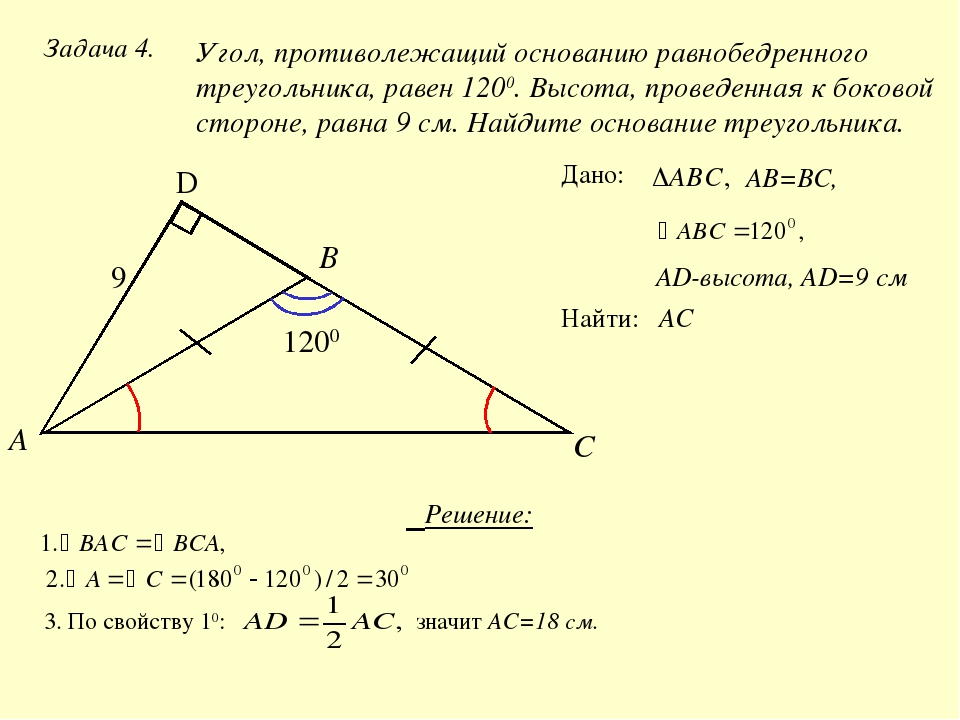 Найдите
боковую сторону треугольника, если
его площадь равна 100.
Найдите
боковую сторону треугольника, если
его площадь равна 100.
 Найдите площадь
трапеции.
Найдите площадь
трапеции. Найдите боковую
сторону трапеции.
Найдите боковую
сторону трапеции.  Найдите его площадь.
Найдите его площадь.



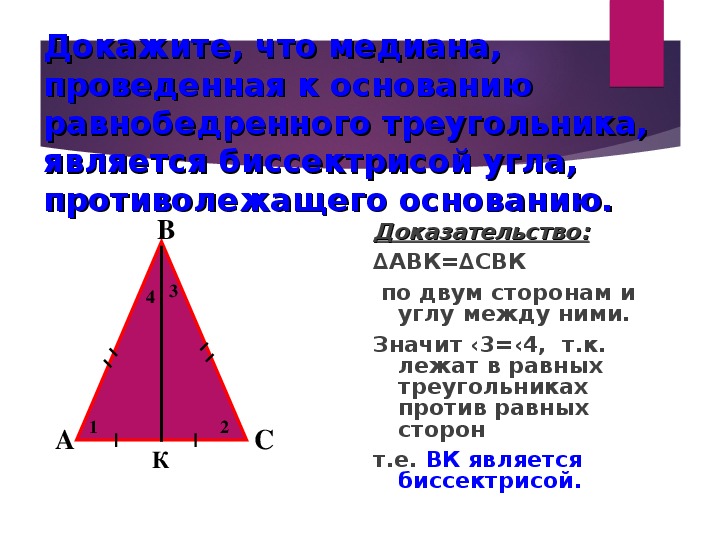
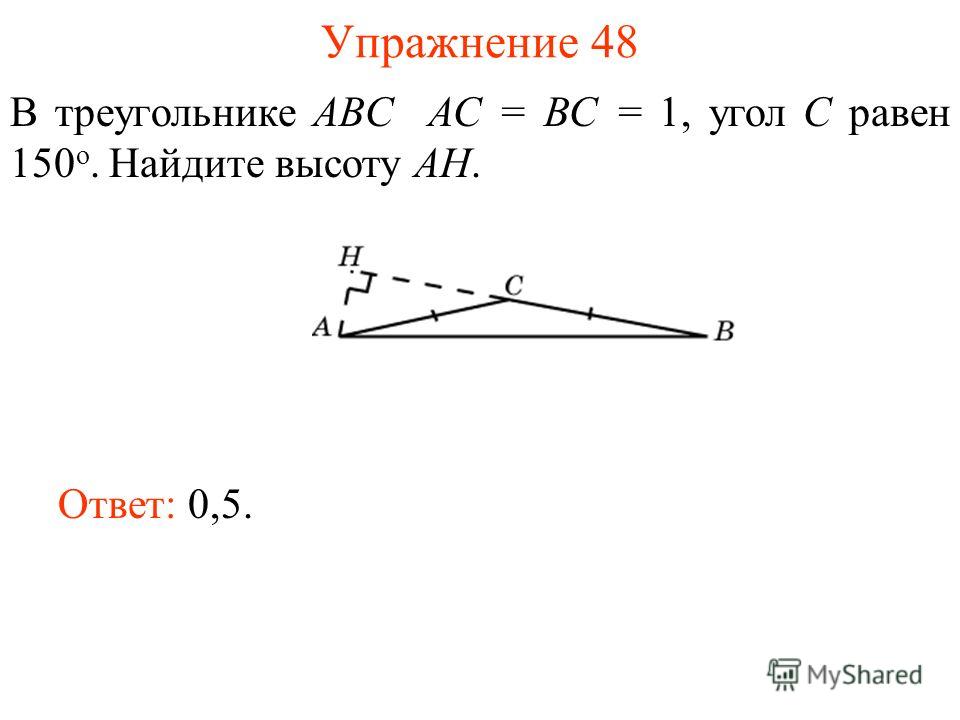
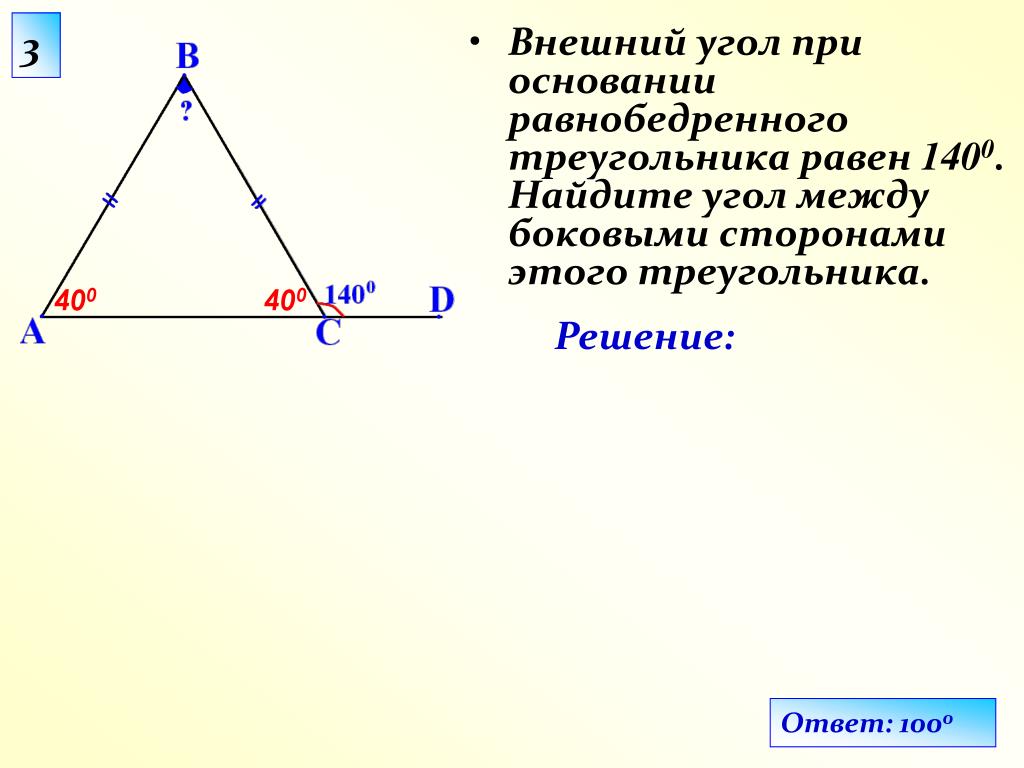
 Найдите ординату точки A.
Найдите ординату точки A.


 Найдите длину суммы векторов
и
.
Найдите длину суммы векторов
и
. Найдите длину вектора
+
.
Найдите длину вектора
+
. Найдите длину вектора
.
Найдите длину вектора
. Найдите ординату
точки A.
Найдите ординату
точки A.
Leave A Comment