Три простых правила относительно квадратного корня. Часть 3
GRE Mathematics
уделяет особое внимание заданиям на квадратный корень. В двух предыдущих частях статьи, мы рассматривали, что делать, если все числа в задании положительные. Если же это не так, то следует применять ещё 2 правила GRE Maths.
Правило №2: если x2 = 9, то x = 3, x = -3
Эта ситуация отлична от
описанных ранее
. Мы больше не имеем знака квадратного корня, зато здесь есть показатель степени. Если 3 возвести в квадрат, то мы получим 9. Если мы возведем -3 в квадрат – мы также получим 9. Следовательно, оба числа являются возможным значением x, потому что оба делают равенство верным.
С математической точки зрения, мы бы сказали, что x = 3 или x = -3. Если вы выполняете задание в разделе Quantitative Comparison, подумайте об этом следующим образом: если одно из них является возможным значением x, то оба варианта должны быть рассмотрены возможными значениями при сравнении Величины А и Величины В.
Правило №3: √(x)2 = 3, если x = 3, x = -3
Итак, вернемся к знаку квадратного корня, но теперь у нас есть и показатель степени! Что дальше? Указывать только положительное число, потому что мы имеем знак корня? Или указывать оба значения, потому что есть показатель степени?
Сначала вычислите значение x: возведите в степень оба значения √(x)2 = 3, чтобы получить x2 = 9. Вычислите квадратный корень, чтобы получить x = 3, x = -3 (как в правиле №2).
Подставьте оба числа в данное равенство, √x2 = 3, и посмотрите, делают ли они равенство верным.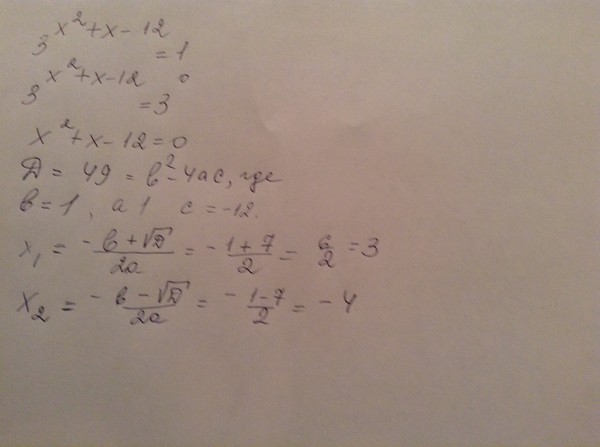 Если мы подставим 3 в равенство √x2 = 3, мы получим: √(3)2 = 3. Верно ли это? Да: √(3)2 = √9 и это действительно равняется 3.
Если мы подставим 3 в равенство √x2 = 3, мы получим: √(3)2 = 3. Верно ли это? Да: √(3)2 = √9 и это действительно равняется 3.
Теперь подставьте в равенство -3: √(-3)2= 3. Под корнем у нас стоит отрицательное число, но также в скобках у нас есть квадратная степень. Следуйте установленному порядку действий: возведите число в квадрат, чтобы получить √9. Больше нет никаких отрицательных чисел под знаком корня! Заканчивая решение задачи, мы получаем √9, и снова это должно равняться 3, поэтому -3 тоже является возможным значением x. X может быть равен как 3, так и -3.
GRE Math Practice: Как это все не забыть?
Запомните: в первом примере представлено либо действительное число, либо очевидная переменная (не возведение в степень!) под знаком квадратного корня. В обоих случаях мы должны получить решение с положительными значениями корня, но не отрицательными.
Второй и третий примеры имеют квадратную степень. Во втором правиле нет знака квадратного корня – в этом случае мы можем получить и положительный, и отрицательный ответ.
Подготовка к GRE Test включает в себя штудирование не только официальных учебников, но также изучение советов и подсказок, которые представлены здесь. Возможно, на самом тесте вам пригодятся именно они!
Пример несложного задания на квадратные корни в тесте GRE:
По материалам сайта: www.manhattanprep.com
Арифметические операции — JavaScript | MDN
Арифметические операции принимают в качестве операндов числовые значения (это может быть и литерал и переменная) и возвращают результат в виде одного числового значения. Стандартными арифметическими операциями являются сложение (
Стандартными арифметическими операциями являются сложение (+), вычитание (-), умножение (*) и деление (
Оператор сложения возвращает сумму числовых операндов или объединяет строки.
Синтаксис
Примеры
1 + 2
true + 1
false + false
5 + "foo"
"foo" + false
"foo" + "bar"
Оператор вычитания вычитает один операнд из другого и возвращает разницу.
Синтаксис
Примеры
Оператор деления производит деление его операндов, где левый операнд — делимый, а правый — делитель.
Синтаксис
Примеры
1 / 2
1 / 2
1.0 / 2.0
2.0 / 0
2.0 / 0.0
2.0 / -0.0 Оператор умножения возвращает произведение операндов.
Синтаксис
Примеры
2 * 2
-2 * 2
Infinity * 0
Infinity * Infinity
"foo" * 2
Оператор возвращает целый остаток от деления левого операнда на правый. Возвращаемое значение всегда получает знак делимого, а не делителя.
modulo, для получения результата, которая является целочисленным остатком деления var1 на var2 — например— var1 modulo var2. Есть предложение добавить оператор modulo в будущие версии ECMAScript, с той разницей, что оператор будет брать знак делителя, а не делимого.Синтаксис
Оператор: var1 % var2
Примеры
12 % 5 -1 % 2 NaN % 2 1 % 2 2 % 3 -4 % 2 5.5 % 2
Оператор возведения в степень возвращает результат первого операнда в степень. это, var1var2, в предыдущем выражении, где var1 и var2 — переменные. Он право ассоциативен. a ** b ** c равно a ** (b ** c).
Синтаксис
Оператор: var1 ** var2
Замечания
Во многих языках, таких как PHP и Python и других, есть оператор возведения возведения в степень (обычно ^ или **), оператор определён имеющим приоритет выше, чем у унарных операторов, таких как унарный + и унарный -, но есть несколько исключений. Например, в Bash оператор ** создан имеющим приоритет ниже, чем у унарных операторов. В JavaScript невозможно написать двухсмысленное выражение, т.е. вы не можете ставить унарный оператор (
Например, в Bash оператор ** создан имеющим приоритет ниже, чем у унарных операторов. В JavaScript невозможно написать двухсмысленное выражение, т.е. вы не можете ставить унарный оператор (+/-/~/!/delete/void/typeof) непосредственно перед базовым числом.
-2 ** 2;
-(2 ** 2);
Примеры
2 ** 3
3 ** 2
3 ** 2.5
10 ** -1
NaN ** 2
2 ** 3 ** 2
2 ** (3 ** 2)
(2 ** 3) ** 2 Изменим знак результата возведения в степень:
-(2 ** 2) Насильная установка основания как отрицательного числа:
(-2) ** 2 Оператор инкремента увеличивает на единицу(инкрементирует) операнд и возвращает значение.
- Если операция используется как постфикс, с оператором после операнда (например, x++), значение операнда возвращается, а затем увеличивается на единицу.
- Если используется префиксная форма с оператором перед операндом (например, ++x), значение операнда возвращается увеличенным на единицу.

Синтаксис
Оператор: x++ или ++x
Примеры
var x = 3;
y = x++;
var a = 2;
b = ++a;
Операция декремента уменьшает на 1 (отнимает единицу) свой операнд и возвращает значение.
- Если операция используется как постфикс (например, x—), значение операнда возвращается, а затем уменьшается на единицу.
- Если используется префиксная форма (например, —x), значение операнда возвращается уменьшенным на единицу.
Синтаксис
Оператор: x-- или --x
Примеры
var x = 3;
y = x--;
var a = 2;
b = --a;
Унарный минус ставится перед своим операндом и возвращает его математическое отрицание.
Синтаксис
Примеры
Оператор унарный плюс предшедствует своему операнду и оценивает его, пытается преобразовать его в число, если он им не является. Хотя, унарное отрицание (-) также конвертирует не числа, унарный плюс — быстрейший и предпочитаемый способ конвертирования чего-либо в число потому, что он не выполняет каких-либо операций с числом. Он может конвертировать строковые представления целых и чисел с плавающей точкой, а также нестроковые значения
Он может конвертировать строковые представления целых и чисел с плавающей точкой, а также нестроковые значения true, false и null. Поддерживаются числа в десятичном и шестнадцатиричном (с префиксом «0x») формате. Отрицательные числа тоже поддерживаются (но не 16-ричные). Если он не может вычислить конкретное значение, выполнится как NaN.
Синтаксис
Примеры
+3
+"3"
+true
+false
+null
Степенные или показательные уравнения.
Приветствую вас дорогие учащиеся!
Рекомендуем подписаться на канал на youtube нашего сайта TutoMath.ru, чтобы быть в курсе всех новых видео уроков.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=an
1. a0 = 1 (a ≠ 0)
a0 = 1 (a ≠ 0)
2. a1 = a
3. an • am = an + m
4. (an)m = anm
5. anbn = (ab)n
6. a-n= 1/an
7. an/am= an — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
6x=36
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2x*5=10
16x — 4x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
2х = 23
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.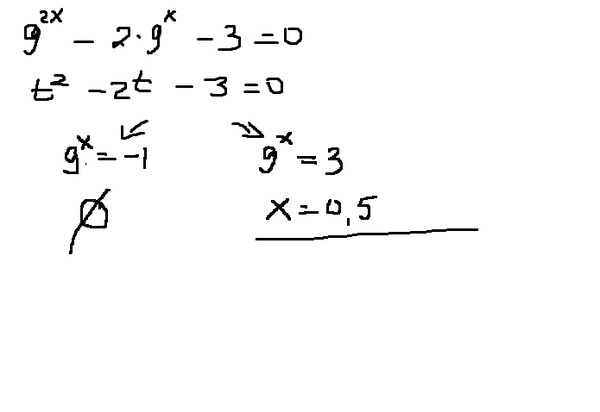
А теперь посмотрим как нужно это решение оформить:
2х = 23
х = 3
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
2х+2 = 24
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
33х — 9х+8 = 0
Для начала переносим девятку в правую сторону, получаем:
33х = 9х+8
Теперь нужно сделать одинаковые основания. Мы знаем что 9=32 . Воспользуемся формулой степеней (an)m = anm.
33х = (32)х+8
Получим 9х+8 =(32)х+8 =3 2х+16
33х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
22х+4 — 10•4х = 24
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (an)m = anm.
4х = (22)х = 22х
И еще используем одну формулу an • am = an + m:
22х+4 = 22х•24
Добавляем в уравнение:
22х•24 — 10•22х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 22х ,вот и ответ — 22х мы можем вынести за скобки:
22х(24 — 10) = 24
Посчитаем выражение в скобках:
24 — 10 = 16 — 10 = 6
6•22х = 24
Все уравнение делим на 6:
22х = 4
Представим 4=22:
22х = 22 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9х – 12*3х +27= 0
Преобразуем:
9х = (32)х = 32х
Получаем уравнение:
32х — 12•3х +27 = 0
Основания у нас одинаковы равны трем.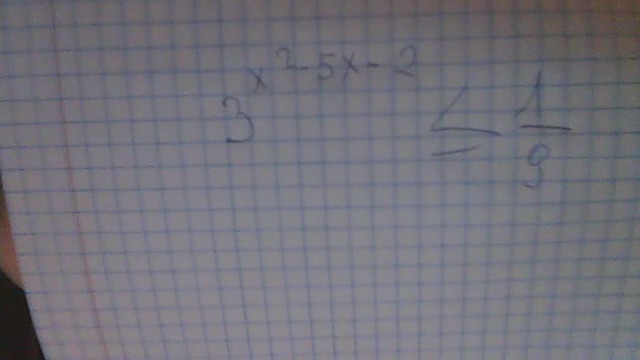 В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
3х = t
Тогда 32х = (3х)2 = t2
Заменяем в уравнении все степени с иксами на t:
t2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
t1 = 9
t2 = 3
Возвращаемся к переменной x.
Берем t1:
t1 = 9 = 3х
Стало быть,
3х = 9
3х = 32
х1 = 2
Один корень нашли. Ищем второй, из t2:
t2 = 3 = 3х
3х = 31
х2 = 1
Ответ: х1 = 2; х2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Уравнения и задачи на подбор параметра в Excel
Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.
Подбор параметра и решение уравнений в Excel
Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:
- y=7 является функцией x;
- нам известно значение y, следует узнать при каком значении x мы получим y вычисляемый формулой.
Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:
- Заполните ячейки листа, так как показано на рисунке:
- Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».

- В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:
В результате мы получили правильное значение 3.
Получили максимально точный результат: 2*3+1=7
Второй пример использования подбора параметра для уравнений
Немного усложним задачу. На этот раз формула выглядит следующим образом:
x2=4
Решение:
- Заполните ячейку B2 формулой как показано на рисунке:
- Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
- Сравните 2 результата вычисления:
Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.
Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:
x=(7-1)/2
Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.
Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:
Таким образом, если нас не устраивает результат вычислений, можно:
- Увеличить в настройках параметр предельного числа итераций.
- Изменить относительную погрешность.
- В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).
Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.
О подборе нескольких параметров в Excel узнаем из примеров следующего урока.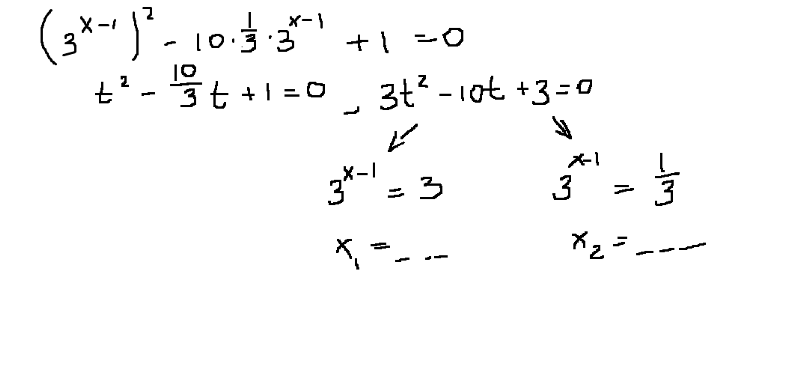
В клавиатуре Razer Huntsman V2 Analog используются аналоговые оптические переключатели
Компания Razer представила многофункциональную клавиатуру Razer Huntsman V2 Analog, оснащенную фирменными аналоговыми оптическими переключателями.
Количество света, проходящего через аналоговый оптический переключатель Razer переключатель, зависит от степени нажатия, что позволяет реализовать три новые возможности: аналоговый ввод, регулировку срабатывания и двухступенчатое срабатывание.
Аналоговый ввод имитирует работу джойстика для плавного управления в играх. В отличие от привычных дискретных переключений при использовании кнопок WASD, игроку становится доступно воздействие, пропорциональное нажатию.
Регулировка срабатывания позволяет настроить рабочий ход каждой клавиши, адаптируя клавиатуру к предпочтительному стилю игры: от быстрого срабатывания на 1,5 мм в динамичных играх до срабатывания на 3,6 мм, требующего «глубоких и продуманных нажатий».
При двухступенчатом срабатывании одно нажатие клавиши может активировать две функции, запрограммированные для разных точек срабатывания. Например, в игре нажатием наполовину можно будет взять гранату, а полным нажатием — метнуть ее в противника.
В отличие от традиционных механических переключателей аналоговые оптические переключатели Razer состоят из меньшего количества движущихся частей и не имеют никаких металлических контактных пар. Отсутствие механического взаимодействия между контактами позволило заявить ресурс 100 млн нажатий. Клавиатура распознает любое количество одновременно нажатых клавиш.
Колпачки клавиш изготовлены методом двойного литья из пластика под давлением, что делает надписи на них нестираемыми. Клавиатура будет доступна в нескольких региональных раскладках, включая русскую.
Устройство подключается к компьютеру с помощью кабеля USB в оплетке. Чтобы использовать сквозной порт USB 3.0, следует подключить второй кабель. Пользователи могут выбирать между подключением USB Type-C или USB Type-A, поскольку в комплект входит переходник.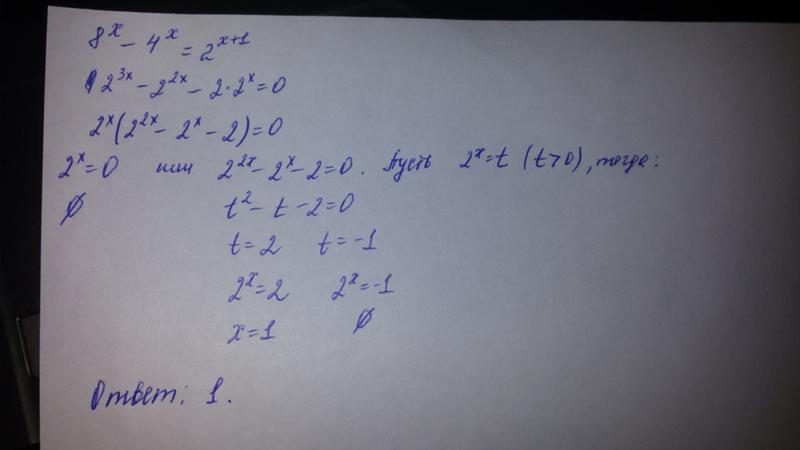 Кроме того, в комплекте есть упор для запястий, обтянутый кожзаменителем и фиксируемый с помощью магнитного крепления. Клавиатура украшена программируемой подсветкой RGB Chroma.
Кроме того, в комплекте есть упор для запястий, обтянутый кожзаменителем и фиксируемый с помощью магнитного крепления. Клавиатура украшена программируемой подсветкой RGB Chroma.
Рекомендуемая розничная цена равна 250 долларам, в Европе — 270 евро.
лидирует Kia Rio — Авторевю
Новый год на российском автомобильном рынке начался с падения продаж: в январе спрос сократился на 4,2%. По данным Ассоциации европейского бизнеса (АЕБ), реализовано 95,2 тысячи новых легковых машин и легких коммерческих автомобилей. Впрочем, это далеко не окончательный показатель, ведь в ежемесячную статистику АЕБ с прошлого года не входят марки Mercedes-Benz, BMW и Mini (они теперь публикуют свои отчеты ежеквартально), а вдобавок недостает узбекских моделей Chevrolet, нескольких китайских марок и элитных брендов. Впрочем, их вклад в общий результат невелик, поэтому картина рынка складывается правдивая.
Интересно, что из пятерки самых популярных марок три показали пусть небольшой, но рост продаж. Лада «вышла в ноль» благодаря Ниве, которая год назад была еще под брендом Chevrolet. А вот продажи Гранты и Весты просели — и бестселлером января стало семейство Kia Rio, показавшее 24-процентный рост! Creta и Solaris тоже «в плюсе», но в целом у компании Hyundai спад продаж на 4%. Зато набирают силу китайские производители: Chery и Haval продали больше автомобилей, чем Lexus или Mitsubishi.
Лада «вышла в ноль» благодаря Ниве, которая год назад была еще под брендом Chevrolet. А вот продажи Гранты и Весты просели — и бестселлером января стало семейство Kia Rio, показавшее 24-процентный рост! Creta и Solaris тоже «в плюсе», но в целом у компании Hyundai спад продаж на 4%. Зато набирают силу китайские производители: Chery и Haval продали больше автомобилей, чем Lexus или Mitsubishi.
В АЕБ ожидают, что в феврале и марте продажи будут расти и по результатам первого квартала выйдут на уровень прошлого года. Однако март 2020-го был действительно ударным на российском рынке: на пороге карантина произошел всплеск продаж, и превзойти тот результат (168 тысяч новых машин) сейчас едва ли удастся.
Продажи легковых и легких коммерческих автомобилей в России в январе 2021 года (в сравнении с январем 2020-го)
| Марка | январь 2021, шт. | январь 2020, шт. | Динамика |
|---|---|---|---|
| Лада | 21857 | 21790 | 0% |
| Kia | 15051 | 14955 | +1% |
| Hyundai | 10949 | 11397 | –4% |
| Renault | 8534 | 8293 | +3% |
| Volkswagen | 6166 | 6653 | –7% |
| Skoda | 6036 | 5945 | +2% |
| Toyota | 5333 | 6405 | –17% |
| Nissan | 3272 | 4938 | –34% |
| Mazda | 2153 | 1899 | +13% |
| ГАЗ | 2102 | 2568 | –18% |
| Chery | 1914 | 417 | +359% |
| Haval | 1567 | 1228 | +28% |
| Lexus | 1428 | 1111 | +29% |
| УАЗ | 1305 | 1942 | –33% |
| Audi | 1085 | 879 | +23% |
| Mitsubishi | 937 | 1539 | –39% |
| Ford | 910 | 368 | +147% |
| Geely | 555 | 778 | –29% |
| Land Rover | 448 | 421 | +6% |
| Volvo | 444 | 281 | +58% |
| Porsche | 412 | 253 | +63% |
| Suzuki | 410 | 521 | –21% |
| Subaru | 404 | 368 | +10% |
| Peugeot | 392 | 225 | +74% |
| Changan | 263 | 241 | +9% |
| Citroen | 213 | 209 | +2% |
| Cadillac | 131 | 60 | +118% |
| Jeep | 107 | 103 | +4% |
| Infiniti | 104 | 104 | 0% |
| FAW | 96 | 86 | +12% |
| Lifan | 83 | 146 | –43% |
| Honda | 82 | 107 | –23% |
| Cheryexeed | 81 | — | — |
| Fiat | 76 | 57 | +33% |
| Genesis | 57 | 110 | –48% |
| Opel | 56 | 2 | +2700% |
| Jaguar | 43 | 74 | –42% |
| Isuzu | 43 | 104 | –59% |
| IVECO | 40 | 20 | +100% |
| GAC | 27 | — | — |
| Chevrolet | 17 | 1231 | –99% |
| Brilliance | 13 | 16 | –19% |
| Zotye | 9 | 36 | –75% |
| Foton | 8 | 3 | +167% |
| Chrysler | 0 | 1 | — |
| Dongfeng | 0 | 82 | — |
| Datsun | 0 | 1403 | — |
Топ-25 самых популярных автомобилей в России в январе 2021 года (в сравнении с январем 2020-го)
| Модель | январь 2021, шт. |
январь 2020, шт. | Динамика |
|---|---|---|---|
| Kia Rio | 7763 | 6258 | +24% |
| Лада Гранта | 7720 | 8470 | –9% |
| Лада Веста | 6347 | 7506 | –15% |
| Hyundai Creta | 5701 | 5376 | +6% |
| Hyundai Solaris | 3481 | 3408 | +2% |
| Volkswagen Polo | 3256 | 3483 | –7% |
| Renault Duster | 2888 | 1773 | +63% |
| Лада Нива/Chevrolet Niva | 2809 | 1194 | +135% |
| Лада Ларгус универсал | 2379 | 2312 | +3% |
| Toyota RAV4 | 2321 | 2618 | –11% |
| Skoda Rapid | 2314 | 2040 | +13% |
| Volkswagen Tiguan | 1955 | 2273 | –14% |
| Renault Sandero | 1938 | 1685 | +15% |
| Kia Sportage | 1819 | 2531 | –28% |
| Skoda Kodiaq | 1760 | 1981 | –11% |
| Renault Logan | 1735 | 2083 | –17% |
| Лада XRAY | 1587 | 1239 | +28% |
| Mazda CX-5 | 1572 | 1380 | +14% |
| Kia Seltos | 1503 | 8 | — |
| Kia K5 | 1463 | 0 | — |
| Nissan Qashqai | 1359 | 1538 | –12% |
| Toyota Camry | 1338 | 1972 | –32% |
| Renault Kaptur | 1158 | 1380 | –16% |
| Hyundai Tucson | 1145 | 1382 | –17% |
| Nissan X-Trail | 1101 | 2073 | –47% |
Использование калькулятора
Это онлайн-калькулятор показателей степени. Вычислите степень больших целых и действительных чисел. Вы также можете вычислять числа в степени большой степени меньше 1000, отрицательной степени и действительных чисел или десятичных знаков для экспонент.
Вычислите степень больших целых и действительных чисел. Вы также можете вычислять числа в степени большой степени меньше 1000, отрицательной степени и действительных чисел или десятичных знаков для экспонент.
Для больших показателей попробуйте Калькулятор больших показателей
В учебных целях решение расширяется, когда основание x и показатель степени n достаточно малы, чтобы поместиться на экране.{4}} \)
\ (= \; \ dfrac {1} {3 \ cdot 3 \ cdot 3 \ cdot 3} \)
\ (= \; \ dfrac {1} {81} \)
\ (= 0,012346 \)
экспонент:
Обратите внимание, что -4 2 и (-4) 2 дают разные ответы: -4 2 = -1 * 4 * 4 = -16, а (-4) 2 = (-4) * (-4) = 16. Если вы вводите отрицательное значение для x, например -4, этот калькулятор принимает (-4) n .
«Когда знак минус встречается в экспоненциальном представлении, следует соблюдать определенную осторожность. Например, (-4) 2 означает, что -4 нужно возвести во вторую степень. Следовательно, (-4) 2 = (-4) * (-4) = 16. С другой стороны, -4 2 представляет аддитивную инверсию 4 2 . Таким образом, -4 2 = -16. Это может помочь подумать о -x 2 как -1 * x 2 … «[1]
Примеры:
- 3 в степени 4 записывается 3 4 = 81.
- -4 в степени 2 записывается (-4) 2 = 16.
- -3 в степени 3 записывается (-3) 3 = -27. Обратите внимание, что в этом случае ответ будет одинаковым для -3 3 и (-3) 3 , однако они все равно рассчитываются по-разному. -3 3 = -1 * 3 * 3 * 3 = (-3) 3 = -3 * -3 * -3 = -27.

- Для 0 в степени 0 ответ — 1, однако это считается определением, а не фактическим вычислением.м} \)
Ссылки
[1] Алгебра и тригонометрия: функциональный подход; М. Л. Киди и Марвин Л. Биттингер; Издательская компания «Аддисон Уэсли»; 1982, стр. 11.
Математический форум: Показатели и отрицательные числа.
Подробнее о теории экспонент см. Экспонентные законы.
Для вычисления дробных показателей используйте нашу Калькулятор дробных показателей.
Для вычисления корня или корней используйте наш Калькулятор корней.
экспонентов
Показатель числа означает , сколько раз использовать при умножении.

В 8 2 «2» означает использование 8 дважды при умножении,
, поэтому 8 2 = 8 × 8 = 64Словами: 8 2 можно назвать «8 в степени 2» или «8 во второй степени», или просто «8 в квадрате»
Показатели также называют степенями или индексами.
Еще несколько примеров:
Пример:
5 3 = 5 × 5 × 5 = 125- Словами: 5 3 можно было бы назвать «5 в третьей степени», «5 в степени 3» или просто «5 кубов»
Пример:
2 4 = 2 × 2 × 2 × 2 = 16- Словами: 2 4 можно было бы назвать «2 в четвертой степени» или «2 в степени 4» или просто «2 к 4»
Показатели упрощают запись и использование множества умножений
Пример: 9 6 легче писать и читать, чем 9 × 9 × 9 × 9 × 9 × 9
Вы можете умножить любое число на само столько раз, сколько хотите, используя экспоненты.
 4 = 2 × 2 × 2 × 2 = 16
4 = 2 × 2 × 2 × 2 = 16
Отрицательные экспоненты
Отрицательный? Что может быть противоположностью умножения? Разделение!
Итак, мы каждый раз делим на число, что аналогично умножению на 1 число
Пример: 8 -1 = 1 8 = 0,125
Мы можем продолжить так:
Пример: 5 -3 = 1 5 × 1 5 × 1 5 = 0.008
Но зачастую проще сделать так:
5 -3 также можно рассчитать как:
1 5 × 5 × 5 = 1 5 3 = 1 125 = 0,008
Отрицательный? Переверните позитив!
Последний пример показал более простой способ справиться с отрицательными показателями:
|
Другие примеры:
| Отрицательная экспонента | Взаимное значение положительной экспоненты | Ответ | ||
|---|---|---|---|---|
| 4 -2 | = | 1/4 2 | = | 1/16 = 0,0625 |
| 10 -3 | = | 1/10 3 | = | 1/1000 = 0.001 |
| (-2) -3 | = | 1 / (-2) 3 | = | 1 / (- 8) = -0,125 |
Что делать, если показатель степени равен 1 или 0?
| 1 | Если показатель степени равен 1, то у вас есть только само число (например, 9 1 = 9 ) | |
| 0 | Если показатель степени равен 0, то вы получите 1 (например, 9 0 = 1 ) | |
А как насчет 0 0 ? Это может быть либо 1, либо 0, поэтому люди говорят, что это «неопределенный» . |
Все имеет смысл
Если вы посмотрите на эту таблицу, вы увидите положительный результат, ноль или отрицательные показатели на самом деле являются частью того же (довольно простого) паттерна:
| Пример: Полномочия 5 | |||
|---|---|---|---|
| .. и т.д .. | |||
| 5 2 | 5 × 5 | 25 | |
| 5 1 | 5 | 5 | |
| 5 0 | 1 | 1 | |
| 5 -1 | 1 5 | 0.2 | |
| 5 -2 | 1 5 × 1 5 | 0,04 | |
. . и т.д .. . и т.д .. | |||
Будьте осторожны при группировке
Во избежание путаницы используйте круглые скобки () в таких случаях:
| С (): | (-2) 2 = (-2) × (-2) = 4 |
| Без (): | -2 2 = — (2 2 ) = — (2 × 2) = -4 |
| С (): | (ab) 2 = ab × ab |
| Без (): | ab 2 = a × (b) 2 = a × b × b |
Три правила экспонент — Полный курс алгебры
Урок 13, Раздел 2
Вернуться в раздел 1
Правило 1. Та же база
Та же база
Правило 2. Мощность продукта
Правило 3. Мощность силы
Правило 1. То же основание
«Чтобы умножить степени одного основания, сложите экспоненты».
Например, a 2 a 3 = a 5 .
Почему мы добавляем экспоненты? Из-за того, что означают символы. Секция 1.
Пример 1. Умножение 3 x 2 · 4 x 5 · 2 x
Решение . Задача означает (Урок 5): умножьте числа, затем сложите степени x :
.3 x 2 · 4 x 5 · 2 x = 24 x 8
Два фактора x — x 2 — умножить на пять факторов x — x 5 — умножить на один фактор x , получить всего 2 + 5 + 1 = 8 множителей x : x 8 .
Задача 1. Умножить. Примените правило Same Base.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
| а) | 5 x 2 · 6 x 4 = 30 x 6 | б) | 7 x 3 · 8 x 6 = 56 x 9 | ||||
| в) | x · 5 x 4 = 5 x 5 | г) | 2 x · 3 x · 4 x = 24 x 3 | ||||
| e) | x 3 · 3 x 2 · 5 x = 15 x 6 | е) | x 5 · 6 x 8 y 2 = 6 x 13 y 2 | ||||
| г) | 4 x · y · 5 x 2 · y 3 = 20 x 3 y 4 | ч) | 2 x y · 9 x 3 y 5 = 18 x 4 y 6 | ||||
| i) | a 2 b 3 a 3 b 4 = a 5 b 7 | к) | a 2 bc 3 b 2 ac = a 3 b 3 c 4 | ||||
| к) | x м y n x p y q = x m41 900 y n + q | л) | a p b q ab = a p + 1 b q + 1 | ||||
Проблема 2. Различают следующие:
Различают следующие:
x · x и x + x .
x · x = x ². х + х = 2 х .
Пример 2. Сравните следующее:
а) x · x 5 б) 2 · 2 5
Решение .
a) x · x 5 = x 6
b) 2 · 2 5 = 2 6
Часть b) имеет ту же форму , что и часть a). Это часть а) с x = 2.
Один множитель 2 умножает пять множителей 2, давая шесть множителей 2.
2 · 2 = 4 здесь неверно.
Проблема 3. Примените правило Same Base.
| а) | x x 7 = x 8 | б) | 3 · 3 7 = 3 8 | в) | 2 · 2 4 · 2 5 = 2 10 | ||
| г) | 10 · 10 5 = 10 6 | д) | 3 x · 3 6 x 6 = 3 7 x 7 | ||||
Проблема 4. Примените правило Same Base.
Примените правило Same Base.
| а) | x n x 2 = x n + 2 | б) | x n x = x n + 1 | ||||
| в) | x n x n = x 2 n | г) | x n x 1- n = x | ||||
| e) | x · 2 x n — 1 = 2 x n | е) | x n x m = x n + m | ||||
| г) | x 2 n x 2- n = x n + 2 | ||||||
Правило 2: Мощность произведения факторов
«Увеличьте каждый коэффициент до той же степени. «
«
Например, ( ab ) 3 = a 3 b 3 .
Почему мы можем это сделать? Опять же, согласно значению символов:
( ab ) 3 = ab · ab · ab = aaabbb = a 3 b 3 .
Порядок факторов не имеет значения:
ab · ab · ab = aaabbb .
Задача 5. Применить правила экспонент.
| а) | ( x y ) 4 = x 4 y 4 | б) | ( pqr ) 5 = p 5 q 5 r 5 | в) | (2 abc ) 3 = 2 3 a 3 b 3 c 3 |
| d) x 3 y 2 z 4 ( xyz ) 5 | = | x 3 y 2 z 4 · x 5 y 5 z 5 Правило 2. |
| = | x 8 y 7 z 9 То же основание. | |
Правило 3: Степень мощности
«Чтобы взять степень степени, умножьте степени».
Например, ( a 2 ) 3 = a 2 · 3 = a 6 .
Почему мы это делаем? Опять же, из-за того, что означают символы:
( a 2 ) 3 = a 2 a 2 a 2 = a 3 · 2 = a 6
Задача 6. Примените правила экспонент.
| а) | ( x 2 ) 5 = x 10 | б) | ( a 4 ) 8 = a 32 | в) | (10 7 ) 9 = 10 63 |
Пример 3. Примените правила экспонент: (2 x 3 y 4 ) 5
Примените правила экспонент: (2 x 3 y 4 ) 5
Решение . В скобках указаны три фактора: 2, x 3 и y 4 . Согласно Правилу 2 мы должны брать пятую степень каждого из них. Но чтобы взять степень степени, мы умножаем показатели. Следовательно,
(2 x 3 y 4 ) 5 = 2 5 x 15 y 20
Проблема 7.Применяйте правила экспонент.
| а) | (10 a 3 ) 4 = 10 000 a 12 | б) | (3 x 6 ) 2 = 9 x 12 | |
| в) | (2 a 2 b 3 ) 5 = 32 a 10 b 15 | г) | ( xy 3 z 5 ) 2 = x 2 y 6 z 10 | |
| e) | (5 x 2 y 4 ) 3 = 125 x 6 y 12 | е) | (2 a 4 bc 8 ) 6 = 64 a 24 b 6 c 48 | |
Проблема 8. Применяйте правила экспонент.
Применяйте правила экспонент.
a) 2 x 5 y 4 (2 x 3 y 6 ) 5 = 2 x 5 y 4 · 2 5 x 15 y 30 = 2 6 x 20 y 34
b) abc 9 ( a 2 b 3 c 4 ) 8 = abc 9 · a 16 b 24 c 32 = a 17 b 25 c 41 9
Проблема 9.Используйте правила экспонент, чтобы вычислить следующее.
а) (2 · 10) 4 = 2 4 · 10 4 = 16 · 10 000 = 160 000
б) (4 · 10 2 ) 3 = 4 3 · 10 6 = 64 000 000
в) (9 · 10 4 ) 2 = 81 · 10 8 = 8 100 000 000
В степенях 10 столько же нулей, сколько в экспоненте 10.
Пример 4. Квадрат x 4 .
Решение . ( x 4 ) 2 = x 8 .
Чтобы возвести в квадрат степень, удвойте экспоненты.
Проблема 10. Возведите следующее.
| а) | x 5 = x 10 | б) | 8 a 3 b 6 = 64 a 6 b 12 | |
| в) | −6 x 7 = 36 x 14 | г) | x n = x 2 n | |
Часть c) иллюстрации: Квадрат числа никогда не бывает отрицательным.
(−6) (- 6) = +36. Правило знаков.
Задача 11. Примените правило экспонент — если возможно.
| а) | x 2 x 5 = x 7 , Правило 1. | б) | ( x 2 ) 5 = x 10 , Правило 3. |
| в) | x 2 + x 5 |
| Невозможно. Правила экспонент применяют только к умножению. |
В итоге: Добавьте показателей степени, когда одно и то же основание появляется дважды: x 2 x 4 = x 6 . Умножьте на степень, когда основание появится один раз — и в скобках: ( x 2 ) 5 = x 10 .
Задача 12. Примените правила экспонент.
| а) | ( x n ) n = x n · n = x n 2 2 | б) | ( x n ) 2 = x 2 n |
Проблема 13. Примените правило экспонент или добавьте похожие термины — если возможно.
Примените правило экспонент или добавьте похожие термины — если возможно.
а) 2 x 2 + 3 x 4 Невозможно. Это не похоже на термины .
б) 2 x 2 · 3 x 4 = 6 x 6 . Правило 1.
в) 2 x 3 + 3 x 3 = 5 x 3 .Как термины. Показатель степени не меняется.
г) x 2 + y 2 Невозможно. Это не термины.
e) x 2 + x 2 = 2 x 2 . Как термины.
е) x 2 · x 2 = x 4 . Правило 1
г) x 2 · y 3 Невозможно.Разные базы.
ч) 2 · 2 6 = 2 7 . Правило 1
i) 3 5 + 3 5 + 3 5 =
3 · 3 5 (При добавлении подобных терминов) = 3 6 .
Мы продолжим правила экспонент в 21 уроке.
Следующий урок: Умножение. Распределительное правило.
Вернуться в раздел 1
Содержание | Дом
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Уроки по упрощению экспонент | Ресурсы Wyzant
Прежде чем мы углубимся в упрощение экспоненты, давайте потратим некоторое время, чтобы узнать, что именно такое экспонента. Показатель — это верхний индекс, или небольшое число, написанное в правом верхнем углу числа, переменной или набора круглых скобок. Пример одного показан ниже.
2 3
Это говорит вам умножить 1 на число столько раз, сколько указано в экспоненте.В приведенном выше примере 2 в третьей степени (в третьей степени
означает, что показатель степени равен 3). Это эквивалентно задаче умножения ниже, потому что 1 умножается на 2 три
раз.
Это эквивалентно задаче умножения ниже, потому что 1 умножается на 2 три
раз.
1 * 2 * 2 * 2
8
Как видите, 1 * 2 * 2 * 2 можно упростить до 8, что является ответом на проблему.
Экспоненты
Изучите следующую проблему:
-3 6
Эта задача заменена задачей умножения, описанной ниже.Из-за порядка операций (объяснено на следующем уроке) сначала упрощается показатель степени, а затем к ответу добавляется отрицательный знак.
1 * 3 * 3 * 3 * 3 * 3 * 3
-729
Как видите, умножение упрощается до числа -729. Вы можете проделать эту работу в уме, на полях бумаги или с помощью калькулятора, если это возможно.
Экспоненты
Следующая проблема показана ниже:
(-3) 6
На этот раз -3 в круглых скобках. Вместо того, чтобы переносить отрицательный знак, каждые 3 становятся отрицательными.
Вместо того, чтобы переносить отрицательный знак, каждые 3 становятся отрицательными.
1 * -3 * -3 * -3 * -3 * -3 * -3
729
Как видите, умножение упрощается до 729. Обратите внимание, что помимо результат предыдущего примера отрицательный, результат вот то же самое. Обратите особое внимание на поиск экспонентов, когда они отрицательны. присутствуют знаки, так как это частый источник ошибок.
Особые случаи
Нулевой показатель
Каждая из этих проблем решается умножением единицы на число, количество раз, которое указывает экспонента. Если показатель равен 0, то 1 не умножить на число вообще. Следовательно, ответ — 1. Это важное правило, о котором следует помнить.
51 0
1
Ноль с показателем степени:
В большинстве случаев ноль с показателем степени можно вычислить как любое другое число. и показатель степени.
и показатель степени.
0 4
1 * 0 * 0 * 0 * 0
0
Обратите внимание, что до тех пор, пока 1 умножается хотя бы на один 0, конечный результат равен 0. Следовательно, мы можем заключить, что 0 для любого положительного показателя всегда равен нулю.
Другой особый случай — 0 0 . Ноль с показателем ноль не определен и не может быть вычислен.
Будьте осторожны, не соблюдайте правила нулевых показателей! От нуля до любой положительной силы всегда равен нулю, потому что сколько бы раз вы ни умножали 1 на ноль ответ всегда будет ноль.Но 0 0 не определено.
1 показатель степени:
Рассмотрим этот пример, в котором rasies число возведено в первую степень.
51 1
1 * 51
51
Если вы попробуете любой аналогичный пример, например 10 1 или 100 1 , вы
обнаружит, что результатом всегда будет исходное число или основание. Это
потому что 1, умноженное на любое другое число, всегда равно второму числу.
Это
потому что 1, умноженное на любое другое число, всегда равно второму числу.
Итак, чтобы упростить случай, когда число возводится в первую степень, мы можем просто удалите показатель степени.
Экспоненты
От десяти до любой степени
Этот совет поможет вам сэкономить много времени: десять в любой степени — это просто цифра 1. за которым следует количество нулей, обозначенных показателем степени. Пример показан ниже.
10 5
100 000
Обратите внимание, что результатом является единица с пятью нулями, поскольку показатель степени 10 было 5.
Показатели чтения
В общем проблема типа
5 10
читается как «пять в десятой степени».
Специальные случаи для чтения экспонент
У некоторых экспонентов есть особые способы произношения. Это делает его
Проще сказать, но совсем не обязательно, чтобы вы их использовали.
Это делает его
Проще сказать, но совсем не обязательно, чтобы вы их использовали.
- Вторая степень: 3 2 — может читаться как «Тройка во второй степени» или «Тройка в квадрате».»
- Третья степень: 10 3 — может читаться как «Десять в третьей степени» или «10 в кубе».
Показатели числа ресурсов
Подпишись бесплатно для доступа к дополнительным ресурсам по алгебре, например. Ресурсы Wyzant содержат блоги, видео, уроки и многое другое по алгебре и более чем 250 другим предметам. Прекратите бороться и начните учиться сегодня с тысячами бесплатных ресурсов!Exponent Calculator — возведен в калькулятор мощности
Exponents Calculator или электронный калькулятор используется для решения экспоненциальных форм выражений.Его также называют возведенным в счетчик мощности.
Свойства калькулятора показателей:
Этот калькулятор решает оснований с и отрицательными показателями и положительными показателями . Он также предоставляет пошаговый метод с точным ответом.
Он также предоставляет пошаговый метод с точным ответом.
Что такое показатель степени?
Показатель степени — это небольшое число, расположенное в верхнем правом положении экспоненциального выражения (основание показателя степени), которое указывает степень возведения основания выражения.
Показатель числа показывает, сколько раз это число должно быть использовано при умножении. Показатели не обязательно должны быть числами или константами; они могут быть переменными.
Часто это положительные целые числа, но они могут быть отрицательными, дробными, иррациональными или комплексными числами. Оно записывается в виде маленького числа справа и над основным числом.
Типы:
Существует два основных типа показателей степени.
Положительная экспонента указывает, сколько раз число необходимо умножить само на себя. Воспользуйтесь нашим калькулятором экспоненты для решения ваших вопросов.
Отрицательный показатель степени показывает, в какой части основания находится решение. Чтобы упростить показателей степени со степенью в виде дробей , используйте наш калькулятор степени .
Пример :Вычислите показатель степени для числа 3 в степени 4 ( 3 в степени 4 ).
Это означает = 3 4
Решение:
3 * 3 * 3 * 3 = 81
4 в 3-й степени = 81
Следовательно, показатель степени равен 81
2 в повышении вычислитель мощности.
Пример :Каково значение экспонента для 2 поднять до степени 9 (2 в 9 степени)
Это означает = 2 9
Решение:
2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 512
2 в 9-й степени = 512
Следовательно, показатель степени равен 512 .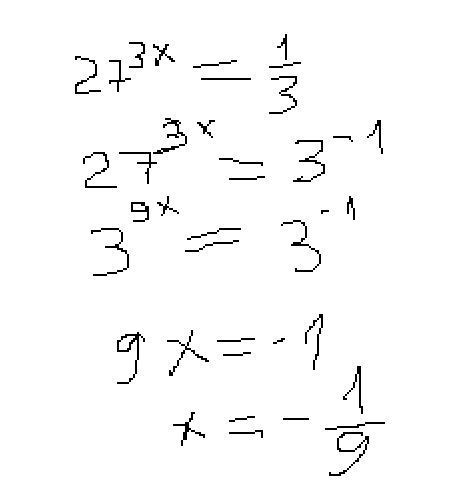
Как вычислить показатели 5,6,7 в степени 4?
Это означает = 5 4 , 6 4 , 7 4
Решение:
5 * 5 * 5 * 5 = 625
6 * 6 * 6 * 6 = 1296
7 * 7 * 7 * 7 = 2401
Следовательно, показателей равны 625, 1296, 2401.
Как вычислить n-ю степень числа?
Энная степень основания, скажем «у», означает, что у умножается на себя в энный раз.Если нам нужно найти пятую степень y, это будет y * y * y * y * y.
Некоторые другие решения для n-й вычислитель мощности приведены в следующей таблице.
| 0,1 в степени 3 | 0,00100 | |||
| 0,5 в степени 3 | 0,12500 | |||
| 0,5 в степени 4 | 0,06250 | 1,2 902 в степени 902 4 | 2,07360 | |
1. 02 в 10-й степени 02 в 10-й степени | 1.21899 | |||
| 1,03 в 10-й степени | 1,34392 | |||
| 1,2 в 5-й степени | 2.48832 | |||
| 1,4 в 10-й степени | 1,03 до степени 5 | 1,27628 | ||
| 1,05 до 10 степени | 1,62889 | |||
| 1,06 до 10 степени | 1,79085 | |||
| 2 до 3 степени | 2 | 2 | степень 3 | 8 |
| 2 в степени 4 | 16 | |||
| 2 в степени 6 | 64 | |||
| 2 в степени 7 | 128 | |||
| 2 в 9 степени | 512 | |||
| 2 в десятой степени | 1024 | |||
| 2 в 15 степени | 9 0230 32768||||
| 2 в 10 степени | 1024 | |||
| 2 в степени 28 | 268435456 | |||
| 3 в степени 2 | 9 | |||
| 9 | ||||
| 27 | ||||
| От 3 до 4 степени | 81 | |||
| От 3 до 8 степени | 6561 | |||
| От 3 до 9 степени | 19683 | |||
| от 3 до | ||||
| 3 в степени, равной 81 | 3 4 | |||
| 4 в степени 3 | 64 | |||
| 4 в степени 4 | 256 | |||
| 4 в степени из 7 | 16384 | |||
| 7 в степени 3 | 343 | |||
| 12 во 2 степени | 144 | |||
2. 5 в степени 3 5 в степени 3 | 15,625 | |||
| 12 в степени 3 | 1728 | |||
| 10 степени 3 | 1000 | |||
| 24 во второй степени (24 2 ) | 57 |
Изучение правил экспоненты вместе с правилами журнала может сделать математику действительно простой для понимания. Есть 7 правил экспоненты.
- Ноль Свойство экспоненты:
Это означает, что если степень основания равна нулю, то значение решения будет равно 1.
Пример: Упростить 5 0 .
В этом вопросе степень основания равна нулю, тогда в соответствии с нулевым свойством экспоненты ответ ненулевого основания равен 1. Следовательно,
5 0 = 1
- Отрицательное свойство экспоненты:
Это означает, что когда степень основания является отрицательным числом, то после умножения нам нужно будет найти обратную величину ответа.
Пример: Упростить 13 -2 .
Сначала сделаем силу положительной, взяв обратную.
1/3 -2 = 3 2
3 2 = 9
- Продукт Свойство экспоненты:
Когда два экспоненциальных выражения с одинаковым ненулевым основанием и разными степенями умножаются, тогда их силы складываются на той же базе.
Пример : Решить (2 6 ) (2 2 ).
Как видно, базы такие же, поэтому силы надо добавлять.Теперь
(2 6 ) (2 2 ) = 2 6 +2
2 8 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2
= 256
- Факторное свойство показателя степени:
Оно противоположно свойству произведения показателя степени. Когда требуется разделить две одинаковые базы с разными показателями, их силы вычитаются.
Пример: Simplify 3 7 /3 2
3 7 /3 2 = 3 7-2
35 = 3 * 3 * 3 * 3 * 3
= 243
- Степень мощности Свойство:
Если в выражении экспоненты еще есть мощность, то сначала вам нужно умножить степени, а затем решить выражение.
Пример: Решить: (x 2 ) 3 .
Учитывая силу степенного свойства показателей, умножим степени.
(x 2 ) 3 = x 2 * 3
= x 6
- Мощность свойства продукта:
Когда продукт баз повышается до некоторой степени, основания будет обладать властью отдельно.
Пример: Упростить (4 * 5) 2
4 2 * 5 2 = 16 * 25
=
- Мощность частного свойства:
Это то же самое, что мощность свойства продукта.Власть принадлежит как числителю, так и знаменателю отдельно.
Пример: Решить (2/3) 2
(2/3) 2 = 2 2 /3 2
2 2 /3 2 = 4 / 9
Инволюция и полномочия, вторая, третья, четвертая степень
Когда количество умножается на само , произведение называется степенью .
Таким образом, 2 × 2 = 4, квадрат или вторая степень двойки.
2 × 2 × 2 = 8, куб или третья степень.
2 × 2 × 2 × 2 = 16, в четвертой степени.
Итак, 10 × 10 = 100, вторая степень 10.
10 × 10 × 10 = 1000, третья степень.
10 × 10 × 10 × 10 = 10000 в четвертой степени.
И a × a = aa, вторая степень a
a × a × a = aaa, третья степень
а × а × а × а = аааа, четвертой степени.
Сама исходная величина, в отличие от исходящих от нее степеней, не порождается умножением, тем не менее, называется первой степенью . Его также называют базовым .
Поскольку записывать все буквы или множители, из которых состоят эти полномочия, неудобно, особенно в случае высоких степеней, обычно применяется сокращенный метод записи. База записывается только один раз, а затем цифра или буква помещаются справа и немного приподняты, чтобы показать, сколько раз основание используется как коэффициент , чтобы произвести мощность. Это число или буква называется показателем степени или показателем степени степени.Таким образом, 2 ставится вместо a × a или aa, потому что a, дважды повторяется как множитель, чтобы получить мощность aa.
А 3 означает aaa; здесь повторяется трижды как множитель.
Это число или буква называется показателем степени или показателем степени степени.Таким образом, 2 ставится вместо a × a или aa, потому что a, дважды повторяется как множитель, чтобы получить мощность aa.
А 3 означает aaa; здесь повторяется трижды как множитель.
Показатель первой степени равен 1; но это обычно опускается. Таким образом, 1 — это то же самое, что и.
Экспоненты не следует путать с коэффициентами . Коэффициент показывает, как часто количество принимается как часть целого.Показатель степени показывает, как часто количество используется в продукте как коэффициент .
Таким образом, 4a = a + a + a + a. Но а 4 = а × а × а × а
Схема обозначения экспонентами имеет особое преимущество, так как позволяет нам выразить неизвестную степень .
Для этого показатель степени представляет собой букву вместо числовой цифры. При решении проблемы может возникнуть величина, которая, как мы знаем, равна , или степени другой величины.Но можно еще не установить, квадрат это, куб или некоторая высшая степень.
При решении проблемы может возникнуть величина, которая, как мы знаем, равна , или степени другой величины.Но можно еще не установить, квадрат это, куб или некоторая высшая степень.
Таким образом, в выражении a x показатель x означает, что a увеличивается до в некоторой степени , хотя он не определяет , какая степень . Итак, b m и d n — степени b и d; и читаются в m-й степени от b и в n-й степени d. Когда значение показателя степени найдено, букву обычно заменяют числом . Таким образом, если m = 3, то b m = b 3 ; а если m = 5, то b m = b 5 .
Метод выражения степеней степенями также имеет большое преимущество в случае соединений величин.
Таким образом, (a + b + d) 3 — это (a + b + d) × (a + b + d) × (a + b + d), то есть куб из (o + 6 + d).
a 3 + 3a 2 b + 3a 2 d + 3ab 2 + 6abd + 3ad 2 + b 3 + d 3 .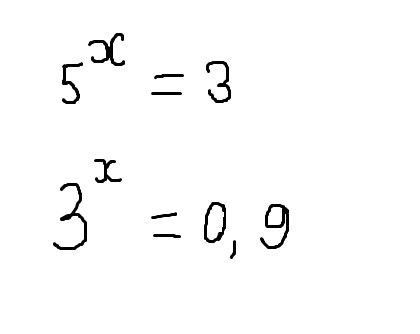
Если мы возьмем ряд степеней, индексы которых увеличиваются или уменьшаются на 1, мы обнаружим, что сами степени увеличиваются на общий множитель или уменьшаются на общий делитель ; и что этот множитель или делитель является исходной величиной, от которой возводятся степени.
Таким образом, в серии ааааа, аааа, ааа, аа, а;
Или 5 , 4 , 3 , 2 , 1 ;
индексы, отсчитываемые справа налево: 1, 2, 3, 4, 5; и общая разница между ними — единица. Если мы начнем с справа, и умножим на a, мы произведем несколько степеней, последовательно, справа налево.
Таким образом, a × a = a 2 второй член. И a 3 × a = a 4
a 2 × a = a 3 третий член.а 4 × а = а 5 .
Если мы начнем с слева , а разделим на a,
У нас есть 5 : a = a 4
и 3 : a = a 2 .
a 4 : a = a 3
a 2 : a = a 1
Но это разделение может быть продолжено еще дальше; и тогда мы получим новый набор величин.
Таким образом, $ a: a = \ frac {a} {a} = 1 $.
$ \ frac {1} {a}: a = \ frac {1} {aa} $
$ 1: a = \ frac {1} {a} $ $ \ frac {1} {aa}: a = \ frac {1} {aaa} $
Тогда вся серия будет aaaaa, aaaa, aaa, aa, a, 1, $ \ frac {1} {a} $, $ \ frac {1} {aa} $, $ \ frac {1} {aaa} $.{-4} $.
И чтобы сделать индексы полной серией, с 1 для общей разницы, термин $ \ frac {a} {a} $ или 1, который рассматривается как отсутствие мощности, записывается как 0 .
Полномочия как прямые, так и взаимные * tnen,
Вместо aaaa, aaa, aa, a, $ \ frac {a} {a} $, $ \ frac {1} {a} $, $ \ frac {1} {aa} $, $ \ frac {1} {aaa} $, $ \ frac {1} {aaaa} $.
будет 4 , 3 , 2 , 1 , 0 , -1 , -2 , -3 , -4 .
Или +4 , +3 , +2 , +1 , 0 , -1 , -2 , -3 , а -4 .
И индексы, взятые сами по себе, будут,
+4, +3, +2, +1, 0, -1, -2, -3, -4.
Основание степени может быть выражено несколькими буквами.
Таким образом, aa × aa, или (aa) 2 — вторая степень aa.
И aa × aa × aa, или (aa) 3 — третья степень aa.
Следовательно, определенная мощность одной величины может быть другой мощностью другой величины. Таким образом, 4 — это вторая степень a и четвертая степень a.
Все степени 1 одинаковы. Для 1 × 1 или 1 × 1 × 1. по-прежнему 1.
Инволюция — это обнаружение любой силы количества путем умножения ее на себя. Причина следующего общего правила очевидна из природы власти.
Умножьте количество на себя, пока оно не будет принято в качестве множителя, столько раз, сколько единиц в мощности, до которой это количество должно быть увеличено.
Это правило охватывает все случаи, которые могут произойти в инволюции. Но будет уместно дать объяснение тому, как это применяется к конкретным случаям.
Отдельная буква возводится в степень, повторяя ее столько раз, сколько ее экспонента.
Четвертая степень a — это 4 или aaaa.
Шестая степень y равна y 6 или yyyyyy.
n-я степень x, x n или xxx ….. n повторений.
Метод включения количества, состоящего из нескольких факторов, зависит от принципа , согласно которому мощность произведения нескольких факторов равна произведению их мощностей.
Таким образом (ay) 2 = a 2 y 2 For (ay) 2 = ay × ay.
Но ay × ay = ayay = aayy = a 2 y 2 .
So (bmx) 3 = bmx × bmx × bmx = bbbmmmxxx = b 3 m 3 x 3 .
Следовательно, обнаруживая силу продукта, мы можем либо возвысить все сразу; или мы можем возвести каждый из факторов отдельно, а затем умножить их несколько степеней друг на друга.
Ex.1. Четвертая степень dhy — это (dhy) 4 , или d 4 h 4 y 4 .
2. 3-я степень 4b: (4b) 3 , или 4 3 b 3 , или 64b 3 .
3. Энная степень числа 6ad равна (6ad) n или 6 n a n d n .
4. Трехмерная степень 3m × 2y равна (3m × 2y) 3 , или 27m 3 × 8y 3 .
Сложная величина, состоящая из десятков, соединенных знаками + и -, возводится в действительное умножение ее нескольких частей.Таким образом,
(a + b) 1 = a + b, первая степень.(a + b) 2 = a 2 + 2ab + b 2 , вторая степень (a + b).
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 , третья степень.
(a + b) 4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4 , четвертая степень.
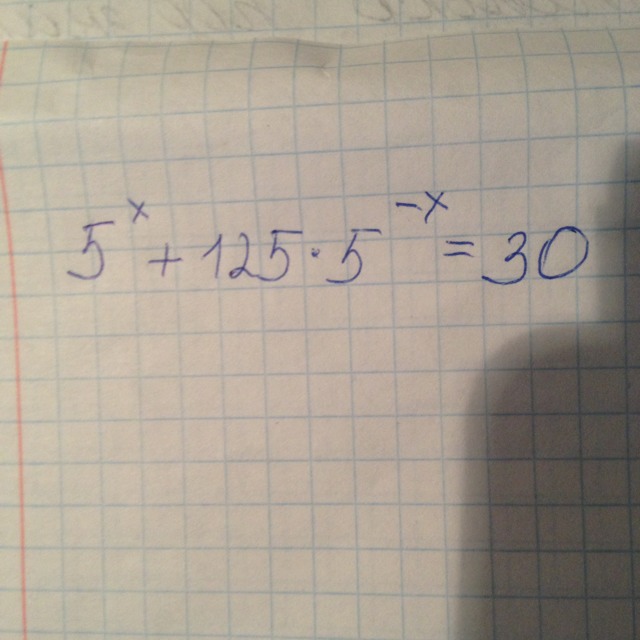
2. Квадрат a — b равен a 2 — 2ab + b 2 .
3. Куб a + 1 — это 3 + 3a 2 + 3a + 1.
4. Квадрат a + b + h равен 2 + 2ab + 2ah + b 2 + 2bh + h 2
5. Требуется куб a + 2d + 3
6. Требуется 4-я степень b + 2.
7. Требуется 5-я степень x + 1.
8. Требуется 6-я степень 1 — b.
Квадраты биномов и остаточных величин встречаются в алгебраических процессах так часто, что важно сделать их знакомыми.
Если умножить a + h на себя, а также a — h,
Имеем (a + h) (a + h) = a 2 + 2ah + h 2
И (a — h) (a — h) = a 2 — 2ah + h 2 .
Здесь будет видно, что в каждом случае первый и последний члены представляют собой квадраты a и h; и что средний член в два раза превышает произведение a на h. Следовательно, квадраты биномиальных и остаточных величин без умножения каждого из членов по отдельности можно найти с помощью следующего предложения.
Квадрат бинома, оба члена которого положительны, равен квадрату первого члена + удвоенного произведения двух членов + квадрату последнего члена.
А квадрат остатка количества равен квадрату первого члена — удвоенному произведению двух членов + квадрату последнего члена.
Пример. 1. Квадрат 2a + b равен 4a 2 + 4ab + b 2 .
2. Квадрат ab + cd равен a 2 b 2 + 2abcd + c 2 d 2 .
3. Квадрат 3d — h, равен 9d 2 + 6dh + h 2 .
4. Квадрат a — 1 равен 2 — 2a + 1.
О методе нахождения более высоких степеней бинома см. В одном из следующих разделов.
Для многих целей будет достаточно выразить степени составных величин с помощью показателей степени без фактического умножения.
Таким образом, квадрат a + b равен (a + b) 2 .
n-я степень bc + 8 + x равна (bc + 8 + x) n
В таких случаях винкулум необходимо провести по всем , из которых состоит составное количество.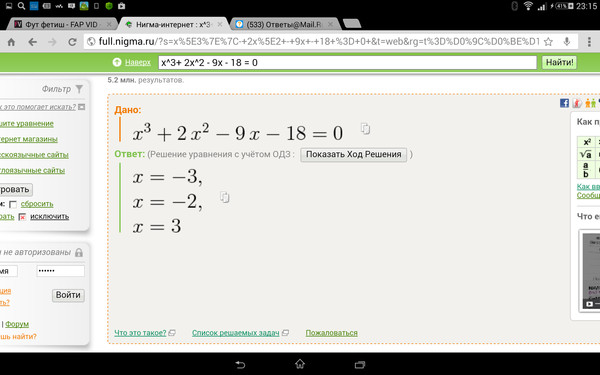
Но если основа состоит из нескольких факторов , винкулум, который используется для выражения силы, может распространяться на все; или может применяться к каждому из факторов отдельно, если этого требует удобство.
Таким образом, квадрат (a + b) (c + d) равен либо [(a + b) × (c + d)] 2 , либо (a + b) 2 × (c + d) 2 .
В самом деле, первое из этих выражений — это квадрат произведения двух факторов, а последнее — произведение их квадратов.Но один из них равен другому.
Куб a × (b + d) равен [a × (b + d)] 3 или a 3 × (b + d) 3 .
Когда величина, мощность которой была выражена переменной и экспонентой, впоследствии возводится до фактического умножения членов, считается, что это развернутое .
Что касается знака, который ставится перед величинами, возведенными в, важно заметить, что когда основание положительно, все его положительные степени также положительны;
но когда база отрицательная, нечетных степеней отрицательны, а четных степеней положительны.
2-я степень -a равна + a 2
3-я степень -a равна -a 3
4-я степень + a 4
5-я степень -a 5 .
215. Следовательно, любая степень с нечетным числом имеет тот же знак, что и его основание. Но степень и даже положительна, независимо от того, положительна она или отрицательна.
Таким образом + a × + a = + a 2
And -a × -a = + a 2
Величина, которая уже является степенью, увеличивается путем умножения ее экспоненты на показатель степени, до которой она должна быть увеличена.
1. 3-я степень 2 равна 2 × 3 = 6 .Для a 2 = aa: и куб aa имеет вид aa × aa × aa = aaaaaa = a 6 ; что является 6-й степенью a, но 3-й степенью 2 .
2. Четвертая степень a 3 b 2 , это 3 × 4 b 2 × 4 = a 12 b 8
3. 3-я степень 4 a 2 x, равна 64a 6 x 3 .
3-я степень 4 a 2 x, равна 64a 6 x 3 .
4.Пятая степень (a + b) 2 , равна (a + b) 10 .
5. Энная степень числа 3 равна 3n
.6. Энная степень (x — y) m , равна (x — y) mn
7. (a 3 × b 3 ) 2 = a 6 × b 6
8. (a 3 b 2 h 4 ) 3 = a 9 b 6 h 12
217. Правило в равной степени применимо к степеням, показатель степени которых равен отрицательным .{-6} $
2. Четвертая степень a 2 b -3 — это 8 b -12 или 8 / b 12 .
3. Квадрат b 3 x -1 , равен b 6 x -2 .
4. Энная степень топора -m равна x -mn , или 1 / x.
Если знак имеет префикс в степени -, он должен быть изменен на +, когда показатель степени становится четным числом.
Пример: квадрат -a 3 , равен + a 6 .Для квадрата -a 3 получается -a 3 . -A 3 , который, согласно правилам умножения знаков, равен + a 6 .
2. Но куб из -a 3 — это -a 9 . Для -a 3 . -A 3 . -A 3 = -a 9 .
3. n-я степень -a 3 , равна ± a 3n .
Здесь степень будет положительной или отрицательной, в зависимости от того, является ли число, которое представляет n, четным или нечетным.2} $
2. 2d, 3d и n-я степени 1 / a равны 1 / a 2 , 1 / a 3 и 1 / a n .
Примеры биномов , в которых один из членов является дробью.
1. Найдите квадрат x + 1/2 и x — 1/2, как в 210.
(x + 1/2) 2 = x 2 + 2. x. (1/2) + 1/2 2 = x 2 + x + 1/4
x. (1/2) + 1/2 2 = x 2 + x + 1/4
(x — 1/2) 2 = x 2 — 2.x. (1/2) + 1/2 2 = x 2 — x + 1/4
2.Квадрат a + 2/3 — это 2 + 4a / 3 + 4/9.
3. Квадрат x + b / 2 = x 2 + bx + b 2 /4.
4 Квадрат x — b / m, равен x 2 — 2bx / m + b 2 / m 2 .
Было показано, что дробный коэффициент может быть переведен из числителя в знаменатель дроби или из знаменателя в числитель. Возвращаясь к схеме обозначения взаимных степеней, можно увидеть, что может быть передан любой множитель , , если знак его экспоненты изменить .
1 Таким образом, в дроби ax -2 / y мы можем перевести x из числителя в знаменатель.
Для ax -2 / y = (a / y) .x -2 = (a / y). (1 / x 2 = a / yx 2 .
2. В дроби a / на 3 мы можем перевести y из знаменателя в числитель.
Для a / by 2 = (a / b). (1 / y 3 ) = (a / b) .y -3 = ay -3 / b.
Таким же образом мы можем перенести множитель с положительным показателем в числителе или отрицательным показателем в знаменателе.
1. Таким образом, ax 3 / b = a / bx -3 . Для x 3 является обратной величиной x -3 , то есть x 3 = 1 / x -3 .
Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть уменьшен до единицы, без изменения значения выражения.
1. Таким образом, a / b = 1 / ba -1 или ab -1 .





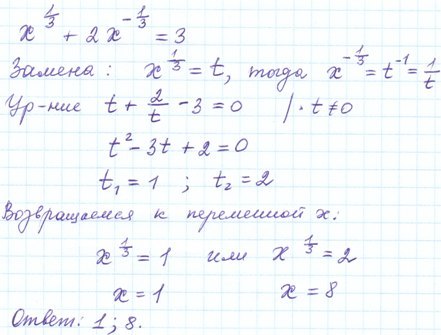 4 = 2 × 2 × 2 × 2 = 16
4 = 2 × 2 × 2 × 2 = 16  е. 1 / а н )
е. 1 / а н ) ЧТО ТАКОЕ ДОКАЗАТЕЛЬ?
ЧТО ТАКОЕ ДОКАЗАТЕЛЬ?  м = 1 / а м
м = 1 / а м 
Leave A Comment