Формула ускорения в проекции: Attention Required!

Ускорение при равноускоренном прямолинейном движении 🐲 СПАДИЛО.РУ

Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
Единица измерения ускорения — метр в секунду в квадрате (м/с²).
Акселерометр — прибор для измерения ускорения.

Формула ускорения

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

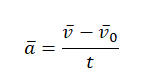
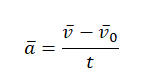
v — скорость тела в данный момент времени, v₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

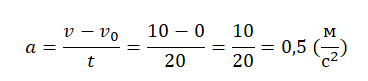
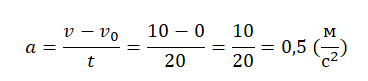
Проекция ускорения

Проекция ускорения на ось ОХ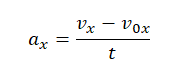

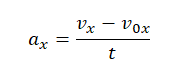
v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

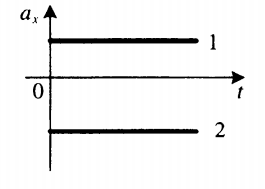
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

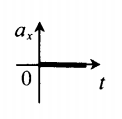
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁= 1 и t₂= 3 с.

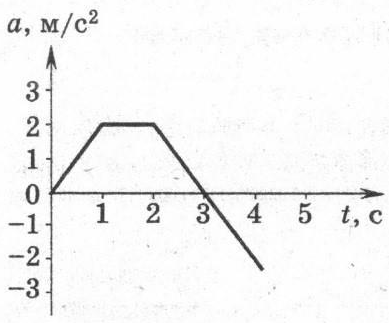
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

В момент времени t₁= 1с ускорение a = 2 м/с². В момент времени t₂= 3 ускорение a = 0 м/с².

Задание EF18027 На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.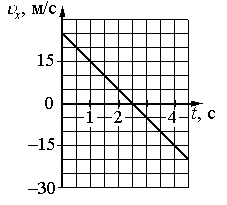

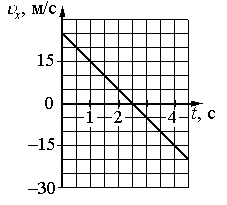
Алгоритм решения

Записать формулу ускорения.
Записать формулу для вычисления модуля ускорения.
Выбрать любые 2 точки графика.
Определить для этих точек значения времени и проекции скорости (получить исходные данные).
Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

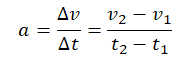
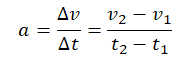
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

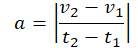
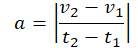
Выбираем любые 2 точки графика. Пусть это будут:

t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10

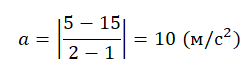
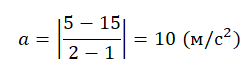
pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18202

Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?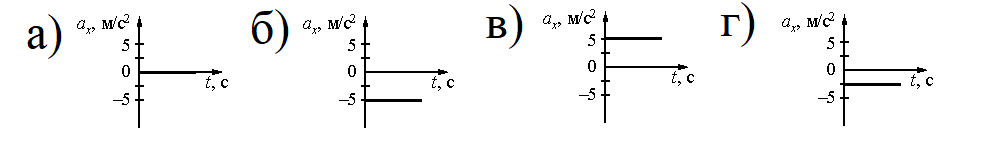

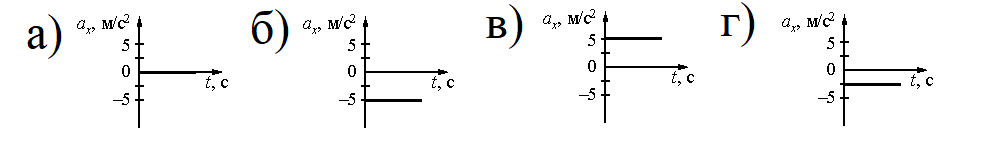
Алгоритм решения

Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
Вычислить ускорение движение тела на этом участке.
Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17992 Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?

Алгоритм решения

Записать исходные данные.
Записать формулу, связывающую известные из условия задачи величины.
Выразить из формулы искомую величину.
Вычислить искомую величину, подставив в формулу исходные данные.

Решение

Запишем исходные данные:

Начальная скорость v₀ = 5 м/с.
Конечная скорость v = 15 м/с.
Пройденный путь s = 40 м.

Формула, которая связывает ускорение тела с пройденным путем:

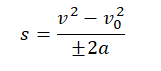
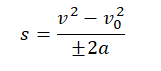
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

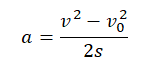
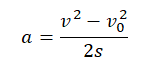
Подставим известные данные и вычислим ускорение автомобиля:

Ответ: 2,5

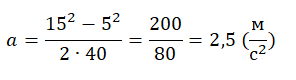
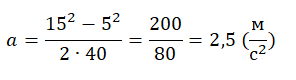
pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

перемещение и путь;
скорость;
ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор | оценить

Движение | Механика | Теория

Движением тела называется изменение его положения в пространстве относительно других.

Координата— величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.

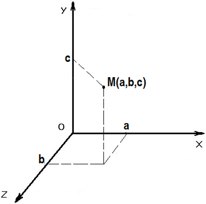
Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.

Траектория — это линия, вдоль которой движется тело.

Путь — это длина траектории, вдоль которой движется тело.

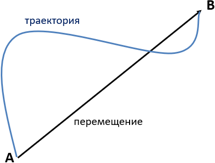
Прямолинейным равномерным движением называется движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Скоростью равномерного прямолинейного движения называется величина, равная отношению перемещения $\overrightarrow{S}$тела к времени 

t, за которое это перемещение произошло .

$\overrightarrow{v} = \frac{\overrightarrow{S}}{t}$

Скорость ― это векторная величина!

В заданиях, где дана зависимость скорости тела от времени,

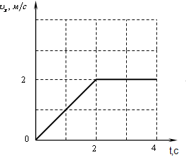
пройденный путь можно вычислить как площадь под графиком:

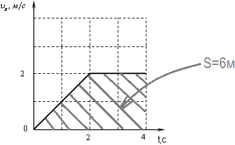
Ускорением тела называется векторная величина, равная отношению изменения скорости за любой промежуток времени к величине этого промежутка:

$\overrightarrow{a} = \frac{\Delta \overrightarrow{v}}{\Delta t}$ 

Зависимость скорости от времени при наличии ускорения определяется выражением:

 $\overrightarrow{v} = \overrightarrow{v_0} + \overrightarrow{a}t$, где:

— скорость тела в момент времени t;

t — время;

— начальная скорость тела;
— ускорение тела.

Равноускоренным движением тела называется движение, при котором его ускорение не меняется, ни по величине, ни по направлению.

Уравнение равноускоренного движения в проекции на ось х  имеет вид:

$x(t) = x_0 +v_{ox}t + \frac{a_xt^2}{2}$, где:

Х₀ — начальная координата тела;

v_ox— проекция начальная скорость на ось x;

a_x — проекция ускорения на ось x;

t — время движения.

Применение производной в кинематике

Если существует зависимость координаты от времени x(t), то зависимость скорости от времени можно получить, взяв производную по времени от этой зависимости. 

Скорость ― это производная координаты тела по времени:

 $v_x(t) = x'(t)$

Например, если зависимость координаты тела при равноускоренном движении имеет вид 

$x(t) = 6-2t + 12t^2$

то взяв первую производную от координаты, мы получим зависимость скорости тела от времени:

$v_x(t) = -2+12\cdot 2t = -2 + 24t$

Точно также, ускорение ― это производная от скорости тела:

$a_x(t) = v_x'(t)$

Скорость при прямолинейном равноускоренном движении тела

Цели урока:

обучающая: повторить понятия равноускоренного движения, ускорения; научить учащихся определять проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени, сформировать навыки построения графика скорости и его анализа.

развивающая: развитие умения наблюдать и анализировать конкретные ситуации; выделять определенные признаки; рассмотрение свойств объектов на основе анализа количественных и качественных характеристик.

воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулирование активности учащихся.

Методы:

словесный — беседа;

наглядный — видеоурок, записи на доске;

контролирующий — тестирование или устный опрос, решение задач.

Связи:

межпредметные: математика — линейная зависимость, график линейной функции;

внутрипредметные: равноускоренное движение, ускорение.

Ход урока:

1. Организационный этап.

Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

На прошлом уроке, мы с вами рассмотрели такой вид движения, при котором тело, за любые равные промежутки времени совершает разные перемещения. Как мы назвали такое движение? {неравномерное}

Какое движение мы назвали ускоренным? {это когда скорость тела увеличивается с течением времени}

А замедленным? {когда скорость тела уменьшается с течением времени}.

Ответьте на вопрос, а что такое средняя скорость? {Средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу времени}

А всегда ли мы можем пользоваться понятием средней скорости при решении задач? Приведите примеры.

Как мы с вами назвали скорость тела в данный момент времени или в данной точке траектории? {мгновенной скоростью}

Как направлена мгновенная скорость? {Она направлена по касательной к траектории в каждой её точке в сторону перемещения}

Что является основной характеристикой неравномерного движения?

{Ускорение — физическая векторная величина, характеризующая быстроту изменения скорости и численно равная отношению изменения скорости тела к промежутку времени, в течение которого это изменение произошло}.

Откройте тетради и запишите число и тему нашего урока: Скорость тела при равноускоренном движении тела.

3. Объяснение нового материала.

Скачать видеоурок Скорость при прямолинейном равноускоренном движении тела

Нам известно, что при прямолинейном равноускоренном движении ускорение тела можно рассчитать по формуле;

Выразим из этой формулы скорость, которую могло бы иметь тело в конце промежутка времени Δt.

Получим

Или

Мы получили формулу, которая называется уравнением скорости при равноускоренном движении.

Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя.

Перепишем нашу формулу в проекци

Задачи на равноускоренное движение

Из кодификатора по физике, 2020:

«1.1.6. Равноускоренное прямолинейное движение:

,
, .»

Теория

В данной статье будем считать, что Вы умеете без проблем находить проекции величин и в примерах не будем подробно объяснять, чему они равны.
В задачах на равноускоренное движение применяют пять величин: проекции перемещения , проекции начальной скорости , проекции конечной скорости , проекции ускорения и времени t. Достаточно знать любые три величины, чтобы найти все остальные.

При решении задач по данной теме применяют два способа решения.

1 способ. При решении запоминаем и применяем две формулы:

А в наиболее сложных случаях решаем систему этих двух уравнений.

2 способ. При решении запоминаем и применяем пять формул (см. таблицу 1).

Таблица 1

Почему пять формул? Каждая из этих формул использует только четыре величины из пяти. Одна из величин не используется при решении (отсутствует) (см. таблицу 1, столбец № 3). Вариантов с одной отсутствующей величиной из пяти может быть только пять.

Алгоритм решения вторым способом.

1) определите, какие величины используются (даны или надо найти), а ка-кая отсутствует;

2) по отсутствующей величину из таблицы выберите рабочую формулу.

Пример 1. Найдите перемещение , если известны , и .

Отсутствующая величина t. Согласно таблице 1 для решения нужно ис-пользовать формулу № 4:
.

Пример 2. Найдите перемещение если известны , и t.

Отсутствующая величина . Согласно таблице 1 для решения нужно использовать формулу № 5

Для сомневающихся и любопытных.

Вывод формулы №3. Из уравнения найдем проекцию начальной скорости:

Подставим полученное выражение в формулу № 2:

${ \upsilon }_{ 0x }={ \upsilon }_{ x }-{ a }_{ x }\cdot t$

Вывод формулы №4. Из уравнения найдем время:

Подставим полученное выражение в формулу № 2:

$t=\frac { { \upsilon }_{ x }-{ \upsilon }_{ 0x } }{ { a }_{ x } }$

Вывод формулы №5. Из уравнения найдем проекцию ускорения:

Подставим полученное выражение в формулу № 2:

${ a }_{ x }=\frac { { \upsilon }_{ x }-{ \upsilon }_{ 0x } }{ t }$

Задачи

Задача 1. Пассажирский поезд тормозит с ускорением 0,2 м/с2. На каком расстоянии от места включения тормоза скорость поезда станет равной 5 м/с, если перед торможением скорость была 15 м/с?

Решение. Скорость поезда уменьшается, поэтому ускорение направлено против начальной скорости. При прямолинейном движении (без поворотов) перемещение поезда равно расстоянию, которое он пройдет, т.е. s = s. Ось 0Х направим по направлению начальной скорости (рис. 1), поэтому

${ s }_{ x }=s,\quad { \upsilon }_{ x }=\upsilon ,\quad { \upsilon }_{ 0x }={ \upsilon }_{ 0 },\quad { a }_{ x }=-a$

1 Способ. Из уравнения находим время:

Перемещение находим из уравнения :

, s = 500 м.

2 Способ. Используются υ0, υ, a и s (надо найти).

Так как отсутствующая величина t, то применяем формулу № 4:

Задача 2. Самолет при взлете за 20 с пробегает по дорожке взлетной полосы 700 м. Какую скорость самолет имеет в конце дорожки взлетной полосы? Движение самолета считайте равноускоренным.

Решение. Скорость самолета увеличивается, поэтому ускорение направлено в сторону движения. Фраза из условия «при взлете» позволяет сделать вывод, что υ0 = 0. Ось 0Х направим по направлению начальной скорости (рис. 2), поэтому

${ s }_{ x }=s,\quad { \upsilon }_{ x }=\upsilon ,\quad { \upsilon }_{ 0x }=0,\quad { a }_{ x }=a$

1 способ. Из уравнения находим ускорение:

${ s }_{ x }={ \upsilon }_{ 0x }\cdot t+\frac { { a }_{ x }\cdot { t }^{ 2 } }{ 2 }$

Конечную скорость находим из уравнения :

м/с.

2 способ. Используются , (надо найти), t и s.

Так как отсутствующая величина a, то применяем формулу № 5:

$\upsilon$

Тогда

$\upsilon$

Задача 3. Шарик в начале наклонного желоба толкнули вниз со скоростью 2 м/с. Определите скорость шарика в конце желоба, если шарик двигался с ускорением 1,25 м/с2, а длина желоба – 2 м.

Решение. Скорость шарика увеличивается, поэтому ускорение направлено в сторону движения. По условию длина желоба – это расстояние, которое пройдет шарик, и при прямолинейном движении s = l. Ось 0Х направим по направлению начальной скорости (рис. 3), поэтому

${ s }_{ x }=l,\quad { \upsilon }_{ x }=\upsilon ,\quad { \upsilon }_{ 0x }={ \upsilon }_{ 0 },\quad { a }_{ x }=a.$

1 способ. Из уравнения находим время:

${ s }_{ x }={ \upsilon }_{ 0x }\cdot t+\frac { { a }_{ x }\cdot { t }^{ 2 } }{ 2 }$

Получили квадратное уравнение относительно t. Корни этого уравнения:

${ s }_{ x }={ \upsilon }_{ 0x }\cdot t+\frac { { a }_{ x }\cdot { t }^{ 2 } }{ 2 }$

находим конечную скорость из уравнения :

м/с.

2 способ. Используются , (надо найти), a и s.

Так как отсутствующая величина t, то применяем формулу № 4:

$\upsilon$

Тогда

$\upsilon$

Задача 4. Хоккейная шайба проскользила по льду 50 м за 2,5 с и остановилась. С каким ускорением двигалась шайба?

Решение. По условию длина поля – это расстояние, которое пройдет шайба, и при прямолинейном движении s = l. «Шайба … остановилась» следовательно, . Скорость шайбы уменьшается, поэтому ускорение направлено против движения. Ось 0Х направим по направлению начальной скорости (рис. 4), поэтому

${ s }_{ x }=l,\quad { \upsilon }_{ x }=0,\quad { \upsilon }_{ 0x }={ \upsilon }_{ 0 },\quad { a }_{ x }=-a$

1 способ. Данную задачу по действиям решить нельзя, т.к. в каждом уравнение неизвестны две величины (ускорение и начальная скорость). Необходимо решать систему уравнений:

${ s }_{ x }=l,\quad { \upsilon }_{ x }=0,\quad { \upsilon }_{ 0x }={ \upsilon }_{ 0 },\quad { a }_{ x }=-a$

или

${ s }_{ x }=l,\quad { \upsilon }_{ x }=0,\quad { \upsilon }_{ 0x }={ \upsilon }_{ 0 },\quad { a }_{ x }=-a$

В итоге получаем:

${ s }_{ x }=l,\quad { \upsilon }_{ x }=0,\quad { \upsilon }_{ 0x }={ \upsilon }_{ 0 },\quad { a }_{ x }=-a$

2 способ. Используются , a (надо найти), t и s.

Так как отсутствующая величина , то применяем формулу № 3:

${ \upsilon }_{ 0 }$

Тогда

${ \upsilon }_{ 0 }$

Вывод.

1) Преимущество первого способа только в том, что нужно запомнить две формулы. При применении второго способа надо запомнить пять формул.

2) При применении первого способа вы можете решать, как линейное уравнение с одним неизвестным, так и квадратные уравнения или систему двух уравнений в общем виде. При применении второго способа вы решаете одно уравнение с одним неизвестным.

Сакович А.Л., 2020

Формула центростремительного ускорения

Когда объект движется по круговой траектории, направление скорости объекта должно постоянно меняться. Изменение скорости означает, что должно быть ускорение. Это ускорение перпендикулярно направлению скорости. Это называется радиальным ускорением или центростремительным ускорением («центростремительное» означает «поиск центра»). Радиальное ускорение равно квадрату скорости, деленной на радиус круговой траектории объекта.Единица центростремительного ускорения — метр на секунду в квадрате ().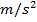

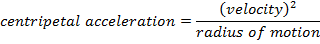
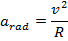
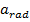= радиальное или центростремительное ускорение (м / с ²)

v = скорость (м / с)

r = радиус движения объекта (м)

Формула центростремительного ускорения Вопросы:

1) Определенный аттракцион в парке развлечений включает круг радиусом 3,00 м, который раскручивает гонщиков со скоростью 6,00 м / с.Что такое центростремительное ускорение всадника?

Ответ: Центростремительное ускорение всадника можно найти по формуле:

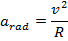
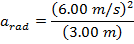
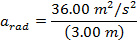
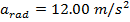
Центростремительное ускорение всадника во время карнавального заезда составляет 12,00 м / с. ².

2) Водитель гоночного автомобиля тренируется на определенном повороте трассы до тех пор, пока не узнает, насколько быстро он может двигаться без заноса. На скорости 45.0 м / с, «датчик бокового ускорения» в ее машине показывает 0,92g, что означает, что ее центростремительное ускорение составляет 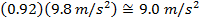. Какой радиус кривой?

Ответ: Радиус кривой можно найти, переставив формулу центростремительного ускорения:

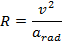
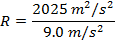
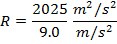
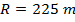
Радиус поворота гоночной трассы составляет 225 м.

Формула центростремительного ускорения

.
Мгновенное ускорение: определение, формула и многое другое
В этой статье вы узнаете, что мы подразумеваем под мгновенным ускорением или, проще говоря, ускорением , когда описываем движение частицы.
Мы увидим определение и формулу мгновенного ускорения на примере, демонстрирующем, как использовать формулу на практике.
Мы также рассмотрим другие важные вещи, которые вам следует знать, например, что мгновенное ускорение представлено на графике зависимости скорости от времени .
Определение и формула для мгновенного ускорения
Ускорение a, которое имеет частица в момент t, равно значению, которое среднее ускорение, вычисленное для интервала времени Δt, который включает момент t, приближается как интервал времени Δt становится все меньше и меньше, то есть по мере того, как Δt приближается к 0.
Мы знаем, что среднее ускорение a для интервала времени Δt выражается как:
, где Δv — изменение скорости, которое происходит в течение Δt.
Формула для мгновенного ускорения a почти такая же, за исключением того, что нам нужно указать, что мы заинтересованы в знании того, какое отношение Δv к Δt приближается, когда Δt приближается к нулю.
Мы можем указать это, используя обозначение пределов.
Итак, формула для мгновенного ускорения:
Чтобы продемонстрировать, как использовать эту формулу на практике, давайте рассмотрим простой пример.
Рассмотрим частицу, скорость которой (в метрах в секунду) в момент t (в секундах) равна 2t ²:
Итак, в 1 секунду скорость равна 2 м / с, в 2 секунды скорость составляет 8 м / с, при 3 с скорость 18 м / с и т. д.
Допустим, мы хотим найти ускорение частицы в момент t = 3 с.
Первое, что нам нужно сделать, это выбрать интервал времени Δt, который включает момент 3 с.
Этот интервал времени Δt начинается в некоторый момент t ₁ и заканчивается в некоторый момент t ₂, так что
Для простоты мы выберем t ₁ = 3 с, чтобы t ₁ было как можно ближе по возможности до 3 с, а Δt можно уменьшить, выбрав значения t ₂, которые ближе к 3 с.
Начнем с выбора t ₂ равным 3,1 с.
t ₁ = 3 с
t ₂ = 3,1 с
Δt = t ₂ — t ₁ = 3,1 с — 3 с = 0,1 с
Среднее ускорение для Δt равно :
a = Δv = v ₂ — v ₁
Δt t ₂ — t ₁
Найдем скорость v ₁ в момент t ₁:
v ₁ = 2t ₁ ²
v ₁ = 2 (3) ² м / с
v ₁ = 18 м / s
и скорость v ₂ в момент t ₂:
v ₂ = 2t ₂ ²
v ₂ = 2 (3.1) ² м / с
v ₂ = 19,22 м / с
Теперь мы можем рассчитать среднее ускорение:
a = 19,22 м / с — 18 м / с
3,1 с — 3 с
a = 12,2 м / с ²
Итак, когда интервал времени Δt составляет от 3 до 3,1 с, среднее ускорение составляет 12,2 м / с ².
Давайте посмотрим, что произойдет, если мы выберем меньший интервал времени Δt, когда t ₂ будет равно 3.01 с.
t ₁ = 3 с
t ₂ = 3,01 с
Δt = 3,01 с — 3 с = 0,01 с
Мы уже знаем, что скорость v ₁ в момент t ₁ равна 18 РС.
Скорость v ₂ в момент t ₂ составляет:
v ₂ = 2t ₂ ²
v ₂ = 2 (3,01) ² м / с
v ₂ = 18,1202 м / с
Среднее ускорение составляет:
a = 18.1202 м / с — 18 м / с
3,01 с — 3 с
a = 12,02 м / с ²
Итак, когда интервал времени Δt составляет от 3 до 3,01 с, среднее ускорение 12,02 м / с ².
В последний раз, давайте выберем еще меньшее Δt, с t ₂ равным 3,001 с.
t ₁ = 3 с
t ₂ = 3,001 с
Δt = 0,001 с
Скорость v ₂ в момент t ₂ составляет:
v ₂ = 2t ₂ ²
v ₂ = 2 (3.001) ² м / с
v ₂ = 18,012002 м / с
Среднее ускорение составляет:
a = 18,012002 м / с — 18 м / с
3,001 с — 3 с
a = 12,002 м / с ²
Таким образом, поскольку Δt становится все меньше и меньше, среднее ускорение приближается к 12 м / с ².
Мы можем продолжать выбирать все меньше и меньше Δt до бесконечности и приближаться к 12 м / с ².
Тем не менее, мы можем показать, что среднее ускорение приближается к 12 м / с ², поскольку Δt становится все меньше и меньше, более строго, чтобы мы могли быть уверены, что ускорение в момент 3 с составляет 12 м / с. с ².
Прежде всего, мы будем ссылаться на момент 3 s как на t, чтобы указать, что то, что мы собираемся сделать, применимо не только к конкретному моменту 3 s, но и к любому моменту t.
Начнем, как и раньше, с рассмотрения интервала времени Δt, который начинается в некоторый момент t ₁ и заканчивается в некоторый момент t ₂, так что
Снова выберем t ₁ = t, поэтому что t ₁ как можно ближе к t, а Δt можно уменьшить, выбрав значения t ₂, которые ближе к t.
Так как Δt = t ₂ — t ₁ и t ₁ = t, мы можем записать:
Δt = t ₂ — t
↓
t ₂ = t + Δt
Это означает, что границами интервала времени Δt являются момент t и момент t + Δt.
Скорость v _t в момент t равна:
, а скорость v _{t + Δt} в момент t + Δt равна:
v _{t + Δt} = 2 (t + Δt) ²
v _{t + Δt} = 2 (t ² + 2tΔt + Δt ²)
v _{t + Δt} = 2t ² + 4tΔt + 2Δt ²
Теперь мы можем рассчитать среднее ускорение для Δt:
a = 2t ² + 4tΔt + 2Δt ² — 2t ²
Δt
a = 4t + 2Δt
Обратите внимание, что это выражение, 4t + 2Δt, объясняет, почему среднее ускорение, которое мы раньше вычисляли вручную, было 12.2 м / с ², когда Δt было 0,1 с, 12,02 м / с ², когда Δt было 0,01 с, и 12,002 м / с ², когда Δt было 0,001 с:
(4 × 3 + 2 × 0,1 ) м / с ² = 12,2 м / с ²
(4 × 3 + 2 × 0,01) м / с ² = 12,02 м / с ²
(4 × 3 + 2 × 0,001 ) м / с ² = 12,002 м / с ²
Теперь вспомним, что мгновенное ускорение равно значению, к которому приближается среднее ускорение, когда интервал времени Δt приближается к 0:
a = lim v _{t + Δt} — v _t
Δt → 0 Δt
В этом случае мы обнаружили, что среднее ускорение равно 4t + 2Δt.Итак,
a = lim 4t + 2Δt
Δt → 0
Когда Δt приближается к 0, член 2Δt в выражении 4t + 2Δt приближается к 0, поэтому выражение приближается 4т.
Следовательно, мгновенное ускорение a определяется как 4t:
Итак, ускорение частицы в любой момент t определяется как 4t.
Таким образом, в момент t = 3 с ускорение составляет 4 × 3 м / с ², то есть 12 м / с ².
Мгновенное ускорение как производная
Предел
lim v _{t + Δt} — v _t
Δt → 0 Δt
называется производной от v относительно t, которое записывается как
Таким образом, мы говорим, что мгновенное ускорение является производной скорости по времени:
Кроме того, поскольку скорость является производной положения по времени:
Мы можем написать мгновенное ускорение как:
a = dv = d dx = d ² x
dt dt dt dt ²
Таким образом, мгновенное ускорение является второй производной позиции по времени:
Ускорение во времени графики
Часто, чтобы показать, как ускорение частицы изменяется во времени, используется график ускорения в зависимости от времени .
Вот как может выглядеть график зависимости ускорения от времени для движущейся частицы:
График ускорения от времени; ускорение в момент времени 0 равно 0, затем становится положительным и, наконец, через 9 секунд оно возвращается обратно к 0. a210864t (s) 897654321O2) (м / с
В этом случае в момент t = 4 с частица имеет ускорение a = 6 м / с ²:
График зависимости ускорения от времени; на 4 секундах ускорение составляет 6 метров в секунду в квадрате. a210864t (с) 897654321O2) (м / с
Напомним, что в предыдущем Например, мы обнаружили, что мгновенное ускорение частицы равно 4t:
. Давайте покажем, как ускорение этой частицы изменяется во времени, с помощью графика зависимости ускорения от времени.
График функции 4t представляет собой линию, поэтому нам нужно найти только две точки, чтобы нарисовать ее.
Для простоты вычислений мы выберем момент t ₁ = 0 с и момент t ₂ = 1 с:
t ₁ = 0 с, a ₁ = (4 × 0 ) м / с ² = 0
t ₂ = 1 с, a ₂ = (4 × 1) м / с ² = 4 м / с ²
Теперь, когда мы нашли два точек, мы готовы построить график зависимости ускорения от времени:
График ускорения от времени, состоящий из линии, проходящей через точки (0, 0) и (1, 4).a210864t (s) 321O2) (м / с
Графики зависимости скорости от времени и мгновенное ускорение
Мгновенное ускорение как наклон касательной линии к графику зависимости скорости от времени
Рассмотрим график зависимости скорости от времени для движения Частица:
График зависимости скорости от времени; скорость в момент времени 0 равна 0, затем становится положительной и, наконец, возвращается к 0. vtO
Помните, что график зависимости скорости от времени показывает, как скорость частицы изменяется во времени.
Как мы видели ранее, когда мы хотим найти ускорение частицы в момент t, мы рассматриваем интервал времени Δt, который начинается в t и заканчивается в t + Δt:
График зависимости скорости от времени; в момент t скорость равна v sub-t; в момент t + Δt скорость равна v sub-t + Δt; указаны Δv и Δt.vtOtΔt + tttΔt + ΔtΔvvv
Ускорение в момент t равно любому среднему ускорению для Δt, которое приближается к Δt, приближающемуся к нулю.
Мы можем использовать эту информацию, чтобы определить, что представляет собой мгновенное ускорение на графике зависимости скорости от времени.
Сначала проведем секущую линию, проходящую через точки t и t + Δt на графике:
График зависимости скорости от времени; секущая линия, которая проходит через точки t и t + Δt на графике. vtOttΔt + ΔttΔt + tΔvvv
Наклон секущей линии равен среднему ускорению за интервал времени Δt, поскольку Δv / Δt представляет собой как среднее ускорение и наклон секущей линии.
Таким образом, ускорение в момент t равно тому, к чему приближается наклон секущей линии, когда Δt приближается к нулю.
По мере того, как Δt становится все меньше и меньше, секущая линия приближается к линии, касательной к графику в точке t:
График зависимости скорости от времени; когда Δt приближается к 0, секущая линия приближается к касательной в точке t на графике. в точке t.
Следовательно, ускорение в момент t равно наклону касательной к графику зависимости скорости от времени в точке t.
График зависимости скорости от времени; касательная линия к графику в точке t.vtOt
Если обозначить наклон касательной с m _T, то мы можем написать
Как определить знак мгновенного ускорения по графику зависимости скорости от времени
Определить знак мгновенного ускорения по графику зависимости скорости от времени довольно просто.
Чтобы показать, как это сделать, давайте вернемся к тому же графику зависимости скорости от времени, который мы видели раньше, и рассмотрим момент t, в который мы хотим узнать знак ускорения:
График зависимости скорости от времени; в момент t скорость равна v sub-t.vtOttv
Мы уже знаем, что ускорение в момент t равно наклону касательной к графику в точке t.
Представим касательную линию и назовем θ углом, который она образует с положительной осью t:
График зависимости скорости от времени; угол θ, который касательная в точке t составляет с положительной осью t.vtOttvθ
Чтобы определить, является ли ускорение в момент t положительным, отрицательным или нулевым, нам просто нужно посмотреть на знак угла θ.
Когда угол θ положительный:
График зависимости скорости от времени; угол θ, который касательная линия образует с положительной осью t, положительный. vtOttvθ
Наклон касательной линии положительный, поэтому мгновенное ускорение положительно.
Когда угол θ отрицательный:
График зависимости скорости от времени; угол θ, который касательная линия составляет с положительной осью t, отрицателен.vtOttvθ
Наклон касательной линии отрицательный, поэтому мгновенное ускорение отрицательно.
Наконец, когда угол θ равен нулю:
График зависимости скорости от времени; касательная линия является горизонтальной линией. vtOttv
Наклон касательной линии равен нулю, и поэтому мгновенное ускорение равно нулю.
Таким образом, знак ускорения в момент t такой же, как знак угла θ, который линия, касательная к графику зависимости скорости от времени в точке t, проходит с положительной осью t.
Итак, мы можем легко определить, когда ускорение положительное, отрицательное или нулевое, просто посмотрев на угол θ в разных точках графика зависимости скорости от времени:
График зависимости скорости от времени; сначала ускорение положительное, затем на мгновение оно становится равным нулю и, наконец, становится отрицательным. vtOa0> a0
Что такое замедление?
Когда ускорение вызывает уменьшение скорости, его иногда называют замедлением .
Итак, когда частица имеет положительную скорость и отрицательное ускорение или отрицательную скорость и положительное ускорение, вы можете услышать, как ускорение частицы называется замедлением.
Вы также можете прочитать:
.
Формула ускорения силы тяжести
Вблизи поверхности Земли ускорение силы тяжести приблизительно постоянно. Однако на больших расстояниях от Земли, вокруг других планет или лун ускорение другое. Ускорение свободного падения зависит от массы тела, расстояния от центра масс и постоянной G, которая называется «универсальной гравитационной постоянной». Его значение = 6,673 x 10 ^-11 Н · м ² / кг ².

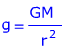
g = ускорение свободного падения (единицы м / с ²)
G = универсальная гравитационная постоянная, G = 6,673 x 10 ^-11 Н · м ² кг ²
м = масса большого тела (например, Земли)
r = расстояние от центра масс большого тела
Ускорение от силы тяжести Вопросы по формуле:
1) Радиус луны равен 1.74 x 10 ⁶ м. Масса Луны 7,35 х 10 ²² кг. Найдите ускорение свободного падения на поверхности Луны.
Ответ: На поверхности Луны расстояние до центра масс такое же, как и радиус: r = 1,74 x 10 ⁶ м = 1 740 000 м. Ускорение свободного падения на поверхности Луны можно найти по формуле:

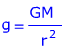
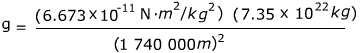
г = 1,620 м / с ²
Ускорение свободного падения на поверхности Луны равно 1.620 м / с ².
2) Радиус Земли составляет 6,38 x 10 ⁶ м. Масса Земли 5,98х 10 ²⁴ кг. Если спутник вращается вокруг Земли на высоте 250 км над поверхностью, какое ускорение свободного падения он испытывает?
Ответ: Ускорение свободного падения зависит от расстояния от центра масс большого тела до спутника. Это расстояние складывается из радиуса Земли и расстояния от спутника до поверхности:
r = (6.38 x 10 ⁶ м) + (250 км)
r = 6 380 000 + 250 000 м
r = 6 630 000 м
Ускорение свободного падения спутника можно найти по формуле:

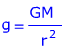
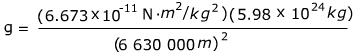
г = 9,078 м / с ²
Ускорение свободного падения на высоте спутника, 250 км над поверхностью Земли, составляет 9,078 м / с ².
.
Формула углового ускорения
Угловое ускорение вращающегося объекта — это скорость, с которой угловая скорость изменяется во времени. Это изменение угловой скорости, деленное на изменение во времени. Среднее угловое ускорение — это изменение угловой скорости, деленное на изменение во времени. Угловое ускорение — это вектор, указывающий в направлении оси вращения. Величина углового ускорения определяется формулой ниже.Единица углового ускорения — радиан / с ².

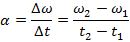
α = угловое ускорение, (радиан / с ²)
Δω = изменение угловой скорости (радиан / с)
Δt = изменение во времени (с)
ω ₁ = начальная угловая скорость (радиан / с)
ω ₂ = конечная угловая скорость (радиан / с)
т ₁ = начальное время (с)
т ₂ = окончательное время (с)
Формула углового ускорения Вопросы:
1) Диск в DVD-проигрывателе запускается из состояния покоя, а затем начинает вращаться, когда пользователь нажимает «Play».Через 4,00 с диск вращается со скоростью 160 радиан / с. Какое было среднее угловое ускорение диска?
Ответ: В начальный момент времени (t ₁ = 0 с) угловая скорость была ω ₁ = 0 радиан / с. В последний момент времени (t ₂ = 4,00 с) угловая скорость диска составила ω ₁ = 160 радиан / с. Среднее угловое ускорение можно найти по формуле:

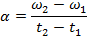
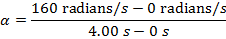
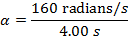
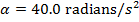
Между начальным и конечным моментами среднее угловое ускорение диска было 40.0 радиан / с ².
2) На некоторых скоростных американских горках есть магнитная тормозная система, которая предназначена для того, чтобы машины американских горок замедляли движение по мере приближения к станции. Магнитные тормоза замедляют автомобили ровно настолько, чтобы сработала другая тормозная система. Если колеса машин изначально вращаются со скоростью 400,0 об / с, а магнитные тормоза применяют постоянное угловое ускорение -440,0 радиан / с

2 в течение 5,00 с, какой будет угловая скорость машин американских горок после были применены магнитные тормоза?
Ответ: Угловая скорость в начальный момент времени (t ₁ = 0 с) дана в оборотах в секунду.Чтобы использовать это значение в формуле углового ускорения, его необходимо преобразовать в радианы в секунду. На оборот приходится 2π радиан, поэтому начальная угловая скорость равна:

ω ₁ = 400,0 об / с

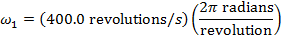
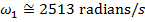
Конечная угловая скорость в момент времени t ₁ = 5,0 с может быть найдена путем преобразования формулы углового ускорения:

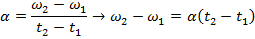
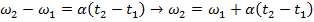
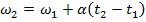
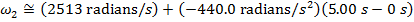
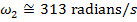
Угловая скорость после применения магнитных тормозов составляет приблизительно 313 радиан / с.Это эквивалентно 49,8 об / с.
.