Как найти производную функции по графику и касательной: Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7

Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7

Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7.

 

Вспомним определение производной:

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

Исходя из этого определения, рассмотрим, каким образом производная функции  связана с графиком этой функции.

Посмотрите ВИДЕОУРОК, в котором я подробно объясняю, в чем заключается геометрический смысл производной, и как выводится уравнение касательной. А затем мы рассмотрим решение задач из Открытого банка заданий для подготовки к ЕГЭ по математике.

 

 

Итак.

Геометрический смысл производной.

Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции   в точке    равен производной функции

в этой точке:

Заметим, что угол  — это угол между прямой и положительным направлением оси ОХ:

Уравнение касательной к графику функции  в точке  имеет вид:

В этом уравнении:

— абсцисса точки касания,

— значение функции  в точке касания,

— значение производной функции  в точке касания.

Приведем несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике, в которых используется знание геометрического смысла производной.

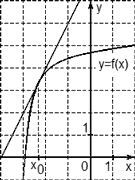
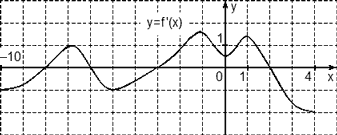
Пример 1. Задание В8 (№ 27504) На рисунке изображены график функции 

 и касательная к нему в точке с абcцисcой  . Найдите значение производной функции  в точке  .

Значение производной функции  в точке  равно тангенсу угла между касательной и положительным направлением оси ОХ. Чтобы его найти, выделим прямоугольный треугольник, гипотенуза которого лежит на касательной, а катеты параллельны осям координат. Обозначим точки с целыми координатами буквами  А и В — эти точки выделены на касательной:

Проведем через точку А прямую параллельно оси ОХ, а через точку В — параллельно оси OY. Получим прямоугольный треугольник ABC:

Угол А  треугольника  АВС равен углу между касательной и положительным направлением оси ОХ.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.

Длины катетов считаем по количеству клеточек.

Ответ: 0,25

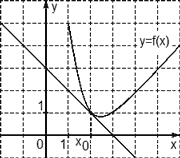
Пример 2. Задание В8 (№ 27506) На рисунке изображены график функции   и касательная к нему в точке с абцисоой 

. Найдите значение производной функции  в точке .

Эта задача очень похожа на предыдущую, за исключением того, что здесь касательная  наклонена влево, и угол

между касательной и положительным направлением оси ОХ расположен так:

Построим, как предыдущей задаче, прямоугольный треугольник АВС:

Угол А треугольника ABC и угол — смежные, то есть их сумма равна 180 градусов. Значит,

Запомните, если прямая наклонена влево, то коэффициент наклона прямой отрицателен.

Ответ: -0,25

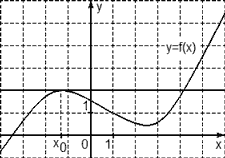
Пример 3. Задание В8 (№ 40129)  На рисунке изображен график функции . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсцссой 8. Найдите значение производной функции в точке

.

Соединим  отрезком точку начала координат с точкой касания:

Производная функции в точке касания равна тангенсу угла  между касательной и положительным направлением оси ОХ:

Чтобы найти тангенс , рассмотрим прямоугольный треугольник АОВ:

 

Ответ: 1,25

И.В. Фельдман, репетитор по математике.

Производная функции. Геометрический смысл производной.

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку  с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Производная функции в точке  равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

.

Величина  в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси .

.

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке  равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке  функция возрастает. Касательная к графику, проведенная в точке , образует острый угол  с положительным направлением оси . Значит, в точке  производная положительна.

В точке  наша функция убывает. Касательная в этой точке образует тупой угол  с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке  производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках  (точка максимума) и  (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка  — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке  с «плюса» на «минус».

В точке  — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

	возрастает	точка максимума	убывает	точка минимума	возрастает
	+	0	—	0	+

Ты нашел то, что искал? Поделись с друзьями!

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке  касательная к графику горизонтальна, и производная равна нулю. Однако до точки  функция возрастала — и после точки  продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных.

Задача 7 — геометрический смысл производной

15 марта 2011

В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:

1. Значение производной в некоторой точке x₀,
2. Точки максимума или минимума (точки экстремума),
3. Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.

Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.

Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.

Вычисление значения производной. Метод двух точек

Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x₀, и требуется найти значение производной в этой точке, применяется следующий алгоритм:

1. Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x₁; y₁) и B (x₂; y₂). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
2. Зная координаты, легко вычислить приращение аргумента Δx = x₂ − x₁ и приращение функции Δy = y₂ − y₁.
3. Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.

Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x₂ − x₁ = −1 − (−3) = 2; Δy = y₂ − y₁ = 6 − 2 = 4.

Найдем значение производной: D = Δy/Δx = 4/2 = 2.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x₂ − x₁ = 3 − 0 = 3; Δy = y₂ − y₁ = 0 − 3 = −3.

Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x₂ − x₁ = 5 − 0 = 5; Δy = y₂ − y₁ = 2 − 2 = 0.

Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.

Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

1. Точка x₀ называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≥ f(x).
2. Точка x₀ называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

1. Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
2. Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x₀ известно, что f’(x₀) ≠ 0, то возможны лишь два варианта: f’(x₀) ≥ 0 или f’(x₀) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
3. Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

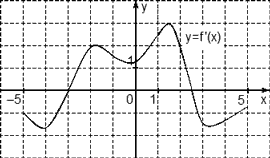
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.

Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:

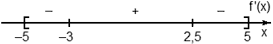
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

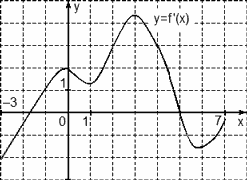
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.

Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

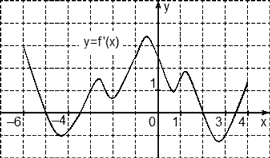
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].

Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

1. Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≤ f(x₂). Другими словами, чем больше значение аргумента, тем больше значение функции.
2. Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≥ f(x₂). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

1. Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
2. Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

1. Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
2. Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
3. Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

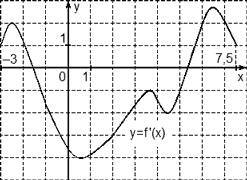
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.

Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

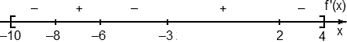
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l₁ = − 6 − (−8) = 2;
l₂ = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l₂ = 5.

Смотрите также:

1. Задача 7: касательная к графику функции
2. Задача 7: касательная к графику функции — 2
3. Пробный ЕГЭ-2011 по математике, вариант №4
4. Пробный ЕГЭ 2012. Вариант 1 (без логарифмов)
5. Так сокращать дроби нельзя!
6. Быстрое возведение чисел в квадрат без калькулятора

Задачи В9. Применение производной к исследованию функции

Часть 3.

Здесь смотрите части 1, 2, 4

Продолжаем разбор  Задач №8 ЕГЭ по математике.

Сегодня нам понадобится при решении задач следующая таблица, показывающая связь знака производной с характером монотонности функции.

Пожалуйста, будьте предельно внимательны в следующем. Смотрите, график ЧЕГО вам дан! Функции или ее производной

Если дан график производной, то интересовать нас будут только знаки функции и нули. Никакие «холмики» и «впадины» не интересуют нас в принципе!

 

Задача 1.

На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции  отрицательна.

Решение: + показать

Задача 2.

На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

Решение:+ показать

Задача 3.

На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции   параллельна прямой   или совпадает с ней.

Решение: + показать

Задача 4.

На рисунке изображен график функции  , определенной на интервале . Найдите количество точек, в которых производная функции   равна 0.

Решение: + показать

Производная равна нулю в точках экстремума. У нас их 4:

Ответ: 4. 

Задача 5.

На рисунке изображён график функции  и одиннадцать точек на оси абсцисс:. В скольких из этих точек производная функции отрицательна?

Решение: + показать

На промежутках убывания  функции  её производная принимает отрицательные значения. А убывает  функция в точках. Таких точек 4.

Ответ: 4. 

Задача 6.

На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции .

Решение: + показать

Точки экстремума – это точки максимума (-3, -1, 1) и точки минимума (-2, 0, 3).

Сумма точек экстремума: -3-1+1-2+0+3=-2.

Ответ: -2. 

Задача 7.

На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение: + показать

Задача 8.

На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.

Решение: + показать

На рисунке выделены цветом все промежутки, на которых производная положительна, а значит  сама функция возрастает на этих промежутках.

 

Длина наибольшего из них – 6.

Ответ: 6. 

Задача 9.

На рисунке изображен график производной функции  , определенной на интервале . В какой точке отрезка    принимает наибольшее значение.

Решение: + показать

Задача 10.

На рисунке изображен график   — производной функции , определенной на интервале . Найдите количество точек максимума функции , принадлежащих отрезку .

 Решение: + показать

На рисунке изображен график производной, значит нас на этом рисунке будут интересовать только знаки и нули производной.

Мы видим на рисунке на указанном отрезке  () три нуля у . Причем, производная мняет знак при переходе через них. Это точки  экстремума функции (точки максимума и минимума).

При этом производная меняет знак с «+» на «-» в  точке 8, помеченной красным цветом, и с «-» на «+» в двух точках (3 и 12), помеченных синим цветом.

Так вот при переходе через точку максимума  функция меняет   возрастание на  убывание, а значит производная меняет знак с  «+» на «-».

Итак, точка максимума одна (помечена красным цветом).

Ответ: 1. 

Задача 11.

На рисунке изображен график функции   и отмечены точки -3, 1, 6, 8. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Решение: + показать

Значение производной в точке касания равно угловому коэффициенту касательной. В свою очередь,  угловой коэффициент касательной  равен тангенсу угла наклона данной касательной к оси .

В точке -3 (точка минимума) производная равна нулю.

В точке 6 производная положительна, так как точки лежат на промежутке возрастания функции.

А вот в точках 1 и 8 производная отрицательна.

При этом в точке 8 угол наклона касательной явно меньше, чем в точке 1.

Поэтому в точке 8 тангенс угла наклона будет наименьшим, а значит и значение производной, будет наименьшее.

Ответ: 8. 

🙂 Самое время немного отдохнуть. Неправда ли? –>+ показать

Вам было нелегко?.. 

Этим ребятам, наверное, тоже не сладко… Не сдавайтесь!

 

Вы можете пройти тест «Применение производной к исследованию функции»

Задание №7. Производная. Поведение функции. Первообразная

Необходимая теория:

Производная функции

Таблица производных

Первообразная функции

Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих встречаются вопросы о первообразной.

Геометрический смысл производной 

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .

Достроив до прямоугольного треугольника АВС, получим:

Ответ: 0,25.

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:

Ответ: −0, 25.

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой в точке

При значения выражений и равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

Из второго уравнения находим или Первому уравнению удовлетворяет только .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени получим:

Ответ: 3

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция возрастает.

Если , то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

 

5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.

Производная функции в точках максимума и минимума функции Таких точек на графике 5.

Ответ: 5.

6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке производная функции положительна.

Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

Ответ: 3.

7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой

Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

Ответ: 7.

8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это

Ответ: 1.

9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.

Значит, является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Функция для которой является производной, называется первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.

Ответ: 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Первообразная функции. Формула Ньютона-Лейбница.

 

Геометрический смысл производной, касательная. Применение производной.

Инфоурок › Математика ›Презентации›Геометрический смысл производной, касательная. Применение производной.

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Геометрический смысл производной, касательная . Применение про­из­вод­ной к ис­сле­до­ва­нию функций. Учитель математики МБОУ СОШ №12 Погорелая С.Н. ст. Павловской Краснодарского края

2 слайд Описание слайда:

Помни, что: Про­из­вод­ная функ­ции по­ло­жи­тель­на на тех ин­тер­ва­лах, на ко­то­рых функ­ция воз­рас­та­ет; Про­из­вод­ная функ­ции от­ри­ца­тель­на на тех ин­тер­ва­лах, на ко­то­рых функ­ция убы­ва­ет; Точки мак­си­му­ма со­от­вет­ству­ют точ­кам смены знака про­из­вод­ной с по­ло­жи­тель­но­го на от­ри­ца­тель­ный, а минимума – с отрицательного на положительный; Точки экс­тре­му­ма со­от­вет­ству­ют точ­кам смены знака про­из­вод­ной;

3 слайд Описание слайда:

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной, ко­то­рый в свою оче­редь равен тан­ген­су угла на­кло­на дан­ной ка­са­тель­ной к оси абс­цисс. Если функ­ция не­пре­рыв­на на от­рез­ке [a; b], а её про­из­вод­ная по­ло­жи­тель­на (от­ри­ца­тель­на) на ин­тер­ва­ле (a; b), то функ­ция воз­рас­та­ет (убы­ва­ет) на от­рез­ке [a; b]. Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной.

4 слайд Описание слайда:

Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания. Ответ: 0,5 Прямая является касательной к графику функции . Найдите абсциссу точки касания. Ответ: -1

5 слайд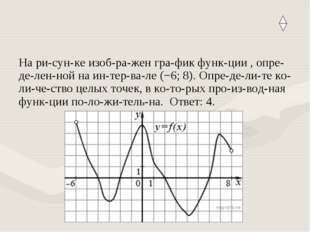 Описание слайда:

На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (−6; 8). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции по­ло­жи­тель­на. Ответ: 4.

6 слайд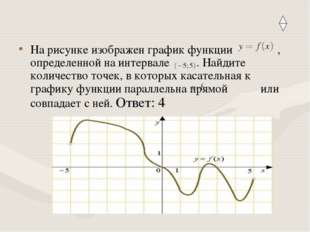 Описание слайда:

На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. Ответ: 4

7 слайд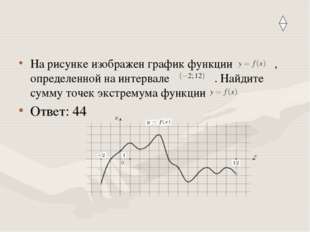 Описание слайда:

На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции Ответ: 44

8 слайд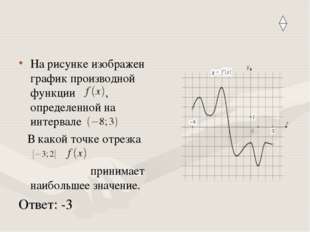 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале В какой точке отрезка принимает наибольшее значение. Ответ: -3

9 слайд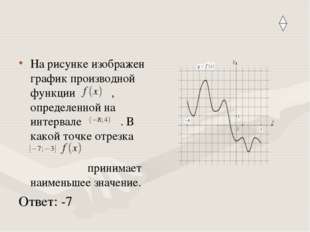 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наименьшее значение. Ответ: -7

10 слайд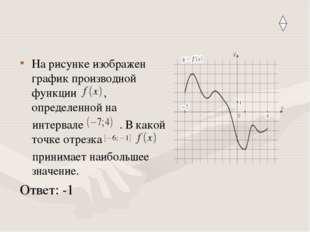 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наибольшее значение. Ответ: -1

11 слайд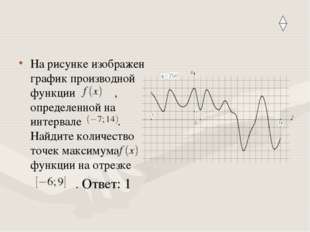 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек максимума функции на отрезке . Ответ: 1

12 слайд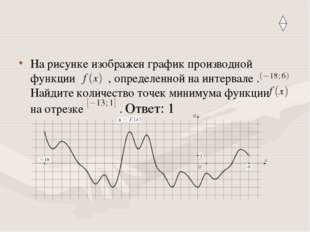 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек минимума функции на отрезке . Ответ: 1

13 слайд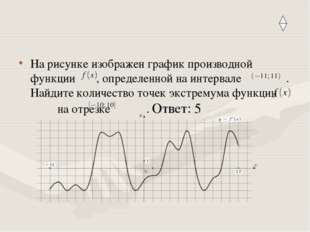 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек экстремума функции на отрезке . Ответ: 5

14 слайд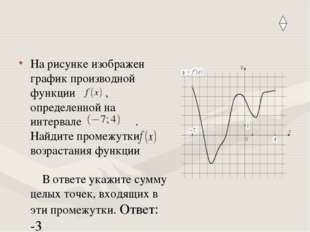 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции В ответе укажите сумму целых точек, входящих в эти промежутки. Ответ: -3

15 слайд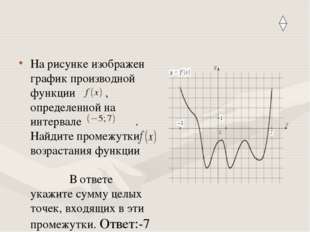 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции В ответе укажите сумму целых точек, входящих в эти промежутки. Ответ:-7

16 слайд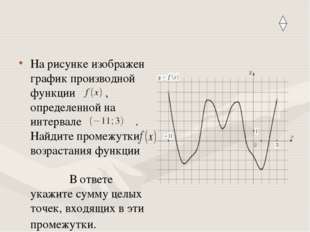 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции В ответе укажите сумму целых точек, входящих в эти промежутки. Ответ: -15

17 слайд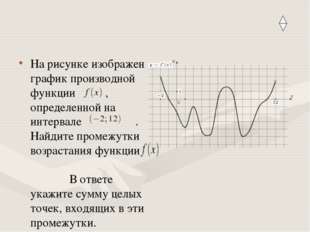 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции В ответе укажите сумму целых точек, входящих в эти промежутки. Ответ: 6

18 слайд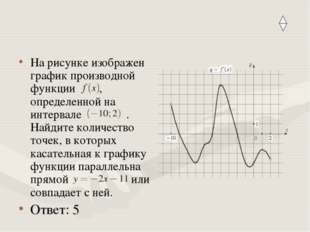 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. Ответ: 5

19 слайд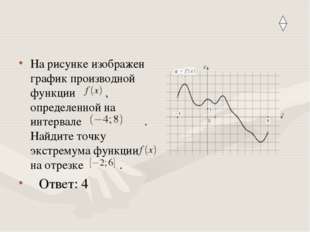 Описание слайда:

На рисунке изображен график производной функции , определенной на интервале . Найдите точку экстремума функции на отрезке . Ответ: 4

20 слайд Описание слайда:

На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции точке Ответ: 2

21 слайд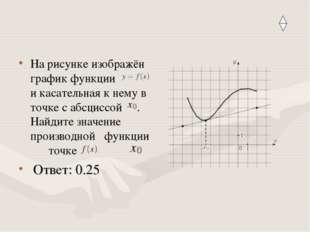 Описание слайда:

На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции точке Ответ: 0.25

22 слайд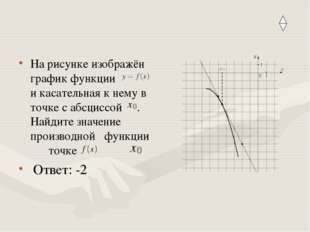 Описание слайда:

На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции точке Ответ: -2

23 слайд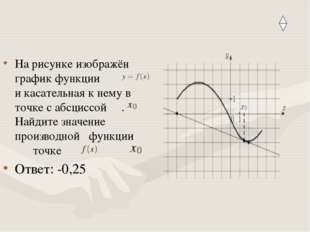 Описание слайда:

На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции точке Ответ: -0,25

24 слайд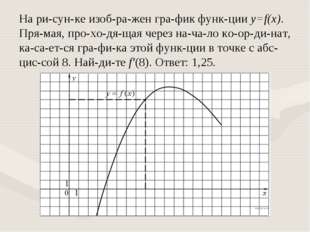 Описание слайда:

На ри­сун­ке изоб­ра­жен гра­фик функ­ции y=f(x). Пря­мая, про­хо­дя­щая через на­ча­ло ко­ор­ди­нат, ка­са­ет­ся гра­фи­ка этой функ­ции в точке с абс­цис­сой 8. Най­ди­те f'(8). Ответ: 1,25.

25 слайд Описание слайда:

Спасибо за внимание

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики и информатики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: 286628

Похожие материалы

Оставьте свой комментарий

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Секущая графика функции. Уравнение секущей графика функции

      Рассмотрим график некоторой функции   y = f (x),   точки   A= (x₀;  f (x₀))   и   B = (x₁;  f (x₁))   на графике, прямую, проходящую через точки   A   и   B,   и произвольную точку   C = (x; y)   на этой прямой (рис. 1).

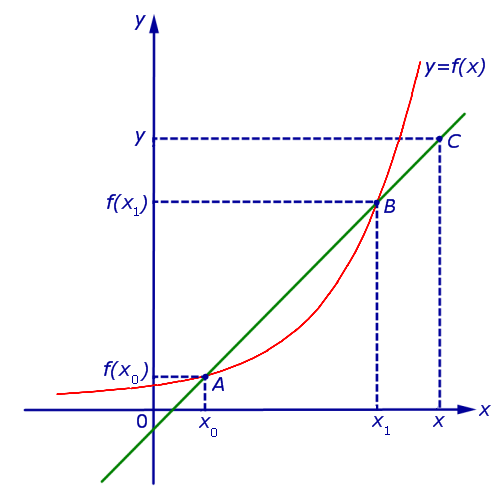
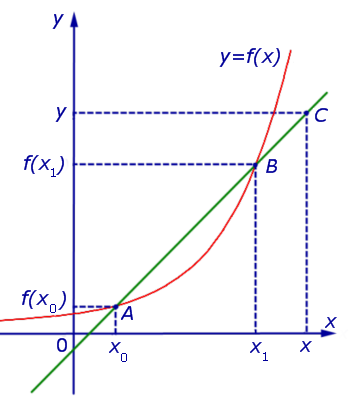
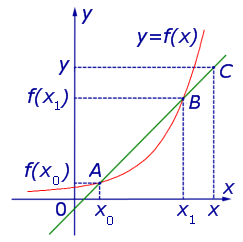
Рис.1

      Определение 1. Прямую, проходящую через две произвольные точки графика функции, называют секущей графика функции.

      В соответствии с определением 1 прямая, проходящая через точки   A   и   B   графика функции   y = f (x),   является секущей этого графика.

      Выведем уравнение секущей графика функции.

      Для этого рассмотрим векторы 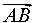и 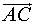, координаты которых имеют вид:

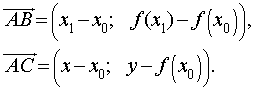
      Поскольку векторы 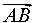и 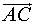лежат на одной прямой, то справедливо равенство

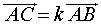(1)

где   k   – некоторое число.

      Переписывая равенство (1) в координатах, получим систему (2):

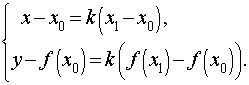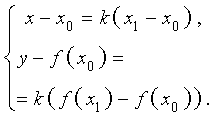(2)

      Исключая из системы (2) переменную   k ,  получим систему (3):

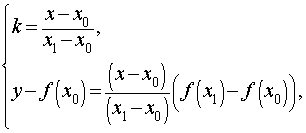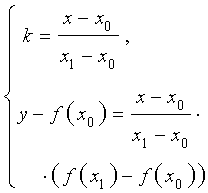(3)

второе уравнение которой можно записать в следующем виде

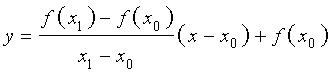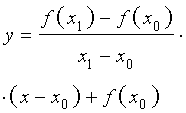(4)

      Уравнение (4) и является уравнением секущей графика функции   y = f (x),   проходящей через точки   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁))   этого графика.

Касательная к графику функции

      Проведем секущую графика функции   y = f (x),   проходящую через точки   A   и   B   этого графика, и рассмотрим случай, когда точка   A   неподвижна, а точка   B   неограниченно приближается к точке   A   по графику функции   y = f (x)   (рис. 2).

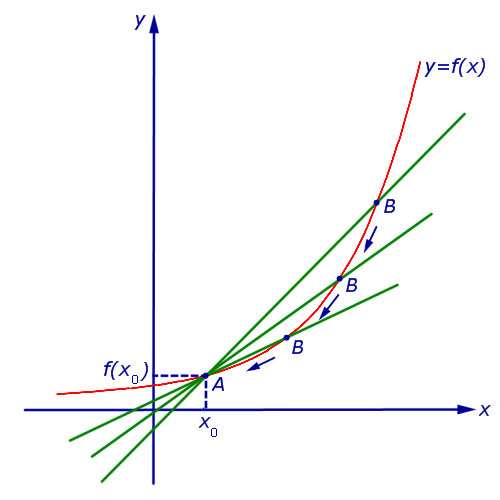
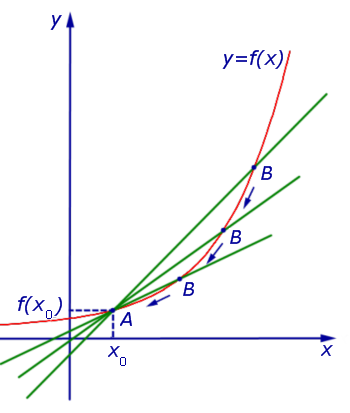
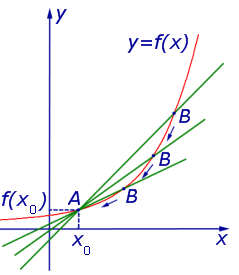
Рис.2

      Неограниченное приближение точки   B   к точке   A   принято обозначать

B → A

и произносить   «B   стремится к   A».

      Заметим, что, если   B → A   для точек   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁))  графика функции  y = f (x),   то это означает, что   x₁ → x₀ .

      Определение 2. Если при   x₁ → x₀   существует предельное положение секущей графика фукнкции   y = f (x),   то это предельное положение секущей называют касательной к графику функции   y = f (x)   в точке   A = (x₀;  f (x₀))  (рис. 3) .

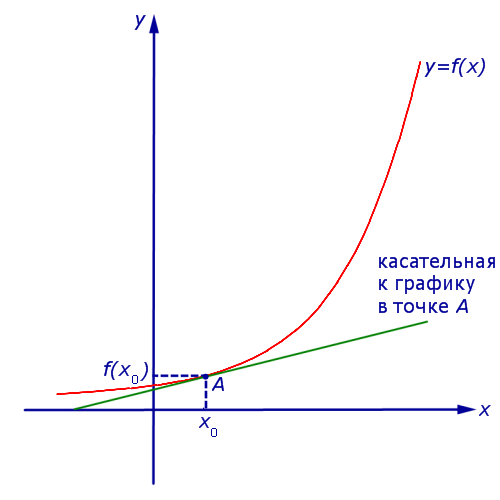
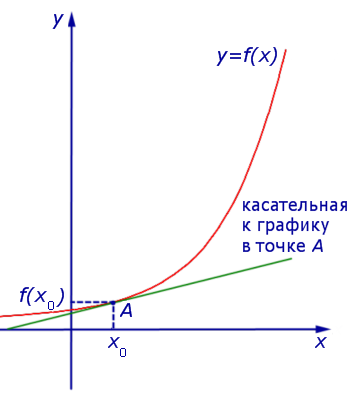
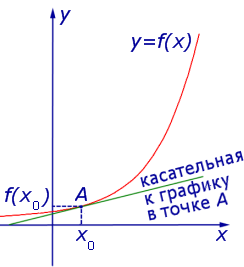
Рис.3

Производная функции

      Определение 3. Если при   x₁ → x₀   отношение

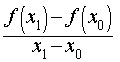(5)

входящее в формулу (4), стремится к некоторому числу, то это число называют производной функции   y = f (x) в точке   x₀ ,   обозначают   f ′(x₀)   или 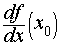и записывают так:

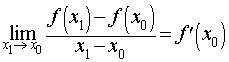(6)

Уравнение касательной к графику функции

      Из формул (4) и (6) вытекает следующее

      Утверждение. Если у функции   y = f (x)   существует производная в точке   x₀ ,   то к графику функции   y = f (x)   в точке с координатами  (x₀;  f (x₀))   можно провести касательную, а уравнение этой касательной имеет вид:

y = f′(x0) (x – x0) + f (x0)

(7)

Геометрический смысл производной

      Рассмотрим сначала возрастающую функцию   y = f (x)   и проведем секущую графика этой функции, проходящую через точки   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁)) (рис. 4).

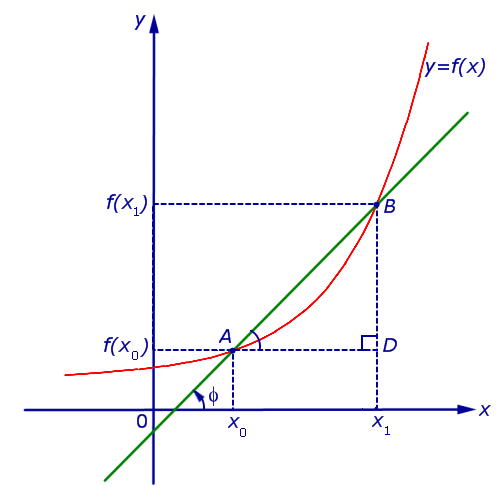
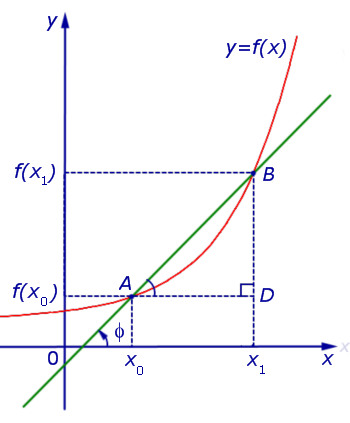
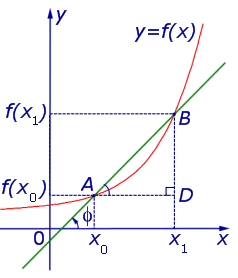
Рис.4

      Обозначим буквой   φ   угол, образованный секущей и положительным направлением оси   Ox,   отсчитываемый против часовой стрелки. Тогда угол   BAD   в треугольнике   ABD   на рисунке 4 равен   φ ,   и по определению тангенса угла получаем равенство

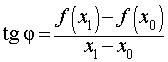(8)

причем по определению углового коэффициента прямой   tg φ   является угловым коэффициентом секущей графика функции   y = f (x),   проходящей через точки   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁))   этого графика.

      Случай, когда функция   y = f (x)   убывает, изображен на рисунке 5

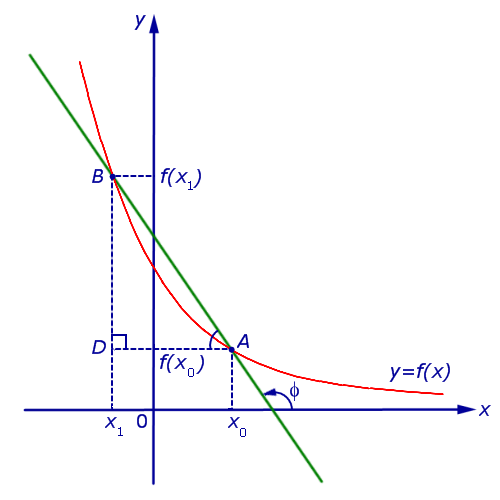
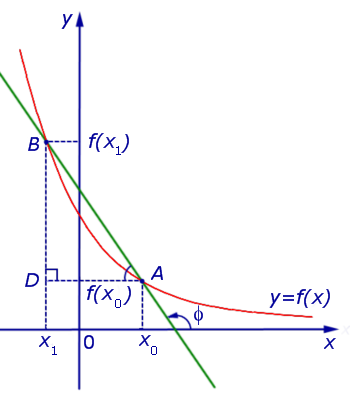
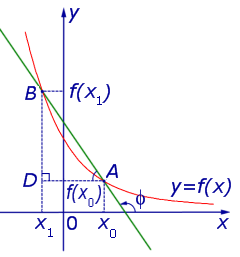
Рис.5

      В этом случае угол   φ  является тупым, причем

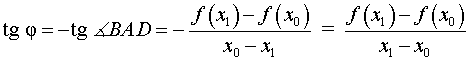
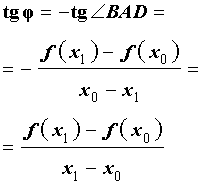
то есть формула (8) справедлива и для случая, когда функция   y = f (x)   убывает.

      Отсюда в соответствии с определением производной функции вытекает соотношение:

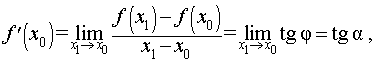
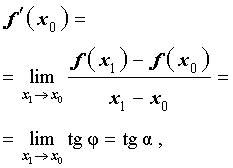
где буквой   α   обозначен угол, образованный касательной к графику функции   y = f (x)   в точке   A = (x₀;  f (x₀))   с положительным направлением оси   Ox   (рис. 6).

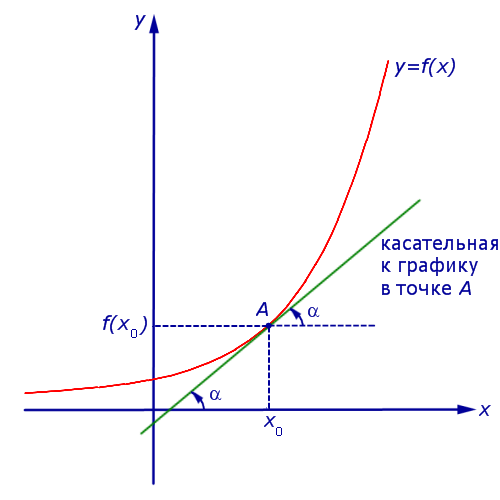
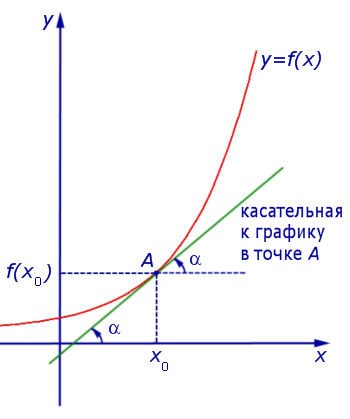
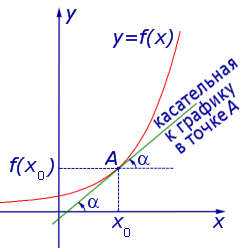
Рис.6

      Таким образом, если у функции   y = f (x)   в точке   x₀   существует производная, то эта производная равна тангенсу угла наклона касательной к графику функции   y = f (x)   в точке   (x₀;  f (x₀)) :

f′(x₀) = tg α ,

где угол наклона   α   образован касательной и положительным направлением оси   Ox   и отсчитывается в положительном направлении (то есть против часовой стрелки).

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Является ли производная функции касательной? — Блог Magoosh

В исчислении мы узнаем, что касательную к функции можно найти, вычислив производную. Таким образом, существует тесная связь между производными и касательными линиями. Однако это не одно и то же. Начнем с того, что производная f ‘( x ) — это функция, а касательная — это прямая.

Вместо этого правильнее утверждение: «Производная измеряет наклон касательных линий.”

Подумайте об этом: часы — это не то же самое, что время . Но если вы хотите узнать время дня, вы можете посмотреть на часы. Часы измеряют время в любой момент дня .

Давайте поближе познакомимся с касательными.

Что такое касательная?

Касательная линия для функции f ( x ) в данной точке x = a — это линия (линейная функция), которая соответствует графику функции при x = a и имеет тот же наклон , что и кривая в этой точке.

Иногда мы можем сказать, что касательная линия « только касается » кривой, или « пересекает кривую только один раз », f но эти идеи иногда могут сбить нас с пути.

На графике ниже показаны касательные линии (красным, пурпурным и пурпурным) в трех разных точках на кривой y = f ( x ) (черным цветом) .

Наклон и производные

Итак, как мы узнаем, каким должен быть наклон касательной? Изучив производных , вы сможете использовать простую формулу

.

м = f ‘( a ).

В этой формуле даны функция f и x -значение a . Ваша задача — найти м , которое представляет собой наклон касательной. Если у вас есть наклон, написать уравнение касательной прямой будет довольно просто.

Нахождение касательной

Предположим, вас попросили найти касательную для функции f ( x ) в заданной точке x = a . Вот пошаговый подход:

1. Найдите производную, f ‘( x ).
2. Подключите x = a , чтобы получить наклон. То есть, вычислим м = f ‘( a ).
3. Если это еще не указано в задаче, найдите координату y точки. Как всегда, вы вставляете в функцию значение x , чтобы получить значение y . Пусть b = f ( a ).
4. Используйте форму точечного уклона и решите относительно y , чтобы найти уравнение касательной.Другими словами, подставьте свои значения м , a и b в уравнение,

   y = м ( x — a ) + b .

Наклон производной меры

Давайте еще раз посмотрим на этот первый шаг: « Найдите производную ». Помните, что производная — это функция (входной переменной x ). Подставляя различные входные значения, x = a , выходные значения f ‘( x ) дают вам наклон касательных линий в каждой точке x = a .

Это то, что мы имеем в виду, когда говорим, что «производная измеряет наклон касательных линий».

Если я хочу узнать наклон f при x = 1, я вычисляю f ‘(1). И если я хочу знать наклон при x = -352/13, я вычисляю f ‘(-352/13). Просто как тот!

Пример: многочлен

Теперь рассмотрим пример функции: f ( x ) = x ³ + 3 x ² + 1.Мы найдем касательные в нескольких разных точках.

Прежде всего найдите производную: f ‘( x ) = 3 x ² + 6 x . (чтобы попрактиковаться в поиске деривативов, прочтите статью Magoosh о деривативах).

Значение функции и значение производной в нескольких точках показаны в таблице ниже:

x	-3	-2	-1	0	1
f ( x ) = x 3 + 3 x 2 + 1	1	5	3	1	5
f ‘( x ) = 3 x 2 + 6 x	9	0	-3	0	9

Для перечисленных точек легко найти уравнение касательной.Обратите внимание, что на экзамене AP Calculus ответы с несколькими вариантами ответов могут быть упрощены. Итак, я показал вам и форму точки-уклона, и упрощенную, или наклон-пересечение , форму касательной.

x	Касательная прямая, форма точка-наклон	Касательная прямая, упрощенная
-3	y = 9 ( x + 3) + 1	y = 9 x + 28
-2	y = 0 ( x + 2) + 5	y = 5
-1	y = -3 ( x + 1) + 3	y = -3 x
0	y = 0 ( x -0) + 1	y = 1
1	y = 9 ( x — 1) + 5	y = 9 x — 4

Теперь давайте посмотрим на график y = f ( x ) вместе с касательными, которые мы только что нашли.

Сводка

Итак, теперь вы знаете. Производная — это не то же самое, что касательная. Вместо этого производная — это инструмент для измерения наклона касательной в любой конкретной точке, точно так же, как часы измеряют время в течение дня. Помня об этом, у вас не возникнет проблем с решением задач касательной на экзамене AP Calculus!

Чтобы узнать больше о наклоне, касательных и производных, ознакомьтесь с соответствующими статьями Magoosh: Является ли производная функции наклоном? и Как найти наклон линии, касающейся кривой.

О Шоне Олте

Шон получил докторскую степень по математике в Университете штата Огайо в 2008 году (Go Bucks !!). В 2002 году он получил степень бакалавра математики и информатику в Оберлинском колледже. Кроме того, Шон получил степень бакалавра искусств. из Консерватории Оберлина в том же году по специальности «музыкальная композиция». Шон по-прежнему любит музыку — почти так же, как математику! — и он (думает, что) может играть на пианино, гитаре и басу.Шон преподавал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!

Политика Magoosh в отношении комментариев в блоге: Чтобы обеспечить максимальное удобство для наших читателей, мы будем одобрять и отвечать на комментарии, относящиеся к статье, достаточно общие, чтобы быть полезными для других студентов, краткие и хорошо написанные! 🙂 Если ваш комментарий не был одобрен, вероятно, он не соответствовал этим правилам. Если вы студент Premium Magoosh и хотите более персонализированное обслуживание, вы можете использовать вкладку «Справка» на панели управления Magoosh.Спасибо!

,

Как сравнить график функции и ее производной — Magoosh Blog

Чтение производного графика — важная часть учебной программы AP Calculus. Типичные задачи исчисления включают задание функции или графика функции и поиск информации о точках перегиба, наклоне, вогнутости или существовании производной.

Существует ли производная?

Во-первых, глядя на график, мы должны знать, существует ли вообще производная функции.В нашем производном блоге есть немного больше информации об этом.

Три ситуации, когда дериватив не существует

Нет производной, если на кривой есть разрыв.

Это любой момент, когда есть разрыв кривой, когда две части кривой не соединяются.

Виды несплошностей:

Имеется устранимый разрыв. Представьте себе линейную функцию, такую ​​как y = x + 3. Если бы мы добавили ограничение, в котором x не определено при x = 0, у нас был бы такой разрыв.

Есть бесконечный разрыв. Это происходит, когда у нас есть какое-либо уравнение, в котором существует разрыв между двумя непрерывными участками кривой из-за того, что асимптоты достигают бесконечности. Например, пусть y = 3 / (x-2). Обратите внимание, у нас есть две вертикальные асимптоты, которые не соединяются.

И, наконец, разрыв скачка. Это происходит с кусочными функциями, где две секции просто не соединяются.

Производная не существует там, где есть острый угол.

Это часто происходит с проблемами абсолютного значения. Посмотрим на график y = √x ²

При x = 0 производной нет, потому что кривая имеет резкий изгиб.

Наконец, нет производной везде, где есть вертикальный разрез графика.

Если есть вертикальный участок графика, наклон не определен; следовательно, производной не существует.

Чтение графика производных.

Глядя на график, мы должны иметь возможность быстро увидеть наклон любого участка и получить приблизительное представление о том, каким должен быть наклон.Это позволяет легко сопоставить график с его производной.

Глядя на первый график, можете ли вы выяснить, какой из трех приведенных ниже графиков является графиком производной?

ф ‘(x):

а

б

с

Несколько ключей к правильному ответу. Сразу должно быть видно, что это некая тригонометрическая функция. Мы знаем, что наклон функции равен 0 в нескольких точках; поэтому график производной в какой-то момент должен проходить через ось абсцисс.Также, глядя на график, мы должны увидеть, что это происходит где-то между -2,5 и 0, а также между 0 и 2,5. Одного этого достаточно, чтобы увидеть, что последний график — правильный ответ.

Построение графика функции на основе производной и двойной производной.

Производная и двойная производная говорят нам несколько ключевых вещей о графике:

(Хорошая практика AP: как определить, минимальное оно или максимальное?)

Ниже приведен график производной функции f (x).

Вот график функции. Можем ли мы увидеть, как они соотносятся?

Умение читать графики производной и знать, какой должна быть общая форма исходной функции, является важной частью учебной программы AP Calculus. Убедитесь, что вы знаете, как определять точки перегиба, локальные минимумы и максимумы, а также места увеличения или уменьшения функции.

О Захари

Захари — бывший инженер-механик, учитель физики, математики и информатики в средней школе.Он окончил Университет Макгилла в 2011 году и работал в автомобильной промышленности в Детройте, прежде чем перейти к образованию. Он преподает и занимается репетиторством в течение последних пяти лет, но вы также можете найти его за приключениями, чтением, скалолазанием и путешествиями всякий раз, когда появляется возможность.

Политика в отношении комментариев в блоге Magoosh: Чтобы обеспечить максимальное удобство для наших читателей, мы будем одобрять и отвечать на комментарии, относящиеся к статье, достаточно общие, чтобы быть полезными для других студентов, краткие и хорошо написанные! 🙂 Если ваш комментарий не был одобрен, вероятно, он не соответствовал этим правилам.Если вы студент Premium Magoosh и хотите более персонализированное обслуживание, вы можете использовать вкладку «Справка» на панели управления Magoosh. Спасибо!

,

Производные правила | Математическое исчисление

Производные правила и законы. Таблица производных функций.

Определение производной

Производная функции — это отношение разности значение функции f (x) в точках x + Δx и x с Δx, когда Δx бесконечно маленький. Производная — это наклон функции или наклон касательной в точке x.

Вторая производная

Вторая производная дается по формуле:

Или просто выведите первую производную:

N-я производная

n -я производная вычисляется путем вычисления f (x) n раз.

Производная n равна производной от (n-1) производная:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] ‘

Пример:

Найдите четвертую производную от

.

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] » ‘ = [10 x ⁴ ] » ‘= [40 x ³ ]’ ‘= [120 x ² ]’ = 240 x

Производная на графике функции

Производная функции — это наклон касательной прямой.

Производные правила

Правило суммы производных

Когда a и b являются константами.

( a f ( x ) + bg ( x ) ) ‘= a f’ ( x ) + bg ‘ ( x )

Пример:

Найти производную от:

3 x ² + 4 x.

Согласно правилу сумм:

a = 3, b = 4

f ( x ) = x ² , г ( x ) = x

f ‘ ( x ) = 2 x , г ‘ ( x ) = 1

(3 x ² + 4 x ) ‘= 3⋅2 x + 4⋅1 = 6 x + 4

Правило производного продукта

( f ( x ) ∙ г ( x ) ) ‘= f’ ( x ) г ( x ) + f ( x ) г ‘ ( x )

Правило частных производных

Правило производной цепочки

f ( g ( x )) ‘= f’ ( г ( x )) ∙ г ‘ ( x )

Это правило можно лучше понять с помощью обозначения Лагранжа:

Функция линейного приближения

При малых Δx мы можем получить приближение к f (x ₀ + Δx), когда мы знаем f (x ₀ ) и f ‘(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f ‘( x ₀ ) ⋅Δ x

Производные функций таблицы

Имя функции	Функция	Производная
	f ( x )	f ‘( x )
Константа	конст.	0
Линейный	x	1
Мощность	x а	a x a- 1
Экспоненциальная	e x	e x
Экспоненциальная	a x	a x ln a
Натуральный логарифм	лин ( x )
Логарифм	бревно b ( x )
Синус	грех x	cos x
Косинус	cos x	-sin x
Касательная	желто-коричневый x
Арксинус	арксин x
Арккосин	arccos x
Арктангенс	арктан x
Гиперболический синус	sinh x	цвет x
Гиперболический косинус	цвет x	sinh x
Гиперболический тангенс	танх x
Обратный гиперболический синус	sinh -1 x
Обратный гиперболический косинус	cosh -1 x
Обратный гиперболический тангенс	tanh -1 x

Производные примеры

, Пример # 1

f ( x ) = x ³ +5 x ² + x +8

f ‘ ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

, пример # 2

f ( x ) = sin (3 x ² )

При применении цепного правила:

f ‘ ( x ) = cos (3 x ² ) ⋅ [3 x ² ] ‘= cos (3 x ² ) ⋅ 6 x

Тест второй производной

Когда первая производная функции равна нулю в точке x ₀ .

f ‘( x ₀ ) = 0

Тогда вторая производная в точке x ₀ , f » (x ₀ ), может указывать тип эта точка:

f » ( x 0 )> 0	местный минимум
f » ( x 0 ) <0	местный максимум
f » ( x 0 ) = 0	неопределенный

---

См. Также

,

Как найти частную производную функции? | by Chi-Feng Wang

Для простых функций, таких как f (x, y) = 3x²y , это все, что нам нужно знать. Однако, если мы хотим вычислить частные производные более сложных функций, например, с вложенными выражениями типа max (0, w ∙ X + b) — нам нужно может использовать правило многомерной цепочки, известное как правило для цепочки полной производной с одной переменной .

Правило одной цепочки переменных

Давайте сначала рассмотрим правило одной цепочки переменных. Рассмотрим функцию y = f (g (x)) = sin (x²). Чтобы получить производную этого выражения, мы умножаем производную внешнего выражения на производную внутреннего выражения или «соединяем части вместе». Другими словами:

Изображение 6: Правило цепочки с одной переменной, где u — промежуточная переменная для вложенных подвыражений

В нашем примере u = x² и y = sin (u) .Следовательно:

Изображение 7: Производные // Источник

и

Изображение 8: Производная всего выражения // Источник

Приятно думать о правиле цепочки с одной переменной как о диаграмме операций, которые проходят x , вот так :

Изображение 9: Схема цепочки операций для y = sin (x ²)

Эта концепция визуализации уравнений в виде диаграмм окажется чрезвычайно полезной при работе с правилом многопараметрической цепочки. Кроме того, если вы используете Tensorflow (или Keras) и TensorBoard, при построении модели и написании обучающего кода вы можете увидеть схему операций, аналогичную этой.

Правило цепочки многих переменных

Правило цепочки нескольких переменных, также известное как правило цепочки полной производной одной переменной , как оно называется в статье, является вариантом правила скалярной цепочки. В отличие от того, что предполагает его название, его можно применять к выражениям только с одной переменной. Однако в выражении должно быть несколько промежуточных переменных.

Чтобы проиллюстрировать этот момент, давайте рассмотрим уравнение y = f (x) = x + x² . Используя правило дополнительной скалярной производной, мы можем немедленно вычислить производную:

Изображение 10: Производная от x + x ²

Давайте попробуем сделать это с помощью цепного правила.Сначала вводятся промежуточные переменные: u₁ (x) = x² и u₂ (x, u₁) = x + u₁. Если мы применим правило цепочки одной переменной, мы получим:

Изображение 11: Использование правила цепочки одной переменной

Очевидно, 2x ≠ 1 + 2x, поэтому здесь что-то не так. Давайте нарисуем график нашего уравнения:

Изображение 12: Схема цепочки операций для y = x + x ² // // Источник

Диаграмма на изображении 12 больше не является линейной, поэтому мы должны рассматривать всех путей на диаграмме, ведущих к окончательному результату.Поскольку u₂ имеет два параметра, в игру вступают частные производные. Чтобы вычислить производную этой функции, мы должны вычислить частную производную по x от u₂ (x, u₁). Здесь изменение x отражается в u₂ двумя способами: как операнд сложения и как операнд оператора квадрата. В символах ŷ = (x + Δx) + (x + Δx) ² и Δy = ŷ-y , и где ŷ — это значение y при измененном x.

Следовательно, чтобы вычислить частичное u₂ (x, u₁) , нам нужно просуммировать все возможные вклады от изменений x в изменение y . Полная производная от u₂ (x, u₁) определяется следующим образом:

Изображение 13: Производная от y = x + x ² // Источник

Проще говоря, складывается из эффекта изменения x непосредственно на u₂ и эффект изменения x через u₁ на u₂. Мне легче визуализировать это в виде графика:

Изображение 14: График y = x + x ² с включенными частичными числами

И все! Получили правильный ответ: 1 + 2x.Теперь мы можем суммировать этот процесс в одном правиле, правиле цепочки многих переменных (или правиле цепочки полной производной одной переменной):

Изображение 15: Правило цепочки нескольких переменных // Источник

Если мы введем псевдоним для x как x = u (n + 1), то мы можем переписать эту формулу в ее окончательном виде, который будет выглядеть немного аккуратнее:

Изображение 16: Правило многопараметрической цепочки // Источник

Вот и все! В качестве примера рассмотрим другой пример: f (x) = sin (x + x²) . Наши 3 промежуточные переменные: u₁ (x) = x², u₂ (x, u₁) = x + u₁, и u₃ (u₂) = sin (u₂) .Еще раз, мы можем нарисовать наш график:

Изображение 17: График y = sin (x + x ²) с включенными частичными числами

и вычислить наши частичные:

Изображение 18: Частичные для функции y = sin (x + x ²)

Следовательно, производная f (x) = sin (x + x²) равна cos (x + x²) (1 + 2x) .

.