Прямолинейное движение: равномерное и равноускоренное
Движением тела называется изменение его положения в пространстве относительно других. Рассмотрим равномерное прямолинейное движение тела, для этого введем следующие понятия.
Определение равномерного прямолинейного движения тела
Равномерное прямолинейное движение тела — это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Координата— величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.
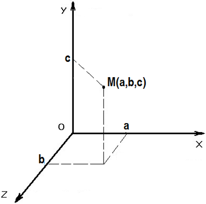
Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.
Траектория — это линия, вдоль которой движется тело.
Путь — это длина траектории, вдоль которой движется тело.

Скоростью равномерного прямолинейного движения называется величина, равная отношению перемещения тела к времени t, за которое это перемещение произошло .
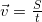
Скорость ― это векторная величина!
В заданиях, где дана зависимость скорости тела от времени,
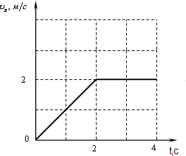
пройденный путь можно вычислить как площадь под графиком:
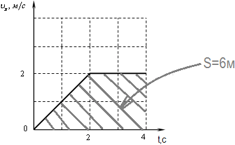
Следующие три переменные включены в равномерное прямолинейное движение:
Координаты: координата, с которой тело начинает двигаться (начальная позиция) 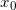 и координата, куда он прибывает через некоторое время (конечная позиция)
и координата, куда он прибывает через некоторое время (конечная позиция) 
Скорость: скорость всегда будет постоянной
 .
.Время: момент, в который объект начинает двигаться (начальное время)
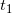 и время, необходимое для прохождения определенного расстояния (конечное время)
и время, необходимое для прохождения определенного расстояния (конечное время) 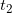
Эти три переменные связаны этой формулой:
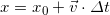 ,
,
где 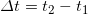 .
.
Равноускоренное прямолинейное движение
Равноускоренное прямолинейное движение тела — движение, при котором его ускорение не меняется, ни по величине, ни по направлению.
Уравнение равноускоренного движения в проекции на ось Ox имеет вид:
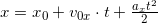 , где:
, где:
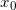 — начальная координата тела;
— начальная координата тела;
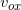 — проекция начальная скорость на ось x;
— проекция начальная скорость на ось x;
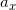 — проекция ускорения на ось x;
— проекция ускорения на ось x;
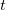 — время движения
— время движения
Ускорением тела называется векторная величина, равная отношению изменения скорости за любой промежуток времени к величине этого промежутка:
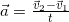
Зависимость скорости от времени при наличии ускорения определяется выражением:
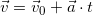 , где:
, где:
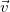 — скорость тела в момент времени t; t — время;
— скорость тела в момент времени t; t — время;
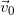 — начальная скорость тела;
— начальная скорость тела;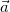 — ускорение тела.
— ускорение тела.
Применение производной в кинематике
Если существует зависимость координаты от времени x(t), то зависимость скорости от времени можно получить, взяв производную по времени от этой зависимости.
Скорость ― это производная координаты тела по времени:
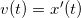
Например, если зависимость координаты тела при равноускоренном движении имеет вид 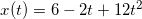 , то взяв первую производную от координаты, мы получим зависимость скорости тела от времени:
, то взяв первую производную от координаты, мы получим зависимость скорости тела от времени:
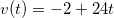
Точно также, ускорение ― это производная от скорости тела:
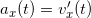 .
.
Примеры выполнения заданий ЕГЭ по физике
Задание 1.
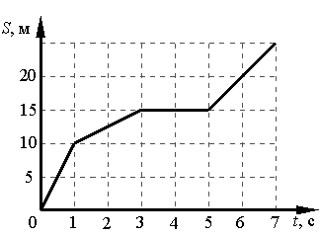
На рисунке представлен график зависимости пути S, пройденного материальной точкой, от времени t. Определите, сколько секунд, после начала движения, когда точка стала двигаться со скоростью 10 м/с.
Ответ:1
Решение: Чтобы определить скорость движения точки на интервале, разделим путь, пройденный точкой, на все время движения на каждом отрезке графика. На интервале с начала движения и до 1 с точка прошла 10 м, следовательно, ее скорость была 10 м/с. Скорость точки на следующих интервалах пути ― 2,5 м/с, 0 м/с и 5 м/с соответственно.
Задание 2.
На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х= 0, а пункт Б ― в точке х= 30 км. Чему равна скорость автобуса на пути из А в Б? Ответ выразить в км/ч.
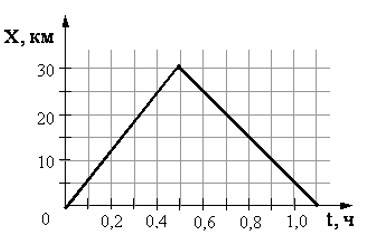
Ответ: 60 км/ч
Решение:
Согласно графику, зависимость пути автобуса от времени линейна, следовательно, скорость автобуса на всех участках пути постоянна. Из пункта А в пункт Б, находящиеся друг от друга на расстоянии S = 30 км автобус идет
t = 0,5 ч.
Уравнение движения автобуса: S = vt, откуда v = S/t = 30 км/ 0,5 ч = 60 км/ч.
Задание 3.
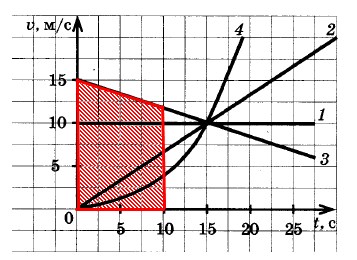
На рисунке изображены графики зависимости модуля скорости движения четырех автомобилей от времени. Какой из автомобилей — 1, 2, 3 или 4 — прошел наибольший путь за первые 10 с движения?
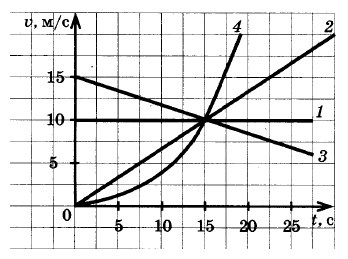
Ответ: 3
Решение:
Путь, пройденный каждым из автомобилей, равен площади под соответствующим графиком зависимости модуля скорости автомобиля от времени движения.
Как видно из следующих рисунков, наименьшая площадь под графиком скорости автомобиля 4, наибольшая ― под графиком скорости автомобиля 3.
Автомобиль 1 прошел путь:
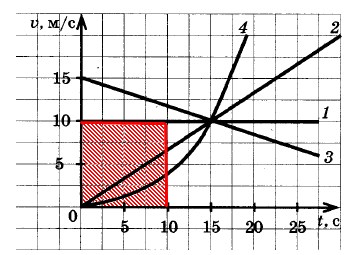
Автомобиль 2 прошел путь:
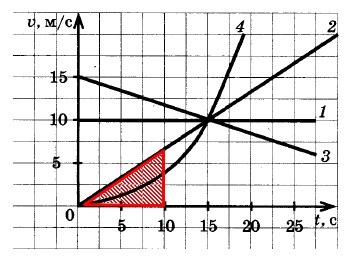
Автомобиль 3:
Путь, который проехал автомобиль 4:
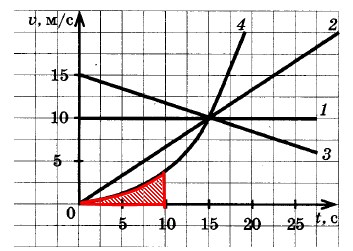
Задание 4.
На рисунке представлен график зависимости скорости v автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 3 с.
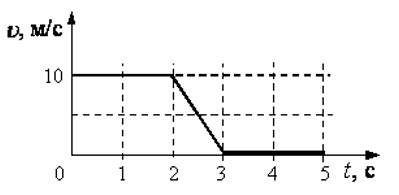
Ответ: 25 м
Решение: Путь, пройденный автомобилем, равен площади под соответствующим графиком зависимости модуля скорости автомобиля от времени движения.
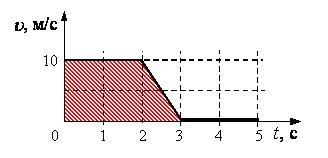
Площадь образовавшейся трапеции равна: 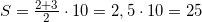 м.
м.
Задание 5.
Тело движется по оси x. По графику зависимости проекции скорости тела υx от времени t установите, какой путь прошло тело за время от t1= 0 до t2= 4 c.
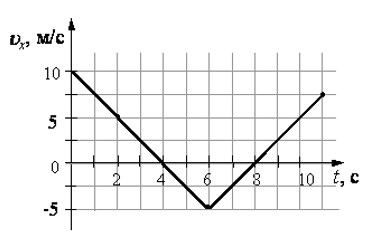
Ответ: 20.
Решение:
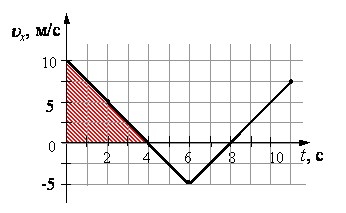
Путь, пройденный телом равен площади под соответствующим графиком зависимости модуля скорости тела от времени движения. Так как тело движется по оси х, других составляющих скорости, кроме υx у тела нет.
Площадь образовавшегося под графиком треугольника равна: 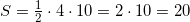
Задание 6
На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите ускорение тела.
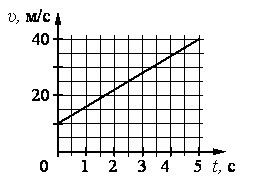
Ответ: 6 м/с2
Решение: Модуль ускорения автомобиля равен 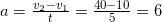 м/с2.
м/с2.
Задание 7
По графику зависимости скорости от времени (см. рисунок) определите ускорение прямолинейно движущегося тела в момент времени 2 с.
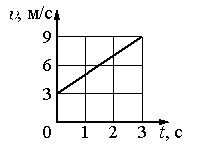
Ответ: 2 м/с2.
Решение: Так как движение равноускоренное, то ускорение постоянная величина и в момент времени 2 с ускорение такое же как и в момент времени 3 с. Определяем ускорение по формуле: 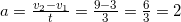
Задание 8
Зависимость пути от времени прямолинейно движущегося тела имеет вид: x(t) = –4t + 10t2, где все величины выражены в СИ. Чему равно ускорение тела?
Ответ: 20 м/с2.
Ускорение есть вторая производная координаты по времени. Имеем 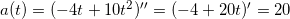 м/с2.
м/с2.
Задание 9
Тело начинает падать из состояния покоя и перед ударом о Землю имеет скорость 80 м/с. Каково время падения? Сопротивлением воздуха пренебречь.
Ответ: 8с.
Решение: Все тела, падающие на Землю из состояния покоя, движутся с ускорением свободного падения g = 10 м/с2. Скорость падающего тела равна v(t) = v0 + gt, так как начальной скорости у тела нет (v0 =0), то время падения тела равно:
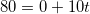 отсюда
отсюда 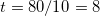 с.
с.
Задание 10
Автомобиль трогается с места и движется с постоянным ускорением 5 м/с2. Какой путь прошёл автомобиль, если его скорость в конце пути оказалась равной 15 м/с?
Ответ: 22,5 м.
Решение: Пройденный автомобилем путь равен 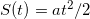 , где a ― ускорение автомобиля, равное a = 5 м/с2, t ― время его движения. Скорость автомобиля равна v(t) = at. Согласно условию, начальной скорости движения автомобиля нет.
, где a ― ускорение автомобиля, равное a = 5 м/с2, t ― время его движения. Скорость автомобиля равна v(t) = at. Согласно условию, начальной скорости движения автомобиля нет.
Определим время, которое понадобилось автомобилю, чтобы развить конечную скорость v = 15 м/с:
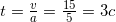
Автомобиль прошел путь: 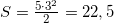 м.
м.
Задание 11.
При равноускоренном движении автомобиля на пути 25 м его скорость увеличилась от 5 до 10 м/с. Чему равно ускорение автомобиля?
Ответ: 1,5 м/с2.
Решение: Уравнение движения автомобиля 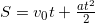 , где v0 ― начальная скорость автомобиля v0 = 5 м/с, а ―постоянное ускорение автомобиля, t ― время движения автомобиля, S = 25 м.
, где v0 ― начальная скорость автомобиля v0 = 5 м/с, а ―постоянное ускорение автомобиля, t ― время движения автомобиля, S = 25 м.
Скорость автомобиля равна v = v0 + at, конечная скорость равна v = 10 м/с. Выразим из этого уравнения время движения автомобиля:
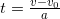
И определим ускорение из уравнения движения:
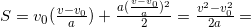
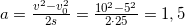 м/с2.
м/с2.
Задание 12.
Скорость пули при вылете из ствола пистолета равна 250 м/с. Длина ствола 0,1 м. Каково ускорение пули в конце ствола, если считать ее движение равноускоренным? Ответ выразить в км/с2.
Ответ: 312,5 км/с2.
Решение: Уравнение движения пули 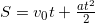 , где v0 ― начальная скорость пули v0 = 0 м/с, а ―постоянное ускорение пули, t ― время движения пули в стволе, S = 0,1 м ― путь, который проходит пуля в стволе.
, где v0 ― начальная скорость пули v0 = 0 м/с, а ―постоянное ускорение пули, t ― время движения пули в стволе, S = 0,1 м ― путь, который проходит пуля в стволе.
Скорость пули при вылете из ствола считается по формуле v = v0 + at и равна по условию v = 250 м/с. Отсюда, время движения пули равно 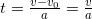 , а пройденный пулей путь:
, а пройденный пулей путь:
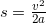
Отсюда, ускорение пули равно:
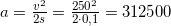 м/с2 или 312,5 км/с2.
м/с2 или 312,5 км/с2.
Таким образом, теперь вы сможете решать задания ЕГЭ по физике на темы равномерное прямолинейное движение и равноускоренное прямолинейное движение.
Равномерное движение тела по окружности – FIZI4KA

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности \( T \) — время, в течение которого тело совершает один полный оборот. Единица периода — \( [\,T\,] \) = 1 с.
Частота обращения \( (n) \) — число полных оборотов тела за одну секунду: \( n=N/t \). Единица частоты обращения — \( [\,n\,] \) = 1 с-1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: \( n=1/T \).
Пусть некоторое тело, движущееся по окружности, за время \( t \) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол \( \varphi \).
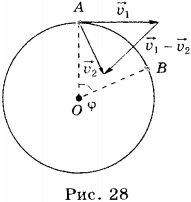

Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость \( \omega \) — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: \( \omega=\varphi/t \). Единица угловой скорости — радиан в секунду, т.е. \( [\,\omega\,] \) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен \( 2\pi \). Поэтому \( \omega=2\pi/T \).
Линейная скорость тела \( v \) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: \( \vec{v}=l/t \). За один оборот точка проходит путь, равный длине окружности. Поэтому \( \vec{v}=2\pi\!R/T \). Связь между линейной и угловой скоростью выражается формулой: \( v=\omega R \).
Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.
4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: \( \vec{a}=\frac{\Delta\vec{v}}{t} \) и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.
Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: \( a=\frac{v^2}{R} \). Так как \( v=\omega R \), то \( a=\omega^2R \).
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости
2. Линейная скорость точки 1, находящейся на расстоянии \( R_1 \) от центра вращающегося колеса, равна \( v_1 \). Чему равна скорость \( v_2 \) точки 2, находящейся от центра на расстоянии \( R_2=4R_1 \)?
1) \( v_2=v_1 \)
2) \( v_2=2v_1 \)
3) \( v_2=0,25v_1 \)
4) \( v_2=4v_1 \)
3. Период обращения точки по окружности можно вычислить по формуле:
1) \( T=2\pi\!Rv \)
2) \( T=2\pi\!R/v \)
3) \( T=2\pi v \)
4) \( T=2\pi/v \)
4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:
1) \( \omega=a^2R \)
2) \( \omega=vR^2 \)
3) \( \omega=vR \)
4) \( \omega=v/R \)
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с
2) 3300 с
3) 3·10-4 с
4) 5·10-6 с
9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?
1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц
10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?
1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с
11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения
ФОРМУЛА
1) \( 1/T \)
2) \( v^2/R \)
3) \( v/R \)
4) \( \omega R \)
5) \( 1/n \)
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
Ответы
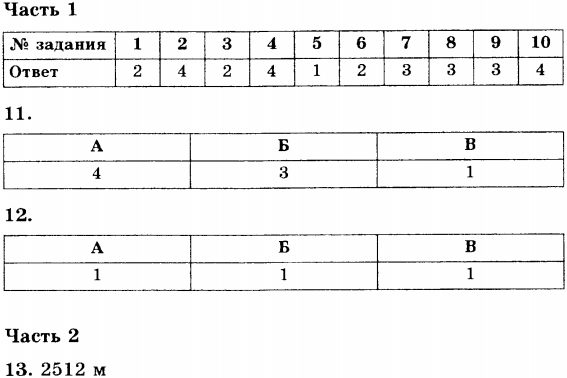

Равномерное движение тела по окружности
5 (100%) 1 voteКинетика — Знаешь как
Движение тела
Содержание статьи
 Механическим движением тела называется изменение с течением времени его положения по отношению к другим телам.
Механическим движением тела называется изменение с течением времени его положения по отношению к другим телам.
Раздел механики, изучающий движение материальных тел в пространстве и времени без рассмотрения вызывающих это движение взаимодействий, называется кинематикой.
Кинетика это наука о движении материи и о её причине, в механике изучение механического состояния тела и т.д. Что характерно для всех наук есть соответствующее название (биологическая кинетика, химическая кинетика, физическая и т.д.).
В природе вообще нет ничего, что можно было бы считать совершенно неподвижным. Только условно некоторые тела в определенных случаях можно считать неподвижными. Например, при изучении движения различных тел во многих случаях в качестве неподвижных принимают Землю и все тела, неизменно с ней связанные (здания, деревья и т. п.).
Любое движущееся тело обладает определенными размерами — протяженностью в пространстве. Его движение происходит также в какой-то части пространства, размер которой называют масштабом движения. Если размеры тела ничтожно малы по сравнению с масштабом движения, то это тело можно называть материальной точкой, считая, что в» этой точке сосредоточена вся масса этого тела. Например, при рассмотрении годичного движения Земли вокруг Солнца Землю можно считать материальной точкой, так как масштаб движения достаточно велик по сравнению с размером планеты.
Материальная точка — это идеализированное понятие. Вводя это понятие, мы отвлекаемся от всех несущественных для данного движения свойств тела, например, его размеров, формы, строения и т. д. Каждая материальная точка, перемещаясь в пространстве, описывает воображаемую линию, называемую траекторией, форма которой может быть самой разнообразной. Если траекторией движения точки является прямая линия, то движение называется прямолинейным, а если кривая линия — криволинейным.
Положение какого-либо тела или материальной точки определяют лишь по отношению к другому материальному телу, условно считаемому неподвижным и называемому телом отсчета. Связанная с этим телом отсчета произвольная система координат называется системой отсчета положений материальной точки. Без выбора системы отсчета описать движение невозможно. Например, при прямолинейном движении можно пользоваться системой координат, состоящей из одной прямой линии OS,вдоль которой происходит движение, с началом отсчета в точке О. В более сложных случаях применяется декартова прямоугольная система координат со взаимно перпендикулярными осями Ох и Оу, пересекающимися точке О, которая является началом отсчета.
Длина части траектории, пройденная точкой с момента начала отсчета времени, называется длиной пути (путем). Путь — скалярная величина, характеризующаяся только численным значением s.
Если начальное положение точки соединить прямой с конечным положением, то получим перемещение ∆r точки за какое-то время t. Перемещение точки является вектором, то есть величиной, характеризующейся численным значением и направлением. При прямолинейном движении абсолютная величина вектора перемещения |∆r| равна пути s.
По траектории различают два основных простейших вида движения твердого тела: поступательное и вращательное. Движение грела, при котором прямая, соединяющая две любые точки тела, перемещается параллельно самой себе в процессе движения тела, называется поступательным.
Что такое вращательное движение это движение тела, при котором все его точки движутся по окружностям, центры которых расположены на одной прямой (оси вращения).
По характеру зависимости пути от времени движения делятся на равномерные и неравномерные.
Равномерное прямолинейное движение
Равномерным прямолинейным движением называют такое движение, при котором материальная точка, двигаясь по прямой, за произвольные равные промежутки времени проходит пути равной длины.
Примером равномерного прямолинейного движения может служить движение ленты заводского сборочного конвейера, поезда на прямолинейном участке пути при постоянной силе тяги и др. Однако следует иметь в виду, что абсолютно равномерных движений в природе не существует, но если отклонения от равномерности незначительны, то ими можно пренебречь.
Для характеристики движения тела вводят векторную физическую величину — скорость. Пусть положение прямолинейно движущегося тела в некоторый момент времени t0 определяется путем s0, а в момент времени t — путем s. Тогда за время t— t0 тело проходит путь s — s0. Математическое выражение для скорости υ можно записать в виде
υ = (s — s0):(t — t0)
В частном случае, когда t0 = 0 и s0 = О,
υ = s : t
Здесь s представляет собой путь, пройденный телом за время t.
Что такое физическая величина это численно равная пути, пройденному телом в единицу времени, называется скоростью υ.
Скорость равномерного движения — величина постоянная. При прямолинейном движении вектор скорости направлен вдоль траектории.
В СИ за единицу измерения скорости принимается скорость такого равномерно движущегося тела, которое за каждую секунду проходит путь, равный одному метру,
υ = (1м):(1с) = 1(м:c)
В системе СГС единица измерения скорости 1(cм:c) Из формулы (1) следует, что
s = s0 + υ(t — t0)
Если t0 = 0 и s0 = 0, то формула (3) примет вид
s = υt,
где s — путь, пройденный телом за время t.
Из формулы (4) видно, что при равномерном движении тела его путь есть линейная функция от времени, так как υ — постоянная величина.
Графики скорости пути равномерного движения
Формула s = υt дает полное описание равномерного движения. Связь между s и t для отдельных моментов времени можно задавать в виде таблицы, содержащей соответственные значения промежутка времени, и пройденного пути.
Например скорость некоторого равномерного движения равна 0,5 —. Формула (4) в этом случае имеет вид s = 0,5 • t. Таблица пути и времени такого движения выглядит следующим образом:
| t, с | 0 | 1 | 2 | 3 | 4 |
| s, М | 0 | 0,5 | 1 | 1,5 | 2 |
Зависимость пути от времени удобнее изображать графиками. Они нагляднее показывают картину изменения пути от времени. Отложим на оси абсцисс значения времени t (рис. 1), а по оси ординат значения пути s. Тогда зависимость пути s от времени t выразится прямой OA. Если тело движется с большей скоростью (υ = 1,25(м:c) , то эта зависимость будет выражаться прямой ОВ. Прямые OA и ОВ называются графиками пути.
 По графику пути равномерного движения можно определить скорость, с которой совершалось движение. Тангенс угла а наклона графика пути к оси времени численно равен отношению ординаты произвольно точки графика к ее абсциссе,.то есть равен отношению s : t, это и есть скорость равномерного движения. Таким образом, υ — tg α. Чем больше скорость, тем больший угол составляет график с осью времени.
По графику пути равномерного движения можно определить скорость, с которой совершалось движение. Тангенс угла а наклона графика пути к оси времени численно равен отношению ординаты произвольно точки графика к ее абсциссе,.то есть равен отношению s : t, это и есть скорость равномерного движения. Таким образом, υ — tg α. Чем больше скорость, тем больший угол составляет график с осью времени.
Рис. 1 — 2 Графики скорости пути равномерного движения
На рис. 2 изображен график скорости равномерного движения, который получен следующим образом: на оси абсцисс отложены значения времени а на оси ординат — значение скорости, которая не меняется с течением времени ( υ = 3 (м:с) = const). Здесь график скорости равномерного движения представляет собой прямую АВ, параллельную оси времени. Пользуясь графиком скорости, можем определить путь, проходимый телом за определенный промежуток времени. При равномерном прямолинейном движении пройденный телом путь s численно равен площади прямоугольника, ограниченного осью времени, графиком скорости и двумя вертикальными отрезками, проведенными из точек, соответствующих началу и концу рассматриваемого промежутка времени.
Переменное движение. Средняя и мгновенная скорости
Неравномерным, или переменным, движением называется такое движение тела, при котором оно за равные промежутки времени проходит неодинаковые отрезки пути.
Скорость при таком движении не остается постоянной на протяжении всего рассматриваемого пути. Такое движение встречается очень часто. Характеристиками неравномерного движения являются средняя и мгновенная скорости. Понятие о средней скорости основано на мысленной замене неравномерного движения равномерным.
Средняя скорость неравномерного движения за данный промежуток времени t — t0 равна скорости такого равномерного движения, при которой тело проходит тот же путь s — s0u3a тот же промежуток времени t — t0, что и при данном неравномерном движении
υср = (s — s0):(t — t0) = ∆s : ∆t
Средняя скорость не дает представления о характере движения. Так, при полете самолета между двумя городами нас может интересовать не только его средняя скорость на всем пути, но скорости, которые самолет развивал на отдельных участках. Если скорость все время меняется, то наилучшее представление о ее величине в данный момент времени или в данной точке пути получим, если промежуток времени ∆t, за который тело будет проходить путь ∆s, возьмем возможно меньшим. Этот промежуток времени можно выбрать настолько малым, что скорость за это время не будет заметно изменяться, и тогда на этом малом участке пути движение можно считать равномерным. Скорость такого движения можно считать мгновенной скоростью неравномерного движения в данный момент времени или в заданной точке траектории. Мгновенная скорость переменного движения точки измеряется той скоростью, с которой двигалась бы точка, если бы, начиная с данного мгновения, ее движение стало равномерным.
Равнопеременное движение Ускорение
 Что такое ускорение это величина, характеризующая изменение скорости движения в единицу времени и обозначается буквой а.
Что такое ускорение это величина, характеризующая изменение скорости движения в единицу времени и обозначается буквой а.
Простейшим видом переменного движения является равнопеременное движение, то есть такое движение, при котором скорость в любые равные промежутки времени изменяется на одну и ту же величину.
Пусть в момент времени t0 скорость имеет значение υ0, а в момент времени t— значение υ, тогда за время t — t0 скорость изменилась на υ — υ0. Разделив разность скоростей на время движения t — t0 получим изменение скорости в единицу времени. Формула для вычисления ускорения равнопеременного движения имеет такой вид:
a = ∆υ : ∆t
В СИ за единицу ускорения принимается ускорение такого движения, при котором скорость меняется на 1 —за каждую секунду (сокращенно 1(м:с2) В СГС единица ускорения 1(см:с2)
Как и скорость, ускорение является векторной величиной. При равнопеременном движении на протяжении всего движения ускорение остается неизменным по величине и направлению.
Ускорение имеет тот же знак, что и изменение скорости υ — υ0 = ∆υ. Если скорость возрастает по численному значению (∆υ> > 0 и а >0), то движение называется равноускоренным. В этом случае вектор скорости и вектор ускорения направлены в одну и ту же сторону. Если скорость убывает по численному значению, то движение называется равнозамедленным. Тогда вектор скорости и вектор ускорения направлены в противоположные стороны (υ = υ0 — at). Из формулы
υ = υ0 + a(t — t0),
Следовательно, при равнопеременном движении скорость меняется со временем линейно. Если t0 = 0, то
υ = υ0 + at
Если начальная скорость υ0 = 0, то
υ = at.
Построим график, отложив по оси абсцисс время г, а по оси ординат скорость υ; зададим начальные условия: υ0 = 2(м:c), а = 2(м:c2)
График скорости (рис. 3) равноускоренного движения есть прямая АВ, наклоненная к оси абсцисс. Отрезок, отсекаемый графиком на оси ординат, показывает величину начальной скорости. Очевидно, если начальная скорость равна нулю, то график проходит через начала координат.
Для равно замедленного движения из формулы
υ = υ0 — a(t — t0).
Если t0 = 0, то υ = υ0 — at.
При равно замедленном движении график скорости есть также прямая линия, пересекающая ось ординат в точке υ0, однако наклоненная вниз.
Статья на тему Кинетика
Тест 1 к разделу «Механика»
Тест к разделу «Механика»
Оценка: «5» — 90% выполнения, «4» — 80%; «3» -60%
Тест №1 Тема. Кинематика
1. Перемещение – это:
1)векторная величина; 2) скалярная величина; 3) может быть и векторной и скалярной величиной; 4) правильного ответа нет.
2.Модуль перемещения при криволинейном движении в одном направлении:
1) равен пройденному пути; 2) больше пройденного пути; 3) меньше пройденного пути; 4) правильного ответа нет.
3. При прямолинейном движении скорость материальной точки направлена:
1) туда же, куда направлено перемещение; 2) против направления перемещения; 4) независимо от направления перемещения;
4. При криволинейном движении мгновенная скорость материальной точки в каждой точке траектории направлена:
1) по траектории; 2) по касательной к траектории в этой точке; 3) по радиусу кривизны траектории.
5. Перемещением движущейся точки называют…
1) …длину траектории; 2) пройденное расстояние от начальной точки траектории до конечной; 3)… направленный отрезок прямой, соединяющий начальное положение точки с его конечным; 4) …линию, которую описывает точка в заданной системе отсчета.
6. Средняя скорость характеризует:
1) равномерное движение; 2) неравномерное движение;
7. Физическая величина, равная отношению перемещения материальной точки к физически малому промежутку времени, в течение которого произошло это перемещение, называется
1) средней скоростью неравномерного движения материальной точки; 2) мгновенной скоростью материальной точки; 3) скоростью равномерного движения материальной точки.
8. Направление ускорения всегда совпадает с:
1) направлением скорости; 2) направлением перемещения; 3) направлением вектора изменения скорости.
9. Ускорение – это:
1) физическая величина, равная отношению изменения скорости к тому промежутку времени, за который это изменение произошло; 2) физическая величина, равная отношению изменения скорости к тому физически малому промежутку времени, за которое это изменение произошло; 3) физическая величина, равная отношению перемещения ко времени.
10. Проекция ускорения на координатную ось может быть:
1) только положительной; 2) только отрицательной; 3) и положительной, и отрицательной, и равной нулю.
11. В каком случае модуль ускорения больше?
1) тело движется с большой постоянной скоростью; 2) тело быстро набирает или теряет скорость; 3) тело медленно набирает или теряет скорость.
12.Два поезда движутся навстречу друг другу по прямолинейному участку пути. Один из них движется ускоренно, второй замедленно. Их ускорения направлены:
1) в одну сторону; 2) в противоположные стороны; 3) однозначно об их направлениях нельзя сказать.
13. Локомотив разгоняется до скорости 20м/с, двигаясь по прямой с ускорением 5м/с2. Начальная скорость его равна нулю. Сколько времени длится разгон?
1) 0,25с; 2) 2с; 3) 100 с; 4) 4с.
14. При подходе к станции поезд уменьшил скорость на 10м/с в течение 20с. С каким ускорением двигался поезд?
1) – 0,5м/с2 ; 2) 2м/с2 ; 3) 0,5 м/с2; 4) – 2м/с2.
15. Автомобиль, трогаясь с места, движется с ускорением 3м/с2. Через 4с скорость автомобиля будет равна:
1)12 м/с; 2) 0,75 м/с; 3) 48 м/с ; 4) 6 м/с.
Кинематика1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
3
1
2
3
2
2
3
2
3
2
1
4
1
1
Тест №2
Тема: Законы Ньютона
16.Какие из величин (скорость, сила, ускорение, перемещение) при механическом движении всегда совпадают по направлению?
1)сила и ускорение; 2) сила и скорость; 3) сила и перемещение; 4) ускорение и перемещение.
17.Какие силы в механике сохраняют свое значение при переходе из одной инерциальной системы в другую?
1) силы тяготения, трения, упругости; 2) только сила тяготения; 3) только сила упругости; 4) только сила трения.
18. Равнодействующая сила – это:
1) сила, действие которой заменяет действие всех сил, действующих на тело; 2) сила, заменяющая действие сил, с которыми взаимодействуют тела.
19. Равнодействующая всех сил, действующих на тело, равна нулю. Какова траектория движения этого тела?
1) парабола; 2) окружность; 3) прямая; 4) эллипс.
20. В инерциальной системе отсчета F сообщает телу массой m ускорение a. Как изменится ускорение тела, если массу тела и действующую на него силу уменьшить в 2 раза?
1) увеличится в 4 раза; 2) уменьшится в 4 раза; 3) уменьшится в 8 раз; 4) не изменится.
21. После открытия парашюта парашютист под действием силы тяжести и силы сопротивления воздуха двигался вниз с ускорением, направленным вверх. Как станет двигаться парашютист, когда при достижении некоторого значения скорости равнодействующая силы тяжести и силы сопротивления воздуха окажется равной нулю?
1) равномерно и прямолинейно вверх; 2) равномерно и прямолинейно вниз; 3) с ускорением свободного падения вниз; 4) будет неподвижным.
22. Закон инерции открыл
1) Демокрит; 2) Аристотель; 3) Галилей; 4) Ньютон.
23. Третий закон Ньютона описывает:
1) действие одного тела на другое; 2) действие одной материальной точки на другую; 3) взаимодействие двух материальных точек.
24. Локомотив сцеплен с вагоном. Сила, с которой локомотив действует на вагон, равна силам, препятствующим движению вагона. Другие силы на движение вагона не влияют. Систему отсчета, связную с Землей, считайте инерциальной. В этом случае:
1) вагон может только покоится; 2) вагон может только двигаться с постоянной скоростью; 3) вагон движется с постоянной скоростью или покоится; 4) вагон движется с ускорением.
25. Яблоко массой 0,3 кг падает с дерева. Выберите верное утверждение
1) яблоко действует на Землю силой 3Н, а Земля не действует на яблоко; 2) Земля действует на яблоко с силой 3Н, а яблоко не действует на Землю; 3) яблоко и Земля не действуют друг на друга; 4) яблоко и Земля действуют друг на друга с силой 3 Н.
26. При действии силы в 8Н тело движется с ускорением 4м/с2. Чему равна его масса?
1) 32 кг; 2) 0,5кг; 3) 2 кг; 4) 20кг.
27.Сила тяги ракетного двигателя первой отечественной экспериментальной ракеты на жидком топливе равнялась 660Н. Стартовая масса ракеты была равна 30кг. Какое ускорение приобретала ракета во время старта?
1) 22м/с2; 2) 45м/с2; 3) 0,1м/с2; 4) 19800 м/с2.
28. Скорость лыжника при равноускоренном спуске с горы за 4с увеличилась на 6м/с. Масса лыжника 60кг. Равнодействующая всех сил, действующих на лыжника, равна
1) 20 Н; 2) 30 Н; 3) 60 Н; 4) 90 Н.
29. Материальная точка массой 1кг движется под действием двух взаимно перпендикулярных сил 8Н и 6Н. Ускорение точки равно
1) 2м/с2; 2) 3,7 м/с2; 3) 10м/с2; 4) 14 м/с2.
30. Какая из физических характеристик не меняется при переходе от одной инерциальной системы отсчета к другой?
1) ускорение; 2) перемещение; 3) траектория; 4) кинетическая энергия.
Законы Ньютона16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1
1
1
3
4
2
3
3
3
4
3
1
4
3
1
Тест №3
Тема. Силы в природе
31.Закон всемирного тяготения позволяет рассчитать силу взаимодействия двух тел, если
1)тела являются телами Солнечной системы; 2) массы тел одинаковы; 3) известны массы тел и расстояние между их центрами; 4) известны массы тел и расстояние между ними, которое много больше размеров тел.
32.Согласно закону Гука сила натяжения пружины при растягивании прямо пропорциональна
1) ее длине в свободном состоянии; 2) ее длине в натянутом состоянии; 3) разнице между длиной в натянутом и свободном состояниях; 4) сумме длин в натянутом и свободном состояниях.
33. Спортсмен совершает прыжок с шестом. Сила тяжести действует на спортсмена
1)только в течение того времени, когда он соприкасается с поверхностью Земли; 2) только в течение того времени, когда он сгибает шест в начале прыжка; 3) только в течение того времени, когда он падает вниз после преодоления планки; 4) во всех этих случаях.
34. Вес тела:
1) свойство тела; 2) физическая величина; 3) физическое явление.
35.Сила тяготения — это сила обусловленная:
1) гравитационным взаимодействием; 2) электромагнитным взаимодействием; 3) и гравитационным, и электромагнитным взаимодействием.
36. Вдоль границ соприкосновения тел направлены силы:
1) вязкого трения; 2) сухого трения; 3) и сухого, и вязкого трения.
37. При сухом трении максимальная сила трения покоя:
1) больше силы трения скольжения; 2) меньше силы трения скольжения; 3) равна силе трения скольжения.
38. Сила упругости направлена:
1) против смещения частиц при деформации; 2) по направлению смещения частиц при деформации; 3) о ее направлении нельзя ничего сказать.
39.Как изменяются масса и вес тела при его перемещении с экватора на полюс Земли?
1) масса и вес тела не изменяются; 2) масса тела не изменяется, вес увеличивается; 3) масса тела не изменяется, вес уменьшается; 4) масса и вес тела уменьшаются.
40. Космический корабль после выключения ракетных двигателей движется вертикально вверх, достигает верхней точки траектории и затем движется вниз. На каком участке траектории в корабле наблюдается состояние невесомости? Сопротивление воздуха пренебрежимо мало.
1) только во время движения вверх; 2) только во время движения вниз; 3) только в момент достижения верхней точки траектории; 4) во время всего полета с неработающими двигателями.
41. Космонавт на Земле притягивается к ней с силой 700Н. С какой приблизительно силой он будет притягиваться к Марсу, находясь на его поверхности, если радиус Марса в 2 раза, а а масса – в 10 раз меньше, чем у Земли?
1) 70Н; 2) 140 Н; 3) 210 Н; 4) 280Н.
42. Под действием силы 3Н пружина удлинилась на 4 см, а под действием силы 6Н удлинилась на 8см. Чему равен модуль силы, под действием которой удлинение пружины составило 6 см?
1) 3,5Н; 2) 4Н; 3) 4,5 Н; 4) 5Н.
43. При скольжении бруска массой 5кг по горизонтальной поверхности сила трения равна 10Н. Чему равен коэффициент трения скольжения для этой пары тел?
1) 0,5; 2) 0,2; 3) 2; 4) 5.
44. Автомобиль массой 1000кг едет по выпуклому мосту с радиусом кривизны 40м. какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали состояние невесомости?
1) 0,05м/с; 2) 20м/с; 3) 25 м/с; 4) 400м/с.
45. Расстояние между центрами двух шаров равно 1м, масса каждого шара 1 кг. Сила всемирного тяготения между ними примерно равна
1) 1Н; 2) 0,001Н; 3) 7·10-5Н; 4) 7·10-11Н.
Силы в природе31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
4
3
4
2
1
3
1
1
2
4
4
3
2
2
4
Тест №4
Тема. Законы сохранения в механике
46.Импульс системы, состоящей из нескольких материальных точек, равен:
сумме модулей импульсов всех ее материальных точек; 2) векторной сумме импульсов всех ее материальных точек; 3) импульсы нельзя складывать.
47.Утверждение о том, что импульсы замкнутой системы тел не изменяются, является:
1) необоснованным; 2) физическим законом; 3) вымыслом; 4) затрудняюсь что-либо сказать по этому поводу.
48. Мальчик массой 50кг, стоя на очень гладком льду, бросает груз массой 8кг под углом 600 к горизонту со скоростью 5м/с. Какую скорость приобретет мальчик?
1)5,8м/с; 2) 1,36 м/с; 3) 0,8м/с; 4) 0,4 м/с.
49. Товарный вагон, движущийся по горизонтальному пути с небольшой скоростью, сталкивается с другим вагоном и останавливается. При этом пружина буфера сжимается. Какое из перечисленных ниже преобразований энергии наряду с другими происходит в этом процессе?
1) кинетическая энергия вагона преобразуется в потенциальную энергию пружины; 2) кинетическая энергия вагона преобразуется в его потенциальную энергию; 3) потенциальная энергия пружины преобразуется в ее кинетическую энергию; 4) внутренняя энергия пружины преобразуется в кинетическую энергию вагона.
50. Кинетическая энергия тела 8 Дж, а величина импульса 4 Н·с, Масса тела равна…
1)0,5кг; 2) 1 кг; 3) 2 кг; 4) 32 кг.
51. Навстречу друг другу летят шарики из пластилина. Модули их импульсов равны соответственно 0,03кгм/с и 0,04 кгм/с. Столкнувшись, шарики слипаются. Импульс слипшихся шариков равен
1).01кг·м/с; 2). 00351кг·м/с; 3).0,05кг·м/с; 4) 0,07кг·м/с;
52. Тело движется по прямой. Под действием постоянной силы величиной 4 Н за 2 с импульс тела увеличился и стал равен 20кг·м/с. Первоначальный импульс тела равен
1) 4кг·м/с; 2) 8кг·м/с; 3) 12кг·м/с; 4) 28кг·м/с;
53. Какую работу надо совершить, чтобы лежащий на земле однородный стержень длиной 2м и массой 100кг поставить вертикально, медленно поднимая один его конец?
1) 100Дж; 2) 200 Дж; 3) 1000 Дж; 4) 2000 Дж.
54. Величина работы может быть отрицательной?
1)может; 2) не может; 3) об этом ничего нельзя сказать.
55. Процесс работы – это:
1) любой процесс превращения энергии; 2) процесс превращения энергии, не связанный с движением тел; 3) процесс превращения энергии при действии сил на движущееся тело.
56.Кинетическая энергия:
1) может быть отрицательной величиной; 2) не может быть отрицательной величиной; 3) может быть и отрицательной, и положительной.
57. Кинетической энергией тело обладает благодаря:
1) взаимодействию с другими телами; 2) благодаря своему движению; 3)благодаря своей деформации.
58. Платформа массой 10т движется со скоростью 2 м/с. Ее нагоняет платформа массой 15т, движущаяся со скоростью 3 м/с. Какой будет скорость этих платформ после автосцепки?
1) 2,6 м/с; 2) 13 м/с; 3) 26м/с; 4) 5м/с.
59. Спортсмен поднял штангу массой 75 кг на высоту 2м. Потенциальная энергия штанги при этом изменилась на
1) 37,5 Дж; 2) 150 Дж; 3) 300 Дж; 4) 1500 Дж.
60. Тело массой 2 кг брошено вертикально вверх с поверхности земли со скоростью 10м/с. На какой высоте потенциальная и кинетическая энергия тела совпадают?
1)1 м; 2) 2 м; 3) 2,5 м; 4) 5 м.
Законы сохранения в механике46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
2
2
4
1
2
1
3
2
1
3
2
2
1
4
3
NCERT Solutions Класс 9 Наука Глава 8 Движение
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРЕНТНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- BNAT 000 Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma класса 8
- Решения RD Sharma класса 9
- Решения RD Sharma класса 10
- Решения RD Sharma класса 11
- Решения RD Sharma класса 12
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0003000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- 000
- 000
- 000
- 000
- 000 BIOG3000
- Математические формулы
- Алгебраные формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 000 PBS4000
- 000
- 000 Физические калькуляторы
- 000
- 000
- 000 PBS4000
- 000
- 000 Калькуляторы для химии Класс 6
- Образцы бумаги CBSE для класса 7
- Образцы бумаги CBSE для класса 8
- Образцы бумаги CBSE для класса 9
- Образцы бумаги CBSE для класса 10
- Образцы бумаги CBSE для класса 11
- Образцы бумаги CBSE чел. для класса 12
- CBSE, вопросник за предыдущий год
- CBSE, вопросник за предыдущий год, класс 10
- CBSE, вопросник за предыдущий год, класс 12
- HC Verma Solutions
- HC Verma Solutions, класс 11, физика
- Решения HC Verma, класс 12, физика
- Решения Лахмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции CBSE
- Примечания к редакции
- CBSE Class
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE Дополнительные вопросы по математике для класса 10
- Дополнительные вопросы по науке, класс 10 по CBSE
- CBSE, класс
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Учебные решения
- CBSE Class
- Решения NCERT
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions Class 11 Business Studies
- NCERT Solutions Class 11 Economics
- NCERT Solutions Class 11 Statistics
- NCERT Solutions Class 11 Commerce
- NCERT Solutions For Class 12
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Бухгалтерский учет 12 класса
- Решения NCERT Класс 12 Бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- NCERT Solutions For Класс 4
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для класса 5
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6
- Решения NCERT для математики 6 класса
- Решения NCERT для науки 6 класса
- Решения NCERT для 6 класса социальных наук
- Решения NCERT для 6 класса Английский
- Решения NCERT для класса 7
- Решения NCERT для класса 7 Математика
- Решения NCERT для класса 7 Наука
- Решения NCERT для класса 7 по социальным наукам
- Решения NCERT для класса 7 Английский
- Решения NCERT для класса 8
- Решения NCERT для класса 8 Математика
- Решения NCERT для класса 8 Наука
- Решения NCERT для социальных наук 8 класса
- Решение NCERT ns для класса 8 Английский
- Решения NCERT для класса 9
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для Математика класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4
- Решения NCERT для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для Математика класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8
- Решения NCERT для математики класса 9 Глава 9 Решения NCERT
- для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для Математика класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13 Решения
- NCERT для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для класса 9 Наука, глава 3
- Решения NCERT для класса 9, наука, глава 4
- Решения NCERT для науки класса 9, глава 5
- Решения NCERT для класса 9, глава 6
- Решения NCERT для науки класса 9, глава 7
- Решения NCERT для класса 9 Наука Глава 8
- Решения NCERT для Науки Класса 9 Глава 9
- Решения NCERT для Науки Класса 9 Глава 10
- Решения NCERT для Науки Класса 9 Глава 12
- Решения NCERT для Науки Класса 9 Глава 11
- Решения NCERT для Класса 9 Наука Глава 13
- Решения NCERT для класса 9 Наука Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- Решения NCERT для математики класса 10 Глава 3
- Решения NCERT для математики класса 10 Глава 4
- Решения NCERT для математики класса 10 Глава 5
- Решения NCERT для математики класса 10 Глава 6
- Решения NCERT для математики класса 10 Глава 7
- Решения NCERT для математики класса 10 Глава 8
- Решения NCERT для математики класса 10 Глава 9
- Решения NCERT для математики класса 10 Глава 10
- Решения NCERT для математики класса 10 Глава 11
- Решения NCERT по математике класса 10 Глава 12
- Решения NCERT по математике класса 10 Глава 13
- NCERT Sol
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса
- Решения NCERT для науки 10 класса Глава 1
- Решения NCERT для науки 10 класса Глава 2
- Решения NCERT для науки класса 10, глава 3
- Решения NCERT для науки класса 10, глава 4
- Решения NCERT для науки класса 10, глава 5
- Решения NCERT для науки класса 10, глава 6
- Решения NCERT для науки класса 10, глава 7
- Решения NCERT для науки класса 10, глава 8
- Решения NCERT для науки класса 10, глава 9
- Решения NCERT для науки класса 10, глава 10
- Решения NCERT для науки класса 10, глава 11
- Решения NCERT для науки класса 10, глава 12
- Решения NCERT для науки 10 класса Глава 13
- Решения NCERT для науки 10 класса Глава 14
- Решения NCERT для науки 10 класса Глава 15 Решения
- NCERT для науки 10 класса Глава 16
- Программа NCERT
- NCERT
- Решения NCERT для класса 11
- Примечания к редакции
- Примечания CBSE класса 7
- FORMULAS
Диалоги о двух новых науках
Авторское право, 1914 г.
КОМПАНИИ MACMILLAN
Настроен и электротипирован. Опубликовано в мае 1914 года.
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
«La Dynamique est la science des force accélératrices или retardatrices, et des mouvemens varés qu’elles doivent produire. Cette science est due entièrement aux modernes, et Galilée est celui qui en a jeté les premiers fondemens ».
Lagrange Mec. Анальный. I. 221.
В течение более чем столетия англоговорящие студенты были помещены в аномальное положение, когда они слышали, как Галилея постоянно называют основателем современной физической науки, не имея возможности прочитать на их родном языке то, что говорит сам Галилей.Архимед был предоставлен Хитом; Свет Гюйгенса был преобразован Томпсоном на английский язык, а Мотт вернул «Начала Ньютона» на язык, на котором он был задуман. Сделать «Физику Галилея» доступной для английских и американских студентов — цель следующего перевода.
Последний из великих творцов Возрождения не был безчестным пророком в свое время; ибо только одна группа его соотечественников не оценила его.Еще при жизни его «Механика» была переведена на французский язык одним из ведущих физиков мира Мерсенном.
В течение двадцати пяти лет после смерти Галилея его «Диалоги по астрономии» и «Диалоги о двух новых науках» были переведены на английский язык Томасом Салусбери и достойно напечатаны в двух красивых четвертных томах. Книга «Две новые науки», содержащая практически все, что Галилей говорит о физике, вышла в английской прессе в 1665 году.Издание: текущее; Страница: [vi] Предполагается, что большая часть копий была уничтожена во время большого лондонского пожара, произошедшего в следующем году. Нам не известно ни одной копии в Америке: даже та, что принадлежит Британскому музею, несовершенна.
Опять же, в 1730 году Томас Вестон перевел на английский язык «Две новые науки»; но эта книга, которой уже почти два столетия, является дефицитной и дорогой. Более того, буквальность, с которой был сделан этот перевод, делает многие отрывки двусмысленными или непонятными для современного читателя.Кроме этих двух, английской версии не было.
Совсем недавно выдающийся итальянский ученый, потратив тридцать из лучших лет своей жизни на эту тему, завершил великое национальное издание сочинений Галилея. Мы ссылаемся на двадцать превосходных томов, в которых профессор Антонио Фаваро из Падуи дал исчерпывающее представление о трудах человека, создавшего современную физическую науку.
Следующая интерпретация не включает в себя ни Le Mechaniche Галилея, ни его статью De Motu Accelerato, поскольку первая из них содержит немного, кроме Статики, которая была актуальна до времен Галилея, а последняя по существу включена в Диалог третьего дня.Динамика была тем предметом, которому в различных формах, таких как баллистика, акустика, астрономия, он последовательно и настойчиво посвятил всю свою жизнь. В один переведенный здесь том он, кажется, собрал за последние годы практически все, что представляет ценность для инженера или физика. Историк, философ и астроном найдут другие тома, наполненные интересным материалом.
Вряд ли есть необходимость добавлять, что мы строго следовали тексту Национального издания — по сути, издания Эльзевира 1638 года.Все комментарии и аннотации опущены, за исключением некоторых сносок, предназначенных для экономии времени читателя. К каждой из этих сносок была приложена подпись [Пер.], Чтобы сохранить оригинал как можно более неповрежденным.
Большая часть ценности любого исторического документа заключается в используемом языке, и это вдвойне верно, когда кто-то пытается Издание: текущее; Страница: [vii] проследить рост и развитие любого набора концепций, например, используемых в современной физике.Поэтому мы сделали этот перевод настолько буквальным, насколько он соответствует ясности и современности. В случаях, когда есть какое-либо существенное отклонение от этого правила, и в случае многих технических терминов, где нет отклонений от него, мы даем исходную итальянскую или латинскую фразу курсивом, заключенную в квадратные скобки. Цель здесь состоит в том, чтобы проиллюстрировать большое разнообразие терминов, используемых ранними физиками для описания одной определенной идеи, и, наоборот, чтобы проиллюстрировать многочисленные значения, в которых тогда, как и сейчас, используется одно слово.За несколько пояснительных английских слов, заключенных в квадратные скобки без курсива, ответственность несут только переводчики. Пейджинг National Edition указан в квадратных скобках, вставленных вдоль средней линии страницы.
Недостатков на следующих страницах было бы намного больше, если бы не помощь трех наших коллег. Профессор Д. Р. Кертисс был достаточно любезен, чтобы помочь в переводе тех страниц, которые обсуждают природу Бесконечности: профессор О.Х. Баскен оказал ценную помощь в переводе главы о сопротивлении материалов; и профессор О. Ф. Лонг прояснил значение ряда латинских фраз.
Профессору А. Фаваро из Падуанского университета переводчики разделяют с каждым читателем чувство искренней ответственности за его Введение.
H. C.
A. de S.
Эванстон, Иллинойс, 15 февраля 1914 года.
ВВЕДЕНИЕ
НАПИСЫВАЯ своему верному другу Элиа Диодати, Галилей говорит о «Новых науках», которые он имел в виду напечатать, как о «превосходящих все остальное из моих, опубликованных до сих пор»; в другом месте он говорит: «они содержат результаты, которые я считаю наиболее важными из всех моих исследований»; и это мнение, которое он высказал относительно своей работы, было подтверждено потомками: «Новые науки» действительно являются шедевром Галилея, который в то время, когда он делал вышеупомянутые замечания, потратил на них более тридцати лет кропотливого труда.
Тот, кто желает проследить историю этого замечательного труда, обнаружит, что великий философ заложил его основы в течение восемнадцати лучших лет своей жизни — тех, которые он провел в Падуе. Как мы узнаем от его последнего ученого, Винченцио Вивиани, многочисленные результаты, к которым пришел Галилей, находясь в этом городе, вызвали сильное восхищение у друзей, которые были свидетелями различных экспериментов, с помощью которых он привык исследовать интересные вопросы физики. Фра Паоло Сарпи воскликнул: Чтобы дать нам Науку Движения, Бог и Природа объединились и создали интеллект Галилея.А когда из прессы вышли «Новые науки», один из его лучших учеников, Паоло Апроино, написал, что в книге содержится многое из того, что он «уже слышал из своих собственных уст» в студенческие годы в Падуе.
Ограничиваясь только наиболее важными документами, которые могут быть процитированы в поддержку нашего заявления, достаточно упомянуть письмо, написанное Гвидобальдо дель Монте 29 ноября 1602 года, относительно падения тяжелых тел. Издание: текущее; Страница: [x] по дугам окружностей и образуемым ими хордам; письмо Сарпи от 16 октября 1604 года о свободном падении тяжелых тел; письмо Антонио Медичи от 11 февраля 1609 г., в котором он заявляет, что «выполнил все теоремы и доказательства, касающиеся сил и сопротивлений балок различной длины, толщины и формы, доказав, что они слабее середина, чем около концов, что они могут нести большую нагрузку, когда эта нагрузка распределена по всей длине балки, чем когда она сосредоточена в одной точке, демонстрируя также, какую форму следует придать балке, чтобы она могла иметь такую же сгибание силы в каждой точке », и что теперь он был занят« некоторыми вопросами, касающимися движения снарядов »; и, наконец, в письме к Белисарио Винте от 7 мая 1610 г., касающемуся его возвращения из Падуи во Флоренцию, он перечисляет различные работы, которые еще не были завершены, и прямо упоминает три книги по совершенно новой науке, посвященной теории. движения.Хотя в разное время после возвращения в родное состояние он уделял много внимания работе, которую даже в то время имел в виду, как показывают некоторые фрагменты, которые явно принадлежат к разным периодам его жизни и которые имеют для впервые опубликовано в National Edition; и хотя эти исследования всегда занимали главное место в его мыслях, не похоже, что он серьезно относился к ним до публикации Диалога и завершения этого судебного процесса, который справедливо был назван позором века.Фактически, уже в октябре 1630 года он почти не упоминает Аггиунти о своих открытиях в теории движения, и только два года спустя, в письме к Марсили относительно движения снарядов, он намекает на почти готовую к публикации книгу, в которой он также рассмотрит эту тему; и всего через год после этого он пишет Арригетти, что у него в руках трактат о сопротивлении твердых тел.
Но определенную форму этой работе придал Галилей во время его вынужденного пребывания в Сиене: за эти пять месяцев, проведенных в спокойной обстановке с архиепископом, он сам пишет, что завершил «трактат по новому разделу механики, полный интересных и полезных идей»; так что через несколько месяцев он смог отправить Издание: текущее; Страница: [xi] слово Миканцио, что «работа была готова»; как только его друзья узнали об этом, они потребовали его публикации.Однако было нелегко напечатать произведение человека, уже осужденного Святой Канцелярией: и, поскольку Галилей не мог надеяться напечатать его ни во Флоренции, ни в Риме, он обратился к верному Миканцио с просьбой выяснить, действительно ли это будет возможно в Венеции, откуда он получил предложение напечатать «Диалог об основных системах», как только там дошли новости о том, что он столкнулся с трудностями. Сначала все шло гладко; так что Галилей начал посылать Миканцио некоторые из рукописей, которые тот принял с энтузиазмом, в котором он не имел себе равных среди самых горячих поклонников великого философа.Но когда Миканцио посоветовался с Инквизитором, он получил ответ, что существует прямой приказ, запрещающий печатать или перепечатывать любые работы Галилея в Венеции или в любом другом месте, nullo excepto.
Как только Галилей получил это обескураживающее известие, он стал более благосклонно относиться к предложениям, поступившим к нему из Германии, где его друг, а также, возможно, его ученый Джованни Баттиста Пьерони, служил у императора в качестве военного инженера. ; следовательно, Галилей дал принцу Маттиа де Медичи, который только что уезжал в Германию, первые два диалога —
.
- BNAT 000 Книги
- BNAT 000 NC
- Классы

Leave A Comment