Онлайн калькулятор системы неравенств с решением онлайн: Калькулятор онлайн - Решение систем неравенств (линейных, квадратных и дробных) (с подробным решением)

Неравенства онлайн

Неравенства онлайн для решения математики. Быстро найти решение неравенства в режиме онлайн. Сайт www.matcabi.net позволяет найти решение почти любого заданного неравенства онлайн. Математические неравенства онлайн для решения математики. Быстро найти решение неравенства в режиме онлайн. Сайт www.matcabi.net позволяет найти решение почти любого заданного алгебраического, тригонометрического или трансцендентного неравенства онлайн. При изучении практически любого раздела математики на разных этапах приходится решать неравенства онлайн. Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.matcabi.net решение неравенства онлайн займет несколько минут. Основное преимущество www.matcabi.net при решении математических неравенства онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические неравенства онлайн, тригонометрические неравенства онлайн, трансцендентные неравенства онлайн, а также неравенства с неизвестными параметрами в режиме онлайн. Неравенства служат мощным математическим аппаратом решения практических задач. C помощью математических неравенств можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины неравенств можно найти, сформулировав задачу на математическом языке в виде неравенств и решить полученную задачу в режиме онлайн на сайте www.matcabi.net. Любое алгебраическое неравенство, тригонометрическое неравенство или неравенства содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения неравенств. При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн. Поэтому для решения математических неравенств онлайн мы рекомендуем сайт www.matcabi.net, который станет вашим незаменимым калькулятором для решения алгебраических неравенств онлайн, тригонометрических неравенств онлайн, а также трансцендентных неравенств онлайн или неравенств с неизвестными параметрами. Для практических задач по нахождению инетравол решений различных математических неравенств ресурса www.matcabi.net вполне достаточно. Решая неравенства онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение неравенств на сайте www.matcabi.net. Необходимо правильно записать неравенство и моментально получите онлайн решение, после чего останется только сравнить ответ с Вашим решением неравенства. Проверка ответа займет не более минуты, достаточно решить неравенство онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении неравенств онлайн будь то алгебраическое, тригонометрическое, трансцендентное или неравенство с неизвестными параметрами.

Как решить неравенство онлайн с подробным решением

Как решать неравенства

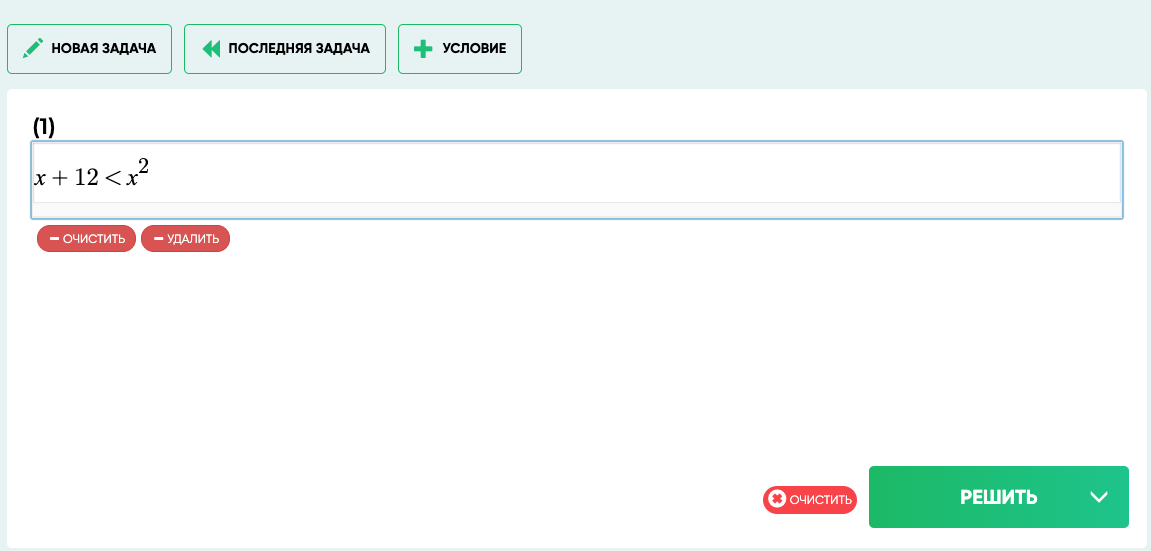
Любое неравенство или система неравенств может быть решена на нашем сайте используя Калькулятор за пару секунд. Решить неравенство с помощью калькулятора просто. Чтобы ввести неравенство, нажмите «+условие»

Например:

x+5

Нажав кнопку Решить вы получите подробное решение неравенств.

Неравенством в математике именуют все уравнения, где знак «=» заменяется на любой из этих значков: \[ > \] \[ \geq \] \[

* линейным;

* квадратным;

* дробным;

* показательным;

* тригонометрическим;

* логарифмическим.

В зависимости от этого и неравенства называются линейными, дробными и т.д.

Об этих знаках нужно знать следующее:

* неравенства со значком больше (>), или меньше (

* неравенства со значками больше или равно \[ \geq \], меньше или равно \[\leq \] называются нестрогими;

* значок не равно \[ \ne \] стоит особняком, но решать примеры с таким значком тоже приходится постоянно.

Неравенства также можно разделить на верные неравенства и неверные неравенства. Например на уроке в школе вы можете часто услышать «запишите верное неравенство»

Как решить неравенство?

Решаются данного рода неравенства при помощи тождественных преобразований.

Допустим, дано неравенство такого вида:

\[x+3 > 5x-5\]

Оно решается точно так же, как и линейное уравнение, но необходимо внимательно следить за знаком неравенства. Изначально выполним перенос членов с неизвестной в левую сторону, с известной в правую, меняя знаки на противоположные:

\[x-5x > -5-3\]

\[-4x > -8\]

Далее выполним деление обеих частей на -4 и меняем знак неравенства на противоположный:

\[x

Это и будет неравенства решение.

Где можно решить неравенства онлайн калькулятор?

Решить неравенства

вы можете на нашем сайте. Бесплатный онлайн решатель позволит решить неравенства x онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как вводить задачи на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Так же читайте нашу статью «Решить целое уравнение онлайн решателем»

Решение показательных неравенств онлайн · Как пользоваться Контрольная Работа РУ

Решим показательное неравенство 5^x + (1/5)^x > 5 с помощью онлайн сервиса, который находится по ссылке

>>решение неравенств онлайн <<

Введём указанное неравенство в данный калькулятор:

Вы получите следующее подробное решение для неравенства:

Дано неравенство: $$5^{x} + \left(\frac{1}{5}\right)^{x} > 5$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$5^{x} + \left(\frac{1}{5}\right)^{x} = 5$$ Решаем:
Дано уравнение: $$5^{x} + \left(\frac{1}{5}\right)^{x} = 5$$ или $$5^{x} + \left(\frac{1}{5}\right)^{x} — 5 = 0$$ Сделаем замену $$v = \left(\frac{1}{5}\right)^{x}$$ получим $$v — 5 + \frac{1}{v} = 0$$ или $$v — 5 + \frac{1}{v} = 0$$ делаем обратную замену $$\left(\frac{1}{5}\right)^{x} = v$$ или $$x = — \frac{\log{\left (v \right )}}{\log{\left (5 \right )}}$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ Данные корни $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_{0} < x_{2}$$ Возьмём например точку $$x_{0} = x_{2} — 1$$ =

             /      ____\    
-log(2) + log\5 - \/ 21 /    
------------------------- - 1
            1                
         log (5)

= $$-1 + \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ подставляем в выражение $$5^{x} + \left(\frac{1}{5}\right)^{x} > 5$$

              /      ____\                       /      ____\        
 -log(2) + log\5 - \/ 21 /          -log(2) + log\5 - \/ 21 /        
 ------------------------- - 1    - ------------------------- + 1    
             1                                  1                    
          log (5)                            log (5)                 
5                              + 5                                > 5


                   /      ____\                     /      ____\    
      -log(2) + log\5 - \/ 21 /        -log(2) + log\5 - \/ 21 /    
 -1 + -------------------------    1 - ------------------------- > 5
                log(5)                           log(5)             
5                               + 5

значит одно из решений нашего неравенства будет при:
$$x < \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$

 _____           _____          
      \         /
-------ο-------ο-------
       x2      x1

Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ: $$x < \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ $$x > \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$

Также вы будете иметь графическое решение показательного неравенства:

Калькулятор онлайн — Решение тригонометрических неравенств

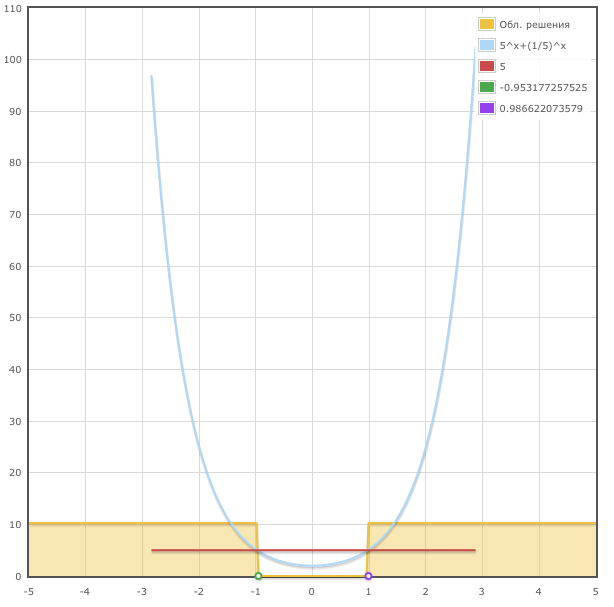
Этот математический калькулятор онлайн поможет вам решить тригонометрическое неравенство. Программа для решения тригонометрического неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Вы можете посмотреть теорию решения тригонометрических неравенств и некоторые методы решения тригонометрических неравенств.

Примеры подробного решения >>

Введите тригонометрическое неравенство

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Сообщение отправлено. Спасибо.

Тригонометрические неравенства

Неравенства вида $ \sin x > a $ и \( \sin x

Пусть дано простейшее неравенство $ \sin x > a $.
1) При $-1
Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (\arcsin a + 2\pi k; \;\; \pi — \arcsin a + 2\pi k), k \in \mathbb{Z} $$
2) При \(а \geq 1 $ неравенство не имеет решений: $ x \in \emptyset $
3) При $а 4) При \(а = -1 $ решением неравенства является любое действительное число, отличное от $ -\frac{\pi}{2} + 2\pi k, \; k \in \mathbb{Z} $

Пусть дано простейшее неравенство $ \sin x
1) При \(-1
Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (\pi — \arcsin a + 2\pi k; \;\; 2\pi + \arcsin a + 2\pi k), k \in \mathbb{Z} $$
2) При \(а > 1 $ решением неравенства является любое действительное число: $ x \in \mathbb{R} $
3) При $а = 1 $ решением неравенства является любое действительное число, отличное от $ \frac{\pi}{2} + 2\pi k, \; k \in \mathbb{Z} $
4) При $а \leq -1 $ неравенство не имеет решений.

Неравенства вида $ \cos x > a $ и \( \cos x

Пусть дано простейшее неравенство $ \cos x > a $.
1) При \(-1

Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (-\arccos(a) + 2\pi k; \;\; \arccos a + 2\pi k), \; k \in \mathbb{Z} $$
2) При $ a \geq 1$ неравенство не имеет решений.
3) При $а 4) При \(а = -1$ решением неравенства является любое действительное число, отличное от $ \pi + 2\pi k, \; k \in \mathbb{Z} $

Пусть дано простейшее неравенство \( \cos x
1) При \(-1
Из данного рисунка видно, что в этом случае решение неравенства будет таким:

$$ x \in (\arccos a + 2\pi k; \;\; 2\pi — \arccos a + 2\pi k), \; k \in \mathbb{Z} $$
2) При $a > 1$ решением неравенства является любое действительное число: $ x \in \mathbb{R} $
3) При $a \leq -1$ неравенство не имеет решений.
4) При $a = 1$ решением неравенства является любое действительное число, отличное от $ 2\pi k, \; k \in \mathbb{Z} $
Неравенства вида $ tg \;x > a $ и \( tg \;x

Пусть дано простейшее неравенство $ tg \;x > a $.
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом $a \in \mathbb{R} $ решение неравенства будет таким:

$$ x \in \left(arctg \;a + \pi k; \;\; \frac{\pi}{2} + \pi k \right), \; k \in \mathbb{Z} $$

Пусть дано простейшее неравенство $ tg \;x
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb{R} $ решение неравенства будет таким:
$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; arctg \;a + \pi k\right), \; k \in \mathbb{Z} $$

Неравенства вида $ ctg \;x > a $ и \( ctg \;x

Пусть дано простейшее неравенство $ ctg \;x > a $.
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом $a \in \mathbb{R} $ решение неравенства будет таким:
$$ x \in ( \pi k; \;\; arcctg \;a + \pi k ), \; k \in \mathbb{Z} $$

Пусть дано простейшее неравенство \( ctg \;x
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом $a \in \mathbb{R} $ решение неравенства будет таким:
$$ x \in ( arcctg \; a + \pi k; \;\; \pi + \pi k ), \; k \in \mathbb{Z} $$

Решение тригонометрических неравенств

ПРИМЕР 1. Решим неравенство $ \sin x > \frac{1}{2} $.
Так как $ -1 $$ x \in \left( \arcsin \frac{1}{2} + 2\pi k; \;\; \pi — \arcsin \frac{1}{2} + 2\pi k \right), \; k \in \mathbb{Z} $$
Так как \( \arcsin \frac{1}{2} = \frac{\pi}{6} $, то решение можно переписать в виде
$$ x \in \left(\frac{\pi}{6} + 2\pi k; \;\; \frac{5\pi}{6} + 2\pi k \right), \; k \in \mathbb{Z} $$

ПРИМЕР 2. Решим неравенство $ \sin \;x Так как \( -1 $$ x \in \left(\pi — \arcsin \left( -\frac{2}{3} \right) + 2\pi k; \;\; 2\pi + \arcsin \left( -\frac{2}{3} \right) + 2\pi k \right), \; k \in \mathbb{Z} $$
Воспользовавшись равенством \( \arcsin(-a) = -\arcsin a $, перепишем решение в виде
$$ x \in \left(\pi + \arcsin \frac{2}{3} + 2\pi k; \;\; 2\pi — \arcsin \frac{2}{3} + 2\pi k \right), \; k \in \mathbb{Z} $$

ПРИМЕР 3. Решим неравенство $ \cos x > \frac{1}{2} $.
Так как \( -1 $$ x \in \left(-\frac{\pi}{3} + 2\pi k; \;\; \frac{\pi}{3} + 2\pi k \right), \; k \in \mathbb{Z} $$

ПРИМЕР 4. Решим неравенство \( \cos x Так как \( -1 $$ x \in (\arccos(-0{,}3) + 2\pi k; \;\; 2\pi — \arccos(-0{,}3) + 2\pi k), k \in \mathbb{Z} $$

Воспользовавшись равенством $ \arccos(-a) = \pi — \arccos a $, перепишем решение в виде
$$ x \in (\pi-\arccos 0{,}3 + 2\pi k; \;\; \pi + \arccos 0{,}3 + 2\pi k), \; k \in \mathbb{Z} $$

ПРИМЕР 5. Решим неравенство $ tg \;x > 1 $.
Очевидно, что решение неравенства будет таким:
$$ x \in \left(\frac{\pi}{4} + \pi k; \;\; \frac{\pi}{2} + \pi k\right), \; k \in \mathbb{Z} $$

ПРИМЕР 6. Решим неравенство \( tg \;x Очевидно, что решение неравенства будет таким:
$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; arctg \left( -\frac{1}{2} \right) + \pi k\right), \; k \in \mathbb{Z} $$

Воспользовавшись равенством $ arctg(-a) = -arctg \; a $, перепишем решение в виде
$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; -arctg \frac{1}{2} + \pi k\right), \; k \in \mathbb{Z} $$

ПРИМЕР 7. Решим неравенство $ ctg \;x > \frac{\sqrt{3}}{3} $.
Очевидно, что решение неравенства будет таким:
$$ x \in \left( \pi k; \;\; \frac{\pi}{3} + \pi k \right), \; k \in \mathbb{Z} $$

ПРИМЕР 8. Решим неравенство \( ctg \;x Очевидно, что решение неравенства будет таким:
$$ x \in \left( arcctg \left( -\frac{5}{4} \right) + \pi k; \;\; \pi + \pi k \right), \; k \in \mathbb{Z} $$

Воспользовавшись равенством $ arcctg(-a) = \pi — arcctg \;a $, перепишем решение в виде
$$ x \in \left( \pi — arcctg \frac{5}{4} + \pi k; \;\; \pi + \pi k \right), \; k \in \mathbb{Z} $$
или в виде
$$ x \in \left( — arcctg \frac{5}{4} + \pi n; \;\; \pi n \right), \; n \in \mathbb{Z} $$

доказать неравенство онлайн с подробным решением

Вы искали доказать неравенство онлайн с подробным решением? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и иррациональные неравенства калькулятор онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «доказать неравенство онлайн с подробным решением».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как доказать неравенство онлайн с подробным решением,иррациональные неравенства калькулятор онлайн,иррациональные неравенства онлайн калькулятор,иррациональные неравенства онлайн решение,иррациональные неравенства решение онлайн,калькулятор иррациональных неравенств,калькулятор неравенств онлайн с модулем,калькулятор неравенств с модулем онлайн,калькулятор онлайн иррациональные неравенства,калькулятор онлайн решение неравенств с модулем,калькулятор онлайн решение систем неравенств,калькулятор онлайн система неравенств,калькулятор онлайн системы неравенств,калькулятор показательных неравенств,калькулятор решение систем неравенств,калькулятор решения систем неравенств,калькулятор решите систему неравенств,калькулятор систем неравенств,калькулятор систем неравенств онлайн,калькулятор систем неравенств онлайн с решением,калькулятор систем неравенств с решением,калькулятор систем неравенств с решением онлайн,калькулятор система неравенств,калькулятор системы неравенств,калькулятор системы неравенств с решением онлайн,калькулятор тригонометрических неравенств,калькулятор тригонометрических неравенств онлайн,логарифмические неравенства онлайн калькулятор,матрицы решить неравенство,неравенства с модулем онлайн калькулятор,неравенство с модулем онлайн калькулятор с решением,онлайн калькулятор неравенств с модулем,онлайн калькулятор решение неравенств с модулем,онлайн калькулятор решение систем неравенств,онлайн калькулятор систем неравенств,онлайн калькулятор систем неравенств с решением,онлайн калькулятор системы неравенств,онлайн калькулятор системы неравенств с решением,онлайн решение иррациональных неравенств,онлайн решение иррациональных неравенств с подробным решением,онлайн решение логарифмических неравенств онлайн с подробным решением,онлайн решение модульных неравенств,онлайн решение неравенств с корнем,онлайн решение неравенств с корнями,онлайн решение неравенств с модулем онлайн,онлайн решение неравенств с модулем онлайн с подробным решением,онлайн решение неравенств система,онлайн решение систем линейных неравенств,онлайн решение систем неравенств,онлайн решение системы неравенств,онлайн решение тригонометрических неравенств с подробным решением,показательные неравенства онлайн калькулятор,построение неравенств онлайн,решатель неравенств онлайн с решением,решение двойных неравенств онлайн,решение двойных неравенств онлайн с подробным решением,решение иррациональные неравенства онлайн,решение иррациональных неравенств онлайн,решение иррациональных неравенств онлайн с подробным решением,решение линейных систем неравенств онлайн,решение логарифмических неравенств онлайн с подробным решением,решение модульных неравенств онлайн,решение неравенств графическим способом онлайн,решение неравенств онлайн с корнем,решение неравенств онлайн с корнями,решение неравенств онлайн с модулем онлайн,решение неравенств онлайн с подробным решением с корнями,решение неравенств с корнем онлайн,решение неравенств с корнями онлайн,решение неравенств с корнями онлайн с подробным решением,решение неравенств с модулем онлайн калькулятор,решение неравенств с параметром онлайн,решение неравенств с параметром онлайн с подробным решением,решение онлайн неравенств с параметром,решение онлайн неравенство с модулем,решение онлайн систем линейных неравенств,решение показательных неравенств онлайн,решение систем линейных неравенств онлайн,решение систем неравенств калькулятор,решение систем неравенств калькулятор онлайн,решение систем неравенств онлайн,решение систем неравенств онлайн калькулятор,решение систем неравенств онлайн с подробным решением,решение системы неравенств калькулятор онлайн,решение системы неравенств онлайн,решение системы неравенств онлайн калькулятор,решение системы неравенств онлайн с подробным решением,решение совокупности неравенств онлайн,решение тригонометрических неравенств онлайн,решение тригонометрических неравенств онлайн с подробным решением,решите двойное неравенство онлайн калькулятор,решите систему неравенств онлайн,решите систему неравенств онлайн с решением,решить двойное неравенство онлайн,решить иррациональное неравенство онлайн с подробным решением,решить логарифмическое неравенство онлайн с подробным решением,решить неравенство матрицы,решить неравенство онлайн с корнем,решить неравенство онлайн с параметром,решить неравенство с корнем онлайн,решить неравенство с модулем онлайн,решить онлайн показательное неравенство,решить онлайн тригонометрическое неравенство,решить показательное неравенство онлайн,решить систему неравенств калькулятор онлайн,решить систему неравенств онлайн,решить систему неравенств онлайн калькулятор,решить систему неравенств онлайн калькулятор с решением,решить систему неравенств онлайн с подробным решением,решить тригонометрическое неравенство онлайн,розв язати нерівність,система неравенств калькулятор,система неравенств калькулятор онлайн,система неравенств онлайн,система неравенств онлайн калькулятор,система решение неравенств онлайн,системы неравенств калькулятор,системы неравенств онлайн,системы неравенств онлайн калькулятор,совокупности неравенств решение онлайн,тригонометрические неравенства онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и доказать неравенство онлайн с подробным решением. Просто введите задачу в окошко и нажмите «решить» здесь (например, иррациональные неравенства онлайн калькулятор).

Где можно решить любую задачу по математике, а так же доказать неравенство онлайн с подробным решением Онлайн?

Решить задачу доказать неравенство онлайн с подробным решением вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Решение линейных неравенств: онлайн калькулятор

Неравенство – это числовое соотношение, иллюстрирующее величину чисел относительно друг друга. Неравенства широко используются при поиске величин в прикладных науках. Наш калькулятор поможет вам разобраться с такой непростой темой, как решение линейных неравенств.

Что такое неравенство

Неравные соотношения в реальной жизни соотносятся с постоянным сравнением различных объектов: выше или ниже, дальше или ближе, тяжелее или легче. Интуитивно или зрительно мы можем понять, что один объект больше, выше или тяжелее другого, однако фактически речь всегда идет о сравнении чисел, которые характеризуют соответствующие величины. Сравнивать объекты можно по любому признаку и в любом случае мы можем составить числовое неравенство.

Если неизвестные величины при конкретных условиях равны, то для их численного определения мы составляем уравнение. Если же нет, то вместо знака «равно» мы можем указать любое другое соотношение между этими величинами. Два числа или математических объекта могут быть больше «>», меньше «<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.

Знаки неравенств в их современном виде придумал британский математик Томас Гарриот, который в 1631 году выпустил книгу о неравных соотношениях. Знаки больше «>» и меньше «<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.

Решение неравенств

Неравенства, как и уравнения, бывают разных типов. Линейные, квадратные, логарифмические или показательные неравные соотношения развязываются различными методами. Однако вне зависимости от метода, любое неравенство вначале требуется привести к стандартному виду. Для этого используются тождественные преобразования, идентичные видоизменениям равенств.

Тождественные преобразования неравенств

Такие трансформации выражений очень похожи на привидение уравнений, однако они имеют нюансы, которые важно учитывать при развязывании неравенств.

Первое тождественное преобразование идентично аналогичной операции с равенствами. К обеим сторонам неравного соотношения можно прибавить или отнять одно и то же число или выражение с неизвестным иксом, при этом знак неравенства останется прежним. Чаще всего этот метод применяется в упрощенной форме как перенос членов выражения через знак неравенства со сменой знака числа на противоположный. Имеется в виду смена знака самого члена, то есть +R при переносе через любой знак неравенства изменится на – R и наоборот.

Второе преобразование имеет два пункта:

Обе стороны неравного соотношения разрешается умножить или разделить на одно и то же положительное число. Знак самого неравенства при этом не изменится.
Обе стороны неравенства разрешается разделить или умножить на одно и то же отрицательное число. Знак самого неравенства изменится на противоположный.

Второе тождественное преобразование неравенств имеет серьезные различия с видоизменением уравнений. Во-первых, при умножении/делении на отрицательное число знак неравного выражения всегда изменяется на обратный. Во-вторых, разделить или умножить части отношения разрешается только на число, а не на любое выражение, содержащее неизвестное. Дело в том, что мы не можем точно знать, число больше или меньше нуля скрывается за неизвестным, поэтому второе тождественное преобразование применяется к неравенствам исключительно с числами. Рассмотрим эти правила на примерах.

Примеры развязывания неравенств

В заданиях по алгебре встречаются самые разные задания на тему неравенств. Пусть нам дано выражение:

6x − 3(4x + 1) > 6.

Для начала раскроем скобки и перенесем все неизвестные влево, а все числа – вправо.

6x − 12x > 6 + 3

−6x > 9

Нам требуется поделить обе части выражения на −6, поэтому при нахождении неизвестного икса знак неравенства изменится на противоположный.

x < −9/6

x < −1,5

При решении этого неравенства мы использовали оба тождественных преобразования: перенесли все числа справа от знака и разделили обе стороны соотношения на отрицательное число.

Наша программа представляет собой калькулятор решения числовых неравенств, которые не содержат неизвестных. В программу заложены следующие теоремы для соотношений трех чисел:

если A < B то A–C< B–C;
если A > B, то A–C > B–C.

Вместо вычитания членов A–C вы можете указать любое арифметическое действие: сложение, умножение или деление. Таким образом, калькулятор автоматически представит неравенства сумм, разностей, произведений или дробей.

Заключение

В реальной жизни неравенства встречаются также часто, как и уравнения. Естественно, что в быту знания о разрешении неравенств могут и не понадобиться. Однако в прикладных науках неравенства и их системы находят широкое применение. К примеру, различные исследования проблем глобальной экономики сводятся к составлению и развязыванию систем линейных или квадратных неравенств, а некоторые неравные отношения служат однозначным способом доказательства существования определенных объектов. Пользуйтесь нашими программами для решения линейных неравенств или проверки собственных выкладок.

Калькулятор неравенства — шаг за шагом

Резюме:

Решатель неравенства, который решает неравенство с деталями расчета: линейное неравенство, квадратное неравенство.

Неравенство_сольвер онлайн

Описание:

Калькулятор неравенств позволяет решать неравенства : он может быть использован как для решения линейного неравенства с одним неизвестным, чтобы решить квадратное неравенство.Во всех случаях этапы расчетов детализированы и дан точный результат.

Расчетных возможностей, предлагаемых калькулятором неравенства , много, поэтому, например, возможно решают неравенство, дробят , — неравенство, которое содержит буквы (символьный расчет).

операторы для решения неравенства

Операторы сравнения для решения неравенства :

> Улучшенный
> = выше или равно

Решение линейного неравенства онлайн

Решение линейного неравенства с одним неизвестным вида `a * x> b` выполняется очень быстро, когда переменная не является неоднозначной, просто введите неравенство , решая и нажмите inequality_solver, точный результат возвращается.

Также даны шагов вычислений , необходимых для решения неравенства .

Калькулятор является мощным инструментом компьютерной алгебры, он способен манипулировать и получить разрешение линейное неравенство , включающее числа, но также буквы, и в этом случае оно должно явно указывать переменная. к решить линейное неравенство, следуя 3x + 5> 0 , просто введите выражение 3 * x + 5> 0 в области исчисления, затем нажмите кнопку вычисления или кнопку Кнопка inequality_solver, точный результат возвращается `[x> -5/3]`.2 + b * x + c> 0` делается очень быстро, когда переменная не является неоднозначной, просто введите неравенство от до решить и нажмите inequality_solver, точный результат затем возвращается.

Также даны шагов вычислений , необходимых для решения неравенства .

Калькулятор является мощным инструментом компьютерной алгебры, он способен манипулировать и получить разрешение квадратное неравенство , включающее числа, но также буквы, и в этом случае оно должно явно указывать переменная.2-5> 0 в области исчисления, затем нажмите на кнопку расчета или кнопку inequality_solver, результат затем возвращается в область, где расчеты детализированы.

Принцип решения неравенства.

Для решения неравенства калькулятор использует следующие принципы:

Он может прибавлять или вычитать одно и то же число к обеим сторонам неравенства.
Он может умножить или разделить каждого члена неравенства на одно и то же число.

Когда это число отрицательное, обратное направление неравенства
Когда это число положительно, оно сохраняет чувство неравенства

Калькулятор неравенства детализирует метод, используемый для решения неравенства.
Решатель неравенства, который решает неравенство с деталями вычисления: линейное неравенство, квадратное неравенство.

Синтаксис:

inequality_solver (уравнение; переменная), параметр переменной является необязательным, если нет неопределенности.

Примеры:

В этом примере показано, как использовать решатель неравенств

Решение неравенств 1-й степени

Рассчитать онлайн с помощью неравенства_сольвер (калькулятор неравенства) ,

Калькулятор неравенства — бесплатный онлайн калькулятор

- Классы
  Класс 1 — 3
  Класс 4 — 5
  Класс 6 — 10
  Класс 11 — 12
- КОНКУРСЫ
  BBS
  000000000000 Книги
  NCERT Книги для 5 класса
  NCERT Книги Класс 6
  NCERT Книги для 7 класса
  NCERT Книги для 8 класса
  NCERT Книги для 9 класса 9
  NCERT Книги для 10 класса
  NCERT Книги для 11 класса
  NCERT Книги для 12-го класса
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT Exemplar Class 12
  9000al Aggar Agard Agard Agard Agard Agulis Class 12
  RS Решения Aggarwal класса 10
  RS Решения Aggarwal класса 11
  RS Решения Aggarwal класса 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  Решения класса RD Sharma
  Решения класса 9 Шарма 7 Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  ФИЗИКА
  Механика
  000000 Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  МАТС
  Теорема Пифагора
  Отношения и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Делительные дроби
  000 ФОРМУЛЫ
  Математические формулы
  Алгебровые формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  S000
  S0003
  Pегипс Класс 6
  Образцы документов CBSE для класса 7
  Образцы документов CBSE для класса 8
  Образцы документов CBSE для класса 9
  Образцы документов CBSE для класса 10
  Образцы документов CBSE для класса 11
  Образец образца CBSE pers for Class 12
  CBSE Предыдущий год Вопросник
  CBSE Предыдущий год Вопросники Класс 10
  CBSE Предыдущий год Вопросник класс 12
  HC Verma Solutions
  HC Verma Solutions Класс 11 Физика
  Решения HC Verma Class 12 Physics
  Решения Lakhmir Singh
  Решения Lakhmir Singh Class 9
  Решения Lakhmir Singh Class 10
  Решения Lakhmir Singh Class 8
  Примечания
  CBSE
  Notes
  CBSE Класс 7 Примечания CBSE
  Класс 8 Примечания CBSE
  Класс 9 Примечания CBSE
  Класс 10 Примечания CBSE
  Класс 11 Примечания CBSE
  Класс 12 Примечания CBSE
  Примечания пересмотра
  CBSE Редакция
  CBSE
  CBSE Class 10 Примечания к пересмотру
  CBSE Class 11 Примечания к пересмотру 9000 4
  Замечания по пересмотру CBSE класса 12
  Дополнительные вопросы CBSE
  Дополнительные вопросы CBSE 8 класса
  Дополнительные вопросы CBSE 8 по естественным наукам
  CBSE 9 класса Дополнительные вопросы
  CBSE 9 дополнительных вопросов по науке CBSE
  9000 Класс 10 Дополнительные вопросы по математике
  CBSE Класс 10 Дополнительные вопросы по науке
  Класс CBSE
  Класс 3
  Класс 4
  Класс 5
  Класс 6
  Класс 7
  Класс 8
  Класс 9
  Класс 10
  Класс 11
  Класс 12
  Решения для учебников
- Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для физики класса 11
  Решения NCERT для класса 11 Химия
  Решения для класса 11 Биология
  NCERT Решения для класса 11 Математика
  9 0003 NCERT Solutions Class 11 Бухгалтерия
  NCERT Solutions Class 11 Бизнес исследования
  NCERT Solutions Class 11 Экономика
  NCERT Solutions Class 11 Статистика
  NCERT Solutions Class 11 Коммерция
  NCERT Solutions для класса 12
  NCERT Solutions для Класс 12 Физика
  Решения NCERT для 12 класса Химия
  Решения NCERT для 12 класса Биология
  Решения NCERT для 12 класса Математика
  Решения NCERT Класс 12 Бухгалтерский учет
  Решения NCERT Класс 12 Бизнес исследования
  Решения NCERT Класс 12 Экономика
  NCERT Solutions Class 12 Бухгалтерский учет Часть 1
  NCERT Solutions Class 12 Бухгалтерский учет Часть 2
  NCERT Solutions Class 12 Микроэкономика
  NCERT Solutions Class 12 Коммерция
  NCERT Solutions Class 12 Макроэкономика
  NCERT Solutions Для Класс 4
  Решения NCERT для класса 4 Maths
  Решения NCERT для класса 4 EVS
  Решения NCERT для класса 5
  Решения NCERT для класса 5
  Решения NCERT для класса 5 EVS
  Решения NCERT для класса 6
  Решения NCERT для класса 6 Математика
  Решения NCERT для класса 6 Наука
  Решения NCERT для класса 6 Общественные науки
  Решения NCERT для класса 6 Английский
  Решения NCERT для класса 7
  Решения NCERT для класса 7 Математика
  Решения NCERT для 7 класса Science
  Решения NCERT для 7 класса Общественные науки
  Решения NCERT для 7 класса Английский
  Решения NCERT для 8 класса Математические решения
  для 8 класса Математика
  Решения NCERT для класса 8 Science
  Решения NCERT для класса 8 Общественные науки
  NCERT Solutio ns для класса 8 Английский
  Решения NCERT для класса 9
  Решения NCERT для класса 9 Общественные науки
  Решения NCERT для класса 9 Математика
  Решения NCERT для класса 9 Математика Глава 1
  Решения NCERT Для класса 9 Математика 9 класса Глава 2
  Решения NCERT для математики 9 класса Глава 3
  Решения NCERT для математики 9 класса Глава 4
  Решения NCERT для математики 9 класса Глава 5
  Решения NCERT для математики 9 класса Глава 6
  Решения NCERT для Математика 9 класса Глава 7
  Решения NCERT для математики 9 класса Глава 8
  Решения NCERT для математики 9 класса Глава 9
  Решения NCERT для математики 9 класса Глава 10
  Решения NCERT для математики 9 класса Глава 11
  Решения NCERT для Математика 9 класса Глава 12
  Решения NCERT для математики 9 класса Глава 13
  Решения NCERT для математики 9 класса Глава 14
  Решения NCERT для математики класса 9 Глава 15
  Решения NCERT для науки 9 класса
  Решения NCERT для науки 9 класса Глава 1
  Решения NCERT для науки 9 класса Глава 2
  Решения NCERT для класса 9 Наука Глава 3
  Решения NCERT для 9 класса Наука Глава 4
  Решения NCERT для 9 класса Наука Глава 5
  Решения NCERT для 9 класса Наука Глава 6
  Решения NCERT для 9 класса Наука Глава 7
  Решения NCERT для 9 класса Научная глава 8
  Решения NCERT для 9 класса Научная глава
  Научные решения NCERT для 9 класса Научная глава 10
  Научные решения NCERT для 9 класса Научная глава 12
  Научные решения NCERT для 9 класса Научная глава 11
  Решения NCERT для 9 класса Научная глава 13
  Решения NCERT для 9 класса Научная глава 14
  Решения NCERT для класса 9 Science Глава 15
  Решения NCERT для класса 10
  Решения NCERT для класса 10 Общественные науки
  Решения NCERT для математики класса 10
  Решения NCERT для математики класса 10 Глава 1
  Решения NCERT для математики класса 10 Глава 2
  решения NCERT для математики класса 10 глава 3
  решения NCERT для математики класса 10 глава 4
  решения NCERT для математики класса 10 глава 5
  решения NCERT для математики класса 10 глава 6
  решения NCERT для математики класса 10 Глава 7
  решения NCERT для математики класса 10 глава 8
  решения NCERT для математики класса 10 глава 9
  решения NCERT для математики класса 10 глава 10
  решения NCERT для математики класса 10 глава 11
  решения NCERT для математики класса 10, глава 12
  Решения NCERT для математики класса 10, глава 13
  соль NCERT Решения для математики класса 10 Глава 14
  Решения NCERT для математики класса 10 Глава 15
  Решения NCERT для науки 10 класса
  Решения NCERT для науки 10 класса Глава 1
  Решения NCERT для науки 10 класса Глава 2
  Решения NCERT для науки 10 класса, глава 3
  Решения NCERT для науки 10 класса, глава 4
  Решения NCERT для науки 10 класса, глава 5
  Решения NCERT для науки 10 класса, глава 6
  Решения NCERT для науки 10 класса, глава 7
  Решения NCERT для науки 10 класса, глава 8
  Решения NCERT для науки 10 класса, глава 9
  Решения NCERT для науки 10 класса, глава 10
  Решения NCERT для науки 10 класса, глава 11
  Решения NCERT для науки 10 класса, глава 12
  Решения NCERT для 10 класса Science Глава 9
  Решения NCERT для 10 класса Science Глава 14
  Решения NCERT для науки 10 класса Глава 15
  Решения NCERT для науки 10 класса Глава 16
  Программа NCERT
  NCERT
- Коммерция
  Класс 11 Коммерческая программа Syllabus
  Учебный курс по бизнес-классу 11000
  Учебная программа по экономическому классу
- Учебная программа по коммерческому классу
  Учебная программа по 12 классу
  Учебная программа по 12 классам
  Учебная записка по 12-му классу
  000000000000
  Образцы коммерческих документов класса 11
  Образцы коммерческих документов класса 12
  Решения TS Grewal
  Решения TS Grewal Класс 12 Бухгалтерский учет
  Решения TS Grewal Класс 11 Бухгалтерский учет
  Отчет о движении денежных средств
  eurship
  Защита потребителя
  Что такое фиксированный актив
  Что такое баланс
  Формат баланса
  Что такое акции
  Разница между продажей и маркетингом
- P000S Документы ICSE
- ML Решения Aggarwal
  ML Решения Aggarwal Class 10 Maths
  ML Решения Aggarwal Class 9 Математика
  ML Решения Aggarwal Class 8 Maths
  ML Решения Aggarwal Class 7 Математические решения
  ML 60004
  ML 6
- Selina Solutions
  Selina Solution для класса 8
  Selina Solutions для класса 10
  Selina Solution для класса 9
- ICSE класс
  ICSE класс 6
  ICSE класс 7
  ICSE
  ICSE
  ICSE Class 9
  ICSE Class 10
  ISC C lass 11
  ISC Class 12
IAS
IAS экзамен
экзамен по гражданской службе
UPSC Syllabus
бесплатный подготовительный IAS
текущие дела
тест IAS
Статьи IAS
IAS 2019 Mock Test 1
IAS 2019 Mock Test 2
Комиссия по государственной службе
KPSC KAS экзамен
UPPSC PCS экзамен
MPSC экзамен
RPSC
группа 1PPS RASP
группа 1PPS
группа 1SPS
группа 1SPS
группа 1SPS
группа 1PPS
группа группа 1SPS 1
Экзамен BPSC
Экзамен WBPSC
Экзамен MPPSC
Экзамен JPSC
Экзамен GPSC
Документ с вопросами UPSC 2019
Ключ ответа UPSC 2019
0008000 Коучинг IAS Дели
Коучинг IAS Ченнаи
Коучинг IAS Хайдарабад
Коуч IAS ing Mumbai
JEE
JEE Программа
JEE Main
JEE Advanced
JEE Образец бумаги
JEE Вопросник
NEET
Программа NEET Byju
NEET 2020
Критерии соответствия требованиям NEET 2020
Образцы документов NEET
Подготовка NEET
Поддержка NEET Syllabus
Поддержка
Служба поддержки клиентов
поддержки клиентов
9000 требует обязательной поддержки для обращения с
государственных советов
GSEB
GSEB Syllabus
Вопросник GSEB
Образец бумаги GSEB
GSEB Книги
MSBSHSE
SBSS000000 MSBSSE Документы estion
AP Board
APSCERT Books
AP SSC Syllabus
AP 1st Year Syllabus
AP 2-й год Syllabus
MP Board
MP000 Sample
MP000 Sample S Board Учебники MP Board
Assam Board
Assam Board Syllabus
Assam Board Учебники
Assam Board Образцы документов
BSEB
Bihar Board
000 Документы для моделей Bihar
9000 9000-е годы
PSE для PSE
S000 PBSS
PS000
P0003000 Доска Syllabus
9000 3 RBSE Учебники
RBSE Документы с вопросами
HPBOSE
HPBOSE Syllabus
HPBOSE Учебники
HPBOSE Вопросы для бумаг
JOSBOSE
JOSBOSE
JOSE S000S
TN Board
TN Board Syllabus
TN Board Вопросные бумаги
TN Образцы документов
Samacheer Kalvi Books
JAC
JAC Syllabus
JAC
JASK
Japers
учебники JAC Совет Телангана

,
Бесплатный онлайн калькулятор — онлайн программное обеспечение компьютерной алгебры.
Калькулятор — это программное обеспечение для компьютерной алгебры , онлайн , и программное обеспечение для численных расчетов, которое имеет много функции для манипулирования выражениями по математике онлайн .
Calculator — мощный интернет-калькулятор который может с его многочисленными функциями, чтобы освободить онлайн расчет, компьютерная алгебра, алгебраические вычисления, числовое исчисление, расчет производной (дифференциальное исчисление), расчет примитива (интегральное исчисление), расчет фракции, расчет комплексного числа, расчет лимита, матричный расчет, калькулятор также может учитывать, уменьшить, расширяться, упростить многие выражения.
С цифрами или буквами, веб-калькулятор можно сделать в точном виде, расчеты , и как подошел в манере научного калькулятора. Это онлайн программное обеспечение для символьных вычислений может сделать все, что калькулятор можно сделать. Мощный онлайн калькулятор, он включает в себя функции: стандартный калькулятор, калькулятор алгебры, научный калькулятор, формальный калькулятор, символический калькулятор, финансовый калькулятор , калькулятор фракций, матричный калькулятор, Калькулятор комплексного числа.
Позволяет вычислять целых, десятичных, вещественных чисел, уравнения, неравенства, функции , фракции, математических выражений , комплексные числа, последовательности:
С уравнениями , калькулятор может решить уравнение с его решателем уравнений. С неравенства , в состоянии решить неравенство с его решающим неравенством.
С фракциями , калькулятор фракций позволяет рассчитывать фракции всех типов, он способен выполнять все арифметические операции, включая дроби.
С алгебраическими выражениями , калькулятор с его возможностями CAS (рассчитывается онлайн с х и у) может развернуть и свернуть выражение, выражение фактора.
С функциями , производный калькулятор умеет рассчитывать производную (производный расчет), примитивный калькулятор способен найти антипроизводные обычных функций.
С векторами , векторный калькулятор может делать векторный расчет: векторное произведение, скалярное произведение, скалярное тройное произведение, векторная сумма, Разница между векторами.
С матриц , матричный калькулятор может сделать матрица какуляции: вычисление определителя матрицы, вычисление обратной квадратной матрицы, вычисление следа матрицы.
С комплексных чисел , калькулятор комплексных чисел может выполнять все арифметические операции, калькулятор имеет функции для поиска сопряженный, реальная часть, мнимая часть, аргумент.
С математическими выражениями калькулятор может выполнять мощные операции буквальный расчет.
С номеров , калькулятор может использовать большинство функций, он может сделать научный калькулятор, это может сделать перевод единиц измерения, расчет длины, расчеты поверхности, объемные расчеты.
С последовательностями , калькулятор позволяет вычислить члены числовой последовательности , даже можно рассчитать условия последовательность определяется повторением , Калькулятор позволяет рассчитать сумму членов последовательности или произведение условий последовательности , можно даже использовать калькулятор серии определить частичные суммы.
В геометрии калькулятор позволяет использовать теорему Пифагора для проверки того, что треугольник является прямоугольником, или определить длину одной стороны, зная две другие.
это даст вам все шаги расчетов, облегчая понимание. Метод расчета благодаря пошаговому режиму вычислений компьютер также является реальным образовательный инструмент, он даст вам все шаги вычислений, облегчая понимание.Этот шаг расчета режима доступен для рассчитать производную, рассчитать антипроизводные, выражение фактора, решить уравнение, решить неравенство, рассчитать дробь.
Решатель уравнений, решатель неравенств, решатель системных уравнений
Калькулятор предлагает различные онлайн решатели.
Решатель уравнений, который позволяет разрешение уравнения, решатель позволяет среди других первое онлайн решение уравнения степени, решение квадратного уравнения онлайн, решение уравнения абсолютного значения, решение показательного уравнения, решение линии логарифмического уравнения, решение уравнения с использованием свойства нулевого продукта.Решатель позволяет решать многие типы уравнений, в частности это позволяет решить уравнение с дробью. Калькулятор возвращает шаги, чтобы добраться до решения уравнения.
С его решающим неравенством, калькулятор адаптирован к разрешение неравенства первой степени онлайн, решатель может также решить квадратное неравенство, решить неравенство с дробью.Все решения снабжены подробными расчетами.
Наконец, калькулятор обеспечивает решение системы уравнений что позволяет решать системы уравнений онлайн.
Калькулятор фракций
Стоит ли рассчитывать дроби или рассчитать дробь, калькулятор фракций умеет делать расчеты с дробями.Этот калькулятор является мощным инструментом расчета, что позволяет рассчитывать фракции используя все обычные арифметические операторы, это позволяет вычитание или сложение дроби с тем же знаменателем, вычитание или сложение дроби с разными знаменателями, умножение дроби на число, умножение двух дробей, деление дроби на число, деление дроби на дробь.Калькулятор позволяет уменьшить дробь, все фракции можно быстро уменьшить, упростить дробь онлайн никогда не было проще, благодаря мощному упрощенному дробнику.
Фракция калькулятор представляет собой числовой калькулятор, но и буквальный т.е. его можно использовать для расчета доли с x, с помощью этой функции можно выполнять все арифметические операции буквально как сложение фракций, вычитание фракций, произведение фракций, поднять фракцию к власти.Расчет дроби буквами не единственная особенность этого калькулятора, он также может предоставить подробную информацию о расчете фракции. Эта функция особенно подходит для расчета доли обучения, помимо пошаговых расчетов фракций, калькулятор фракций возвращает результаты в виде неприводимая дробь.
В дополнение к калькулятору мощности на сайте подсчет фракций инструментов для манипулирования фракциями, это возможно благодаря одноименным функциям найти числитель и знаменатель дроби.Калькулятор позволяет сравнивать дроби онлайн, снова указав шаги для достижения результата.
С онлайн-калькулятором фракций, можно проводить расчеты по фракциям онлайн так как :
Разверните, сверните, разложите выражение.
Компьютер имеет мощные функции символьных вычислений, которые позволяют ему развернуть алгебраическое выражение онлайн, упростить алгебраическое выражение онлайн, факторизовать алгебраическое выражение онлайн, факторизовать специальные расширения.
С помощью формального калькулятора можно упростить алгебраическое выражение, как символический калькулятор или буквальный калькулятор, он позволяет среди прочего уменьшить алгебраическое выражение, расширить выражение, расширить и свернуть выражение в Интернете, факторизовать выражение. Упрощение выражения относится к обеим числовым формулам как к буквальным формулам.Расширение выражения относится ко всем типы выражения. Факторинг относится ко многим типы математических выражений, или что различные механизмы используются для поиска общих факторов, выражение факторизации со специальными расширениями, факторизация онлайн квадратичных полиномов. Используя эти методы, калькулятор может Факторизация выражения онлайн с подробным описанием различных этапов расчета.Калькулятор сопоставим с программным обеспечением факторизации.
Производный калькулятор, антипроизводный калькулятор.
Калькулятор позволяет символическая дифференциация и символическая антидифференциация. Калькулятор предоставляет функции, которые позволяют дифференцировать онлайн (Дифференциация), расчет производной функции онлайн, расчет антидеривативной функции онлайн (Antidifferentiation), вычисление интеграла функции онлайн.
Калькулятор умеет находить антипроизводные или искать антипроизводные, для этого, имеет интуитивно понятный интерфейс ввода, который позволяет автоматически определять переменные функции когда нет никакой двусмысленности. Таким образом, чтобы определить антидериватив или поиск производной функции выполняется быстро.
Производный калькулятор позволяет расчет производной онлайн.Калькулятор использует обычные функции и производное свойство для расчета производная онлайн. Антидеривативный калькулятор позволяет Рассчитать правило цепочки производных. Калькулятор предоставляет подробную информацию о расчете производной.
Примитивный калькулятор позволяет антидеривативный расчет онлайн.Антидеривативный калькулятор онлайн использует обычные примитивные функции, интеграция по частям и свойства интеграции в рассчитать антипроизводные онлайн. Антидеривативный калькулятор также позволяет рассчитать цепочку правил антидериватива. Калькулятор также предоставляет подробную информацию о расчете антипроизводных
Векторное исчисление
Доступно несколько функций векторного исчисления, которые помогают выполнять различные виды онлайн-вычислений для векторов. онлайн расчеты по векторам.Можно сделать:
Матричный расчет
Доступны несколько функций расчета матриц, эти функции позволяют делать разные типы расчеты онлайн на матрицах. Можно сделать, например: Вот полный список функций матрицы :
Калькулятор комплексных чисел
Символ, используемый для комплекса: и .
Калькулятор комплексного числа позволяет выполнять расчеты с комплексными числами, можно делать арифметические операции:
Калькулятор комплексного числа позволяет:
Калькулятор комплексного числа обеспечивает упрощение комплексного числа, после вычисления комплексное число возвращается в его упрощенной алгебраической форме.
Символьные вычисления
Большинство доступных функций способны выполнять символические вычисления, т.е. расчет с буквами. Эта функция позволяет делать символьные вычисления дроби, упростить символьную дробь калькулятор фракций, расширить алгебраическое выражение с функция расширения, упростить алгебраическое выражение с функцией упростить, разложить алгебраическое выражение на функция факторизации, решить уравнение с решатель уравнений.Эта возможность расчета с линией букв также относится к производный расчет и антидеривативный расчет. Одним из преимуществ использования символьных вычислений является умение делать точные расчеты.
Научный калькулятор
Калькулятор обеспечивает функциональность научного калькулятора онлайн, это включает в себя все стандартные научные функции: абсолютное значение функции (abs), функция arccosine (арккос), функция arcsine (арксин), функция arctangent (арктан), функция гиперболический косинус (ch), функция косинус (cos), функция котангенс (cotan), функция гиперболический котангенс (coth) , корень куба функции (cube_root), экспонента функции (exp), логарифм функции Напиера (ln), логарифм функции (log), гиперболический синус функции (sh), синус функции (sin), корень квадратный функции (sqrt), тангенс функции ( tan), функция гиперболического тангенса (th) и других научные функции онлайн.
Тригонометрические функции доступны для этого калькулятора, Тригонометрический калькулятор завершен завершен, следующие функции могут быть использованы: функция арккосин (arccos), функция арксинус (arcsin), функция арктангенс (арктан), функция косинус (cos), функция котангенс (котан), функция тригонометрического расширения (expand_trigo), функция тригонометрическая линеаризация (linearization_trigo), функция Simplify Calculator (упрощение) , функция синуса (sin), функция тангенса (tan), функция тригонометрического калькулятора (trig_calculator).
Как и гиперболический калькулятор , калькулятор также имеет все гиперболические функции : функция гиперболического косинуса (ch), функция гиперболического котангенса (coth), функция гиперболического синуса (sh), функция гиперболического тангенса (th).
Калькулятор предоставляет доступ ко многим математическим формулам , которые позволяют ему сделать онлайн преобразования единиц, функция преобразования позволяет преобразовывать длину, преобразование поверхности, или преобразование объема.Периметр круга, периметр квадрата, периметр прямоугольника, площадь круга, площадь квадрата, площадь прямоугольника, объем сферы, объем куба или объем прямоугольного параллелепипеда может быть легко вычислено с помощью мощных онлайн-функций расчета , доступных для бесплатно .
Пошаговый расчет
Некоторые функции, предоставляемые калькулятором , могут предоставить подробностей вычислений .Таким образом, различные калькуляторы возвращают этапы и детали вычислений . Производный калькулятор, антидеривативный калькулятор, решатель, калькулятор фракций, Функция факторизации позволяет получить подробных расчетов .
Производный пошаговый расчет
Производный калькулятор позволяет разложить производные вычисления шагов, облегчая понимание расчетов и помогая механизмам обучения, связанным с производные вычисления.
Пошаговое антидеривативное вычисление
Антидеривативный калькулятор позволяет разложить антидеривативные расчеты шагов, облегчая понимание расчетов и помогая механизмам обучения, связанным с производные вычисления.
Уравнение пошаговый расчет
калькулятор уравнений позволяет прервать вычисления, чтобы найти решения уравнения по шагам облегчение понимания расчетов и помощь в изучении механизмов обучения в разрешении уравнения.
Неравенство пошаговый расчет
Калькулятор неравенства позволяет разбить вычисления, чтобы найти решения неравенства в шагах, облегчающих понимание расчетов и помощь механизмов обучения, связанных с разрешение неравенства.
Дробный пошаговый расчет
Калькулятор фракции с помощью пошагового режима вычисления позволяет выполнять сломать расчет фракции: это позволяет разложить дробь сложение, вычитание дроби, умножение дроби, фракции подразделений.Приложения калькулятора фракций многочисленны : его можно использовать среди других решить упражнения по дробям, проверить , результаты расчетов дробей .
Факторизация : пошаговый расчет
«Калькулятор факторизации» с его расчет шаг за шагом режим позволяет разбить расчеты до разложить выражение на поэтапно облегчение понимания расчетов и помощь в изучении механизмов, связанных с факторизация выражения.
Этот шаг вычислений шаг за шагом , предложенный этими калькуляторами, является действительно полезной функцией, позволяющей лучше понять различные конкатенации, которые позволяют достичь заданного результата.
Чтобы использовать программное обеспечение для формального онлайн-расчета, щелкните онлайн-калькулятор, Вы можете получить помощь по использованию программного обеспечения компьютерной алгебры, нажав на Руководство по калькуляторам.
,2 + 1 (пример графика), 4x + 2 = 2 (x + 6) (пример решения)
Алгебра Калькулятор — это калькулятор, который предоставляет пошаговую помощь по задачам алгебры.
Смотрите другие примеры »
Отказ от ответственности: Этот калькулятор не идеален. Пожалуйста, используйте на свой страх и риск, и, пожалуйста, предупредите нас, если что-то не работает. Спасибо.
Как использовать калькулятор
Введите проблему алгебры в текстовое поле.
Например, введите 3x + 2 = 14 в текстовое поле, чтобы получить пошаговое объяснение того, как решить 3x + 2 = 14.
Попробуйте этот пример сейчас! »
Дополнительные примеры
Пробуя примеры на Примеры страница — это самый быстрый способ научиться пользоваться калькулятором. Калькулятор
Примеры »
Математические символы
Если вы хотите создать свои собственные математические выражения, вот некоторые символы, которые калькулятор понимает:
+ (дополнение)
— (вычитание)
* (умножение)
/ (отдел)
^ (Экспонент: «возведен во власть»)
sqrt (квадратный корень) (пример: sqrt (9))
Дополнительные математические символы
Учебное пособие
Прочитайте полное руководство, чтобы узнать, как составить график уравнений и проверить домашнюю работу по алгебре.Учебник по калькулятору
»
Мобильное приложение
Получить мобильное приложение MathPapa! Работает в автономном режиме!
Обратная связь (Для студентов 13+)
Пожалуйста, используйте эту форму обратной связи, чтобы отправить свой отзыв. Спасибо!
Нужно больше практических проблем? Попробуйте MathPapa Математическая практика
Share This Story, Choose Your Platform!
Facebook Twitter LinkedIn Reddit Whatsapp Google+Tumblr Pinterest Vk Email
Related Posts
Насморк при прорезывании зубов у детей: причины, симптомы и лечение
Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша
Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования
Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов
УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров
Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ
Comment

Save my name, email, and website in this browser for the next time I comment.

Неравенства онлайн

Как решать неравенства

Где можно решить неравенства онлайн калькулятор?

Тригонометрические неравенства

Неравенства вида \( \sin x > a \) и \( \sin x

Неравенства вида \( \cos x > a \) и \( \cos x

Неравенства вида \( tg \;x > a \) и \( tg \;x

Неравенства вида \( ctg \;x > a \) и \( ctg \;x

Решение тригонометрических неравенств

доказать неравенство онлайн с подробным решением

Где можно решить любую задачу по математике, а так же доказать неравенство онлайн с подробным решением Онлайн?

Решение линейных неравенств: онлайн калькулятор

Что такое неравенство

Решение неравенств

Тождественные преобразования неравенств

Примеры развязывания неравенств

Заключение

Калькулятор неравенства — шаг за шагом

Резюме:

Описание:

Синтаксис:

Примеры:

Решение неравенств 1-й степени

Решатель уравнений, решатель неравенств, решатель системных уравнений
Калькулятор предлагает различные онлайн решатели.

Как использовать калькулятор

Дополнительные примеры

Математические символы

Учебное пособие

Мобильное приложение

Обратная связь (Для студентов 13+)

Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ

Онлайн калькулятор системы неравенств с решением онлайн: Калькулятор онлайн — Решение систем неравенств (линейных, квадратных и дробных) (с подробным решением)

Неравенства онлайн

Как решать неравенства

Где можно решить неравенства онлайн калькулятор?

Тригонометрические неравенства

Неравенства вида \( \sin x > a \) и \( \sin x

Неравенства вида \( \cos x > a \) и \( \cos x

Неравенства вида \( tg \;x > a \) и \( tg \;x

Неравенства вида \( ctg \;x > a \) и \( ctg \;x

Решение тригонометрических неравенств

доказать неравенство онлайн с подробным решением

Где можно решить любую задачу по математике, а так же доказать неравенство онлайн с подробным решением Онлайн?

Решение линейных неравенств: онлайн калькулятор

Что такое неравенство

Решение неравенств

Тождественные преобразования неравенств

Примеры развязывания неравенств

Заключение

Калькулятор неравенства — шаг за шагом

Резюме:

Описание:

Синтаксис:

Примеры:

Решение неравенств 1-й степени

Решатель уравнений, решатель неравенств, решатель системных уравнений Калькулятор предлагает различные онлайн решатели.

Как использовать калькулятор

Дополнительные примеры

Математические символы

Учебное пособие

Мобильное приложение

Обратная связь (Для студентов 13+)

Share This Story, Choose Your Platform!

Related Posts

Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ

Решатель уравнений, решатель неравенств, решатель системных уравнений
Калькулятор предлагает различные онлайн решатели.