График функции модуль х в квадрате: Построение функций, содержащих модули

Построение функций, содержащих модули

Здравствуйте, уважаемые посетители! В этой статье мы попробуем подробно разобраться, как построить график функции, если эта функция содержит модуль. В статье разобраны различные примеры с пошаговым построением и подробным объяснением, как получен тот или иной график.

1. Начнем с построения графика

В “основе” его лежит график функции

и все мы знаем, как он выглядит:

Теперь построим график

Чтобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:

Теперь необходимо умножить на два все ординаты, чтобы получить график функции

Наконец, сдвигаем график вверх на две единицы:

Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):

2. Теперь построим график функции

Выражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:

При х>2/3 функция запишется так:

То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (правее) мы строим функцию

а в другой (левее) – график функции

Строим:

3. Следующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:

Посмотрим, в каких точках подмодульные выражения меняют знак:

Расставим знаки для подмодульных выражений на координатной прямой:

Раскрываем модули на первом интервале:

На втором интервале:

На третьем интервале:

Таким образом, на интервале (-∞; 1.5] имеем график, записанный первым уравнением, на интервале [1.5; 2] – график, записанный вторым уравнением, и на интервале [2;∞) – график по третьему уравнению:

Строим:

4. Теперь можем построить график, похожий на один из предыдущих, и все же отличающийся:

В основе опять знакомый нам график функции

но, если в знаменателе x стоит под знаком модуля,

то график имеет вид:

Теперь произведем сдвиг на три единицы,

при этом сдвинутся обе части: правая – вправо, левая – влево (своеобразное зеркало : отходишь дальше – видно больше)

График этой функции, умноженной на два,

выглядит так:

Теперь можно поднять график по оси у:

и тогда он будет таким:

Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:

5.Очень интересно выглядит график функции

В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) – второе:

6. Две следующие функции отличаются знаком, и графики их выглядят по-разному:

7. Еще два похожих графика, вид которых меняется в зависимости от х в показателе степени:

Первый:

Второй:

8.Теперь построим график такой функции:

Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:

А на интервале [4; ∞) так:

Точка вершины первой параболы (2;-12), она обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее обращены вверх. В итоге имеем:

9. Построим график функции, которая, на первый взгляд, выглядит устрашающе:

Однако многочлен в числителе раскладывается на множители:

Точки перемен знака подмодульных выражений – 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

Строим:

Внесем небольшие изменения, добавив двойку в знаменатель исходной функции:

Тогда точки перемены знака остаются те же, но функция выглядит иначе на разных интервалах:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

График изменится:

10. Наконец, последний график мы построим для функции

Начнем построение с “базовой” для этого графика функции

она выглядит так:

Далее добавим знак модуля под корень:

Теперь опустим этот график вниз на 4 единицы по оси у:

“Опрокинем” все, что ниже оси х, вверх,

и не забудем поделить все ординаты на 2:

Графики прямой, параболы, гиперболы, с модулем

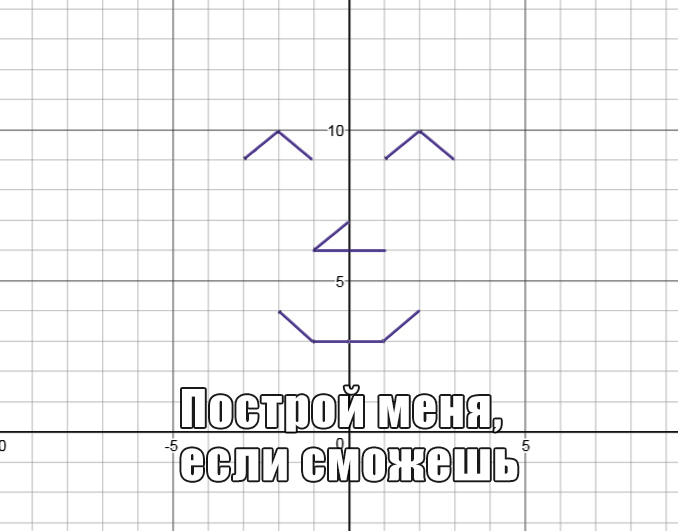
Пошаговое построение графиков.

«Навешивание» модулей на прямые, параболы, гиперболы.

Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.

Для понимания друг друга введу немного «обзываний» системы координат:

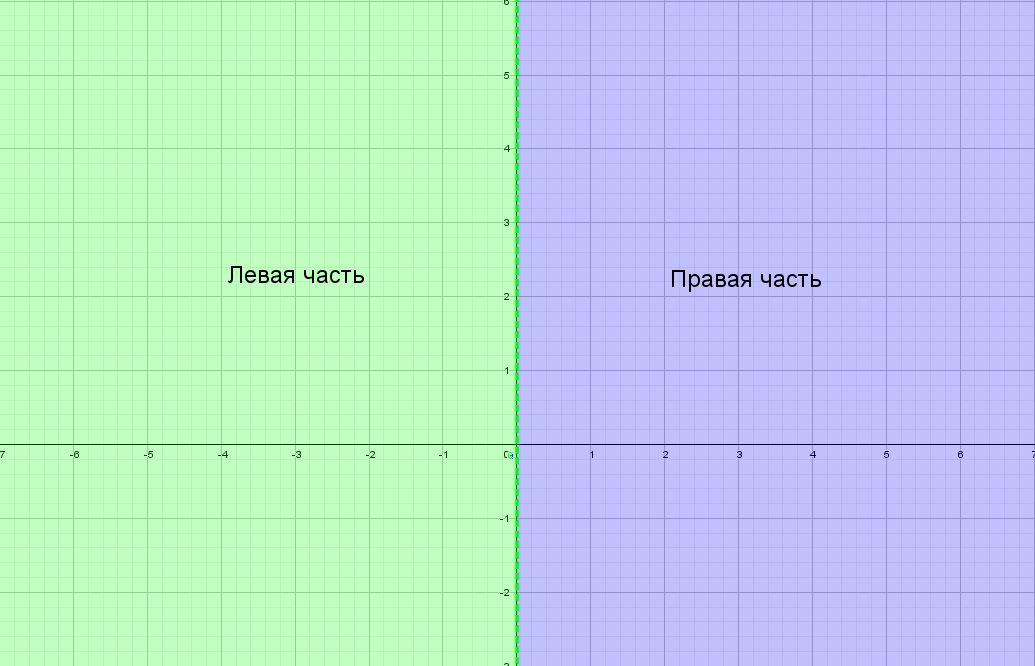
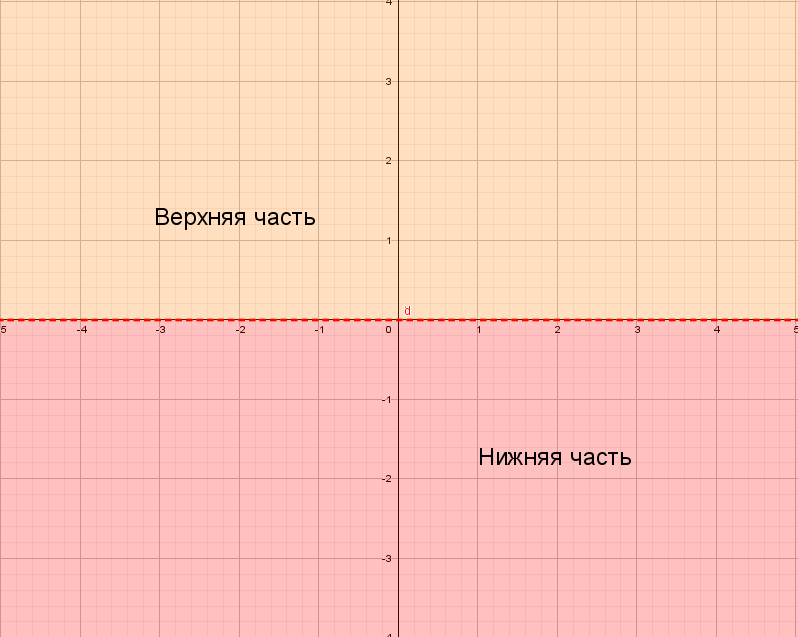
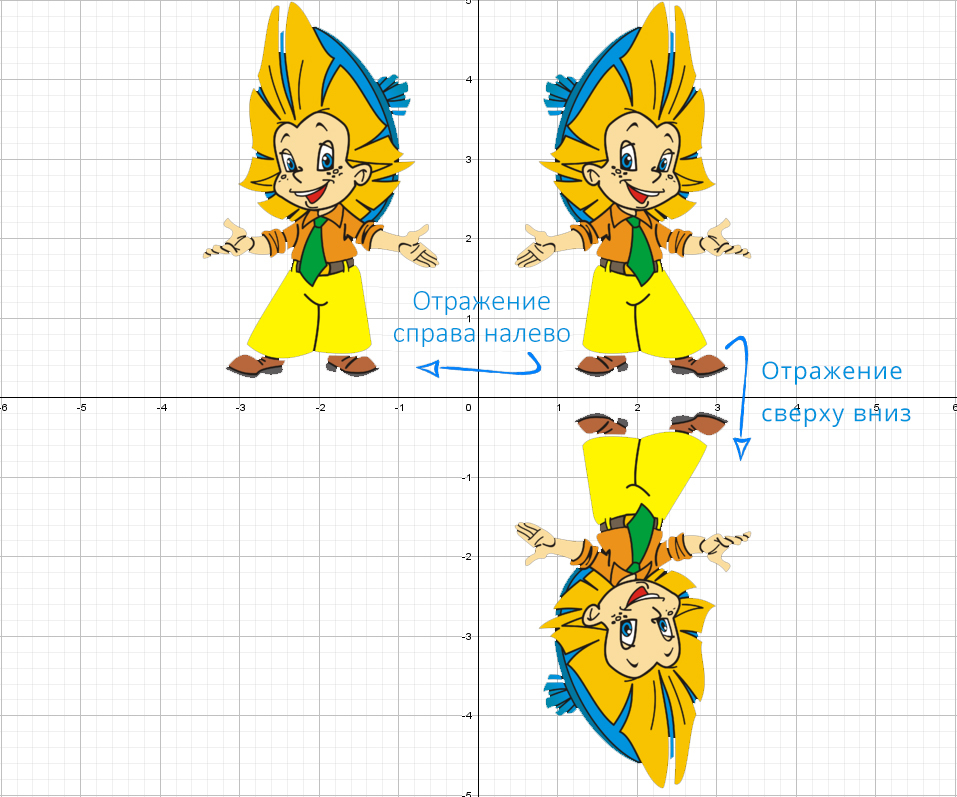
Для начала построим график прямой y = 2x − 1.

Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.

Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1

Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:

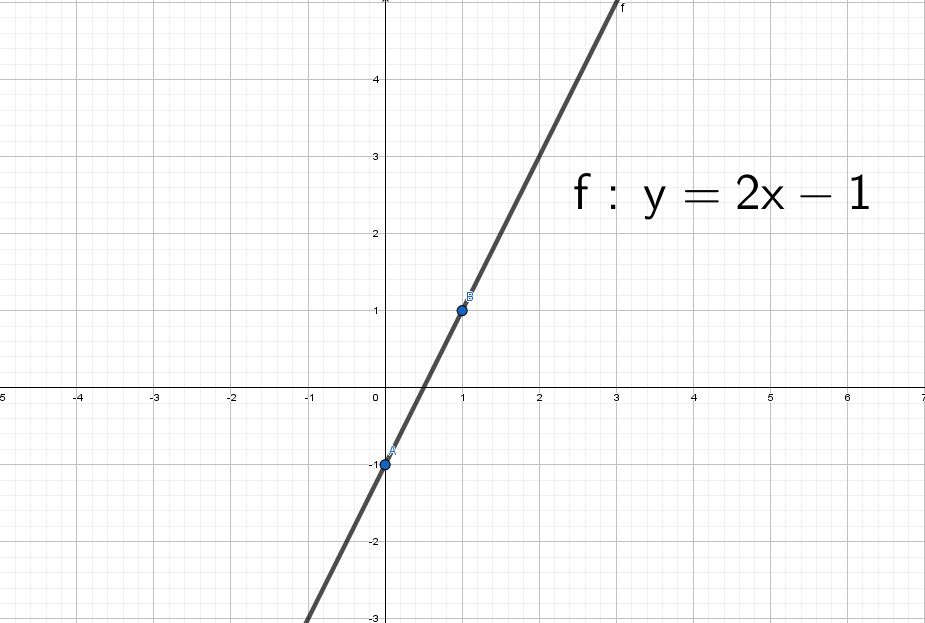
А если теперь добавить модуль y = |2x − 1|.

Модуль — это всегда положительное значение, получается, что «y» должен быть всегда положительным.

Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).

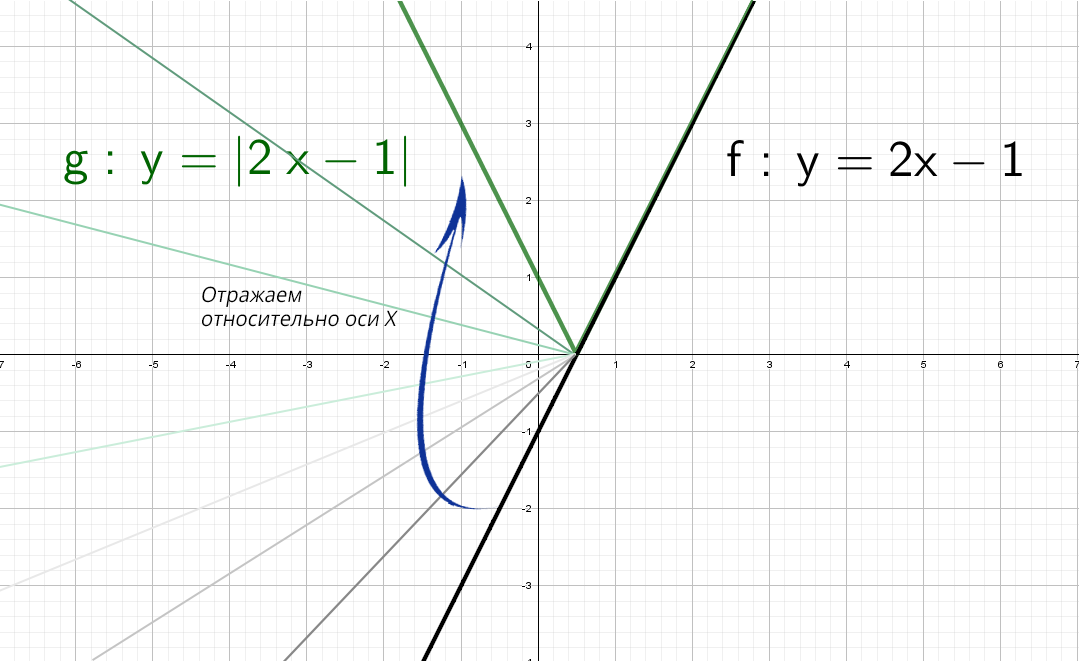Получается такая зеленая «галочка».

Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?

Одна строчка рассуждений и рисуем:

Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.

Здесь отражаем относительно оси «y». Такая же галочка, только теперь через другую ось.

Смертельный номер: y = |2|x| − 1|.

Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.

В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!

А после этого отражаем относительно оси «y» то, что мы получили справа налево:

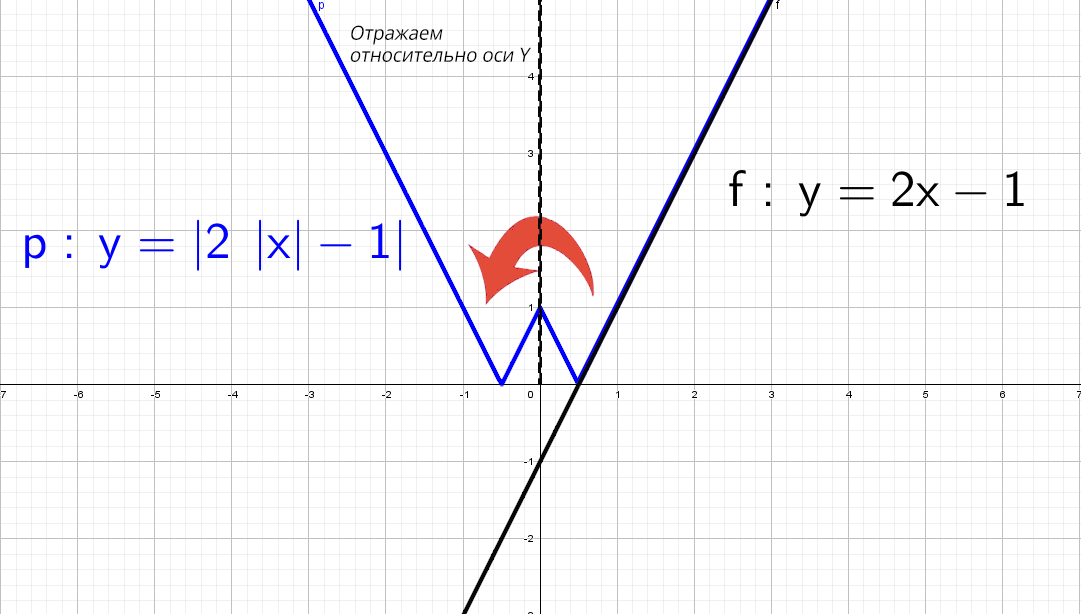
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.

Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x₁ = 1 и x₂ = -2.

Можно найти вершину у параболы и взять пару точек для точного построения.

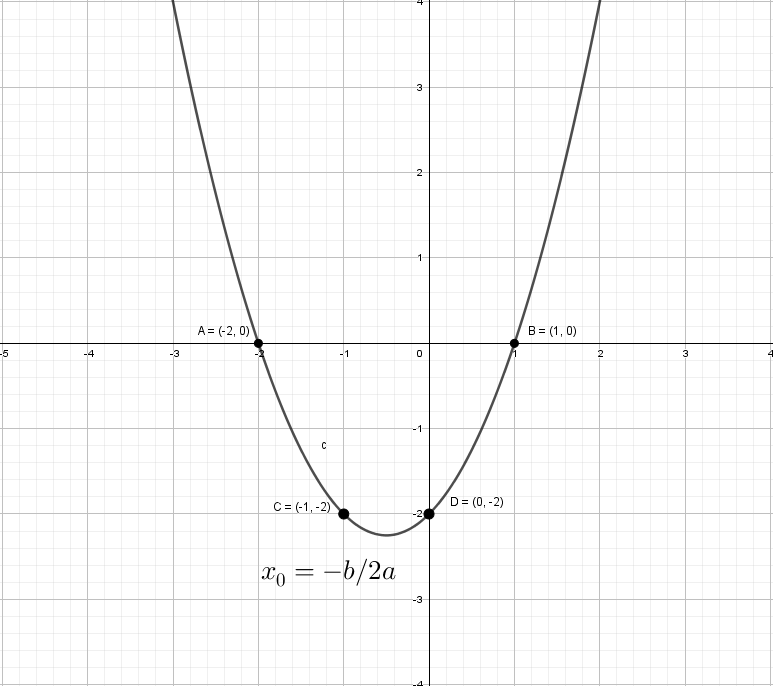
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.

При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:

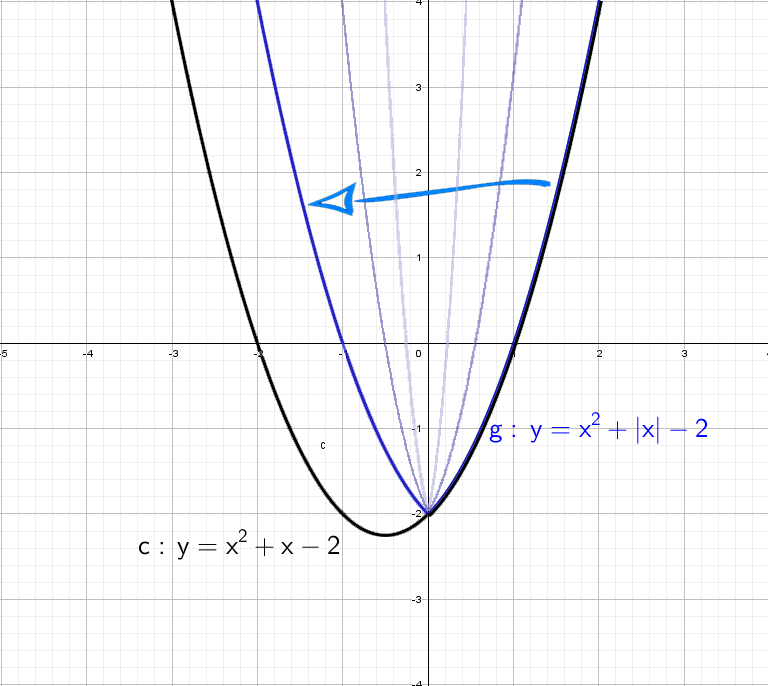
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!

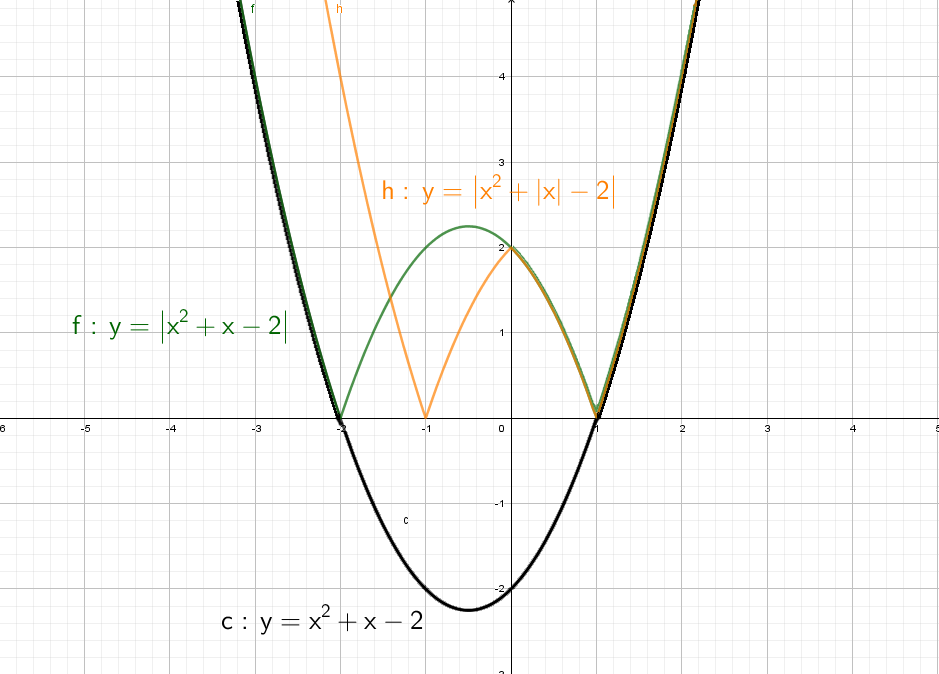
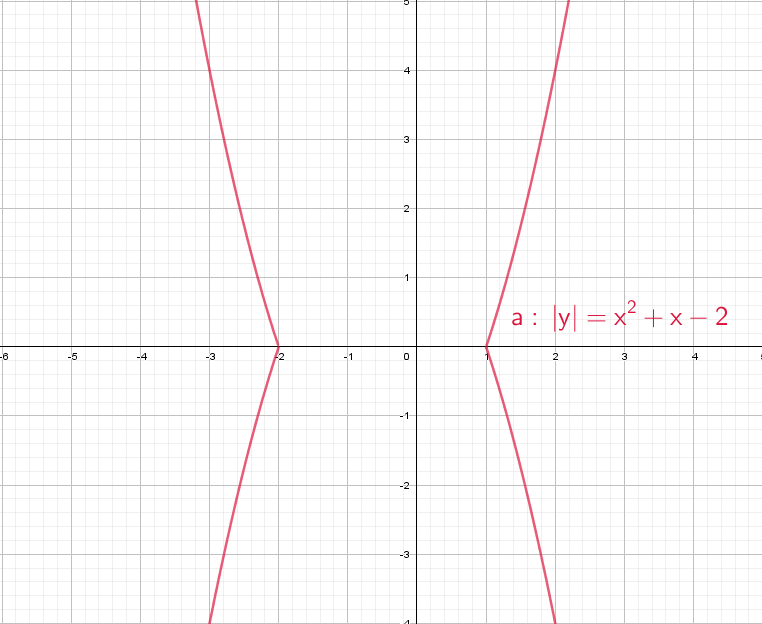
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.

При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!

Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.

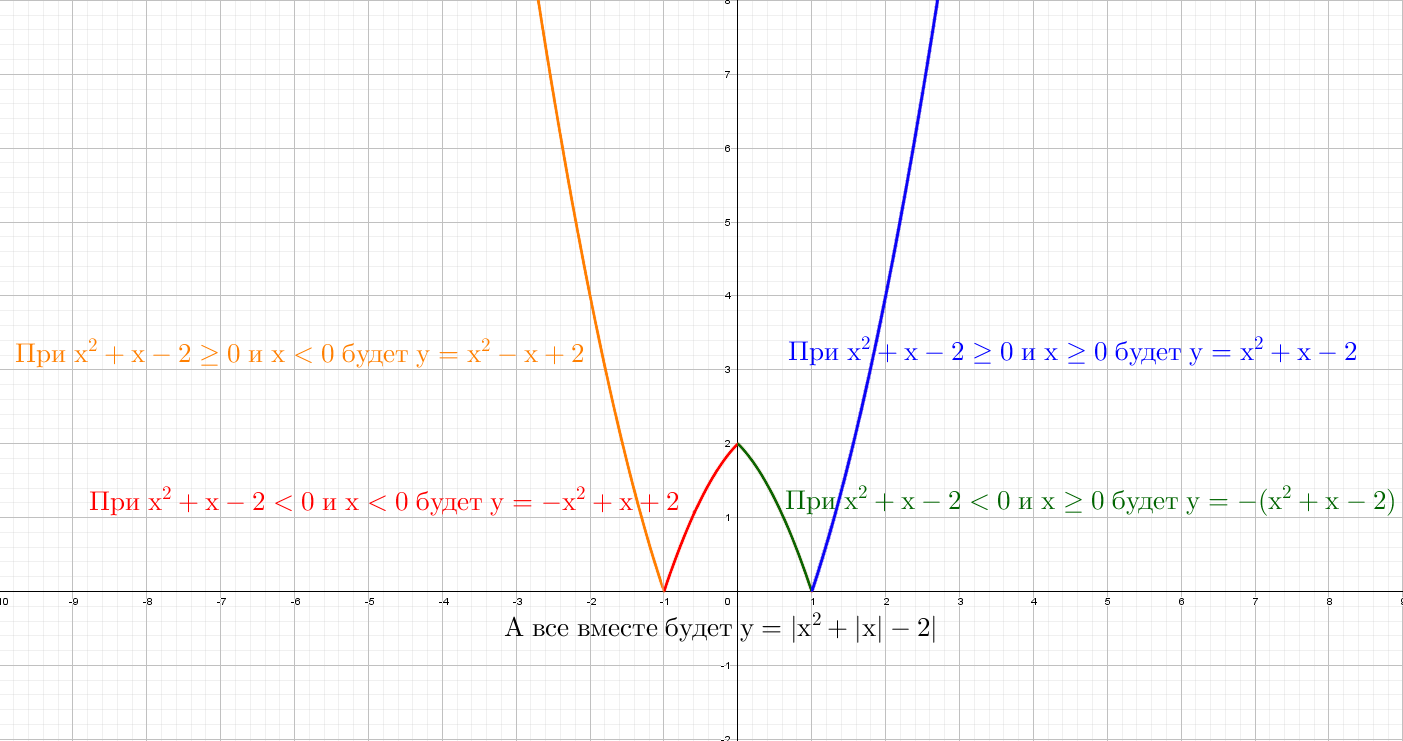
А теперь сразу комбо:

Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.

Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.

Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.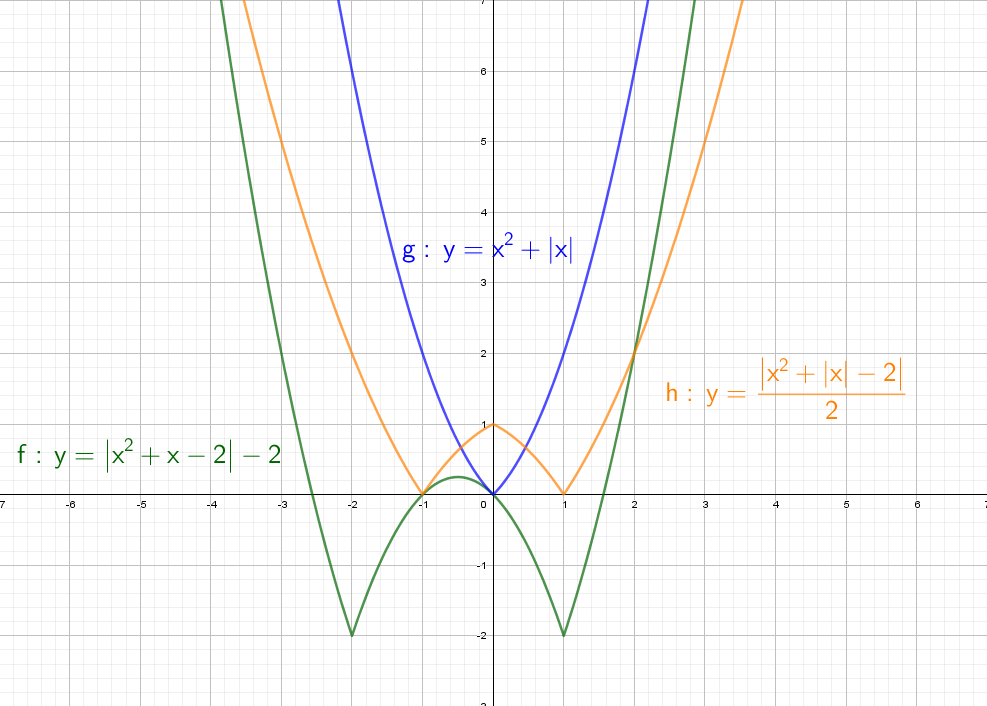

Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.

y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:

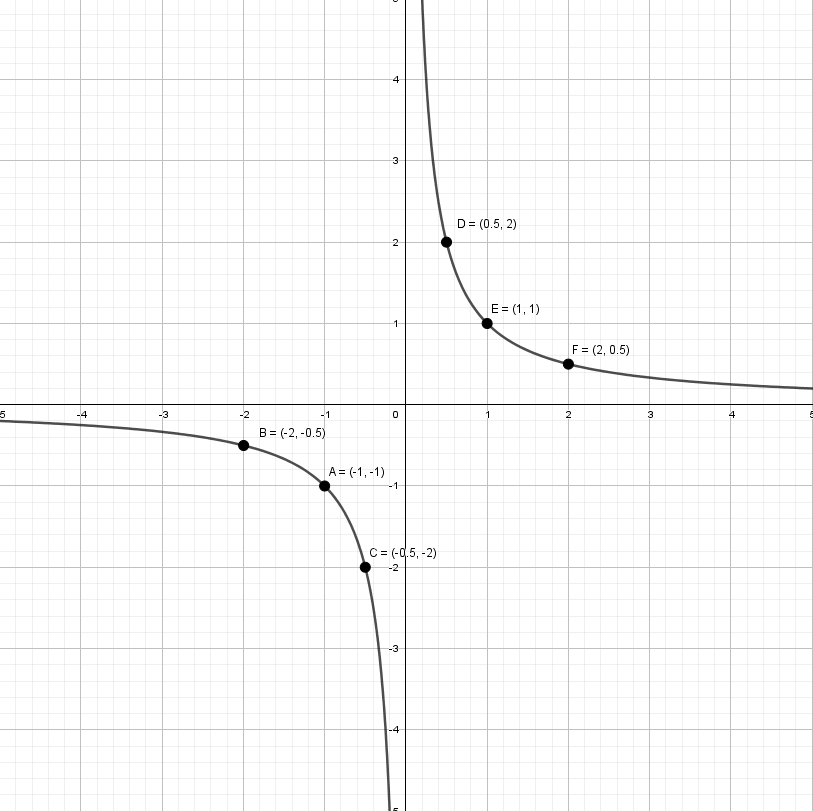
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:

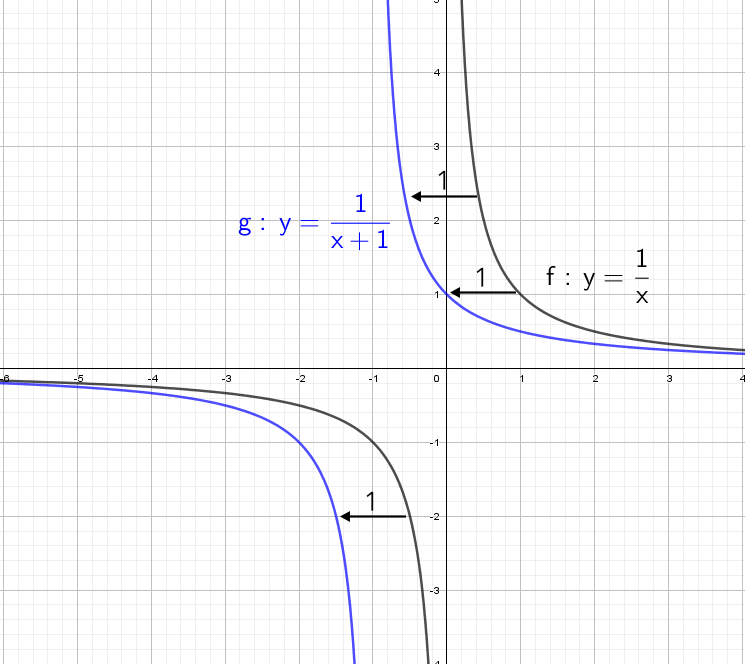
А что будет, если мы добавим в знаменателе «−1»? График сдвинется вправо на единицу.

А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!

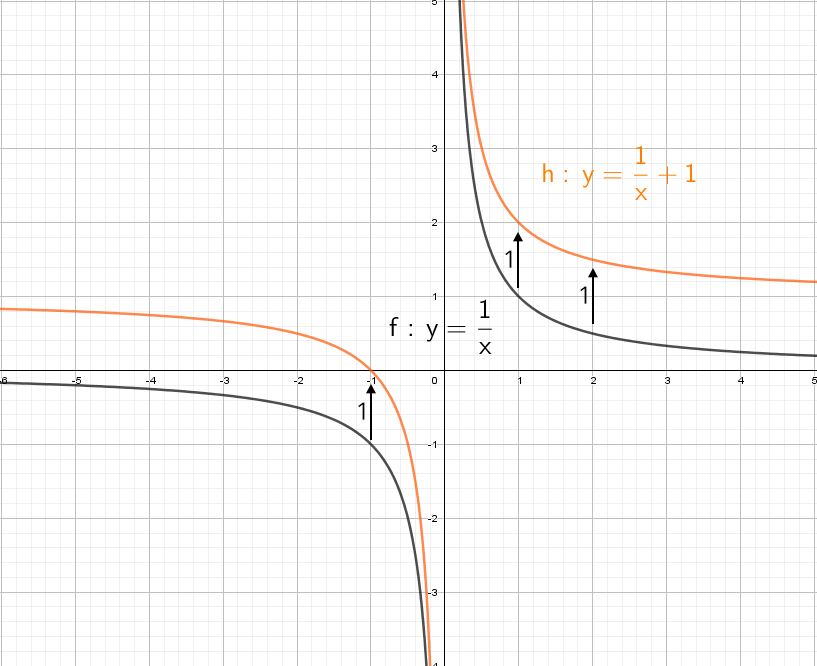Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!

Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.

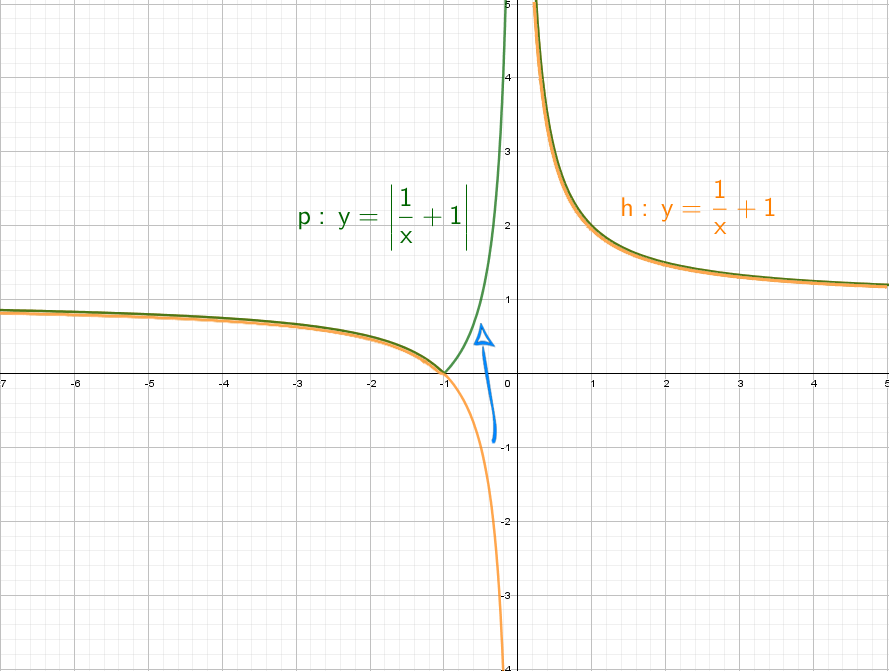
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.

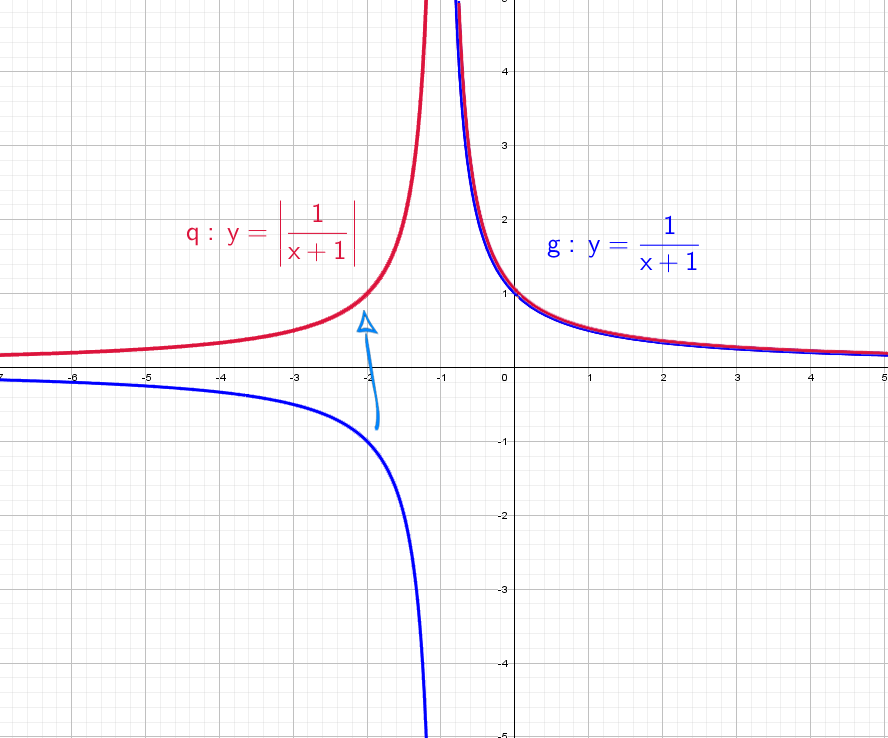
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.

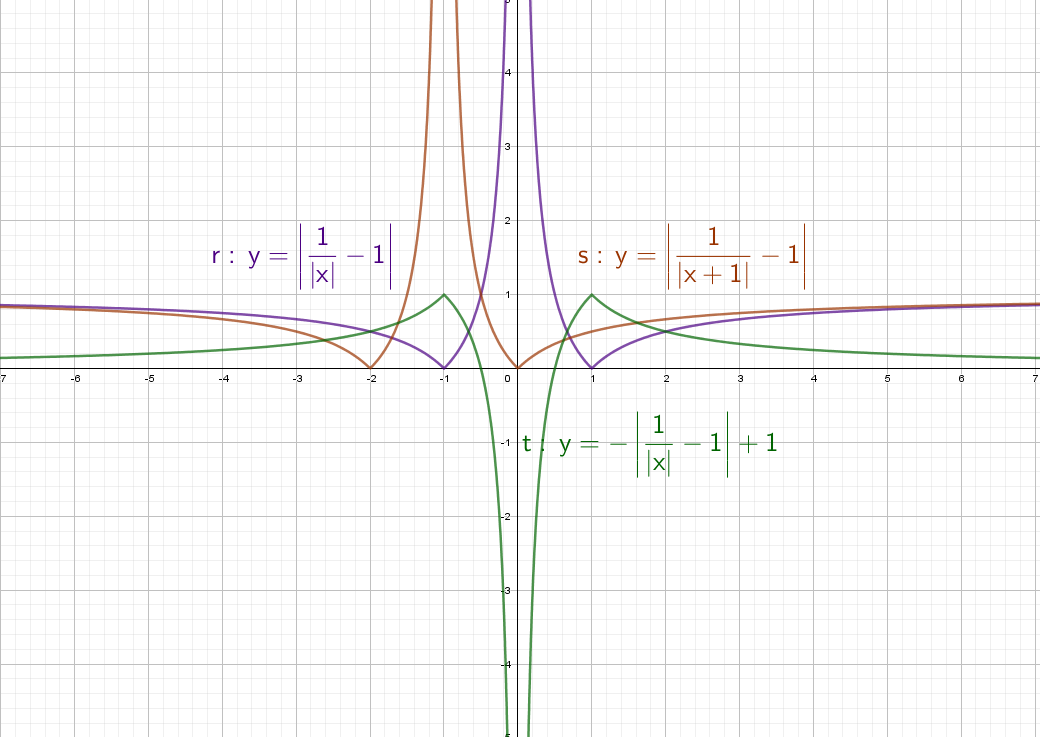
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.

Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.

Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.

Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:

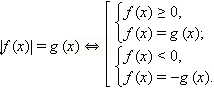
И построить график, разбив его на кусочно-заданные функции.

Например для прямой:

Для параболы с одним модулем будет два кусочно-заданных графика: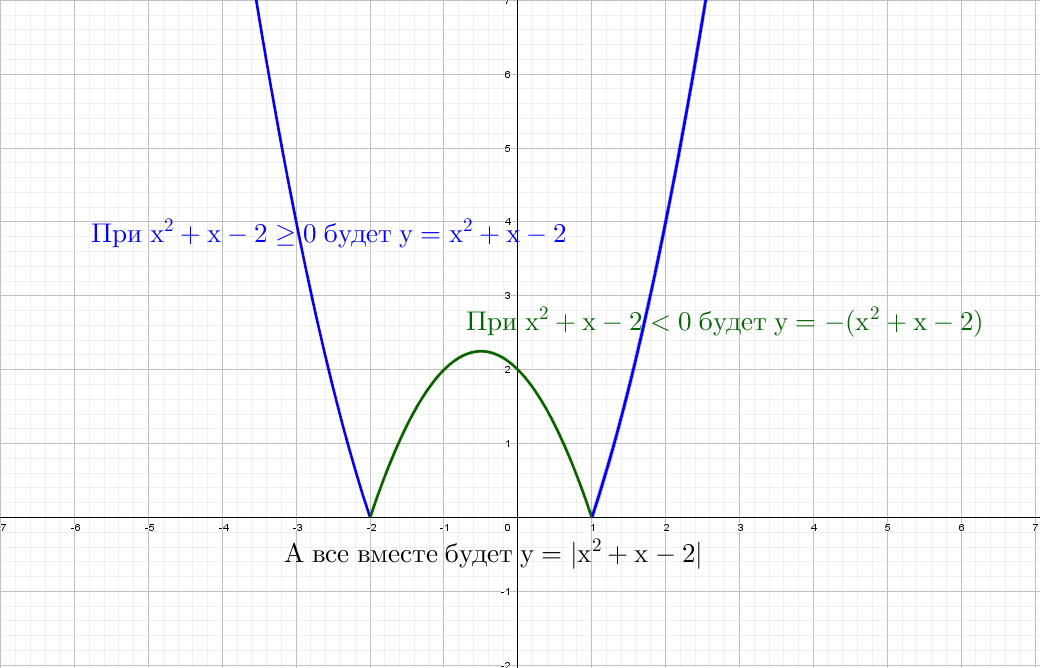

C двумя модулями кусочно-заданных графиков будет четыре:

Таким способом, медленно и кропотливо можно построить любой график!

Выводы:

Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:

Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.

Будь в курсе новых статеек, видео и легкого математического юмора.

Методы построения графиков функций содержащих модуль

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока:

повторить построение графиков функций содержащих знак модуля;
познакомиться с новым методом построения графика линейно-кусочной функции;
закрепить новый метод при решении задач.

Оборудование:

мультимедиа проектор,
плакаты.

Ход урока

Актуализация знаний

На экране слайд 1 из презентации.

Что является графиком функции y=|x| ? (слайд 2).

(совокупность биссектрис 1 и 2 координатных углов)

Найдите соответствие между функциями и графиками, объясните ваш выбор (слайд 3).

Рисунок 1

y=| x+3|

y=| x| +3

y=-2| x| -2

y=6-| x-5|

y=1/3| x-6| -3

Расскажите алгоритм построения графиков функций вида y=|f(x)| на примере функции y=|x²-2x-3| (слайд 4)

Ученик: чтобы построить график данной функции нужно

— построить параболу y=x²-2x-3

— часть графика над ОХ сохранить, а часть графика расположенную ниже ОХ отобразить симметрично относительно оси ОХ (слайд 5)

Рисунок 2

Рисунок 3

Расскажите алгоритм построения графиков функций вида y=f(|x|) на примере функции y=x²-2|x|-3 (слайд 6).

Ученик: Чтобы построить график данной функции нужно:

— построить параболу.

— часть графика при х 0 сохраняется и отображается симметрии относительно оси ОУ (слайд 7)

Рисунок 4

Расскажите алгоритм построения графиков функций вида y=|f(|x|)| на примере функции y=|x²-2|x|-3| (слайд 8).

Ученик: Чтобы построить график данной функции нужно:

— нужно построить параболу у=x²-2x-3

— строим у= x²-2|x|-3, часть графика сохраняем и симметрично отображаем относительно ОУ

— часть над ОХ сохраняем, а нижнюю часть симметрично отображаем относительно ОХ (слайд 9)

Рисунок 5

Следующее задание выполняем письменно в тетрадях.

1. Построить график линейно-кусочной функции у=|х+2|+|х-1|-|х-3|

Ученик на доске с комментарием:

— находим нули подмодульных выражений х₁=-2, х₂=1, х₃=3

— разбиваем ось на промежутки

— для каждого промежутка запишем функцию

при х < -2, у=-х-4

при -2 х<1, у=х

при 1 х<3, у = 3х-2

при х 3, у = х+4

— строим график линейно-кусочной функции.

Мы с вами построили график функции используя определение модуля (слайд 10).

Рисунок 6

Предлагаю вашему вниманию “метод вершин”, который позволяет строить график линейно-кусочной функции (слайд 11). Алгоритм построения дети записывают в тетрадь.

Метод вершин

Алгоритм:

Найдем нули каждого подмодульного выражения
Составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
Нанесем точки на координатную плоскость и соединим последовательно

2. Разберем этот метод на той же функции у=|х+2|+|х-1|-|х-3|

Учитель на доске, дети в тетрадях.

Метод вершин:

— найдем нули каждого подмодульного выражения;

— составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа

х -3 -2 1 3 4

у -1 -2 1 7 8

— нанесем точки на координатную плоскость и соединим последовательно.

Графиком линейно-кусочной функции является ломанная с бесконечными крайними звеньями (слайд 12) .

Рисунок 7

Каким же методом график получается быстрее и легче?

3. Чтобы закрепить данный метод предлагаю выполнить следующее задание:

При каких значения х функция у=|х-2|-|х+1| принимает наибольшее значение.

Следуем алгоритму; ученик на доске.

у=|х-2|-|х+1|

х₁=2, х₂=-1

у(-2)=4-1=3

у(-1)=3

у(2)=-3

у(3)=1-4=3, соединяем последовательно точки.

у_наиб= 3

4. Дополнительное задание

При каких значениях а уравнение ||4+x|-|x-2||=a имеет два корня.

5. Домашняя работа

а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2| принимает наименьшее значение.

б) Построить график функции y=||x-1|-2|-3| .

«Построение графика квадратной функции, содержащей модуль»

Тема: “Построение графика квадратной функции, содержащей модуль”.
(На примере графика функции у = х²— 6x + 3.)

Цель.

Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
Развить навыки построения графика функции, содержащей модуль.

Ход урока.

1. Этап актуализации знаний.

а) Проверка домашнего задания.

Пример 1. Построить график функции у = х² — 6х + 3. Найти нули функции.

Решение.

1. Направление “ветвей” параболы: если а = 1, а > 0, то “ветви” параболы направлены вверх.

2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).

3. Уравнение оси симметрии: х = 3.

4. Нули функции: у(х) = 0, х² — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,

x _1,2 = (6 ± )/2 = 3 ± ; В(3 — ;0), С(3 + ;0).

График на рис.1.

Рис.1.

Алгоритм построения графика квадратной функции.

1. Определить направление “ветвей” параболы.

2. Вычислить координаты вершины параболы.

3. Записать уравнение оси симметрии.

4. Вычислить несколько точек.

б) Рассмотрим построение графиков линейных функций, содержащих модуль:

1. у = |х|. График функции на рисунке 2.

Рис. 2.

2.у = |х| + 1. График функции на рисунке 3.

Рис.3.

3. у = |х + 1|. График функции рисунке 4.

Рис.4.

Вывод.

1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.

2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.

2.Опирационно-исполнительная часть.

Этап исследовательской работы. Работа в группах.

Группа 1. Построить графики функций:

а) у = х² — 6|x| + 3,

б) у = |х² — 6х + 3|.

Решение.

а)

1.Построить график функции у = х²-6х+3.

2. Отобразить его симметрично относительно оси Оу.

График на рисунке 5.

Рис.5.

б) 1. Построить график функции у = х² — 6х + 3.

2. Отобразить его симметрично относительно оси Ох.

График функции на рисунке 6.

Рис. 6.

Вывод.

1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.

2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.

Группа 2.Построить графики функций:

а) у = |x² — 6|x| + 3|;

б) y = |x² — 6x + 3| — 3.

Решение.

а)

1. График функции у = х² + 6x + 3 отображаем относительно оси Оу, получается график функции у = х² — 6|x| + 3.

2. Полученный график отображаем симметрично относительно оси Ох.

График функции на рисунке 7.

Рис.7.

Вывод.

График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.

б)

1. График функции у = х² — 6х + 3 отображаем относительно оси Ох.

2. Полученный график переносим на вектор {0;-3}.

График функции на рисунке 8.

Рис.8.

Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.

Группа 3.Построить график функции:

а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.

Решение.

а) у = |x| (x — 6) + 3, имеем совокупность систем:

Строим график функции у = -х² + 6x + 3 при х < 0 для точек у(0) = 3, у( — 1) = — 4.

График функции на рисунке 9.

Рис.9.

б) у = х |х — 6| + 3, имеем совокупность систем:

Строим график функции у = — х² + 6х + 3 при х 6.

1. Направление “ветвей” параболы: а = — 1, а < 0, “ветви” параболы направлены вниз.

2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2, А(3;12).

3. Уравнение оси симметрии: х = 3.

4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.

Строим график функции у = х² — 6х + 3 при х = 7 у(7) = 10.

График на рис.10.

Рис.10.

Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.

(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения.)

Получили сводную таблицу для графиков функций, содержащих модуль.

Таблица построения графиков функций, содержащих модуль.

Вид функции

Способ построения графика функции

1. у = f(|x|)

2. у = |f(x)|

3. у = |f(|x|)|

4. у = |f(x)| + a

1. Отобразить график функции у = f(x) симметрично относительно оси Оу.

2. Отобразить график функции у = f(x) симметрично относительно оси Ох.

3. Последовательно отобразить график функции у = f(x) симметрично относительно осей координат.

4. Параллельный перенос перенос графика функции у = |f(x)|на вектор {0;а}.

Группа 4.

Построить график функции:

а) у = х² — 5x + |x — 3|;

б) у = |x² — 5x| + x — 3.

Решение.

а) у = х² — 5х + |х — 3|, переходим к совокупности систем:

Строим график функции у = х² -6х + 3 при х 3,
затем график функции у = х² — 4х — 3 при х > 3 по точкам у(4) = -3, у(5) = 2, у(6) = 9.

График функции на рисунке 11.

Рис.11.

б) у = |х² — 5х| + х — 3, переходим к совокупности систем:

Строим каждый график на соответствующем интервале.

График функции на рисунке 12.

Рис.12.

Вывод.

Выяснили влияние модуля в каждом слагаемом на вид графика.

Самостоятельная работа.

Построить график функции:

а) у = |х² — 5х + |x — 3||,

б) у= ||x² — 5x| + х — 3|.

Решение.

Предыдущие графики отображаем относительно оси Ох.

Рис.13.

Рис. 14.

Группа.5

Построить график функции: у =| х — 2| (|x| — 3) — 3.

Решение.

Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.

Имеем совокупность систем уравнений:

Строим график на каждом из интервалов.

График на рисунке 15.

Рис.15.

Вывод. Два модуля в предложенных уравнениях существенно усложнили построение общего графика, состоящего из трех отдельных графиков.

Учащиеся записывали выступления каждой из групп, записывали выводы, участвовали в самостоятельной работе.

3. Задание на дом.

Построить графики функций с различным расположением модуля:

1. у = х² + 4х + 2;

2. у = — х² + 6х — 4.

4. Рефлексивно – оценочный этап.

1.Оценки за урок складываются из отметок:

а) за работу в группе;

б) за самостоятельную работу.

2. Какой момент был наиболее интересен на уроке?

3. Трудное ли домашнее задание?

Урок окончен.

Урок алгебры в 8-м классе по теме: «Модуль и квадратичная функция»

“Великое множество функций
Любой может школьник назвать.
Но лишь о немногих сегодня
Решили мы вам рассказать”

Изучение квадратичной функции с модулем позволяет углубить знания учащихся в преобразовании графиков квадратичной функции. Учащиеся с большим интересом выполняют любые задания с модулем. Рассмотренные приемы построения графиков функции являются общими и применяются не только к квадратичной, но и к другим функциям.

Ход урока

I. Вводное слово учителя

Функция – одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Математика рассматривает абстрактные переменные величины, изучает законы их взаимосвязи, не углубляясь в природу задачи. Например, в соотношении Y = Х²математик или геодезист увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может увидеть зависимость силы Y сопротивления воздуха или воды от скорости Х движения.

Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение Х в 2 раза приведет к увеличению Y в 4 раза, и это заключение может применяться в любой конкретной ситуации.

Модуль и квадратичная функция

Построение графиков функций:

Y = АХ² + ВX + C,
Y = АХ² + ВX + C ,
Y = АХ²+ ВХ + С

II. Устная работа

1) Дать определение модуля числа Х

2) Дать определение квадратичной функции, рассказать все, что известно об этой функции (график, свойства).

3) Найти на рисунке график функции Y = –Х²+ 4Х – 3.

4) На каком рисунке изображен график функции Y = –(Х + 1)(2 – Х)?

5) Вспомнить, как построить график функции Y = Х

По определению модуля

График функции Y = Х симметричен относительно оси У.

III. Построение графиков функций:

Y = АХ² + ВX + C,

Y = АХ²+ ВХ + С

Работа проводится в группах, т.к. графики в К–1 в) и К–3 в) одинаковы, их необходимо сравнить и сделать вывод (всего 3 группы). Каждой группе выдается карточка, в ней 3 задания. Учащиеся должны построить графики квадратичной функции, содержащей модуль, используя определение модуля и сделать вывод: как построить график данной функции, используя график квадратичной функции и симметрию относительно осей координат.

Работа в группах.

Задание: построить график функции, используя:

а) определение модуля;
б) график функции Y = АХ²+ ВХ + С;
в) симметрию относительно осей координат.

а) Y = Х² – 4 Х + 3
б) Y = Х² – 4 Х + 3
в) Y = Х² – 4 Х + 3

а) Y = Х² + 2 Х – 3
б) Y = Х² + 2 Х – 3
в) Y = Х² + 2 Х – 3

а) Y = –Х² + 4 Х – 3
б) Y = –Х² + 4 Х – 3
в) Y = –Х² + 4 Х – 3

IV. Учащиеся делают вывод о расположении графиков указанных функций

Вопрос: а) Как построить график функции Y = f (X)?

(1 способ. Построить график функции Y = f (X), если Х 0 и Y = f (–Х), если Х< 0.
2 способ. Построить график функции Y = f (X) и отобразить правую часть графика симметрично относительно оси Y).

б) Как построить график функции Y = f (X) ?

(Построить график функции Y = f (X) и точки с отрицательными ординатами симметрично отобразить относительно оси Х).

в) Как построить график функции Y = f (X) ?

(Построить график функции Y = f (X), если Х 0 и эту часть графика симметрично отобразить относительно оси Y, а потом точки с отрицательными ординатами отобразить симметрично относительно оси Х.)

г) Почему графики функций Y = –Х² + 4X – 3 и Y = Х² – 4X + 3 одинаковы?

(Так как А = А , –А = А)

V.

У рассмотренных функций под знаком модуля была независимая переменная. Теперь рассмотрим функции, где под знаком модуля стоит либо сама функция, либо и функция, и независимая переменная одновременно, т.е. зависимости вида

Y = АХ² + ВX+ C и Y = АХ² + ВX + C

Приведем конкретные примеры.

а) Y = Х² – 4X+ 3

По определению

Построим график функции Y = f (X) и берем ту его часть, которая расположена выше оси Х, т.к. Х² – 4X+ 3 0 и добавим к ней ее симметричное отображение относительно оси Х.

б) Y = Х² – 4X+ 3

Сначала строим график функции Y = Х² – 4X+ 3 , а затем множество точек, координаты которых удовлетворяют условию Y = Х² – 4X+ 3 , т.е. график функции Y = Х² – 4X+ 3 отображаем относительно оси Х.

VI. Творческое задание

Дана функция Y = Х² + 2X– 3

Выполнить всевозможные преобразования данной квадратичной функции с модулем.

График функции с модулем | Алгебра

Построить график функции с модулем — один из видов задания 23 ОГЭ по математике.

Рассмотрим примеры таких заданий.

1) Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.

Решение:

Область определения функции D(y): x∈R.

1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

x-2=0, x=2.

Найдём значение функции при x=2.

y(2)=5·0-2²+5∙2-3∙0-6=0.

Получили точку (2;0).

2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения.

Если x-2>0, то есть при x>2, |х-2|=x-2,

y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16.

y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).

Координаты вершины параболы

то есть вершина параболы — точка (5;9). От вершины строим график функции y=-x² (так как a=-1).

3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения.

Если x-2<0, то есть при x<2, |х-2|=-(x-2),

y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4.

y=-x²+4 — квадратичная функция. График — парабола ветвями вниз.

Координаты вершины параболы

то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x².

Прямая x=2 разбивает координатную плоскость на две полуплоскости. Слева от неё, для x<2, строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:

График функции с модулем можно рассматривать и как график кусочной функции:

Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4:

Ответ: 0; 4.

2) Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

|6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1.

y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0).

Координаты вершины параболы

Так как a=1, от вершины (3;-10) строим график y=x².

|6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1.

y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх.

Координаты вершины параболы

от вершины (-3;-8) строим график y=x².

Или:

Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8:

Ответ: -8; 1/36.

3) Постройте график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Если x=0, y=|0|·0+3·|0|-5·0=0.

2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x.

y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0).

Координаты вершины параболы

От вершины (1;-1) строим параболу y=x² (так как a=1).

3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x.

y=-x²-8x — квадратичная функция. График — парабола ветвями вниз (a=-1<0).

Координаты вершины параболы

От вершины (-4;16) строим параболу y=-x² (так как a=-1).

Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x:

Альтернативный вариант:

Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16:

Ответ: -1; 16.

4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Решение:

Область определения функции D(y): x∈R.

Построим график функции y=x²+2x-3.

Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх.

Координаты вершины параболы

, то есть вершина параболы — точка (-1;-4).

От вершины строим график функции y=x²:

График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox.

Или y=|x²+2x-3|

Вершина параболы (-1;-4) при этом переходит в точку (-1;4):

Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках).

Ответ: 4.

График функции с модулем и дробью

График функции с модулем и дробью — ещё одна группа заданий номера 23 ОГЭ по математике.

Подобно функциям с переменной в знаменателе, графики таких функций могут содержать выколотую точку. Как и при построении графиков функций с модулем, рассматриваем два варианта раскрытия модуля.

1) Построить график функции

и определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:

Так как x²=|х|², формулу, задающую функцию, перепишем в виде

В знаменателе общий множитель |х| вынесем за скобки

Найдём область определения функции.

|х|(|х|-1)≠0

|х|≠0; |х|-1≠0

x≠0; |х|≠1

x≠0, x≠±1.

D(y):x∈(-∞;-1)∪(-1;0)∪(0;1)∪(1;∞).

Сократив дробь на (|х|-1), получаем

При x>0 |х|=x,

— функция обратной пропорциональности. График — гипербола. Для построения гиперболы возьмём несколько точек (включая выколотую x=1):

При x<0 |х|=-x,

— функция обратной пропорциональности.

Прямая y=kx не имеет с графиком общих точек, если она проходит через выколотые точки либо совпадает с осью Ox, то есть при k=±1 и k=0:

Ответ: -1; 0; 1.

2)Постройте график функции

и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.

Решение:

В числителе вынесем за скобки общий множитель 0,25x:

Ищем область определения функции.

x+2≠0

x≠-2.

D(y):x∈(-∞;-2)∪(-2;∞).

Сокращаем дробь на (x+2):

Получили функцию, содержащую переменную под знаком модуля (при условии x≠-2).
При x=0, y=0,25·0·|0|=0.

При x>0 |х|=x, y=0,25·x·|x|= y=0,25·x·x=0,25x².

y=0,25x² или

— квадратичная функция. График — парабола, полученная из параболы y=x² сжатием к оси Ox в 4 раза.

При x<0 |х|=-x, y=0,25·x·|x|= y=0,25·x·(-x)=-0,25x².

— квадратичная функция. График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза.

Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку, то есть при m=-1:

Ответ: -1.

3) Построить график функции

и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.

Решение:

Найдём область определения функции: x≠0.

D(y):x∈(-∞;0)∪(0;∞).

Если

то есть при x∈[-4;0)∪[4;∞), то

y=x/4 -функция прямой пропорциональности. График — прямая, проходящая через начало координат.

Для построения прямой достаточно взять одну точку, например, при x=4 y=4/4=1. Вторая точка — точка O — на графике выколотая, так как x≠0. Для более точного построения прямой лучше взять ещё одну точку: при x=-4 y=-4/4=-1.

Если

то есть при x∈(-∞;-4)∪(0;4), то

y=4/x — функция обратной пропорциональности. График — гипербола.

Для построения гиперболы возьмём несколько точек из промежутков (-∞;-4)∪(0;4) (-4 и 4 также лучше взять для уточнения построения графика).

Прямая y=m имеет с графиком ровно одну общую точку при m=1 и m=-1:

Ответ: -1; 1.

квадратичных функций и их графики

График квадратичной функции

Квадратичная функция — это полиномиальная функция степени 2, которая может быть записана в общем виде,

f (x) = ax2 + bx + c

Здесь a , b и c представляют действительные числа, где a ≠ 0. Функция возведения в квадрат f (x) = x2 является квадратичной функцией, график которой следует.

Эта общая криволинейная форма называется параболой. U-образный график любой квадратичной функции, определенной как f (x) = ax2 + bx + c, где , , b, и c — действительные числа и a ≠ 0. ,и разделяется графиками всех квадратичных функций. Обратите внимание, что график действительно является функцией, поскольку он проходит тест вертикальной линии. Кроме того, область этой функции состоит из набора всех действительных чисел (−∞, ∞), а область состоит из набора неотрицательных чисел [0, ∞).

При построении графиков парабол, мы хотим включить в график определенные специальные точки. Пересечение и — это точка, где график пересекает ось и . Точки пересечения x — это точки, где график пересекает ось x .ВершинаТочка, определяющая минимум или максимум параболы. это точка, которая определяет минимум или максимум графика. Наконец, линия симметрии: вертикальная линия через вершину x = −b2a, относительно которой парабола симметрична. (также называется осью симметрии. Термин, используемый при ссылке на линию симметрии.) — это вертикальная линия, проходящая через вершину, относительно которой парабола симметрична.

Для любой параболы мы найдем вершину, а и — перехват.Кроме того, если существуют перехваты x , мы также захотим определить их. Гадать по значениям x этих особых точек нецелесообразно; поэтому мы разработаем методы, которые облегчат их поиск. Многие из этих методов будут широко использоваться по мере нашего продвижения в нашем изучении алгебры.

Для заданной квадратичной функции f (x) = ax2 + bx + c найдите пересечение y , вычислив функцию, где x = 0. В общем, f (0) = a (0) 2 + b (0) + c = c, и мы имеем

y-перехват (0, c)

Далее, напомним, что x -приятий, если они существуют, можно найти, установив f (x) = 0.Делая это, мы имеем a2 + bx + c = 0, который имеет общие решения, заданные квадратичной формулой, x = −b ± b2−4ac2a. Следовательно, x -приятия имеют такую общую форму:

x-перехватывает (-b-b2-4ac2a, 0) и (-b + b2-4ac2a, 0)

Используя тот факт, что парабола симметрична, мы можем определить вертикальную линию симметрии, используя x -цепки. Для этого находим среднее значение x между перехватами x , взяв среднее значение следующим образом:

x = (- b − b2–4ac2a + −b + b2−4ac2a) ÷ 2 = (- b − b2−4ac − b + b2−4ac2a) ÷ (21) = — 2b2a⋅12 = −b2a

Следовательно, линия симметрии — это вертикальная линия x = −b2a.Мы можем использовать линию симметрии, чтобы найти вершину.

Линия симметрии Vertexx = −b2a (−b2a, f (−b2a))

Обычно три точки определяют параболу. Тем не менее, в этом разделе мы найдем пять точек, чтобы мы могли получить лучшее приближение к общей форме. Шаги для построения графика параболы описаны в следующем примере.

Пример 1

График: f (x) = — x2−2x + 3.

Решение:

Шаг 1 : Определить точку пересечения и .Для этого установите x = 0 и найдите f (0).

f (x) = — x2−2x + 3f (0) = — (0) 2−2 (0) + 3 = 3

Пересечение и равно (0,3).

Шаг 2 : Определить перехватчики x , если таковые имеются. Для этого установите f (x) = 0 и решите для x .

f (x) = — x2−2x + 3 Задайте f (x) = 0.0 = −x2−2x + 3 Умножьте обе стороны на −1.0

.Функция модуля

— определение, область, диапазон и график

Последнее обновление: 12 июля 2018 года, Teachoo

Изучите все понятия главы 2 «Отношения и функции класса 11» — БЕСПЛАТНО. Проверка — связь и функциональный класс 11 — все концепции

е: р → р

f (x) = | x | для каждого x ∈ р

Здесь | х | известен как модуль х

| Х | всегда позитивно

Итак, | –1 | = 1

| -2 | = 2

| 1 | = 1

| 2 | = 1

| 0 | = 0

Давайте перепишем функцию

Давайте проверим для различных значений х

Для х = –1

х <0

Итак, f (x) = — x

f (x) = — (–1) = 1

Для х = -2

х <0

Итак, f (x) = — x

f (x) = — (–2) = 2

Для х = 1

х> 0

Итак, f (x) = x

f (x) = 1

Для х = 2

х> 0

Итак, f (x) = x

f (x) = 2

Для х = 0

х ≥ 0

Итак, f (x) = x

f (x) = 0

Сейчас,

График построения

Вот,

Домен = Все значения х = R

Ассортимент = Все значения у

Поскольку у всегда будет положительным или 0

Диапазон = все положительные вещественные числа и 0

Функциональный Графер и Калькулятор

Описание :: Все функции

Описание

Function Grapher — это полнофункциональная графическая утилита, которая поддерживает отображение двух функций вместе.

Он обладает уникальной функцией, которая позволяет сохранять свою работу в виде URL (ссылка на веб-сайт).

Использование

Для построения функции просто введите ее в поле функции.2)
(х-3) (х + 3)

Масштабирование и перецентровка

Для увеличения используйте ползунок масштабирования. Слева увеличено, справа уменьшено. Когда вы отпускаете ползунок, он возвращается к середине, чтобы вы могли увеличить масштаб.

Вы можете нажать и перетащить, чтобы переместить график.

Если вы просто нажмете и отпустите (не двигаясь), то место, на котором вы щелкнули, будет новым центром

Чтобы восстановить исходное масштабирование, нажмите кнопку «Сброс ».

Использование значений «a»

Есть слайдер с «a =» на нем. Вы можете использовать «a» в своей формуле, а затем с помощью ползунка изменить значение «a», чтобы увидеть, как оно влияет на график.

Обратите внимание, как я использовал * x для умножения на и x . Если бы я использовал ax (или xa ), программа просто запуталась.

Все функции

Операторы

	+	Оператор сложения
	—	Оператор вычитания
	*	Оператор умножения
	/	Оператор подразделения
	^	Экспонент (Мощность) оператор

Функции

	кв.	квадратный корень значения или выражения.
	грех	синус значения или выражения
	cos	косинус значения или выражения
	загар	тангенса значения или выражения
	asin	обратный синус (арксинус) значения или выражения
	acos	обратный косинус (арккос) значения или выражения
	атан	обратный тангенс (арктангенс) значения или выражения
	синх	Гиперболический синус (sinh) значения или выражения
	кош 9009	Гиперболический косинус (кош) значения или выражения
	tanh	Гиперболический тангенс (танх) значения или выражения
	exp	e (постоянная Эйлера), возведенная в степень значения или выражения
	ln	натуральный логарифм значения или выражения
	бревно	Логарифм по основанию-10 значения или выражения
	этаж	Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и равно математическому целому числу.
	ceil	Возвращает наименьшее (ближайшее к отрицательной бесконечности) значение, которое не меньше аргумента и равно математическому целому числу.
	абс	Абсолютное значение (расстояние от нуля) значения или выражения
	знак	Знак (+1 или -1) значения или выражения
	факт	факторная функция

Константы

	пи	Константа π (3.141592654 …)
	е	число Эйлера (2.71828 …), основание для натурального логарифма

,
Функция преобразования графиков модуля
Здесь мы увидим преобразование графиков функции модуля.
Отражение:
Отражение — это зеркальное отображение графика, где линия l — это отражение отражения.
(i) График y = −f (x) является отражением графа f относительно оси x.
(ii) График y = f (−x) является отражением графа f относительно оси y.
(iii) График y = f ^-1 (x) является отражением графика f в y = x.
Перевод:
Перевод графика — это вертикальный или горизонтальный сдвиг графика, который создает конгруэнтные графики.
График
y = f (x + c), c> 0 вызывает сдвиг влево.
y = f (x — c), c> 0 вызывает сдвиг вправо.
y = f (x) + d, d> 0 вызывает сдвиг вверх.
y = f (x) — d, d> 0 вызывает смещение вниз.
Дилатация:
Дилатация — это также преобразование, которое вызывает растяжение кривой (расширение) или сжатие (сжатие).Умножение функции на положительную постоянную вертикально растягивает или сжимает ее график; то есть график перемещается от оси x или к оси x.
Если положительная константа больше единицы, график отходит от оси x. Если положительная константа меньше единицы, график перемещается в направлении оси x.
Практический вопрос
Задача 1:
Из кривой y = | x | нарисуем
(i) y = | x — 1 | + 1
(ii) y = | x + 1 | — 1
(iii) y = | x + 2 | — 3
Решение:
Сначала нарисуем график y = | x |, для любых отрицательных значений x мы получим положительные значения y.
Итак, график будет
(i) y = | x — 1 | + 1
Первое 1 вычитается из x в функции модуля, поэтому мы должны переместить единицу кривой 1 вправо.
1 добавляется к | x — 1 |, поэтому мы должны переместить график y = | x — 1 | На 1 единицу вверх.,
Задача 2:
Из кривой y = sin x нарисуйте y = sin | x | (Подсказка: sin (−x) = −sin x.)
Решение:
График y = sin x

Если x = 0
y = sin 0
y = 0
Если x = π / 2
y = sin π / 2
y = 1
Если x = π
y = sin π
y = 0
Если x = 3π / 2
y = sin 3π / 2
y = -1
Если x = 2π
y = sin 2π
y = 0
(0, 0) (π / 2, 1) (π, 0) (3π / 2, — 1) и (2π, 0)
Чтобы нарисовать график y = sin | x |, воспользуемся подсказкой
sin (−x) = −sin x
Если x = 0
y = sin 0
y = 0
Если x = -π / 2
y = -sin π / 2
y = -1
Если x = π / 2
y = sin π / 2
y = 1
Если x = -π
y = -sin π
y = 0
Если x = π
y = sin π
y = 0
Если x = -3π / 2
y = -sin 3π / 2
y = -1
Если x = 3π / 2
y = sin 3π / 2
y = -1
Если x = -2π
y = -sin 2π
y = 0
Если x = 2π
y = sin 2π
y = 0
Помимо материалов, приведенных выше, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Вы также можете посетить следующие веб-страницы по различным материалам по математике.
ЗАДАЧИ СЛОВА
Задачи со словами в HCF и LCM
Задачи со словами в простых уравнениях
Задачи со словами в линейных уравнениях
Задачи в словах по квадратным уравнениям

Проблемы со словами в поездах
Проблемы со словами в области и по периметру
Проблемы со словами при прямом и обратном изменении
Проблемы со словами в цене за единицу
Проблемы со словами в скорости за единицу
задачи по сравнению курсов
Преобразование обычных словесных задач
Преобразование метрических единиц проблем слов
Задачи по простым интересам
Задачи по сложным интересам
Задачи по типам слов ngles
и дополнительные углы проблема слова
Двойных проблемы фактов слова
Тригонометрии проблема слова
проблем Процента слов
Прибыль и потеря слова проблема
Markup и уценки слово задачи
задачи с десятичными словами
задачи со словами о дробях
задачи о словах на смешанных дробях
задачи с одним уравнением в одном слове задачи
линейные неравенства о словах

задачи
Проблемы со временем и рабочим словом
Задачи со словами на множествах и диаграммах Венна
Задачи со словами в возрасте
Проблемы со словами теоремы Пифагора
Процент числа oblems
Задачи на слово на постоянной скорости
Задачи на слово на средней скорости
Задачи на слово на сумму углов треугольника составляет 180 градусов
ДРУГИЕ ТЕМЫ
короткие убытки Прибыль и прибыль
Процентные ярлыки
Сочетания временного расписания
Сочетания времени, скорости и расстояния
Сочетания соотношений и пропорций

Область 9 и область рациональных функций функции с отверстиями
Графические рациональные функции
Графические рациональные функции с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
длинных корней
Поиск квадрата зрение
л.Метод CM для решения задач времени и работы Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, кратных 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
,

График функции модуль х в квадрате: Построение функций, содержащих модули

Построение функций, содержащих модули

Графики прямой, параболы, гиперболы, с модулем

Будь в курсе новых статеек, видео и легкого математического юмора.

1. Этап актуализации знаний.

2.Опирационно-исполнительная часть.

Самостоятельная работа.

3. Задание на дом.

4. Рефлексивно – оценочный этап.

Ход урока

I. Вводное слово учителя

II. Устная работа

III. Построение графиков функций:

IV. Учащиеся делают вывод о расположении графиков указанных функций

V.

VI. Творческое задание

График функции с модулем | Алгебра

График функции с модулем и дробью

квадратичных функций и их графики

График квадратичной функции

Пример 1

— определение, область, диапазон и график

Для х = –1

Для х = -2

Для х = 1

Для х = 2

Для х = 0

Функциональный Графер и Калькулятор

Описание

Использование

Для построения функции просто введите ее в поле функции.2) (х-3) (х + 3)

Масштабирование и перецентровка

Использование значений «a»

Все функции

Операторы

Функции

Константы

Функция преобразования графиков модуля

Практический вопрос

Share This Story, Choose Your Platform!

Related Posts

Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ

Для построения функции просто введите ее в поле функции.2)
(х-3) (х + 3)