9 класс
Контрольная работа №2
Тема: «Углы, вписанные в окружность. Пропорциональность отрезков хорд и секущих»
Вариант I
1. Хорды окружности 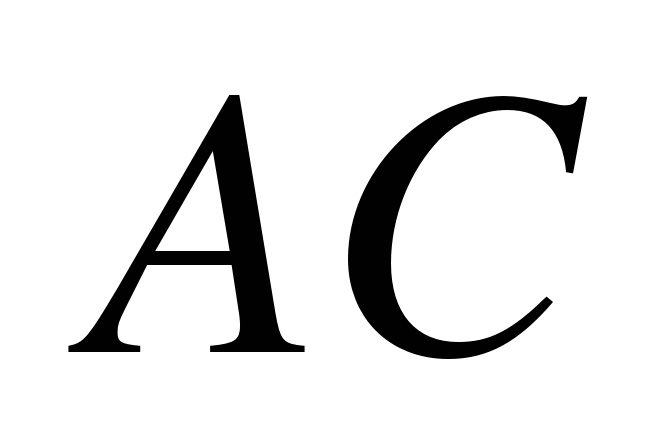 и
и 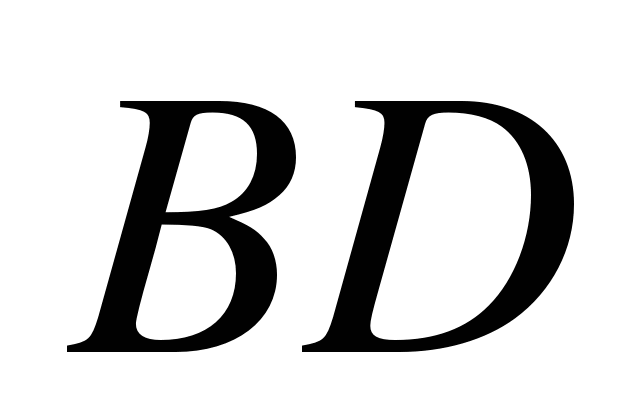 пересекаются. Найти
пересекаются. Найти 


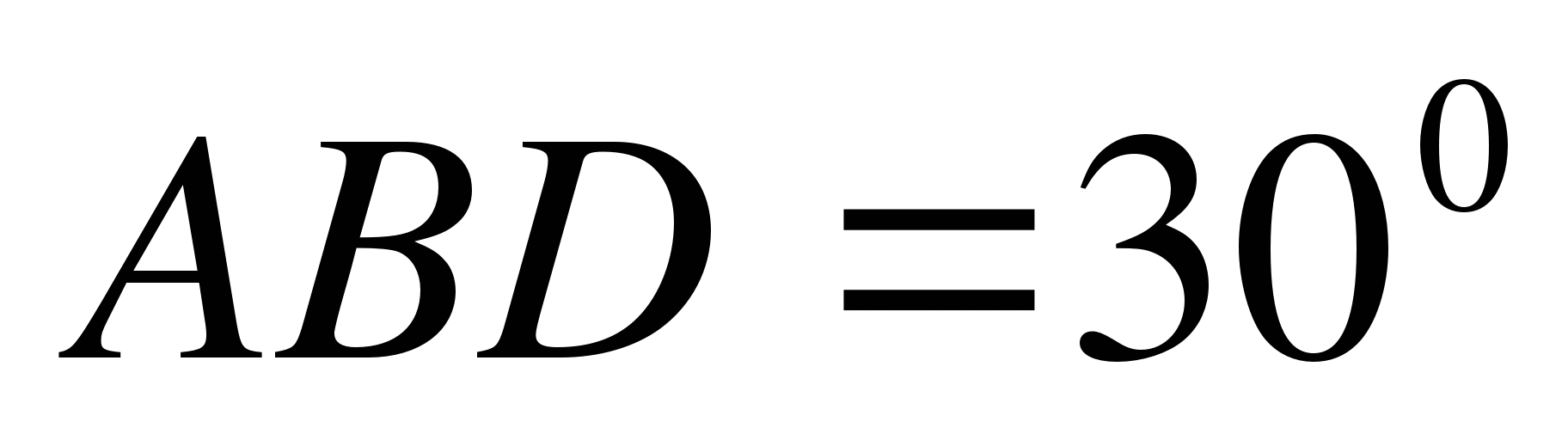 ,
, 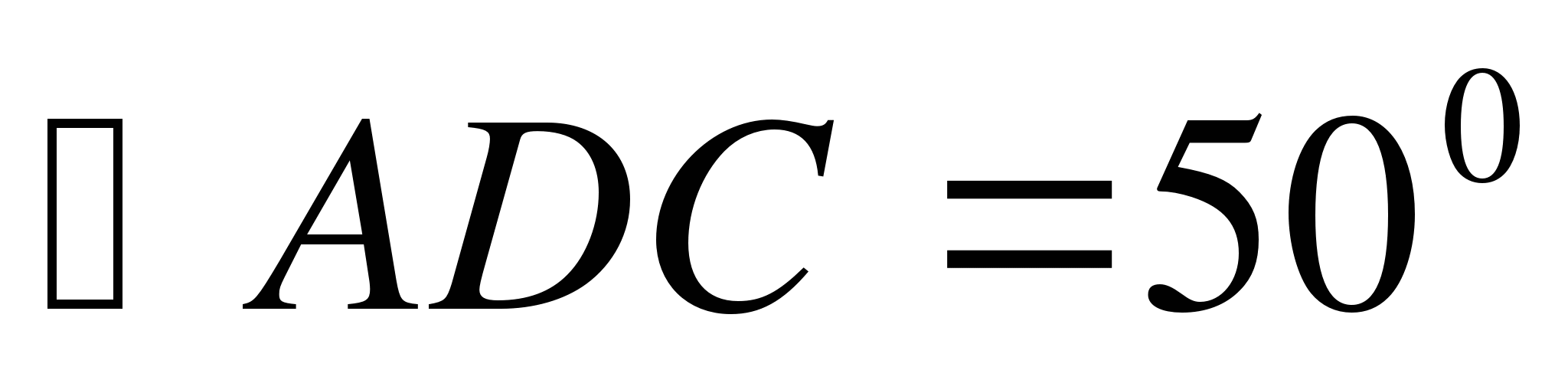 .
.
2. Как далеко видно из самолета, летящего на высоте 6 км над Землей, если
радиус Земли 6370 км?
3. В равнобедренном треугольнике боковые стороны равны 5 см, а высота
опущенная на основание – 3 см. Найдите радиус окружности, описанной
около этого треугольника.
Контрольная работа №2
Тема: «Углы, вписанные в окружность. Пропорциональность отрезков хорд и секущих»
Вариант II
1. Хорды окружности  и
и 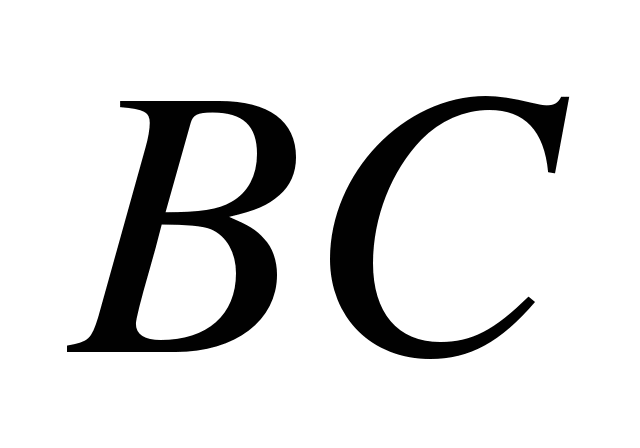 пересекаются. Найти
пересекаются. Найти 
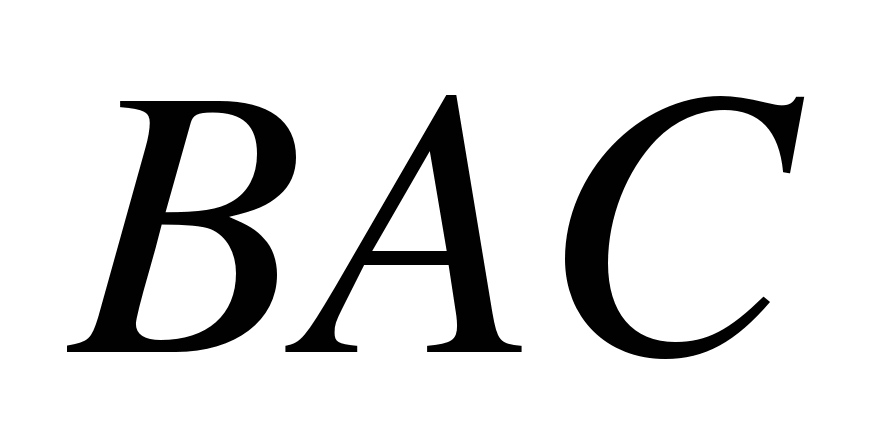

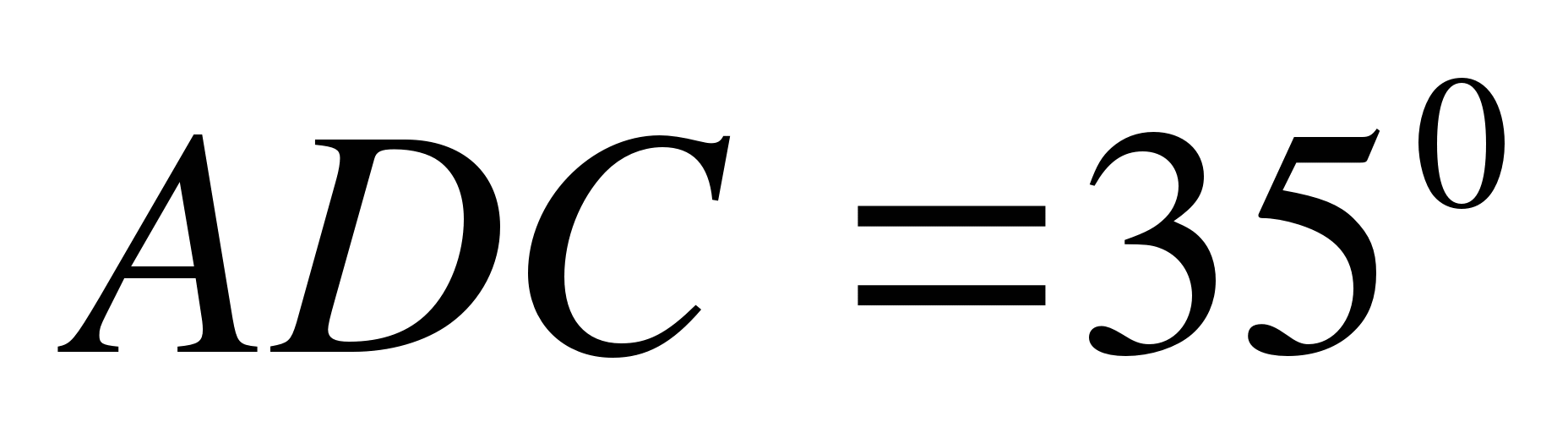 ,
, 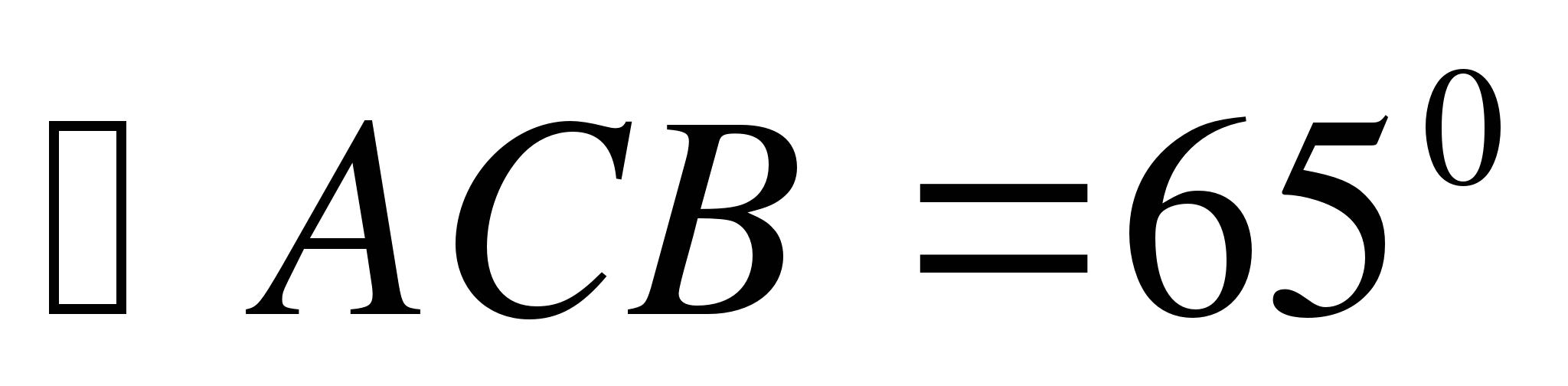 .
.
2. Как далеко видно из самолета, летящего на высоте 8 км над Землей, если
радиус Земли 6370 км?
3. В равнобедренном треугольнике боковые стороны равны 10 дм, а высота
опущенная на основание – 8 дм. Найдите радиус окружности, описанной
около этого треугольника.
Вариант 1
| Вариант 2
|
Вариант 1
| Вариант 2
|
Вариант 1
| Вариант 2
|
Вариант 1
| Вариант 2
|
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 1
а) в одной полуплоскости относительно прямой MN;
б) в разных полуплоскостях относительно прямой MN.
По данным рисунка определите градусную меру угла α.
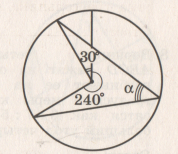
Хорды АВ и CD пересекаются в точке Е. Найдите величину CD, если АЕ = 4см, ВЕ = 9см, а длина СЕ в четыре раза больше длины DE.
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 2
Углы АВС и ADC вписаны в одну окружность. Найдите градусную меру угла АВС, если угол ADC равен 1200 и точки В и D лежат:
а) в одной полуплоскости относительно прямой АС;
б) в разных полуплоскостях относительно прямой АС.

Хорды АВ и CD пересекаются в точке М. АМ = 9см, МВ = 4см, СМ=MD. Вычислите длину хорды CD.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 3:7:8 соответственно. Найдите градусную меру большего угла треугольника АВС.
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 1
Углы MNK и MPN вписаны в одну окружность. Найдите градусную меру угла MKN, если угол MPN равен 400 и точки К и Р лежат:
а) в одной полуплоскости относительно прямой MN;
б) в разных полуплоскостях относительно прямой MN.
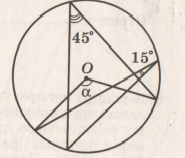
По данным рисунка определите градусную меру угла α.

Хорды АВ и CD пересекаются в точке Е. Найдите величину CD, если АЕ = 4см, ВЕ = 9см, а длина СЕ в четыре раза больше длины DE.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 2:4:6 соответственно. Найдите градусную меру большего угла треугольника АВС.
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 2
Углы АВС и ADC вписаны в одну окружность. Найдите градусную меру угла АВС, если угол ADC равен 1200 и точки В и D лежат:
а) в одной полуплоскости относительно прямой АС;
б) в разных полуплоскостях относительно прямой АС.
По данным рисунка определите градусную меру угла α

Хорды АВ и CD пересекаются в точке М. АМ = 9см, МВ = 4см, СМ=MD. Вычислите длину хорды CD.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 3:7:8 соответственно. Найдите градусную меру большего угла треугольника АВС.
«Центральные и вписанные углы окружности»
Вариант 1
Углы MNK и MPN вписаны в одну окружность. Найдите градусную меру угла MKN, если угол MPN равен 400 и точки К и Р лежат:
а) в одной полуплоскости относительно прямой MN;
б) в разных полуплоскостях относительно прямой MN.
По данным рисунка определите градусную меру угла
·.
Хорды АВ и CD пересекаются в точке Е. Найдите величину CD, если АЕ = 4см, ВЕ = 9см, а длина СЕ в четыре раза больше длины DE.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 2:4:6 соответственно. Найдите градусную меру большего угла треугольника АВС.
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 2
Углы АВС и ADC вписаны в одну окружность. Найдите градусную меру угла АВС, если угол ADC равен 1200 и точки В и D лежат:
а) в одной полуплоскости относительно прямой АС;
б) в разных полуплоскостях относительно прямой АС.
По данным рисунка определите градусную меру угла
·
Хорды АВ и CD пересекаются в точке М. АМ = 9см, МВ = 4см, СМ=MD. Вычислите длину хорды CD.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 3:7:8 соответственно. Найдите градусную меру большего угла треугольника АВС.
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 1
Углы MNK и MPN вписаны в одну окружность. Найдите градусную меру угла MKN, если угол MPN равен 400 и точки К и Р лежат:
а) в одной полуплоскости относительно прямой MN;
б) в разных полуплоскостях относительно прямой MN.
По данным рисунка определите градусную меру угла
·.
Хорды АВ и CD пересекаются в точке Е. Найдите величину CD, если АЕ = 4см, ВЕ = 9см, а длина СЕ в четыре раза больше длины DE.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 2:4:6 соответственно. Найдите градусную меру большего угла треугольника АВС.
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 2
Углы АВС и ADC вписаны в одну окружность. Найдите градусную меру угла АВС, если угол ADC равен 1200 и точки В и D лежат:
а) в одной полуплоскости относительно прямой АС;
б) в разных полуплоскостях относительно прямой АС.
По данным рисунка определите градусную меру угла
·
Хорды АВ и CD пересекаются в точке М. АМ = 9см, МВ = 4см, СМ=MD. Вычислите длину хорды CD.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 3:7:8 соответственно. Найдите градусную меру большего угла треугольника АВС.
15
Приложенные файлы
ТЕСТ №11.
1В угол C величиной 107° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
2Центральный угол AOB опирается на хорду АВтак, что угол ОАВ равен 60° . Найдите длину хорды АВ, если радиус окружности равен 8.
Ответ: 8
3. В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
4. Центральный угол AOB, равный 60° , опирается на хорду АВ длиной 4. Найдите радиус окружности.
5. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
6. Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно.
7В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину углаOAB.
8. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
9. Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.
10. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?
11. Точка О — центр окружности, ∠ACB = 24° (см. рисунок). Найдите величину угла AOB (в градусах).
12.. На окружности с центром O отмечены точки A и B так, что ∠AOB = 66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
13. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 112°. Найдите вписанный угол ACB. Ответ дайте в градусах.
14. На окружности по разные стороны от диаметра ABвзяты точки M и N. Известно, что ∠NBA = 38°. Найдите угол NMB. Ответ дайте в градусах.
15.. AC и BD — диаметры окружности с центром O. Угол ACBравен 79°. Найдите угол AOD. Ответ дайте в градусах.
По теме: методические разработки, презентации и конспекты
Подготовка к ГИА. Окружность.Центральные и вписанные углы.Презентация по теме «Окружность.Центральные и вписанные углы» . Материал содержит повторение вопросов теории и задачи для подготовки к ГИА по этой теме….
 Уроки модульной технологии по геометрии. * класс тема: «Окружность, касательная к окружности, центральные и вписанные углы»
Уроки модульной технологии по геометрии. * класс тема: «Окружность, касательная к окружности, центральные и вписанные углы»Касательная к окружности. Центральные и вписанные углы.Комплексная дидактическая цель – расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью….
 Презентация по теме «Касательная к окружности. Центральные и вписанные углы» — диктант
Презентация по теме «Касательная к окружности. Центральные и вписанные углы» — диктантДанная работа представлена в виде презентации, на которой представлен диктант по теме «касательная к окружности. Центральные и вписанные углы». Диктант для двух вариантов состоит из 10 вопросов в кажд…
 Презентация для урока по теме «Дуга окружности. Центральные и вписанные углы». 8 класс
Презентация для урока по теме «Дуга окружности. Центральные и вписанные углы». 8 классДанную презентацию можно использовать при изучении нового материала….
 тест Окружность. центральные и вписанные углы.
тест Окружность. центральные и вписанные углы.Данный материал предназначен для подготовки к ОГЭ…
 Опрос-тест по геометрии на тему «Окружность. Центральные и вписанные углы» (8 класс)
Опрос-тест по геометрии на тему «Окружность. Центральные и вписанные углы» (8 класс)Тест по геометрии в 8 классе направленный на знание учащимися темы «Окружность. Центральные и вписанные углы» . В каждом из двух вариантов 10 вопросов с выбором одного правильного из четырёх предложен…
 Презентация » Окружность. Центральные и вписанные углы. «
Презентация » Окружность. Центральные и вписанные углы. «Презентация по решению задач по готовым чертежам…
Контрольные работы Г-9 по Бурмистрову
Контрольная работа №1 «Подобие фигур» вариант-1
№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см
№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см
а) вычислите длину проекции стороны ВС на прямую СD.
в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СД)
Контрольная работа № 1 «Подобие фигур» вариант 2
а) вычислите длины отрезков ВО и ОD.
в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).
Контрольная работа №2 «Углы, вписанные в окружность» вариант-1
№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.
№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:
а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.
в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см
Контрольная работа №2 «Углы, вписанные в окружность» вариант-2
№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.
№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:
а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.
в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.
Контрольная работа №3 «Решение треугольников» 1 вариант.
В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.
Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5
 см и 3 см.
см и 3 см.Сторона параллелограммам равна 2
 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.*Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.
Контрольная работа №3 «Решение треугольников» 2 вариант.
В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.
Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4
 см и 7 см.
см и 7 см.Найдите углы равнобокой трапеции, в которой боковая сторона равна 2
 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.*Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.
Контрольная работа №4 «Многоугольники» вариант-1
№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.
№2. Около правильного треугольника со стороной 5см описана окружность. Найдите
а) радиус описанной окружности;
в) сторону правильного шестиугольника, вписанного в эту окружность.
№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.
Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.
Контрольная работа №4 «Многоугольники» вариант-2
№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.
№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите
а) радиус окружности;
в) сторону правильного треугольника, описанного около данной окружности.
№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.
Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.
Контрольная работа №5 «Площади многоугольников» вариант-1
№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.
№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.
№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.
Контрольная работа №5 «Площади многоугольников» вариант-2
№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм.
№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.
№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45 . Вычислите площадь трапеции, если основания её равны 24см и 60см.
Контрольная работа №6 «Площадь круга и его частей» вариант-1
№1. Найдите площадь круга, диаметр которого 6см.
№2. Площади двух подобных многоугольников пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.
№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.
Контрольная работа №6 «Площадь круга и его частей» вариант-2
№1. Найдите площадь круга, диаметр которого 8см.
№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.
№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.
Контрольная работа № 1
«Подобие фигур»
вариант-1
№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см
№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см
а) вычислите длину проекции стороны ВС на прямую СD.
в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СD)
Контрольная работа № 1
«Подобие фигур»
вариант -2
а) вычислите длины отрезков ВО и ОD.
в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).
Контрольная работа №1
«Подобие фигур»
вариант-1
№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см
№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см
а) вычислите длину проекции стороны ВС на прямую СD.
в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СD)
Контрольная работа № 1
«Подобие фигур»
вариант -2
а) вычислите длины отрезков ВО и ОD.
в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).
Контрольная работа № 1
«Подобие фигур»
вариант-1
№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см
№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см
а) вычислите длину проекции стороны ВС на прямую СD.
в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СD)
Контрольная работа № 1
«Подобие фигур»
вариант -2
а) вычислите длины отрезков ВО и ОD.
в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).
Контрольная работа №2
«Углы, вписанные в окружность»
вариант-1
№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.
№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:
а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.
в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см
Контрольная работа №2 «Углы, вписанные в окружность»
вариант-2
№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.
№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:
а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.
в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.
Контрольная работа №2
«Углы, вписанные в окружность»
вариант-1
№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.
№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:
а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.
в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см
Контрольная работа №2 «Углы, вписанные в окружность»
вариант-2
№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.
№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:
а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.
в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.
Контрольная работа №2
«Углы, вписанные в окружность»
вариант-1
№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.
№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:
а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.
в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см.
Контрольная работа №2 «Углы, вписанные в окружность»
вариант-2
№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.
№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:
а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.
в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.
Контрольная работа №3
«Решение треугольников»
вариант-1
В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.
Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5
 см и 3 см.
см и 3 см.Сторона параллелограммам равна 2
 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.*Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.
Контрольная работа №3
«Решение треугольников»
вариант-2
В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.
Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4
 см и 7 см.
см и 7 см.Найдите углы равнобокой трапеции, в которой боковая сторона равна 2
 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.*Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.
Контрольная работа №3
«Решение треугольников»
вариант-1
В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.
Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5
 см и 3 см.
см и 3 см.Сторона параллелограммам равна 2
 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.*Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.
Контрольная работа №3
«Решение треугольников»
вариант-2
В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.
Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4
 см и 7 см.
см и 7 см.Найдите углы равнобокой трапеции, в которой боковая сторона равна 2
 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
4* Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.
Контрольная работа №3
«Решение треугольников»
вариант-1
.
В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.
Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5
 см и 3 см.
см и 3 см.Сторона параллелограммам равна 2
 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.*Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.
Контрольная работа №3
«Решение треугольников»
вариант-2
. В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.
Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4
 см и 7 см.
см и 7 см.Найдите углы равнобокой трапеции, в которой боковая сторона равна 2
 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
4* Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.
Контрольная работа №4
«Многоугольники»
вариант-1
№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.
№2. Около правильного треугольника со стороной 5см описана окружность. Найдите
а) радиус описанной окружности;
в) сторону правильного шестиугольника, вписанного в эту окружность.
№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.
Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.
Контрольная работа №4
«Многоугольники»
вариант-2
№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.
№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите
а) радиус окружности;
в) сторону правильного треугольника, описанного около данной окружности.
№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.
Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.
Контрольная работа №4
«Многоугольники»
вариант-1
№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.
№2. Около правильного треугольника со стороной 5см описана окружность. Найдите
а) радиус описанной окружности;
в) сторону правильного шестиугольника, вписанного в эту окружность.
№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.
Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.
Контрольная работа №4
«Многоугольники»
вариант-2
№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.
№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите
а) радиус окружности;
в) сторону правильного треугольника, описанного около данной окружности.
№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.
Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.
Контрольная работа №4
«Многоугольники»
вариант-1
№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.
№2. Около правильного треугольника со стороной 5см описана окружность. Найдите
а) радиус описанной окружности;
в) сторону правильного шестиугольника, вписанного в эту окружность.
№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.
Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.
Контрольная работа №4
«Многоугольники»
вариант-2
№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.
№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите
а) радиус окружности;
в) сторону правильного треугольника, описанного около данной окружности.
№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.
Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.
Контрольная работа №5
«Площади многоугольников»
вариант-1
№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.
№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.
№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.
Контрольная работа №5
«Площади многоугольников»
вариант-2
№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм
.
№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.
№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45º . Вычислите площадь трапеции, если основания её равны 24см и 60см.
Контрольная работа №5
«Площади многоугольников»
вариант-1
№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.
№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.
№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.
Контрольная работа №5
«Площади многоугольников»
вариант-2
№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм
.
№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.
№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45º . Вычислите площадь трапеции, если основания её равны 24см и 60см.
Контрольная работа №5
«Площади многоугольников»
вариант-1
№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.
№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.
№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.
Контрольная работа №5
«Площади многоугольников»
вариант-2
№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм
.
№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.
№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45º . Вычислите площадь трапеции, если основания её равны 24см и 60см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-1
№1. Найдите площадь круга, диаметр которого 6см.
№2. Площади двух подобных многоугольников
пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.
№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-2
№1. Найдите площадь круга, диаметр которого 8см.
№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников
№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.
№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-1
№1. Найдите площадь круга, диаметр которого 6см.
№2. Площади двух подобных многоугольников
пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.
№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-2
№1. Найдите площадь круга, диаметр которого 8см.
№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников
№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.
№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-1
№1. Найдите площадь круга, диаметр которого 6см.
№2. Площади двух подобных многоугольников
пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.
№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-2
№1. Найдите площадь круга, диаметр которого 8см.
№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников
№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.
№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.
дуг, центральные и вписанные углы, полный круг
Транскрипция






1 rcs, центральные и надписанные иглы ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: Совместное чтение, обобщение / перефразирование / пересказ, визуализация Крис любит играть в футбол.Когда ему было семь лет, его семья записала его в футбольный лагерь, чтобы он мог начать изучать навыки, необходимые для хорошего игрока. В течение двух лет Крис добивался прогресса в своей команде, но он хотел улучшаться. Поэтому в этом году на девятый день рождения Криса мистер Грин, друг семьи, опытный футболист, вызвался тренировать Криса по несколько часов каждые выходные. Во время их первых сессий Крис хорошо справлялся с мячом, бегая взад и вперед по полю, но ему было очень трудно бить по точному голу.Г-н Грин предложил сосредоточиться на улучшении этого конкретного навыка на будущих сессиях. На каждой тренировке мистер Грин стоит в центре между стойками ворот, и Крис пытается забить гол с разных позиций на поле. Он заметил, что выстрелы Криса идут где угодно от цели до 15 по обе стороны от его цели. Обладая этой информацией, мистер Грин полагает, что он и Крис могут найти места на футбольном поле, с которых Крис может быть уверен в том, что они будут пробивать между воротами. хотя его удары могут быть заблокированы вратарем, по крайней мере, у Криса будет больше шансов сделать гол.Ваш учитель предоставит вам схему части футбольного поля, цель шириной 24 фута и точку X, на которой г-н Грин планирует встать. Очки и представляют собой стойки ворот, которые находятся на расстоянии 24 фута друг от друга. Крис будет направлять свои удары прямо в мистера Грина из разных точек игрового поля, чтобы попытаться найти места, где даже с допустимой погрешностью его удары будут попадать между стойками ворот. Ваш учитель также предоставит вам диаграмму из 30 углов, которая имеет биссектрису. Вершина S представляет точку, из которой Крис наносит удар, биссектриса — путь к цели, на которую нацелен Крис, а стороны 30-градусного угла образуют внешние границы возможных ударов Криса, учитывая, что его край ошибки до 15 по обе стороны от цели.CTIVITY 4.2 Блок 4 Круги и конструкции 285
2 CTIVITY 4.2 rcs, центральные и вписанные ngles ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: Закрыть Чтение, Думать / Пара / Поделиться, Использовать Манипуляторы, Опрашивать текст, Визуализация, Создавать представления, Искать шаблон Ваш учитель даст вам листы, содержащие диаграмму футбольного поля и диаграмму 30-треугольника. Угловая диаграмма будет использоваться в качестве инструмента для оценки внешних границ удара Криса, когда он нацеливается на точку X из различных мест на футбольном поле.1. На диаграмме футбольного поля вы увидите три точки, обозначенные как Точки 1, 2 и 3. Эти три точки представляют различные позиции на поле, с которых Крис попытается пробить по воротам. Поместите вершину вашего угла в точку 1 и убедитесь, что точка X лежит на биссектрисе угла. Будет ли гарантирован удар Криса между воротами с этой позиции на поле? Объясните. 2. Поочередно поместите вершину угла в точку 2, а затем в точку 3. Каждый раз, убедитесь, что точка X лежит на биссектрисе угла.Определите, будут ли удары Криса попадать между воротами с этих позиций на поле. Какая позиция, если таковая есть, является верным ударом по цели для Криса? 3. Экспериментируя, вы должны обнаружить, что есть область игрового поля, из которой Крис наверняка пробьет в зону ворот, несмотря на свою погрешность. Используйте диаграмму футбольного поля и угловую диаграмму, чтобы проверить точки на поле, пока вы не сможете сделать обоснованное предположение о форме этого региона.Напишите описание региона. На диаграмме футбольного поля четко обозначьте не менее восьми точек на внешней границе этого региона. 286 Springoard Математика со смыслом TM Geometry
3 rcs, центральные и вписанные иглы CTIVITY 4.2 ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: поощрение предварительного знания, внимательное чтение, интерактивная стена слов, словарный органайзер 4. elow — это схема круга O. O и O называются , O Q CDEMIC VOCULRY центральный угол Обведите точки и разделите круг на две дуги.Меньшая дуга называется малой дугой, а большая дуга называется большой дугой Q. Угол, образованный двумя радиусами O, называется центральным углом этого круга. В общем, центральный угол — это угол, вершина которого находится в центре круга, а стороны которого содержат радиусы круга. n дуга, перехваченная центральным углом, является второстепенной дугой, которая находится внутри угла. Обратите внимание, что главная дуга связана с точками и лежит снаружи O, а малая дуга лежит внутри O.говорят, что он перехвачен по определению O. y, мера малой дуги равна мере центрального угла, который пересекает малую дугу. Обозначение для меры является м. Для обозначения малой дуги требуются конечные точки дуги. Для обозначения большой дуги требуется точка на дуге, включенная между конечными точками дуги, Q. Полукруги называются основными дугами. Мера малой дуги должна быть от 0 до 180. Мера крупной дуги должна быть не менее 180 и не более 360.Мера полукруга 180. Единица 4 Круги и конструкции 287
4 CTIVITY 4.2 rcs, центральное и вписанное ngles ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: Думайте / Соединяйте / Делитесь, Быстро пишите ПОПРОБУЙТЕ ПОПРОБУЙТЕ ДАННЫЕ С учетом круга ниже с центром C, диаметрами JR и KQ и m RCQ = 50. Используйте определения для центрального угла и перехваченной дуги вместе со свойствами треугольника, чтобы найти каждое из следующего. а. m RQ = b. m JQ = c. м CRQ = д. m JQR = e. м JKQ = ф. JK. Напишите определение для конгруэнтных дуг.J K C Q R ПОПРОБУЙТЕ ДАННЫЙ круг ниже с центром С и диаметрами JR, KQ и PL. PL JR и KQ делят PCR. P Q a. Объясните, почему PQ QR. J C 2 1 R b. m 1 + m 2 = с. m JP + m PQ = m. Объясните. д. m JQ = e. m JRQ = f. м JL = г. м JRL =. Объясните. K L 288 Springoard Математика со значением TM Geometry
5 rcs, центральные и вписанные иглы CTIVITY 4.2 ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: Используйте Манипуляторы, Интерактивную Стену Слова, Словарный органайзер, Думайте / Соединяйте / Делитесь, Создавайте представления, Быстрое написание, Опрашивая текст O 5.Используйте транспортир, чтобы найти меру центрального угла O. m O = и m = 6. Выберите любую точку на главной дуге и обозначьте точку P. Нарисуйте P и P. P и P образуют вписанный угол. а. Назовите дугу, перехваченную P. CDEMIC VOCULRY с вписанным углом b. Перечислите характеристики вписанного угла. 7. Используйте транспортир, чтобы найти меру вписанного угла P. m P =. 8. Нарисуйте другую точку R на круге. Затем нарисуйте новый вписанный угол, который имеет вершину R и перехватывает. Найдите меру нового вписанного угла.м р =. 9. Сделайте предположение о мере перехвата любого вписанного угла этого круга. Проверьте свою гипотезу, создав и измерив еще три вписанных угла, которые пересекаются. Блок 4 Круги и конструкции 289
6 CTIVITY 4.2 rcs, центральные и подписанные иглы ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: подумайте / спаритесь / поделитесь, найдите шаблон, быстрое написание 10. См. «Попробуйте это, попробуйте это», а также пункты 5 и 7 для завершения следующая таблица. Попробуйте эти Попробуйте эти Попробуйте эти пункты 5 и 7 Измерение перехваченной дуги Измерение центрального угла Измерение вписанного угла m JQ = m JCQ = m JRQ = m JQ = m JCQ = m JRQ = m JL = m JCL = m JRL = m = m O = m P = 11.В ответ на любые закономерности, которые вы видите в таблице выше, напишите гипотезу о связи между мерой вписанного угла и мерой центрального угла, который пересекает ту же дугу. Доказательство. Доказательство гипотезы, которую вы написали в пункте 11, рассматривает каждое из трех возможных положений центра круга относительно вписанного угла: (Случай 1) центр лежит на стороне вписанного угла; (Случай 2) центр находится внутри вписанного угла; и (Случай 3) центр лежит вне вписанного угла.Если мы сможем доказать, что эта гипотеза верна для каждого из этих трех случаев, мы можем сформировать одну теорему, которая охватывает все возможные положения центра круга относительно вписанного угла. Случай 1 Случай 2 Случай Springoard Математика со значением TM Geometry
7 rcs, центральные и вписанные иглы CTIVITY 4.2 ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: Представление в группе, думай / пара / делись, идентифицируй подзадачу, Quickwrite 12. На рисунке ниже показан круг с центром О.Значения a, b, c и d относятся к степени измерения каждого указанного угла. Определите каждое из следующего. O a d b C c a. мера степени центрального угла перехвата b. мера степени вписанного угла перехвата c. в соответствии с вашей гипотезой в пункте 11, b = используйте круг и свойства треугольника, чтобы выполнить каждый из следующих ключевых шагов в доказательстве для случая 1 вашей гипотезы. а. потому что O является внешним углом к OC, a =. б. О. Объясни. с. OC — это треугольник d. б =Объясните. е. Используйте ваши ответы для частей a и d, чтобы проверить свой ответ на часть c в пункте 12. Блок 4 Круги и конструкции 291
8 CTIVITY 4.2 rcs, центральное и вписанное ngles ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: воспитание предшествующего знания, представление группы, мышление / пара / Поделиться, Определить подзадачу, QuickWrite 14. На рисунке ниже показан круг с центром O, который (согласно случаю 2 для доказательства вашей гипотезы в пункте 11) находится внутри вписанного угла, P.Для углов, показанных ниже, используйте гипотезу, которую вы сделали в пункте 11, чтобы завершить следующее уравнение. м р = 1 м. 2 P a O c d e f C b 15. Диаметр CP обозначен точечным сегментом. Используйте строчные переменные в круге выше и результаты пунктов 12 и 13 (случай 1), чтобы выполнить следующее: a. с = 1 1 и d = 2 2 б. m O = + и m P = +. Объясните. с. Напишите полный и убедительный аргумент для случая 2, который объясняет утверждение, которое вы выполнили в статье «Весенняя математика по смыслу» со значением TM TM Geometry
9 rcs, центральные и вписанные иглы CTIVITY 4.2 ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: Групповая презентация, Думай / Пару / Делись, Идентифицируй подзадачу, Быстрая запись 16. На рисунке ниже показан круг с центром O, который (в соответствии с делом 3 для доказательства вашей гипотезы в пункте 11) находится в за пределами вписанного угла, P. Обратите внимание, что диаметр PC снова обозначен пунктирной линией, а переменные в нижнем регистре представляют меры степени указанных углов. b c P a d O C Используйте строчные переменные на диаграмме выше, чтобы выполнить каждое из следующих действий.а. c = 1 1 и b + c = 2 2 b. Напишите полный и убедительный аргумент для случая 3, который объясняет, почему мера вписанного угла, который перехватывает, составляет половину меры центрального угла, который перехватывает. Блок 4 Круги и конструкции 293
10 CTIVITY 4.2 rcs, центральный и вписанный ngles ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: Quickwrite, Self / Peer Revision, Групповая презентация, Think / Pair / Share 17. Мы теперь доказали гипотезу из пункта 11 для каждого из три возможных местоположения центра круга относительно вписанного угла.Поскольку эта гипотеза доказана для каждого, теперь мы можем сформулировать одну теорему, которая включает все три случая. Заполните нижеприведенную теорему о мерной метке: Вписанная теорема о мерной мере В круге мера вписанного угла равна половине. ПОПРОБУЙТЕ С Данным кругом с центром, C, ниже, и m HC = 50. Найдите каждое из следующего. H a. м HI = b. m HCR = c. m HIR = d. m IR = R C I P 18. Учитывая круг справа с PL США. а. Заполните следующие доказательства: Заявления 1.PL US Причины 1. Дано Если две параллельные линии отрезаны поперечным, чередуются внутренние углы. 3. m 1 = m 2 = замена PS 6. L U 1 2 S b. Напишите теорему, предложенную этим доказательством. 294 Springoard Matmatics with Значение TM Geometry
11 rcs, центральные и вписанные иглы CTIVITY 4.2 ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: ДУМАЙТЕ / ПАРУ / ДЕЛИТЕ, ИСПОЛЬЗУЙТЕ МАНИПУЛЯТИВЫ В начале этого занятия Крис и тренер Грин пытались определить места на футбольном поле. поле, с которого Крис мог забить гол и быть уверенным в том, что, прицелившись в центр зоны ворот, он может поместить мяч между стойками ворот.В пункте 3 вы и ваша группа высказали предположение об области поля, которая определяется всеми точками, из которых Крис наверняка поставит цель. Давайте посмотрим, как доказанная нами теорема о знакопеременной мере может либо поддержать вашу гипотезу, либо помочь вам пересмотреть ее. В круге ниже вписанный угол равен P, а m P = 30. PX делит пополам P. XP 19. Поместите 30-угольную диаграмму, которую вы использовали в начале упражнения, так, чтобы вершина S находилась в точке P, и поэтому угол биссектрисы совпадают.Сдвиньте S так, чтобы он был ближе к X, чем к P, сохраняя угловые биссектрисы друг над другом. Затем сдвиньте S от X так, чтобы S находился за пределами круга и чтобы угловые биссектрисы оставались выровненными. Подумайте о местах S, из которых Крис наверняка сделает удар в зону ворот. Используя круг как точку отсчета, из каких точек вдоль PX Крис будет уверен, что пробьет в зону ворот? Блок 4 Круги и конструкции 295
12 ЗДАНИЕ 4.2 rcs, центральный и вписанный ngles ПРЕДЛАГАЕМЫЕ СТРАТЕГИИ ОБУЧЕНИЯ: Думать / Соединять / Делить, Создавать Представления, Быстрое Написание, Групповое Представление, Использовать Манипуляторы, Самостоятельная / Одноранговая Редакция 20. В кружке ниже выберите новую точку W на главной дуге, определяемой точки и, и осторожно нарисуйте W. X 21. м W =. Объясните. 22. При осторожном использовании транспортира или по построению нарисуйте биссектрису угла W. Ваш новый биссектриса угла также проходит точку X? Используйте свойства, которые вы изучили в этой статье, чтобы поддержать ваш вывод.23. Поместите вершину S вашего 30-го угла на окружность выше, чтобы угол биссектрисы совпадал. Сдвиньте S из начальной позиции в точке W ближе и дальше от точки X. Используя круг как точку отсчета, из каких точек этого биссектрисы угла Крис будет уверен в том, что он выстрелит в зону цели? 24. Перескажите или пересмотрите свою гипотезу в пункте 3 о регионе, в котором Крис хочет оказаться, когда бьет по воротам. 296 Springoard Математика со смыслом ТМ Геометрия
13 rcs, центральные и надписанные иглы CTIVITY 4.2 ПРОВЕРЬТЕ СВОЕ ПОНИМАНИЕ Запишите свои ответы на блокноте. Показать свою работу. 1. У круга есть центр O. Пусть E IS и m TOE = 36. Найдите каждое из следующего. а. т TE б. м ST c. м сидеть м с е. м IS ф. м IOT г. м. ч. m TI 2. Найти значение x в каждом из следующих. а. 96 8x S O I T E 3. Используйте кружок ниже, чтобы выполнить следующее. а. Если С тогда. б. Напишите убедительный аргумент в поддержку вашего ответа на Часть а. Подсказка: нарисуйте C или три радиуса, которые содержат точки, и C. 4. Если многоугольник вписан в окружность, то каждая из его вершин лежит на окружности.Что из следующего правильно изображает вписанный многоугольник? а. б. С б. с. 10x 5 16x m 1 = 7x + 4 и m 2 = 5x + 10 c. д. 5. Найдите длину одной стороны квадрата, вписанного в круг с радиусом 4 см. а. 4 см б. 4 2 см c. 8 см д. 8 2 см Единица 4 Круги и конструкции 297

14 CTIVITY 4.2 rcs, центральное и начертанное углы ПРОВЕРЬТЕ СВОЕ ПОНИМАНИЕ () Напишите 6. Всегда используйте ответы, всегда, на блокноте или никогда на бумаге.Покажите каждому свою работу. 8. а. м E =. Объясните. из следующих утверждений верно. б. м F =. Объясните. а. Треугольники могут быть вписаны в круг. с. Заполните таблицу ниже. б. Трапеции могут быть вписаны в круг. м 1 м 2 х у в. Параллелограммы, которые не являются прямоугольниками 40, могут быть вписаны в круг. 90 дней Равносторонние треугольники могут быть вписаны в полукруг. е. Прямоугольные треугольники могут быть вписаны полукругом. е. Трапеции могут быть вписаны полукругом. 7. МАТЕМАТИЧЕСКОЕ ОТРАЖЕНИЕ, которое можно вписать в круг? Что должно быть правдой относительно углов любого четырехугольника. Используйте этот рисунок и предоставленную информацию, чтобы ответить на пункт 8.Дан круг с центром С и диаметром. DE касается окружности в точке. D C x y 2 1 F E a d. Как в каждом случае m 1 сравнивается с y? е. Используйте информацию в таблице, чтобы выполнить следующее. Теорема: мера угла, образованного касательной к окружности и хордой, которая содержит точку касания, равную. 298 Весенняя математика со смыслом ТМ Геометрия
.дуг и вписанных углов
Обратитесь к рисунку 3 и сопровождающему его примеру.
Рисунок 3 Круг с двумя диаметрами и (недиаметровым) поясом.
Обратите внимание, что м is3 — это ровно половина от м  , а м — это половина от м
, а м — это половина от м  203 и ∠4 — вписанные углы, а
203 и ∠4 — вписанные углы, а  и
и  — их перехваченные дуги, что приводит к следующей теореме.
— их перехваченные дуги, что приводит к следующей теореме.
Теорема 70: Мера вписанного угла в окружности равна половине меры его перехваченной дуги.
Следующие две теоремы непосредственно следуют из . Теорема 70 .
Теорема 71: Если два вписанных угла окружности пересекают одну и ту же дугу или дуги одинаковой меры, то вписанные углы имеют одинаковую меру.
Теорема 72: Если вписанный угол пересекает полукруг, то его мера равна 90 °.
Пример 1: Найдите м × C на рисунке 4.
Рисунок 4 Поиск меры вписанного угла.

Пример 2: Найдите м ∠ A и м ∠ B на рисунке 5.
Рисунок 5 Два вписанных угла с одинаковой мерой.

Пример 3: На рисунке 6 QS — диаметр. Найти м ∠ R . м R = 90 ° (теорема 72).
Рисунок 6 Вписанный угол, который пересекает полукруг.
Пример 4: На рисунке 7 окружности O , м  60 ° и м =1 = 25 °.
60 ° и м =1 = 25 °.
Рисунок 7 Круг с вписанными углами, центральными углами и соответствующими дугами.
Найдите каждое из следующего.
а. м ∠ CAD
b . м 
в. м ∠ BOC
д . м 
е .м ∠ ACB
ф. м ∠ ABC
,Руководство по оценке спортивных карточек, полезные советы, информация, детали оценки
Руководство по оценке спортивных карточекИтак, вы хотите узнать больше о оценочных карточках, но не знаете, с чего начать? Наш гид здесь, чтобы помочь.
Оценочные компании
Beckett Grading Services (BGS), PSA и SGC являются основными компаниями, используемыми для оценки карточек. В общем, BGS предпочтительнее для современных карт, в то время как PSA является фаворитом для винтажных карт.
Шкала оценок
Беккет оценивает свои карты по шкале 1-10 с подклассами (.5s). Оценки PSA по плоской шкале 1–10 и оценки SGC по шкале из 100, которые затем используются для присвоения карте оценки 1–10.
Карты классифицируются на основе следующих факторов: Центрирование, Углы, Края и Поверхность. Они дают каждому атрибуту оценку 1-10, а затем объединяют их, чтобы получить окончательную оценку 1-10. Все, что выше 9, стоит балансовой стоимости или выше, так как BGS 9 (известный как «Монетный двор 9») является условием, ожидаемым от карты из колоды. 9,5 балла — Gem-Mint, карта, которая почти безупречна.Это условие, которого хочет большинство коллекционеров. Тогда есть «PRISTINE 10», который является святым Граалем картона. Нетронутые 10 редко выдаются. Pristine 10 может превратить карту за 10 долларов в карту за 1000 долларов.
Введение условий в контекст
Бренд
Это, вероятно, больше всего смущает людей. Ожидание высокой оценки для определенных марок карт не только нереально, но и практически невозможно. Хорошим примером этого является карта Джека Джетера 1993 года SP SP .Запас фольги карты привел к безумному количеству недостатков «из колоды». В результате, старшие классы продаются за тысячи, а средние — намного меньше.
С другой стороны, есть случайные наборы, в которых большинство карт выходит из колоды почти в идеальном состоянии. В этом случае BGS 9.5 едва ли что-то изменяет. Если вы хотите понять, как подойти к этому, подумайте об открытии колоды и представьте, как карты будут удерживаться с течением времени (процесс сматывания, плавный удар в угол или края, влажность и т. Д.)…).
Год
Год довольно прост, поскольку у старых карт оценка ниже, чем у новых. Это не означает, что старые карты стоят меньше, это просто означает, что с точки зрения условий ожидается меньше. Чем старше карты, тем хуже состояние. Цель состоит в том, чтобы найти карты, о которых хорошо заботятся и которые находятся в лучшем состоянии, чем норма.
Что делать, если вы не можете видеть карту лично
Самый сложный и рискованный способ купить карту — это когда вы не видите ее лично.Если скан карты, которую вы хотите купить, кажется, что-то скрывает или не дает точного или видимого изображения, пришло время закрыть глаза и напечатать. Просто задавайте вопросы продавцу, чтобы выяснить, в чем вы не уверены. Несколько примеров вопросов приведены ниже.
- Все 4 угла острые?
- я заметил _____. Это на карте или на корпусе карты?
- Есть ли заметные недостатки?
Теперь вы готовы к практике «Око коллекционера»
Это очень просто.Благодаря Beckett Grading Services мы знаем пять основных атрибутов, используемых для оценки карты.
- Центрирование: Центрирование — это, в основном, ширина границы. В идеале размеры границы должны быть одинаковыми слева, справа, сверху и снизу. Иногда оценить центрирование не так просто, как поиск равных границ. Суть в том, что карта должна чувствовать себя сбалансированной. Если карта выглядит перекошенной, это означает, что центрирование отключено.
- Углы: Это, пожалуй, самый важный и наиболее тщательно изученный атрибут оценки.Карта с четырьмя острыми углами может облегчить другие проблемы, особенно на старых картах. Сначала изучите все четыре угла, глядя на переднюю часть карты, затем посмотрите на заднюю часть карты. Это лучший способ перепроверить. Если угол показывает недостатки с обеих сторон, это не ваши глаза, играющие с вами шутки. Иногда чернила, фольга или другие факторы могут создать иллюзию слабого угла, поэтому всегда проверяйте обратную сторону. Если угол или два — это бельмо на глазу, вы, вероятно, смотрите на карту с оценкой ниже 85. Незначительные угловые дефекты, такие как едва видимый белый, могут быть различием между BGS 9 и BGS 9.5, но также могут не привести к изменениям.
- Края: Также важны четыре края карты. Некоторые бренды печально известны своими краями, особенно карты с темными или черными рамками. В то же время от них ожидается меньше, поэтому снизьте свои ожидания. Грейдеры тоже смотрят на это сзади. Края должны быть острыми, а цвет должен быть постоянным.Несовершенные края имеют вмятины, вмятины или тонкие изменения цвета. Как и в углах, едва видимый белый не конец света.
- Поверхность: Поверхность — это состояние картона в целом. С глянцевыми картами, такими как Bowman Chrome, царапины на поверхности могут быть проблемой, а также выцветшие автографы. Кроме того, карты, сделанные с использованием фольги, склонны к отрыву небольших кусочков фольги, оставляя белые пятна на карте. У старых карт основная проблема — это складки и повреждение от влаги.Многие карты 1980-х годов страдают от размазывания чернил и следов от штампов, которые возникают, когда карта проходит через печатный станок. Во многих случаях на первых порах трудно заметить складку, так как изображение на карте может очень хорошо скрыть ее.
- Автографы: Оценка автографа не имеет ничего общего с оценкой самой карты. Если чернила не смазываются, а автограф не выцветает, обычно это будет 10. Все оцененные автографы должны быть «без упаковки» (не подписанными вручную или лично). Очень легко «оценить» автограф.
Хотя технически процесс оценки может быть научным, изучение того, как смотреть на карту, имеет больше общего с вашей реакцией на интуицию. Если карта выглядит великолепно, она выглядит великолепно. Существует тонкая грань между высокими ожиданиями по поводу состояния и параноидальным отношением к совершенству.
Хотите купить оцененные карты?
Обязательно ознакомьтесь с нашими дополнительными руководствами для получения дополнительной информации о классификации.

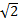 см и 3 см.
см и 3 см.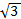 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.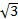 см и 7 см.
см и 7 см.
Leave A Comment