ЭДС. Закон Ома для полной цепи

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная

против движения заряда (т.е. против направления тока).

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

\vec{F_E}

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят,

неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда

по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

(1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

R

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:

(2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

(4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

(5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока

. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .

Если сила тока в цепи равна , то

Некоторое количество теплоты выделяется также на источнике тока:

Полное количество теплоты, которое выделяется в цепи, равно:

КПД электрической цепи — это отношение полезного тепла к полному:

КПД цепи равен единице лишь в том случае, если источник тока идеальный .

Закон Ома для неоднородного участка

Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).

R + r

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло: .

Подставляем сюда выражения для , и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает

положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

b

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Источники тока и напряжения — Студопедия

Под источником понимают элемент, питающий цепь электромагнитной энергией. Эта энергия потребляется пассивными элементами цепи — запасается в индуктивностях и емкостях и расходуется в активном сопротивлении. Примерами реальных источников электромагнитной энергии могут служить генераторы постоянных, синусоидальных и импульсных сигналов разнообразной формы, сигналы, получаемые от различных датчиков, антенн радиоприемных устройств, источники питания, сигналы, поступающие с выходов электронных устройств и т.д.

Для анализа цепей удобно вводить идеализированные источники двух видов: источник напряжения и источник тока, которые учитывают главные свойства реальных источников. При соответствующем дополнении идеализированных источников пассивными элементами можно передать все свойства реальных источников по отношению к их внешним выводам.

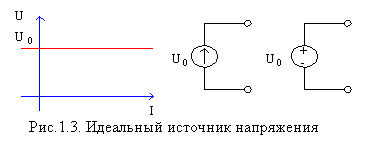
Источник напряжения. Подисточником напряжения понимают такой элемент с двумя выводами (полюсами), напряжение между которыми задано в виде некоторой функции времени независимо от тока, отдаваемого во внешнюю цепь. Зависимость напряжения от тока идеального источника напряжения показана на рис. 1.3. Такой идеализированный источник способен отдавать неограниченную мощность. Наиболее часто применяемые условные графические изображения источника напряжения показаны на том же рисунке, где принятая положительная полярность напряжения источника указывается либо стрелкой внутри кружочка, либо знаками “+”, “-”.


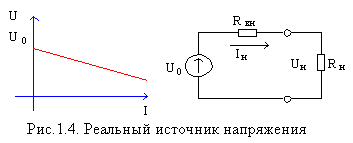
Реальные источники сигнала имеют внутренние сопротивления. К источнику напряжения внутреннее сопротивление подключается последовательно. На рис. 1.4 показаны вольтамперная характеристика и схема реального источника напряжения. Для реального источника выходное напряжение будет равно

Uн = U0 – URвн = U0 – Iн Rвн.

Из формулы видно, что выходное напряжение реального источника тока зависит от тока нагрузки Iн. Чем больше ток нагрузки, тем больше падает напряжение на внутреннем сопротивлении источника, и меньшая часть напряжения U0 поступает на нагрузку (на выход). С другой стороны, чем больше внутреннее сопротивление Rвн при неизменном токе нагрузки, тем больше падает на нем напряжения, что ведет к уменьшению напряжения на выходе источника. Применительно к электронным схемам внутреннее сопротивление источника часто называют выходным сопротивлением.


В случае идеального источника напряжения, его внутреннее сопротивление равно 0 и напряжение на нагрузке не зависит от тока нагрузки. При этом ток нагрузки может возрастать до бесконечности, если сопротивление нагрузки будет стремиться к 0. В действительности невозможно построить идеальный источник напряжения во всем диапазоне изменения выходного тока. Однако, во многих случаях, для ограниченного диапазона изменения выходного тока некоторые источники можно рассматривать как идеальные.

Например, источник питания в диапазоне рабочих токов имеет очень малое внутреннее сопротивление, которым можно пренебречь, по сравнению с сопротивлением нагрузки. Или другой пример, выходное сопротивление операционного усилителя, охваченного отрицательной обратной связью, может достигать нескольких сотых долей Ома. Таким внутренним сопротивлением можно пренебречь и рассматривать выход операционного усилителя как идеальный источник напряжения в диапазоне допустимых выходных токов.

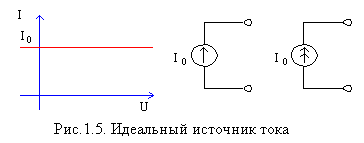
Источник тока. Под идеальным источником тока понимают такой элемент цепи, через выводы которого протекает ток с заданным законом изменения во времени независимо от напряжения между выводами. Вольтамперная характеристика и условные графические изображения идеального источника тока показана на рис. 1.5. Независимость тока от напряжения означает, что внутренняя проводимость источника, куда может ответвляться ток, равна 0, а внутреннее сопротивление равно бесконечности. Вольтамперная характеристика и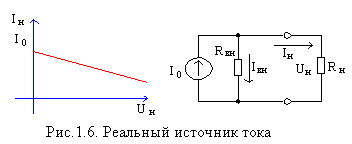

схема реального источника тока показана на рис. 6. При увеличении напряжения на нагрузке за счет увеличения сопротивления нагрузки увеличивается внутренний ток источника тока. При этом меньшая часть тока I0 поступает в нагрузку. Выходной ток Iн будет равен

Iн = I0 – Iвн = I0 – Uн / Rвн.

Из формулы видно, что чем больше внутреннее сопротивление источника тока, тем меньше внутренний ток Iвн и большая часть тока I0 отдается в нагрузку. В пределе при Rвн = ∞ весь ток I0 отдается в нагрузку, и ток нагрузки не будет зависеть от напряжения на нагрузке. В этом случае имеем дело с идеальным источником тока. Итак, в идеальном источнике тока внутреннее сопротивление равно бесконечности. В идеальном источнике тока при бесконечной величине сопротивления нагрузки (обрыв цепи нагрузки) на его зажимах будет напряжение бесконечной величины.

Это конечно идеализация – нельзя построить источник тока, у которого величина внутреннего сопротивления рана бесконечности. Однако на практике используются источники тока, построенные на транзисторах, с внутренним сопротивлением, достигающим величин многих мегом и более, работающие в ограниченном диапазоне выходных напряжений. Такие источники тока широко используются в схемах дифференциальных и операционных усилителей, при построении цифро-аналоговых преобразователей, при передаче сигналов по токовой петле и др.

Реальные источники напряжения и тока эквивалентны. Это означает, что относительно своих зажимов схемы ведут себя одинаковым образом, т.е. при анализе схемы один и тот же источник можно рассматривать как реальный источник напряжения или реальный источник тока. Условия эквивалентности можно получить из выражения для напряжения реального источника напряжения

Uн = U0 – Iн Rвн.

Разделим правую и левую части уравнения на Rвн, получим

Uн /Rвн = U0 /Rвн – Iн .

Введем обозначения U0 /Rвн = I0 = const; U0 /Rвн = Iвн и запишем уравнение в следующем виде

Iвн = I0 — Iн или I0 = Iвн + Iн.

Причем на сопротивлениях Rвн и Rн падает одно и то же напряжение Uн, т.е. они соединены параллельно

I0 = Uн /Rвн + Uн /Rн .

Отсюда приходим к схеме реального источника тока, показанного на рис.1.6.

Раз схемы реальных источников напряжения и тока эквивалентны, то возникает вопрос, когда использовать при анализе схемы тот или иной источник? Ответ простой. Используйте тот тип источника, при котором проще анализировать работу схемы. На практике часто поступают следующим образом. Если внутреннее сопротивление источника намного меньше сопротивления нагрузки, то такой источник целесообразно рассматривать как источник напряжения. И в первом приближении величиной внутреннего сопротивления можно пренебречь. Если внутреннее сопротивление намного больше сопротивления нагрузки, то такой источник рассматривают как источник тока. И при первоначальном анализе считают его идеальным. При более детальном анализе схемы учитывают не идеальность источника тока.

Закон Ома для полной цепи

Если закон Ома для участка цепи знают почти все, то  закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!

Идеальный источник ЭДС

Имеем источник ЭДС

источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС – это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Внутреннее сопротивление источника ЭДС

Дело все в том, что в аккумуляторе “спрятано” сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой “r “.

Выглядит все это в аккумуляторе примерно вот так:

Цепляем лампочку

Итак, что у нас получается в чистом виде?

Лампочка – это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью  делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.

На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .

Теперь вспоминаем статью делитель тока. Сила тока, протекающая  через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Закон Ома для полной цепи

Далее

Закон Ома для полной цепи

Закон Ома для полной цепи

формула закон Ома для полной цепи

Закон Ома для полной цепи

Итак, последнее выражение носит название “закон Ома для полной цепи”

закон Ома для полной цепи формула

где

Е – ЭДС источника питания, В

R – сопротивление всех внешних элементов в цепи, Ом

I – сила ток в цепи, А

r – внутреннее сопротивление источника питания, Ом

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем  галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Как найти внутреннее сопротивление источника ЭДС

Давайте снова вернемся к этой фотографии

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

как найти внутреннее сопротивление

Закон Ома для полной цепи

Вывод

Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.

Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.

Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.

Определение напряжений на источниках тока.

⇐ ПредыдущаяСтр 5 из 17Следующая ⇒

Общая стандартная форма записи системы уравнений по МКТ для резистивных цепей с источниками постоянного действия

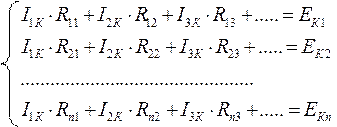Записывают уравнения и в матричном виде. Например,

.

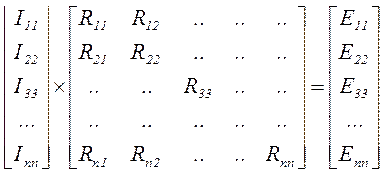Здесь: Inn (InK ) – соответствующие контурные токи,

R11 –собственное контурное сопротивление первого контура, равное сумме сопротивлений элементов входящих в 1 контур, R22 –контурное сопротивление второго и т.д.;

R12 – взаимное сопротивление между первым и вторым контурами (учитывается с +, если контурные токи совпадают и с “- ”, если не совпадают) и аналогично;

E11 – контурная ЭДС 1 контура, которая содержит алгебраическую сумму ЭДС входящих в 1-ый контур (c + если совпадает с контурным током) и включает влияние источников тока на контур (после переноса из левой части). Далее аналогично.

Причем обычно R12 = R21 а если есть управляемые источники, то R12 и R21 могут быть не равны.

6. Применение МКТ

Целесообразно применять для сложных схем с несколькими однотипными источниками, у которых частота одна и та же. Если есть L— и C-элементы и частоты источников одинаковые, то применяется в комплексной форме. Если частоты действия разные, то можно применять совместно с методом наложения для расчета частичных токов.

1.8. Метод узловых напряжений (МУН)

В качестве основных неизвестных используются так называемые узловые напряжения – это напряжения между узлом схемы или цепи и некоторым опорным или базисным узлом, который выбирается один для всей цепи или схемы. В качестве дополнительных неизвестных используются токи в некоторых «вырожденных» ветвях, которые содержат только идеальные источники напряжения (или ЭДС) без других элементов. Система уравнений по МУН составляется на основе первого закона Кирхгофа. Второй закон и закон Ома используются как вспомогательные.

2. Определение количества уравнений и выбор базисного узла

Количество уравнений определяется по формуле:

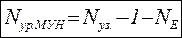, где NE – число «вырожденных» ветвей которые содержат только идеальные источники напряжения (или ЭДС) без других элементов.

Базисный узел выбирается из узлов, прилегающих к ветви «вырожденной» (где есть одиночный идеальный источник напряжения) и отмечается знаком заземления или корпуса.

I1 E1

Из этих двух узлов обычно берут тот узел, где больше подходит ветвей.

Берут там, где удобнее при взгляде на схему.

Начинается метод с определения числа «вырожденных» ветвей и базисного узла, потом составляется и решается система уравнений.

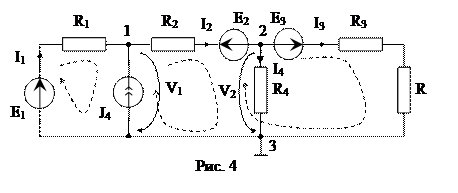Пример расчета цепи с помощью метода узловых напряжений по схеме

1. При расчёте цепи по методу узловых напряжений определяем число узлов схемы. Один из этих узлов принимаем за базисный. Остальные узлы называются независимыми. Базисный узел – это узел от которого ведется отсчет. Его выбирают в первую очередь там, где есть ветвь, содержащая только одиночный идеальный источник ЭДС, и сходится много ветвей или это тот узел, который удобнее для наглядности (в нашей схеме это узел 3 ). Базисный узел часто заземляют, при этом его потенциал (напряжение) равен нулю V3=0. Из свойств идеального источника напряжения, следует отметить, что если в схеме имеются ветви, состоящие из одиночных идеальных источников напряжения, то их сопротивление равно нулю, а проводимость – бесконечности. В нашем случае таких ветвей нет NE=0. Для ветвей с источниками тока все наоборот.

2. Определяем число независимых уравнений, составляемых методом узловых напряжений NМУН=NУЗ-1-NЕ=2.

Составляем систему алгебраических уравнений методом узловых напряжений, согласно первому закону Кирхгофа.

I1+J4-I2=0

I2-I3-I4=0

4. V1,V2 – узловые напряжения узлов 1 и 2 соответственно. Выражаем токи ветвей через узловые напряжения на основе 2 закона Кирхгофа для вспомогательных контуров, которые обязательно проходят через базисный узел, и закона Ома:

I1∙R1+V1 =E1, I2∙R2+V2-V1= -E2, I3∙(R3+R)-V2 =E3 (V=U).

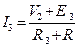
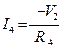
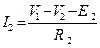
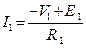
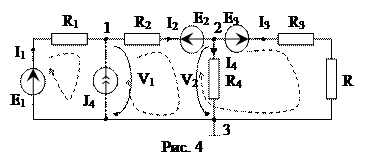
После подстановки формул токов данная система уравнений переводится в систему узловых уравнений, записанную в канонической форме. Число уравнений должно быть равно числу неизвестных узловых напряжений.

Для 1 уравнения получим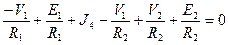

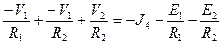. Затем можно поменять знаки и получить уравнение 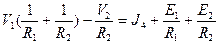. Аналогично для 2 уравнения получим

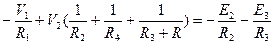. Эти уравнения приводят к стандартному каноническому виду:

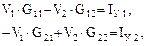
где 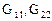– это собственные проводимости соответственно узлов 1 и 2.

.

.

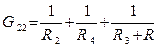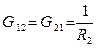– взаимные проводимости между узлами 1 и 2.

IУ1, IУ2 – собственные или задающие узловые токи, соответственно, независимых узлов 1 и 2. В общем виде их можно представить в следующем виде:

,

,

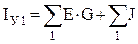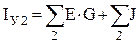где 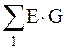– алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 1, на их проводимости, 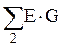– алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу 2, на их проводимости; при этом со знаком «+» берутся те ЭДС, которые действуют в направлении узла, и со знаком «–» – в направлении от узла; 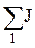– алгебраическая сумма токов источников тока, присоединенных к узлу 1, 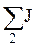– алгебраическая сумма токов источников тока, присоединенных к узлу 2; при этом со знаком «+» берутся те токи, которые направлены к узлу, а со знаком «–» в направлении от узла. Для нашего случая токи IУ1, IУ2 имеют следующий вид:

.

.

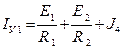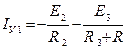Узловое напряжение – это напряжение между независимым и базисным узлами и направлено оно к базисному узлу. V1,V2 – узловые напряжения узлов 1 и 2 соответственно. Знак «+» перед узловым напряжением берётся, если это собственное узловое напряжение, в противном случае берётся знак «–».

Данную систему решаем методом Крамера. Составляем определитель второго порядка, в первую и вторую строки которого ставим значения проводимостей стоящих при напряжениях, соответственно в первом и во втором уравнениях нашей системы.

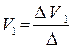Затем составляем определитель 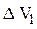, для этого в определителе 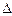в первом столбе значения проводимостей заменяем значениями токов, стоящих в правой части нашей системе.

После чего вычисляем напряжение 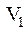по следующей формуле:

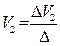Аналогично находим напряжение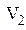

6. Находим токи ветвей через узловые напряжения:

 

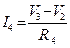
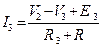
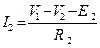
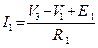
Общая форма записи системы уравнений по МУН с узловыми напряжениями (потенциалами) VK, собственными проводимостями узлов GKK, взаимными проводимостями между узлами GKM и узловыми токами.



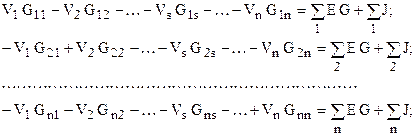
Формула коэффициента полезного действия в источниках электротока

Для работы электронных и электрических устройств необходимо подключать их к источникам питания. Источники питания могут быть как стационарные, так и автономные. В качестве питающих устройств используются гальванические элементы или преобразователи электроэнергии. И те, и другие являются источниками тока или напряжения.

Источники электрического тока и напряжения

Источники электрического тока и напряжения

Что такое источник тока

Это устройство или элемент, в общем понимании – двухполюсник, у которого проходящий через него ток не зависит от величины напряжения на полюсах. Основные характеристики источника тока (ИТ):

  • величина;
  • внутренняя проводимость (импеданс).

Внутреннее сопротивление такого двухполюсника очень мало. У идеального источника (ИИТ) оно приближается к нулю.

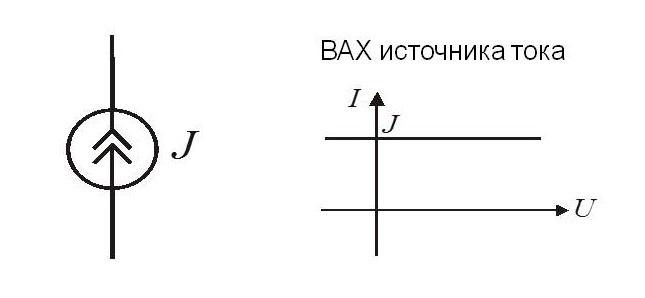
Графическое обозначение и вольт-амперная характеристика (ВАХ) ИТ

Графическое обозначение и вольт-амперная характеристика (ВАХ) ИТ

Генераторы движения электронов могут быть как независимыми, так и зависимыми.

Первые представляют собой идеальный двухполюсник, с двумя зажимами. У них ток, движущийся от одного зажима к другому, не зависит от формы и величины разности потенциалов на зажимах. Его изменения происходят по своим законам.

Второй тип ИТ – идеальный двухполюсник, с двумя зажимами, у которого движение зарядов от одного зажима к другому зависит от формы и величины напряжения на этих зажимах.

Существует управляемый зависимый ИТ. Он представляет собой идеальный двухполюсник, имеющий 2 зажима на входе и 2 зажима на выходе. Его особенность в том, что выходное значение тока на выходе зависит от его величины на входе. В таком ИТ происходит усиление мощности. Изменяя нулевое значение мощности на его входе, управляют величину мощности на выходных зажимах.

Информация. Управление производителем энергии может осуществляться напряжением (ИТУН) или током (ИТУТ). Одни находят применение для полевых триодов и электровакуумных ламп, вторые – для транзисторов биполярного типа.

В реальности генераторы тока имеют определённые ограничения по напряжению. Они далеки от идеальных ИТ и создают движение электричества в таком интервале напряжений, где их верхняя граница зависит от Uпит ИТ. Следовательно, у реального источника тока есть существенные пределы по нагрузке.

КПД электрической цепи

Выполняя продвижения зарядов через замкнутую цепь, двухполюсник проделывает некоторую работу. Когда генератор двигает заряды по внешнему контуру цепи, то это полезная работа. Когда ИТ продвигает электрические носители по всей цепи, говорят о полной работе.

Внимание! В этой цепочке перемещения зарядов особое значение имеет КПД (коэффициент полезного действия) источника. Он равен соотношению сопротивлений внешней цепи и полному сопротивлению цепи.

Обращая внимание на КПД электроцепи, нужно отметить, что он напрямую зависит от физических величин, определяющих скорость передачи или трансформации электрической энергии. Одной из таких величин является мощность Р (Вт).

Формулы мощности:

P = U * I = U2/R = I2 * R,

где:

  • U – напряжение на нагрузке, В;
  • I – ток, А;
  • R – сопротивление нагрузки, Ом.

Для разных цепей значения напряжения и сила тока различаются, следовательно, производимая ими работа будет разной. Когда предстоит оценить скорость передачи и преобразования электрического тока, то обращают внимание на Р. Она соответствует работе, проделанной за единицу времени:

P = A/∆t,

где:

  • P – мощность, Вт;
  • A – работа, Дж;
  • ∆t – временной интервал, с.

Исходя из этой формулы, чтобы найти работу А, нужно умножить Р на время:

A=P∙∆t

Чтобы найти КПД (η) электроцепи, нужно найти отношение полезно потраченной энергии к количеству всей энергии, поданной в цепь. Формула для расчёта:

η = A/Q *100%,

где:

  • А – проделанная потребителем работа, Дж;
  • Q – количество энергии, взятой от источника, Дж.

Важно! КПД не может быть выше единицы. В основном он или равен ей, или меньше её. Этому причина – Закон сохранения энергии. Согласно ему, полезная совершённая работа никогда не превысит затраты энергии, необходимые для её выполнения.

Наглядно это можно объяснить на примере электрической цепи, в которую включен проводник, имеющий определённое сопротивление. При прохождении электричества через цепь часть энергии будет рассеиваться на проводнике, превращаясь в тепло и нагревая его. Потери мощности будут зависеть от величины этого сопротивления.

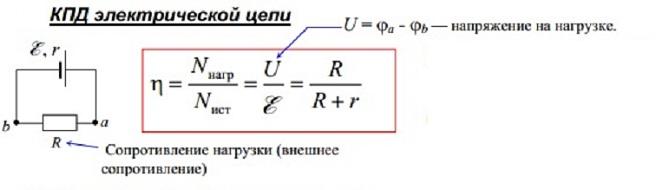
КПД электрической цепи

КПД электрической цепи

Что такое КПД ИТ

Когда речь идёт о кпд источника тока, также рассматривают полезную и полную работу, совершаемую двухполюсником. Перемещая электроны во внешней цепи, он выполняет полезную работу, двигая их по всей цепи, включая и свою внутреннюю, он производит полную работу.

В виде формул это выглядит так:

  • А полезн. = q*U = I*U*t = I2*R*t;
  • А полн. = q*ε = I* ε*t = I2*(R+r)*t.

где:

  • q – количество энергии, Дж;
  • U – напряжение, В;
  • ε – ЭДС, В;
  • I – ток, А;
  • R – сопротивление нагрузки, Ом;
  • r – импеданс источника, Ом;
  • t – время, за которое совершается работа, с.

С учётом этого можно выразить мощности двухполюсника:

  • Р полезн. = А полезн./t = I*U = I2*R;
  • P полн. = А полн./t = I*ε = I2*(R+r).

Формула кпд источников тока имеет вид:

η = Р полезн./P полн.= U/ε = R/ R+r.

Исследование мощности и КПД генератора тока

Максимальная полезная Pmax и максимальный КПДmax – несовместимые понятия. Нельзя добиться максимального КПД источника при максимальной мощности. Это обусловлено тем, что Р, отдаваемая двухполюсником, достигнет своего максимального значения только при условии согласования сопротивления нагрузки и внутреннего импеданса ИТ:

R = r.

В этом случае КПД источника будет:

η = R/ R+r = r/ r+r = 1/2, что составляет всего 50%.

Для согласования двухполюсника и нагрузки применяют электронные схемы или согласующие блоки, для того чтобы добиться максимального отбора мощности от источника.

Мощность ИТ и внутреннее сопротивление

Можно собрать последовательную схему, в которую войдут гальванический двухполюсник и сопротивление нагрузки. Двухполюсник, имеющий внутренний импеданс r и ЭДС – Е, отдаёт на внешнюю нагрузку R ток I. Задача цепи – питание электричеством активной нагрузки, выполняющей полезную работу. В качестве нагрузки может быть применена лампочка или обогреватель.

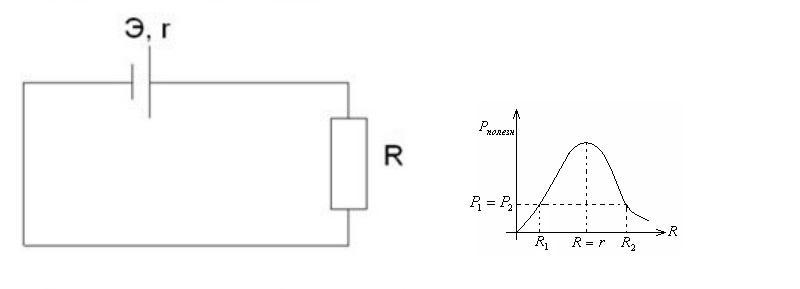
Простая схема для исследования зависимости Рполезн. от R

Простая схема для исследования зависимости Рполезн. от R

Рассматривая эту цепь, можно определиться с зависимостью полезной мощности от величины сопротивления. Для начала находят R-эквивалентное всей цепи.

Оно выглядит так:

Rэкв. = R + r.

Движение электричества в цепи находится по формуле:

I = E/(R + r).

В таком случае Р ЭДС на выходе составит Рвых. = E*I = E²/(R + r).

Далее можно найти Р, рассеиваемую при нагреве генератора из-за внутреннего сопротивления:

Pr = I² * r = E² * r/(R + r)².

На следующем этапе определяются с мощностью, отбираемой нагрузкой:

PR = I² * R = E² * R/(R + r)².

Общая Р на выходе двухполюсника будет равна сумме:

Рвых. = Рr + PR.

Это значит, что потери энергии изначально происходят при рассеивании на импедансе (внутреннем сопротивлении) двухполюсника.

Далее, чтобы увидеть, при какой величине нагрузки достигается максимальная величина полезной мощности Рполезн., строят график.

При его рассмотрении видно, что самое большое значение мощности – в точке, где R и r сравнялись. Это точка согласования сопротивлений генератора и нагрузки.

Внимание! Когда R > r, то ток, возникающий в цепи, мал для передачи энергии нагрузке с достаточной скоростью. При R < r значительная доля энергии превращается в тепло в самом двухполюснике.

Наиболее наглядный пример согласования можно увидеть в радиотехнике при согласовании выходного сопротивления УНЧ (усилителя низкой частоты) и звуковых динамиков. На выходе усилителя сопротивление находится в пределах от 4 до 8 Ом, в то время как Rвх динамика составляет 8 Ом. Устройство позволяет подключить к своему выходному каскаду, как один динамик на 8 Ом, так и параллельно два по 4 Ома. И в том, и в другом случае УНЧ будет работать в заданном режиме, без потерь мощности.

В процессе разработок тех или иных реальных источников тока пользуются представлением его в виде эквивалентного блока. В его состав входят два компонента, с которыми ведётся работа: это идеальный источник и его импеданс.

Видео

Расчет внутреннего сопротивления источника тока

Есть несколько вариантов замера внутреннего сопротивления.

  1. Зная сопротивление нагрузки и просадку напряжения при ней.
  2. Замерять ток и напряжение при двух разных сопротивлениях.

В двух примерах расчёта ниже внутреннее сопротивление будет определятся у двух последовательно соединённых батареек по 1.5 вольта

Теория о внутреннем сопротивлении.

Первый вариант:

  1. Измерьте сопротивление нагрузки и ЭДС.
  2. Измерьте напряжение при подключенной нагрузке.
  3. Рассчитаем падение напряжения на источнике тока. U2=E-U1  U2=3.145-3.015=0.13 Вольта проседает на внутреннем сопротивлении.
  4. Теперь ЭДС разделим на падение напряжения. разница напряжений = E/U2 разница напряжений = 3.145/0.13 =24.19.
  5. Зная что ЭДС распределяется по участкам цепи в зависимости от сопротивлений на них делаем вывод, что r в 24.19 раза меньше чем R нагрузки. r = R/разница напряжений r=24.3/24.19 ≈ 1 Om Внутреннее сопротивление.

Второй вариант:

Для расчета нам понадобится сделать два замера тока и напряжения при разных нагрузках.

И рассчитать внутреннее сопротивление по формуле:

r = U1-U2 / I1-I2

  • r — Внутреннее сопротивление
  • U — Напряжение
  • I — ток

Вот пример:

Замеряем ток и напряжение при разном сопротивлении.

Закон Ома кратко и понятно для чайников

Закон Ома является одним из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Его важно знать и понимать. Понятное объяснение вы найдёте в статье.

Закон Ома официально и абсолютно оправдано можно отнести к ряду основополагающих в физике по нескольким признакам. Данный закон объясняют в школе на базовом уровне, а после, более углубленно, в учреждениях, специализирующихся на изучении технических аспектов технологий.

Закон Ома – определение

Впервые данный закон был официально зафиксирован и сформулирован в восемнадцатом веке, благодаря сделанному сейчас уже широко известным всем Георгом Симоном Омом открытию. Благодаря данному закону получило грамотное и исчерпывающее объяснение наличие количественной связи между тремя фигурирующими в определении параметрами. Зависимость рассматривается как пропорциональная. Когда данное явление только было выявлено, закон несколько раз формулировали. В итоге сейчас всем известно данное определение: «величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению».

Для лучшего понимания разделим определение на две части и разберём отдельно более понятным языком смысл каждой.

  1. Первая часть определения указывает на то, что если на определенной отрезке цепи происходит количественный скачок напряжения, то величина тока также увеличивается на данном участке. Важно упомянуть, что становится больше и величина тока на заданном участке цепи.
  2. Концовка определения расшифровывается также просто. Выше напряжение – меньше сила тока.

Закон Ома – формула

Иллюстрация связи сопротивленияИллюстрация связи сопротивленияИллюстрация связи сопротивления

Рисунок наглядно демонстрирует связь фигурирующих в понятии «участников». Таким образом, вытекают простые выводы:

1. При данных условиях: на конкретном отрезке увеличивается напряжение, но при том сопротивление остаётся прежним, ток резко возрастает;

2. Иная ситуация: наоборот, изменяется сопротивление, а точнее возрастает, при том что уровень напряжения не меняется вовсе, тока становится меньше.

В итоге в законе Ома участвуют всего три величины.

Готовая формула выглядит так:

I = U/R

Фигурируют и другие две переменные, их также можно вычислить, при условии, что другие два значения известны. Видоизменив формулу, получим:

Формула сопротивленияR = U/I
Формула напряженияU = I × R
Формула силы токаI = U/R

Важно!

Шпаргалка для закона ОмаШпаргалка для закона ОмаШпаргалка для закона Ома

На начальном этапе, когда составлять формулы ещё сложно, можно воспользоваться небольшой шпаргалкой.

На треугольнике просто нужно закрыть то значение, которое необходимо найти.

Закон Ома для участка цепи

Итоговая формула не видоизменяется вовсе. Обычно сопротивление в данном законе является явной характеристикой проводника, потому что это значение не постоянная величина: в зависимости от материала и других параметров число может увеличиваться или уменьшаться. Закон применим как при расчёте с использованием металлов, так и растворов электролитов, однако существует важный нюанс: в цепи не должно быть реального источника тока, или же источник должен быть идеальным, то есть он не должен создавать дополнительное сопротивление.

Шпаргалка для использования закона ОмаШпаргалка для использования закона ОмаШпаргалка для использования закона Ома

С ЭДС

Обобщённый закон Ома формулируется так:

I = (Uab+E)/R

Также формулу можно выразить через проводимость:

I = (Uab + E) × G, как понятно, G – проводимость участка электрической цепи. Эти формулы можно использовать, если сохраняются условия, зафиксированные на рисунке.

Участок цепи с ЭДСУчасток цепи с ЭДСУчасток цепи с ЭДС

Без ЭДС

Для начала определим, что положительное направление – это то, что слева направо. Только в этом случае напряжение на участке будет равняться разности потенциалов.

Разность потенциаловРазность потенциаловРазность потенциалов

Если сохраняется условие и потенциал конечный меньше потенциала начального, то напряжение будет больше нуля. Значит, как и полагается, направление линий напряженности в проводнике будет от начала к концу, следовательно, направление тока будет идентичным. Именно такое направление тока принято считать положительным, I > O. Данный вариант самый простой для расчётов. Формула действительна с любыми числами.

Закон Ома для полной (замкнутой) цепи

При данной вариации закона выявляется значение тока при реальных условиях, то есть в настоящей полной цепи. Важно учитывать то, что получившееся в результате расчетов число зависит от нескольких параметров, а не только от сопротивления нагрузки.

Сопротивление нагрузки – внешнее сопротивление, а сопротивление самого источника тока – внутреннее сопротивление (обозначается маленькой r).

Вывод формулы закона Ома для замкнутой цепи

Если к цепи подключено напряжение и в цепи замечено напряжение (ток), то, чтобы поддержать его во внешней цепи, необходимо создать условия, при которых между её концами возникнет разность потенциалов. Это число будет равняться I × R. Однако важно помнить о том, что вышеупомянутый ток будет и во внутренней цепи и его также необходимо поддерживать, поэтому нужно создать разность потенциалов между концами сопротивления r. Эта разность равняется I × r.

Чтобы поддержать ток в цепи, электродвижущая сила (ЭДС) аккумулятора должна иметь величину:

E = I × r + I × R

Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:

E = I(r + R)

или

I = E / (r + R)

Две последние формулы выражают закона Ома для полной цепи.

Закон Ома в дифференциальной форме

Дифференциальная форма закона ОмаДифференциальная форма закона ОмаДифференциальная форма закона Ома

Закон можно представить таким образом, чтобы он не был привязан к размерам проводника. Для этого выделим участок проводника Δl, на концах которой расположены ф1 и ф2. Среднюю площадь проводника обозначают ΔS , а плотность тока j, при таких условиях сила тока будет равняться:

I = jΔS = (ф1- ф2) / R = -(((ф1 — ф2)ΔS) / pΔl , отсюда следует, что j = -y × (Δф/Δl)

При условии, что Δl будет равен 0, то, взяв предел отношения:

lim (-(Δф/Δl)) = -(dф/dl) = Е,

окончательное выражение будет выглядеть так:

j = yE

Данное выражение закона находит силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.

Закон Ома в интегральной форме

В данной интерпретации закона не содержится в условиях ЭДС, то есть формула выглядит так:

I = U/R

Чтобы найти значение для однородного линейного проводника, выразим R через p и получим:

R = p (l/S), где за р принимаем удельное объёмное сопротивление.

Линией тока принято называть кривую, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. При таких условиях вектор плотности находится из отношения J = jt, где t – это единичный вектор касательной к линии тока.

Для лучшего понимания предположим, что удельное сопротивление, а также напряженность поля движущих сил на поперечном сечении проводника однородны. При таком условии Е однородна, а значит, и j также однородная величина. Примем произвольное значение поперечного сечения цепи S, тогда pl/s = E. Получившееся равенство умножим на dl. Тогда Edl = (Е эл.ст.+Е стор.) dl = Е эл.ст. dl + Е стор. dl = -dф + dE. Отсюда получим (pI/S) dl = -dф + dE. Возьмём в учёт, что p/s dl = dR и запишем закон Ома в интегральной форме:

IdR = -dф + dE.

Закон Ома в комплексной форме

Чтобы провести анализ электрических цепей синусоидального тока, комфортнее использовать закон Ома в комплексной форме. Для лучшего понимания введем основное понятие, фигурирующее в данной интерпретации закона: синусоидальный ток – это линейные цепи с установившимся режимом работы, после того, как переходные процессы в них завершены, уровень напряжения резко уменьшается на конкретной дистанции, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В противном случае, когда данные параметры не соблюдаются, закон не может быть применим. Чем отличается эта форма от обычной? Ответ прост: токи, сопротивление и ЭДС фиксируются как комплексные числа. Это обусловлено тем, что существуют как активные так и реактивные значения напряжений, токов и сопротивлений, а в результате этого требуется внесение определенных коррективов.

Вместо активного сопротивления используется полное, то есть комплексное сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже превращаются в комплексные величины. При реальных расчетах лучше и удобнее применять действующие значения. Итак, закон в комплексной форме выглядит так:

i = U/Z, i = UY

В данной формуле Z – комплексное сопротивление, Y – комплексная проводимость.

Чтобы выявить эти величины, выведены формулы. Пропустим шаги их создания и приведем готовые формулы:

Z = ze = z cosф + jz sinф = r + jx

Y = 1/ ze = ye = y cos ф — jy sin ф = g + jb

Закон Ома для переменного тока

После того как Фарадей открыл электромагнитную индукцию, стали активно использовать генераторы сперва постоянного, а после и переменного тока.

Используется уже известная формула:

I = U/Z

Полное сопротивление тока – это совокупность активного, а также индуктивного и емкостного сопротивлений. Проще говоря, ток в цепи переменного тока зависит от многих параметров, в том числе от величины ёмкости и индуктивности. Полное сопротивление вычисляется по формуле.

Формула полного сопротивленияФормула полного сопротивленияФормула полного сопротивления

Полное сопротивление можно изобразить как гипотенузу прямоугольного треугольника, катетами которого является активное и индуктивное сопротивление.

Треугольник полного сопротивленияТреугольник полного сопротивленияТреугольник полного сопротивления

Итак, формула амплитудного значения силы тока будет выглядеть так:

Im = Um/ ((R^2 + (ωL — (1/ωC)^2

ЦепьЦепьЦепь

В такой цепи колебания тока и напряжения разные по фазе, а разность фаз зависит от индуктивности катушки и ёмкости конденсатора:

U = Um sin (ωt)

I = Im sin (ωt + ф)

Закон Ома для постоянного тока

В данном случае частота будет равняться нулевому значению, поэтому остальные показатели также будут нулевыми соответственно, в то время как значение ёмкости достигнет бесконечности. Цепь разорвётся. Поэтому отсюда вытекает логичный вывод: реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.

Закон Ома для однородного участка цепи

Формула выглядит уже известным образом:

I = U/R

В данном случае главной характеристикой проводника остаётся сопротивление. От того, как выглядит проводник, зависит количество узлов кристаллической решётки и атомов примесей. Поэтому электроны могут замедляться или ускоряться.

Сопротивление будет зависеть от вида проводника, а именно от его сечения, материала и длины:

R = p (L/S)

Закон Ома для неоднородного участка цепи

При решении задачи становится понятным, что для того, чтобы поддерживался стабильный ток в замкнутой цепи, нужны силы совершенной другой природы, а не кулоновские. В этом случае можно заметить такую закономерность: заряды, которые никак не соприкасаются друг с другом, выступают в двух ролях одновременно, то есть они являются силами электрического поля и силами иного вида – сторонними в это же время. Участок, на котором замечена данная закономерность, называется неоднородным.

Неоднородный участок цепиНеоднородный участок цепиНеоднородный участок цепи

Формула принимает вид:

E = Eq + Est

Закон Ома в данном подразделе был сформулирован таким образом: сила тока прямо пропорциональна напряжению на данном участке и обратно пропорциональна его полному сопротивлению.

Итак, готовая формула:

I = U12/R, где U12

Закон Ома для магнитной цепи

В каждом электромагните совмещены несколько важных элементов: стальной сердечник и катушка. По последней протекает ток. При совмещении нескольких участков образуется магнитная цепь.

При кольцевом магнитопроводе все поле находится внутри кольца. Тогда поток в магнитопроводе равен:

Ф = Вср S = μHср S

Формула закона для магнитной цепи:

Формула закона ома для магнитной цепиФормула закона ома для магнитной цепиФормула закона ома для магнитной цепи

Задачи с решениями на закон Ома

Задача №1

Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 127 В. Определить силу тока в проволоке.

Дано:

  • l = 120 м,
  • S = 0,5 мм,
  • U = 127 В,
  • p = 1,1 Ом*мм2 /м.

Найти: I — ?

Решение:

  • R = p * l / S,
  • R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
  • I = 127 В : 264 Ом = 0,48 А.

Ответ: I = 0,48 Ом

Задача №2

Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 220 В. Определить силу тока в проволоке.

Дано:

  • l = 120 м,
  • S = 0,5 мм,
  • U = 220 В,
  • p = 1,1 Ом*мм2 /м.

Найти: I — ?

Решение:

  • R = p * l / S,
  • R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
  • I = 220 В : 264 Ом = 0,83 А.

Ответ: I = 0,83 Ом

Задача №3

Дано:

  • U = 15 В,
  • R1 = 3 Ом,
  • R2 = R3 = 4 Ом.

Найти: I — ?

Решение:

  • R2 и R3 соединены параллельно R2 = R3, R2.3 = R2 / 2 = 2 Ом, составим эквивалентную схему:
Формула закона ома для магнитной цепиФормула закона ома для магнитной цепи
  • R = R1 + R2,3
  • R = 3 Ом + 2 Ом = 5 Ом
  • Найдем силу тока на участке цепи по закону Ома I = U / R
  • I = 15 В / 5 Ом = 3 А

Ответ: I = 3 A.

Что такое преобразование источника — преобразование напряжения в ток и ток в источник напряжения

Преобразование источника означает просто замену одного источника эквивалентным. Практический источник напряжения может быть преобразован в эквивалентный практический источник тока и аналогичным образом практический источник тока в источник напряжения.

Любой практический источник напряжения или просто источник напряжения состоит из идеального источника напряжения, включенного последовательно с внутренним сопротивлением или импедансом (для идеального источника этот импеданс будет равен нулю), выходное напряжение становится независимым от тока нагрузки.Ячейки, батареи и генераторы являются примером источника напряжения.

Для любого практического источника тока или просто источника тока существует идеальный источник тока, параллельный внутреннему сопротивлению или импедансу, для идеального источника тока этот параллельный импеданс равен бесконечности.

Полупроводниковые устройства, такие как транзисторы и т. Д., Рассматриваются как источник тока или выходной сигнал, генерируемый источником постоянного или переменного напряжения, называется источником постоянного и переменного тока соответственно.

Источник напряжения и тока являются взаимно передаваемыми или, другими словами, может быть выполнено преобразование источника, то есть напряжения на источник тока и тока на источник напряжения. Позвольте нам понять это, рассмотрев схему, приведенную ниже:

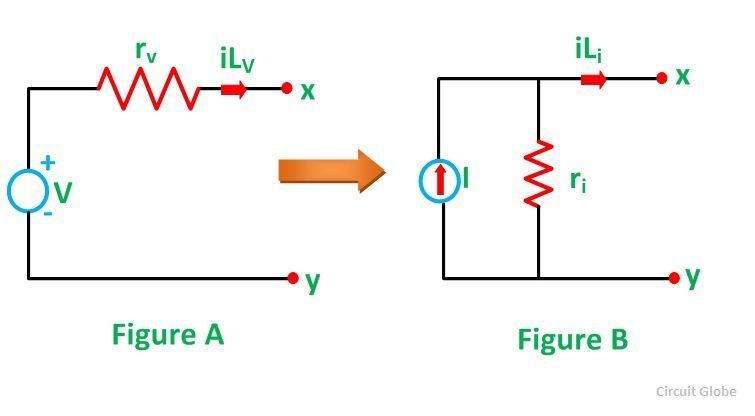SOURCE-TRANSFORMATION-FIGURE-1 На рисунке A показан практический источник напряжения, включенный последовательно с внутренним сопротивлением r v , а на рисунке B представлен практический источник тока с параллельным внутренним сопротивлением r i

.

Для практического источника напряжения ток нагрузки будет определяться уравнением:
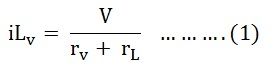SOURCE-TRANSFORMATION-EQ1 Где,

iL v — ток нагрузки для практического источника напряжения
В — напряжение
r v — внутреннее сопротивление источника напряжения
r L — сопротивление нагрузки

Предполагается, что сопротивление нагрузки r L подключено на клемме x-y.Аналогично для практического источника тока ток нагрузки задается как:
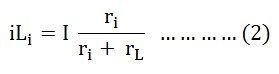SOURCE-TRANSFORMATION-EQ2, где,

iL i — ток нагрузки для практического источника тока

это текущий

r i — внутреннее сопротивление источника тока

r L — сопротивление нагрузки, подключенное через клемму x-y на рисунке B

Два источника становятся идентичными, когда мы будем уравнять уравнение (1) и уравнение (2)

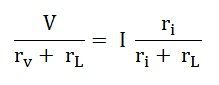
SOURCE-TRANSFORMATION-EQ3

Однако для источника тока напряжение на клеммах x-y будет равно Iri, клемма x-y открыта.то есть

V = I x r i

Таким образом, мы получим,
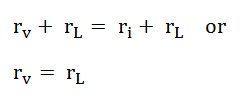
SOURCE-TRANSFORMATION-EQ4

Следовательно, для любого практического источника напряжения, если идеальное напряжение равно V, а внутреннее сопротивление равно r v , источник напряжения может быть заменен источником тока I с внутренним сопротивлением, параллельным источнику тока.

Преобразование источника: преобразование источника напряжения в источник тока

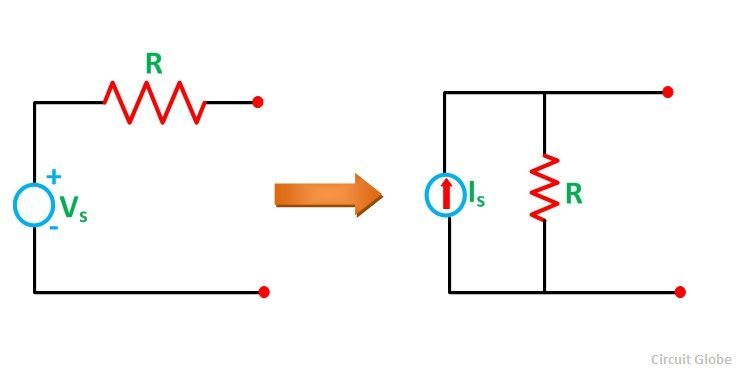SOURCE-TRANSFORMATION-FIGURE Когда источник напряжения подключен к сопротивлению последовательно и его необходимо преобразовать в источник тока, тогда сопротивление подключается параллельно с источником тока, как показано на рисунке выше.

, где I с = V с / R

Преобразование источника тока в источник напряжения

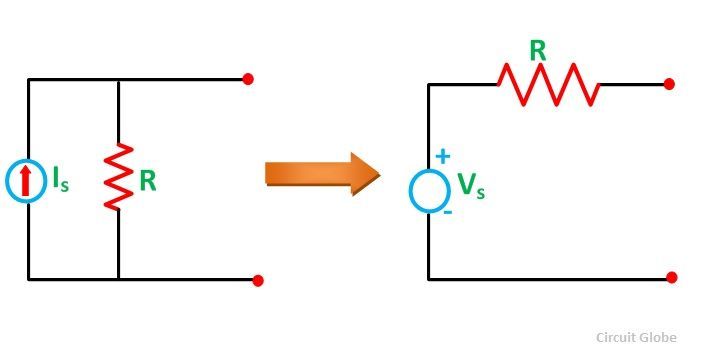SOURCE-TRANSFORMATION-FIGURE-3 На приведенной выше принципиальной схеме источник тока, который подключен параллельно с сопротивлением, преобразуется в источник напряжения путем последовательного размещения сопротивления с источником напряжения.

где, V с = I с / R

,Формула падения напряжения

с примерами

    • Классы
      • Класс 1 — 3
      • Класс 4 — 5
      • Класс 6 — 10
      • Класс 11 — 12
    • КОНКУРСЫ
      • BBS
      • 000000000 Книги
        • NCERT Книги для 5 класса
        • NCERT Книги Класс 6
        • NCERT Книги для 7 класса
        • NCERT Книги для 8 класса
        • NCERT Книги для 9 класса
        • NCERT Книги для 10 класса
        • NCERT Книги для 11 класса
        • NCERT Книги для 12-го класса
      • NCERT Exemplar
        • NCERT Exemplar Class 8
        • NCERT Exemplar Class 9
        • NCERT Exemplar Class 10
        • NCERT Exemplar Class 11
        • NCERT Exemplar Class 12
          • 9000al Aggar Agard Agard Agard Agard Agulis Class 12
          • RS Решения Aggarwal класса 10
          • RS Решения Aggarwal класса 11
          • RS Решения Aggarwal класса 10
            • 90 003 Решения RS Aggarwal класса 9
          • Решения RS Aggarwal класса 8
          • Решения RS Aggarwal класса 7
          • Решения RS Aggarwal класса 6
        • Решения RD Sharma
          • Решения класса RD Sharma
          • Решения класса 9 Шарма 7 Решения RD Sharma Class 8
          • Решения RD Sharma Class 9
          • Решения RD Sharma Class 10
          • Решения RD Sharma Class 11
          • Решения RD Sharma Class 12
        • ФИЗИКА
          • Механика
          • 000000 Электромагнетизм
        • ХИМИЯ
          • Органическая химия
          • Неорганическая химия
          • Периодическая таблица
        • МАТС
          • Теорема Пифагора
          • Отношения и функции
          • Последовательности и серии
          • Таблицы умножения
          • Детерминанты и матрицы
          • Прибыль и убыток
          • Полиномиальные уравнения
          • Делительные дроби
        • 000 ФОРМУЛЫ
          • Математические формулы
          • Алгебровые формулы
          • Тригонометрические формулы
          • Геометрические формулы
        • КАЛЬКУЛЯТОРЫ
          • Математические калькуляторы
          • S000
          • S0003
          • Pегипс Класс 6
          • Образцы документов CBSE для класса 7
          • Образцы документов CBSE для класса 8
          • Образцы документов CBSE для класса 9
          • Образцы документов CBSE для класса 10
          • Образцы документов CBSE для класса 11
          • Образец образца CBSE pers for Class 12
        • CBSE Документ с вопросами о предыдущем году
          • CBSE Документы за предыдущий год Class 10
          • CBSE Вопросы за предыдущий год Class 12
        • HC Verma Solutions
          • HC Verma Solutions Класс 11 Физика
          • Решения HC Verma Class 12 Physics
        • Решения Lakhmir Singh
          • Решения Lakhmir Singh Class 9
          • Решения Lakhmir Singh Class 10
          • Решения Lakhmir Singh Class 8
        • Примечания
        • CBSE
        • Notes
            CBSE Класс 7 Примечания CBSE
          • Класс 8 Примечания CBSE
          • Класс 9 Примечания CBSE
          • Класс 10 Примечания CBSE
          • Класс 11 Примечания CBSE
          • Класс 12 Примечания CBSE
        • Примечания пересмотра
        • CBSE Редакция
        • CBSE
        • CBSE Class 10 Примечания к пересмотру
        • CBSE Class 11 Примечания к пересмотру 9000 4
        • Замечания по пересмотру CBSE класса 12
      • Дополнительные вопросы CBSE
        • Дополнительные вопросы CBSE 8 класса
        • Дополнительные вопросы CBSE 8 по естественным наукам
        • CBSE 9 класса Дополнительные вопросы
        • CBSE 9 дополнительных вопросов по науке CBSE
          • 9000 Класс 10 Дополнительные вопросы по математике
        • CBSE Класс 10 Дополнительные вопросы по науке
      • Класс CBSE
        • Класс 3
        • Класс 4
        • Класс 5
        • Класс 6
        • Класс 7
        • Класс 8
        • Класс 9
        • Класс 10
        • Класс 11
        • Класс 12
      • Решения для учебников
    • Решения NCERT
      • Решения NCERT для класса 11
          Решения NCERT для физики класса 11
        • Решения NCERT для класса 11 Химия
          • Решения для класса 11 Биология
        • NCERT Решения для класса 11 Математика
          • 9 0003 NCERT Solutions Class 11 Бухгалтерия
        • NCERT Solutions Class 11 Бизнес исследования
        • NCERT Solutions Class 11 Экономика
        • NCERT Solutions Class 11 Статистика
        • NCERT Solutions Class 11 Коммерция
      • NCERT Solutions для класса 12
        • NCERT Solutions для Класс 12 Физика
        • Решения NCERT для 12 класса Химия
        • Решения NCERT для 12 класса Биология
        • Решения NCERT для 12 класса Математика
        • Решения NCERT Класс 12 Бухгалтерский учет
        • Решения NCERT Класс 12 Бизнес исследования
        • Решения NCERT Класс 12 Экономика
        • NCERT Solutions Class 12 Бухгалтерский учет Часть 1
        • NCERT Solutions Class 12 Бухгалтерский учет Часть 2
        • NCERT Solutions Class 12 Микроэкономика
        • NCERT Solutions Class 12 Коммерция
,
Согласно закону Ома, I ∝ V, но I ∝ 1 / V в уравнении мощности. Как?

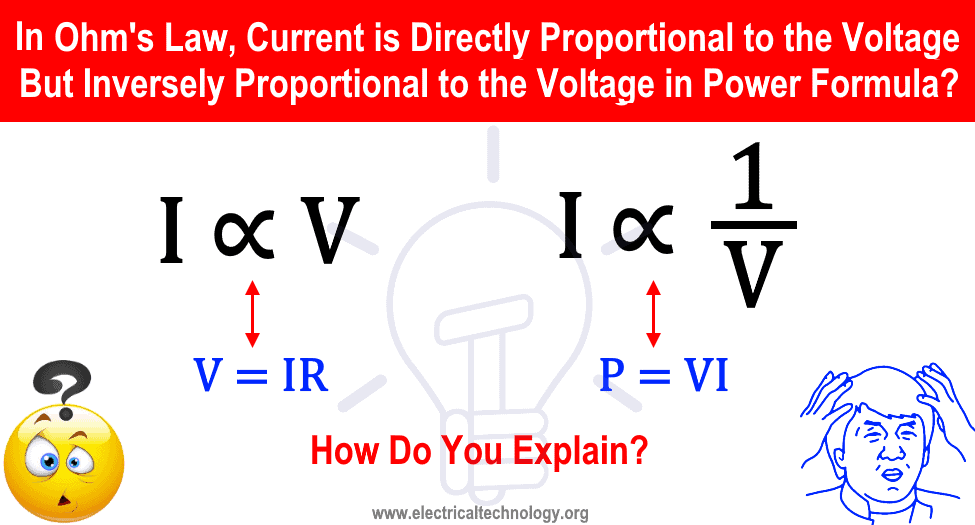
В I = V / R, ток прямо пропорционален напряжению, но ток обратно пропорционален напряжению в P = VI?

Это еще один запутанный вопрос, который чаще всего задают в интервью по электротехнике и электронике.

Согласно закону Ома, ток увеличивается при увеличении напряжения (I = V / R), но ток уменьшается при увеличении напряжения согласно формуле (P = VI).Как вы объясните?

, т. Е.

  • Согласно закону Ома: I ∝ V (ток прямо пропорционален напряжению. I = V / R)
  • Согласно формуле мощности: I ∝ 1 / V (ток обратно пропорционален напряжению. I = P / V)

Короче говоря, согласно закону Ома (V = IR или I = V / R), который показывает, что ток прямо пропорционален напряжению, но согласно P = VI или I = P / V , это показывает, что ток обратно пропорционален напряжению.

According to Ohm According to Ohm

Давайте разберемся с этим утверждением.

P = V x I

На самом деле, это зависит от того, как вы увеличиваете параметры, т.е. увеличиваете ли вы напряжение, поддерживая постоянную мощность источника или изменяясь.

  • Если мощность источника постоянна, то при увеличении напряжения ток уменьшается.
  • Если вы не заботитесь о мощности и просто замените батарею на новую с более высокой номинальной мощностью, это может увеличить ток при увеличении напряжения, так как мощность больше не постоянна i.е. мощность также была увеличена.

В случае трансформатора, когда напряжение увеличивается, ток уменьшается, потому что мощность остается постоянной, то есть мощность обеих сторон равна P = VI (без учета коэффициента мощности: Cos θ).

В = I x R

По закону Ома ток (I) прямо пропорционален напряжению (В), если сопротивление (R) и температура остаются постоянными.

Согласно формуле мощности, он говорит, что ток обратно пропорционален напряжению, если мощность остается неизменной.

Как мы уже знаем, что в повышающем трансформаторе, если напряжение увеличивается, ток уменьшается там, где мощность одинакова (так как трансформатор только увеличивает или понижает значение тока и напряжения и не меняет значение мощность). Аналогично, напряжение уменьшается при увеличении тока в понижающем трансформаторе.

Та же история есть на электростанции, где выработка электроэнергии постоянна. Если мощность на стороне генерации улучшится, ток и напряжение будут увеличены.

Вкратце:

  • Если мощность постоянна = Напряжение обратно пропорционально току , т.е. В ∝ 1 / I в P = VxI .
  • Если сопротивление и температура постоянны: Напряжение прямо пропорционально току , то есть В ∝ I в В = IxR .

Именно по этой причине объясняет, почему в законе Ома ток прямо пропорционален напряжению, но обратно пропорционален формуле напряжения в мощности.

Похожие вопросы / ответы:

.

Related Posts

Leave A Comment