обозначение на схеме, как увеличить, что делать, если нет подходящего
В схемах радиоэлектронной аппаратуры одним из наиболее часто встречающихся элементов является резистор, другое его название это сопротивление. У него есть целый ряд характеристик, среди которых есть мощность. В этой статье мы поговорим о резисторах, что делать, если у вас нет подходящего по мощности элемента, и почему они сгорают.Характеристики резисторов
1. Основной параметр резистора – это номинальное сопротивление.
2. Второй параметр, по которому его выбирают – это максимальная (или предельная) рассеиваемая мощность.
3. Температурный коэффициент сопротивления – описывает, насколько изменяется сопротивление, при изменении его температуры на 1 градус Цельсия.
4. Допустимое отклонение от номинала. Обычно разброс параметров резистора от одного заявленного в пределах 5-10%, это зависит от ГОСТ или ТУ по которому он произведен, существуют и точные резисторы с отклонением до 1%, обычно стоят дороже.
5. Предельное рабочее напряжение, зависит от конструкции элемента, в бытовых электроприборах с напряжением питания 220В могут применяться практически любые резисторы.
6. Шумовые характеристики.
7. Максимальная температура окружающей среды. Это такая температура, которая может быть при достижении максимальной рассеиваемой мощности самого резистора. Об этом подробнее поговорим позже.
8. Влаго- и термоустойчивость.
Есть еще две характеристики, о которых начинающие чаще всего не знают, это:
1. Паразитная индуктивность.
2. Паразитная ёмкость.
Оба параметра зависят от типа и конструктивных особенностей резистора. Индуктивность имеет в любом проводнике, вопрос в её величины. Типовые величины паразитных индуктивностей и емкостей приводить бессмысленно. Паразитные составляющие следует учитывать при проектировании и ремонте высокочастотных приборах.
На низких частотах (например, в пределах звукового диапазона до 20 кГц), существенного влияния в работу схемы они не вносят. В высокочастотных приборах, с рабочими частотами в сотни тысяч и выше герц существенное влияние вносит даже расположение дорожек на плате и их форма.
В высокочастотных приборах, с рабочими частотами в сотни тысяч и выше герц существенное влияние вносит даже расположение дорожек на плате и их форма.
Мощность резистора
Из курса физики многие отлично помнят формулу мощности для электричества, это: P=U*I
Отсюда следует, что она линейно зависит от тока и напряжения. Ток же через резистор зависит от его сопротивления и приложенного к нему напряжению, то есть:
I=U/R
Падение напряжения на резисторе (сколько на его выводах остаётся напряжения от приложенного к цепи, в которой он установлен), так же зависит от тока и сопротивления:
I=U/R
Теперь объясним простыми словами, что такое мощность у резистора и куда она выделяется.
У любого металла есть своё удельное сопротивление, это такая величина, которая зависит от структуры этого самого металла. Когда носители зарядов (в нашем случае электроны), под воздействием электрического тока протекают через проводник, они сталкиваются с частицами, из которого состоит металл.
В результате этих столкновений затрудняется движение тока. Если очень обобщенно сказать, то получается, так, что чем плотнее структура металла, тем сложнее протекать току (тем больше сопротивление).
На картинке пример кристаллической решетки, для наглядности.
Из-за этих столкновений выделяется тепло. Это можно представить, как если бы вы шли через толпу (большое сопротивление), где вас еще и толкают, или если бы шли по пустому коридору, где вы сильнее вспотеете?
То же самое происходит и с металлом. Мощность выделяется в виде тепла. В некоторых случаях это плохо, потому что так снижается коэффициент полезного действия прибора. В других ситуациях – это полезное свойство, например в работе ТЭНов. В лампах накаливания за счет своего сопротивления спираль раскаляется до яркого свечения.
Но как это относится к резисторам?
Дело в том, что резисторы применяют для ограничения тока при питании каких-либо устройств, или элементов цепи, или для задания режимов работы полупроводниковым приборам.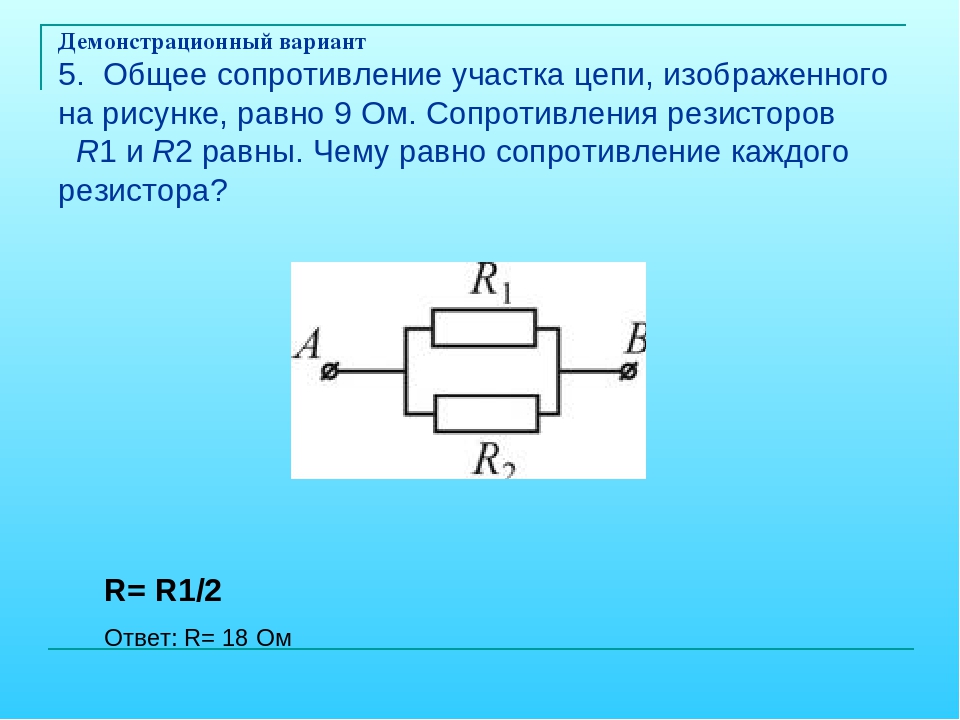 2/1=144/1=144 Вт.
2/1=144/1=144 Вт.
Всё сходится. Резистор будет выделять тепло с мощностью в 144Вт. Это условные значения, взятые в качестве примера. На практике таких резисторов вы не встретите в радиоэлектронной аппаратуре, исключением являются большие сопротивления для регулирования двигателей постоянного тока или пуска мощных синхронных машин в асинхронном режиме.
Какие бывают резисторы и как они обозначаются на схеме
Ряд мощностей резисторов стандартен: 0.05 (0.62) – 0.125 – 0.25 – 0.5 – 1 – 2 – 5
Это типовые номиналы распространенных резисторов, бывают и большие значения, или другие величины. Но этот ряд наиболее распространен. При сборке электроники используют схему электрическую принципиальную, с порядкового номера элементов. Реже указываться номинальное сопротивление, еще реже указывается номинальное сопротивление и мощность.
Чтобы быстро определить мощность резистора на схеме были введены соответствующие УГО (условные графические обозначения) по ГОСТ. Внешний вид таких обозначений и их расшифровка представлены в таблице ниже.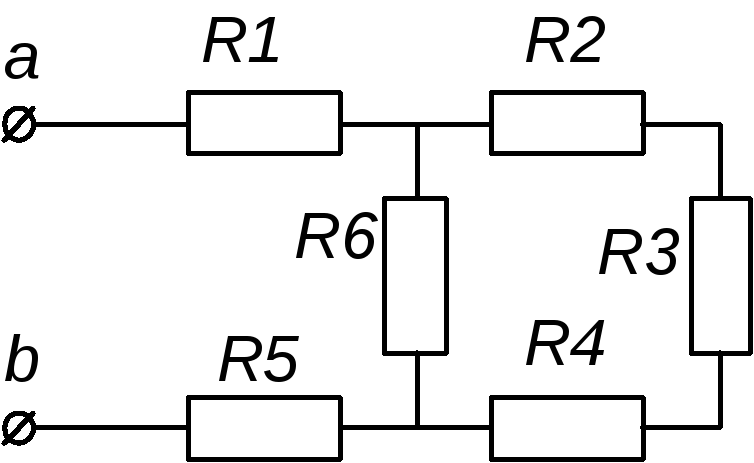
Вообще эти данные, а также название конкретного типа резистора указываются в перечне элементов, там же указывается и разрешенный допуск в %.
Внешне, они отличаются размером, чем мощнее элемент, тем больше его размер. Больший размер увеличивает площадь теплообмена резистора с окружающей средой. Поэтому тепло, которое выделяется при прохождении тока через сопротивление, быстрее отдаётся воздуху (если окружающая среда воздух).
Это значит, что резистор может греться с большей мощностью (выделять определенное количество тепла в единицу времени). Когда температура сопротивления достигает определенного уровня, сначала начинает выгорать внешний слой с маркировкой, дальше сгорает резистивный слой (пленка, проволока или что-то другое).
Чтобы вы оценили, как сильно может греться резистор, взгляните на нагрев спирали разобранного мощного резистора (более 5 Вт) в керамическом корпусе.
В характеристиках был такой параметр, как допустимая температура окружающей среды. Она указывается, для правильного подбора элемента. Дело в том, что раз мощность резистора ограничена способностью отдать тепло и, при этом, не перегреться, а для отдачи тепла, т.е. охлаждения элемента путем конвекции или принудительным потоком воздуха должна быть как можно большая разница температур элемента и окружающей среды.
Дело в том, что раз мощность резистора ограничена способностью отдать тепло и, при этом, не перегреться, а для отдачи тепла, т.е. охлаждения элемента путем конвекции или принудительным потоком воздуха должна быть как можно большая разница температур элемента и окружающей среды.
Поэтому если вокруг элемента слишком жарко он быстрее нагреется и сгорит, даже если электрическая мощность на нем ниже максимально рассеиваемой. Нормальной температурой является 20-25 градусов Цельсия.
В продолжение этой темы:
Как понизить напряжение с помощью резистора
Расчет и подбор резистора для светодиода
Расчет делителя напряжения на резисторах
Применение добавочных резисторов
Что делать, если нет резистора нужной мощности?
Частой проблемой радиолюбителей является отсутствия резистора нужной мощности. Если у вас есть резисторы мощнее, чем нужно – ничего страшного в этом нет, можно ставить не задумываясь. Лишь бы он влез по размеру. Если все имеющиеся резисторы по мощности меньше, чем нужно – это уже проблема.
На самом деле решить этот вопрос достаточно просто. Вспомните законы последовательного и параллельного соединения резисторов.
1. При последовательном соединении резисторов сумма падений напряжений на всей цепочке равняется сумме падений на каждом из них. А ток, протекающий через каждый резистор равен общему току, т.е. в цепи из последовательно соединенных элементов протекает ОДИН ток, но приложенные к каждому из них напряжения РАЗНЫЕ, определяются по закону Ома для участка цепи (см. выше) Uобщ=U1+U2+U3
2. При параллельном соединении резисторов падение на всех напряжения равны, а ток, протекающий в каждой из ветвей обратно пропорционален сопротивлению ветви. Общий ток цепочки из параллельно соединенных резисторов равен сумме токов каждой из ветвей.
На этой картинке изображено всё вышесказанное, в удобной для запоминания форме.
Так, как при последовательном соединении резисторов снизится напряжение на каждом из них, а при параллельном соединении ток, то если P=U*I
Мощность, выделяемая на каждом из них, снизится соответствующим образом.
Поэтому, если у вас нет резистора 100 Ом на 1 Вт, его можно почти всегда заменить 2 резисторами на 50 Ом и 0.5 Вт соединенными последовательно, или 2 резисторами на 200 Ом и 0.5 Вт соединенными параллельно.
Я не просто так написал «ПОЧТИ ВСЕГДА». Дело в том, что не все резисторы одинаково хорошо переносят ударные токи, в некоторых цепях, например связанные с зарядом конденсаторов большой ёмкости, в первоначальный момент времени переносят большую ударную нагрузку, которая может повредить его резистивный слой. Такие связки нужно проверять на практике или путем долгих расчетов и чтением технической документации и ТУ на резисторы, чем почти никогда и никто не занимается.
Заключение
Мощность резистора – это величина не менее важная, чем его номинальное сопротивление. Если не уделять внимания подбору сопротивлений нужно мощности, то они будут перегорать и сильно греться, что плохо в любой цепи.
При ремонте аппаратуры, особенно китайской, ни в коем случае не пытайтесь ставить резисторы меньшей мощности, лучше поставить с запасом, если есть такая возможность поместить его по габаритам на плате.
Для стабильной и надежной работы радиоэлектронного устройства нужно подбирать мощность, как минимум, с запасом в половину от предполагаемой, а лучше в 2 раза больше. Это значит, что если по расчетам на резисторе выделяется 0.9-1 Вт, то мощность резистора или их сборки должна быть не меньше, чем 1.5-2 Вт.
Алексей Бартош
Источник: http://electrik.info
Постоянно ли напряжение в серии: 3 важных пояснения —
By Кошики Банерджи
Напряжение на каждом резисторе в последовательной цепи различается в зависимости от значения сопротивления. Таким образом, последовательное напряжение не является постоянным. Только резисторы одинакового номинала могут дать такое же падение напряжения.
Мы используем слово «константа», чтобы указать фиксированное значение количества, которое остается неизменным. Напряжение никогда не может быть постоянным параметром в любой электрической цепи. У каждого резистора в последовательной комбинации разное падение напряжения. Следовательно, напряжение в последовательных цепях не является ни одинаковым, ни постоянным.
Следовательно, напряжение в последовательных цепях не является ни одинаковым, ни постоянным.
Когда мы соединяем несколько резисторов или параметров импеданса в линию один за другим, это называется последовательной схемой. Последовательная комбинация имеет одинаковый ток повсюду в цепи.
Эквивалентное сопротивление в последовательной схеме — это сумма всех индивидуальных сопротивлений. Падения напряжения на всех резисторах в сумме составляют общее напряжение. Падение напряжения на каждом компоненте в цепи разное. Эти падения напряжения рассчитываются путем умножения общего тока на номинал резистора.
Rузнать больше о… функциях цепи .series
Как рассчитать напряжение в последовательной цепи? Объясните числовым примером.Вышеупомянутая схема представляет собой простую последовательную схему с тремя резисторами по 5 Ом, 10 Ом и 20 Ом. Наша цель — найти через них падения напряжения. Сначала мы выясним эквивалентное сопротивление.
Наша цель — найти через них падения напряжения. Сначала мы выясним эквивалентное сопротивление.
Эквивалентное сопротивление R = R1+R2+R3= 5 + 20 + 10 = 35 Ом
Итак, общий ток = общее напряжение / эквивалентное сопротивление = 10/35 = 0.29 ампер.
Напряжение через резистор 5 Ом = 5 * 0.29 = 1.45 Вольт
Напряжение через резистор 10 Ом = 10 * 0.29 = 2.9 Вольт
Напряжение через резистор 20 Ом = 20 * 0.29 = 5.8 Вольт
Постоянно ли напряжение в серии — FAQsКак напряжение влияет на ток в последовательных цепях?Каждый резистор в последовательной цепи получает одинаковый ток при последовательном включении. Рассчитываем падение напряжения на них по известным номиналам резисторов.
Последовательная цепь представляет собой соединение нескольких элементов полного сопротивления. Таким образом, если цепь в любой момент разомкнется, произойдет сбой всей цепи, и ток не будет протекать. Очень распространенный пример — последовательное соединение лампочек разной яркости. Если мы продолжим добавлять лампы, яркость в конечном итоге снизится.
Очень распространенный пример — последовательное соединение лампочек разной яркости. Если мы продолжим добавлять лампы, яркость в конечном итоге снизится.
Схема, изображенная выше, представляет собой четыре последовательно соединенных резистора. В цепи присутствует аккумулятор с неизвестным напряжением В. Ток составляет 0.25 А. Мы должны выяснить ценность V.
Падение напряжения через резистор 6 Ом = 6 * 0.25 = 1.5 Вольт
Падение напряжения через резистор 8 Ом = 8 * 0.25 = 2 Вольт
Падение напряжения через резистор 10 Ом = 10 * 0.25 = 2.5 Вольт
Падение напряжения через резистор 12 Ом = 12 * 0.25 = 3 Вольт
Следовательно, общее напряжение АКБ = В = 1.5 + 2 + 2.5 + 3 = 9 Вольт.
Каковы применения последовательного напряжения?Последовательные и параллельные цепи считаются строительными блоками схемотехники. Они обычно используются для многих приложений с ограничением тока, таких как деление напряжения, смещение транзистора и т. Д.
Д.
Напряжение в последовательной цепи может быть различным. Некоторые распространенные применения последовательного напряжения:
- Цепи делителя напряжения
- Батарейки для пульта ТВ
- Пожарная тревога
- Аналоговые фильтры
- Резонансные схемы
- Сетевые фильтры
- Гирлянды светодиодных ламп
- Внутренние компоненты автомобильной техники
Отдельные напряжения резисторов в последовательной цепи получают из общего тока, умноженного на номинал резистора.
Допустим, есть два резистора R1 и R2 соединены последовательно с батареей V. Следовательно, эквивалентное сопротивление Req R1+R2. Итак, напряжение на любом резисторе = значение резистора x общий ток.
Напряжение на R1 V =1 = VR1 / Р1+R2 Вольт
Напряжение на R2 V =2 = VR2 / Р1+R2 Вольт
Последовательно ли напряжение одинаково?Напряжение в последовательной цепи не является ни одинаковым, ни постоянным. Падение напряжения на каждом резисторе во всех случаях разное, кроме одного, когда все резисторы в последовательной сети имеют одинаковое значение.
Когда резисторы в цепи равны, то только падения напряжения будут одинаковыми для всех резисторов. Предположим, что в схеме, содержащей три резистора, все резисторы имеют сопротивление R Ом. Эквивалентное значение сопротивления = R + R + R = 3R. Напряжение на любом резисторе = V * R / 3R = V / 3 вольта.
Последовательно объясните напряжение на практическом примере.Один очень интересный пример последовательной схемы в практической жизни — это классическое освещение рождественской елки. В этом освещении многие крошечные лампочки соединены последовательно.
В этом освещении многие крошечные лампочки соединены последовательно.
Мы используем эти лампочки годами. Мы видим, что определенная часть света не работает. Это связано с последовательным подключением. Светильники представляют собой комбинацию множества таких последовательно соединенных струн. Таким образом, даже если одна лампочка в сети выходит из строя, вся ее часть перестает работать.«Это сезон» by ДонкерДинк под лицензией CC BY-NC-ND 2.0
резисторов
резисторовРезисторы последовательно и параллельно, правила Кирхгофа
Резисторы, включенные последовательно и параллельно
Проблема:
Четыре одинаковые лампочки сопротивлением R являются подключен, как показано на рисунке.
Батарея обеспечивает разность потенциалов В 0 .
Переключатели S 1 и S 2 могут быть разомкнуты и/или
закрыто в четырех различных комбинациях: открыто-открыто, закрыто-закрыто, открыто-закрыто,
закрыто-открыто.
(a) Рассмотрите лампочку A: определите, какая
комбинации переключателей дадут самый яркий и самый тусклый свет в лампе A.
(b) Рассмотрите лампочку B: определите, какая
комбинации переключателей будут давать самый яркий и самый тусклый свет в лампе B.
Решение:
- Концепты:
Резисторы последовательно и параллельно - Рассуждение:
Проанализируйте простую схему. - Детали расчета:
(a) самый яркий: S 1 закрытый, S 2 разомкнут, I A = 2В/(5R).
самый тусклый: S 2 закрытый, I A = 0,
(b) самый яркий: S 2 закрытый, S 1 открытый, I B = V/(2R).
самый тусклый: S 1 закрытый, S 2 открытый, I B = V/(5R).
Проблема:
схема, показанная на схеме, содержит идеальную батарею и два резистора R 1 и R 2 .
Вольтметром измеряют напряжение на R 1 ,
затем через R 2 ,
затем через аккумулятор.
Его показания соответственно 2,0 В; 3,0 В; 6,0 В.
Каковы фактические напряжения на резисторах?
Решение:
- Концепты:
Резисторы последовательно и параллельно - Рассуждение:
Вольтметр также имеет шунтирующее сопротивление R. Он считывает напряжение на это сопротивление. При размещении в цепи он правильно считывает напряжение батареи, а не напряжения на резисторах невозмущенного схема.
Напряжение батареи V = 6 В.
Напряжения на R 1 и R 2 (без вольтметра в схеме)
V 1 = 6V R 1 /(R 1 + R 2 ) и V 2 = 6V R 2 /(R 1 + R 2 ) соответственно.
В 1 = 6В /(1 + R 2 /R 1 ), В 2 = 6В /(1 + R 1 /R 2 ).
Нам нужно найти соотношение R 1 /R 2 . - Детали расчета:
С вольтметром в схеме имеем:
2В = 6В [R 1 R/(R 1 + R)]/[ (R 1 R/(R 1 + R)) + R 2 ] или 2 В = 6 В/[1 + R 2 (R 1 + R)/(R 1 R)]
3В = 6В [R 2 R/(R 2 + R)]/[ (R 2 R/(R 2 + Р)) + Р 1 ] или 3 В = 6 В/[1 + R 1 (R 2 + R)/(R 2 R)]
[1 + R 2 (R 1 + R)/(R 1 R)] = 3, R 2 (R 1 + R)/(R 1 R) = 2, R 2 /R + R 2 /R 1 = 2, 1/R = 2/R 2 — 1/R 1
[1 + R 1 (R 2 + R)/(R 2 R)] = 2, R 1 (R 2 + R)/(R 2 R) = 1, R 1 /R + R 1 /R 2 = 1. 1/R = 1/R 1 — 1/R 2
1/R = 1/R 1 — 1/R 2
Следовательно, 3/R 2 = 2/R 1 , R 1 /R 2 = (2/3).
В 1 = 6 В * 2/5 = 2,4 В, В 2 = 6 В * 3/5 = 3,6 В.
Проблема:
Что сопротивление следующей сети? Каждый омический резистор имеет сопротивление R
.Решение:
- Концепты:
Резисторы последовательно и параллельно - Рассуждение:
Схема имеет достаточную симметрию, чтобы мы могли анализировать ее как простую схему. схема с резисторами последовательно и параллельно. - Детали расчета:
р всего = (3/2)р.
Проблема:
(a) Четыре конденсатора подключены, как показано на рисунке.
С 1 = С 2 = С 3 = С 4 = 1
мкФ.
Чему равна общая емкость между точками А и В?
(b) Пять одинаковых резисторов 1 Ом соединены и образуют четыре стороны квадрата. и его диагонали. Чему равно сопротивление между точками А и В?
и его диагонали. Чему равно сопротивление между точками А и В?
Решение:
- Концепты:
Конденсаторы и резисторы последовательно и параллельно - Рассуждение:
Нас просят найти эффективную емкость и сопротивление заданного конфигурации. - Детали расчета:
(a) Обратная эквивалентная емкость для подсхема с двумя конденсаторами C 3 и C 4 —
1/C eq = 1/1 + 1/1 = 2, таким образом, C eq = ½. Сейчас эквивалентная емкость для подсхемы с C 2 , C 3 , и C 4 представляет собой C eq ‘= C + C eq = 1 + ½ = 3/2. Наконец, эквивалентная емкость для всей цепи составляет 1/C экв. » = 1/C 1 + 1/C eq ‘ = 1 + (2/3) = 5/3, таким образом, C eq »= 3/5. Суммарная емкость 0,6 мкФ.(b) Эквивалентное сопротивление подцепи с R 3 а R 4 равно 2.
 Эквивалентное сопротивление подцепи с R 3 ,
R 4 и R 5 равно 1/R экв. =1/1 + ½ = 3/2, таким образом, R экв. = (2/3). Эквивалентное сопротивление подцепи с R 2 , Р 3 ,
R 4 и R 5 равно R eq ‘ = R 2 + Re q = 1 + (2/3) = 5/3. Наконец, эквивалентное сопротивление всей цепи равно 1/R eq »=
1/1 + 3/5 = 8/5, таким образом, R eq »= 5/8. Сопротивление между точками A
и B составляет 5/8 Ом.
Эквивалентное сопротивление подцепи с R 3 ,
R 4 и R 5 равно 1/R экв. =1/1 + ½ = 3/2, таким образом, R экв. = (2/3). Эквивалентное сопротивление подцепи с R 2 , Р 3 ,
R 4 и R 5 равно R eq ‘ = R 2 + Re q = 1 + (2/3) = 5/3. Наконец, эквивалентное сопротивление всей цепи равно 1/R eq »=
1/1 + 3/5 = 8/5, таким образом, R eq »= 5/8. Сопротивление между точками A
и B составляет 5/8 Ом.
Проблема:
Найдите максимальную мощность
нагревательный элемент , который можно сконструировать из куска проволоки с сопротивлением 536 Ом. Элемент должен быть запитан
постоянным напряжением V = 110В. Ток по проводу
не может превышать 2,0 А.
(а) Предположим, что вы
допускается выбраковка отрезка провода,
(б) Предположим, что вам НЕ разрешено выбрасывать часть провода,

Решение:
- Концепты:
Закон Ома, I = V/R, мощность P = IV, резисторы в последовательно и параллельно - Рассуждение:
Мы можем разрезать провод на N кусков и соединить эти куски параллельно источник питания. - Детали расчета:
Поскольку V постоянно, мы должны максимизировать I, чтобы максимизировать P.
На каждый из отрезков провода, соединенных параллельно, имеем
I = V/R, I макс. = 2 A = 110 В/R мин. , R мин. = 55 Ом.
(a) Мы можем отрезать 9 кусков по 55 Ом и выбросить один кусок по 41 Ом.
Тогда общий ток равен 9*2 А, а рассеиваемая мощность 1980 Вт.
(b) Мы можем отрезать 8 кусков по 55 Ом и 1 кусок по 96 Ом. Суммарный ток их
I всего = 8*110 В/(55 Ом) + 110 В/(96 Ом). Мощность P = VI всего = 1886 Вт.
А что, если мы отрежем небольшой кусок провода 96 Ом и присоединим его к одному из провода 55 Ом?
I = V/R, dI = -(V/R 2 )dR
Суммарное изменение тока по проводам в них равно dI = -(V/R 2 55 Ом )dR + (V/R 2 96 Ом )dR.
dI отрицательный, меньше ток течет, меньше мощность рассеивается при нагреве элемент. Максимальная мощность, рассеиваемая при обогреве элемент 1886Вт.
Проблема:
В
бесконечная цепь, показанная на схеме, каждая батарея имеет ЭДС ε и внутреннюю
сопротивление р. Каждый резистор имеет сопротивление 2r. Найдите ЭДС и внутреннюю
сопротивление эквивалентной батареи.
Решение:
- Концепты:
Ан бесконечная лестничная сеть - Рассуждение:
Поскольку лестница бесконечна, ток через эквивалентную ЭДС и внутреннее сопротивление не будет изменить, если к передней части лестницы добавляется дополнительная секция. - Детали расчета:
Любая комбинация батарей и сопротивлений с двумя клеммами может быть заменены одним источником напряжения V и одним последовательным резистором R. Напряжение V является идеальным источником напряжения, равным разомкнутой цепи. напряжение на клеммах. Сопротивление Thevenin R — это сопротивление измеряется на клеммах со всеми источниками напряжения, замененными короткозамкнутыми цепи и все источники тока заменены разомкнутыми цепями. Пусть
Напряжение сети равно V, а сопротивление R.
Пусть
Напряжение сети равно V, а сопротивление R.
Сеть состоит из бесконечного числа секций.
Давайте построим новую двухполюсную сеть, добавив еще один участок в сеть. перед старой двухтерминальной сетью.Пусть напряжение Thevenin новой сети равно V’ и пусть Thevenin сопротивление R’.
У нас есть
V’ = ε + V2r/(2r + R), R’ = 2rR/(R + 2r) + r = (3rR + 2r 2 )/(R + 2р).
Полагая R’ = R, V’ = V, получаем
R 2 — rR — 2r 2 = 0, R = r/2 + ((r/2) 2 + 2r 2 ) ½ = 2р.
V = (2r + R)ε/R = 2ε.
ЭДС эквивалентной батареи равна 2ε, а внутреннее сопротивление равно 2r.
Проблема:
(a) Рассчитайте сопротивление между двумя точками A
и B бесконечной системы резисторов.
(b) Рассчитайте сопротивление между точками A и
B куба из одинаковых резисторов r.
Решение:
Проблема:
Какое эквивалентное сопротивление показанной сети? Каждый резистор имеет сопротивление R.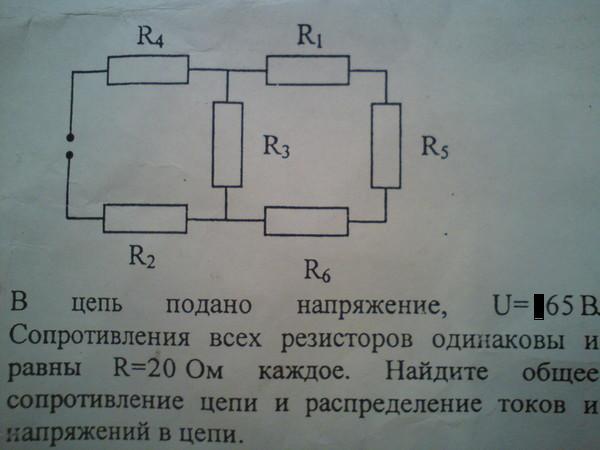
Решение:
- Концепции:
Резисторы последовательно и параллельно - Обоснование:
Через центральный резистор не протекает ток. Его можно игнорировать. Затем схема имеет достаточную симметрию, чтобы мы могли анализировать ее как простую схему с двумя пары резисторов последовательно. Пары параллельны друг другу. - Детали расчета:
Для двух последовательно соединенных резисторов: R эфф = R 1 + R 2 .
Для двух резисторов, включенных параллельно: 1/R эфф = 1/R 1 + 1/R 2 .
Каждый резистор имеет сопротивление R, эквивалентное сопротивление равно R.
Правила Кирхгофа
Проблема:
Найдите эквивалентное сопротивление между точками А и В цепи показано на рисунке ниже.
Решение:
- Концепты:
Правила Кирхгофа - Рассуждение:
Мы можем найти эквивалентное сопротивление, используя правила Кирхгофа. Правило соединения гласит, что сумма токов, входящих в соединение, должна
равна сумме токов, выходящих из этого соединения. Правило цикла гласит
что сумма разностей потенциалов вокруг любой замкнутой цепи должна
быть нулем.
Правило соединения гласит, что сумма токов, входящих в соединение, должна
равна сумме токов, выходящих из этого соединения. Правило цикла гласит
что сумма разностей потенциалов вокруг любой замкнутой цепи должна
быть нулем.
Предположим, что ток, протекающий в каждой части цепи, имеет некоторое направление.Если резистор перемещается в направлении тока, изменение потенциала на резисторе равно -IR.
Если резистор перемещается в направлении, противоположном этому тока изменение потенциала на резисторе равно +IR.
Если источник напряжения пересекается в направлении от — до +, изменение потенциала равно +V.
Если источник напряжения перемещается в направлении от + к -, изменение потенциала равно -V.
Мы можем использовать правило соединения столько раз, сколько возможно включить в него ток, который не использовался в предыдущем правиле соединения уравнение.
 Количество уравнений должно быть равно количеству неизвестных.
Количество уравнений должно быть равно количеству неизвестных. - Детали расчета:
Предположим, вы подключили батарею между A и B, так что A находится под некоторым напряжением V. и B находится на земле. Ток I начнет течь по цепи от A к B. V = IR, R = V/I. Если ты знаешь меня, то ты знаешь Р.Чтобы найти R для цепи, нам нужно знать токи, протекающие через 6 резисторы. Пусть I(1) обозначает ток, протекающий через резистор 1 Ом, I(2) обозначает ток через резистор 2 Ом и так далее. Общая текущая точка выхода A обозначается I. Нам нужно использовать правила Кирхгофа, чтобы найти 7 уравнений для семи токов, а затем использовать алгебру, чтобы решить эти семь уравнений одновременно.
(1) Для соединения с номером J1 имеем I(1) + I(2) + I(5) — I = 0,
(2) Для соединения с номером J2 имеем I(2) — I(7) — I(9) = 0
(3) Для соединения с номером J3 имеем I(13) — I(7) — I(5) = 0
(4) Для петли 1 имеем V — 1*I(1) = 0
(5) Для цикла 2 имеем 1*(I1) — 2*I(2) — 9*I(9) = 0
(6) Для цикла 3 имеем 9*I(9) — 7*I(7) — 13*I(13) = 0
(7) Для контура 4 имеем 2*I(2) + 7*I(7) — 5*I(5) = 0Теперь воспользуемся уравнением 4, чтобы исключить I(1) из других уравнений.

I(1) = V. Теперь у нас есть шесть уравнений.
(1) Для соединения с номером J1 имеем V + I(2) + I(5) — I = 0,
(2) Для соединения с номером J2 имеем I(2) — I(7) — I(9) = 0
(3) Для соединения с номером J3 имеем I(13) — I(7) — I(5) = 0
(5) Для петли 2 имеем V — 2*I(2) — 9*I(9) = 0
(6) Для цикла 3 имеем 9*I(9) — 7*I(7) — 13*I(13) = 0
(7) Для контура 4 имеем 2*I(2) + 7*I(7) — 5*I(5) = 0Теперь воспользуемся уравнением 2, чтобы исключить I(2) из других уравнений.
Я(2) = Я(7)+Я(9). Теперь у нас есть пять уравнений.
(1) Для соединения с номером J1 имеем V + I(7) + I(9) + I(5) — I = 0,
(3) Для соединения с номером J3 имеем I(13) — I(7) — I(5) = 0
(5) Для петли 2 имеем V — 2*I(7) — 11*I(9) = 0
(6) Для цикла 3 имеем 9*I(9) — 7*I(7) — 13*I(13) = 0
(7) Для контура 4 имеем 9*I(7) + 2*I(9) — 5*I(5) = 0Теперь воспользуемся уравнением 3, чтобы исключить I(5) из других уравнений.

I(5) = I(13)-I(7). Теперь у нас есть 4 уравнения.
(1) Для соединения с номером J1 имеем V + I(9) + I(13) — I = 0,
(5) Для петли 2 имеем V — 2*I(7) — 11*I(9) = 0
(6) Для цикла 3 имеем 9*I(9) — 7*I(7) — 13*I(13) = 0
(7) Для контура 4 имеем 14*I(7) + 2*I(9) — 5*I(13) = 0Теперь воспользуемся уравнением 5, чтобы исключить I(7) из других уравнений.
2*I(7) = V-11*I(9). Теперь у нас есть три уравнения.
(1) Для соединения с номером J1 имеем V + I(9) + I(13) — I = 0,
(6) Для петли 3 имеем -7*V + 95*I(9) — 26*I(13) = 0
(7) Для контура 4 имеем 7*V — 75*I(9) — 5*I(13) = 0Теперь воспользуемся уравнением 7, чтобы исключить I(9) из других уравнений.
75*I(9) = 7*V — 5*I(13). Теперь у нас есть 2 уравнения.
(1) Для соединения J1 имеем 82*V + 70*I(13) — 75*I = 0,
. (6) Для контура 3 имеем 140*V — 2425*I(13) = 0Теперь воспользуемся уравнением 6, чтобы исключить I(13) из других уравнений.

485*I(13) = 28*V. Теперь у нас есть 1 уравнение.
(1) Для соединения J1 имеем 41730*V — 36375*I = 0,I = (41730/36375)*V = 1,147*V
R = V/I = 0,87 ОмСопротивление 0,87 Ом.
Проблема:
В приведенной выше схеме выразите ток в резисторе 3R через V и R.
Решение:
- Концепты:
Правила Кирхгофа - Рассуждение:
Мы можем найти токи I 1 , I 2 и I 3 используя правила Кирхгофа. Правило соединения гласит, что сумма токи, входящие в соединение, должны быть равны сумме токов, выходящих из этого соединения. узел. Правило петли гласит, что сумма разностей потенциалов вокруг любого замкнутого контура должно быть равно нулю.
- Детали расчета:
Я 1 + Я 2 = I 3 , I 1 = I 2 , В — 3РИ 3 — РИ 2 = 0. И 3 = 2В/(7R).
Резисторы в цепях — Практика — Гиперучебник по физике
[закрыть]практическая задача 1
Определите следующие величины для каждой из двух цепей, показанных ниже…- эквивалент сопротивления
- ток от блока питания
- ток через каждый резистор
- падение напряжения на каждом резисторе
- мощность, рассеиваемая на каждом резисторе
раствор
Соблюдайте правила для последовательных цепей.
Сопротивления последовательно складываются.
Р Т = Р 1 + Р 2 + Р 3 Р Т = 20 Ом + 30 Ом + 50 Ом R T = 100 Ом Суммарный ток определяется напряжением источника питания и эквивалентным сопротивлением цепи.

И Т = В T / R T
I T = 125 В/100 Ом
I T = 1,25 АПостоянный ток через последовательно соединенные резисторы.
I T = I 1 = I 2 = I 9001 5 3 = 1,25 А
Падение напряжения можно найти по закону Ома.
В 1 = I 1 Р 1
В 1 = (1,25 А)(20 Ом)
В 1 = 25,0 ВВ 2 = I 2 R 2
В 2 = (1,25 А)(30 Ом)
В 2 = 37,5 ВВ 3 = I 3 R 3
9 0662 В 3 = (1,25 А)(50 Ом)
В 3 = 62,5 ВПроверьте свои расчеты, добавив падение напряжения.
 В последовательной цепи они должны равняться увеличению напряжения источника питания.
В последовательной цепи они должны равняться увеличению напряжения источника питания.В Т = В 1 + В 2 + В 3 125 В = 25,0 В + 37,5 В + 62,5 В 125 В = 125 В Мы в порядке, так что давайте закончим.
Есть три уравнения для определения мощности. Поскольку у нас есть три резистора, давайте в качестве упражнения применим к каждому отдельное уравнение.
P 1 = В 1 I 1
9066 2 P 1 = (25,0 В)(1,25 A)
P 1 = 31,250 ВтP 2 = I 2 2 R 2
P 2 = (1,25 А) 2 (30 Ом)
P 2 = 46,875 ВтP 3 = В 3 2 / R 3
P 3 = (62,5 В) 2 /(50 Ом)
P 3 = 78,125 ВтВ последовательной цепи элемент с наибольшим сопротивлением потребляет наибольшую мощность.

Соблюдайте правила для параллельных цепей.
Параллельные сопротивления объединяются по правилу суммы обратных величин.
1 = 1 + 1 + 1 Р Т Р 1 Р 2 Р 3 1 = 1 + 1 + 1 Р Т 20 Ом 100 Ом 50 Ом 1 = 5 + 1 + 2 Р Т 100 Ом 100 Ом 100 Ом 1 = 8 Р Т 100 Ом Р Т = 100 Ом = 12,5 Ом 8 Суммарный ток определяется напряжением источника питания и эквивалентным сопротивлением цепи.

I T = V T / R T
I T = 125 В/12,5 Ом
I T = 10 A(Примечание: мы ответим на часть 4 перед частью 3.) В параллельной цепи каждая ветвь испытывает одинаковое падение напряжения.
В Т = В 1 = В 2 = В 9001 5 3 = 125 В
Ток в каждой ветви можно найти по закону Ома.
I 1 = V 1 / R 1
I 1 = (125 В)/(20 Ом)
I 1 = 6.25 АI 2 = V 2 / R 2
I 2 = (125 В)/(100 Ом)
I 2 = 1,25 АI 3 = V 3 / R 3
I 3 = (125 В)/(50 Ом)
I 3 = 2,50 АПроверьте свои расчеты, добавив токи.
 При параллельной схеме они должны суммироваться с током от источника питания.
При параллельной схеме они должны суммироваться с током от источника питания.I Т = я 1 + I 2 + I 3 10 А = 6,25 А + 1,25 А + 2,50 А 10 А = 10 А Хорошо, работает.
Снова в качестве упражнения используйте другое уравнение для определения электрической мощности каждого резистора.
P 1 = В 1 I 1
P 1 = (125 В)(6,25 А)
P 1 = 781,25 ВтP 2 = I 2 2 R 2
P 2 = (1,25 А) 2 (100 Ом)
P 2 = 156,25 ВтP 3 = В 3 2 / R 3
P 3 = (125 В) 2 /(50 Ом)
P 3 = 312,50 ВтВ параллельной цепи элемент с наименьшим сопротивлением потребляет наибольшую мощность.

практическая задача 2
На кухне в Северной Америке есть три прибора, подключенных к сети 120 В с автоматическим выключателем на 15 А: кофеварка мощностью 850 Вт, микроволновая печь мощностью 1200 Вт и тостер мощностью 900 Вт.- Нарисуйте принципиальную схему этой цепи.
- Какие из этих приборов могут работать одновременно без срабатывания автоматического выключателя?
раствор
Розетки подключаются параллельно , так что приборы в цепи независимы друг от друга. Выключение кофеварки не приведет к отключению тостера (при условии, что оба были включены одновременно). Каждый прибор также получит одинаковое регулируемое напряжение, что упрощает конструкцию электрических устройств. Недостатком этой схемы является то, что параллельные токи могут составлять опасно высокие уровни. А 9Автоматический выключатель 0710 в серии перед параллельными ответвлениями может предотвратить перегрузку, автоматически размыкая цепь.

Цепь 15 А, работающая при напряжении 120 В, потребляет 1800 Вт общей мощности.
P = VI = (120 В)(15 А) = 1800 Вт
Суммарная мощность в параллельной цепи равна сумме мощностей, потребляемых на отдельных ветвях.
кофеварка + микроволновая печь 850 Вт + 1200 Вт 2050 Вт микроволновая печь + тостер 1200 Вт + 900 Вт 2100 Вт тостер + кофеварка 900 Вт + 850 Вт 1750 Вт В этом контуре одновременно могут работать только кофеварка и тостер .
 Все другие комбинации вызовут размыкание автоматического выключателя.
Все другие комбинации вызовут размыкание автоматического выключателя.
практическая задача 3
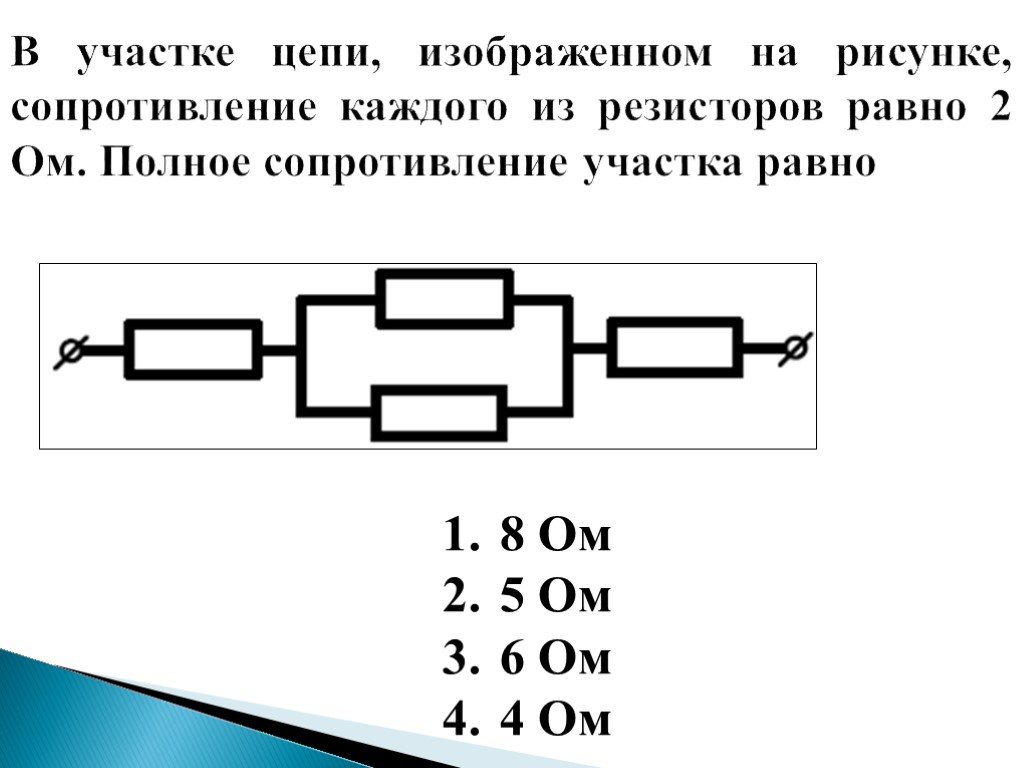
На приведенной ниже схеме показана схема с одной батареей и 10 резисторами; 5 слева и 5 справа. Определять…- ток через
- падение напряжения на
- мощность, рассеиваемая каждым резистором
раствор
Чтобы решить сложную проблему, нужно разбить ее на ряд более простых задач. Однако будьте осторожны, чтобы не упустить из виду свою цель среди всех кусочков. Перед началом проложите свой курс. В этом случае мы начнем с нахождения эффективного сопротивления всей цепи и тока от батареи. Это позволяет нам получить ток во всех различных сегментах цепи. (Ток делится и снова делится, пытаясь следовать по пути наименьшего сопротивления.) После этого легко рассчитать падение напряжения на каждом резисторе, используя В = IR и мощность, рассеиваемая при использовании P = VI . Никакая часть этой задачи не является сложной сама по себе, но поскольку схема очень сложна, мы некоторое время будем очень заняты.
Никакая часть этой задачи не является сложной сама по себе, но поскольку схема очень сложна, мы некоторое время будем очень заняты.
Начнем процесс с объединения резисторов. В этой цепи четыре последовательных пары.
слева R с = 3 Ом + 1 Ом
R с = 4 Ом
R с = 4 Ом + 2 Ом
Ч с = 6 Омсправа R с = 2 Ом + 3 Ом
R с = 5 Ом
R с 90 665 = 1 Ом + 4 Ом
R с = 5 ОмЭти пары образуют две параллельные цепи, одну слева и одну справа.
слева 1 = 1 + 1 Р р 4 Ом 6 Ом 1 = 5 Р р 12 Ом Р р = 12 Ом = 2,4 Ом 5 справа 1 = 1 + 1 Р р 5 Ом 5 Ом 1 = 2 Р р 5 Ом Р р = 5 Ом = 2,5 Ом 2 Каждая группа из четырех резисторов соединена последовательно с другой.

слева R с = 2,4 Ом + 0,6 Ом
R с = 3 Омсправа R s = 2,5 Ом + 0,5 Ом
R с = 3 ОмЛевая и правая половины схемы параллельны друг другу и батарее.
1 = 1 + 1 = 2 Р р 3 Ом 3 Ом 3 Ом Р р = 3 Ом = 1,5 Ом 2 Теперь, когда у нас есть эффективное сопротивление всей цепи, определим ток от источника питания по закону Ома.

I всего = В Всего + 24 В = 16 А R всего 1,5 Ом Теперь пройдемся по цепи (не буквально, конечно). В каждом соединении ток будет делиться на большее количество проводников по пути с меньшим сопротивлением и на меньшее количество по пути с большим сопротивлением. Поскольку заряд нигде не вытекает из полной цепи, ток будет одинаковым для всех элементов, соединенных последовательно друг с другом.
Левая и правая половины цепи имеют одинаковое общее сопротивление, а значит, ток будет делиться между ними поровну.
8 A для резистора 0,6 Ом
на слева .
8 A для резистора 0,5 Ом
на справа .С каждой стороны ток снова разделяется на две параллельные ветви.

Ответвления на слева имеют сопротивления в соотношении… Р 1 и 3 = 4 Ом + 2 Р 2 и 4 6 Ом 3
, что означает, что токи будут делиться в соотношении…Р 1 и 3 = 3 Р 2 и 4 2 3 8А = 4,8А 5 для резисторов 1 Ом и 3 Ом
на слева .2 8А = 3,2 А 5 для резисторов 2 Ом и 4 Ом
на слева .
Ответвления на справа идентичны, поэтому ток разделяется на две равные половины. ☟ ☟ ☟ ☟ ☟ 1 8А = 4,0 А 2 для резисторов 2 Ом и 3 Ом
на справа .1 8А = 4,0 А 2 для резисторов 1 Ом и 4 Ом
на справа .Используйте V = IR снова и снова, чтобы определить падение напряжения. (См. таблицы в конце этого решения.)
Использовать P = VI (или P = I 2 R или P = 9 0662 В 2 / R ) несколько раз для определения рассеиваемой мощности .
 Эти последние две задачи настолько утомительны, что вам следует использовать какое-нибудь приложение для работы с электронными таблицами. Введите заданные значения сопротивления и текущие значения, только что рассчитанные, в столбцы и дайте указание выбранному электронному устройству умножить их соответствующим образом. Как-то так…
Эти последние две задачи настолько утомительны, что вам следует использовать какое-нибудь приложение для работы с электронными таблицами. Введите заданные значения сопротивления и текущие значения, только что рассчитанные, в столбцы и дайте указание выбранному электронному устройству умножить их соответствующим образом. Как-то так…
| сопротивление (Ом) | ток (А) | напряжение (В) | мощность (Вт) |
|---|---|---|---|
| 0,6 | 8,0 | 04.8 | 38,40 |
| 1,0 | 4,8 | 04.8 | 23.04 |
| 2,0 | 3,2 | 06.4 | 20,48 |
| 3,0 | 4,8 | 14,4 | 69,12 |
| 4,0 | 3,2 | 12,8 | 40,96 |
| сопротивление (Ом) | ток (А) | напряжение (В) | мощность (Вт) |
|---|---|---|---|
| 0,5 | 8 | 04 | 32 |
| 1,0 | 4 | 04 | 16 |
| 2,0 | 4 | 08 | 32 |
| 3,0 | 4 | 12 | 48 |
| 4,0 | 4 | 16 | 64 |
практическая задача 4
Учитывая приведенную ниже схему…- Рассчитайте эквивалентное сопротивление цепи.

- Рассчитайте ток через батарею.
- Нарисуйте график зависимости напряжения от положения в цепи, предполагая, что В a = 0 В на отрицательной клемме аккумулятора.
- График тока в зависимости от положения в цепи.
раствор
Вот решения…
Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений…
Р Т = Р 1 + R 2 + R 3
R T = 3 Ом + 9 Ом + 6 Ом
R T = 18 ОмСуммарный ток можно найти по закону Ома…
I T = V T / R T
I T = (12 В)/(18 Ом) = ⅔ A
I T = 0,667 АНапряжение в цепи повышается в батарее и падает в резисторе (когда мы следим за течением обычного тока).
 Повышение напряжения в батарее указано как 12 В, а падение напряжения на каждом резисторе можно найти, многократно применяя закон Ома…
Повышение напряжения в батарее указано как 12 В, а падение напряжения на каждом резисторе можно найти, многократно применяя закон Ома…В 1 = I 1 Р 1
В 1 = (⅔ А)(3 Ом)
В 1 = 2 ВВ 2 = I 2 R 2
В 2 = (⅔ А)(9 Ом)
В 2 = 6 ВВ 3 = I 3 R 3
В 3 = (⅔ А)(6 Ом)
В 3 = 4 ВНачиная с нулевого напряжения на отрицательной клемме аккумулятора, напряжение повышается на 12 В, затем падает на 2 В, 6 В и 4 В, что возвращает нас к нулю. (Мы предполагаем, что батарея и провода имеют незначительное сопротивление.



 1/R = 1/R 1 — 1/R 2
1/R = 1/R 1 — 1/R 2  Эквивалентное сопротивление подцепи с R 3 ,
R 4 и R 5 равно 1/R экв. =1/1 + ½ = 3/2, таким образом, R экв. = (2/3). Эквивалентное сопротивление подцепи с R 2 , Р 3 ,
R 4 и R 5 равно R eq ‘ = R 2 + Re q = 1 + (2/3) = 5/3. Наконец, эквивалентное сопротивление всей цепи равно 1/R eq »=
1/1 + 3/5 = 8/5, таким образом, R eq »= 5/8. Сопротивление между точками A
и B составляет 5/8 Ом.
Эквивалентное сопротивление подцепи с R 3 ,
R 4 и R 5 равно 1/R экв. =1/1 + ½ = 3/2, таким образом, R экв. = (2/3). Эквивалентное сопротивление подцепи с R 2 , Р 3 ,
R 4 и R 5 равно R eq ‘ = R 2 + Re q = 1 + (2/3) = 5/3. Наконец, эквивалентное сопротивление всей цепи равно 1/R eq »=
1/1 + 3/5 = 8/5, таким образом, R eq »= 5/8. Сопротивление между точками A
и B составляет 5/8 Ом.
 Пусть
Напряжение сети равно V, а сопротивление R.
Пусть
Напряжение сети равно V, а сопротивление R.  Правило соединения гласит, что сумма токов, входящих в соединение, должна
равна сумме токов, выходящих из этого соединения. Правило цикла гласит
что сумма разностей потенциалов вокруг любой замкнутой цепи должна
быть нулем.
Правило соединения гласит, что сумма токов, входящих в соединение, должна
равна сумме токов, выходящих из этого соединения. Правило цикла гласит
что сумма разностей потенциалов вокруг любой замкнутой цепи должна
быть нулем.  Количество уравнений должно быть равно количеству неизвестных.
Количество уравнений должно быть равно количеству неизвестных.

 В последовательной цепи они должны равняться увеличению напряжения источника питания.
В последовательной цепи они должны равняться увеличению напряжения источника питания.

 При параллельной схеме они должны суммироваться с током от источника питания.
При параллельной схеме они должны суммироваться с током от источника питания.

 Все другие комбинации вызовут размыкание автоматического выключателя.
Все другие комбинации вызовут размыкание автоматического выключателя.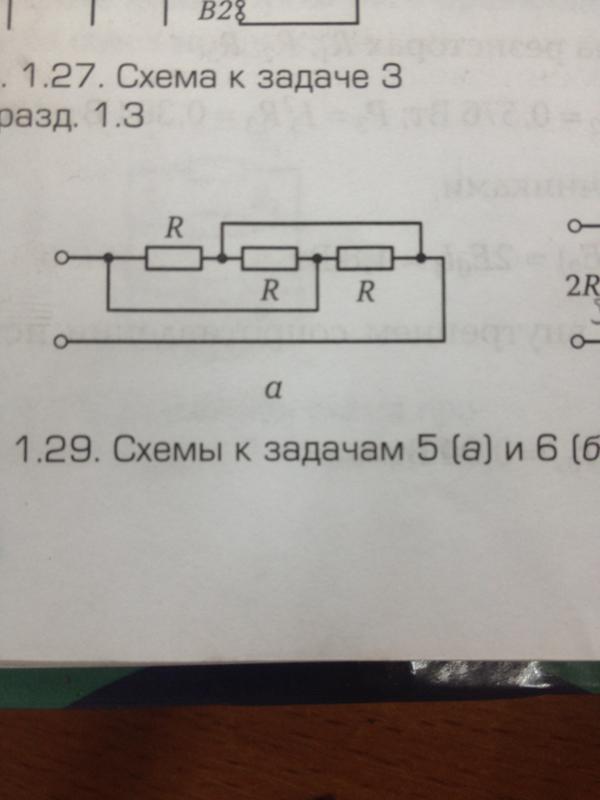

 Эти последние две задачи настолько утомительны, что вам следует использовать какое-нибудь приложение для работы с электронными таблицами. Введите заданные значения сопротивления и текущие значения, только что рассчитанные, в столбцы и дайте указание выбранному электронному устройству умножить их соответствующим образом. Как-то так…
Эти последние две задачи настолько утомительны, что вам следует использовать какое-нибудь приложение для работы с электронными таблицами. Введите заданные значения сопротивления и текущие значения, только что рассчитанные, в столбцы и дайте указание выбранному электронному устройству умножить их соответствующим образом. Как-то так…
 Повышение напряжения в батарее указано как 12 В, а падение напряжения на каждом резисторе можно найти, многократно применяя закон Ома…
Повышение напряжения в батарее указано как 12 В, а падение напряжения на каждом резисторе можно найти, многократно применяя закон Ома…
Leave A Comment