Под действием горизонтальной силы равной 12 н тело движется по закону: Под действием горизонтальной силы, равной 12 Н, тело движется по горизонтальной

СУНЦ УрФУ

Расписание

Электронный журнал

Поступающим

Олимпиады, турниры, конкурсы

Планы работы

Подготовительные курсы

Новости:

25.05.2023

Прозвенел последний звонок!

В СУНЦ УрФУ 23 мая для 237 выпускников прозвенел последний звонок.

21.05.2023

Два диплома на театральном фестивале

Литературный театр СУНЦ с успехом принял участие в региональном фестивале-конкурсе школьных театров «СоБытие».

15.05.2023

Проект из «магии и кирпичей»

Литературный театр СУНЦ показал спектакль «История одного рассказчика».

15.05.2023

«Милосердие сильнее мести»

Состоялась премьера спектакля литературного театра СУНЦ.

12.05.2023

И снова май, цветы, салют и слёзы

В преддверии Дня Победы в СУНЦ состоялся концерт, подготовленный учащимися и педагогами.

11.05.2023

«Бронза» наша!

Ученица СУНЦ (в составе команды) стала бронзовым призером чемпионата России по чир спорту.

Больше новостей

Видеогалерея:

Дом в котором (Литературный театр СУНЦ УрФУ, май 2023)

День Победы (04.05.2023)

Игра в Шекспира (Литературный театр СУНЦ УрФУ, апрель 2023)

Больше видео

О нас:

Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).

В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским  программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.

Иногородние обучающиеся проживают в уютном общежитии.

Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы.

Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону +7 343 367-82-22

и в разделе нашего сайта «Поступающим».

Как нас найти:

Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝

Проезд:

• автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
• автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
• троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
• троллейбусами № 4 до остановки «Сулимова», № 19, 32 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.

Сила трения — определение, формула, виды, как найти?

Покажем, как применять знание физики в жизни

Начать учиться

196. 2K

Когда вы гладите кота, катаетесь на велосипеде, моете полы и чешете пятку, вы сталкиваетесь с таким понятием, как сила трения. Что это такое, и как влияет на нашу жизнь — в этой статье.

Сила трения: величина, направление

С силой трения вы сталкиваетесь буквально каждую секунду. Каждый раз, когда вы взаимодействуете с любой поверхностью — идете по асфальту, сидите на стуле, пьете чай из чашки — на вас действует сила трения.

Трение — это и есть взаимодействие в плоскости соприкосновения двух поверхностей. Чтобы перевести трение на язык физики, вводится понятие сила трения. Сила трения — это величина, которая характеризует процесс трения по величине и направлению.

Измеряется сила трения, как и любая сила — в Ньютонах.

Возникает сила трения по двум причинам:

• Различные шероховатости, царапины и прочие «несовершенства» поверхностей. Эти дефекты задевают друг друга при соприкосновении и создается сила, тормозящая движение.
• Когда контактирующие поверхности практически гладкие (до идеала довести невозможно, но стремиться к нему — значит устремлять силу трения к нулю), то расстояние между ними становится минимальным. В этом случае возникает взаимное притяжение молекул вещества этих поверхностей. Притяжение обусловлено взаимодействием между электрическими зарядами атомов. В связи с этим можно часто услышать формулировку «Сила трения — сила электромагнитной природы»

Направлена сила трения всегда против скорости тела. В этом плане все просто, но всегда есть вопрос:

В задачах часто пишут что-то вроде: «Поверхность считать идеально гладкой». Это значит, что сила трения в данной задаче отсутствует. Да, в реальной жизни это невозможно, но во имя красивой математической модели трением часто пренебрегают.

Не переживайте из-за этой несправедливости, а просто решайте задачи без трения, если увидели словосочетание «гладкая поверхность».

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Сухое и вязкое трение

Есть очень большая разница между вашим соприкосновением с водой в бассейне во время плавания и соприкосновением между асфальтом и колесами вашего велосипеда.

В случае с плаванием мы имеем дело с вязким трением — явлением сопротивления при движении твердого тела в жидкости или воздухе. Самолет тоже подвергается вязкому трению и вон тот наглый голубь из вашего двора.

А вот сухое трение — это явление сопротивления при соприкосновении двух твердых тел. Например, если школьник ерзает на стуле или злодей из фильма потирает ладоши — это будет сухое трение.

А если злодей чистоплотный и потирает ладоши, капнув на них антисептик?

Тогда это вязкое трение, не смотря на то, что руки — твердые тела. В данном случае есть влажная прослойка.

Вязкое трение в школьном курсе физики не рассматривается подробно, а вот сухое — разбирают вдоль и поперек. У сухого трения также есть разновидности, давайте о них поговорим.

Трение покоя

Если вы решите сдвинуть с места грузовик, вряд ли у вас это получится. Не то, чтобы мы в вас не верим — просто это невозможно сделать из-за того, что масса человека во много раз меньше массы грузовика, да еще и сила трения мешает это сделать. Мир жесток, что тут поделать.

В случае, когда сила трения есть, но тело не двигается с места, мы имеем дело с силой трения покоя.

Сила трения покоя равна силе тяги. Например, если вы пытаетесь сдвинуть с места санки, действуя на них с силой тяги 10 Н, то сила трения будет равна 10 Н.

Сила трения покоя Fтр = Fтяги Fтр — сила трения покоя [Н] Fтяги — сила тяги [Н]

Немного потренируемся!

Задача

Найти силу трения покоя для тела, на которое действуют сила тяги в 4 Н.

Решение:

Тело покоится, значит

F_тр = Fтяги = 4 Н

Ответ: сила трения равна 4 Н.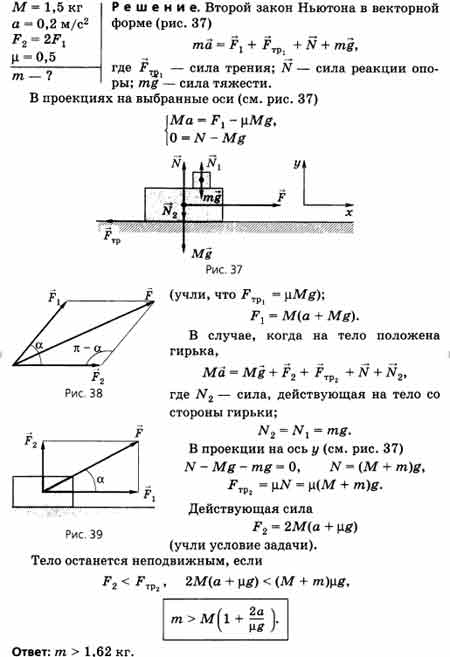

Трение скольжения

А теперь давайте скользить на коньках по льду. Каток достаточно гладкий, но, как мы уже выяснили, сила трения все равно будет присутствовать и вычисляться будет по формуле:

Сила трения скольжения Fтр = μN Fтр — сила трения скольжения [Н] μ — коэффициент трения [—] N — сила реакции опоры [Н]

Сила трения, которую мы получим по этой формуле будет максимально возможной — то есть больше уже некуда.

Сила реакции опоры — это сила, с которой опора действует на тело.

Она численно равна силе нормального давления и противоположна по направлению.

Сила нормального давления — это то же самое, что и вес тела?

Не совсем. Сила нормального давления направлена всегда перпендикулярно поверхности (нормаль — перпендикуляр к поверхности). Вес не обязательно направлен перпендикулярно поверхности.

В рамках школьного курса вес всегда направлен перпендикулярно поверхности, поэтому силу реакции опоры можно численно приравнивать к весу.

Подробнее про вес тела читайте в нашей статье😇

Также, если тело находится на горизонтальной поверхности, сила реакции опоры будет равна силе тяжести: N = mg.

Коэффициент трения — это характеристика поверхности. Он определяется экспериментально, не имеет размерности и показывает, насколько поверхность гладкая — чем больше коэффициент, тем более шероховатая поверхность. Коэффициент трения положителен и чаще всего меньше единицы.

Будем бдительны!

Из формулы не следует зависимость силы трения от площади соприкосновения. Например, если вы положите брусок на один бок и протащите по столу, а потом перевернете на другой, не равный по площади, и сделаете то же самое — сила трения не изменится.

Задача 1

Масса котика, лежащего на столе, составляет 5 кг. Коэффициент трения µ = 0,2. К коту прилагают внешнюю силу, равную 2,5 Н. Какая сила трения при этом возникает?

Решение:

По условию данной задачи невозможно понять, двигается наш котик или нет. Решение о том, приравниваем ли мы к силе тяги силу трения, принять сразу нельзя. В таких случаях нужно все-таки рассчитать по формуле:

F = μN

Так как котик лежит на горизонтальной поверхности, сила реакции опоры в данном случае равна силе тяжести: N = mg.

F = μmg = 0,2 · 5 · 10 = 10Н

Мы получили максимально возможную силу трения. Внешняя сила по условию задачи меньше максимальной. Это значит, что котик находится в покое. Сила трения уравновешивает внешнюю силу. Следовательно, она равняется 2,5 Н.

Ответ: возникает сила трения величиной 2,5 Н

Задача 2

Барсук скользит по горизонтальной плоскости. Найти коэффициент трения, если сила трения равна 5 Н, а сила давления тела на плоскость — 20 Н.

Решение:

В данной задаче нам известно, что барсучок скользит. Значит нужно воспользоваться формулой:

F_тр = μN

Так как барсук находится на горизонтальной поверхности, сила реакции опоры в данном случае равна силе давления на плоскость: N = F_д.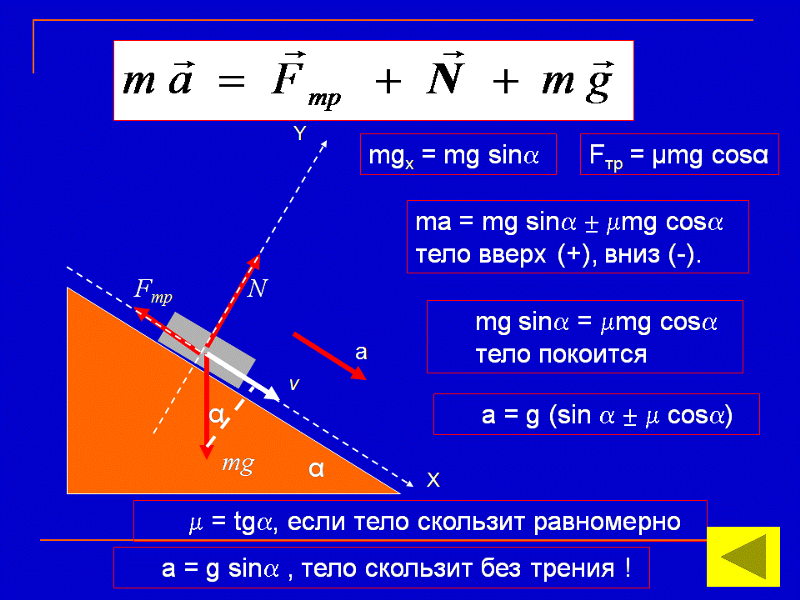

F_тр = μF_д

Выражаем коэффициент трения:

μ = F_тр / F_д = 5 / 20 = 0,25

Ответ: коэффициент трения равен 0,25

Задача 3

Пудель вашей бабушки массой 5 кг скользит по горизонтальной поверхности. Сила трения скольжения равна 20 Н. Найдите силу трения, если пудель сильно похудеет, и его масса уменьшится в два раза, а коэффициент трения останется неизменным.

Решение:

В данной задаче нам известно, что пудель скользит. Значит, нужно воспользоваться формулой:

F_тр = μN

Так как пудель находится на горизонтальной поверхности, сила реакции опоры в данном случае равна силе тяжести: N = mg.

F_тр = μmg

Выразим коэффициент трения:

μ = F_тр / mg = 20 / 5 · 10 = 0,4

Теперь рассчитаем силу трения для массы, меньшей в два раза:

Ответ: сила трения будет равна 10 Н.

Задача 4

Ученик провел эксперимент по изучению силы трения скольжения, перемещая брусок с грузами равномерно по горизонтальным поверхностям с помощью динамометра.

Результаты экспериментальных измерений массы бруска с грузами m, площади соприкосновения бруска и поверхности S и приложенной силы F представлены в таблице.

 

№ эксперимента	Поверхность	m, г	S, см2	F, H
1	деревянная рейка	200	30	0,8±0,1
2	пластиковая рейка	200	30	0,4±0,1
3	деревянная рейка	100	20	0,4±0,1
4	пластиковая рейка	400	20	0,8±0,1

Какие утверждения соответствуют результатам проведенных экспериментальных измерений? Из предложенного перечня утверждений выберите два правильных.

1. Коэффициенты трения скольжения во втором и третьем опытах равны.

2. Коэффициент трения скольжения между бруском и деревянной рейкой больше коэффициента трения скольжения между бруском и пластиковой рейкой.

3. Сила трения скольжения зависит от площади соприкосновения бруска и поверхности.

4. Сила трения скольжения зависит от рода соприкасающейся поверхности.

Решение:

Подробно рассмотрим каждое утверждение.

1. В данном случае сила реакции опоры равна силе тяжести. Значит F_тр = μN = μmg.

   Выразим коэффициент трения скольжения:
   μ = F_тр / mg

   Коэффициент трения скольжения во втором опыте равен 0,4 / (0,2 · 10) = 0,2.

   В третьем опыте — 0,4 / (0,1 · 10) = 0,4.

   Следовательно, утверждение «Коэффициенты трения скольжения во втором и третьем опытах равны» неверно.

2. Как и в первом утверждении, коэффициент трения будет вычисляться по формуле:
   μ = F_тр / mg

   Для деревянной рейки μ = F_тр / mg = 0,8 / 0,2 · 10 = 0,4

   Для пластиковой рейки μ = F_тр / mg = 4,8 / 0,2 · 10 = 0,2

   Следовательно утверждение «Коэффициент трения скольжения между бруском и деревянной рейкой больше коэффициента трения скольжения между бруском и пластиковой рейкой» верно.

3. Согласно формуле F_тр = μN, сила трения не зависит от площади поверхности соприкосновения. Значит утверждение «Сила трения скольжения зависит от площади соприкосновения бруска и поверхности» неверно.

4. Если проанализировать первый и второй эксперимент, можно увидеть, что при прочих равных данных сила меняется. Это значит, что утверждение «Сила трения скольжения зависит от рода соприкасающейся поверхности» верно.

Ответ: 25

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Трение качения

Про колесо совершенно точно нельзя сказать, что оно скользит или покоится. При этом сила трения явно возникает, так как существует соприкосновение двух поверхностей.

В этом случае мы говорим о трении качения — сопротивлению движения, если одно тело катится по поверхности другого. При равных силах нормального давления сила трения скольжения больше силы трения качения. Это явление часто используют, например, ставя колесики на чемодан. Да и вообще, ставя колесики куда угодно.

Сила трения качения Fтр = (λN)/R Fтр — сила трения качения [Н] λ — коэффициент трения качения [м] N — сила реакции опоры [Н] R — радиус колеса [м]

Задачи на трение качения встречаются только в задачах высокого уровня сложности (например, в олимпиадах). Однако на формулу посмотреть полезно, даже если вы не планируете покорять самую высокую вершину.

Если приглядеться, она очень похожа на формулу трения скольжения, только в знаменателе появляется радиус. Если мы будем увеличивать знаменатель, то сила трения будет уменьшаться. То есть, чем больше радиус колеса, тем меньше трение.

Ладно, давайте все-таки решим задачу на силу трения качения — только никому об этом не рассказывайте 😉

Задача

Какого радиуса понадобится установить колесо, чтобы уменьшить силу трения, равную 17 Н — на 5 Н. При коэффициенте трения 0,6 мм и силе нормального давления тела равной 10 кН.

Решение:

Берем формулу силы трения качения:

F_тр = (λN)/R

Выражаем из нее радиус:

R = (λN)/F_тр

Коэффициент трения качения и сила нормального давления нам даны, а чтобы найти силу трения, нам нужно вычесть из начальной силы трения ее изменение:

F_{тр 2} = F_{тр 1} − ΔF_тр = 17 − 5 = 12Н

Подставляем числа в формулу, предварительно переведя их в СИ:

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

R = (λN)/F_тр = 0,0006 · 10 000 / 12 = 0,5 м

Ответ: необходимо поставить колесо радиусом 0,5 м.

Избавиться от трения: возможно ли это

Итак, идеально гладких поверхностей в реальной жизни не бывает. Это значит, что стараясь делать поверхность идеально гладкой — например, натирая ее миллион часов супер-мелкой наждачной бумагой — мы минимизируем трение, но не избавляемся от него.

Но это не значит, что способов избавиться от трения не существует. Например, вполне себе реальны поезда на магнитных подушках. Благодаря магнитному полю, которое создается между рельсом и вагоном, поезд как будто бы парит. Так он ликвидирует соприкосновение различных поверхностей, из-за которого и создается трение.

Карина Хачатурян

К предыдущей статье

Инерция

К следующей статье

Сила тяжести

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

4.2 Первый закон движения Ньютона: инерция

Цели обученияПервый закон Ньютона и трениеМасса и инерцияПроверить свое понимание

Обсудите связь между массой и инерцией.

Основные термины раздела

трение	инерция	закон инерции
масса	Первый закон движения Ньютона	система

Первый закон Ньютона и трение

Первый закон движения Ньютона гласит следующее:

1. Тело в состоянии покоя стремится оставаться в покое.
2. Движущееся тело имеет тенденцию оставаться в движении с постоянной скоростью, если на него не действует результирующая внешняя сила. (Напомним, что постоянная скорость означает, что тело движется прямолинейно и с постоянной скоростью.)

На первый взгляд может показаться, что этот закон противоречит вашему повседневному опыту. Вы, наверное, замечали, что движущийся объект обычно замедляется и останавливается, если не предпринимать никаких усилий для поддержания его движения. Ключ к пониманию того, почему, например, скользящий ящик замедляется (по-видимому, сам по себе), заключается в том, чтобы сначала понять, что на ящик действует чистая внешняя сила, заставляющая ящик замедляться. Без этой чистой внешней силы коробка продолжала бы скользить с постоянной скоростью (согласно первому закону движения Ньютона). Какая сила действует на ящик, чтобы замедлить его? Эта сила называется трением. Трение — это внешняя сила, действующая против направления движения (см. рис. 4.3). Думайте о трении как о сопротивлении движению, которое замедляет работу.

Рассмотрим стол для аэрохоккея. Когда воздух отключен, шайба скользит только на короткое расстояние, прежде чем трение замедляет ее до остановки. Однако, когда воздух включен, он немного приподнимает шайбу, поэтому шайба испытывает очень мало трения при движении по поверхности. Благодаря почти устраненному трению шайба скользит с очень небольшим изменением скорости. На поверхности без трения шайба не будет подвергаться чистой внешней силе (без учета сопротивления воздуха, которое также является формой трения). Кроме того, если мы достаточно знаем о трении, мы можем точно предсказать, как быстро объекты будут замедляться.

Теперь давайте подумаем о другом примере. Человек толкает коробку по полу с постоянной скоростью, прикладывая к ней силу

+ 50 Н. (Положительный знак означает, что по соглашению движение движется вправо.) Какова сила трения, противодействующая движение? Сила трения должна быть -50 Н.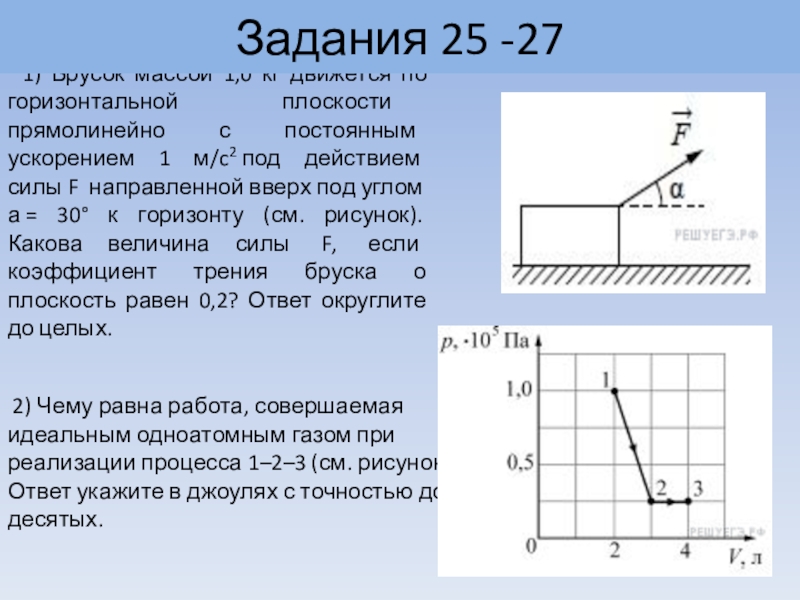 Почему? Согласно первому закону движения Ньютона, на любой объект, движущийся с постоянной скоростью, не действует никакая внешняя сила, а это означает, что сумма сил, действующих на объект, должна быть равна нулю. Математический способ сказать, что никакая внешняя сила не действует на объект, это  Fnet= 0  Fnet= 0  или  ΣF=0. ΣF=0. Таким образом, если человек прикладывает силу +50 Н, то сила трения должна быть равна -50 Н, чтобы сумма двух сил равнялась нулю (то есть, чтобы две силы равнялись отменить друг друга). Всякий раз, когда вы сталкиваетесь с фразой при постоянной скорости , первый закон Ньютона говорит вам, что чистая внешняя сила равна нулю.

Рис. 4.3. Для коробки, скользящей по полу, трение действует в направлении, противоположном скорости.

Сила трения зависит от двух факторов: коэффициента трения и нормальной силы. Для любых двух поверхностей, соприкасающихся друг с другом, коэффициент трения является постоянной величиной, зависящей от природы поверхностей. Нормальная сила — это сила, действующая на поверхность, которая давит на объект в ответ на гравитацию, тянущую объект вниз. В форме уравнения сила трения равна

4.1f=мкН,f=мкН,

, где μ — коэффициент трения, а Н — нормальная сила. (Коэффициент трения обсуждается более подробно в другой главе, а нормальная сила обсуждается более подробно в разделе Третий закон Ньютона .)

Напомним из раздела о силе, что результирующая внешняя сила действует от снаружи на интересующий объект. Более точное определение состоит в том, что он действует на интересующую систему. Система — это один или несколько объектов, которые вы выбрали для изучения. Важно определить систему в начале проблемы, чтобы выяснить, какие силы являются внешними и их необходимо учитывать, а какие являются внутренними и ими можно пренебречь.

Например, на рис. 4.4 (а) двое детей толкают третьего ребенка в тележке с постоянной скоростью. Интересующая система — это повозка плюс маленький ребенок, как показано в части (b) рисунка. Двое детей позади повозки воздействуют на эту систему извне ( F 1, F 2). Трение f , действующее на оси колес и на поверхность, где колеса касаются земли, две другие внешние силы, действующие на систему. На систему действуют еще две внешние силы: вес Вт опускания системы и нормальная сила Н толкания грунта вверх. Обратите внимание, что повозка не движется вертикально, поэтому первый закон Ньютона говорит нам, что нормальная сила уравновешивает вес. Поскольку тележка движется вперед с постоянной скоростью, сила трения должна быть равна сумме сил, приложенных двумя детьми.

Рисунок 4.4 (a) Повозка и всадник образуют систему , на которую действуют внешние силы. (b) Двое детей, толкающих тележку, и ребенок создают две внешние силы. Трение, действующее на оси колес и на поверхность шин, где они соприкасаются с землей, создает внешнюю силу, действующую против направления движения. Вес Вт и нормальная сила Н от земли — еще две внешние силы, действующие на систему. Все внешние силы представлены на рисунке стрелками. Все внешние силы, действующие на систему, складываются, но поскольку вагон движется с постоянной скоростью, сумма всех сил должна равняться нулю.

Масса и инерция

Инерция — это склонность покоящегося объекта оставаться в покое или движущегося объекта оставаться в прямолинейном движении с постоянной скоростью. Это ключевое свойство объектов впервые было описано Галилеем. Позже Ньютон включил понятие инерции в свой первый закон, который часто называют законом инерции.

Как мы знаем из опыта, одни объекты обладают большей инерцией, чем другие. Например, изменить движение большого грузовика сложнее, чем изменить движение игрушечного грузовика. На самом деле инерция объекта пропорциональна массе объекта. Масса — это мера количества материи (или вещества ) в объекте.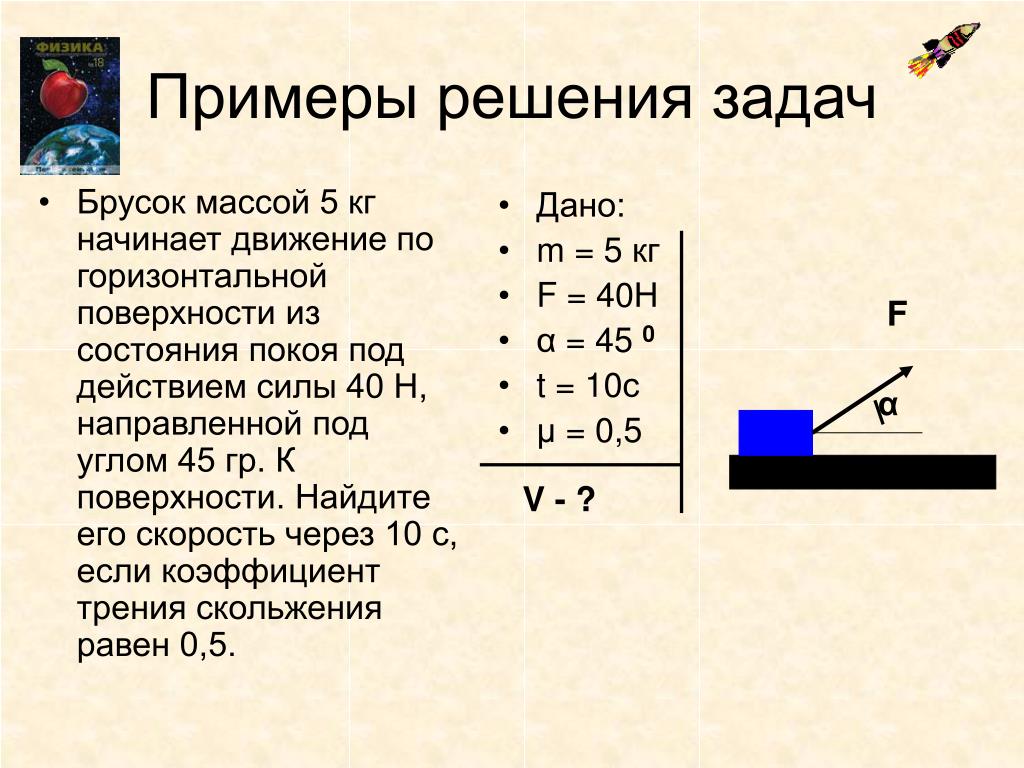 Количество или количество материи в объекте определяется количеством и типами атомов, содержащихся в объекте. В отличие от веса (который изменяется при изменении силы гравитации), масса не зависит от гравитации. Масса объекта одинакова на Земле, на орбите или на поверхности Луны. На практике очень сложно сосчитать и идентифицировать все атомы и молекулы в объекте, поэтому массу таким способом обычно не определяют. Вместо этого масса объекта определяется путем сравнения ее со стандартным килограммом. Поэтому масса выражается в килограммах.

Советы для достижения успеха

В повседневном языке люди часто используют термины вес и масса взаимозаменяемо, но это неправильно. Вес на самом деле является силой. (Мы рассмотрим эту тему более подробно в разделе Второй закон Ньютона .)

Смотреть физику

Первый закон движения Ньютона

В этом видео показано, как мы думали о движении и силе во времена, предшествовавшие концепции инерции Галилея и первому закону движения Ньютона, и то, как мы понимаем силу и движение сейчас.

Щелкните, чтобы просмотреть содержание

Проверка на хватку

До того, как мы поняли, что объекты имеют тенденцию сохранять свою скорость по прямой линии, если на них не действует результирующая сила, люди думали, что объекты имеют тенденцию останавливаться сами по себе. Это произошло потому, что конкретная сила еще не была понята. Что это была за сила?

1. Гравитационная сила
2. Электростатическая сила
3. Ядерная сила
4. Сила трения

Виртуальная физика

В этой симуляции вы сначала исследуете общую силу, размещая синих человечков с левой стороны каната для перетягивания каната, а красных — с правой стороны (щелкая людей и перетаскивая их мышью). Поэкспериментируйте с изменением количества и размера людей с каждой стороны, чтобы увидеть, как это повлияет на исход матча и общую силу. Нажмите кнопку «Вперед!» кнопку, чтобы начать матч, и кнопку «сбросить все», чтобы начать заново.

Далее перейдите на вкладку Трение. Попробуйте выбрать разные объекты, которые человек будет толкать. Сдвиньте приложил силу кнопку вправо, чтобы приложить силу вправо, и влево, чтобы приложить силу влево. Сила будет продолжать действовать до тех пор, пока вы удерживаете кнопку. Посмотрите на стрелку, показывающую изменение силы трения по величине и направлению в зависимости от того, какую силу вы прикладываете. Попробуйте увеличить или уменьшить силу трения, чтобы увидеть, как это изменение повлияет на движение.

Рисунок 4.5 Щелкните здесь для имитации

Проверка захвата

Щелкните вкладку для Acceleration Lab и отметьте опцию Сумма сил . Сдвиньте коробку вправо, а затем отпустите. Обратите внимание, в каком направлении указывает стрелка суммы сил после того, как человек перестанет толкать коробку и позволит ей продолжить движение вправо самостоятельно. В этой точке, в каком направлении направлена ​​результирующая сила, сумма сил? Почему?

1. Суммарная сила действует вправо, потому что приложенная внешняя сила действовала вправо.
2. Суммарная сила действует слева, потому что приложенная внешняя сила действовала слева.
3. Суммарная сила действует вправо, потому что сила трения действует вправо.
4. Суммарная сила действует слева, потому что слева действует сила трения.

Проверьте свое понимание

Упражнение 5

Что утверждает первый закон Ньютона?

1. Тело в состоянии покоя имеет тенденцию оставаться в состоянии покоя, а тело в движении имеет тенденцию оставаться в движении с постоянным ускорением, если на него не действует результирующая внешняя сила.
2. Тело в состоянии покоя имеет тенденцию оставаться в покое, а тело в движении имеет тенденцию оставаться в движении с постоянной скоростью, если на него не действует результирующая внешняя сила.
3. Скорость изменения количества движения тела прямо пропорциональна внешней силе, приложенной к телу.
4. Скорость изменения импульса тела обратно пропорциональна внешней силе, приложенной к телу.

Упражнение 6

Согласно первому закону Ньютона, движущееся тело стремится оставаться в движении с постоянной скоростью. Однако, когда вы перемещаете объект по поверхности, он в конце концов замедляется и останавливается. Почему?

1. На объект действует сила трения о поверхность, препятствующая его движению.
2. Объект испытывает гравитационную силу Земли, которая препятствует его движению
3. На объект действует внутренняя сила, создаваемая самим телом, которая противодействует его движению.
4. На объект действует псевдосила движущегося тела, противодействующая его движению.

Упражнение 7

Что такое инерция?

1. Инерция — это тенденция объекта сохранять свою массу.
2. Инерция — это тенденция объекта оставаться в состоянии покоя.
3. Инерция — это тенденция объекта оставаться в движении
4. Инерция — это тенденция объекта оставаться в покое или, если он движется, оставаться в движении.

Упражнение 8

Что такое масса? От чего это зависит?

1. Масса — это вес объекта, зависящий от силы гравитации, действующей на объект.
2. Масса — это вес объекта, зависящий от количества и типов атомов в объекте.
3. Масса – это количество материи, содержащейся в объекте, и она зависит от гравитационной силы, действующей на объект.
4. Масса — это количество материи, содержащейся в объекте, и она зависит от количества и типов атомов в объекте.

• Печать
• Поделиться

Законы движения Ньютона

Теперь, когда мы знаем законы движения Ньютона, как мы применять их? Как они могут позволять нам предсказывать движение объекта, если мы знаем все силы, действующие на него? Как может они позволяют нам предсказывать силы на объекте, если мы знаем его движение?

Сказать, что остальная часть этого конечно просто ищет окольные способы применить

F = м и

---

Пример 1: Предположим, ящик тянут по трение меньше пол (пока такой пол очень трудно найти, такой еще будет помогите нам понять концепцию и мы можем вернуться к этому ситуация позже, после учитывая трение, и решить ее более реалистично).

Представьте, что ящик тянут по горизонтали, трение меньше эт. Вокруг него привязана веревка, и человек тянет за веревку с силой Т. Т — натяжение в веревка. Что происходит с ящиком?

Прежде чем мы сможем применить второй закон Ньютона,

F = м а

мы должны найти чистую силу — вектор сумму все силы — действующие на объект. В добавок к сила T действующая на веревку, какие другие силы действуют на объект ?

Как обсуждалось в классе, на механике мы можем ограничить внимание на «контактные» силы и «гравитацию». Это означает гравитацию тянет вниз по этому ящику с силой, равной его весу, с . Но пол поддерживает ящик. Пол отвечает толкать вверх на ящике с силой, которую мы называем нормальной сила . «Нормальный» означает «перпендикулярный». Мы назовем эту силу н ; вы также можете встретить его с пометкой Н или Ф _Н .

Эти силы показаны на «диаграмме свободного тела» выше. Мы нарисовали в все силы, действующие на объект. Суммарная сила равна вектору сумме этих сил.

F _нетто = F = T + n + w

где , греческий верхний регистр «сигма» означает «сумма». Помни, хотя, векторное обозначение равно всегда элегантная стенографическая запись. Когда мы пишем

F _нетто = F = T + n + w

мы действительно написали

F _{нетто, х} = F _x = T _x + n _x + w _х

и

F _{нетто,у} = F _y = T _y + n _y + ш _г

Каковы эти x- и y-компоненты сил T, n, и с ? Для этого первого простого примера мы можем найти — по осмотр — что эти компоненты

Т _х = Т

Т _у = 0

н _х = 0

п _д = п

ш _х = 0

ш _г = — ш

Теперь мы готовы применить

F = м а

Но это нужно сначала записать в терминах компонентов,

F _x = F _{нетто, x} = F _x = m a _x

F _x = F _{нетто, x} = F _x = T _x + n _x + w _x = T = m _x

Т = м а _х

а _х = Т/м

Ящик имеет горизонтальное ускорение равное натяжение T разделить на m, массу ящика. Что насчет силы в вертикальном направлении?

F _y = F _нетто,y = F _y = m a _y

F _y = F _net,y = F _y = T _y + n _y + w _y = n — w = m а _у

н — ш = м а _у

Поскольку мы знаем, что ящик не ускоряется в направлении Y — не вскакивает с пола и не закапывается в пол — мы знаем _y = 0, поэтому

н = ш

Нормальная восходящая сила, действующая на ящик со стороны пола, в этой ситуации, равна весу, направленной вниз силе сила тяжести.

---

Пример 2: Какие силы действуют на книгу, если ее толкнуть вниз по нему с силой F пока он сидит на ровной, горизонтальный стол, как показано на рисунке ниже?

Собери все силы. Это называется «свободное тело». диаграмме». В этом курсе механики мы ограничимся «контактные силы» и сила тяжести. Контактные силы, для в этом случае будет «нормальная» сила — перпендикулярная сила — под воздействием стола — обозначенного на схеме n — и сила F с помощью руки. Гравитация оказывает силу вниз, называется весом и маркируется w . Так же, как в предыдущий пример, мы можем сразу написать

F = м а

, но это действительно элегантное сокращение для

. F _x = F _{нетто, x} = F _x = м а _х

и

F _y = F _нетто,y = F _и = м а _г

В этом примере, хотя ничего не происходит по горизонтали направление. Все силы есть только вертикальные компоненты, так что все, что у нас есть, это

F _y = F _нетто,y = F _y = м а _г

Принимая за положительное, имеем

F _y = F _нетто,y = F _y = п — ш — F

Поскольку книга лежит на столе, мы знаем, что она не ускоряется поэтому _y = 0. Это означает

н — ш — Ж = 0

н = ш + Ж

Мы можем использовать законы Ньютона, чтобы определить значение нормального заставить н.

---

Эта же идея и техника могут быть использованы немного по-другому. ситуация,

Пример 3: Рассмотрим лампу, подвешенную на цепи. Что натяжение в цепи?

Как всегда, начнем со «схемы свободного тела». Натяжение Т воздействует вверх на лампу, в то время как сила тяжести притягивает вниз с усилием w , вес светильника. Чистая сила является векторной суммой этих двух сил. Лампа не ускоряет , поэтому усилие до должно равна сила вниз . По величине это означает

Т = ш

---

Напряжение: Напряжение величина силы при помощи цепи, веревки или веревки. Направление этого сила зависит от остальной ситуации и объекта, который мы концентрируемся на данный момент. Если мы сосредоточимся на цепи, показанной ниже, направленная вниз сила T’ — это сила сила, действующая на цепь со стороны лампы, в то время как направленная вверх сила Т» сила, действующая на цепь со стороны потолка. Здесь нет заменить хорошие диаграммы свободного тела.

---

Пример 4: Рассмотрим светофор, подвешенный на шнурах, как показано на эскизе ниже. Каково напряжение в каждом из этих шнуры?

Натяжение T ₃ легко, поэтому мы рассмотрим первое. Как мы видели в предыдущих двух примерах; это напряжение в вертикальный шнур, поддерживающий вес, как раз равен весу. В На приведенной ниже схеме мы нарисовали силы, действующие на светофор. На светофор действуют только силы w , вес действует вниз, и T ₃ , восходящая сила из-за вертикального троса.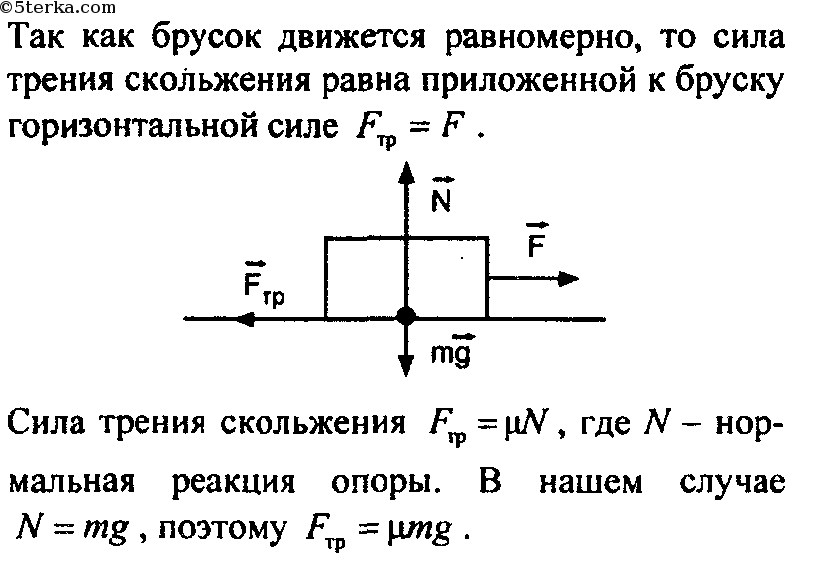 Т ₃ это натяжение этого троса. Ясно

Т ₃ = ш

А как насчет натяжения двух других тросов, T ₂ и Т ₁ ? Чтобы найти их, мы должны посмотреть на перекресток где три кабеля сходятся вместе. Этот перекресток находится в равновесие так

F нетто = 0

Ж _нетто = Ж = Т ₁ + Т ₂ + Т ₃ = 0

Однако мы должны помнить, что этот единственный вектор уравнение является элегантным, сокращенная запись для два скаляра уравнения,

F _нетто,x = F _х = Т _{1 х} + Т _{2 х} + Т _{3 х} = 0

F _нетто,y = F _г = Т _{1 г} + Т _{2 г} + Т _{3 г} = 0

Итак, мы должны разложить все эти силы на их x- и Y-компоненты,

T _1x = — T ₁ cos 37 ^o = — 0,8 T ₁

T _{1 год} = T ₁ sin 37 ^o = 0,6 Т ₁

T _2x = T ₂ cos 53 ^о = 0,6 Т ₂

T _2y = T ₂ sin 53 ^o = 0,8 Т ₂

Т _3x = 0

T _{3 года} = — T ₃ = — w

знаки важны! Теперь мы можем вернуться к уравнения компонентов и решить для растяжения T ₁ и Т ₂ .

F _нетто,x = F _х = Т _{1 х} + Т _{2 х} + Т _{3 х} = 0

T _{1 x} + T _{2 x} + T _{3 x} = 0

— 0,8 Т ₁ + 0,6 Т ₂ + 0 = 0

Т ₁ = 0,75 Т ₂

F _{нетто, у} = F _г = Т _{1 г} + Т _{2 г} + Т _{3 г} = 0

Т _{1 год} + Т _{2 года} + Т _{3 года} = 0

0,6 Т ₁ + 0,8 Т ₂ 2 — ш = 0

0,6 Т ₁ + 0,8 Т ₂ = w

0,6 (0,75 Т ₂ ) + 0,8 Т ₂ = w

1,25 Т ₂ = ш

Т ₂ = 0,8 Вт

T ₁ = 0,75 (0,8 Вт)

T ₁ = 0,6 Вт

---

Теперь мы расширяем наши приложения и смотрим на Этвудс Машина

Пример 5 : Рассмотрим показанную здесь машину Этвуда с массы m ₁ и m ₂ . Они прикреплены к легкий шнур над шкивом, как показано на рисунке. Что такое ускорение системы?

	Мы можем сказать «ускорение системы» для масс 1 и 2 будут иметь то же ускорение , так как они крепятся шнуром. Если m 2 > m 1 и Этвудс машина выходит из состояния покоя, масса m 1 будет ускорение вверх в сторону массы m 2 разгоняет до направления. Собственно, это будет их ускорений независимо от того, вышла ли система из состояния покоя или двигается. Вероятно, это легче представить, если вы подумайте о том, что система выходит из состояния покоя. Как мы можем применить F = m a ? Применим F = m a к массам, по одной на время.
Посмотрите на меньшую массу, m 1 . Какие силы, действующие на эту массу? Натяжение струны создает силу вверх в то время как гравитация оказывает силу вниз . Мы ожидаем этого масса, имеющая ускорение a, равное и . Там горизонтальных сил нет. Мы возьмем вверх по как положительное . F нетто = F = Т — ш 1 = м 1 а F нетто = F = Т — м 1 г = м 1 а Т — м 1 г = м 1 а Это одно уравнение имеет два неизвестных — напряжение T и ускорение a. Так что нам нужно еще информация .
Мы получаем эту дополнительную информацию, просматривая силы, действующие на более тяжелую массу, м 2 и применяя второй закон Ньютона, F = m a , к эта масса. Горизонтальных сил нет. Натяжение струны создает силу вверх в то время как гравитация оказывает силу вниз . Мы ожидаем этого масса, чтобы иметь ускорение a, которое вниз . Мы можно назвать вниз «положительным» для этой массы или мы можем позвонить до «положительно» и дальше ожидаем эта масса должна иметь ускорение — а. Любой выбор Это хорошо. На этот раз давайте выберем из как «положительное». F нетто = F = ш 2 — Т = м 2 а F нетто = F = м 2 г — Т = м 2 а м 2 г — Т = м 2 а Конечно, это одно уравнение также имеет два неизвестные — напряжение T и ускорение a.

Но теперь у нас есть два уравнения с двумя неизвестными и этого достаточно. Мы можем найти напряжение T в первое уравнение,

Т — м ₁ г = м ₁ а

Т = м ₁ г + м ₁ а

, а затем подставьте это во второе уравнение

. м ₂ г — Т = м ₂ а

м ₂ г — ( м ₁ г + м ₁ а ) = м ₂ а

м ₂ г — м ₁ г — м ₁ а = м ₂ а

м ₂ г — м ₁ г = м ₁ а + м ₂ а

( м ₂ — м ₁ ) г = ( м ₁ + м ₂ ) а

( м ₁ + м ₂ ) а = ( м ₂ — м ₁ ) г

а = ( м ₂ — м ₁ ) г / ( м ₁ + м ₂ )

---

Пример 6: Теперь давайте рассмотрим наклонную машину Этвуда. Массы м ₁ и м ₂ соединены нитью который наезжает на шкив и массой m ₂ находится на гладкой наклонная плоскость. Помните, что «гладкий» — это просто кодовое слово для «без трения»; мы скоро перейдем к трениям. Это наклонно Машина Этвудса нарисована здесь:

Теперь мы хотим применить второй закон Ньютона, F = m и . Второй закон Ньютона описывает действие сил на один объект. Итак, мы должны изолировать все силы от массы м ₁ и применить его. Затем мы изолируем все силы на массу m ₂ и нанесите еще раз. Это требует хорошего свободного тела диаграммы.

На подвешенный груз m1 действуют только две силы; струна тянет вверх с силой, которую мы обозначаем буквой Т, в то время как гравитация тянет вниз с силой мы маркируем w:

Мы ожидаем, что ускорение будет восходящим, и нарисовали его. рядом с диаграммой свободного тела. Как всегда, мы готовы подать заявку Ф = m a к этим силам, действующим на этот объект.

F _нетто = F = T — m ₁ g = m ₁ а

Т — м ₁ г = м ₁ а

Как мы уже могли ожидать, это одно уравнение имеет два неизвестные — напряжение T и ускорение a — так что надо искать в другом месте для получения дополнительной информации. Конечно, где посмотреть находится на другой массе.

Тщательно постройте диаграмму свободного тела, показывающую все силы действующая на массу m ₂ . Действуют три сил. на эту массу — струна действует с силой Т , (без трения) наклонная плоскость оказывает «нормальную» силу n , и гравитация тянет вниз с силой w ₁ = м ₁ г. Чтобы найти чистую силу , мы должны решить эти векторы на их компоненты. Так как ускорение будет быть вдоль направления плоскости, мы выбрали это направление как ось х.

Обратите внимание, что угол в эта диаграмма измерена от оси y . Это означает, что вес имеет компоненты

w _x = m ₂ g sin

w _y = — m ₂ g cos

А у нас

н _х = 0

п _д = п

и

Т _х = — Т

Т _у = 0

Убедитесь, что вы понимаете знаки и синусы! Не продолжай пока все эти составляющие вам не понятны!

Теперь мы можем применить второй закон Ньютона к этой массе:

F = м а

F = F _нетто = T + n + ш = м а

F _x = F _{нетто, x} = F _x = м ₂ a _x

Ф _х = T _x + n _x + w _x = m ₂ а _х

— Т _{+ 0 + м ​​ 2 г синх = m 2 a x = m 2 a}

, где мы использовали

а _х =

, поскольку ускорение происходит только в положительном направлении x.

— Т _{+ м ​​ 2 г грех = м 2 а}

Это дает всю информацию, необходимую для решения T и a. Как и раньше, мы можем решить одно из этих уравнений относительно T и подставьте это в другое уравнение и найдите а.

Т = м ₂ г sin — м ₂ а

[м ₂ г sin — м ₂ а] — м ₁ г = м ₁ а

м ₁ а + м ₂ а = м ₂ г sin — м ₁ г

( м ₁ + м ₂ ) а = ( м ₂ sin — м ₁ ) г

а = ( м ₂ грех — м ₁ ) г/( м ₁ + м ₂ )

Как насчет y-компонент сил на массу м ₂ , на наклонной плоскости?

F _y = F _нетто,y = F _и = м ₂ а _у

F _у = T _y + n _y + w _y = m ₂ а _у = 0

, где мы использовали

а _у = о

, так как ускорение происходит только в положительном направлении x и ускорение перпендикулярно плоскости отсутствует.

Т _у + п _у + ш _у = 0

0 + n — m ₂ г cos = 0

n = m ₂ г cos

Из y-компонент сил на массу m ₂ получаем можно найти нормальную силу. Это будет важно, когда мы учитывать трение .

---

Пример 7: Два блока масс m ₁ и m ₂ соприкасаются друг с другом на гладкой, горизонтальной плоскости, как показано здесь. Постоянная горизонтальная сила F применяется к m ₁ . Каково ускорение каждая масса?

В каком-то смысле мы можем (почти) решить этот пример интуитивно — в нашей голове. Сила F приложена к телу, масса которого равна m = м ₁ + м ₂ . Значит его ускорение должно быть

а = Ф/м

или

а = F / (м ₁ + м ₂ )

Это правильный ответ! Но больше ничего в этом нет вопрос? Простые вопросы — интуитивно очевидные — заставляют замечательные шаблоны или примеры для более сложных задач.

Посмотреть все силы на m ₁ . Сделать хорошее свободное тело диаграмма сил, действующих на m ₁ .

Конечно, внешняя сила F толкает вправо на масса m ₁ . Гравитация тянет вниз с силой ш ₁ = м ₁ г и самолет отвечает с нормальной силой н ₁ . Но другой масса — m ₂ — действует на массу m 9 с силой0302 1 . Эта сила обозначена P’ и направлена ​​влево. Мы можем примените второй закон Ньютона к силам, составляющим y, и найдите, что n ₁ = w ₁ 1. Но теперь есть дополнительная и неизвестная сила в x-компоненте второго закона Ньютона,

F _{1, нетто} = F — P’ = m ₁ a

Нам нужно больше информации поэтому мы обратимся к другой массе, м ₂

Первая масса m1 действует на эту массу с силой P , m2. Применяя y-компоненту F = m a , мы легко найти

п ₂ = ш ₂

Для x-компонентов только сила, действующая на м2, равна P так

F _{2, нетто} = P = m ₂ a

Однако из третьего закона Ньютона F ₁₂ = — F ₂₁ , мы знаем, что P = P’, поэтому

F — P’ = м ₁ а

F — м ₂ а = м ₁ а

F = м ₁ а + м ₂ а

F = ( м ₁ + м ₂ ) a

а = F / ( м ₁ + м ₂ )

Это тот же самый ответ, который мы так быстро нашли ранее, но этот может предоставить шаблон для использования в более сложных ситуациях.

---

Пример 8: Этот конкретный пример сформулирован в терминах весом рыба в ускоряющемся лифте. это тоже весело думать о взвешивании себя в разгоняющемся лифте. Когда лифт разгоняется до градусов? Когда лифт ускорить вниз вардов?

Силы, действующие на рыбу, показаны в свободном теле. диаграмма. T — натяжение, обеспечиваемое весами. Это значение шкала читает. Мы можем назвать это кажущимся весом рыба. Чистая сила, действующая на рыбу, равна

F _нетто = T — w

или

F _нетто = T — мг

Суммарная сила ( всегда! ) равна произведению массы на ускорение. Эта рыба движется вместе с лифтом. В этом диаграмме мы приняли ускорение от до , так что оно положительный.

F _нетто = T — m g = m a

Т = м г+ м а

Т = м (г + а)

Пока лифт разгоняет до , кажущийся вес рыбы на больше ее истинного веса, мг.