Главная → Видеоуроки → ЕГЭ по математике. Профильный уровень. Задание 6. Описание видеоурока: Основания равнобедренной трапеции равны 120 и 50. Центр окружности, описанной около трапеции, лежит внутри трапеции, а радиус окружности равен 65. Найдите высоту трапеции. Валерий Волков 5 09.02.2018 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математикеЗадача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. 5 класс.Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс.Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс.Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс.Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс.Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. 10 — 11 класс.Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки?Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
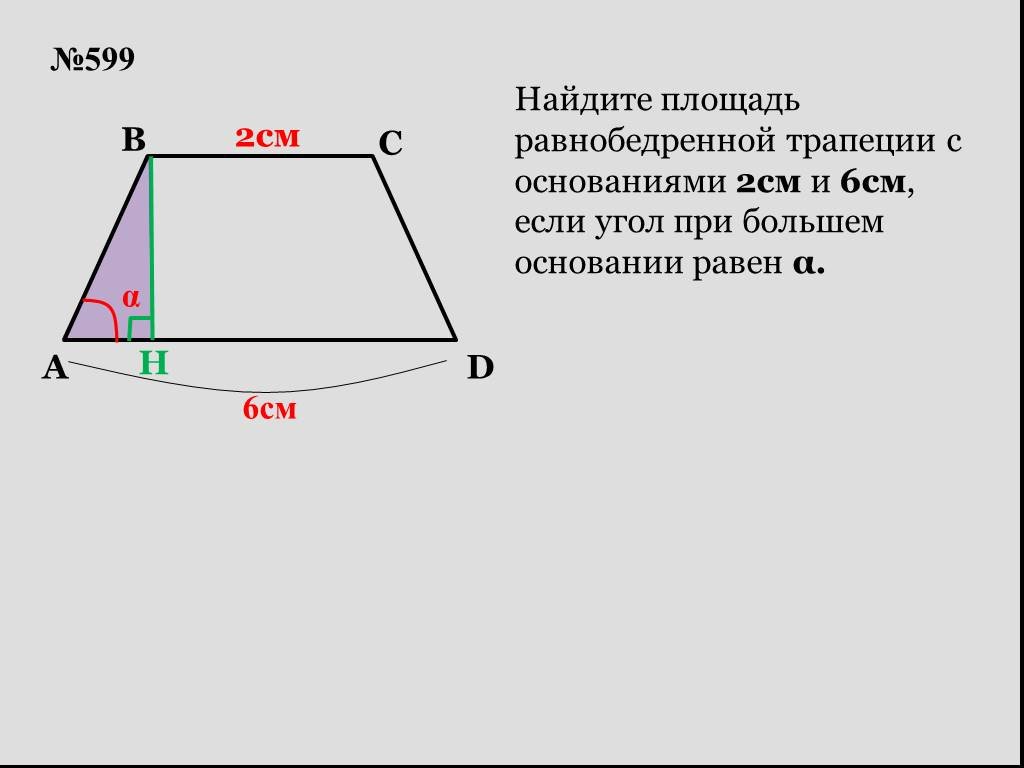
Использование материалов сайта возможно только с разрешения администрации портала.Основание равнобедренной трапеции равны 6 и 54, боковая сторона 25 см Найдите высоту h и площадь S трапеции — Знания.site
Кто не видел белого медведя? В зоопарках он – обычный гость. Нет нужды описывать, каков он на вид. Напомним лишь, что у него только нос черный, сам медведь белый и зимой, и летом (а не как, скажем, песец или заяц-беляк – те лишь зимой белые). Подошвы лап у белого медведя густой шерстью поросли, а пальцы примерно на половину своей длины соединены плавательными перепонками.
Плавают и ныряют белые медведи отлично. Две минуты могут пробыть под водой, но погружаются в нее редко глубже двух метров. Далеко в открытом море не раз видели белых медведей, даже медведиц с медвежатами. Плывут со скоростью 5 километров в час, не беспокоясь, что ни земли, ни льдов нигде вблизи не видно.
Белый медведь и тюленей ловит не только на льду, украдкой к ним подползая.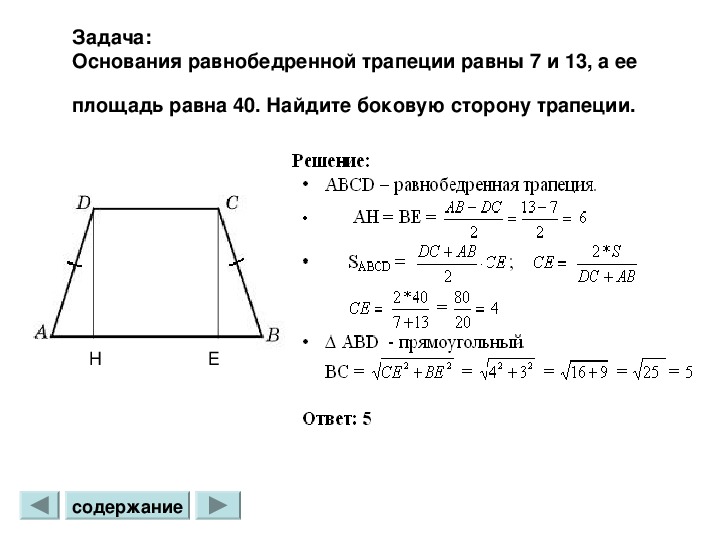
Обычный его прием, так сказать, атаки с моря такой: поблизости от лежбищ тюленей медведь осторожно, без плеска и шума, сползает в воду, плывет туда, где заметил тюленей. Затем он бесшумно ныряет и выныривает уже у самого лежбища, быстро карабкается на лед, отрезая тем самым тюленям путь к спасительной воде. По отвесным ледяным стенам медведь может прямо из воды выпрыгнуть на льдину, даже если высота ее над водой два метра.
Тюлени – главная охотничья добыча белого медведя весной. За год ловит и съедает он примерно 50 тюленей. Летом меню его более разнообразно. Ловит он рыбу на мелкой воде, на берегу – леммингов, песцов, лакомится яйцами птиц. Когда голоден, ест ягоды, водоросли, мхи, лишайник, грибы.
Белый медведь – самый могучий из сухопутных хищных зверей. Лев и тигр в сравнении с ним легковесы: средний вес медведиц 310 килограммов, медведей-самцов – 420 килограммов. Если медведь матерый и хорошо упитанный, то он может весить целую тонну!
Акимушкин И.И. Мир животных: Млекопитающие, или звери.
– М., 1988 г
IV. Тест по русскому языку
1. В тексте про белых медведей больше всего предложений:
а) повествовательных; б) вопросительных
2. Восклицательное предложение находится:
а) в начале текста; б) в конце текста
3. Вопросительное предложение находится
а) в начале текста; б) в конце текста
4. Выпиши из второй части текста (из второго абзаца) первое предложение. Разбери его по членам предложения. Что ты можешь сказать о сказуемых? Они являются
а) родственными словами; б) однородными членами предложения
5. Что можно сказать о глаголах, которыми выражены сказуемые? Эти глаголы:
а) I спряжения; б) II спряжения
6. Эти глаголы стоят в форме:
а) настоящего времени; б) будущего времени; в) прошедшего времени
7. Эти глаголы стоят в форме:
а) единственного числа; б) множественного числа
8. Эти глаголы стоят в форме:
а) 1-го лица; б) 2-го лица; в) 3-го лица; г)нельзя определить лицо
9.
Эти глаголы стоят в форме:
а) ж.р.; б) м.р.; в) ср.р.; г) нельзя определить род
10. Найди во второй части текста (во втором абзаце) все слова, которые являются родственными существительному, являющемуся подлежащим в первом предложении. Запиши их столбиком, поставив в начальную форму. У тебя получилось:
а) два слова; б) три слова
11. Найди во второй части текста (во втором абзаце) другую форму слова, которое является подлежащим в первом предложении. Выпиши такое словосочетание с формой этого слова, из которого можно определить его падеж. Этот падеж:
а) Р.п.; б) В.п.
равнобедренная трапеция
Равнобедренная трапеция — это трапеция с конгруэнтными катетами (http://planetmath.org/Leg) и двумя конгруэнтными углами, так что их общая сторона (http://planetmath.org/Side3) является основанием трапеция. Таким образом, в равнобедренной трапеции любые два угла, общая точка которых является основанием трапеции, равны.
В евклидовой геометрии принято давать определение равнобедренной трапеции без условия конгруэнтности катетов, поскольку этот факт может быть доказан в евклидовой геометрии из других требований.
Для других геометрий, таких как гиперболическая геометрия и сферическая геометрия, условие конгруэнтности катетов используется для определения равнобедренной трапеции, поскольку другие требования не подразумевают конгруэнтность катетов.
Общий перпендикуляр к основаниям равнобедренной трапеции всегда делит четырехугольник на две конгруэнтные прямые трапеции. В других , каждая равнобедренная трапеция симметрична относительно общего перпендикуляра к своим основаниям.
Ниже приведено изображение равнобедренной трапеции. Общий перпендикуляр к его основаниям показан голубым цветом.
В некоторых диалектах английского языка (например, (http://planetmath.org/Eg) британский английский) эта фигура обозначается как равнобедренная трапеция . Из-за модификатора «равнобедренный» при таком использовании не должно возникнуть путаницы.
Все прямоугольники являются равнобедренными трапециями (если не используется определение трапеции, см. статью о трапеции (http://planetmath.
В евклидовой геометрии в окружности концы двух параллельных хорд являются вершинами равнобедренной трапеции. И наоборот, можно использовать четыре подходящие точки на окружности для получения параллельных хорд (и, следовательно, параллельных линий).
А — трапеция, являющаяся одновременно прямоугольной и равнобедренной трапецией. В евклидовой геометрии такие трапеции автоматически являются прямоугольниками. В гиперболической геометрии такие трапеции автоматически являются четырехугольниками Саккери. Таким образом, словосочетание «правильная равнобедренная трапеция» встречается редко.
Трехсторонняя трапеция представляет собой равнобедренную трапецию, имеющую по крайней мере три конгруэнтные стороны. Ниже приведено изображение трапеции с тремя сторонами.
В некоторых диалектах английского языка (например, в британском английском) эта цифра обозначается как 9.
0003 Трехсторонняя трапеция . Из-за модификатора «3 стороны равны» при таком использовании не должно возникнуть путаницы.
Редкое, но удобное альтернативное название трапеции с тремя сторонами —
| Титул | равнобедренная трапеция |
| Каноническое имя | Равнобедренная трапеция |
| Дата создания | 22.03.2013 17:11:59 |
| Последнее изменение | 22.03.2013 17:11:59 |
| Владелец | Wkbj79 (1863) |
| Последнее изменение: | Wkbj79 (1863) |
| Числовой идентификатор | 25 |
| Автор | Wkbj79 (1863) |
| Тип ввода | Определение |
| Класс | мск 51-00 |
| Синоним | Равнобедренная трапеция |
| Связанная тема | СаккериЧетырехугольник |
| Определяет | Трехсторонняя трапеция |
| Определяет | 3-х сторонняя трапеция |
| Определяет | Трехсторонняя трапеция |
| Определяет | 3-х сторонняя трапеция |
| Определяет | Трехбедренная трапеция |
| Определяет | Трехбедренная трапеция |
Формулы равнобедренной трапеции Он также известен как Трапеция.
Есть три типа трапеций, и равнобедренная трапеция является одним из ее типов. Типы трапеций:- Правая трапеция
- Равнобедренная трапеция
- Разносторонняя трапеция
Равнобедренная трапеция
Равнобедренная трапеция — это трапеция с конгруэнтными углами основания и конгруэнтными непараллельными сторонами. Трапеция называется равнобедренной, если две противоположные стороны (основания) параллельны, а две другие стороны (катеты) имеют одинаковую длину.
Площадь и Периметры являются формулами равнобедренной трапеции.
Площадь равнобедренной трапеции
Площадь равнобедренной трапеции можно рассчитать, сложив длины двух параллельных сторон (оснований), разделив полученное значение на 2 и умножив результат на высоту трапеции, чтобы получить площадь. Формула площади дается выражением-
Площадь = ((a+b)/2) × h
Где
a, b — длина параллельных сторон
, а h — высота.
Чтобы лучше понять, давайте решим несколько примеров
Примеры задач на площадь равнобедренной трапеции
Вопрос 1: Какова площадь равнобедренной трапеции, если длины параллельных сторон 7 см, 5 см, а высота 4 см.
Решение:
Дано
Длина параллельных сторон (a) = 7 см, b = 5 см
Высота (h) = 4 см
Площадь = ((a + b)/2) × h
= ((7 + 5)/2) × 4
= (12/2) × 4
= 6 × 4
= 24 см 2
Площадь заданной равнобедренной кости трапеция 24см 2 .
Вопрос 2: Найдите высоту равнобедренной трапеции, если длины параллельных сторон равны 6см, 4см и площадь 24см 2 .
Решение:
Дано
Длина параллельных сторон (a) = 6 см, b = 4 см
Площадь = 24 см 2
900 02 Площадь = ((a+b)/2) × h24 = ((6+4)/2) × h
24 = (10/2) × h
24 = 5 × h
h = 24/5
= 4,8 см
901 53 Итак, из данного площадь, длина основания высота равнобедренной трапеции 4,8см
Периметр равнобедренной трапеции
Периметр равнобедренной трапеции можно вычислить, сложив все стороны трапеции.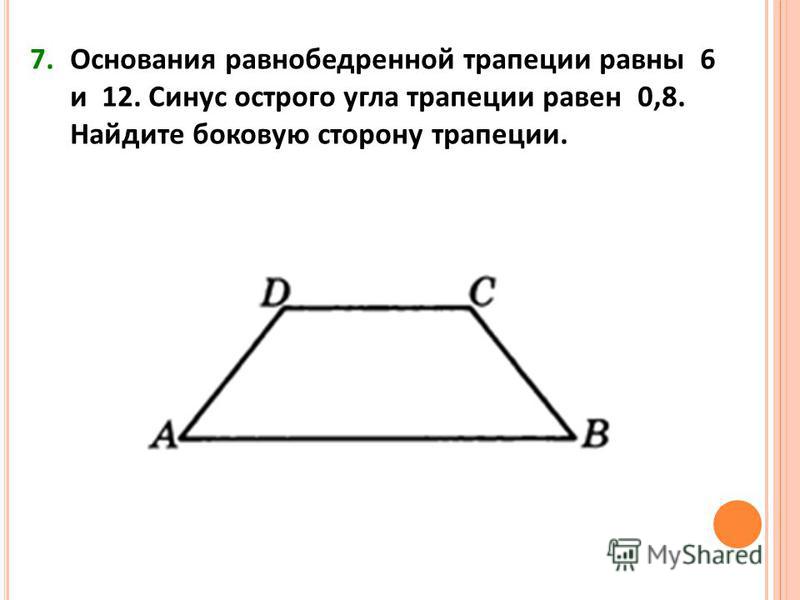
Формула периметра:
Периметр = a+b+c+d
Где
a,b — длины двух параллельных сторон
c,d — длины двух непараллельных сторон
Примечание: Для равнобедренной трапеции c = d (длины непараллельных сторон равны)
Давайте рассмотрим несколько примеров, чтобы лучше понять.
Примеры задач на периметр равнобедренной трапеции
Вопрос 1: Чему равен периметр равнобедренной трапеции, если длины сторон равны 7см, 5см, 3см, 3см.
Решение:
Дано,
Длина параллельных сторон (a) = 7 см, (b) = 5 см
Длина непараллельных сторон (c) = 3 см, (d) = 3 см
Периметр = a + b + c + d
= 7+5+3+3
= 18 см
Значит периметр данной равнобедренной трапеции равен 18см.
Вопрос 2: Чему равен периметр равнобедренной трапеции , если длины параллельных сторон 8 см, 4 см и длина сторон равной длины 2 см.
Решение:
Дано,
Длина параллельных сторон (оснований) (a) = 8см, (b) = 4см
Длина непараллельных сторон (ног) (c) = 2см, (d ) = 2 см
Периметр = a + b + c + d
= 8 + 4 + 2 + 2
= 16 см
Итак, периметр данной равнобедренной трапеции равен 16 см.
Вопрос 3: Каковы площадь и периметр равнобедренной трапеции с длинами оснований 3см, 6см и длинами двух других сторон, равных по длине 2,5см и высоте 1,5см.
Решение:
Дано
Длина оснований (a) = 6 см, (b) = 3 см
Длина ног, т.е. стороны с одинаковой длиной (c) = 2,5 см, (d) = 2,5 см
Высота (h) = 1,5 см
Площадь = ((a+b)/2) × h
= ((6+3)/2) × 1,5
= (9/2) × 1,5
= 4,5 × 1,5
= 6,75 см 2 9000 7
Периметр = a + b + c + d
= 6 + 3 + 2,5 + 2,5
= 14 см
Итак, для данных данных площадь равна 6,75 см 2 , а периметр равен 14 см.
Leave A Comment