Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20

Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 4. Найдите объём куба

Мы знаем, что объем треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух ребер, выходящих …

Подробнее →

Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах

Для решения данной задачи нужно знать, что в равнобедренном треугольнике два угла равны. Из условия задачи известно …

Подробнее →

Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2 корень из 3, а высота равна 2

Для решения задачи нам нужно знать формулу для нахождения площади боковой поверхности правильной треугольной призмы .

..

Подробнее →

Моторная лодка прошла против течения реки 135 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 12 км/ч

Для решения данной задачи необходимо использовать формулу: скорость течения = (расстояние в одну сторону — расстояние …

Подробнее →

Вершина A куба ABCDA_1B_1C_1D_1 с ребром 0,9 является центром сферы, проходящей через точку A_1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину S/ Пи

Из условия задачи мы знаем, что вершина A куба является центром сферы. Это значит, что расстояние от вершины A до любой …

Подробнее →

Вероятность купить качественную посуду на фабрике

На фабрике керамической посуды изготавливают тарелки, из которых 10% имеют дефект. Это значит, что из 100 произведенных . ..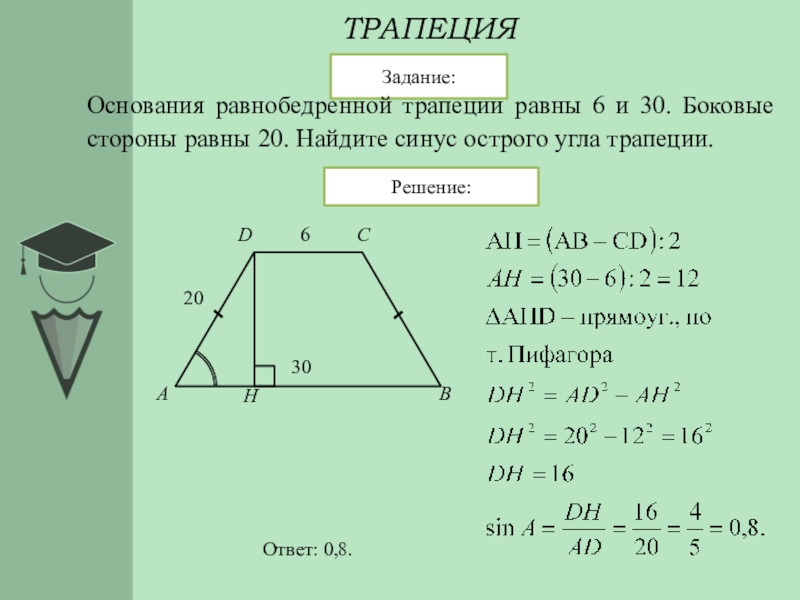

Подробнее →

Игральную кость бросают два раза. Найдите вероятность того, что выпавшие значения совпадают. Ответ округлите до сотых

У нас есть игральная кость, которую бросают два раза. Каждый раз при броске выпадает число от 1 до 6. Нам нужно найти …

Подробнее →

В треугольнике ABC известно, что АС = 36,ВС = 15, а угол \angle C=90 градусов. Найдите радиус вписанной в этот треугольник окружности

Для решения данной задачи нам понадобятся знания из геометрии и тригонометрии. Первым шагом найдем длину стороны AB с …

Подробнее →

Вероятность выбора докладчика из Швейцарии на конференции.

Всего на конференцию приехало 7+5+4=16 ученых. Если каждый из них делает один доклад, то всего будет прозвучано 16 …

Подробнее →

Вероятность наличия доклада профессора М. на последнем дне конференции

Итак, в задаче дано, что научная конференция будет проходить 3 дня, на которых запланировано провести 40 докладов.

В …

Подробнее →

Основания равнобедренной трапеции равны 8 и 20, а её площадь равна 112. Найдите периметр трапеции

Из условия задачи известны значения оснований равнобедренной трапеции и её площадь. Для решения задачи необходимо найти …

Подробнее →

Вероятность выбора пенсионера среди мужчин города

Дано: — в городе 52% взрослого населения — мужчины — пенсионеры составляют 17,8% взрослого населения — доля пенсионеров …

Подробнее →

Карточки для подготовки к ЕГЭ на профильном уровне. Задание №6 «Планиметрия»

Вариант 1 6. Планиметрия

1. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

2. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

3.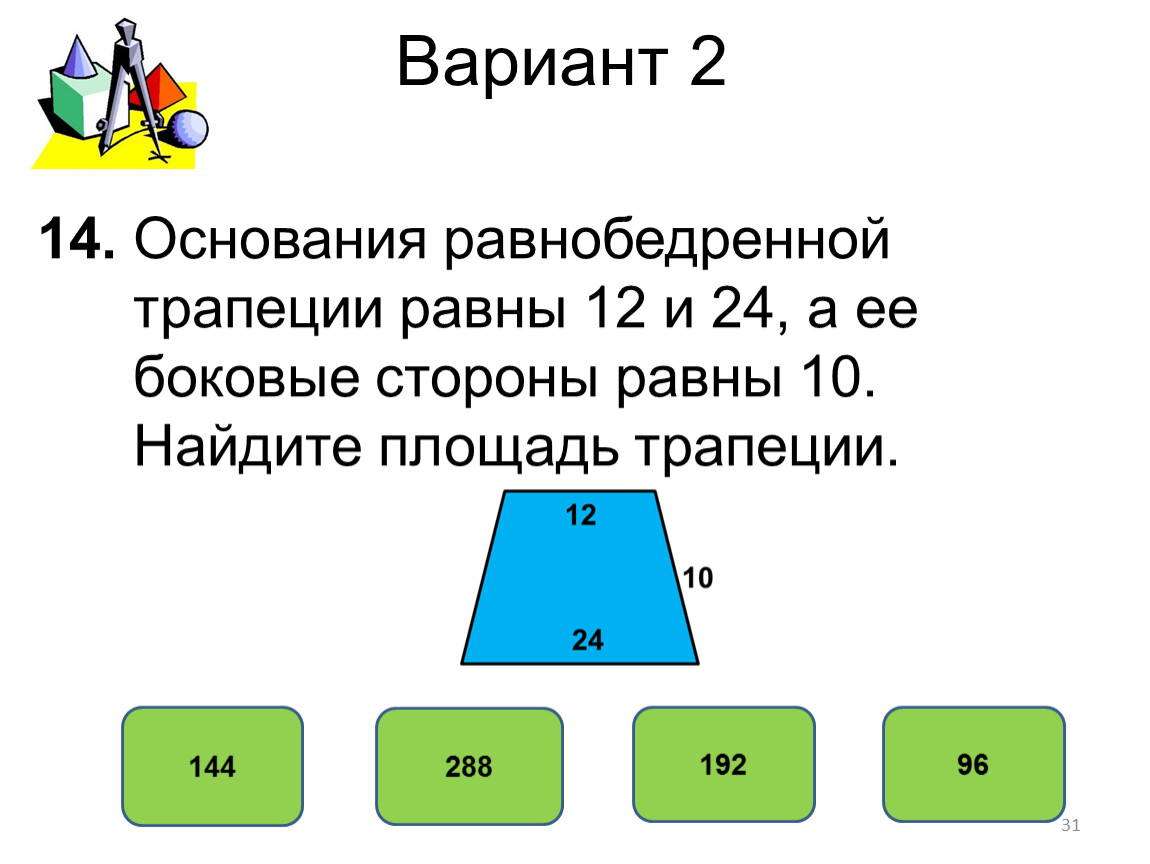  Найдите синус угла АОВ.  В ответе укажите значение синуса, умноженное на 2.

4. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

5. Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

6. Угол между хордой AB и касательной BC к окружности равен  35°.  Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

7. Около трапеции описана окружность. Периметр трапеции равен 24, средняя линия равна 11. Найдите боковую сторону трапеции.

8. Найдите величину угла АВС.  Ответ дайте в градусах.

9. Угол ACO равен 35°, где O — центр окружности.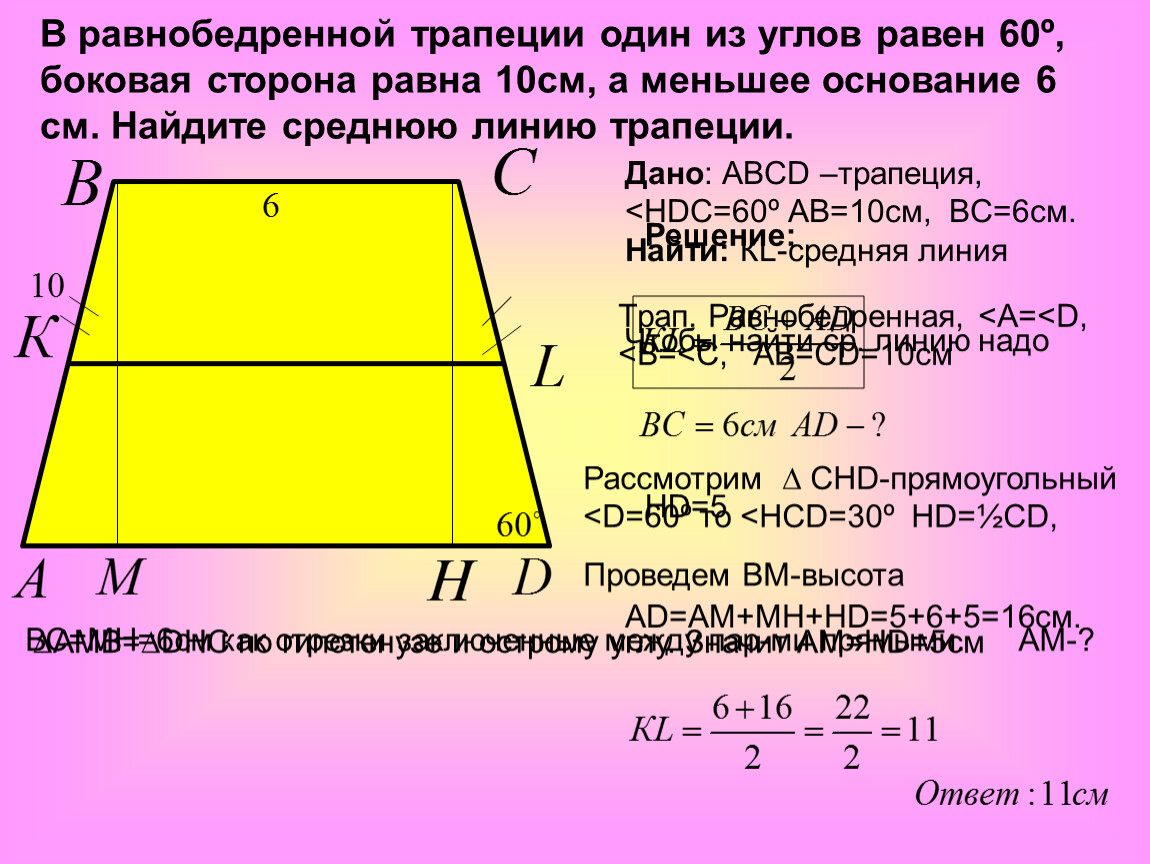 Его сто­ро­на CA ка­са­ет­ся окружности. Най­ди­те ве­ли­чи­ну мень­шей дуги AB окружности, за­клю­чен­ной внут­ри этого угла. Ответ дайте в градусах.

10. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.

Вариант 2 6. Планиметрия

В 1. Сторона правильного треугольника равна  Найдите радиус окружности, вписанной в этот треугольник.

2. Две стороны параллелограмма относятся как  9:11, а периметр его равен 40. Найдите большую сторону параллелограмма.

3. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.

4. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

5. Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.

6. Найдите радиус окружности, вписанной в треугольник , считая стороны квадратных клеток равными 1.

7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

8. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

9. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.

10. Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника.

Вариант 3 6. Планиметрия

1. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах.

2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.

3. В треугольнике АВС АС = ВС = 4 , cos ВАС = 0,25.   Найдите высоту АН.

4. В ромбе ABCD угол DAB равен 136°. Най­ди­те угол BDC. Ответ дайте в градусах.

5. В треугольнике АВС угол  С  равен 90°, СН – высота, АС = 3, cos А =  . Найдите ВН.

6. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

7. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите 

8. Найдите площадь ромба, если его диагонали равны 4 и 12.

9. В треугольнике АВС АС = ВС = 4, угол  С  равен 30°.  Найдите высоту  АН.

10. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах

Вариант 4 6. Планиметрия

1. В треугольнике ABC угол C равен 90°, CH  — высота, АВ = 15,  tg А = . Найдите BH.

2. Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.

3. Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.

4.Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

5. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника.

6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB.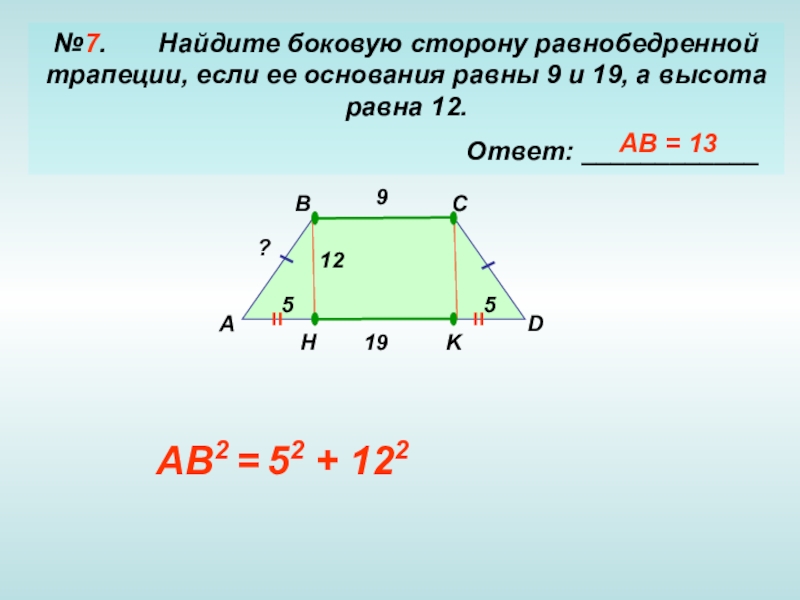 Ответ дайте в градусах.

7. Катеты равнобедренного прямоугольного треугольника равны 82 + 41   

Найдите радиус окружности, вписанной в этот треугольник.

8. В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

9. В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4,  ВН = 4. Найдите 

10. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.

Вариант 5 6. Планиметрия

1. Найдите косинус угла  АОВ.  В ответе укажите значение косинуса, умноженное на 2.

2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

3. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 3, sin А =  . Найдите АН.

4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

5. Катеты равнобедренного прямоугольного треугольника равны  2+ Найдите радиус окружности, вписанной в этот треугольник.

6. Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции.

7. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

8.Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.

9. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

10. Стороны параллелограмма равны 38 и 76. Высота, опущенная на первую сторону, равна 57. Найдите высоту, опущенную на вторую сторону параллелограмма.

Вариант 6 6. Планиметрия

1. Сторона АВ треугольника АВС равна 42. Противолежащий ей угол С равен 150° . Найдите радиус окружности, описанной около этого треугольника.

2. Через концы A, B дуги окружности в  114°  проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

3. В треугольнике АВС АС=ВС, АН  – высота, АВ=5, sinВАС= .  Найдите 

4. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

5. Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.

6. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен  Найдите высоту трапеции.

7. В треугольнике ABC угол C равен 90°, АС = 8, cos А =   Найдите АВ.

8. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.

9. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

10. В треугольнике ABC угол ACB равен °, угол B равен °, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Вариант 7 6. Планиметрия

1. Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

2. Две сто­ро­ны па­рал­ле­ло­грам­ма от­но­сят­ся как  3:17, а пе­ри­метр его равен 40. Най­ди­те боль­шую сто­ро­ну параллелограмма.

3. В треугольнике ABC AC = BC, AB = 22, tg А =  .  Найдите AC.

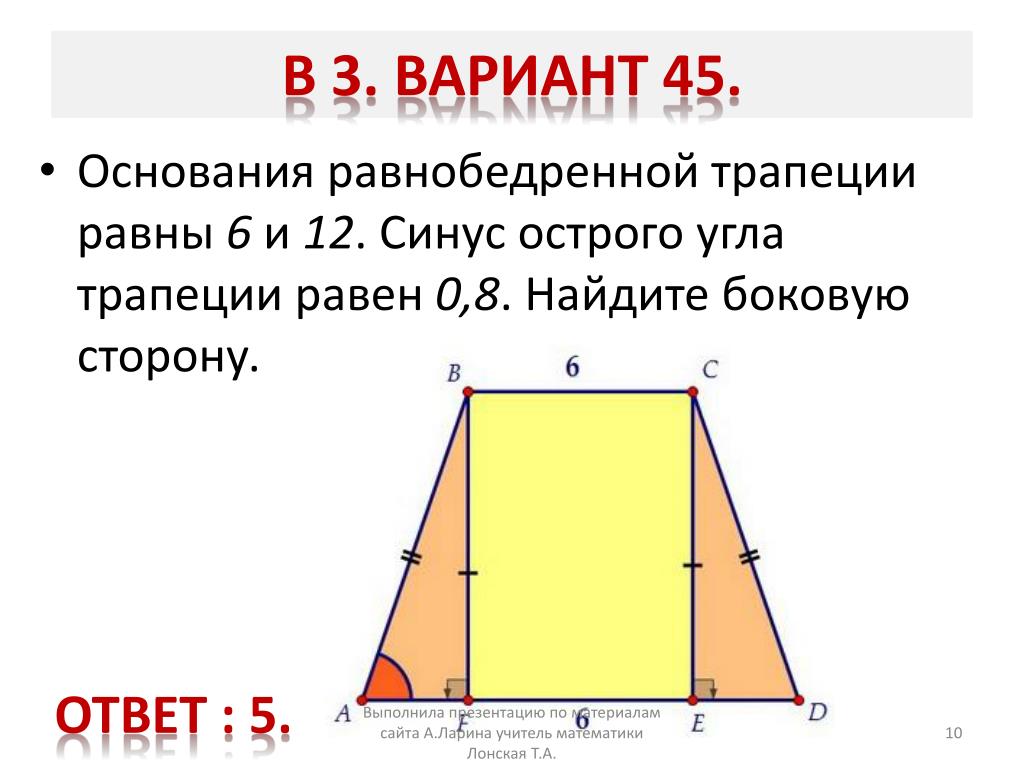
4. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.

5. В треугольнике ABC угол C равен  90°, АС = 17, sin А = .  Найдите BC.

6. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.

7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

8. Угол ACO равен 35°, где O — центр окружности. Его сто­ро­на CA ка­са­ет­ся окружности. Най­ди­те ве­ли­чи­ну мень­шей дуги AB окружности, за­клю­чен­ной внут­ри этого угла. Ответ дайте в градусах.

9. Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.

10.Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.

Вариант 8 6. Планиметрия

1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

2. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции.

3. Найдите вписанный угол, опирающийся на дугу, которая составляет  окружности. Ответ дайте в градусах.

4. В треугольнике ABC угол C равен  90°, АС = 17, sin А = .    Найдите BC.

5. Площадь тре­уголь­ни­ка ABC равна 136. DE — сред­няя линия. Най­ди­те площадь тре­уголь­ни­ка CDE.

6. В треугольнике ABC AC = BC, AB = 8, tg А =  .  Найдите AC.

7. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.

8. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.

9. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен  47.

10. Найдите синус угла  АОВ. В ответе укажите значение синуса, умноженное на 2

Вариант 9 6. Планиметрия

1.  Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

2. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 

4. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах.

5. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.

6. В треугольнике АВС АС = ВС, АВ = 7 , tg ВАС = , Найдите высоту 

7. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен  80°.  Найдите n.

8. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.

9. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.

10. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла.

Вариант 10 6. Планиметрия

1. Найдите величину угла АВС. Ответ дайте в градусах.

2. В треугольнике ABC угол C равен 76°, AC = BC. Найдите угол A. Ответ дайте в градусах.

3. Площадь треугольника  АВС  равна 129.  ДE  – средняя линия, параллельная стороне  АВ.  Найдите площадь трапеции АВЕД.

4. В треугольнике  АВС  угол  С  равен 90°, СН – высота, АН = 12 , cos А =  .  Найдите АВ.

5.  Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника.

6. Основания рав­но­бед­рен­ной тра­пе­ции равны 5 и 11, а её пло­щадь равна 32. Най­ди­те пе­ри­метр трапеции.

7. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.

8. Хорда AB делит окружность на две части, градусные величины которых относятся как 3:5.  Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

9. В треугольнике  известно, что , , угол равен  90°.  Найдите радиус вписанной окружности.

10. В треугольнике АВС АС = ВС = 27 ,  — высота, sin ВАС =  .  Найдите 

6. Планиметрия

Вариант 1

  1. 0,5

  2. 3

  3. 2

  4. 30

  5. 16

  6. 70

  7. 1

  8. 135

  9. 55

  10. 52

Вариант 2

  1. 0,5

  2. 11

  3. 62

  4. 57

  5. 132

  6. 1

  7. 34

  8. 6

  9. 5

  10. 93

Вариант 3

  1. 40

  2. 2

  3. 7,5

  4. 22

  5. 17,5

  6. 160

  7. 0,6

  8. 24

  9. 2

  10. 56

Вариант 4

  1. 9,6

  2. 20

  3. 5

  4. 42

  5. 25

  6. 57

  7. 41

  8. 115

  9. 0,5

  10. 4,5

Вариант 5

  1. 2

  2. 122

  3. 17,5

  4. 46

  5. 1

  6. 1,5

  7. 2

  8. 41

  9. 30

  10. 28,5

Вариант 6

  1. 42

  2. 66

  3. 4,8

  4. 36

  5. 104

  6. 10

  7. 12

  8. 304

  9. 6

  10. 23

Вариант 7

  1. 150

  2. 17

  3. 22

  4. 0,8

  5. 34

  6. 10,5

  7. 24

  8. 55

  9. 21

  10. 10

Вариант 8

  1. 122

  2. 10

  3. 36

  4. 34

  5. 34

  6. 7

  7. 26

  8. 44

  9. 94

  10. 2

Вариант 9

  1. 24

  2. 9

  3. 1

  4. 53

  5. 15,5

  6. 4

  7. 18

  8. 141,75

  9. 36

  10. 1

Вариант 10

  1. 45

  2. 52

  3. 96,75

  4. 27

  5. 22

  6. 26

  7. 8

  8. 112,5

  9. 4

  10. 30

Задача по математике: Равнобедренная трапеция — вопрос №30171, алгебра

Найти площадь равнобедренной трапеции; если основания 12 см и 20 см, длина руки 16 см.

Правильный ответ:

S =  263,8788 см 2

Пошаговое объяснение:

a=12 см c=20 см r=16 см x=(c−a)/2=(20− 12)/2=4 см h=x2+r2

​=42+162

​=4 17

​ см ≐ 16,4924 см S=2a+c ⋅ h=212+20 ⋅ 16,4924=6 4 17

​=263,8788 см2


Нашли ошибку или неточность? Не стесняйтесь

пишите нам . Спасибо!

Советы по использованию связанных онлайн-калькуляторов

См. также наш калькулятор прямоугольного треугольника.

Для решения этой словесной задачи по математике необходимо знать следующие знания:

  • алгебра
  • выражение переменной из формулы
  • планиметрия 900 39
  • Теорема Пифагора
  • Прямоугольный треугольник
  • площадь фигуры
  • трапеция
Уровень задачи:
  • практика для 13-летних
  • практика для 14-летних
 

Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче. : видео1   видео2

  • Длина окружности 7686
    Длина окружности равнобедренной трапеции равна 34 см. Разница в длине оснований 6 см. Длина руки составляет одну треть длины более длинного основания. Найдите длины сторон трапеции.
  • Рассмотрим 3
    Рассмотрим равнобедренную трапецию PQRS. Базы |PQ|=120 мм, |RS|=62 мм и плечо s=48 мм. Найдите высоту трапеции, длину диагонали и площадь трапеции.
  • Трапеция IS
    Равнобедренная трапеция длиной 35 см. Высота 30 см, а средний сегмент 65 см. Найдите длину его оснований.
  • Равнобедренная трапеция
    Основания равнобедренной трапеции относятся как 5:3. Руки имеют длину 5 см и высоту = 4,8 см. Вычислите длину окружности и площадь трапеции.
  • Равнобедренная трапеция
    Вычислите длину окружности и площадь равнобедренной трапеции, если известны размеры оснований 8 и 12 см, а размер плеч 5 см.
  • Равнобедренная 27793
    Равнобедренная трапеция LICH имеет плечи длиной 5,2 см и основания 7,6 см и 3,6 см.
    Найдите площадь трапеции LICH.
  • Площадь изоловушки
    Найдите площадь равнобедренной трапеции, если длины ее оснований 16 см и 30 см, а диагонали перпендикулярны друг другу.
  • Высота — 6183
    В равнобедренной трапеции ABCD длина основания равна а = 10 см, с = 6 см, а длина плеча — 4 см. Вычислите его высоту — результат округлите до десятых.
  • Параметры: 36691
    Рассчитайте длину плеч и площадь равнобедренной трапеции, если известны следующие параметры: o = 20 см a = 10 см, c = 4 см h = 2 см
  • Окружность 7065
    В равнобедренный треугольник, длина основания которого равна 75% длины руки. Определить площадь треугольника, если длина его окружности 22 см.
  • Окружность 3160
    В равнобедренном треугольнике длина основания составляет 75% длины плеча. Вычислите площадь треугольника, если длина его окружности 22 см.
  • Равнобедренная трапеция
    Вычислите площадь равнобедренной трапеции, основания которой относятся как 5:3.