егэ. задача B6. рабочая тетрадь смирнов в.а 2010 -48с
егэ. задача B6. рабочая тетрадь смирнов в.а 2010 -48сAdvertisement
Advertisement
Advertisement
Advertisement
Advertisement
Advertisement
Advertisement
Advertisement
Advertisement
Upcoming SlideShareМатематикаLoading in … 3
1 of 42
Top clipped slideDownload to read offlineEducation
Advertisement
Advertisement
Advertisement
егэ. задача B6. рабочая тетрадь смирнов в.а 2010 -48с
- Содержание
Введение …………………………………………………………………
Диагностическая работа ………………………………………………..
Решения задач диагностической работы ……………………………..
Тренировочные работы …………………………………………………
1. Площадь треугольника ………………………………………………
2. Площадь прямоугольника, квадрата, параллелограмма, ромба ….
3. Площадь трапеции ……………………………………………………
4. Площадь выпуклых и невыпуклых четырехугольников …………..
5. Площадь круга и его частей ………………………………………….
6.
 Площадь фигур на координатной плоскости ……………………….
Самостоятельные работы ……………………………………………….
Самостоятельная работа 1 ……………………………………………….
Самостоятельная работа 2 ……………………………………………….
Самостоятельная работа 3 ……………………………………………….
Площадь фигур на координатной плоскости ……………………….
Самостоятельные работы ……………………………………………….
Самостоятельная работа 1 ……………………………………………….
Самостоятельная работа 2 ……………………………………………….
Самостоятельная работа 3 ………………………………………………. - Диагностическая работа 1. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1. 2. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1. 3. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
- 4. Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1. 5. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1. 6. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- 7. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1. 8. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
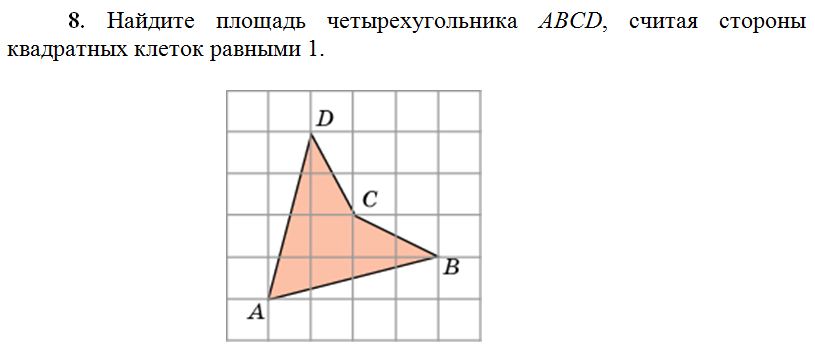
- 9. Найдите площадь S сектора, считая стороны квадратных клеток
S
π
равными 1.

- 12. Найдите площадь четырехугольника, вершины которого имеют
координаты (1, 0), (0, 2), (4, 4), (5, 2).
Решения задач диагностической работы
1. Первое решение. Заметим, что данный треугольник ABC является
прямоугольным ( A = 90о). Воспользуемся тем, что диагональ квадратной
∠
2
клетки со сторонами, равными 1, равна . Тогда катеты AB и AC данного
3 2
треугольника будут равны . Так как площадь прямоугольного
треугольника равна половине произведения его катетов, то площадь
3 2 ⋅3 2
2
данного треугольника будет равна , т.

- Ответ. 9.
2
2. Первое решение. Так как диагональ квадрата со стороной 1 равна ,
5 2
то сторона AC треугольника ABC равна , высота BH, проведенная к этой
3 2
2
стороне, равна . Следовательно, площадь данного треугольника равна
3 2 ⋅5 2
4
, т.е. равна 7,5.
Второе решение. Разобьем данный треугольник ABC на два
треугольника ABD и BDC. Их общая сторона BD равна 3, а высоты, к ней
проведенные, равны соответственно 1 и 4. Площадь треугольника ABD равна
1,5, а площадь треугольника BDC равна 6. Площадь треугольника ABC равна
сумме площадей этих треугольников и, следовательно, равна 7,5.

- Ответ. 7,5. 3. Первое решение. Найдем стороны данного прямоугольника. Рассмотрим прямоугольный треугольник ADE. Катет AE равен 4, катет DE равен 2. Следовательно, по теореме Пифагора гипотенуза AD равна 20 . Аналогично, для прямоугольного треугольника ABF катет AF равен 1, катет BF равен 2, Следовательно, по теореме Пифагора гипотенуза AB равна 5 . Так как площадь прямоугольника равна произведению его смежных сторон, 20 ⋅ 5 то площадь данного прямоугольника будет равна , т.е. равна 10. Второе решение. Разобьем данный прямоугольник ABCD на два треугольника ABD и BCD. Сторона BD у них общая и равна 5. Высоты AE и CF, опущенные на эту сторону, равны 2. Так как площадь треугольника равна половине произведения стороны на высоту, опущенную на эту сторону, то площадь каждого из этих двух треугольников будет равна 5 и, следовательно, площадь прямоугольника будет равна 10.
- Ответ. 10.
4. Первое решение.
 Напомним, что площадь ромба равна половине
произведения его диагоналей. Воспользуемся тем, что диагональ
2
квадратной клетки со сторонами, равными 1, равна . Тогда диагонали
4 2 2 2
AС и BD данного ромба будут равны соответственно и , а его
2 2 ⋅4 2
2
площадь будет равна , т.е. равна 8.
Второе решение. Достроим на сторонах ромба четыре равных
прямоугольных треугольника, катеты которых равны 1 и 3. Площадь
каждого такого треугольника равна 1,5. Ромб вместе с этими
треугольниками образует фигуру, состоящую из четырнадцати единичных
квадратов. Следовательно, ее площадь равна 14. Вычитая из нее площадь
четырех треугольников, получим, что площадь ромба равна 8.
Напомним, что площадь ромба равна половине
произведения его диагоналей. Воспользуемся тем, что диагональ
2
квадратной клетки со сторонами, равными 1, равна . Тогда диагонали
4 2 2 2
AС и BD данного ромба будут равны соответственно и , а его
2 2 ⋅4 2
2
площадь будет равна , т.е. равна 8.
Второе решение. Достроим на сторонах ромба четыре равных
прямоугольных треугольника, катеты которых равны 1 и 3. Площадь
каждого такого треугольника равна 1,5. Ромб вместе с этими
треугольниками образует фигуру, состоящую из четырнадцати единичных
квадратов. Следовательно, ее площадь равна 14. Вычитая из нее площадь
четырех треугольников, получим, что площадь ромба равна 8. - Ответ. 8.
5. Первое решение. Основания AD и BC данной трапеции равны
соответственно 4 и 2. Высотой является боковая сторона CD.
 Она равна 3.
Так как площадь трапеции равна произведению полусуммы оснований на
4+ 2
⋅3
2
высоту, то площадь данной трапеции будет равна , т.е. равна 9.
Второе решение. Из точки B опустим перпендикуляр BH на AD. Он
разобьет трапецию на прямоугольный треугольник ABH и прямоугольник
HBCD. Катеты прямоугольного треугольника равны 2 и 3, следовательно,
его площадь равна 3. Смежные стороны прямоугольника равны 2 и 3,
следовательно, его площадь равна 6. Площадь трапеции равна сумме
площадей треугольника и прямоугольника и, следовательно, равна 9.
Она равна 3.
Так как площадь трапеции равна произведению полусуммы оснований на
4+ 2
⋅3
2
высоту, то площадь данной трапеции будет равна , т.е. равна 9.
Второе решение. Из точки B опустим перпендикуляр BH на AD. Он
разобьет трапецию на прямоугольный треугольник ABH и прямоугольник
HBCD. Катеты прямоугольного треугольника равны 2 и 3, следовательно,
его площадь равна 3. Смежные стороны прямоугольника равны 2 и 3,
следовательно, его площадь равна 6. Площадь трапеции равна сумме
площадей треугольника и прямоугольника и, следовательно, равна 9. - Ответ. 9.
6. Первое решение. Основания AD и BC трапеции равны
3 2
4 2 2 2 2
соответственно и . Высота BH трапеции равна .
 Так как
площадь трапеции равна произведению полусуммы оснований на высоту, то
4 2 +2 2 3 2
⋅
2 2
площадь данной трапеции будет равна и, следовательно,
будет равна 9.
Второе решение. Разобьем трапецию на параллелограмм ABCE и
треугольник CDE. Сторона AB параллелограмма ABCE равна 3, высота EH,
к ней проведенная, равна 2, следовательно, площадь этого параллелограмма
равна 6. Сторона CE треугольника CDE равна 3, высота DG, к ней
проведенная, равна 2, следовательно, площадь этого треугольника равна 3.
Площадь трапеции равна сумме площадей параллелограмма и треугольника
и, следовательно, равна 9.
Так как
площадь трапеции равна произведению полусуммы оснований на высоту, то
4 2 +2 2 3 2
⋅
2 2
площадь данной трапеции будет равна и, следовательно,
будет равна 9.
Второе решение. Разобьем трапецию на параллелограмм ABCE и
треугольник CDE. Сторона AB параллелограмма ABCE равна 3, высота EH,
к ней проведенная, равна 2, следовательно, площадь этого параллелограмма
равна 6. Сторона CE треугольника CDE равна 3, высота DG, к ней
проведенная, равна 2, следовательно, площадь этого треугольника равна 3.
Площадь трапеции равна сумме площадей параллелограмма и треугольника
и, следовательно, равна 9.  Второе решение. Разобьем данный четырехугольник на два
треугольника ABD и BCD. Сторона BD у них общая и равна 4. Высоты AH и
CH равны соответственно 3 и 1. Следовательно, площади этих
треугольников равны соответственно 6 и 2. Значит, площадь
четырехугольника равна 8.
Ответ. 8.
Второе решение. Разобьем данный четырехугольник на два
треугольника ABD и BCD. Сторона BD у них общая и равна 4. Высоты AH и
CH равны соответственно 3 и 1. Следовательно, площади этих
треугольников равны соответственно 6 и 2. Значит, площадь
четырехугольника равна 8.
Ответ. 8.- 8. Первое решение. Разобьем данный четырехугольник на два
2 2
треугольника ACB и ACD. Сторона AC у них общая и равна . Высоты
3 2
2
BH и DH равны . Следовательно, площади этих треугольников равны 3.
Значит, площадь четырехугольника равна 6.
Второе решение. Площадь данного четырехугольника равна разности
площадей треугольников ABD и CBD. В треугольнике ABD сторона BD
5 2
3 2 2
равна , высота AH равна . Следовательно, его площадь равна 7,5. В
2
3 2 2
треугольнике CBD сторона BD равна , высота CH равна .

- Подставляя данные значения R и ϕ
в формулу площади сектора, получим
5π S
= 1,25
4 π
S= .
 Откуда .
Второе решение. Заметим, что данный сектор является одной
четвертой частью круга и, следовательно, его площадь равна одной
четвертой площади круга. Площадь круга равна π R , где R – радиус круга.
2
5π
5 4
В нашем случае R = и, следовательно, площадь S сектора равна .
S
= 1,25
π
Откуда .
Ответ. 1,25.
10. Площадь кольца равна разности площадей внешнего и
внутреннего кругов. Радиус R внешнего круга равен 2 2 , радиус r
внутреннего круга равен 2. Следовательно, площадь S кольца равна 8π−4π ,
S
=4
π
т.
Откуда .
Второе решение. Заметим, что данный сектор является одной
четвертой частью круга и, следовательно, его площадь равна одной
четвертой площади круга. Площадь круга равна π R , где R – радиус круга.
2
5π
5 4
В нашем случае R = и, следовательно, площадь S сектора равна .
S
= 1,25
π
Откуда .
Ответ. 1,25.
10. Площадь кольца равна разности площадей внешнего и
внутреннего кругов. Радиус R внешнего круга равен 2 2 , радиус r
внутреннего круга равен 2. Следовательно, площадь S кольца равна 8π−4π ,
S
=4
π
т. е. S = 4π
и, следовательно, .
е. S = 4π
и, следовательно, . - Ответ. 4. 11. Из вершины B треугольника ABC опустим высоту BH. Она равна 3. Сторона AC равна 4. Следовательно, площадь треугольника равна 6. Ответ. 6. 12. Разобьем четырехугольник ABCD на два треугольника ABD и BCD. Высоты AG и CH этих треугольников, опущенные на сторону BD, равны 2, сторона BD равна 5. Следовательно, площади этих треугольников равны 5 и, значит, площадь четырехугольника ABCD равна 10. Ответ. 10.
- Тренировочные работы 1. Площадь треугольника 1. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1. 2. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1. 3. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
- 4. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1.
5. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1.
 6. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1.
7. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1.
6. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1.
7. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1. - 8. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
- 2. Площадь прямоугольника, квадрата, параллелограмма, ромба 1. Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1. 2. Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1. 3. Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1.
- 4. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1. 5. Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1. 6. Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1.
- 7. Найдите площадь параллелограмма ABCD, считая стороны
квадратных клеток равными 1.
8. Найдите площадь параллелограмма ABCD, считая стороны
квадратных клеток равными 1.

- 3. Площадь трапеции 1. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1. 2. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1. 3. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- 4. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1. 5. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1. 6. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- 7. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1. 8. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- 4. Площадь выпуклых и невыпуклых четырехугольников
1. Найдите площадь четырехугольника ABCD, считая стороны
квадратных клеток равными 1.
2. Найдите площадь четырехугольника ABCD, считая стороны
квадратных клеток равными 1.
3. Найдите площадь четырехугольника ABCD, считая стороны
квадратных клеток равными 1.
 4. Найдите площадь четырехугольника ABCD, считая стороны
квадратных клеток равными 1.
4. Найдите площадь четырехугольника ABCD, считая стороны
квадратных клеток равными 1. - 5. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1. 6. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1. 7. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
- 8. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
- 5. Площадь круга и его частей
1. Найдите площадь S сектора, считая стороны квадратных клеток
S
π
равными 1. В ответе укажите .
2. Найдите площадь S сектора, считая стороны квадратных клеток
S
π
равными 1. В ответе укажите .
3. Найдите площадь S сектора, считая стороны квадратных клеток
S
π
равными 1. В ответе укажите .

- 4. Найдите площадь S сектора, считая стороны квадратных клеток S π равными 1. В ответе укажите . 5. Найдите площадь S сектора, считая стороны квадратных клеток S π равными 1. В ответе укажите .
- 6. Найдите площадь S сектора, считая стороны квадратных клеток S π равными 1. В ответе укажите . 7. Найдите площадь S кольца, считая стороны квадратных клеток S π равными 1. В ответе укажите . 8. Найдите площадь S кольца, считая стороны квадратных клеток S π равными 1. В ответе укажите .
- 6. Площадь фигур на координатной плоскости
1. Найдите площадь треугольника, вершины которого имеют
координаты (1, 1), (4, 4), (3, 1).
 2. Найдите площадь квадрата, вершины которого имеют координаты
(2, 1), (1, 3), (3, 4), (4, 2).
3. Найдите площадь параллелограмма, вершины которого имеют
координаты (1, 1), (1, 3), (5, 4), (5, 2).
2. Найдите площадь квадрата, вершины которого имеют координаты
(2, 1), (1, 3), (3, 4), (4, 2).
3. Найдите площадь параллелограмма, вершины которого имеют
координаты (1, 1), (1, 3), (5, 4), (5, 2). - 4. Найдите площадь параллелограмма, вершины которого имеют координаты (1, 1), (2, 4), (5, 4), (4, 1). 5. Найдите площадь трапеции, вершины которой имеют координаты (1, 1), (2, 4), (4, 4), (5, 1). 6. Найдите площадь ромба, вершины которого имеют координаты (1, 1), (2, 4), (5, 5), (4, 2).
- 7. Найдите площадь треугольника, вершины которого имеют координаты (1, 3), (4, 4), (4, 1). 8. Найдите площадь прямоугольника, вершины которого имеют координаты (0, 2), (1, 4), (5, 2), (4, 0).
- Самостоятельные работы
Самостоятельная работа 1
1. Найдите площадь параллелограмма ABCD, считая стороны
квадратных клеток равными 1.
2. Найдите площадь треугольника ABC, считая стороны квадратных
клеток равными 1.
3. Найдите площадь трапеции ABCD, считая стороны квадратных
клеток равными 1.

- 4. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1. 5. Найдите площадь S сектора, считая стороны квадратных клеток S π равными 1. В ответе укажите . 6. Найдите площадь треугольника, вершины которого имеют координаты (1, 1), (1, 4), (4, 3).
- Самостоятельная работа 2 1. 1. Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1. 2. 2. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1. 3. 3. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- 4. Найдите площадь четырехугольника ABCD, считая стороны
квадратных клеток равными 1.
5. Найдите площадь S сектора, считая стороны квадратных клеток
S
π
равными 1. В ответе укажите .
6. Найдите площадь параллелограмма, вершины которого имеют
координаты (1, 2), (1, 4), (5, 3), (5, 1).

- Самостоятельная работа 3 1. 1. Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1. 2. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1. 3. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- 4. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1. 4. 4. Найдите площадь S кольца, считая стороны квадратных клеток S π равными 1. В ответе укажите . 6. Найдите площадь трапеции, вершины которой имеют координаты (1, 1), (1, 4), (3, 4), (5, 1).
Advertisement
площади дз
Тренировочные работы
1. Площадь треугольника
1. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
2. Найдите площадь треугольника ABC,
считая стороны квадратных клеток равными
1.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток равными
1.
3. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
4. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
5. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
6. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
7. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
8. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
2. Площадь прямоугольника, квадрата, параллелограмма, ромба
1. Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток равными
1.
2. Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
3. Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1.
4. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
5. Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1.
6. Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1.
7. Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток равными
1.
Найдите площадь параллелограмма ABCD,
считая стороны квадратных клеток равными
1.
8. Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
3. Площадь трапеции
1. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
2. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
3. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
4. Найдите площадь трапеции ABCD,
считая стороны квадратных клеток равными
1.
5. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
6. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
7. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
8. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
4. Площадь выпуклых и невыпуклых четырехугольников
1. Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток равными
1.
2. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
3. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
4. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
5. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
6. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
7. Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток равными
1.
8. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
5. Площадь круга и его частей
1. Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите .
2. Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите .
3. Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите .
4. Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите.
5.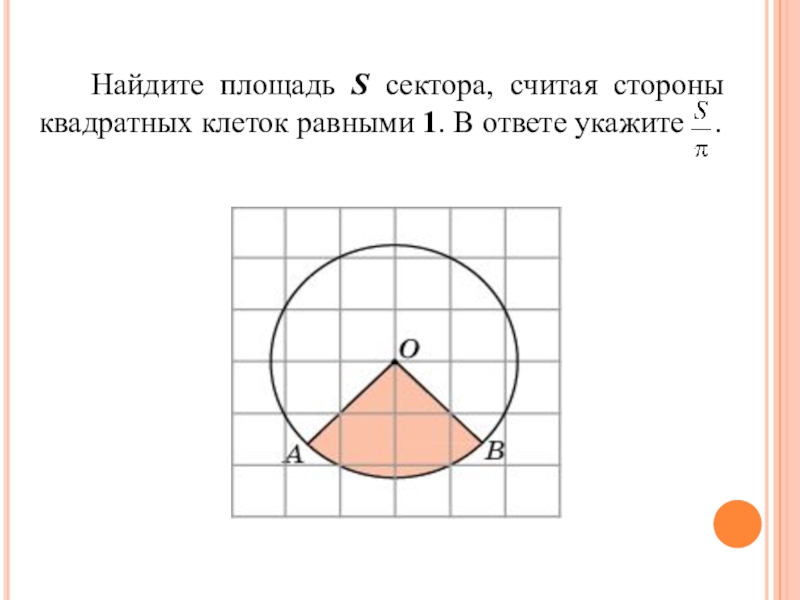 Найдите площадь S сектора,
считая стороны квадратных клеток равными
1. В ответе укажите
.
Найдите площадь S сектора,
считая стороны квадратных клеток равными
1. В ответе укажите
.
6. Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите .
7. Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите.
8. Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите .
6. Площадь фигур на координатной плоскости
1. Найдите площадь треугольника, вершины которого имеют координаты (1, 1), (4, 4), (3, 1).
2.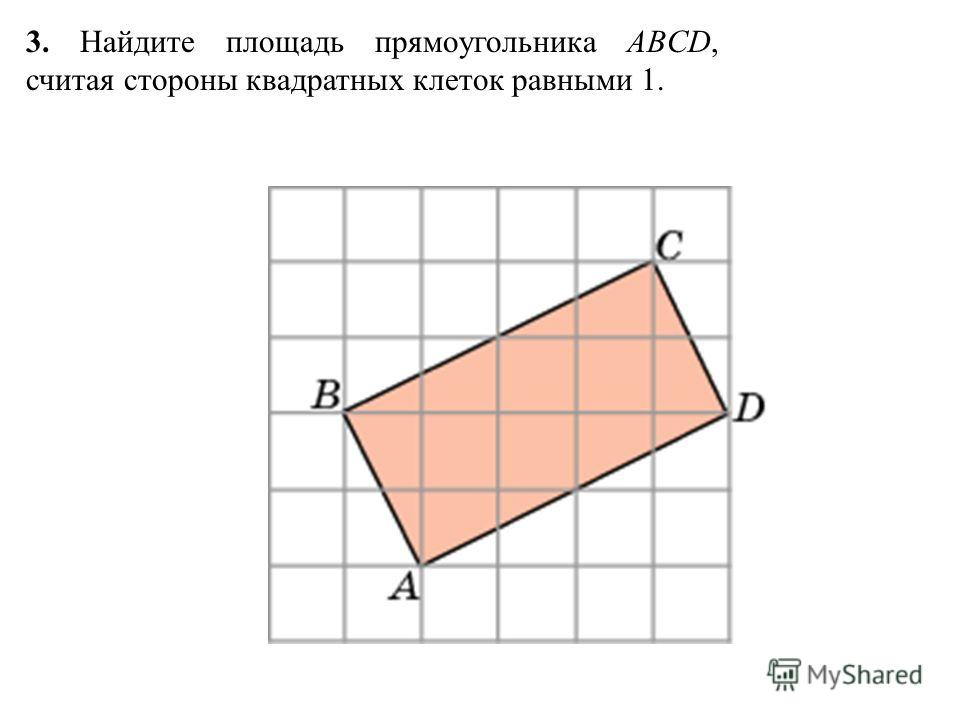 Найдите площадь квадрата, вершины
которого имеют координаты (2, 1), (1, 3), (3,
4), (4, 2).
Найдите площадь квадрата, вершины
которого имеют координаты (2, 1), (1, 3), (3,
4), (4, 2).
3. Найдите площадь параллелограмма, вершины которого имеют координаты (1, 1), (1, 3), (5, 4), (5, 2).
4. Найдите площадь параллелограмма, вершины которого имеют координаты (1, 1), (2, 4), (5, 4), (4, 1).
5. Найдите площадь трапеции, вершины которой имеют координаты (1, 1), (2, 4), (4, 4), (5, 1).
6. Найдите площадь ромба, вершины которого имеют координаты (1, 1), (2, 4), (5, 5), (4, 2).
7. Найдите площадь треугольника, вершины
которого имеют координаты (1, 3), (4, 4), (4,
1).
Найдите площадь треугольника, вершины
которого имеют координаты (1, 3), (4, 4), (4,
1).
8. Найдите площадь прямоугольника, вершины которого имеют координаты (0, 2), (1, 4), (5, 2), (4, 0).
Как найти площадь круга
Все математические ресурсы GRE
13 Диагностические тесты 452 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
GRE Math Help » Геометрия » Плоская геометрия » Круги » Радиус » Как найти площадь круга
Какова площадь круга, четверть длины окружности которого равна 5,5 дюйма?
Возможные ответы:121π
π/3
121/π
225π
Правильный ответ:121/№
Объяснение: Здесь вам нужно «решить в обратном направлении» из данных, которые вам дали. Мы знаем, что 0,25С = 5,5; следовательно, C = 22. Чтобы найти площадь, нам понадобится радиус окружности. Это можно получить, если вспомнить, что C = 2πr. Заменив 22 на C, мы получим 22 = 2πr.
Мы знаем, что 0,25С = 5,5; следовательно, C = 22. Чтобы найти площадь, нам понадобится радиус окружности. Это можно получить, если вспомнить, что C = 2πr. Заменив 22 на C, мы получим 22 = 2πr.
Найдите r: r = 22/2π = 11/π.
Теперь найдем площадь: A = πr 2 . Замена 11 / π вместо r: A = π (11 / π) 2 = (121π) / (π 2 ) = 121 / π.
Сообщить об ошибке
На приведенной выше диаграмме квадрат ABCD вписан в окружность. Если площадь квадрата 9, то какова площадь круга?
Возможные ответы:3√(2)π
4,5π
3π
9π
18π
Правильный ответ:4,5π
Объяснение: Если площадь квадрата равна 9, то s 2 = 9 и s = 3. Если таким образом стороны равны 3, мы можем вычислить диагонали (CB или AD), используя 45-45- Соотношение треугольников 90. Для стороны 3 диагональ будет 3√(2). Обратите внимание, что поскольку квадрат вписан в круг, эта диагональ также является диаметром круга.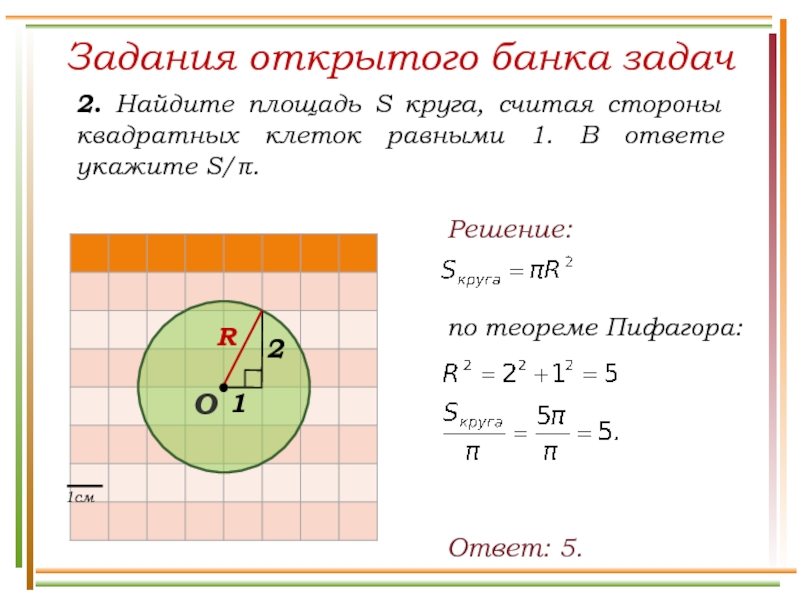 Если это так, радиус составляет половину этого или 1,5 √ (2).
Если это так, радиус составляет половину этого или 1,5 √ (2).
На основе этого значения мы можем вычислить площадь круга:
A = πr 2 = π(1,5√(2)) 2 = (2,25 * 2)π = 4,5π
Сообщить об ошибке 9000 5
Количественное сравнение
Количество A: Площадь круга с радиусом r
Количество B: Периметр круга с радиусом r
Возможные ответы:Отношение не может быть определено из предоставленной информации.
Количество A больше.
Количество B больше.
Обе величины равны.
Правильный ответ:Связь не может быть определена на основе предоставленной информации.
Объяснение:Попробуйте разные значения радиуса, чтобы увидеть, возникает ли закономерность. Необходимые формулы: Площадь = π r 2 и Периметр = 2 πr .
Если r = 1, то Площадь = π и Периметр = 2 π , поэтому периметр больше.
Если r = 4, то площадь = 16 π и периметр = 8 π , поэтому площадь больше.
Таким образом, на основе предоставленной информации нельзя определить родство.
Сообщить об ошибке
Количественное сравнение
Круг имеет радиус 2.
Количество A: Площадь круга
Количество B: Длина окружности
Возможные ответы :Связь не может быть определена на основании предоставленной информации.
Количество B больше.
Количество A больше.
Обе величины равны.
Правильный ответ:Обе величины равны.
Объяснение:Это один из немногих особых случаев, когда площадь равна длине окружности. Площадь = πr 2 = 4 π . Окружность = 2 πr = 4 π .
Примечание. Для количественного сравнения, такого как это, где столбцы имеют числовые значения вместо переменных, ответ редко будет «невозможно определить».
Сообщить об ошибке
Количественное сравнение
Количество A: Площадь прямоугольного треугольника со сторонами 7, 24, 25
Количество B: Площадь круга с радиусом 5
Возможные ответы:Две величины равны.
Количество A больше.
Количество B больше.
Связь не может быть определена на основании предоставленной информации.
Правильный ответ:Количество А больше.
Объяснение:Количество A: площадь = основание * высота / 2 = 7 * 24/2 = 84
Количество B: площадь = πr 2 = 25 π
Теперь нам нужно вспомнить, что такое π есть. Используя π = 3, площадь приблизительно равна 75. Используя π = 3,14, площадь немного увеличивается, но каким бы точным ни было приближение для π , эта площадь никогда не будет больше, чем количество A.
Сообщить об ошибке
Если круговой сад радиусом 3 фута граничит с круглым тротуаром шириной 2 фута, какова площадь тротуара?
Возможные ответы: Правильный ответ: Пояснение: Чтобы решить эту задачу, вы должны найти площадь всего круга (сада и тротуара) и вычесть ее из площади внутреннего сада. Вся область имеет радиус 5 футов (3 фута радиуса сада плюс 2 фута ширины тротуара), что дает площадь . Внутренний сад имеет радиус 3 фута и площадь . Разница в том, что площадь тротуара.
Вся область имеет радиус 5 футов (3 фута радиуса сада плюс 2 фута ширины тротуара), что дает площадь . Внутренний сад имеет радиус 3 фута и площадь . Разница в том, что площадь тротуара.
Сообщить об ошибке
Если круглый памятник радиусом 30 футов окружен круглым садом шириной 20 футов, какова площадь сада?
Возможные ответы: Правильный ответ: Пояснение:Чтобы найти площадь сада, вам нужно найти всю площадь и вычесть ее из площади внутреннего круга или памятника. Радиус большего круга равен 50, что составляет его площадь. Радиус внутреннего круга равен 30, что составляет его площадь. Разница в том.
Сообщить об ошибке
Маленький круг радиусом 5 лежит внутри большего круга радиусом x. Чему равна площадь области внутри большего круга, но за пределами меньшего круга в единицах x?
Возможные ответы: Правильный ответ: Объяснение:Поскольку ответы выражены в виде пи, просто найдите площадь каждого круга в единицах x и ∏:
Меньше: ∏(5) 2 = 25∏
Больше: ∏x 2
Мы должны вычесть внутренний круг из внешнего круга; это переводится как ∏x 2 -25∏ .
Сообщить об ошибке
Даны круг O диаметром 2 и квадрат ABCD , вписанный в круг O , какова площадь заштрихованной области?
Возможные ответы:4
4π – 2
π – 2
2
Правильный ответ:π – 2
Объяснение:Эта задача состоит из двух шагов: определение площади круга и определение площади квадрата. Площадь круга равна πr 2 , что равно π(2/1) 2 или π. AD является диаметром окружности O и образует два равнобедренных прямоугольных треугольника с ACD и ABD. Отношение сторон равнобедренного прямоугольного треугольника равно 1 : 1 : √2. Таким образом, стороны квадрата ABCD равны √2, а площадь равна 2. Площадь заштрихованной области равна площади круга минус площадь квадрата, или π – 2,9.0005
Сообщить об ошибке
Для , Челси может получить пиццу диаметром или два диаметра. Какая сделка лучше?
Возможные ответы: Два значения равны.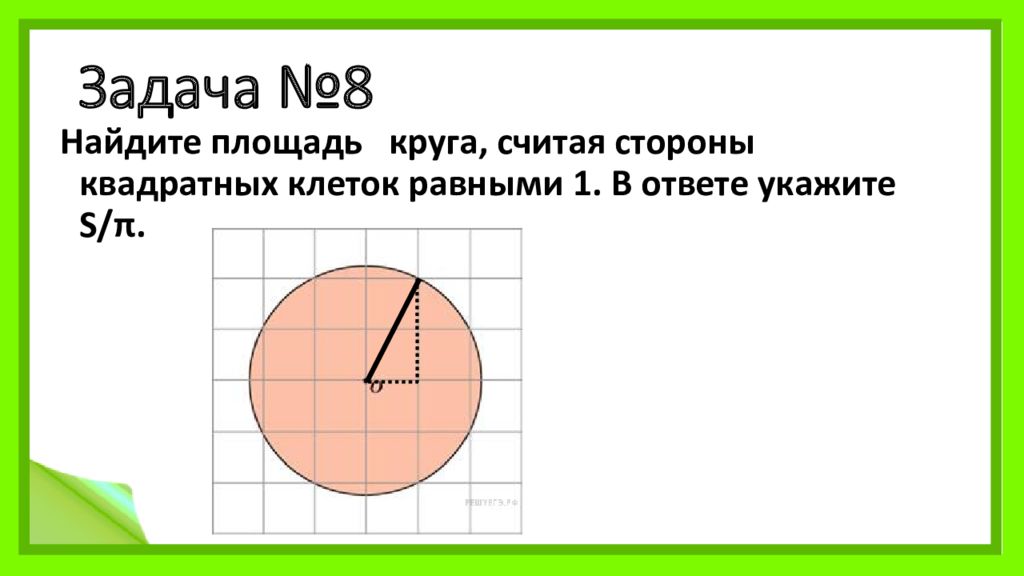
Невозможно определить.
два
Правильный ответ: Объяснение:
Таким образом, 16-дюймовая пицца — лучшее предложение.
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все математические ресурсы GRE
13 Диагностические тесты 452 практических теста Вопрос дня Карточки Learn by Concept
геометрия — Ожидаемая площадь, покрытая кругами внутри квадрата
- геометрический подход
Проблема явно масштабно-инвариантна.
$, когда квадрат почти полностью покрыт, за исключением углов, где пространство с касательными окружностями всегда останется.
Для нашей цели мы берем случайную «точку исследования» $X=(x,y)$, равномерно распределенную на $Q$, и вычисляем
вероятность того, что он выпадет за пределы любой из монет, которая представляет собой отношение $A/|Q| = А/4$.
Это эквивалентно фиксации окружности радиуса $r$ вокруг исследуемой точки, заданной как $X \in [x, x+dx) \times [y+dy) \subset Q$,
и определить вероятность того, что все $n$ центральные точки $(x_k,y_k)$ попадают за его пределы и в пределах $R$. 9{\,n} dxdy} } \cr}
\тег{1} }$$
где последний шаг исходит из симметрии $\lambda$.
2) Вычислительные аспекты
Точная общая формулировка $\lambda (x,y,r)$ довольно громоздка, так как сильно фрагментирована. в соответствии с различными относительными положениями круга и квадрата.
Однако, чтобы найти хорошее асимптотическое приближение для больших $n$ и малых $r$, мы можем начать с более простой версии что получается
в случае, если $r \le 1/2$.
В этом случае точная формула в первом квадранте равна
$$ \bbox[lightyellow] {
\left\{ \begin{массив}{l}
u = \left( {x — \left( {1 — r} \right)} \right)/r\quad v = \left( {y — \left( {1 — r} \right)} \right) /р \\
0 \le x,y \le 1\quad \Leftrightarrow \quad 1 — \frac{1}{r} \le u,v \le 1 \\
g(t) = \left[ {t < - 1} \right]\left( { - \frac{\pi }{2}} \right) + \left[ { - 1 \le t < 1} \right ]
\left ( {\ arcsin t + t \ sqrt {1 - t ^ {\, 2} } } \ right) + \ left [ {1 \ le t} \ right] \ left ( {\ frac {\ pi} { 2}} \справа) \\
\ lambda (u, v) = \ frac {1} {{2 \ pi}} \ left \ { {\ begin {array} {* {20} c}
{\ frac {\ pi} {2} + 2uv - g (u) - g (v)} & {\ left | {\;u^{\,2} + v^{\,2} < 1} \right.

 Площадь фигур на координатной плоскости ……………………….
Самостоятельные работы ……………………………………………….
Самостоятельная работа 1 ……………………………………………….
Самостоятельная работа 2 ……………………………………………….
Самостоятельная работа 3 ……………………………………………….
Площадь фигур на координатной плоскости ……………………….
Самостоятельные работы ……………………………………………….
Самостоятельная работа 1 ……………………………………………….
Самостоятельная работа 2 ……………………………………………….
Самостоятельная работа 3 ……………………………………………….


 Напомним, что площадь ромба равна половине
произведения его диагоналей. Воспользуемся тем, что диагональ
2
квадратной клетки со сторонами, равными 1, равна . Тогда диагонали
4 2 2 2
AС и BD данного ромба будут равны соответственно и , а его
2 2 ⋅4 2
2
площадь будет равна , т.е. равна 8.
Второе решение. Достроим на сторонах ромба четыре равных
прямоугольных треугольника, катеты которых равны 1 и 3. Площадь
каждого такого треугольника равна 1,5. Ромб вместе с этими
треугольниками образует фигуру, состоящую из четырнадцати единичных
квадратов. Следовательно, ее площадь равна 14. Вычитая из нее площадь
четырех треугольников, получим, что площадь ромба равна 8.
Напомним, что площадь ромба равна половине
произведения его диагоналей. Воспользуемся тем, что диагональ
2
квадратной клетки со сторонами, равными 1, равна . Тогда диагонали
4 2 2 2
AС и BD данного ромба будут равны соответственно и , а его
2 2 ⋅4 2
2
площадь будет равна , т.е. равна 8.
Второе решение. Достроим на сторонах ромба четыре равных
прямоугольных треугольника, катеты которых равны 1 и 3. Площадь
каждого такого треугольника равна 1,5. Ромб вместе с этими
треугольниками образует фигуру, состоящую из четырнадцати единичных
квадратов. Следовательно, ее площадь равна 14. Вычитая из нее площадь
четырех треугольников, получим, что площадь ромба равна 8.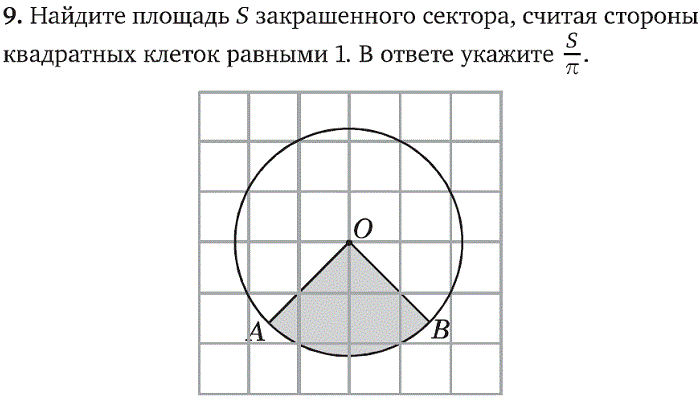 Она равна 3.
Так как площадь трапеции равна произведению полусуммы оснований на
4+ 2
⋅3
2
высоту, то площадь данной трапеции будет равна , т.е. равна 9.
Второе решение. Из точки B опустим перпендикуляр BH на AD. Он
разобьет трапецию на прямоугольный треугольник ABH и прямоугольник
HBCD. Катеты прямоугольного треугольника равны 2 и 3, следовательно,
его площадь равна 3. Смежные стороны прямоугольника равны 2 и 3,
следовательно, его площадь равна 6. Площадь трапеции равна сумме
площадей треугольника и прямоугольника и, следовательно, равна 9.
Она равна 3.
Так как площадь трапеции равна произведению полусуммы оснований на
4+ 2
⋅3
2
высоту, то площадь данной трапеции будет равна , т.е. равна 9.
Второе решение. Из точки B опустим перпендикуляр BH на AD. Он
разобьет трапецию на прямоугольный треугольник ABH и прямоугольник
HBCD. Катеты прямоугольного треугольника равны 2 и 3, следовательно,
его площадь равна 3. Смежные стороны прямоугольника равны 2 и 3,
следовательно, его площадь равна 6. Площадь трапеции равна сумме
площадей треугольника и прямоугольника и, следовательно, равна 9. Так как
площадь трапеции равна произведению полусуммы оснований на высоту, то
4 2 +2 2 3 2
⋅
2 2
площадь данной трапеции будет равна и, следовательно,
будет равна 9.
Второе решение. Разобьем трапецию на параллелограмм ABCE и
треугольник CDE. Сторона AB параллелограмма ABCE равна 3, высота EH,
к ней проведенная, равна 2, следовательно, площадь этого параллелограмма
равна 6. Сторона CE треугольника CDE равна 3, высота DG, к ней
проведенная, равна 2, следовательно, площадь этого треугольника равна 3.
Площадь трапеции равна сумме площадей параллелограмма и треугольника
и, следовательно, равна 9.
Так как
площадь трапеции равна произведению полусуммы оснований на высоту, то
4 2 +2 2 3 2
⋅
2 2
площадь данной трапеции будет равна и, следовательно,
будет равна 9.
Второе решение. Разобьем трапецию на параллелограмм ABCE и
треугольник CDE. Сторона AB параллелограмма ABCE равна 3, высота EH,
к ней проведенная, равна 2, следовательно, площадь этого параллелограмма
равна 6. Сторона CE треугольника CDE равна 3, высота DG, к ней
проведенная, равна 2, следовательно, площадь этого треугольника равна 3.
Площадь трапеции равна сумме площадей параллелограмма и треугольника
и, следовательно, равна 9. Второе решение. Разобьем данный четырехугольник на два
треугольника ABD и BCD. Сторона BD у них общая и равна 4. Высоты AH и
CH равны соответственно 3 и 1. Следовательно, площади этих
треугольников равны соответственно 6 и 2. Значит, площадь
четырехугольника равна 8.
Ответ. 8.
Второе решение. Разобьем данный четырехугольник на два
треугольника ABD и BCD. Сторона BD у них общая и равна 4. Высоты AH и
CH равны соответственно 3 и 1. Следовательно, площади этих
треугольников равны соответственно 6 и 2. Значит, площадь
четырехугольника равна 8.
Ответ. 8.
 Откуда .
Второе решение. Заметим, что данный сектор является одной
четвертой частью круга и, следовательно, его площадь равна одной
четвертой площади круга. Площадь круга равна π R , где R – радиус круга.
2
5π
5 4
В нашем случае R = и, следовательно, площадь S сектора равна .
S
= 1,25
π
Откуда .
Ответ. 1,25.
10. Площадь кольца равна разности площадей внешнего и
внутреннего кругов. Радиус R внешнего круга равен 2 2 , радиус r
внутреннего круга равен 2. Следовательно, площадь S кольца равна 8π−4π ,
S
=4
π
т.
Откуда .
Второе решение. Заметим, что данный сектор является одной
четвертой частью круга и, следовательно, его площадь равна одной
четвертой площади круга. Площадь круга равна π R , где R – радиус круга.
2
5π
5 4
В нашем случае R = и, следовательно, площадь S сектора равна .
S
= 1,25
π
Откуда .
Ответ. 1,25.
10. Площадь кольца равна разности площадей внешнего и
внутреннего кругов. Радиус R внешнего круга равен 2 2 , радиус r
внутреннего круга равен 2. Следовательно, площадь S кольца равна 8π−4π ,
S
=4
π
т. е. S = 4π
и, следовательно, .
е. S = 4π
и, следовательно, .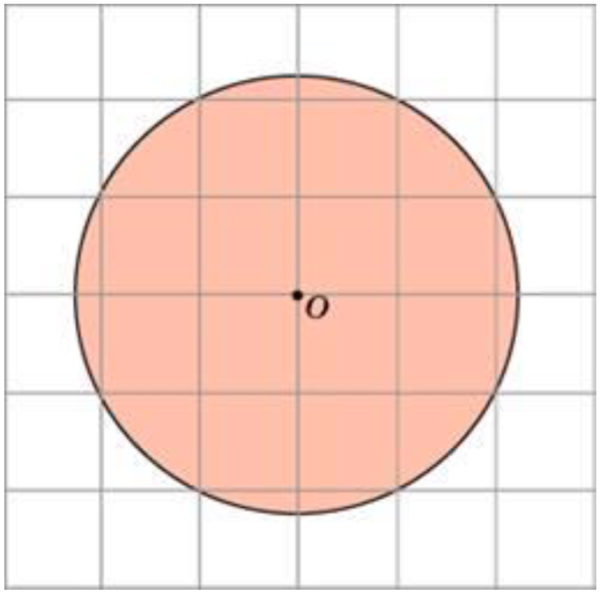 6. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1.
7. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1.
6. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1.
7. Найдите площадь треугольника ABC, считая стороны квадратных клеток
равными 1.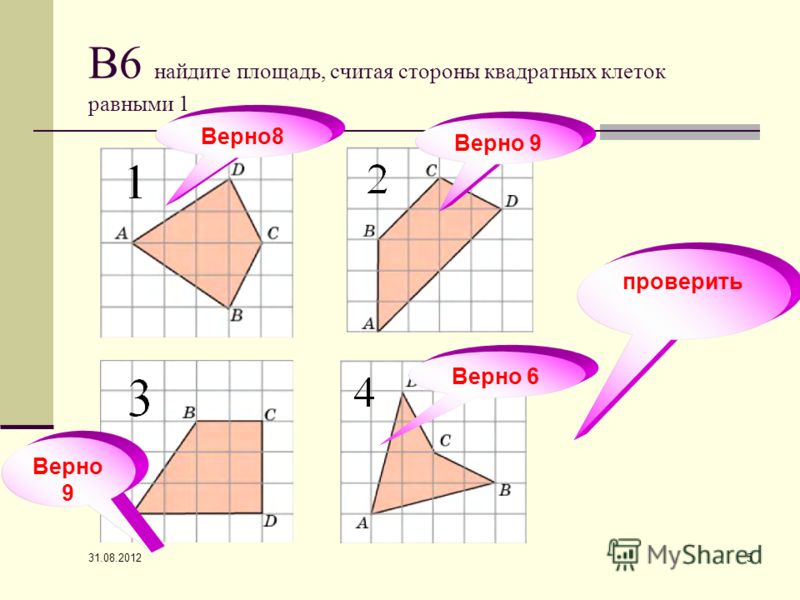
 4. Найдите площадь четырехугольника ABCD, считая стороны
квадратных клеток равными 1.
4. Найдите площадь четырехугольника ABCD, считая стороны
квадратных клеток равными 1.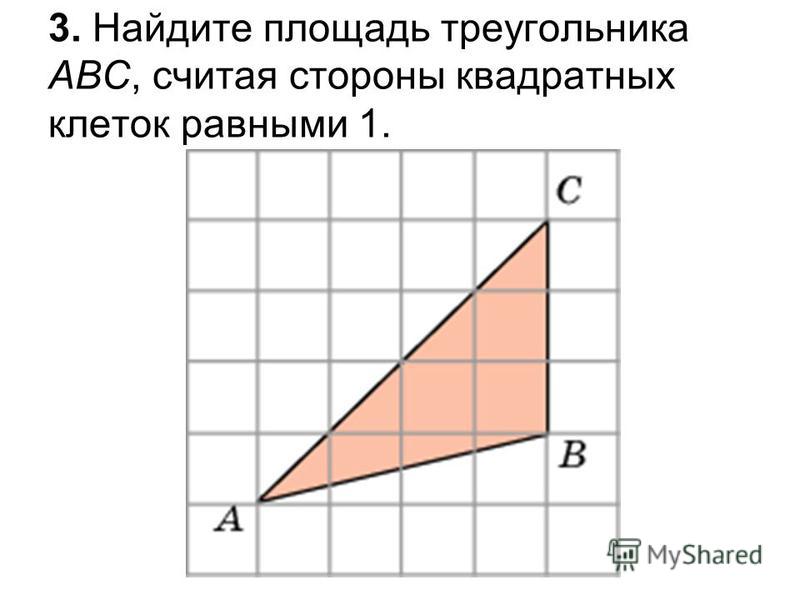
 2. Найдите площадь квадрата, вершины которого имеют координаты
(2, 1), (1, 3), (3, 4), (4, 2).
3. Найдите площадь параллелограмма, вершины которого имеют
координаты (1, 1), (1, 3), (5, 4), (5, 2).
2. Найдите площадь квадрата, вершины которого имеют координаты
(2, 1), (1, 3), (3, 4), (4, 2).
3. Найдите площадь параллелограмма, вершины которого имеют
координаты (1, 1), (1, 3), (5, 4), (5, 2).

Leave A Comment