Тест по математике (геометрии) для 10 класса «Параллельность прямых, прямой и плоскости»
Тест по математике (геометрии), 10 класс
«Параллельность прямых, прямой и плоскости»
1 вариант
1. Точки А, В, С, D не лежат в одной плоскости. Точки K, L, M, N — середины отрезков AB, BC, CD, AD соответственно. Укажите прямые, параллельные прямой АС.
1) KL и ML; | 2) MN и BD; | 3) KL и MN; | 4) нет. |
2. Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С — параллельные прямые, пересекающие эту плоскость в точках B1 и C1. Найдите длину отрезка CC1, если AC:CB=3:2 и BB1=20 см.
Найдите длину отрезка CC1, если AC:CB=3:2 и BB1=20 см.
1) 12 см; | 2) 8 см; | 3) 16 см; | 4) 4 см. |
3. Вершина А треугольника АВС лежит в плоскости α, вершины В и С расположены по одну сторону от этой плоскости. Отрезок AD — медиана треугольника АВС. Через точки B, D и C проведены параллельные прямые, пересекающие плоскость α в точках B1, D1, C1 соответственно. Найдите длину DD1, если BB1=2 см и CC1=2 см.
1) 7 см; | 2) 5 см; | 3) 10 см; | 4) 8 см. |
4. В тетраэдре ABCD точки K, L, M, N — середины рёбер АС, ВС, BD, AD, соответственно. Определите вид четырехугольника KLMN и его периметр, если АВ=16 см и CD=18 см.
Ответ: _______________.
5. Точки А и В лежат по одну сторону от плоскости α Точка С лежит на отрезке АВ и АС:СВ=2:3. Через точки А, В, С проведены параллельные прямые, пересекающие плоскость α соответственно в точках A1, B1, C1. Найдите CC1 , если AA1=a, BB1=b (ba).
Ответ: _______________.
6. Даны параллелограмм ABCD и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках A1, B1, C1, D1. Найдите DD1, если AA1=2 см, BB1=3 см, CC1=8 см.
Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках A1, B1, C1, D1. Найдите DD1, если AA1=2 см, BB1=3 см, CC1=8 см.
Ответ: _______________.
Кличи к тесту:
1 | 2 | 3 | 4 | 5 | 6 |
3 | 1 | 2 | параллелограмм; 34 см | 7 см |
Тест по математике (геометрии), 10 класс
«Параллельность прямых, прямой и плоскости»
2 вариант
1.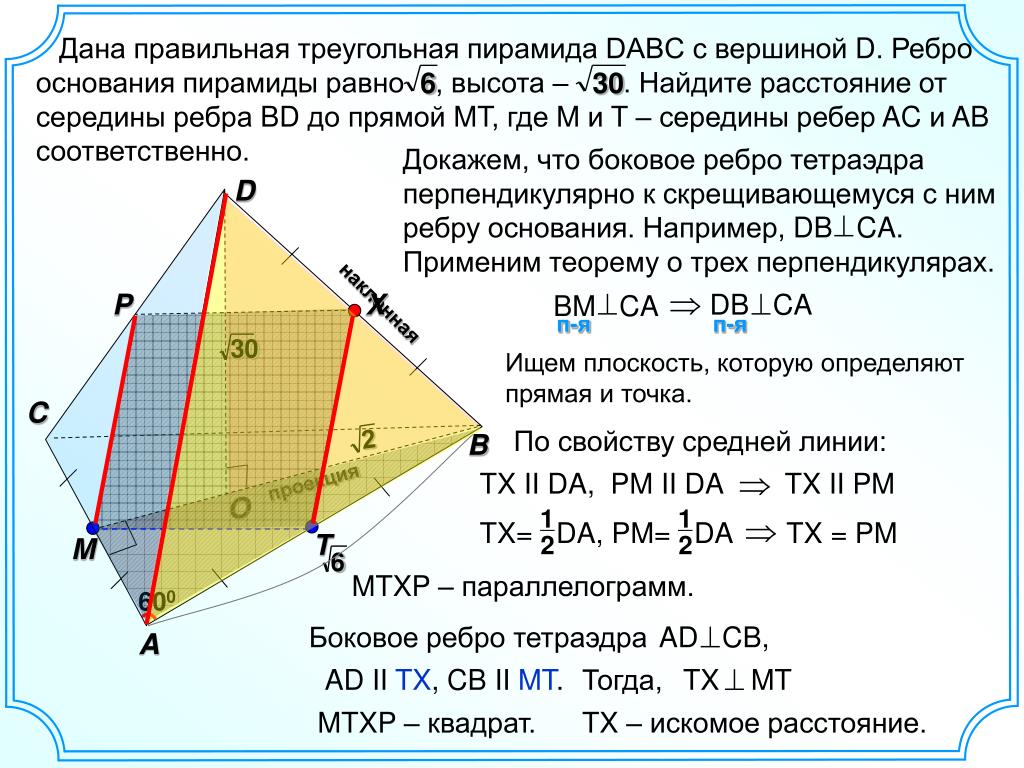 Точки А, В, С, D не лежат в одной плоскости. Точки K, L, M, N — середины отрезков AB, BC, CD, AD соответственно. Укажите прямые, параллельные прямой BD.
Точки А, В, С, D не лежат в одной плоскости. Точки K, L, M, N — середины отрезков AB, BC, CD, AD соответственно. Укажите прямые, параллельные прямой BD.
1) LM и MN; | 2) KN и LM; | 3) KN и AC; | 4) нет. |
2. Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С — параллельные прямые, пересекающие эту плоскость в точках B1 и C1. Найдите длину отрезка CC1, если AC:CB=4:3 и BB1=14 см.
1) 12 см; | 2) 7 см; | 3) 8 см; | 4) 6 см. |
3. Вершина А треугольника АВС лежит в плоскости α, вершины В и С расположены по одну сторону от этой плоскости. Отрезок AD — медиана треугольника АВС. Через точки B, D и C проведены параллельные прямые, пересекающие плоскость α в точках B1, D1, C1 соответственно. Найдите длину DD1, если BB1=14 см и CC1=8 см.
1) 3 см; | 2) 11 см; | 3) 6 см; | 4) 7 см. |
4. В тетраэдре ABCD точки K, L, M, N — середины рёбер АС, ВС, BD, AD, соответственно.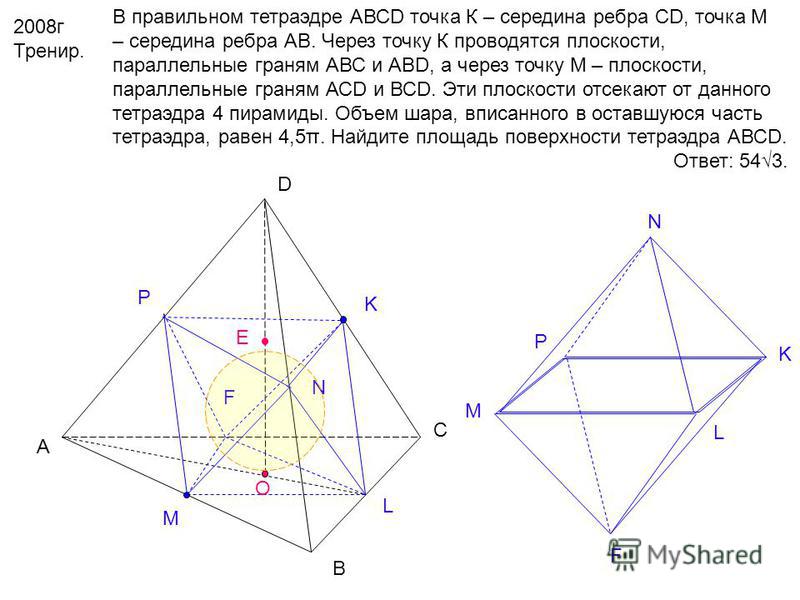 Определите вид четырехугольника KLMN и его периметр, если АВ=12 см и CD=24 см.
Определите вид четырехугольника KLMN и его периметр, если АВ=12 см и CD=24 см.
Ответ: _______________.
5. Точки А и В лежат по одну сторону от плоскости α. Точка С лежит на отрезке АВ и АС:СВ=3:4. Через точки А, В, С проведены параллельные прямые, пересекающие плоскость α соответственно в точках A1, B1, C1. Найдите CC1 , если AA1=a, BB1=b (ba).
Ответ: _______________.
6. Даны параллелограмм ABCD и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках A1, B1, C1, D1. Найдите DD1, если AA1=6 см, BB1=4 см, CC1=10 см.
Найдите DD1, если AA1=6 см, BB1=4 см, CC1=10 см.
Ответ: _______________.
Кличи к тесту:
1 | 2 | 3 | 4 | 5 | 6 |
2 | 3 | 1 | параллелограмм; 36 см | 12 см |
Контрольно-измерительные материалы. Геометрия. 10 класс
%PDF-1.7 % 164 0 obj > endobj 20 0 obj >>> endobj 197 0 obj >stream application/pdf
 Н. Рурукин
Н. Рурукин

Эйлер Учителя МО 2007-20 62 стр
Точка $K$ лежит на стороне $BC$ параллелограмма $ABCD$, а точка $M$ лежит на стороне $AD$
. Отрезки $CM$ и $DK$ пересекаются в точке $L$, а отрезки $AK$ и $BM$ пересекаются в точке $N$.
Найдите наибольшее значение отношения площадей четырехугольников $KLMN$ и $ABCD$.
2011 Олимпиада учителей Эйлера I стр. 4
Олимпиада учителей Эйлера 2011 I стр. 6
Сфера касается всех ребер тетраэдра, два противоположных ребра которого равны $a$ и $b$, а все остальные ребра равны между собой. Найдите радиус этой сферы.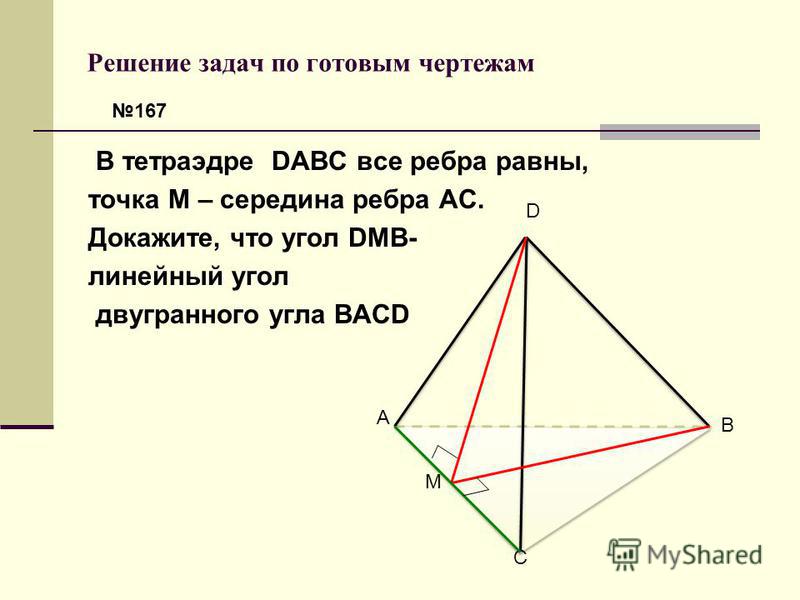
2011 Олимпиада учителей Эйлера I стр.10
На гипотенузе $ABDE$ прямоугольного треугольника $ABC$ в полуплоскости, которой треугольник $ABC$ не принадлежит, построен квадрат $ABDE$. Найти расстояние от вершины $C$ до центра квадрата, если известно, что $BC=a$ и $AC= b$
Олимпиада учителей Эйлера 2011 I стр. 12
Докажите неравенство $P> 4R$, где $P$ — периметр, а $R$ — радиус описанной окружности остроугольного треугольника.
2011 Олимпиада учителей Эйлера II с.3
Основанием пирамиды $PABCD$ является трапеция $ABCD$, основание которой $AD$ вдвое больше основания BC. Прямая $MN$ — это средняя линия треугольника $ABP$, параллельная стороне $AB$. Найдите отношение объемов тел, на которое плоскость $DMN$ делит данную пирамиду.
2012 Олимпиада учителей Эйлера I с.6
Докажите, что сумма квадратов расстояний от вершин правильного семиугольника до произвольной прямой, проходящей через его центр, не зависит от положения этой прямой.
Олимпиада учителей Эйлера 2012 I с.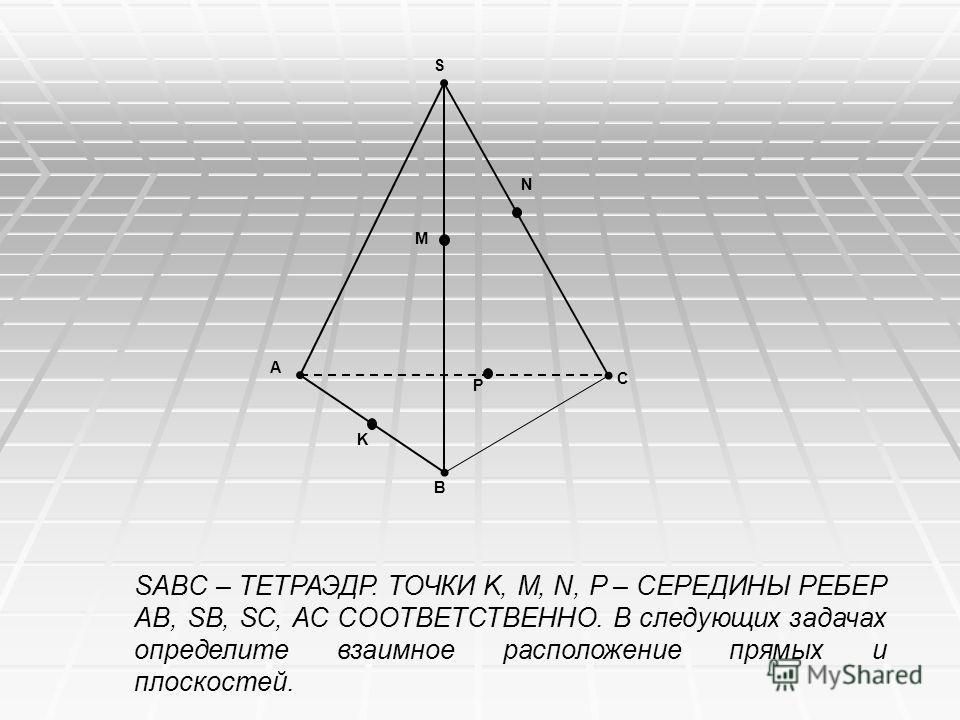 7
7
Окружность и парабола имеют ровно две общие точки, одна из которых является точкой касания этой параболы и этой окружности. Верно ли вообще, что вторая общая точка окружности и параболы является также точкой их касания? 9о$.
2012 Олимпиада учителей Эйлера II с.3
Постройте прямую, проходящую через вершину выпуклого четырехугольника и делящую его на две равные части (площади).
2012 Олимпиада учителей Эйлера II с.4
а) Докажите, что любое сечение правильного тетраэдра плоскостью, проходящей через середины двух его пересекающихся ребер, делит тетраэдр на две равные части.
б) Докажите, что утверждение, сформулированное в пункте (а), верно для любого (не обязательно правильного) тетраэдра.
2012 Олимпиада учителей Эйлера II с.7
Четырехугольник вписан в прямоугольник так, что на каждой стороне прямоугольника лежит одна вершина четырехугольника. Докажите, что периметр четырехугольника не менее чем в два раза больше диагонали прямоугольника.
2013 Олимпиада учителей Эйлера I с4
Пусть $A, B$ и $C$ — вершины равностороннего треугольника, $P$ — произвольная точка в плоскости этого треугольника. Докажите, что $AP\le BP+CP$.
2013 Олимпиада учителей Эйлера I с5
В правильной четырехугольной пирамиде косинус угла между противоположными боковыми гранями равен $8/9$ . Найдите сечение этой пирамиды плоскостью, проходящей через ребро основания, площадь которого наибольшая.
2013 Олимпиада учителей Эйлера I стр.9
Две окружности радиусов $4$ и $8$ касаются в точке $A$. Через точку $A$ прямую, пересекающую большую окружность в точке $B$ и меньшую окружность в точке $C$. Найдите $AB$, если известно, что $BC = 6\sqrt2$.
2013 Олимпиада учителей Эйлера I стр. 12
Постройте треугольник $ABC$ по двум сторонам $AC$ и $AB$, если известно, что $\угол BAC = 2 \угол ABC$ .
2013 Олимпиада учителей Эйлера II с.3
Докажите, что существует треугольная пирамида с площадями граней, равными $3, 4, 5$ и $10$.
2014 Олимпиада учителей Эйлера I стр.2
Сторона квадрата равна a. Середины сторон квадрата соединены отрезками с его противоположными вершинами (см. рисунок). Найдите площадь получившегося восьмиугольника.
2014 Олимпиада учителей Эйлера I с.6
Олимпиада учителей Эйлера 2014 I с.9
Проведите прямую через вершину $A$ треугольника $ABC$ так, чтобы сумма расстояний от этой прямой до точек $B$ и $C$ была наибольшей.
2014 Олимпиада учителей Эйлера II с.5
На сторонах $AB, BC$ и $AC$ треугольника $ABC$ выбраны точки$ K, L$ и $M$ соответственно так, что отрезки $AL, BM$ и $CK$ пересекаются в одной точке и $\overrightarrow{AL}+\overrightarrow{BM} + \overrightarrow{CK}= \overrightarrow{0}$ .
2015 Олимпиада учителей Эйлера I с.2
Четырехугольник называется равнодиагональным, если его диагонали равны. Докажите, что если отрезок, соединяющий середины противоположных сторон выпуклого четырехугольника $ABCD$, делит его на два равнодиагональных четырехугольника, то четырехугольник $ABCD$ также является равнодиагональным.
2015 Олимпиада учителей Эйлера I стр.7
В основании пирамиды объема $V$ лежит параллелограмм. Длины боковых ребер этой пирамиды различны и отличаются от длин ребер ее основания. Найдите объем треугольной пирамиды, составленной из боковых граней этой пирамиды.
Олимпиада учителей Эйлера 2015 II стр. 2
В тетраэдре $ABCD$: $AB=8, BC=10, AC=12, BD=15$. Известно, что четыре отрезка, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.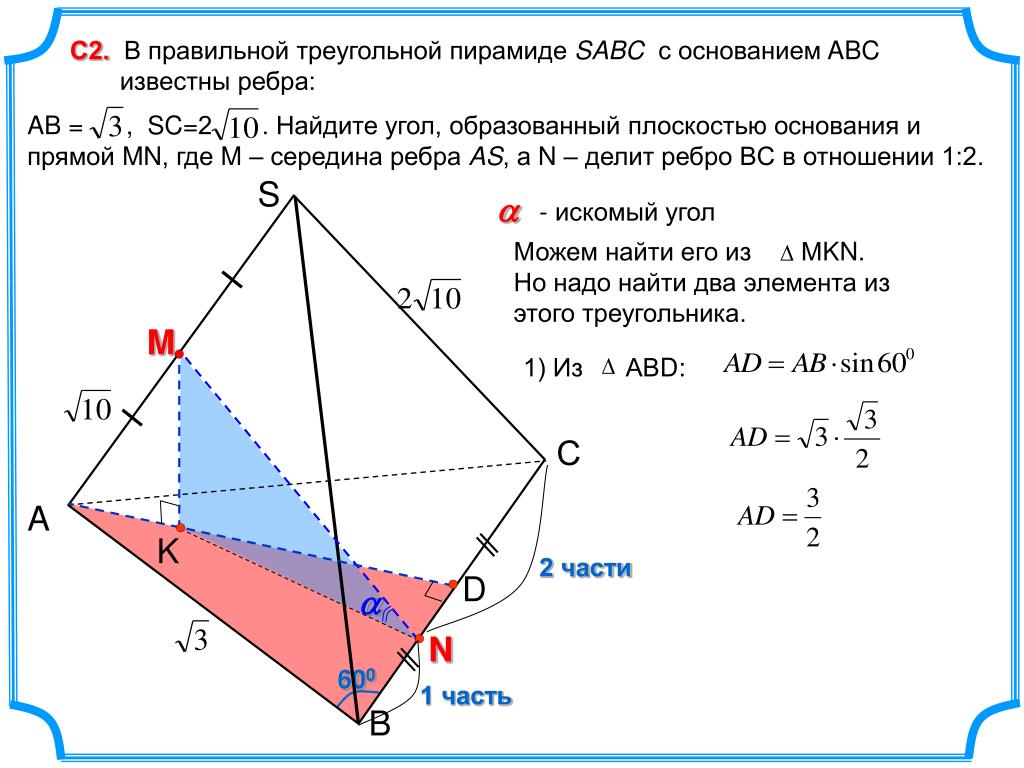 Найдите длины ребер $DA$ и $DC$
Найдите длины ребер $DA$ и $DC$
2016 Олимпиада учителей Эйлера I стр.5
В основании пирамиды с вершиной $S$ лежит квадрат $ABCD$. Известно, что $AS = 7, BS= DS = 5$. Какие значения может принимать длина стороны квадрата $ABCD$? Найдите также длину бокового ребра $CS$ такой пирамиды.
2016 Олимпиада учителей Эйлера I стр.9
В треугольнике $ABC$ проведены биссектрисы $AD$ и $BE$. Оказалось, что $DE$ является биссектрисой треугольника $ADC$. Найдите угол $\angle BAC$
Олимпиада учителей Эйлера 2016 I с11 92)$.
2016 Олимпиада учителей Эйлера II с.4
В основании четырехугольной пирамиды $PABCD$ лежит параллелограмм $ABCD$. На боковых ребрах $PC$ и $PD$ выбраны точки $M$ и $N$ соответственно так, что точки $A, B, M$ и $N$ лежат в одной плоскости, а объем $ Пирамида PABMN$ в $4,5$ меньше объемной пирамиды $PABCD$ (соотношение объемов $=2:9$). Найдите отношение $PM:MC$.
Олимпиада учителей Эйлера 2017 I с.6
Найдите наименьшую площадь общей части правильного восьмиугольника и его изображения при повороте на некоторый угол относительно центра исходного восьмиугольника.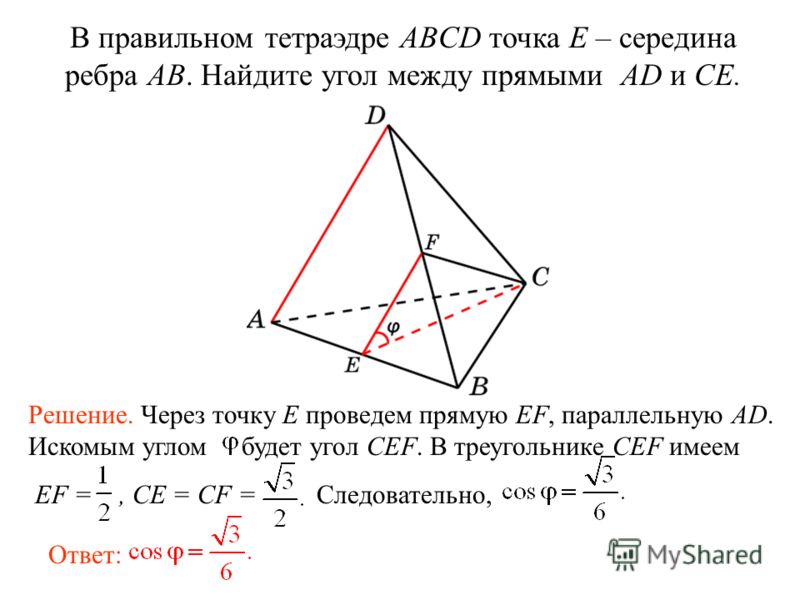 2}{2}$
2}{2}$
2017 Олимпиада учителей Эйлера II с.6
а) Докажите, что любой трехгранный угол с вершиной $P$ имеет луч $PO$, образующий равные углы с ребрами этого треугольного угла.
б) Пусть каждый из лучей $AK, BL, CM$ и $DN$ в тетраэдре $ABCD$ образует равные углы с ребрами «своего» треугольного угла. Сформулируйте и докажите хотя бы одно необходимое и достаточное условие пересечения лучей $AK, BL, CM$ и $DN$ в одной точке. Какая теорема планиметрии аналогична этому утверждению?
2018 Олимпиада учителей Эйлера I с.5
Рассмотрим тетраэдр $ABCD$, высота которого $DH$ проходит через точку пересечения высот треугольника $ABC$.
а) Докажите, что противоположные ребра этого тетраэдра перпендикулярны.
б) Докажите, что прямые, на которых лежат высоты этого тетраэдра, проходят через одну точку.
в) Выясните, верно ли обратное: «Если прямые, на которых лежат высоты тетраэдра, проходят через одну точку, то основания высот этого тетраэдра являются точками пересечения высот соответствующих граней . 92+14x-7=0$
92+14x-7=0$
Олимпиада учителей Эйлера II 2018 p5
Дан тетраэдр с длинами ребер, равными $1$. Докажите, что на поверхности этого тетраэдра существует набор отрезков общей длины меньше $1+\sqrt3$, таких что любые две вершины тетраэдра соединены ломаной, состоящей из этих отрезков.
2018 Олимпиада учителей Эйлера II с.7
Пусть $a, b, c$ — длины сторон треугольника, $r$ — радиус вписанной окружности в этот треугольник. Докажите, что если $r=\frac{a+b-c}{2}$, то этот треугольник прямоугольный.»
Олимпиада учителей Эйлера 2019 I стр.1
В треугольнике $ABC$ известны длины двух сторон: $AB = 1$ и $AC = 3$. Найдите все значения, которые могут принимать:
а) длину $h$ высоты, опущенной из вершины $A$,
б) длину $m$ медианы, проведенной из вершины $A$,
в) длину $ l$ биссектрисы, проведенной из вершины $A$.
Обоснуйте свои ответы.
Олимпиада учителей Эйлера 2019 I стр.9
Стороны треугольника $ABC$ известны: $AB = 5, BC = 6, AC = 7$. Окружность, проходящая через точки $A$ и $C$, пересекает прямые $BA$ и $BC$ в точках $E$ и $F$ соответственно, отличных от вершин треугольника. Отрезок $EF$ касается вписанной окружности треугольника $ABC$. Найдите длину отрезка $EF$.
Окружность, проходящая через точки $A$ и $C$, пересекает прямые $BA$ и $BC$ в точках $E$ и $F$ соответственно, отличных от вершин треугольника. Отрезок $EF$ касается вписанной окружности треугольника $ABC$. Найдите длину отрезка $EF$.
2019 Олимпиада учителей Эйлера I с10
Докажите, что на плоскости нет равносторонних треугольников, все координаты вершин целые числа.
2019 Олимпиада учителей Эйлера II с.3
В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ длины трех его ребер: $AB= 5$,$AD= 12$,$AA_1 = 8$. Точка $M$ на ребре $AA_1$ такова, что $AM = 5$. Найдите объем пирамиды $MB_1C_1D$.
2019 Олимпиада учителей Эйлера II с.7
Постройте квадрат $ABCD$ в его вершине $A$ и двух точках $M$ и $N$, лежащих на прямых $BC$ и $CD$ соответственно.
Олимпиада учителей Эйлера 2020 I стр. 10
Квадраты $ABCD, DCGH, BEFG$ и $ELKM$ расположены, как показано на рисунке. Найдите площадь треугольника $DGK$, если известно, что площадь квадрата $ABCD$ равна $20$
Олимпиада учителей Эйлера 2020 I стр. 12
12
Найдите условия, при которых изображение угла в его ортогональной проекции на плоскость меньше исходного угла.
Кен Монкс | Профессор математики
- Докажите каждую из следующих теорем и запишите свое доказательство дважды один раз в качестве полуформального доказательства и второй раз в качестве традиционного, неформального пояснительного доказательства. Запишите их все в один файл проекта LaTeX, используя приведенный ниже шаблон домашнего задания в стиле статьи (не обычный шаблон). Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 22».
- 1. Thm (лучше поздно, чем никогда) Если у функции есть обратная функция, то она биективна.
- 2. Thm 10.30 ( даже больше Де Моргана ) Для любого множества $I$ и $A_i$ с $i\in I$, $$\displaystyle\left(\bigcup_{i\in I} A_i\right)’ = \bigcap_{j\in I} A_j’$$
- 3.
 Thm 10.60 ( не отношение эквивалентности ) Предположим, что $\sim$ есть множество
$$\sim = \Set{ (1,1),(2,2),(3,3),(1,2),(2,1),(1,3),(3,1)} $$
Тогда $\sim$ не является отношением эквивалентности на множестве $\Set{1,2,3}$.
Thm 10.60 ( не отношение эквивалентности ) Предположим, что $\sim$ есть множество
$$\sim = \Set{ (1,1),(2,2),(3,3),(1,2),(2,1),(1,3),(3,1)} $$
Тогда $\sim$ не является отношением эквивалентности на множестве $\Set{1,2,3}$. - 4. Thm 10.65 ( конгруэнция есть отношение эквивалентности ) Пусть $m$ — натуральное число. Отношение $\underset{m}{\equiv}$ является отношением эквивалентности на любом множестве целых чисел
- Запомните определения теории основных множеств из таблицы на странице 60 конспекта лекций для короткого теста в начале занятия.
- Докажите каждую из следующих теорем и запишите свое доказательство дважды один раз в качестве полуформального доказательства и второй раз в качестве традиционного, неформального пояснительного доказательства, такого как пример, который я делал в классе. Запишите их все в один файл проекта LaTeX, используя приведенный ниже шаблон домашнего задания в стиле статьи (не обычный шаблон).
 Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 21».
Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 21».- 1. Thm 10.48 : Композиция сюръективных функций сюръективна. 9-{у}$$ тогда $\sim$ — отношение эквивалентности.
- Запомните определения теории основных множеств из таблицы на странице 60 конспекта лекций для короткого теста в начале занятия.
- Смешанный пакет. Докажите каждую из следующих теорем и запишите свое полуформальное доказательство в одном проекте файла LaTeX. Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 20». В этих задачах множествами являются $A , B, C$ и $D$.
- а. Thm 10,2 ( Порядок не имеет значения ) $\{\,a,b\,\}=\{\,b,a\,\}$
- б. Thm 10.35 ( Powerset и Union ) $\mathcal{P}(A)\cup\mathcal{P}(B) \subseteq \mathcal{P}(A\cup B)$
- с.
 Thm 10.32 ( Подмножества заразны ) Если $A\subseteq C$ и $B\subseteq D$, то $A\times B\subseteq C\times D$.
Thm 10.32 ( Подмножества заразны ) Если $A\subseteq C$ и $B\subseteq D$, то $A\times B\subseteq C\times D$. - д. Thm 10,57 ( тождество для состава ) Если $f\colon A\to A$, то $$f\circ \text{id}_A=\text{id}_A\circ f=f$$
- эл. Thm 10.40 ( Композиция ассоциативна ) Если $h\colon A\to B$, $g\colon B\to C$ и $f\colon C\to D$, то $$f\circ (g\circ h)=(f\circ g)\circ h$$
- ф. Теория 10.47 ( Композиция инъективов инъективна ) Если $f\colon A\to B$ и $g\colon B\to C$ инъективны, то $g\circ f$ инъективно.
- Докажите каждую из следующих теорем и запишите свое полуформальное доказательство в одном проекте файла LaTeX. Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 19».
- 1. Набор наборов ( Thm 10.
 4 ): $\{\,1,2\,\}\in\{\,A : \{\,1\,\}\subseteq A\ ,\}$
4 ): $\{\,1,2\,\}\in\{\,A : \{\,1\,\}\subseteq A\ ,\}$ - 2. Модульное сложение: Пусть $a,b,c,d$ — целые числа, а $m$ — целое положительное число. Если $a\underset{m}{\equiv}b$ и $c\underset{m}{\equiv}d$, то $$a+c\underset{m}{\equiv}b+d$$
- 1. Набор наборов ( Thm 10.
Смешанный пакет. Докажите каждую из следующих теорем и запишите свое полуформальное доказательство в одном проекте файла LaTeX. Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 18». Доказательство каждой теоремы может использовать только результаты из предыдущих глав, а также аксиомы, определения и ранее доказанные результаты из той же главы, из которой взята теорема.
- 9-{1}\cdot х$.
- д. Thm 10.11 ( транзитивность $\subseteq$ ) $A\subseteq B\text{ и } B\subseteq C \Rightarrow A\subseteq C$
- эл. Thm 10.
 35 ( степенных множеств дополнений ) $A\subseteq B\Rightarrow \mathcal{P}(B’)\subseteq\mathcal{P}(A’)$
35 ( степенных множеств дополнений ) $A\subseteq B\Rightarrow \mathcal{P}(B’)\subseteq\mathcal{P}(A’)$ - ф. Thm 10.59 ( линейных биекций ) Линейная функция биективна тогда и только тогда, когда она имеет ненулевой наклон.
Здесь мы определяем линейную функцию как отображение $f\colon\mathbb{R}\to\mathbb{R}$ такое, что для некоторых $m,b\in\mathbb{R}$ $$f(x)=m\cdot x+b$$ В этой ситуации мы говорим, что $m$ — это наклон $f$.
- Запомните аксиомы действительных чисел (кроме аксиомы полноты) для викторины в четверг.
- Докажите каждую из следующих теорем и запишите свое полуформальное доказательство в одном проекте файла LaTeX. Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 17». Вам не нужно и не следует использовать ничего из главы 7 конспекта лекций. Вам не нужно использовать аксиому полноты, поэтому я сэкономлю вам время, сказав, что нет необходимости даже пытаться идти по этому пути.
 n$$
9п-1$$
n$$
9п-1$$
- Давайте говорить по-настоящему. Докажите каждую из следующих теорем и запишите свое полуформальное доказательство в одном проекте файла LaTeX. Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 15». Вы можете использовать только аксиомы действительных чисел и все, что предшествует главе 9.-=\frac{1}{x}$.
- 2. Уникальность предшественников Пусть $x$ и $y$ — вещественные числа. Если $x+1=y+1$, то $x=y$.
- 3. Не оба Не существует таких действительных чисел $x$ и $y$, что $x\lt y$ и $y\lt x$.
- 4. Ностальгия по M1 Пусть $x$ и $y$ — действительные числа. Тогда $x\cdot(y+1)=x+x\cdot y$.
- 5. Да, не так просто, как можно было ожидать $$0\lt 1$$
(где 0 и 1 — константы вещественных чисел, а не константы натуральных чисел).

- 1. Докажите три теоремы – (8.2(c), 8.5 (a) и 8.7) в конце нашего общего документа на обороте, который я сделал в классе (Math 299 – в классе 2023). Тот, которым я поделился с вами, доступен только для чтения, поэтому сделайте копию и удалите доказательства, которые уже есть. У меня есть probmems и среды проверки, уже напечатанные для вас там, так что вам просто нужно заполнить доказательства. Когда вы закончите, загрузите PDF-файл и поместите его в папку Dropbox в подпапку с именем «Задание № 15». Если у вас есть какие-либо вопросы о Overleaf или $\LaTeX$, просто задайте их мне по горячей линии домашних заданий.
- 1. Повторить. Выберите любую домашнюю задачу, которая была задана после промежуточного экзамена, и запишите ее доказательство на обороте, используя полуформальный стиль доказательства, показанный в классе.
- 2. Докажите следующую теорему в том же проекте на обороте, что и предыдущую задачу.
 Загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 14». Если у вас есть какие-либо вопросы о Overleaf или $\LaTeX$, просто задайте их мне по горячей линии домашних заданий.
Загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 14». Если у вас есть какие-либо вопросы о Overleaf или $\LaTeX$, просто задайте их мне по горячей линии домашних заданий.- Теорема Натуральное число $k!$ всегда положительно.
- Запомните определения – в таблице Ароматы индукции и таблице Определения теории чисел на страницах 39-49 конспекта лекций для викторины во вторник. (Вам не нужно запоминать аксиомы Пеано.)
- Докажите каждую из следующих теорем. Введите свои полуформальные корректуры в Lurch. Используйте полуформальный стиль, показанный в классе. При доказательстве теорем в задаче, поставленной в конце главы 7, вы можете использовать любую более раннюю пронумерованную теорему в качестве правила вывода, чтобы помочь вам доказать более позднюю пронумерованную теорему (но не наоборот, если вы не докажете ее раньше).


 Thm 10.60 ( не отношение эквивалентности ) Предположим, что $\sim$ есть множество
$$\sim = \Set{ (1,1),(2,2),(3,3),(1,2),(2,1),(1,3),(3,1)} $$
Тогда $\sim$ не является отношением эквивалентности на множестве $\Set{1,2,3}$.
Thm 10.60 ( не отношение эквивалентности ) Предположим, что $\sim$ есть множество
$$\sim = \Set{ (1,1),(2,2),(3,3),(1,2),(2,1),(1,3),(3,1)} $$
Тогда $\sim$ не является отношением эквивалентности на множестве $\Set{1,2,3}$. Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 21».
Когда вы закончите, загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 21». Thm 10.32 ( Подмножества заразны ) Если $A\subseteq C$ и $B\subseteq D$, то $A\times B\subseteq C\times D$.
Thm 10.32 ( Подмножества заразны ) Если $A\subseteq C$ и $B\subseteq D$, то $A\times B\subseteq C\times D$. 4 ): $\{\,1,2\,\}\in\{\,A : \{\,1\,\}\subseteq A\ ,\}$
4 ): $\{\,1,2\,\}\in\{\,A : \{\,1\,\}\subseteq A\ ,\}$ 35 ( степенных множеств дополнений ) $A\subseteq B\Rightarrow \mathcal{P}(B’)\subseteq\mathcal{P}(A’)$
35 ( степенных множеств дополнений ) $A\subseteq B\Rightarrow \mathcal{P}(B’)\subseteq\mathcal{P}(A’)$ n$$
9п-1$$
n$$
9п-1$$
 Загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 14». Если у вас есть какие-либо вопросы о Overleaf или $\LaTeX$, просто задайте их мне по горячей линии домашних заданий.
Загрузите pdf-файл с Overleaf и поместите его в папку Dropbox в подпапку с именем «Задание № 14». Если у вас есть какие-либо вопросы о Overleaf или $\LaTeX$, просто задайте их мне по горячей линии домашних заданий.
Leave A Comment