Задание №14 на ЕГЭ-2019. Различные методы и способы решения.
Задание № 14 на ЕГЭ-2019. Различные методы и способы решения.
№1.1.(а) В правильной треугольной пирамиде SABC точка P — делит сторону AB в отношении 2:3, считая от вершины A , точка K — делит сторону BC в отношении 2:3, считая от вершины C . Через точки P и K параллельно SB проведена плоскость .
а) Докажите, что сечение пирамиды плоскостью является прямоугольником.
б) Найдите расстояние от точки S до плоскости , если известно, что SC=5, AC=6.
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Дальний Восток. Вариант Р.Я.
Дано: SABC—правильная пирамида , AP:PB=CK:KB=2:3,-плоскость.
а) сечение пирамиды плоскостью

б)Найти — расстояние от точки S до плоскости , если известно, что SC=5, AC=6.
Решение:
1-й способ (метод координат).
Пусть точка O – центр равностороннего треугольника, BH – высота ,
Введем прямоугольную систему координат, как показано на рисунке: точка A – начало отсчета; оси x, y, z лучи AC, AV, AW соответственно, где лучи AV и BH сонаправлены, луч AW сонаправлен с лучом
Координаты
некоторых точек найдем более подробно: , так как в равностороннем треугольнике
высота является медианой и биссектрисой треугольника; ,так как катет равен произведению
гипотенузы на синус противолежащего угла; , так как медианы треугольника
пересекаются в одной точке и делятся в отношении 2:1, считая от вершины; по
теореме Пифагора .
Координаты точек .
Координаты этих точек находим из векторных равенств и
Уравнение плоскости имеет вид . Так как из параллельности прямой и плоскости получим .
Подставляя координаты точек P и K в уравнение плоскости и определения скалярного произведения векторов получим систему уравнений.
Значит уравнение плоскости где — вектор нормали к плоскости .
Найдем точку M – точку пересечения прямой AS и плоскости , уравнение прямой AS: пусть , тогда и получим уравнение прямой AS в параметрическом виде и подставляя его в уравнение плоскости получим Получим .
Найдем точку N – точку пересечения прямой CS и плоскости , уравнение прямой CS: пусть , тогда и получим уравнение прямой
Получили
четырехугольник MNKP – сечение
пирамиды плоскостью . Докажем, что MNKP – параллелограмм,
так как , то , значит MNKP – параллелограмм. Докажем, что MNKP – прямоугольник,
так как ,значит , тогда и MNKP – прямоугольник,
что и требовалось доказать.
Докажем, что MNKP – прямоугольник,
так как ,значит , тогда и MNKP – прямоугольник,
что и требовалось доказать.
б) Расстояние от точки S до плоскости найдем по
формуле , где .
По условию , значит . Тогда – расстояние от точки
Ответ: б)
Решение: 2-й способ (геометрический метод).
Дано: SABC—правильная пирамида , AP:PB=CK:KB=2:3,-плоскость.
а) сечение пирамиды плоскостью является прямоугольником.
б)Найти — расстояние от точки S до плоскости , если известно, что SC=5, AC=6.
Решение:
Так как AP:PB=CK:KB=2:3

На грани SCB проведем прямую , на грани SAB проведем прямую , проведем отрезок MN в грани SAC, отрезок PK в грани ABC и получим PKNM – четырехугольник, который является сечением пирамиды плоскостью .
по двум углам: общий, как соответственные углы при параллельных прямых KN и BS, и секущей CB. Тогда получим, что соответствующие стороны пропорциональны, то есть
по двум углам: общий, как соответственные углы при параллельных прямых PM и BS, и секущей AB. Тогда получим, что соответствующие стороны пропорциональны, то есть AP:AB=AM:AS=PM:BS=2:5, значит .
Следовательно, , значит PKNM – параллелограмм,
так как противоположные стороны параллельны и равны.
Прямые и прямая BH является проекцией прямой BS, тогда по теореме о трех перпендикулярах . Поэтому будут перпендикулярны соответственно параллельные им прямые PM и PK, поэтому и PKNM – прямоугольник, что и требовалось доказать.
б) Проведем высоту BH в треугольнике АВС, которая пересекает отрезок PK в точке R. SH является высотой боковой грани ACS и пересекает MN в точке T. Получим . Так как по пропорциональности двух сторон и равенству углов между ними BK:BC=BP:BA=3:5, а значит и их высоты BR
Так как по пропорциональности двух сторон и равенству углов между ними NS:CS=MS:AS=3:5, а значит и их высоты ST:SH=3:5.
Тогда HT:HS=HR:HB=2:5 и – общий угол, значит поэтому и эти углы являются соответственными
углами для прямых RT и BS, и
секущей HS, поэтому и высоты этих треугольников относятся как
2:5.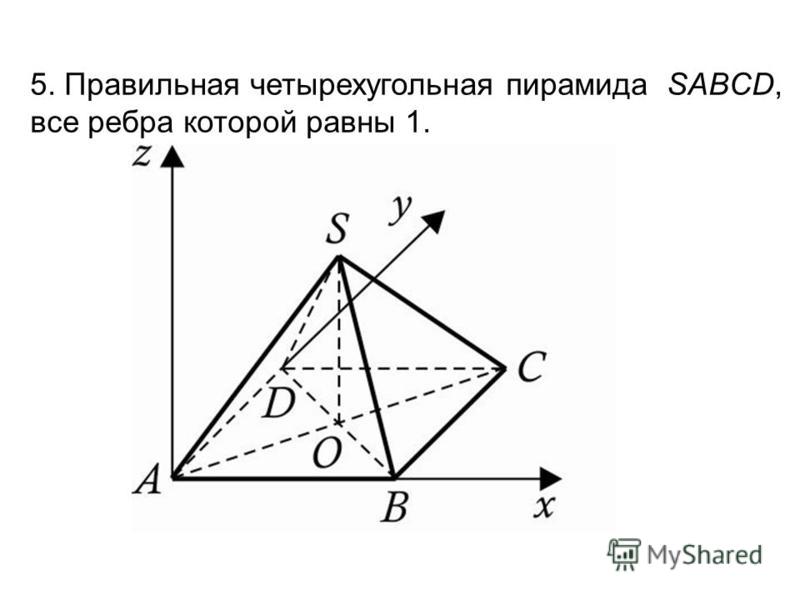
Значит , где площадь найдем по формуле Герона: BS=5, , , , .
Ответ:
Задание № 14 на ЕГЭ — 2019 по математике, профиль. Дидактические материалы.
№1.1.(а) В правильной треугольной пирамиде SABC точка P — делит сторону AB в отношении 2:3, считая от вершины A , точка K — делит сторону BC в отношении 2:3, считая от вершины C . Через точки P и K параллельно SB проведена плоскость .
а) Докажите, что сечение пирамиды плоскостью является прямоугольником.
б) Найдите расстояние от точки S до плоскости , если известно, что SC=5, AC=6.
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Дальний Восток. Вариант Р.Я.
№1.2.(а) В правильной треугольной пирамиде
 На рёбрах AB и SC отмечены точки K и M соответственно, причём AK:KB = SM:MC = 2:7. Плоскость содержит прямую KM и параллельна
прямой SA.
На рёбрах AB и SC отмечены точки K и M соответственно, причём AK:KB = SM:MC = 2:7. Плоскость содержит прямую KM и параллельна
прямой SA.а) Докажите, что плоскость делит ребро SB в отношении 2:7, считая от вершины S .
б) Найдите расстояние между прямыми SA и KM .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. С.Петербург. Вариант Р.Я.
№1.3.(а) В правильной треугольной пирамиде SABC сторона основания
а) Докажите, что сечение пирамиды SABC плоскость является прямоугольником.
б) Найдите объем
пирамиды, вершиной которой является точка А, основание – сечение
пирамиды плоскостью .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант Я.
№1.3.(б) В правильной треугольной пирамиде SABC сторона основания
а) Докажите, что сечение пирамиды SABC плоскостью является прямоугольником.
б) Найдите объем пирамиды, вершиной которой является точка А, основание – сечение пирамиды плоскостью .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант .Л.
№1.4.(а) В
правильной треугольной пирамиде SABC точка K — делит сторону SC в отношении 1:2, считая от вершины S , точка N — делит сторону SB в отношении 1:2, считая от вершины S . Через точки N и K параллельно SA проведена плоскость .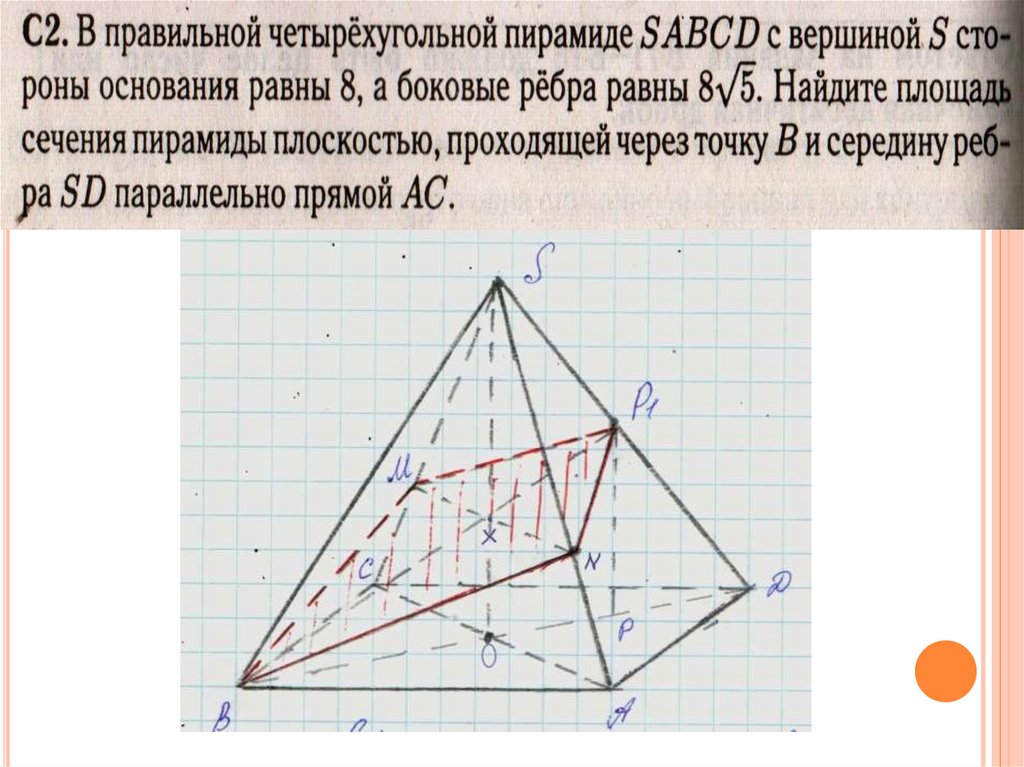
а) Докажите, что сечение пирамиды плоскостью параллельно прямой BC.
б) Найдите расстояние от точки B до плоскости , если известно, что SA=9, AB=6.
Отве: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Центр Вариант Р.Я.
№1.5.(а) В правильной треугольной пирамиде SABC сторона основания AB равна 5, а боковое ребро SA равно 3. На ребрах AB и SC отмечены точки K и М соответственно, причем АК:КВ = SM:MC = 1:4. Плоскость содержит прямую КМ и параллельна прямой SA.
а) Докажите, что плоскость делит ребро AC в отношении 1:4, считая от вершины А.
б) Найдите расстояние между прямыми SA и KM.
Ответ: . Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант М.
№1.6.(а) В
правильной треугольной пирамиде SABC сторона основания AB=3, а
боковое ребро SA=2. На
рёбрах AB и SC отмечены точки K и M соответственно,
причём AK:KB=SM:MC=1:2.Плоскость содержит прямую KM и
параллельна SA.
На
рёбрах AB и SC отмечены точки K и M соответственно,
причём AK:KB=SM:MC=1:2.Плоскость содержит прямую KM и
параллельна SA.
а) Докажите, что плоскость делит ребро AC в отношении 1:2, считая от вершины A .
б) Найдите расстояние между прямыми SA и KM.
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №316.Р.
№1.7.(а) В правильной треугольной пирамиде SABC сторона основания AB=3, а боковое ребро SA=4. На рёбрах AB и SC отмечены точки K и M соответственно, причём AK:KB=SM:MC=1:2. Плоскость содержит прямую KM и параллельна BC.
а) Докажите, что плоскость параллельна прямой SA.
б) Найдите угол между плоскостями и SBC.
Ответ: Источник: ЕГЭ —
2019. Основная волна 29.05.2019. Вариант №324.Я.
Основная волна 29.05.2019. Вариант №324.Я.
№1.7.(б) В правильной треугольной пирамиде SABC сторона основания AB=6, а боковое ребро SA=7. На рёбрах AB и SC отмечены точки K и M соответственно, причём AK:KB=SM:MC=1:5. Плоскость содержит прямую KM и параллельна BC.
а) Докажите, что плоскость параллельна прямой SA.
б) Найдите угол между плоскостями и SBC.
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №324.Я.
№1.8.(а) В правильной четырехугольной пирамиде SABCD AB=7; AS=14. На сторонах CD и SC взяты точки N и K соответственно, причем DN:NC=SK:KC=2:5. Плоскость содержит прямую NK и параллельна ребру AS.
а) Докажите, что плоскость параллельна ВС.
б) Найдите
расстояние от точки B до плоскости .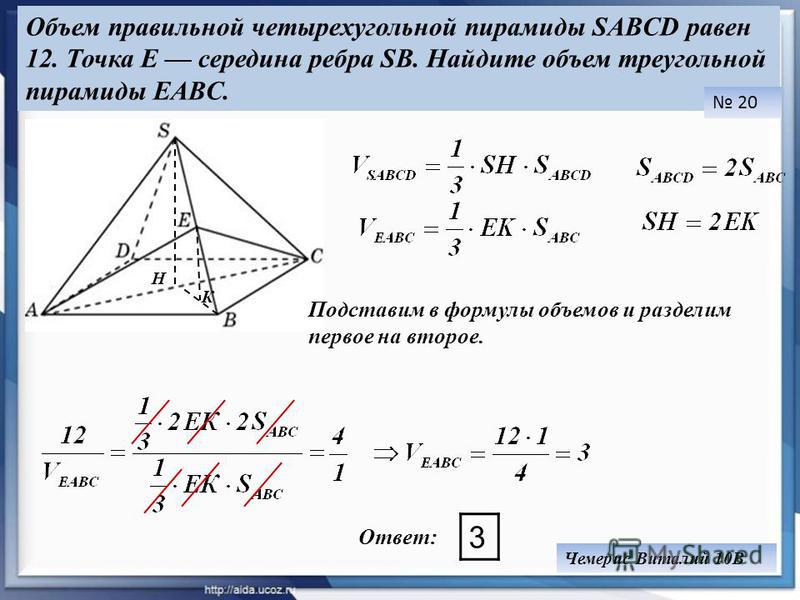
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант Л.А.Я.
№1.9.(а) В правильной четырёхугольной пирамиде SABCD сторона основания AB= 4, а боковое ребро SA = 8. На рёбрах CD и SC отмечены точки N и K соответственно, причём DN:NC = SK:KC =1:3. Плоскость α содержит прямую KN и параллельна прямой BC.
а) Докажите, что плоскость делит ребро AB в отношении 1:3, считая от вершины A .
б) Найдите расстояние между прямыми SA и KN.
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №405.Р.
№1.9.(б) В
правильной четырёхугольной пирамиде SABCD сторона основания AB=8,
а боковое ребро SA=10. На рёбрах CD и SC отмечены точки N и K соответственно, причём DN:NC = SK:KC =1:7.Плоскость содержит прямую KN и параллельна
прямой BC.
а) Докажите, что плоскость делит ребро SB в отношении 1:7, считая от вершины S .
б) Найдите расстояние между прямыми SA и KN.
Ответ:б) Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №409.Р.Я.
№1.10.(а) В правильном тетраэдре ABCD точки K и M — середины рёбер AB и CD соответственно. Плоскость содержит прямую KM и параллельна прямой AD.
а) Докажите, что сечение тетраэдра плоскостью — квадрат.
б) Найдите площадь сечения тетраэдра ABCD плоскостью, если
Ответ:б)3 Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №991.Р.
№1.11.(а) В
правильной треугольной пирамиде SABC сторона основания AB=6, а
боковое ребро SA=7. На
рёбрах AB и SC отмечены точки K и M соответственно,
причём AK:KB=SM:MC=5:1.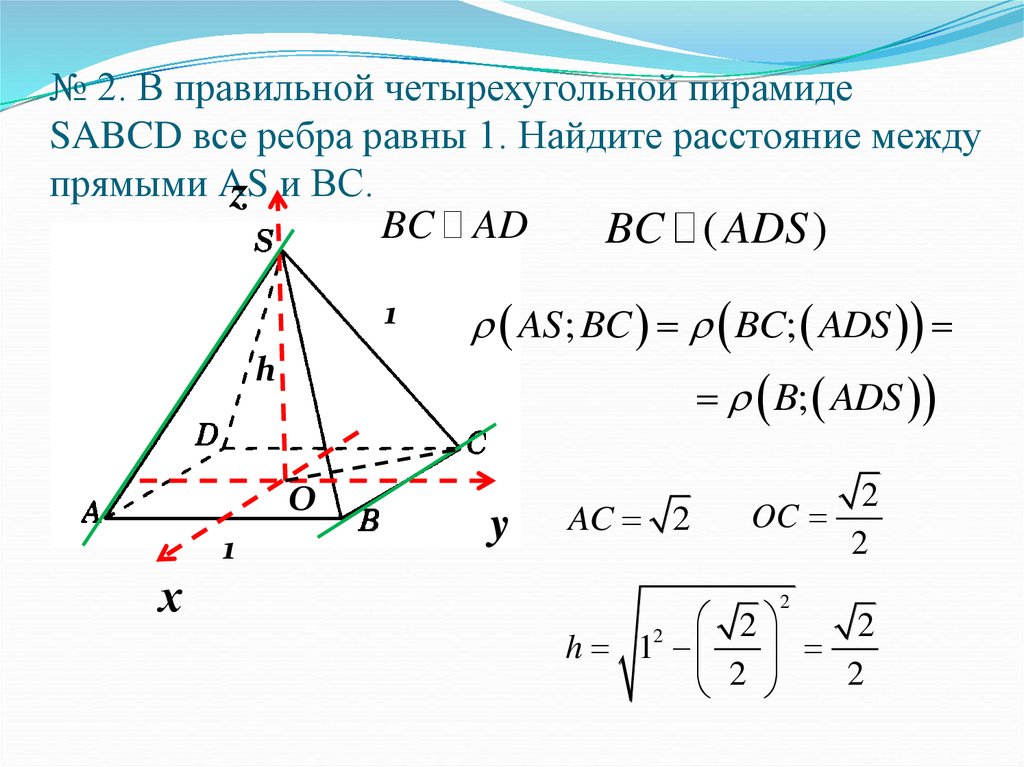 Плоскость
содержит прямую KM и параллельна
прямой BC.
Плоскость
содержит прямую KM и параллельна
прямой BC.
а) Докажите, что сечение пирамиды SABC плоскостью является прямоугольником.
б) Найдите расстояние от точки C до плоскости угол .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант № .Я.
№1.12.(а) В правильной четырёхугольной пирамиде SABCD сторона основания AB=3, а боковое ребро SA=6. Точка K делит ребро SC , причём SK:KC =1:2.Плоскость проходит через точку K и параллельна плоскости SAD.
а) Докажите, что сечение пирамиды плоскостью является равнобедренной трапецией.
б) Найдите объем пирамиды, вершиной которой является точка S, а основание – сечение пирамиды SABCD плоскостью .
Ответ:б) Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант № .Я.
Основная
волна. Резерв. 24.06.2019.
Резерв. 24.06.2019.
№1.13.(а) В правильной треугольной призме сторона основания равна 4, а боковое ребро равно 2. Точка M — середина ребра , а точка O — точка пересечения диагоналей боковой грани .
а) Докажите, что точка пересечения диагоналей четырёхугольника, являющегося сечением призмы плоскостью AMB лежит на отрезке .
б) Найдите угол между прямой , и плоскостью AMB.
Ответ: Источник: ЕГЭ — 2019. Основная волна. Резерв. 24.06.2019. Вариант №503.и Кавказ. Р.
№1.13.(б) В правильной треугольной призме сторона основания равна 4, а боковое ребро равно 6. Точка M — середина ребра , а точка O — точка пересечения диагоналей боковой грани .
а) Докажите, что точка пересечения диагоналей четырёхугольника, являющегося сечением призмы плоскостью AMB лежит на отрезке .
б) Найдите угол между прямой , и плоскостью AMB.
Ответ: Источник: ЕГЭ — 2019.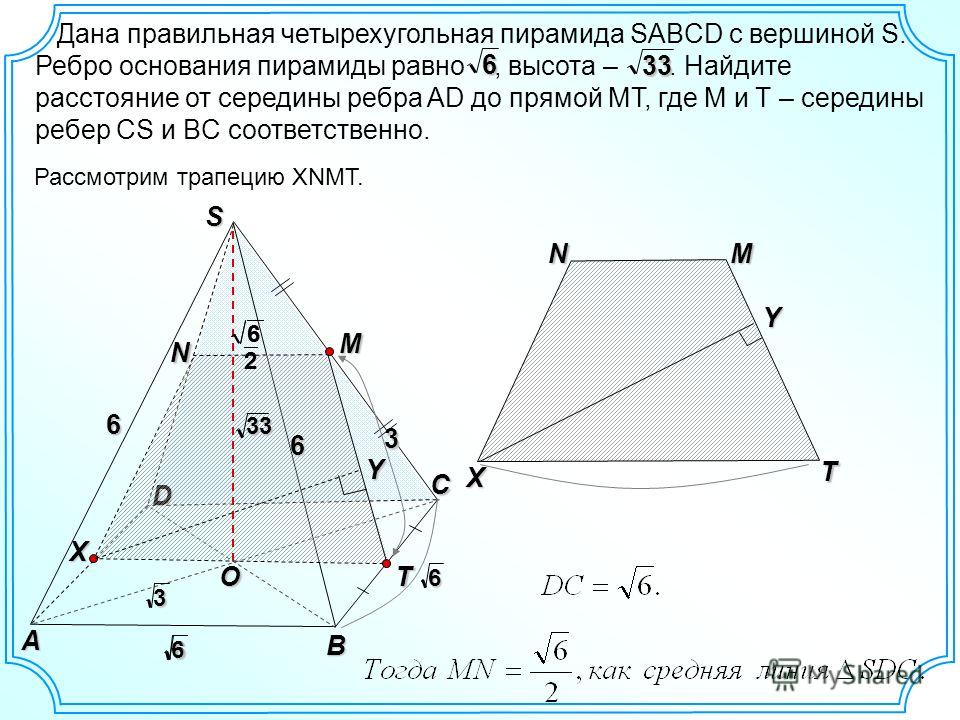 Основная волна.
Резерв. 24.06.2019. Вариант Л.
Основная волна.
Резерв. 24.06.2019. Вариант Л.
№1.14.(а) В кубе рёбра равны 1. На продолжении отрезка за точку отмечена точка M так, что , а на продолжении отрезка за точку C отмечена точка N так, что .
а) Докажите, что .
б) Найдите расстояние между прямыми и MN .
Ответ: Источник: ЕГЭ — 2019. Основная волна. Резерв. 24.06.2019. Вариант 992.Р.
Досрочная волна (29.03.19).
№1.15.(а) Дана пирамида SABC, в которой SC=SB=AB=AC=, SA=BC=.
а) Докажите, что ребро SA перпендикулярно ребру BC.
б) Найдите расстояние между ребрами BC и SA.
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. 29.03.2019. Вариант
№1.15.(б) Дана
пирамида SABC, в
которой SC=SB=AB=AC=, SA=BC=.
а) Докажите, что ребро SA перпендикулярно ребру BC.
б) Найдите расстояние между ребрами BC и SA.
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. 29.03.2019. Вариант
№1.16.(а) В треугольной пирамиде PABC с основанием ABC известно, что AB=13, PB=15, . Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC.
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. 29.03.2019. Вариант
Досрочная волна, резерв. (10.04.19).
№1.17.(а) В конусе
с вершиной S и центром
основания O, радиус
основания равен 13, а высота равна . Точки A и B – концы
образующих, M –
середина SA, N – точка в
плоскости основания такая, что прямая MN параллельна
прямой SB.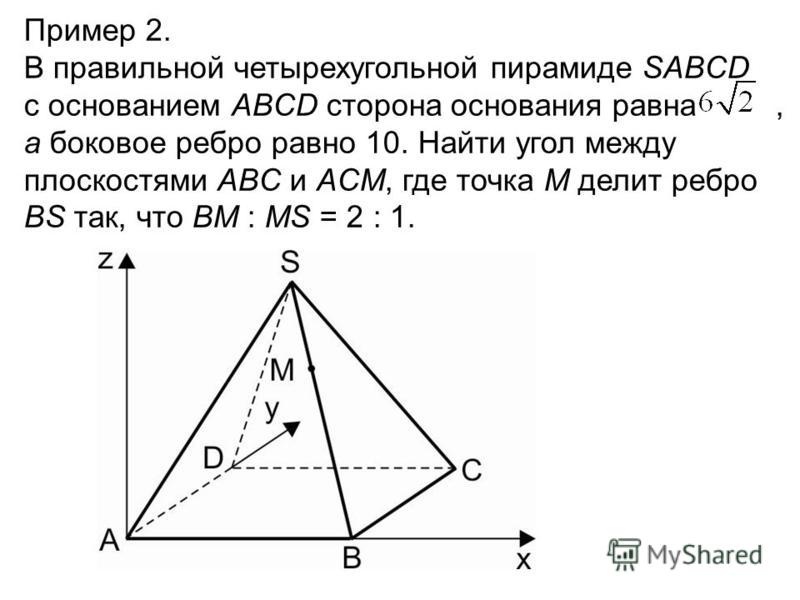
а) Докажите, что .
б) Найдите угол между прямой MB и плоскостью основания конуса, если известно, что AB=10.
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. Резерв. 10.04.2019. Вариант
№1.17.(б) В конусе с вершиной S и центром основания O, радиус основания равен 5, а высота равна . Точки A и B – концы образующих, M – середина SA, N – точка в плоскости основания такая, что прямая MN параллельна прямой SB.
а) Докажите, что .
б) Найдите угол между прямой MB и плоскостью основания конуса , если известно, что AB=8.
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. Резерв. 10.04.2019. Вариант
Решутест. Продвинутый тренажёр тестов
Решутест. Продвинутый тренажёр тестов- Главная
- ЕГЭ
- Математика профильная
- Стереометрия
- Расстояние от точки до прямой, от точки до плоскости
Решил заданий
Не решил заданий
Осталось заданий
История решения
5072 — не приступал 1208 — не приступал 9943 — не приступал 4063 — не приступал 1077 — не приступал 3883 — не приступал 2266 — не приступал 7857 — не приступал 5680 — не приступалФормат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Раскрыть Скрыть
№1В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, рёбра которой равны 1, найдите расстояние от точки А до прямой ВС1.
ответ
1) Искомое расстояние — перпендикуляр, опущенный из точки А на прямую ВС1. По сути, перпендикуляр — это высота в треугольнике АВС1, опущенная из вершины А на сторону ВС1. Будем её искать.
2) В квадрате ВСС1В1 диагональ ВС1 равна √2.
В прямоугольном треугольнике АСD находим AC по теореме Пифагора:
AC2 = AD2 – DC2.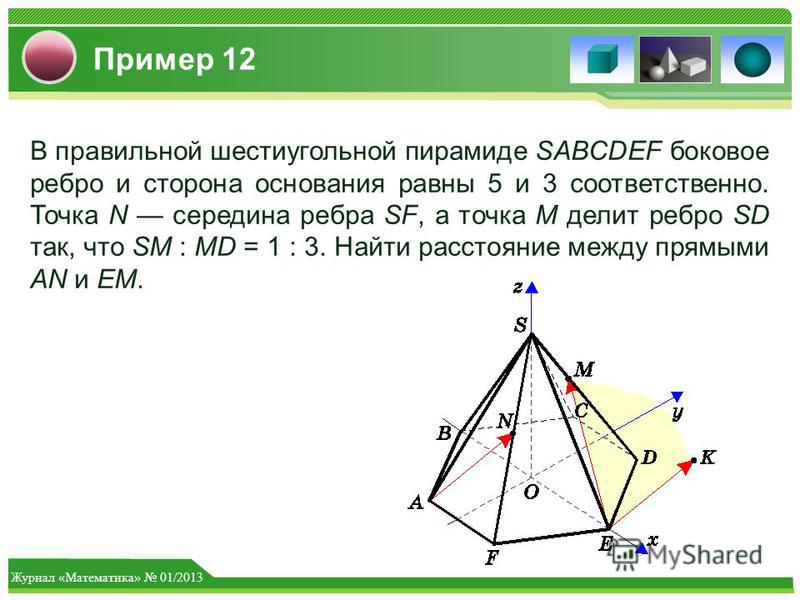 2}=2$ по теореме Пифагора.
2}=2$ по теореме Пифагора.
3) В треугольнике АВС1, используя теорему косинусов, получаем:
B AB2 = AC12 + BC12 – 2 ∙ AC1 ∙ BC1 ∙ cosAC1B;
1 = 4 + 2 – 2 ∙ 2 ∙ √2 ∙ cosAC1B;
cosAC1B = $\displaystyle\frac{5}{4\sqrt{2}}$.
Найдем высоту АН:
$\sin AC_1B=\displaystyle\frac{AH}{AC_1}=\frac{AH}{2}$;
AH = sinAC1B ∙ 2.
Найдем sinAC1B через основное тригонометрическое тождество:
sin2AC1B = 1 – cos2AC1B = $1-\displaystyle\frac{25}{32}=\frac{7}{32}=\frac{14}{64}$;
sinAC1B = $\displaystyle\frac{\sqrt{14}}{8}$.
Тогда АН равно:
AH = $2\cdot\displaystyle\frac{\sqrt{14}}{8}=\frac{\sqrt{14}}{4}$.
В основании прямого параллелепипеда ABCDA1B1C1D1 лежит ромб со стороной 8 и острым углом BAD, равным 30º. Площадь боковой поверхности параллелепипеда равна 128. Найдите расстояние от середины ребра A1B1 до прямой CD.
ответ
1)Дополнительное построение: проведем MN параллельно АА1. Так как АА1 — перпендикуляр к плоскости основания параллелепипеда, то MN также является перпендикуляром к плоскости основания.
Отрезок NH, проведенный перпендикулярно прямой CD является проекцией наклонной MH на плоскость АВС.
$\left.\begin{gathered}MN\perp ABC\rightarrow MN\perp CD \\ NH\perp CD \\ MH\ -\ наклонная\end{gathered}\right\}\rightarrow MH\perp CD\ {(по\ теореме\ о\ трёх\atop перпендикулярах)}$
MH — искомое расстояние.
2) Посмотрим, что дано в условии:
Sбок = $4S_{AA_1B_1B}$ = 4AB · AA1 = 32AA1 = 128;
AA1 = 4.
3) MN = AA1 = 4, а KD — высота ромба, длина которой вычисляется из треугольника AKD, в котором катет KD лежит напротив угла в 30º, значит, NH = KD = 4.
По теореме Пифагора из треугольника MNH получим:
МН2 = MN2 + NH2
МН2 = 16 + 16 = 32
МН = 4√2.
№3Основанием прямой призмы АВСDA1B1C1D1 служит трапеция с основаниями АD = 3, ВС = 1 и боковыми сторонами АВ = СD = 2. Боковое ребро призмы равно 2. Найдите расстояние от точки А1 до прямой ВС.
ответ
1) Искомое расстояние d есть длина перпендикуляра А1М, опущенного на прямую ВС. Поскольку A1D1|| BC, это расстояние равно также высоте ВН трапеции А1ВСD1.
2) Боковая сторона данной трапеции:
AA12 + AB2 = A1B2;
4 + 4 = 8 = A1B2;
A1B = 2√2.
Нарисуем эту трапецию отдельно:
Легко находим: A1H = $\displaystyle\frac{A_1D_1-BC}{2}$ = 1.
Тогда найдем d по теореме Пифагора:
d2 = A1B2 – A1H2 = 8 – 1 = 7
d = √7.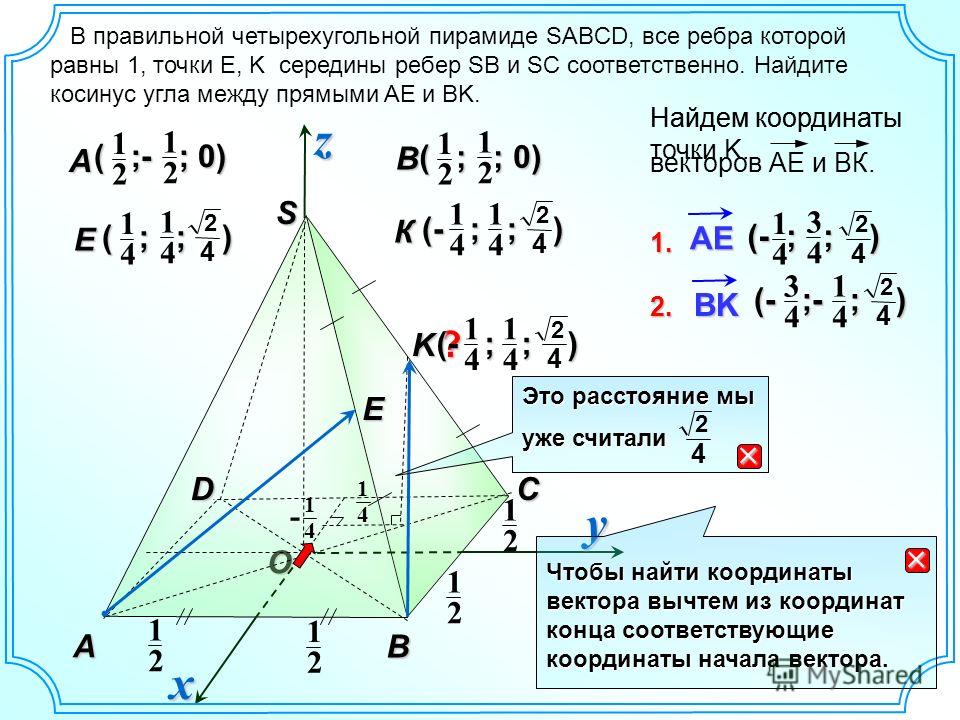
В единичном кубе ABCDA1B1C1D1 найдите расстояние от точки А до плоскости BDA1.
ответ
Первый способ
1) Дополнительной построение: пусть О — середина отрезка BD.
АО — медиана в равнобедренном треугольнике ABD. Значит, по свойству равнобедренного треугольника, АО — высота.
$\left.\begin{gathered}AO\perp BD \\ BD\perp AA_1 \\ AO\cap AA_1=A\end{gathered}\right\}\rightarrow BD\perp AA_1O\ {(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)}$
Значит, BD перпендикулярно любой прямой, лежащей в этой плоскости.
Дополнительное построение. АН перпендикулярно А1О.
$\left.\begin{gathered}AH\perp A_1O \\ BD\perp AH \\ AO\cap BD=O\end{gathered}\right\}\rightarrow AH\perp A_1BD\ {(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)}$
Следовательно, искомым перпендикуляром, опущенным из точки А на плоскость ВDА1, является высота АН прямоугольного треугольника АОА1, в котором:
АА1 = 1, АО = $\displaystyle\frac{\sqrt{2}}{2}$ (как половина диагонали грани куба). 2\sqrt{3}}{4}}=\frac{4\cdot3\cdot6\cdot6}{2\cdot6\cdot6\cdot2\cdot\sqrt{3}}=\sqrt{3}$.
2\sqrt{3}}{4}}=\frac{4\cdot3\cdot6\cdot6}{2\cdot6\cdot6\cdot2\cdot\sqrt{3}}=\sqrt{3}$.
Второй способ
Пусть искомое расстояние от точки М до плоскости ВС1D равно d. Тогда расстояние от точки D1 до этой плоскости равно 2d. Отрезок D1C делится плоскостью ВС1D пополам, поэтому расстояние от точки С до данной плоскости также равно 2d.
С другой стороны, расстояние от точки С до плоскости ВС1D есть высота СН треугольной пирамиды ВС1DC. Основанием этой пирамиды служит равносторонний треугольник ВС1D со стороной 6√2. Боковые рёбра пирамиды равны 6. Стало быть, данная пирамида является правильной, и точка Н — центр треугольника ВС1D.
Отрезок С1Н есть радиус окружности, описанной вокруг треугольника ВС1D. 2}=\sqrt{1+1}=\sqrt{2} \\[10pt] S_{BCS}=\displaystyle\frac{1}{2}\cdot h_{BC}\cdot BC=\frac{1}{2}\cdot\sqrt{2}\cdot2=\sqrt{2} \\[15pt] h=\displaystyle\frac{\left(\frac{1}{2}\cdot CD\cdot BC\cdot ST\right)}{S_{BCS}}=\frac{\frac{1}{2}\cdot2\cdot2\cdot1}{\sqrt{2}}=\sqrt{2}$
2}=\sqrt{1+1}=\sqrt{2} \\[10pt] S_{BCS}=\displaystyle\frac{1}{2}\cdot h_{BC}\cdot BC=\frac{1}{2}\cdot\sqrt{2}\cdot2=\sqrt{2} \\[15pt] h=\displaystyle\frac{\left(\frac{1}{2}\cdot CD\cdot BC\cdot ST\right)}{S_{BCS}}=\frac{\frac{1}{2}\cdot2\cdot2\cdot1}{\sqrt{2}}=\sqrt{2}$
Второй способ
Пусть SТ — высота пирамиды. Точка Т является серединой отрезка DВ. Тогда искомое расстояние d от точки D до плоскости ВСS равно удвоенному расстоянию от точки Т до этой плоскости по теореме Фалеса.
Расстояние от точки Т до плоскости ВСS равно высоте ТН треугольника SТМ (точка М — середина ВС). Действительно, ТН перпендикулярна также прямой ВС ( BC ⊥ TM, BC ⊥ SM ⇒ BC ⊥ STM ⇒ BC ⊥ TH), и потому ТН — перпендикуляр к плоскости ВСS. Из треугольника SТМ легко находим: ТН = $\displaystyle\frac{\sqrt{2}}{2}$. Тогда d = 2 · TH = √2.
Тогда d = 2 · TH = √2.
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точка N — середина ребра AC, точка O — центр основания пирамиды, точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая NP перпендикулярна прямой BS.
б) Найдите расстояние от точки B до прямой NP.
ответ
а) SABC — правильная пирамида, значит, О — центр вписанной и описанной окружности основания АВС. Таким образом, точки В, О и N лежат на одной прямой.
Пусть прямая NP пересекает прямую BS в точке К.
Рассмотрим треугольник SNB. Он равнобедренный, так как SN и BN — медианы в равных равносторонних треугольниках.
Найдем величину ON и ОР.
$ON=\displaystyle\frac{1}{3}BN=\frac{1}{3}\cdot\frac{AB\sqrt{3}}{2}=\frac{1}{3}\cdot\frac{4\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}$;
$OB=\displaystyle\frac{2}{3}BN=\frac{4\sqrt{3}}{3}$. 2 \displaystyle\frac{SNB}{2}=\frac{2}{3}; \\[15pt] \cos\displaystyle\frac{SNB}{2}=\sqrt{{\small\frac{2}{3}}}=\frac{\sqrt{6}}{3}=\cos ONP.$
2 \displaystyle\frac{SNB}{2}=\frac{2}{3}; \\[15pt] \cos\displaystyle\frac{SNB}{2}=\sqrt{{\small\frac{2}{3}}}=\frac{\sqrt{6}}{3}=\cos ONP.$
Значит, угол ОNP является половиной угла SNB. Следовательно, NK — биссектриса в равнобедренном треугольнике, проведенная на основание, а по свойству равнобедренного треугольника эта биссектриса является высотой. Значит, что прямая NP перпендикулярна прямой BS.
б) Так как NK является и высотой, и медианой в равнобедренном треугольнике SNB, то расстояние от точки B до прямой PN равно $BK=\displaystyle\frac{1}{2}BS=2$.
№8В правильной треугольной пирамиде SABC сторона основания AB равна 60, а боковое ребро SA равно 37. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5 : 1, считая от точки C.
б) Найдите расстояние от вершины A до плоскости α.
ответ
а) Прямая MN параллельна плоскости ABC, поэтому сечение пересекает плоскость ABC по прямой PQ, параллельной MN. Рассмотрим плоскость SCE. Пусть K — точка пересечения этой плоскости и прямой MN, L — точка пересечения этой плоскости и прямой PQ, O — центр основания пирамиды.
Плоскости SCE и MNQ перпендикулярны плоскости ABC, поэтому прямая KL перпендикулярна плоскости ABC, а значит, параллельна прямой SO.
Поскольку MN — средняя линия треугольника ASB, точка K является серединой ES. Следовательно, L — середина EO. Медиана CE треугольника ABC делится точкой O в отношении 2 : 1. Значит, CL : LE = 5 : 1.
б) Прямая CE перпендикулярна KL и PQ, поэтому прямая CE перпендикулярна плоскости MNQ. Прямые AB и PQ параллельны, значит, расстояние от вершины A до плоскости сечения равно расстоянию от точки E до плоскости сечения, то есть $EL=\displaystyle\frac{CE}{6}=5\sqrt{3}$.
№9Ребро SA пирамиды SABC перпендикулярно плоскости основания ABC.
а) Докажите, что высота пирамиды, проведенная из точки A, делится плоскостью, проходящей через середины рёбер AB, AC и SA, пополам.
б) Найдите расстояние от вершины A до этой плоскости, если SA = √5, AB = AC = 5, BC = 2√5.
ответ
а) 1) Дополнительное построение: пусть М — середина AS, K — середина АС, Т — середина АВ. Если мы соединим эти три точки, то получим плоскость.
Отрезки МК, КТ, МТ для треугольников ASC, SCB, ASB будут являться средними линиями.
2) Также давайте посмотрим на плоскости МКТ и SCB. Они параллельные, причем этому способствует признак параллельных плоскостей (две пересекающиеся прямые МК и МТ, принадлежащие плоскости МКТ, соответственно параллельны пересекающимся прямым SC и SB, принадлежащим плоскости SCB).
3) Отпустим перпендикуляр из точки А на плоскость МКТ и назовем его h1. Тогда продолжение этого перпендикуляра до плоскости SBC будет являться высотой, так как плоскости МКТ и SBC параллельны. Назовем этот перпендикуляр h2.
4) У нас есть два перпендикуляра, которые мы не можем изобразить. Давайте найдем отношение объемов пирамиды МАТК и SABC.
$V_{MATK}=\displaystyle\frac{1}{3}\cdot MA\cdot S_{ATK}$
$V_{SABC}=\displaystyle\frac{1}{3}\cdot SA\cdot S_{ABC}$
По условию $\displaystyle\frac{MA}{SA}=\frac{1}{2}$, так как М — середина. 2=\frac{1}{4}$
2=\frac{1}{4}$
Найдем отношение объемов:
$\displaystyle\frac{V_{MATK}}{V_{SABC}}=\frac{\frac{1}{3}\cdot MA\cdot S_{ATK}}{\frac{1}{3}\cdot SA\cdot S_{ABC}}=\frac{MA}{SA}\cdot\frac{S_{ATK}}{S_{ABC}}=\frac{1}{2}\cdot\frac{1}{4}=\frac{1}{8}$.
Используем метод двойного выражения объемов, тогда:
$V_{MATK}=\displaystyle\frac{1}{3}\cdot h_1\cdot S_{MTK}$
$V_{SABC}=\displaystyle\frac{1}{3}\cdot h_2\cdot S_{SBC}$
Треугольники МТК и SBC подобны по трем сторонам, следовательно, их площади относятся, как $\displaystyle\frac{1}{4}$.
Тогда запишем отношение объемов:
$\displaystyle\frac{V_{MATK}}{V_{SABC}}=\frac{\frac{1}{3}\cdot h_1\cdot S_{MTK}}{\frac{1}{3}\cdot h_2\cdot S_{SBC}}=\frac{h_1}{h_2}\cdot\frac{S_{MTK}}{S_{SBC}}=\frac{h_1}{h_2}\cdot\frac{1}{4}=\frac{1}{8}$
Откуда получим, что $\displaystyle\frac{h_1}{h_2}=\frac{1}{2}$. Что и требовалось доказать.
б) 1) Мы знаем, что расстояние от точки А до плоскости МКТ меньше в два раза, чем до плоскости SBC. 2=30-5=25 \\[9pt] SD=5$
2=30-5=25 \\[9pt] SD=5$
Найдем площадь треугольника SBC:
$S=\displaystyle\frac{1}{2}\cdot5\cdot2\sqrt{5}=5\sqrt{5}$
4) Подставим всё найденное в формулу:
$\displaystyle\frac{1}{3}\cdot SA\cdot S_{ABC}=\frac{1}{3}\cdot h_2\cdot S_{SBC} \\[15pt] SA\cdot S_{ABC}=h_2\cdot S_{SBC} \\[10pt] \sqrt{5}\cdot10=h_2\cdot5\sqrt{5}$
Откуда $h_2=2$.
Тогда $h_1=\displaystyle\frac{h_2}{2}=\frac{2}{2}=1$.
Так твой прогресс будет сохраняться.
Регистрация
Мы отправили код на:
ИзменитьПолучить код повторно через 00:00
Я прочитал(-а) Политику конфиденциальности и согласен(-на) с правилами использования моих персональных данных
Ништяк!
Решено верно
Браво!
Решено верно
Крутяк!
Решено верно
Зачёт!
Решено верно
Чётко!
Решено верно
Бомбезно!
Решено верно
Огонь!
Решено верно
Юхууу!
Решено верно
Отпад!
Решено верно
Шикарно!
Решено верно
Блестяще!
Решено верно
Волшебно!
Решено верно
Боковая площадь квадратной пирамиды
LearnPracticeDownload
Боковая площадь квадратной пирамиды определяется как площадь, покрытая наклоном ее боковых граней. Пирамида — это трехмерный объект, основание которого может быть любым многоугольником, а все его боковые грани — конгруэнтными треугольниками. Одна сторона каждого из этих треугольников совпадает с одной стороной базового многоугольника. Пирамиды названы в соответствии с формой их оснований. Квадратная пирамида — это пирамида, основание которой — квадрат. Как и другие трехмерные фигуры, квадратная пирамида также имеет два типа областей.
Пирамида — это трехмерный объект, основание которого может быть любым многоугольником, а все его боковые грани — конгруэнтными треугольниками. Одна сторона каждого из этих треугольников совпадает с одной стороной базового многоугольника. Пирамиды названы в соответствии с формой их оснований. Квадратная пирамида — это пирамида, основание которой — квадрат. Как и другие трехмерные фигуры, квадратная пирамида также имеет два типа областей.
- Площадь боковой поверхности (LSA)
- Общая площадь поверхности (TSA)
Давайте узнаем о боковой площади квадратной пирамиды вместе с формулой и несколькими примерами решения здесь. В конце вы также найдете несколько практических вопросов для практики.
| 1. | Какова боковая площадь квадратной пирамиды? |
| 2. | Формула площади поперечного сечения квадратной пирамиды |
| 3. | Как рассчитать латеральную площадь квадратной пирамиды? |
4. | Часто задаваемые вопросы о боковой площади квадратной пирамиды |
Какова боковая площадь квадратной пирамиды?
Слово «боковой» означает «принадлежащий стороне». Таким образом, площадь боковой стороны квадратной пирамиды равна сумме площадей ее боковых граней. Это также известно как площадь боковой поверхности (LSA) квадратной пирамиды. Мы знаем, что квадратная пирамида имеет:
- основание, представляющее собой квадрат.
- 4 боковые грани, каждая из которых представляет собой треугольник.
Все эти треугольники конгруэнтны и равнобедренны, каждый из которых имеет сторону, совпадающую со стороной основания (квадрата).
Итак, площадь боковой поверхности квадратной пирамиды равна сумме площадей четырех ее треугольных боковых граней.
Формула площади поперечного сечения квадратной пирамиды
Рассмотрим квадратную пирамиду, длина основания (длина стороны квадрата) которой равна ‘a’, а высота каждой боковой грани (треугольника) равна ‘l’ (это также называется наклонной высотой).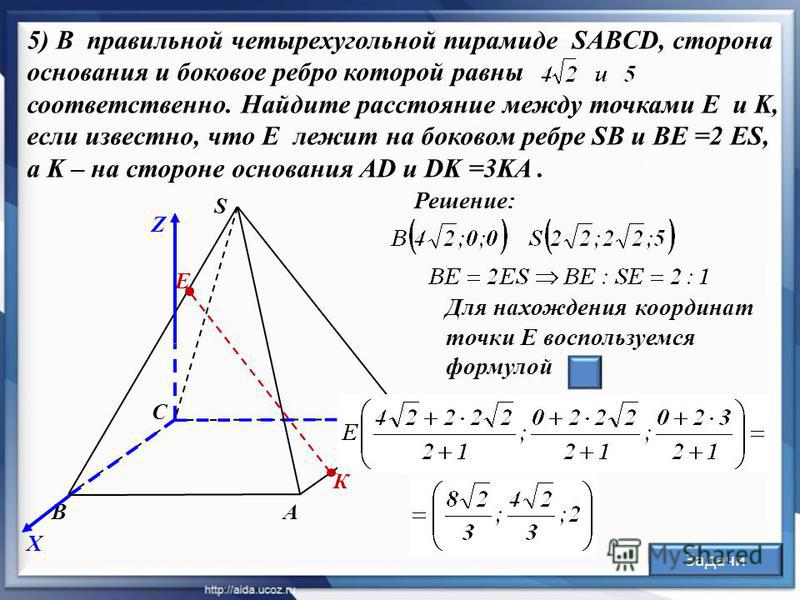 т. е. основание и высота каждой из четырех треугольных граней равны «a» и «l» соответственно. Таким образом, площадь каждой такой треугольной грани равна 1/2 × a × l. Таким образом, сумма площадей всех 4 треугольных граней равна 4 (½ al) = 2 al. Таким образом, площадь поперечной стороны квадратной пирамиды = 2al
т. е. основание и высота каждой из четырех треугольных граней равны «a» и «l» соответственно. Таким образом, площадь каждой такой треугольной грани равна 1/2 × a × l. Таким образом, сумма площадей всех 4 треугольных граней равна 4 (½ al) = 2 al. Таким образом, площадь поперечной стороны квадратной пирамиды = 2al
Что если нам дана высота пирамиды, а не высота наклона? Предположим, что высота пирамиды (высота) равна «h». Затем, применяя теорему Пифагора (см. рисунок ниже),
l=√[(a 2 /4) + h 2 ]
. квадратная пирамида = 2al = 2a√[(a 2 /4) + h 2 ]
Примечание: √[(a 2 /4) + h 2 ] может быть упрощено как (1/2)√(a 2 + 4h 2 ). Таким образом, формула площади поперечной стороны квадратной пирамиды может быть записана как 2a[(1/2)√(a 2 + 4h 2 )] = a√(a 2 + 4h 2 ).
Как рассчитать боковую площадь квадратной пирамиды?
Площадь поверхности боковой пирамиды можно рассчитать, следуя указанным шагам,
- Запишите данные размеры квадратной пирамиды и убедитесь, что они должны иметь одинаковые единицы измерения.

- Применить формулу для расчета площади поперечной стороны квадратной пирамиды,
Боковая площадь квадратной пирамиды = 2al = 2a√[(a 2 /4) + h 2 ], где «a» — длина основания, «h» — высота, а «l» — наклонная высота пирамиды. квадратная пирамида. - Выразите ответ в квадратных единицах.
Теперь, когда мы поняли площадь боковой стороны квадратной пирамиды, давайте посмотрим на несколько решенных примеров, чтобы лучше понять.
Пример 1: Найти площадь боковой стороны квадратной пирамиды с длиной основания 10 см и высотой наклона 16 см.
Решение:
Длина основания квадратной пирамиды а = 10 см.
Его наклонная высота l = 16 см.
Площадь боковой стороны = 2al = 2 (10) (16) = 320 см 2
Ответ: Площадь боковой стороны данной квадратной пирамиды = 320 см 2 .
Пример 2: Площадь основания квадратной пирамиды составляет 256 квадратных единиц, а ее высота – 25 единиц.
 Найдите его боковую площадь. Округлите ответ до сотых.
Найдите его боковую площадь. Округлите ответ до сотых.Решение:
Пусть сторона основания (квадрата) равна а единицам.
Тогда дано, что a 2 = 256 ⇒ a = 16 единиц.
Высота данной квадратной пирамиды, h = 25 единиц.
Используя формулу площади поперечного сечения квадратной пирамиды,
Боковая площадь = 2a√[(a 2 /4) + h 2 ]
= 2 (16) √(16 2 /4) + 25 2 ] ≈ 8 39,96 квадратных единиц.
Окончательный ответ округляется до сотых.
Ответ: Площадь боковой стороны данной квадратной пирамиды = 839,96 квадратных единиц.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о боковой площади квадратной пирамиды
Что такое боковая площадь квадратной пирамиды?
Площадь боковой поверхности квадратной пирамиды равна сумме площадей всех ее четырех треугольных боковых граней. Если a, h и l — длина основания, высота пирамиды и наклонная высота соответственно, то площадь боковой поверхности квадратной пирамиды = 2al (или) 2a√[(a 2 /4) + h 2 ].
Если a, h и l — длина основания, высота пирамиды и наклонная высота соответственно, то площадь боковой поверхности квадратной пирамиды = 2al (или) 2a√[(a 2 /4) + h 2 ].
Как найти площадь боковой поверхности квадратной пирамиды?
Чтобы найти площадь боковой стороны квадратной пирамиды, найдите площадь одной боковой грани (треугольника) и умножьте ее на 4. Если a и l — длина основания и наклонная высота квадратной пирамиды, то площадь боковой стороны квадратная пирамида = 4 (½ × a × l) = 2al. Если h — высота пирамиды, то ее площадь = 2a√[(a 2 /4) + h 2 ].
Какова площадь одной из треугольных граней квадратной пирамиды?
Если a и l — длина основания и наклонная высота квадратной пирамиды, то площадь одной из 4 треугольных боковых граней составляет ½ × a × l.
Как найти площадь боковой поверхности и общую площадь поверхности квадратной пирамиды?
Площадь боковой поверхности квадратной пирамиды представляет собой сумму площадей только боковых граней, тогда как площадь поверхности представляет собой площадь боковой поверхности + площадь основания.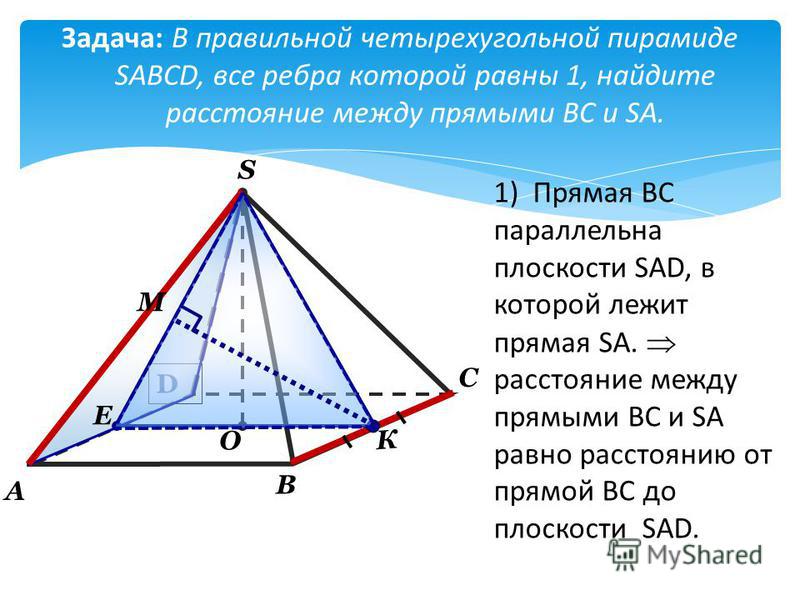

 Найдите его боковую площадь. Округлите ответ до сотых.
Найдите его боковую площадь. Округлите ответ до сотых.
Leave A Comment