Трапеция. Задачи категории В8 егэ по математике
Задача 1. Основания равнобедренной трапеции равны и Боковые стороны равны Найдите синус острого угла трапеции.
Решение: + показать
Задача 2. Большее основание равнобедренной трапеции равно Боковая сторона равна Синус острого угла равен Найдите меньшее основание.
Решение: + показать
Задача 3. Основания равнобедренной трапеции равны и Тангенс острого угла равен . Найдите высоту трапеции.
Решение: + показать
Задача 4. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
Решение: + показать
Задача 5. Найдите среднюю линию трапеции, если ее основания равны и
Решение: + показать
Задача 6. Средняя линия трапеции равна а меньшее основание равно Найдите большее основание трапеции.
Решение: + показать
Задача 7. Основания трапеции равны и Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Основания трапеции равны и Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Решение: + показать
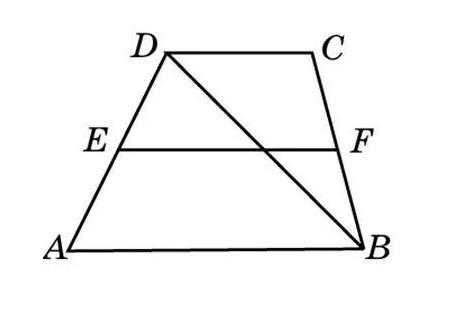
Задача 8. Основания трапеции равны и Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение: + показать
Задача 9. В равнобедренной трапеции основания равны и острый угол равен . Найдите ее периметр.
Решение: + показать
Задача 10. Основания трапеции равны и боковая сторона равна Площадь трапеции равна Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
Решение: + показать
Задача 11. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного отсекает треугольник, периметр которого равен Найдите периметр трапеции.
Решение: + показать
Задача 12. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины и Найдите среднюю линию этой трапеции.
Решение: + показать
Задача 13. Основания трапеции относятся как а средняя линия равна Найдите меньшее основание.
Решение: + показать
Задача 14. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна Найдите ее среднюю линию.
Решение: + показать
Задача 15. Найдите площадь прямоугольной трапеции, основания которой равны и большая боковая сторона составляет с основанием угол
Решение: + показать
Задача 16. Основания равнобедренной трапеции равны и а ее периметр равен Найдите площадь трапеции.
Решение: + показать
Задача 17. Найдите среднюю линию трапеции , если стороны квадратных клеток равны .
Решение: + показать
Вы можете пройти тест по теме «Трапеция»
Повторение по теме «Подобные треугольники» Вариант 1 В треугольнике ABC угол C равен 90°, AC=6, AB=10. В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB. В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN. Основания трапеции равны 17 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей. Катеты прямоугольного треугольника равны 18 и 24. Найдите высоту, проведённую к гипотенузе. | Повторение по теме «Подобные треугольники» Вариант 2 В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB. В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB. В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 83, сторона BC равна 62, сторона AC равна 104. Найдите MN. Основания трапеции равны 16 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей. Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведённую к гипотенузе. |
Повторение по теме «Подобные треугольники» Вариант 3 В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB. В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB. В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN. Основания трапеции равны 14 и 19. Катеты прямоугольного треугольника равны 21 и 28. Найдите высоту, проведённую к гипотенузе. | Повторение по теме «Подобные треугольники» Вариант 4 В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB. В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB. В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 66, сторона BC равна 37, сторона AC равна 74. Найдите MN. Основания трапеции равны 1 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей. Катеты прямоугольного треугольника равны 10 и 24. Найдите высоту, проведённую к гипотенузе. |
Повторение по теме «Подобные треугольники» Вариант 5 В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB. В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB. В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 95, сторона BC равна 80, сторона AC равна 128. Найдите MN. Основания трапеции равны 1 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей. Катеты прямоугольного треугольника равны 15 и 36. Найдите высоту, проведённую к гипотенузе. | Повторение по теме «Подобные треугольники» Вариант 6 В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB. В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB. В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 31, сторона BC равна 27, сторона AC равна 40. Найдите MN. Основания трапеции равны 2 и 9. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей. Катет и гипотенуза прямоугольного треугольника равны 20 и 52. Найдите высоту, проведённую к гипотенузе |
Повторение по теме «Подобные треугольники» Вариант 7 В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB. В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB. В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 42, сторона BC равна 44, сторона AC равна 62. Основания трапеции равны 8 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей. Катет и гипотенуза прямоугольного треугольника равны 16 и 34. Найдите высоту, проведённую к гипотенузе. | Повторение по теме «Подобные треугольники» Вариант 8 В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB. В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB. В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 31, сторона BC равна 42, сторона AC равна 50. Найдите MN. Основания трапеции равны 3 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей. Катет и гипотенуза прямоугольного треугольника равны 24 и 51. |
2.5: Численное интегрирование — средняя точка, трапеция, правило Симпсона
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10269
Эта страница является черновиком и находится в активной разработке.
Первообразные многих функций либо не могут быть выражены, либо не могут быть легко выражены в замкнутой форме (то есть через известные функции). Следовательно, вместо непосредственного вычисления определенных интегралов этих функций мы прибегаем к различным методам численного интегрирования
 Кроме того, мы исследуем процесс оценки ошибки при использовании этих методов.
Кроме того, мы исследуем процесс оценки ошибки при использовании этих методов.n_{i=1}f(m_i)Δx\) соответствует сумме площадей прямоугольников, аппроксимирующих площадь между графиком \(f(x)\) и осью \(x\) над \([ а, б]\). На графике показаны прямоугольники, соответствующие \(M_4\) для неотрицательной функции на замкнутом интервале \([a,b].\)
Рисунок \(\PageIndex{1}\): Правило середины аппроксимирует площадь между график \(f(x)\) и оси \(x\) путем суммирования площадей прямоугольников со средними точками, являющимися точками на \(f(x)\).Пример \(\PageIndex{1}\): использование правила средней точки с \(M_4\) 92\,dx\) с использованием четырех подынтервалов. Сравните результат с действительным значением этого интеграла.
Решение: Каждый подинтервал имеет длину \( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Следовательно, подынтервалы состоят из
\[\left[0,\ tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2} ,\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right]. \nonumber\]
\nonumber\]
Середины этих подинтервалов являются \(\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right \}.\) Таким образом, 92_1\frac{1}{x}\,dx.\)
- Подсказка
\( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)
- Ответить
\(\dfrac{24}{35}\)
Правило трапеций
Мы также можем аппроксимировать значение определенного интеграла, используя трапеции, а не прямоугольники. На рисунке \(\PageIndex{2}\) область под кривой аппроксимирована трапециями, а не прямоугольниками.
Рисунок \(\PageIndex{2}\): Трапеции можно использовать для аппроксимации площади под кривой, таким образом, аппроксимируя определенный интеграл. Правило трапеций для оценки определенных интегралов использует трапеции, а не прямоугольники для аппроксимации площади под кривой. Чтобы получить представление об окончательной форме правила, рассмотрите трапеции, показанные на рисунке \(\PageIndex{2}\).
Обобщая, сформулируем формально следующее правило.
Правило трапеций
Предположим, что \(f(x)\) непрерывно над \([a,b]\). Пусть \(n\) — натуральное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \( P=\{x_0,x_1,x_2…,x_n\}.\ )
Набор
\[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_ {n−1})+f(x_n)\big).\] 9nf(x_i)Δx.\)
То есть \(L_n\) и \(R_n\) аппроксимируют интеграл, используя левую и правую конечные точки каждого подинтервала соответственно. Кроме того, внимательное изучение рисунка \(\PageIndex{3}\) позволяет нам сделать следующие замечания об использовании правил трапеций и правил середины для оценки определенного интеграла неотрицательной функции. Правило трапеций имеет тенденцию систематически завышать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически занижать значение определенного интеграла на интервалах, где функция вогнута вниз. С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично занижая значение определенного интеграла на тех же самых типах интервалов. Это приводит нас к гипотезе о том, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеций. 92_1\frac{1}{x}\,dx.\)
Кроме того, внимательное изучение рисунка \(\PageIndex{3}\) позволяет нам сделать следующие замечания об использовании правил трапеций и правил середины для оценки определенного интеграла неотрицательной функции. Правило трапеций имеет тенденцию систематически завышать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически занижать значение определенного интеграла на интервалах, где функция вогнута вниз. С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично занижая значение определенного интеграла на тех же самых типах интервалов. Это приводит нас к гипотезе о том, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеций. 92_1\frac{1}{x}\,dx.\)
- Подсказка
Множество \(Δx=\dfrac{1}{2}.\) Концы подинтервалов являются элементами множества \(P=\left\{1,\frac{3}{2},2\right \}.\)
- Ответить
\(\dfrac{17}{24}\)
Абсолютная и относительная погрешность
Важным аспектом использования этих правил численной аппроксимации является вычисление погрешности их использования для оценки значения определенного интеграла. 2\,dx\), используя правило средней точки, найденное в Пример \(\PageIndex{1}\). 92_1\frac{1}{x}\,dx\) в \(\frac{24}{35}\) с использованием \(T_2\). Фактическое значение этого интеграла равно \(\ln 2\). Используя \(\frac{24}{35}≈0,6857\) и \(\ln 2≈0,6931,\), вычислите абсолютную ошибку и относительную ошибку.
2\,dx\), используя правило средней точки, найденное в Пример \(\PageIndex{1}\). 92_1\frac{1}{x}\,dx\) в \(\frac{24}{35}\) с использованием \(T_2\). Фактическое значение этого интеграла равно \(\ln 2\). Используя \(\frac{24}{35}≈0,6857\) и \(\ln 2≈0,6931,\), вычислите абсолютную ошибку и относительную ошибку.
- Подсказка
Используйте предыдущие примеры в качестве руководства.
- Ответить
абсолютная ошибка \(\приблизительно 0,0074,\) и относительная ошибка \(\приблизительно 1,1\%\)
Границы погрешности для средней точки и правил трапеций
В двух предыдущих примерах мы смогли сравнить нашу оценку интеграла с фактическим значением интеграла; однако у нас обычно нет такой роскоши. В общем, если мы аппроксимируем интеграл, мы делаем это потому, что не можем легко вычислить точное значение самого интеграла. Поэтому часто полезно иметь возможность определить верхнюю границу ошибки приближения интеграла.
- Подсказка
\(f»(x)=2,\) поэтому \(M=2.\)
- Ответить
\(\dfrac{1}{192}\)
Правило Симпсона
С помощью правила средней точки мы оценили площади областей под кривыми с помощью прямоугольников. В некотором смысле мы аппроксимировали кривую кусочно-постоянными функциями. С помощью правила трапеций мы аппроксимировали кривую, используя кусочно-линейные функции. Что, если бы мы вместо этого аппроксимировали кривую с помощью кусочно-квадратичных функций? С 9{x_4}_{x_2}f(x)\,dx\) с интегралом от другой квадратичной функции, проходящей через \( (x_2,f(x_2)), \,(x_3,f(x_3)),\) и \((x_4,f(x_4)).\) Этот процесс продолжается с каждой последующей парой подынтервалов.
Рисунок \(\PageIndex{4}\): С помощью правила Симпсона мы аппроксимируем определенный интеграл, интегрируя кусочно-квадратичную функцию. Чтобы понять формулу, которую мы получаем для правила Симпсона, мы начнем с вывода формулы для этой аппроксимации для первых двух подынтервалов. Проходя через вывод, мы должны помнить о следующих соотношениях: 9{x_4}_{x_0}f(x)\,dx=\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f( x_3)+f(x_4)).\nonumber\]
Проходя через вывод, мы должны помнить о следующих соотношениях: 9{x_4}_{x_0}f(x)\,dx=\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f( x_3)+f(x_4)).\nonumber\]
Шаблон продолжается, когда мы добавляем пары подынтервалов к нашему приближению. Общее правило можно сформулировать следующим образом.
Правило Симпсона
Предположим, что \(f(x)\) непрерывно над \([a,b]\). Пусть \(n\) — четное положительное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \(P=\{x_0,x_1,x_2,…,x_n\}. \) Набор 9b_af(x)\,dx.\nonumber\]
Точно так же, как правило трапеций является средним значением правил левой и правой руки для оценки определенных интегралов, правило Симпсона может быть получено из правил средней точки и правил трапеций с помощью взвешенное среднее. Можно показать, что \(S_{2n}=(\dfrac{2}{3})M_n+(\dfrac{1}{3})T_n\).
Также можно ограничить ошибку при использовании правила Симпсона для аппроксимации определенного интеграла. Граница ошибки задается следующим правилом: 92_1\frac{1}{x}\,dx.\)
Граница ошибки задается следующим правилом: 92_1\frac{1}{x}\,dx.\)
- Подсказка
\[S_2=(\frac{1}{3}Δx(f(x_0)+4f(x_1)+f(x_2))\]
- Ответить
\(\ гидроразрыва{25}{36}\)
Ключевые понятия
- Мы можем использовать численное интегрирование для оценки значений определенных интегралов, когда сложно найти замкнутую форму интеграла или когда требуется приблизительное значение только определенного интеграла.
- Наиболее часто используемыми методами численного интегрирования являются правило средней точки, правило трапеций и правило Симпсона.
- Правило средней точки аппроксимирует определенный интеграл, используя прямоугольные области, тогда как правило трапеций аппроксимирует определенный интеграл, используя трапециевидные приближения.
- Правило Симпсона аппроксимирует определенный интеграл, сначала аппроксимируя исходную функцию с помощью кусочно-квадратичных функций.

- числовое интегрирование
- разнообразие численных методов, используемых для оценки значения определенного интеграла, включая правило средней точки, правило трапеций и правило Симпсона
- относительная ошибка Ошибка
- в процентах от фактического значения, определяемая как \[\text{относительная ошибка}=∣\frac{A−B}{A}∣⋅100\%\nonumber\]
- Правило Симпсона 9b_af(x)\,dx\) задается как \[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+ 2\, f(x_{n−1})+f(x_n)\big).\nonnumber\]
Авторы
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- да
- Стадия
- Проект
- Теги
- расчетный график:да
- юпитер: питон
- правило средней точки
- Сумма Римана
- Правило Симпсона
ПАРКЦ | Облегчение синдрома спешки
Я заметил следующий вопрос в практическом тесте PARCC Grade 4 Mathematics EOY Spring 2014. Не знаю, почему этот вопрос показался мне сомнительным. Должно быть, он прошел довольно много обзоров, прежде чем попал в релиз.
Не знаю, почему этот вопрос показался мне сомнительным. Должно быть, он прошел довольно много обзоров, прежде чем попал в релиз.
Интересно, что означает параллельность сторон? Интересно, что значит, если сторона перпендикулярна?
Сколько перпендикулярных сторон, по вашему мнению, имеет прямоугольник? Как вы думаете, сколько пар перпендикулярных сторон имеет прямоугольник?
PARCC определяет трапецию как четырехугольник, по крайней мере, с одной парой параллельных сторон.
Сколько параллельных сторон, по вашему мнению, имеет следующая фигура?
Можно ли сказать, что у фигуры 3 перпендикулярные стороны?
Недавно я прочитал статью Ву «Преподавание геометрии через общие базовые стандарты», где он говорит: «Перпендикулярность — это одно из двух особых отношений между двумя линиями. Другой — параллелизм». Он предупреждает нас, чтобы мы ограничивали наши разговоры о параллелизме линиями, поскольку существует множество непересекающихся отрезков, для которых пересекаются содержащие их прямые.
Далее Ву определяет параллелограмм как четырехугольник с параллельными противоположными сторонами, и поэтому я знаю, что мы имеем в виду линии, содержащие стороны. Но почему-то язык этого вопроса кажется мне предполагающим, что сторона может быть параллельной сама по себе. Может ли кто-нибудь убедить меня, что это нормально, как написано?
Итак, путешествие к внимание к точности продолжается…
Метки: внимание к точности, атрибуты многоугольников, параллельные стороны, PARCC EOY Grade 4 элемент, перпендикулярные стороны
PARCC наконец-то выпустила образец предмета по геометрии для средней школы.
Мне не терпелось щелкнуть по нему, чтобы увидеть, с чем мы столкнулись.
Утверждение о доказательствах: автономно стройте цепочки рассуждений, которые будут подтверждать или опровергать геометрические утверждения или предположения.
Наиболее актуальные стандарты: G-CO.D: Создание геометрических конструкций
12. Создание формальных геометрических конструкций с помощью различных инструментов и методов (циркуль и линейка, шнур, отражающие устройства, складывание бумаги, динамическое геометрическое программное обеспечение, и т. д.). Копирование сегмента; копирование угла; разделение сегмента пополам; деление угла пополам; построение перпендикулярных линий, включая перпендикулярную биссектрису отрезка прямой; и построение прямой, параллельной заданной прямой, через точку, не лежащую на этой прямой.
Создание формальных геометрических конструкций с помощью различных инструментов и методов (циркуль и линейка, шнур, отражающие устройства, складывание бумаги, динамическое геометрическое программное обеспечение, и т. д.). Копирование сегмента; копирование угла; разделение сегмента пополам; деление угла пополам; построение перпендикулярных линий, включая перпендикулярную биссектрису отрезка прямой; и построение прямой, параллельной заданной прямой, через точку, не лежащую на этой прямой.
13. Постройте равносторонний треугольник, квадрат и правильный шестиугольник, вписанный в окружность.
Образец:
Что мне нравится в этом задании, так это то, что оно заставляет учащихся обращать внимание на этапы построения, а не просто слепо следовать указаниям, не думая о результатах.
Поскольку в этом году мы занимались построением, мы сосредоточились на том, чтобы выяснить, что конгруэнтно в конце каждого шага. Какие отрезки, углы, дуги и треугольники равны в результате построения? CCSS-M заставил меня изменить это. В прошлом строительство представляло собой контрольный список шагов. Я не заставлял своих учеников думать о том, что они делают.
В прошлом строительство представляло собой контрольный список шагов. Я не заставлял своих учеников думать о том, что они делают.
Эта конкретная конструкция предоставляет учащимся прекрасную возможность искать и использовать структуру . Эта математическая практика указана как дополнительная. Две практики, которые PARCC выделяет для этой задачи: построить жизнеспособный аргумент и критически оценить рассуждения других и обратить внимание на точность .
Итак, вот что меня разочаровывает в этой задаче. Стандарты геометрии были написаны для определения конгруэнтности и подобия с точки зрения преобразований. Две фигуры конгруэнтны, если существует жесткое движение (или набор жестких движений), которое отображает одну фигуру на другую. Две фигуры подобны, если существует растяжение (и, если необходимо, набор жестких движений), отображающее одну фигуру на другую. Информация об оценке этого задания требует, чтобы учащиеся доказали конгруэнтность полученных треугольников с помощью SSS и конгруэнтность углов с помощью CPCTC. Мне это кажется геометрией старой школы.
Мне это кажется геометрией старой школы.
Итак, я дал задание своим ученикам. Я переиграл анимацию построения биссектрисы угла, которую нашел в сети, пока они спокойно работали минут 10-15.
Согласно руководству по подсчету очков, учащиеся получают 1 балл, если считают, что настройки компаса образуют конгруэнтные сегменты. Они отмечают, что третья сторона конгруэнтна по рефлексивности. Поймут ли учащиеся суть, если они не заметят, что третья пара сторон конгруэнтна по рефлексивному свойству? Студенты получают 1 балл, если считают, что треугольники конгруэнтны по SSS. Студенты получают 3 rd и конечная точка, если они считают, что углы конгруэнтны по CPCTC, таким образом образуя биссектрису угла.
Из примечаний: «Рассуждение должно включать утверждение о конгруэнтности треугольника и то, как этапы построения образуют пары конгруэнтных сторон».
Я не оценил все свои студенческие работы в соответствии с рекомендациями. Я так не думаю. Но хочу поделиться некоторыми результатами.
Из 60 студентов у меня было около 10, которые доказали или попытались доказать, что треугольники, отмеченные в решении PARCC, конгруэнтны SSS.
У меня было около 5 человек, которые говорили о точках биссектрисы, равноудаленных от двух концов отрезка, и о точках биссектрисы угла, равноудаленных от двух сторон угла.
У меня было несколько человек, которые признали, что ∆ABC равнобедренный, и использовали свойства равнобедренных треугольников, чтобы показать, что угол был разделен пополам.
И у меня было по крайней мере 40 студентов, которые искали и использовали структуру . Они увидели воздушного змея. И они использовали свойства воздушного змея, чтобы доказать, что луч является биссектрисой угла.
Так что теперь? Если бы это был экзамен AP, я был бы уверен, что мои ученики получат признание за свои ответы. Или, по крайней мере, некоторая заслуга — я признаю, что не все дали пошаговое объяснение/объяснение ответа, и я признаю, что все не указали, почему фигурка была воздушным змеем.
Так что мне интересно. Путешествие продолжается…
Теги: конструкция биссектрисы угла, CCSS-M G-CO.12, CCSS-M G-CO.13, воздушные змеи, ищите и используйте структуру, образец PARCC
Таблица с доказательствами PARCC для геометрии EOY, G-CO.3, говорит: Трапеция определяется как «четырехугольник с хотя бы одной парой параллельных сторон».
Усыскин (и я уверен, что другие — он просто был первым, от кого я это прочитал) называют это инклюзивным определением трапеции.
Я предлагал это определение своим ученикам как возможность уже несколько лет. что будет , если мы определили трапецию как четырехугольник хотя бы с одной парой параллельных сторон? Тогда параллелограмм тоже трапеция. Наши всегда/иногда/никогда не заполняют пустые утверждения «Параллелограмм — это ____ трапеция» или «Трапеция — это ____ квадрат» меняются с никогда на иногда. Но поскольку в нашем учебнике трапеция определяется как четырехугольник с ровно одной парой параллельных сторон, мы тоже так поступили. В этом году мы определили трапецию, как будет PARCC. Мои коллеги и я думали о влиянии этого определения на нашу дедуктивную систему.
В этом году мы определили трапецию, как будет PARCC. Мои коллеги и я думали о влиянии этого определения на нашу дедуктивную систему.
Кстати, я искал реальные ресурсы по геометрии CCSS. Я обычно сначала смотрю, где находится блок по преобразованиям. Если не 1-й и не 2-й, то для меня это явный признак того, что текст действительно не редактировался для CCSS-M. Я все забыл посмотреть, как они говорят о трапециях. Не то, чтобы каждый ресурс учебника CCSS-M должен определять трапеции, как это делает PARCC, но предлагают ли они вообще инклюзивное определение как возможность?
Наше расположение четырехугольников на диаграмме Венна было удалено.
Некоторые из наших практических задач пришлось переписать:
Старое: По определению, что такое четырехугольник, у которого ровно одна пара противоположных сторон параллельна?
Новое: По определению, что такое четырехугольник с хотя бы одной парой противоположных сторон, параллельных?
Old: По определению, что такое четырехугольник, в котором обе пары противоположных сторон параллельны?
Новое: По определению, что такое трапеция , у которой обе пары противоположных сторон параллельны?
Технически мы могли бы сохранить старый вопрос, но мы изменили его, поскольку хотим подчеркнуть новое определение.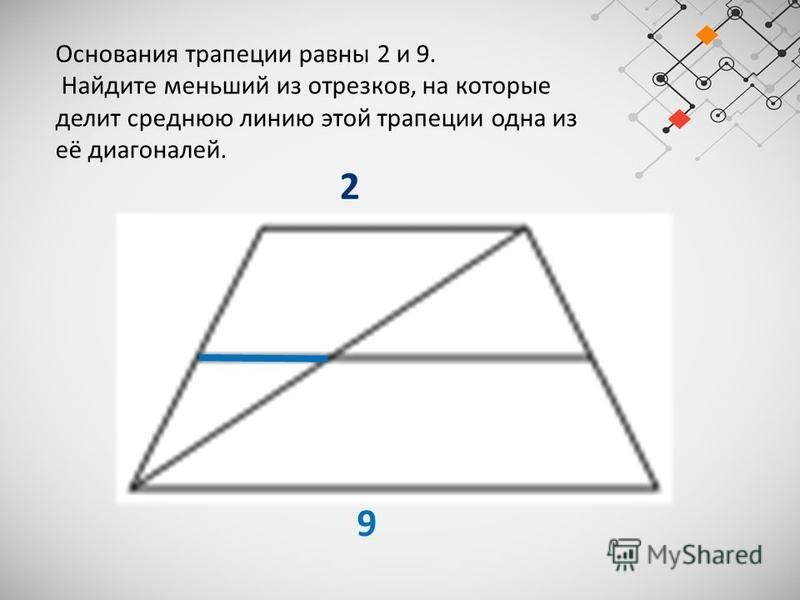
Старый: Какое утверждение НИКОГДА не верно?
A. Квадрат ABCD является ромбом.
B. Параллелограмм PQRS представляет собой квадрат.
C. Трапеция GHJK является параллелограммом.
D. Квадрат WXYZ является параллелограммом.
E. Трапеция EFGH – равнобедренная трапеция.
Новое: мы полностью удалили этот вопрос. Но теперь, когда я смотрю на это более внимательно, я думаю, что мы могли бы изменить параллелограмм в выборе C на воздушный змей .
Старое: Два последовательных угла трапеции прямые. Четыре из следующих утверждений о трапеции могут быть верными. Какое утверждение НЕ МОЖЕТ быть верным?
A. Два прямых угла являются углами при основании.
B. Диагонали не равны.
C. Две стороны конгруэнтны.
D. Никакие две стороны не конгруэнтны.
E. Ровно две стороны параллельны.
Новое: мы добавили слово Ровно в начало основы вопроса.
Старый: Напишите номер каждой из пяти фигур в соответствующей области схемы.
Новое: нам не нужно было менять вопрос… только решение.
Другие разговоры, которые у нас были, были о том, как определять другие четырехугольники. Если мы определим трапецию как четырехугольник, по крайней мере, с одной парой параллельных сторон, то не должен ли параллелограмм быть трапецией, у которой обе пары противоположных сторон параллельны? Мы всегда определяли прямоугольник как параллелограмм с четырьмя конгруэнтными углами, ромб как параллелограмм с четырьмя конгруэнтными сторонами и квадрат как параллелограмм, который одновременно является прямоугольником и ромбом. Эти определения, кажется, все еще работают. Но являются ли они лучшими определениями? Изменим ли мы наше определение воздушного змея с четырехугольника с двумя парами последовательных конгруэнтных сторон на четырехугольник с по крайней мере двумя парами последовательных конгруэнтных сторон? И если да, то должны ли мы определять ромб как воздушный змей с четырьмя конгруэнтными сторонами? Как определить равнобедренную трапецию в этой дедуктивной системе? Кажется, что трапеция с конгруэнтными катетами больше не работает.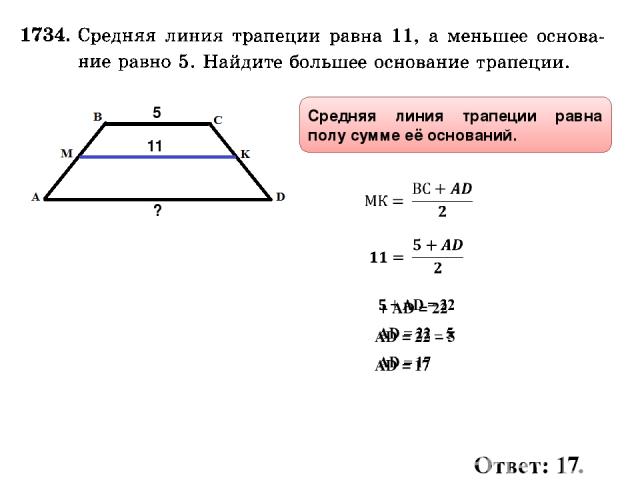 А трапеция с равными диагоналями? Или трапеция с равными углами при основании? Мы вообще говорим о основаниях и катетах трапеции?
А трапеция с равными диагоналями? Или трапеция с равными углами при основании? Мы вообще говорим о основаниях и катетах трапеции?
Еще один вопрос, который у меня возник, заключается в том, знают ли учителя K-8 об этом исчерпывающем определении трапеции. Беспокоит ли учащихся изменение определения в середине школьных лет? Или нам нужно начать кампанию по информированию учителей об этом определении, которые, возможно, не читают таблицу утверждений PARCC для геометрии EOY? Просто для протокола: я думаю, мои ученики согласны с этим определением. На самом деле они были более гибкими в своем мышлении, чем учителя.
В прошлом году моя ученица 2-го класса -го и -го классов пришла домой с этим вопросом в рабочем листе, который я поделился со своими учениками.
К сожалению, я хотел отметить один ответ, хотя моя дочь отметила более одного ответа.
Можете ли вы представить себе страдания, связанные с наличием 4-й -й -й фигуры, которая не является специальной трапецией с указаниями «Отметить трапецию»?
Что касается изучения свойств трапеции, мне очень нравится всеобъемлющее определение трапеции. Мы построили трапецию, используя наше программное обеспечение для динамической геометрии. Мы признаем, что две пары последовательных углов являются дополнительными. Но когда мы перемещаем вершины, чтобы наблюдать, что остается неизменным, а что изменяется, мы понимаем, что бывают моменты, когда все пары последовательных углов являются дополнительными. Трапеция может быть параллелограммом.
Мы построили трапецию, используя наше программное обеспечение для динамической геометрии. Мы признаем, что две пары последовательных углов являются дополнительными. Но когда мы перемещаем вершины, чтобы наблюдать, что остается неизменным, а что изменяется, мы понимаем, что бывают моменты, когда все пары последовательных углов являются дополнительными. Трапеция может быть параллелограммом.
Мы также использовали наше программное обеспечение для динамической геометрии, чтобы наблюдать, что происходит, когда мы создаем средний сегмент трапеции. Что верно в отношении середины трапеции? Она параллельна основаниям. Он разрезает трапецию на две меньшие трапеции. Откуда вы знаете? Как мы можем показать, что ABNM также является трапецией?
А что верно в отношении длины среднего сегмента по сравнению с основаниями? Это половина суммы оснований. Как показать, что длина среднего отрезка всегда равна половине суммы оснований?
Я рад, что этот разговор был начат в другом месте, и что я легко нашел его через Google.

 Найдите sinB.
Найдите sinB.
 Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

 Найдите MN.
Найдите MN. Найдите высоту, проведённую к гипотенузе.
Найдите высоту, проведённую к гипотенузе.
Leave A Comment