2. Диагонали осевого сечения усеченного конуса взаимно перпендикулярны. Зив Б.Г. Геометрия 11 класс ГДЗ. Самостоятельные работы. С-8. В-7.
2. Диагонали осевого сечения усеченного конуса взаимно перпендикулярны. Зив Б.Г. Геометрия 11 класс ГДЗ. Самостоятельные работы. С-8. В-7. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
2.
перпендикулярны. Площадь боковой поверхности усечен-
ного конуса относится к площади боковой поверхности
конуса, образующей которого служит диагональ сечения,
а радиусом основания — его высота, как √6 : 3. Найдите
угол наклона образующей к плоскости основания.
ответы
ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Юмор
Олимпиады
ЕГЭ
Компьютерные игры
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее.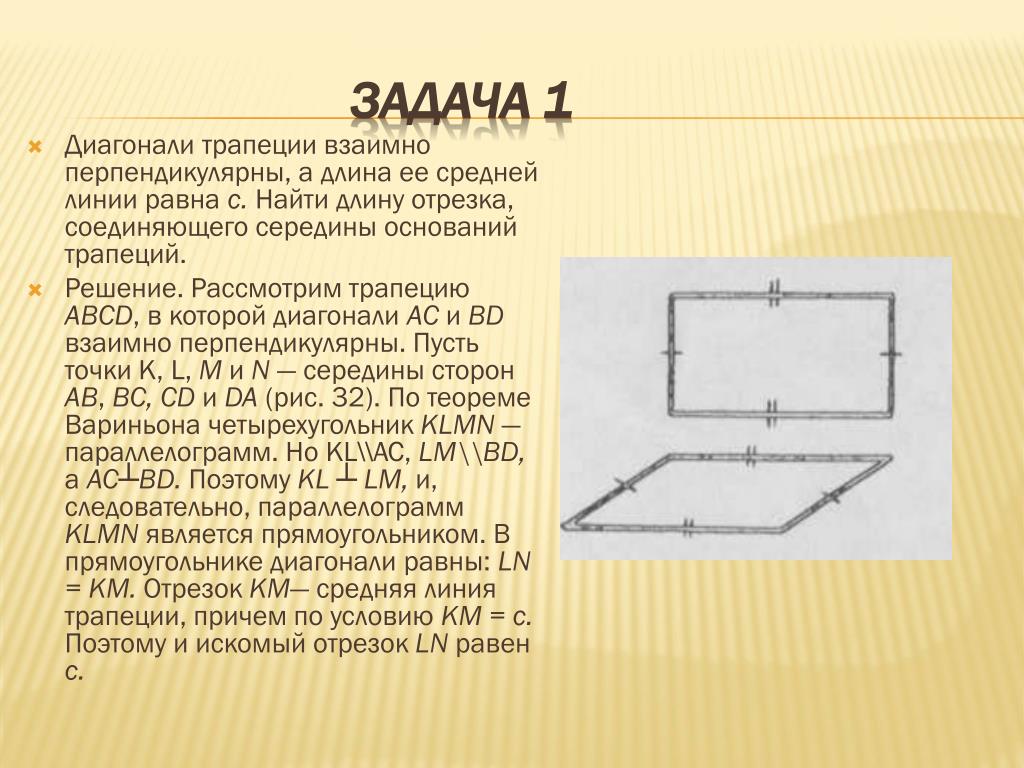 ..)
..)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
С чем связано окончание приема учащихся в Московский институт телевидения и радиовещания «Останкино»? (Подробнее…)
ВузыПоступление11 классНовости
Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее. ..)
..)
Поступление11 классЕГЭНовости
В прямоугольной трапеции диагонали взаимно. Диагонали трапеции
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм (BC∥ DF как основания трапеции, BD∥ CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.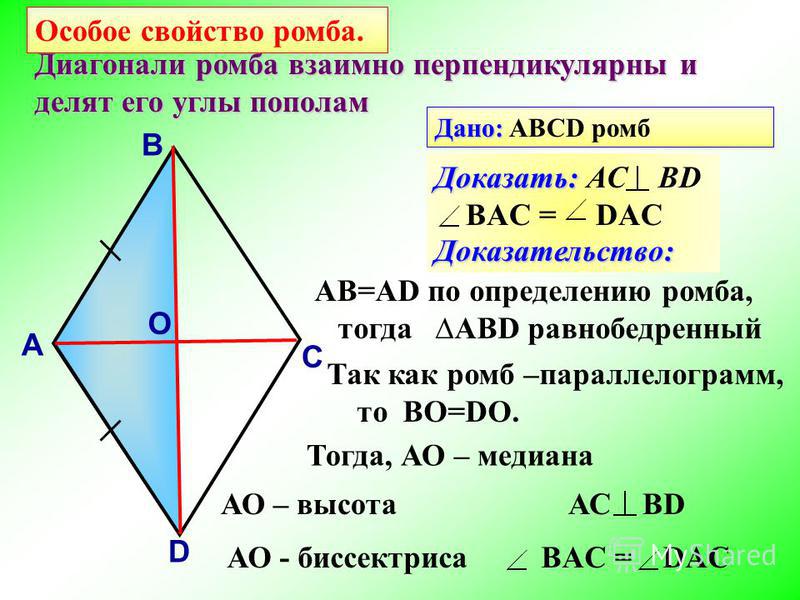
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
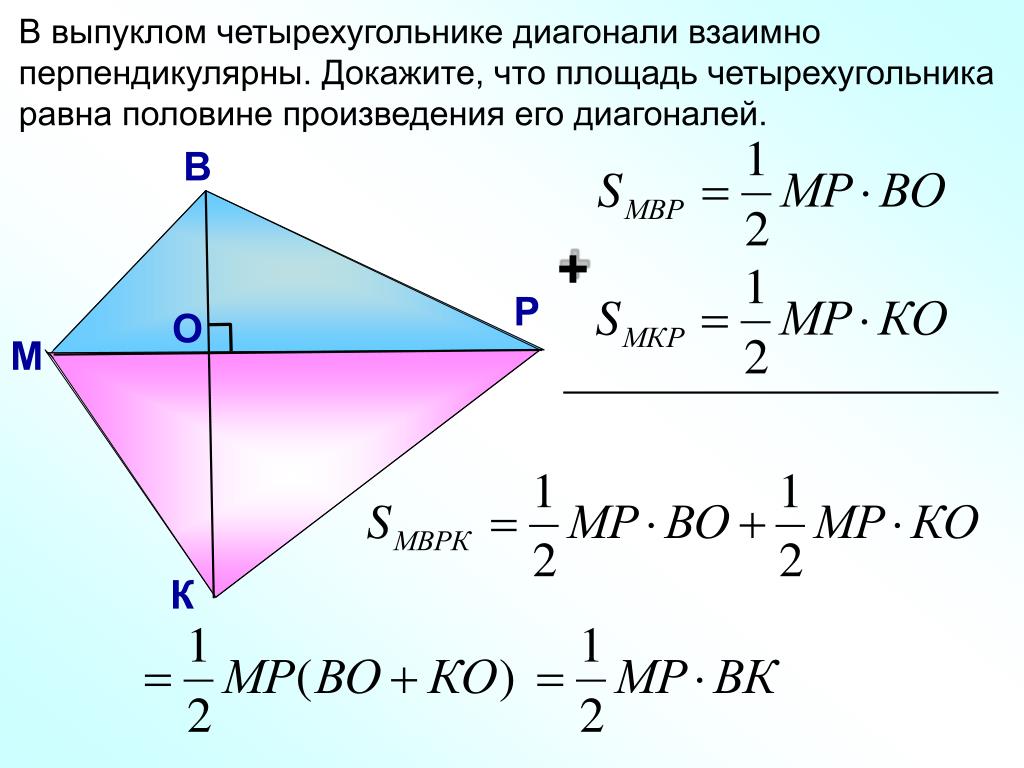
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует. х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Похожие задачи:
1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с.
3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата если его диагональ составляет 10 см
2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?
4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.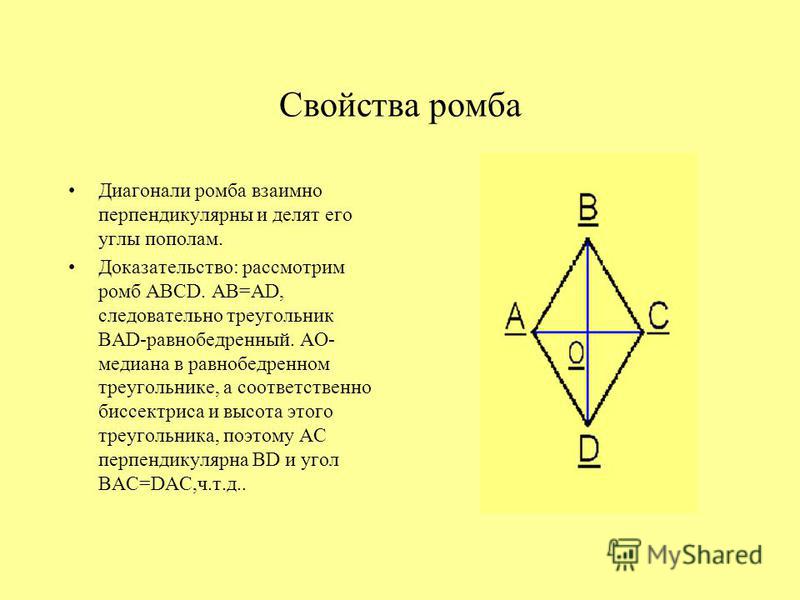
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .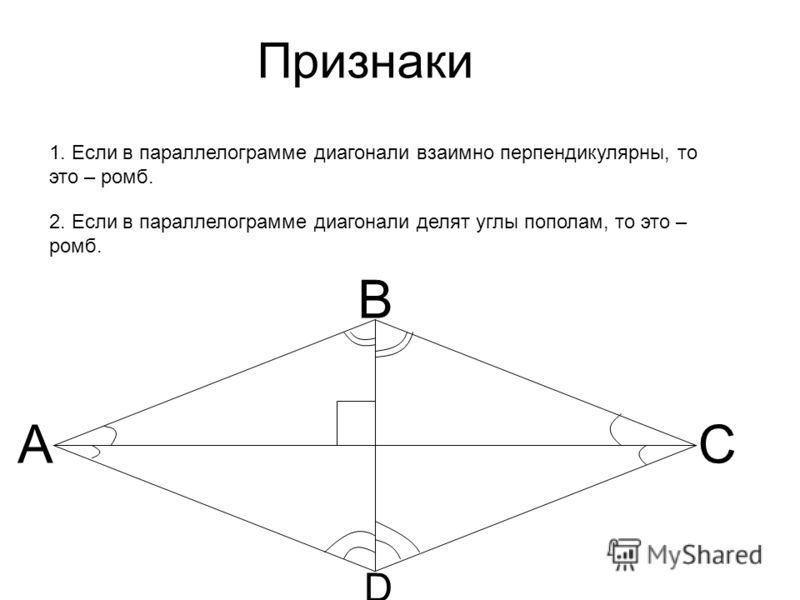
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание . В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме .
Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме .
Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .
Диагонали прямоугольной трапеции взаимно перпендикулярны углу между ними. Диагонали трапеции
Опять пифагорейский треугольник :))) Если отрезок большой диагонали от большого основания до точки пересечения обозначить через x, то из очевидного подобия прямоугольных треугольников с одинаковыми углами это следует. х/64 = 36/х, следовательно, х = 48; 48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Единственным исключением является треугольник, образованный отрезками диагоналей и косой стороны, но он нас не интересует :). (Для ясности, рассматриваемое подобие — это просто ДРУГИЕ НАЗВАННЫЕ тригонометрические функции углов 🙂 мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, поэтому синус равен 3/5, а косинус 4/5 :)) можно сразу написать
Ответы. Нижнее основание 80, высота трапеции будет 60, а верхнее 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Смежные задачи:
1. Основанием призмы является треугольник, у которого одна сторона равна 2 см, а две другие по 3 см. Боковой край равен 4 см и образует с плоскостью основания угол 45°. Найдите ребро равнобедренного куба.
Основанием призмы является треугольник, у которого одна сторона равна 2 см, а две другие по 3 см. Боковой край равен 4 см и образует с плоскостью основания угол 45°. Найдите ребро равнобедренного куба.
2. Основанием наклонной призмы является равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, меньшая диагональ которого равна c. Найдите объем призмы.
3. У наклонной призмы основанием является прямоугольный треугольник, гипотенуза которого равна с, один острый угол равен 30, боковое ребро равно и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата, если его диагональ равна 10 см
2. В равнобедренной трапеции тупой угол на 135 градусов меньше, чем основание равно 4 см, а высота равна 2 см. Найдите площадь трапеция?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту, если площадь трапеции равна 168 см в квадрате?
4. В треугольнике ABC угол A = угол In = 75 градусов. Найдите ВС, если площадь треугольника равна 36 см в квадрате.
В треугольнике ABC угол A = угол In = 75 градусов. Найдите ВС, если площадь треугольника равна 36 см в квадрате.
1. Диагонали трапеции ABCD со сторонами AB и CD пересекаются в точке O
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите, что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эта высота делится биссектрисой угла при основании.
3. Линия АМ-касательная к окружности, АВ-хорда этой окружности. Докажите, что угол MAB измеряется половиной дуги AB, лежащей внутри угла MAB.
- Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения, подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если мы продолжим стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой линией, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной отношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции и проведенный через точку пересечения диагоналей, делится этой точкой пополам, и его длина равна 2ab/(a+b), где а и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединяем середины диагоналей трапеции ABCD, в результате чего у нас получится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции , лежит на средней линии трапеции .
Этот отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, образованные основаниями трапеции и точкой пересечения диагоналей трапеция — аналогичны .
Треугольники BOC и AOD подобны. Поскольку углы BOC и AOD вертикальны, они равны.
Углы OCB и OAD внутренние крест-накрест, лежащие на параллельных прямых AD и BC (основания трапеций параллельны друг другу) и секущей AC, следовательно, равны.
Углы OBC и ODA равны по той же причине (внутреннее пересечение).
Поскольку все три угла одного треугольника равны соответствующим углам другого треугольника, эти треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если известны длины двух соответствующих элементов подобных треугольников, то находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов связаны друг с другом точно такой же величиной.
Если известны длины двух соответствующих элементов подобных треугольников, то находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов связаны друг с другом точно такой же величиной.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на сторонах трапеции AB и CD. Это треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон этих треугольников могут быть совершенно разными, но площади треугольников, образованных сторонами и точкой пересечения диагоналей трапеции, равны , то есть треугольники равны.
Если стороны трапеции продолжить в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, проходящей через середины оснований .
Таким образом, любую трапецию можно продолжить до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продолженных сторон, подобны
- Прямая, соединяющая середины оснований трапеции, является одновременно медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, лежащей в точке пересечения диагоналей трапеции (КН), то отношение составляющих ее отрезков от стороны основания до точки пересечения диагоналей (КО/ОН) будет равно отношению оснований трапеции (ВС/АД).
КО/ОН=БК/АД
Это свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами :
- Заданное расстояние (км) делит пополам точку пересечения диагоналей трапеции
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна КМ = 2ab/(a + b)
а, б — основания трапеции
в, d — стороны трапеции
d1 d2 — диагонали α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов сторон плюс удвоенное произведение ее оснований. Это свойство диагоналей трапеции можно доказать как отдельную теорему
Сумма квадратов диагоналей трапеции равна сумме квадратов сторон плюс удвоенное произведение ее оснований. Это свойство диагоналей трапеции можно доказать как отдельную теорему
2 . Эта формула получается преобразованием предыдущей формулы. Квадрат второй диагонали набрасывается на знак равенства, после чего из левой и правой частей выражения извлекается квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с тем отличием, что в левой части выражения
оставлена еще одна диагональ. Следующая группа формул (4-5) аналогична по смыслу и выражает подобное отношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание . В этом уроке дается решение задач по геометрии о трапециях. Если вы не нашли решение задачи по геометрии интересующего вас типа — задайте вопрос на форуме .
Если вы не нашли решение задачи по геометрии интересующего вас типа — задайте вопрос на форуме .
Задача .
Диагонали трапеции ABCD (AD | | BC) пересекаются в точке O. Найдите длину основания BC трапеции, если основание AD = 24 см, длина AO = 9 см, длина OS = 6 см.
Решение .
Решение этой задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC подобны по трем углам — AOD и BOC вертикальны, а остальные углы попарно равны, так как образованы пересечением одной прямой и двух параллельных прямых.
Так как треугольники подобны, то все их геометрические размеры связаны друг с другом, как известные нам по условию задачи геометрические размеры отрезков АО и ОС. то есть
AO/OC=AD/BC
9 / 6 = 24 / B.C.
БК = 24 * 6 / 9 = 16
Ответ : 16 см
Задание .
В трапеции ABCD известно, что AD=24, BC=8, AC=13, BD=5√17. Найдите площадь трапеции.
Решение .
Чтобы найти высоту трапеции из вершин меньшего основания В и С, опускаем две высоты на большее основание. Так как трапеция неравнополочная, обозначим длину АМ = а, длину КД = b (не путать с символами в формуле нахождения площади трапеции). Так как основания трапеции параллельны и мы опустили две высоты, перпендикулярные большему основанию, то MBCK является прямоугольником.
Среднее
AD=AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK прямоугольные, поэтому их прямые углы образованы высотами трапеций. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Считаем, что a = 16 — b , то в первом уравнении
ч 2 + (24 — 16 + b) 2 = 425
ч 2 = 425 — (8 + b) 2
Подставляем значение квадрата высоты во второе уравнение, полученное по теореме Пифагора. Получаем:
425 — (8 + б) 2 + (24 — б) 2 = 169
— (64 + 16б + б) 2 + (24 — б) 2 = -256
-64 — 16б — б 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, КД = 12
Где
ч 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдите площадь трапеции, используя ее высоту и половину суммы оснований
, где а b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см2.
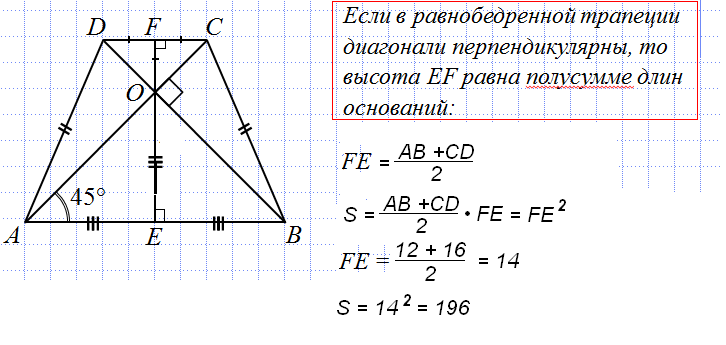
Если диагонали в равнобедренной трапеции перпендикулярны, то при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, то высота трапеции равна половине суммы оснований.
Проведем прямую CF через точку C параллельно BD и продолжим прямую AD до пересечения с CF.
Четырехугольник BCFD является параллелограммом (BC∥ DF как основание трапеции, BD∥ CF по построению). Итак, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Так как в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF равнобедренный с основанием AF. Следовательно, его высота CN также является медианой. А так как медиана прямоугольного треугольника, проведенного к гипотенузе, равна ее половине, то
, что можно записать в общем виде как
, где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна половине суммы оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высота трапеции (или квадрат полусуммы оснований, или квадрат средней линии).
Так как площадь трапеции находится по формуле
и высота, то половины суммы оснований и средней линии равнобедренной трапеции с перпендикулярными диагоналями равны между собой:
4 Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
Q4 Назовите четырехугольник, диагонали которого i делят друг друга пополам ii являются перпендикулярными биссектрисами каждого.
 ..
..Перейти к
- Упражнение 3.1
- Упражнение 3.2
- Упражнение 3.3
- Упражнение 3.4
- Рациональное число
- Линейные уравнения с одной переменной
- Понимание четырехугольников
- Практическая геометрия
- Обработка данных
- Квадраты и квадратные корни
- Кубы и кубические корни
- Сравнение количеств
- Алгебраические выражения и тождества
- Визуализация твердых фигур
- Измерение
- Показатели и силы
- Прямые и обратные пропорции
- Факторизация
- Введение в графики
- Игра с числами
Главная >
Решения НЦЭРТ
Класс 8
Математика
>
Глава 3. Понимание четырехугольников
>
Упражнение 3.4
>
Вопрос 14
Понимание четырехугольников
>
Упражнение 3.4
>
Вопрос 14
Вопрос 14 Упражнение 3.4
Q4) Назовите четырехугольник, диагонали которого:
(i) делят друг друга пополам.
(ii) перпендикулярны друг другу.
(iii) равны.
Ответ:
Решение:
(i) Если диагонали четырехугольника делят друг друга пополам, то это ромб, параллелограмм, прямоугольник или квадрат.
(ii) Если диагонали четырехугольника взаимно перпендикулярны, то это ромб или квадрат.
(iii) Если диагонали равны, то это квадрат или прямоугольник.
Связанные вопросы
**Укажите, верно это или нет:** **Все ромбы — воздушные змеи.**
**Укажите, верно это или нет:** **Все параллелограммы являются трапециями.**
**Укажите, верно это или нет:** **Все прямоугольники являются квадратами.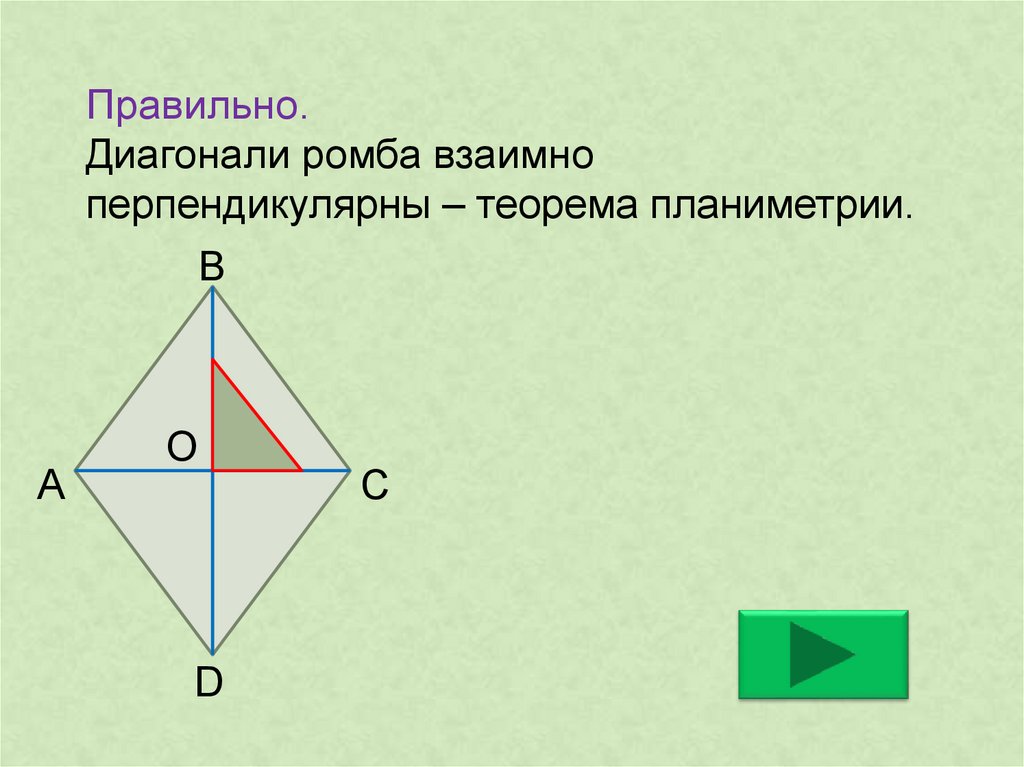 **
**
**Укажите, верно это или нет:** **Все ромбы являются параллелограммами.**
**Укажите, верно это или нет:** **Все квадраты не являются параллелограммами.**
**Укажите, верно это или нет:** **Все воздушные змеи представляют собой ромбы.**
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 3.1
Упражнение 3.2
Упражнение 3.3
Упражнение 3.4 2 Понимание четырёхугольников
Практическая геометрия
Обработка данных
Квадраты и квадрат Корни
Кубы и кубические корни
Сравнение величин.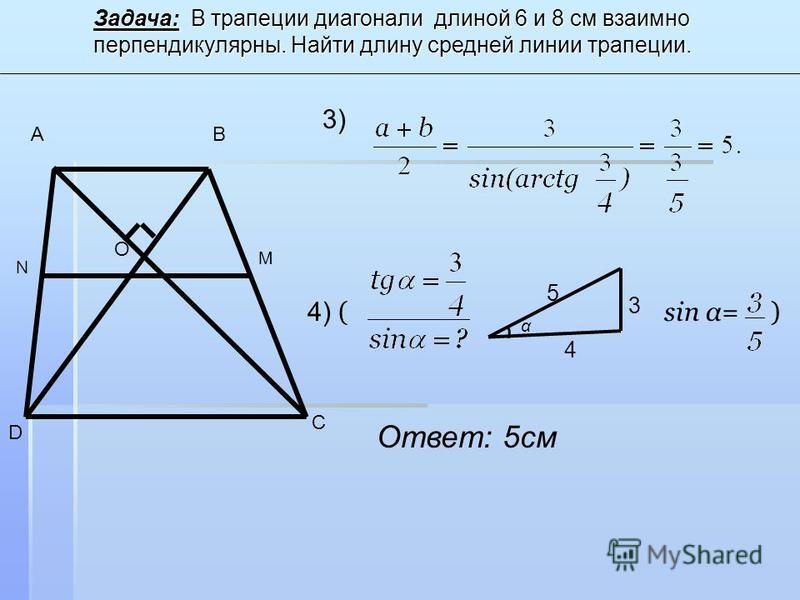

Leave A Comment