Страница 15 (учебник Моро 1 часть 4 класс) ответы по математике
74. Выполни деление с объяснением: 832 : 4, 924 : 3, 618 : 2, 603 : 3. 75. В одном автобусе 48 пассажиров, а в другом — в 3 раза больше. На сколько человек в первом автобусе меньше, чем во втором?1) 48 * 3 = 144 пассажира во втором автобусе.
2) На 144 — 48 = 96, пассажиров больше во втором автобусе, чем в первом.Ответ: на 96 пассажиров.
1) 8 * 10 = 80 банок съели туристы через 10 дней.
2) 96 — 80 = 16 банок у них осталось.Ответ: 16 банок.
1) Найди массу 1 таких пачек.
2) Сколько таких пачек содержат 100 г чая?
150 : 3 = 50 г — масса одной пачки чая.
1) 7 * 50 = 350 г — масса 7 пачек чая.
2) 100 : 50 = 2 пачки чая содержат 100 г чая.
Ответ: 350 г., 2 пачки. 78. Вычисли и проверь деление умножением.
1)
960 : 3 = 320
780 : 6 = 130
945 — 9 * 5 : 3 = 945 — 45 : 3 = 945 — 15 = 930
600 + 6 * 7 : 2 = 600 + 42 : 2 = 600 + 21 = 621
(200 + 450) : 5 = 650 : 6 = 130
(720 — 120) : 3 = 600 : 3 = 200
2)
507 + 230 + 187 = 924
367 + 178 + 264 = 809
Площадь прямоугольника 4 * 3 = 12 см2.
75 → 15 → 60 → 10 → 70 → 7 → 63 → 100.
gdzmoro.ru
Танграм своими руками (схемы игры, фигуры)
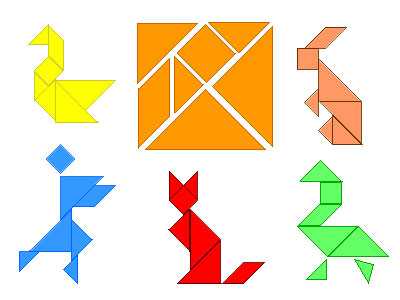
Танграм — старинная восточная головоломка из фигур, получившихся при разрезании квадрата на 7 частей особым образом: 2 больших треугольника, один средний, 2 маленьких треугольника, квадрат и параллелограмм. В результате складывания этих частей друг с другом получаются плоские фигуры, контуры которых напоминают всевозможные предметы, начиная от человека, животных и заканчивая орудиями труда и предметами обихода. Такого рода головоломки часто называют «геометрическими конструкторами», «головоломками из картона» или «разрезными головоломками».
С танграмом ребенок научится анализировать изображения, выделять в них геометрические фигуры, научится визуально разбивать целый объект на части, и наоборот — составлять из элементов заданную модель, а самое главное — логически мыслить.
Как сделать танграм
Танграм можно сделать из картона или бумаги, распечатав шаблон и разрезав по линиям. Вы можете скачать и распечатать схему квадрата танграма, кликнув по картинке и выбрав «печать» или «сохранить картинку как…».
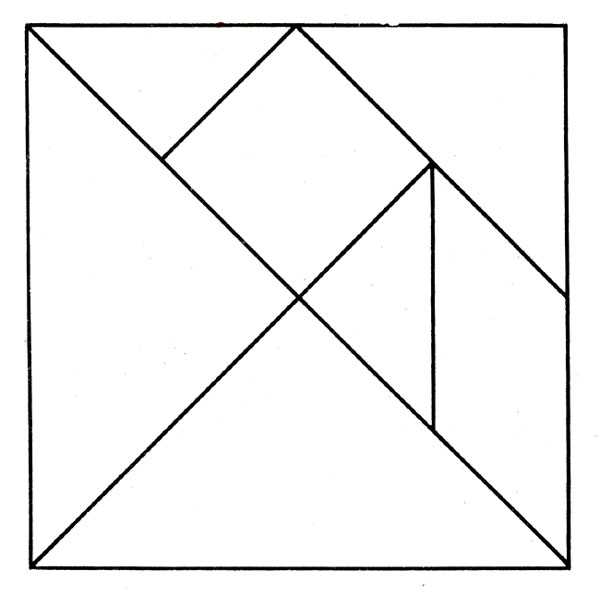
Можно и без шаблона. В квадрате чертим диагональ — получается 2 треугольника. Один из них разрезаем пополам на 2 небольших треугольника. Отмечаем на каждой стороне второго большого треугольника середину. Отсекаем по этим отметкам средний треугольник и остальные фигуры. Есть и другие варианты, как расчертить танграм, но когда вы его разрежете на части, они будут абсолютно те же самые.
Более практичный и долговечный танграм можно вырезать из жесткой офисной папки или пластиковой коробки из под DVD. Можно немного усложнить себе задачу, вырезав танграм из кусочков разного фетра, обметав их по краям, или вовсе из фанеры или дерева.
Как играть в танграм
Каждая фигура игры должна складываться из семи частей танграма, и при этом они не должны перекрываться.
Самый легкий вариант для детей дошкольников 4-5 лет — собирать фигуры по расчерченным на элементы схемам (ответам), как мозаику. Немного практики, и ребенок научится составлять фигуры по образцу-контуру и даже придумывать свои фигуры по такому же принципу.
Схемы и фигуры игры танграм
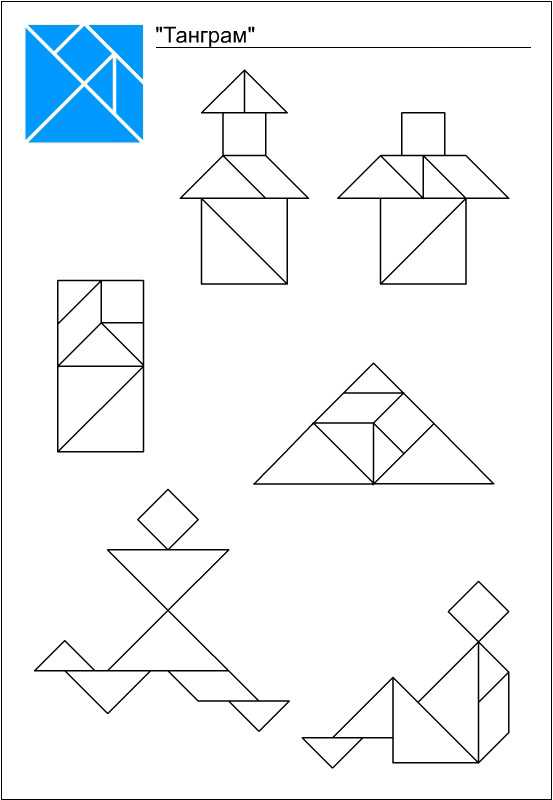

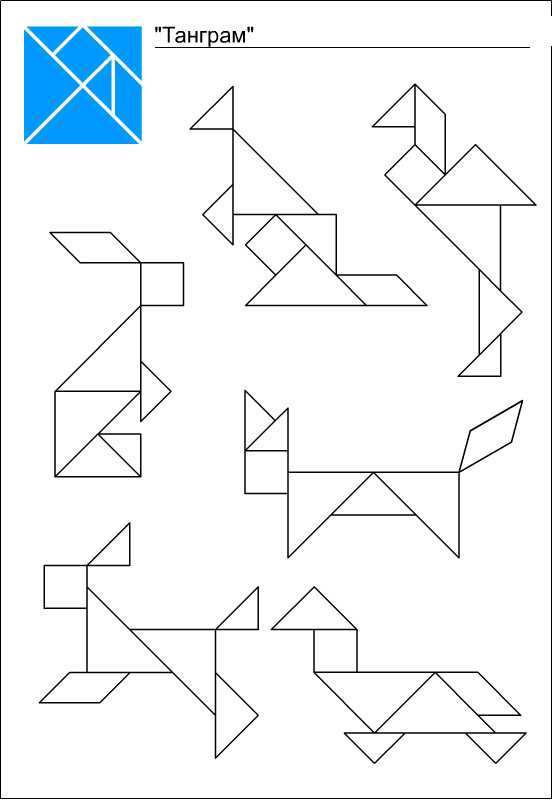
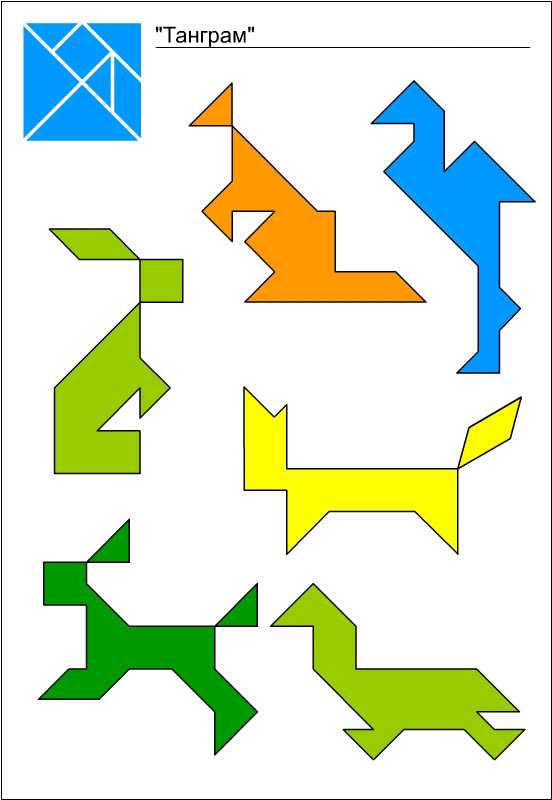
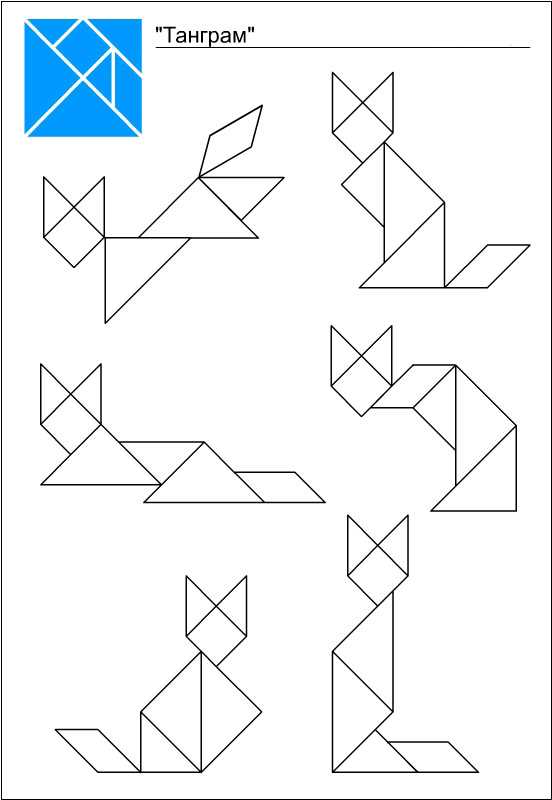
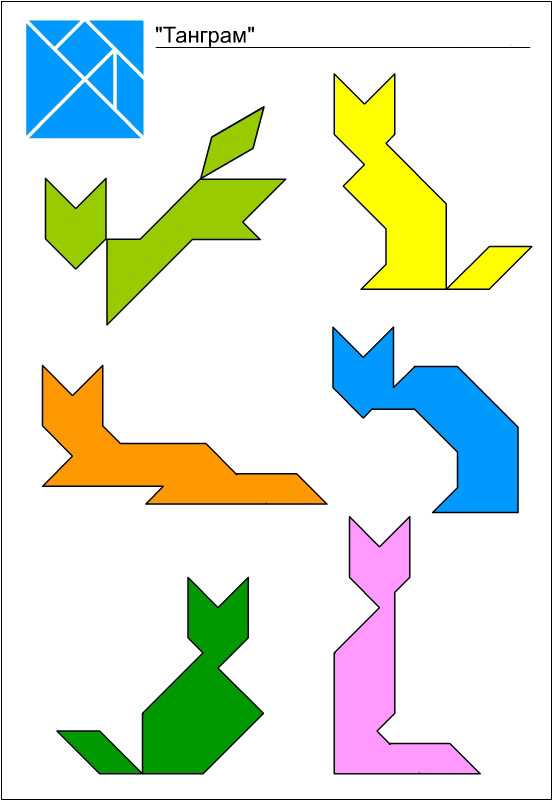
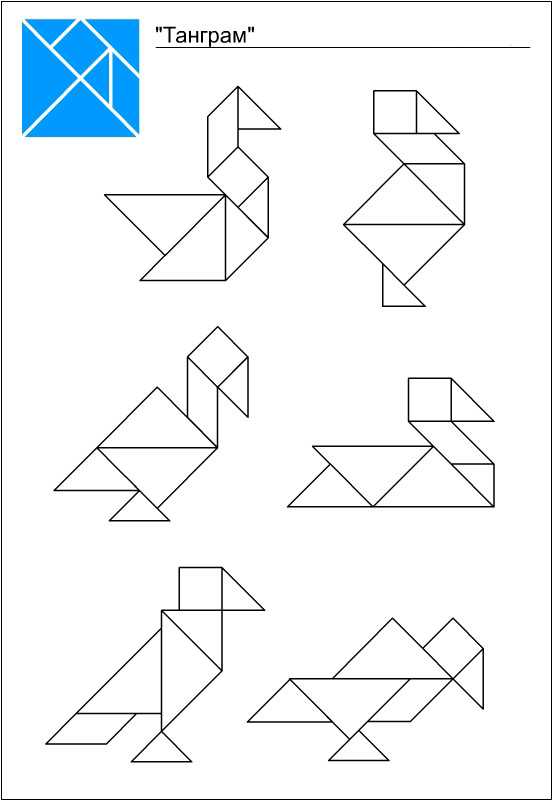
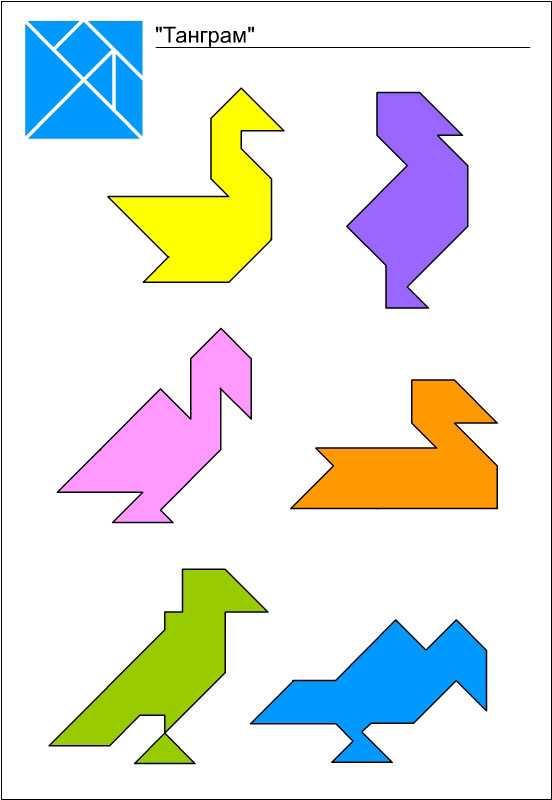




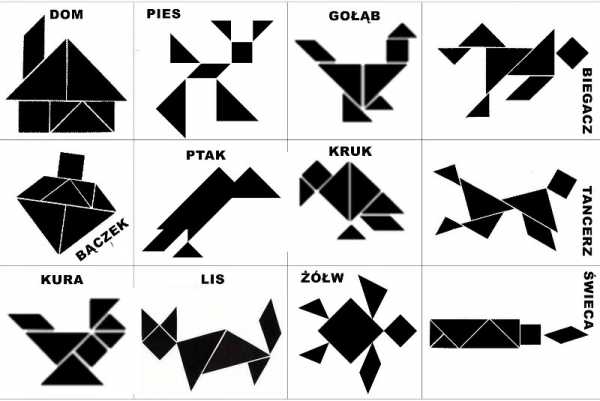



В последнее время танграм частенько используют дизайнеры. Самое удачное применение танграма, пожалуй, в качестве мебели. Есть и столы-танграмы, и трансформируемая мягкая мебель, и корпусная мебель. Вся мебель, построенная по принципу танграма, довольно удобна и функциональна. Она может видоизменятся в зависимости от настроения и желания хозяина. Сколько всевозможных вариантов и комбинаций можно составить из треугольных, квадратных и четырехугольных полок. При покупке такой мебели вместе с инструкцией покупателю выдаются несколько листов с картинками на разные темы, которые можно сложить из этих полок. В гостиной можно повесить полки в виде людей, в детской из этих же полок можно сложить котов, зайцев и птиц, а в столовой или библиотеке — рисунок может быть на строительную тему — дома, замки, храмы.
Вот такой многофункциональный танграм.
ПНШ 3 класс. Математика. Учебник № 2, с. 126
Составление и разрезание фигур
Ответы к с. 126
383. Составь из двух равных прямоугольных треугольников прямоугольник.
384. Составь из двух равных прямоугольных треугольников один равнобедренный треугольник.
385. Предложи как можно больше вариантов разрезания квадрата на две равные части.
386. Разрежь прямоугольник со сторонами 4 см и 2 см на четыре части так, чтобы из этих частей можно было составить квадрат.
Покажи на рисунке в тетради, как это можно сделать.
Будут ли данный прямоугольник и построенный квадрат являться равносоставленными фигурами?
Чему будет равна площадь составленного квадрата?
И квадрат и прямоугольник состоят из четырёх одинаковых прямоугольных треугольников, следовательно, являются равносоставленными. Так как равносоставленные фигуры состоят из одних и тех же фигур, можно заключить, что они имеют одинаковую площадь, то есть площадь квадрата будет равна площади прямоугольника: 4 см • 2 см = 8 см2.
Ответы к заданиям. Математика. Учебник. Часть 2. Чекин А.Л. 2013 г.
Математика. 3 класс. Чекин А.Л.
ПНШ 3 класс. Математика. Учебник № 2, с. 126
e-razumniki.ru
Презентация. Тема: Создать робота из предложенных фигур.4 класс
Слайд 1
Презентация к факультативному занятию по программе курса «Развитие творческого мышления». Тема: Создать робота из предложенных фигур. Презентацию выполнила учащаяся 9 «А» класса МОБУ «Сясьстройская средняя общ Презентацию выполнила учащаяся 9 «А» класса МОБУ «Сясьстройская средняя общеобразовательная школа №1» Харитонова Ксения Всеволодовна, 15 лет Презентацию выполнила учащаяся 9 «А» класса сь общеобразовательная школа №1» Харитонова Ксения Всеволодовна, 15 лееобразовател5 лет Презентацию выполнила учащаяся 4 «Б» класса МОБУ «Сясьстройская средняя общеобразовательная школа №1» Миронова Яна Юрьевна, 10 летСлайд 2
Цель: Узнать, что такое «прямоугольник» и «треугольник», какие образы можно создать из этих фигур.
Слайд 3
Задача: 1.Объяснить, что такое «треугольник» и «прямоугольник»; 2.Придумать образцы роботов, которые можно создать из этих фигур; 3.Уменьшая или увеличивая размеры этих фигур, поворачивая их под любым углом составить образ робота; 4.Оформить рисунок с помощью РС; 5.Предложить практическое применение робота.
Слайд 4
Треугольник — это геометрическая фигура, образованная тремя отрезками.
Слайд 5
Прямоугольник — это геометрическая фигура, у которой все углы прямые (равны 90 градусам).
Слайд 6
Располагая фигуры треугольников и прямоугольников под разным углом можно получить разных роботов похожих на животных.
Слайд 7
Из прямоугольников и треугольников получился «Огне — робот».
Слайд 8
Однажды на металлургическом заводе исчез огонь в плавильной печи и работа вдруг остановилась, но один человек Иван Умный изобрёл «Огне — робота». Робот помогал людям во всём.
Слайд 9
Вывод: Я узнала, что «прямоугольник» и «треугольник» – это геометрические фигуры с помощью которых можно составить и нарисовать разные образы. .
Слайд 10
В ПРЕЗЕНТАЦИИ ИСПОЛЬЗОВАНЫ МАТЕРИАЛЫ ИЗ СЛЕДУЮЩИХ ИСТОЧНИКОВ : 1.Математика.4 кл . Учеб. для ощеобразоват . организаций с приложен. на электрон. носителе. В 2ч. Ч1/ [ М.И.Моро, М.А.Бантова , Г.В.Бельтюкова и др. ] .-М.:Просвещение,2013.-(Школа России).-112с.:ил.- ISBN 978-5-09-023199-2. 2. 1.Математика.3 кл . Учеб. для ощеобразоват . организаций с приложен. на электрон. носителе. В 2ч. Ч1/ [ М.И.Моро, М.А.Бантова , Г.В.Бельтюкова и др. ] .-3-е Изд.-М.:Просвещение,2013.-(Школа России).-112с.:ил.- ISBN 978-5-09-029637-3. 3. http://www.treugolniki.ru/vidy-treugolnikov/ 4. Справочник. http://www.univer.omsk.su/omsk/Edu/Rusanova/triangls.htm
Слайд 11
Спасибо за внимание! .
nsportal.ru
ПНШ 3 класс. Математика. Учебник № 1, с. 127
Прямоугольный треугольник
Ответы к с. 127
419. Начерти прямоугольный треугольник, у которого одна сторона равна 3 см, а другая — 4 см. Измерь длину его третей стороны.
Длина третей стороны — 5 см.
420. Начерти прямоугольник со сторонами 3 см и 4 см. Проведи отрезок, который разбивает этот прямоугольник на два треугольника.
Проверь, являются ли эти треугольники прямоугольными. Измерь и запиши длины сторон каждого треугольника.
Получились два одинаковых треугольника с прямым углом и со сторонами 3 см, 4 см и 5 см.
421. Начерти два равных прямоугольных треугольника со сторонами 3 см и 4 см. Начерти прямоугольник, составленный из этих прямоугольных треугольников.
Какие ещё фигуры можно составить из 2 равных прямоугольных треугольников? Покажи это с помощью рисунка.
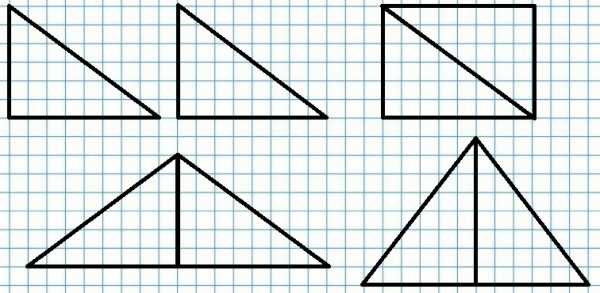
422. Начерти треугольник. Разбей его на 2 прямоугольных треугольника.
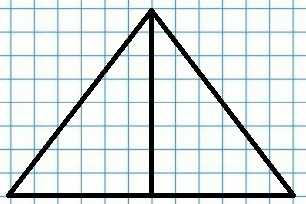
424. Начерти прямоугольный треугольник, у которого две стороны равны.
Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2013 г.
Математика. 3 класс. Чекин А.Л.
ПНШ 3 класс. Математика. Учебник № 1, с. 127
2.8 (55%) от 4 голосующихe-razumniki.ru
Как собрать прямоугольник из четырех фигур
Мало кто в детстве любил математику, зато математические головоломки в интернете всегда становятся хитами, ведь для их решения обычно не требуется углубленных знаний, зато требуются смекалка и нестандартное мышление. Предлагаем вам проверить себя на пяти главных логических задачках этого года.
Задача №1
Кумар Анкит предложил пользователям Facebook посчитать, сколько треугольников изображено на его рисунке. С простым, казалось бы, заданием подсчитать фигуры не справился практически никто из пользователей. Близки к правильному ответу оказываются многие, но большинству не хватает чуть-чуть внимательности.
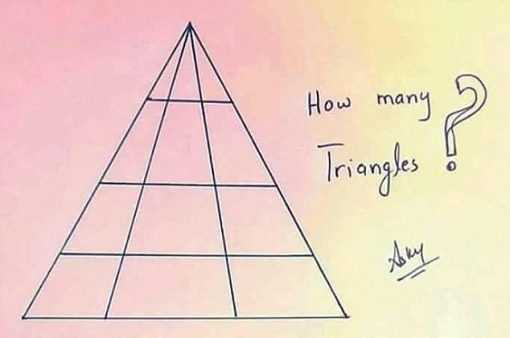
Ответ:
Внутри большого треугольника находится 24 треугольника, посчитать это несложно, но большинство пользователей не обратили внимание на еще один треугольник, скрытый в подписи автора. Таким образом, всего на картинке 25 треугольников.

Задача №2
Необычную задачку с двумя решениями предложили пользователям интернета создатели сайта gotumble.com. По их словам, одно решение головоломки более простое, его способны найти около 10% людей, а вот дойти до второго решения получается у одного человека из тысячи. Попробуйте сделать это сами.
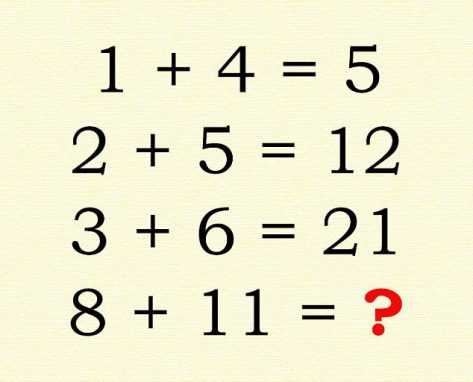
Ответ:
Первое решение состоит в том, чтобы прибавлять к каждому следующему примеру результат предыдущего. Так, прибавив 5 к сумме 2 и 5, мы получим 12. Прибавив 12 к сумме 3 и 6, получим 21. И так далее. В таком случае правильным ответом головоломки будет 40.
А вот второе решение, до которого доходит лишь один человек из тысячи, состоит в том, чтобы сложить первую цифру примера с произведением двух цифр:
1 + 1*4 = 5,
2 + 2*5 = 12, 3 + 3*6 = 21, 8 + 8*11 = 96.Задача №3
У нас есть треугольник, состоящий из четырех частей, но если перегруппировать части, то в нем появляется пустой квадрат. Как такое может быть?
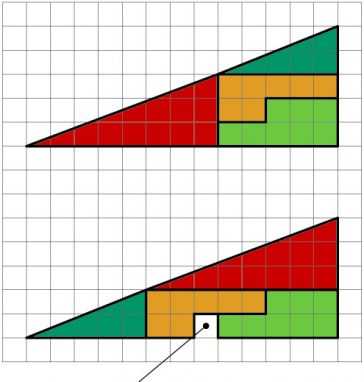
Ответ:
Это вовсе не оптический обман. Все дело в разных углах наклона гипотенузы красного и бирюзового треугольника — отсюда и разные размеры фигур.

Задача №4
Колумнист издания The Guardian Алекс Беллос предложил читателям решить задачку, которая является частью выпускного экзамена по математике в некоторых странах. По статистике ее решает всего один человек из 10.
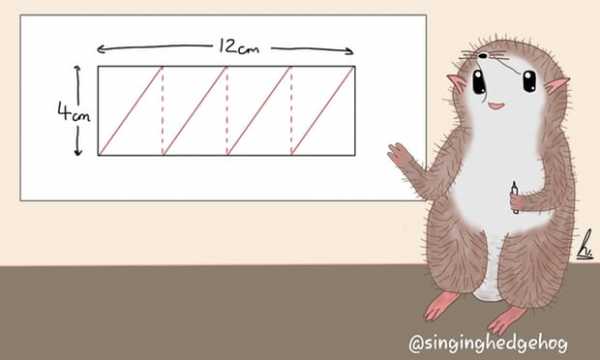
У нас есть цилиндр, вокруг которого симметрично четыре раза обмотана нить. Окружность цилиндра составляет 4 см, а его длина – 12 см. Нужно найти длину нити.
Ответ:
Задача кажется большинству школьников слишком сложной, на самом же деле надо лишь понять, что, развернув цилиндр на плоскость, мы получим обыкновенный прямоугольник со сторонами — 4 и 12 см, который можно разделить на четыре прямоугольника поменьше со сторонами — 4 и 3 см. Нить в этом случае будет гипотенузой прямоугольного треугольника и ее длину в каждой из четырех фигур можно вычислить по простой школьной формуле, она равняется 5 см. В результате общая длина нити равняется 20 сантиметрам.
Задача №5
И наконец, последняя математическая головоломка, взорвавшая соцсети. По словам автора поста, на ней изображена загадка, которую дают в качестве бонусного вопроса студентам в Сингапуре. Составители загадки предлагают изучить числовую последовательность и заполнить четыре свободных окошка недостающими числами.

Ответ:
Пользователи сети долго ломали голову над этой задачкой, но справиться с ней не смогли даже серьезные математики. А министерство образования Сингапура от этого задания открестилось, заявив, что никакого отношения к нему не имеет. Так что скорее всего головоломка была просто чьей-то злой шуткой.
www.eg.ru
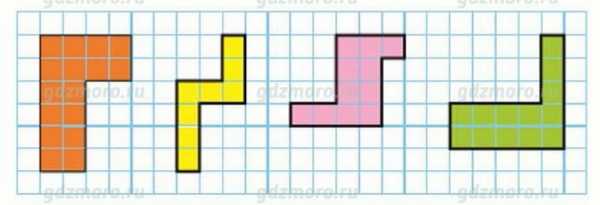
Собери прямоугольник
спасибо огромное!!!!
Marina ответил 2 года назадА можно и логическую цепочку как собрать добавить?
Qwe Asd ответил 2 года назадВсего 33 кубика во всех деталях, таким образом фигура может быть лишь 3х11
пасябкииииииии
просто очень выручили
Алгоритм решения (вариант):
1) Считаем общую площадь имеющихся 6-ти фигур — 33 (клеточки) — это значит, что получившийся прямоугольник будет иметь такую же площадь. Чтобы получить такую площадь, длины сторон прямоугольника могут быть только 3 и 11 клеточек. Положим высоту прямоугольника — 3 клеточки, длину — 11 клеточек.
2) Строим прямоугольник. Учитываем, что все фигуры имеют разную длину, но одинаковый «носик» в 1 клеточку высотой. Расположим фигуру длиной 3 клеточки (оранжевую) буквой Г. В верхнем ряду нам осталось заполнить 11-2=9 клеточек, в среднем и нижнем по 11-1=10 клеточек. Следовательно, верхний ряд нам надо сложить из фигур длиной 5 и 4 клеточек (зеленая и голубая) «носиками» вниз. У нас остаются фигуры длиной 2 (красная), 6 (розовая) и 7 (фиолетовая) клеточек. Видим, что в среднем ряду не заполнено 8 клеточек. Средний ряд можно заполнить только фигурой длиной 6 клеток (розовой), и двумя «носиками» других фигур, (если заполним фигурой 7 клеток длиной, расположив ее между «носиками» голубой и зеленой фигур, то для завершения построения прямоугольника нам потребуются фигуры без «носиков», а таких у нас нет по условию задачи). Ориентируем розовую фигуру так, чтобы «носик» был справа и смотрел вниз, а левый край длинной стороны примыкал к зеленой фигуре. Если «носик» будет слева, то мы не сможем достроить прямоугольник, т.к. получившиеся пустоты мы не сможем ничем заполнить. Нижний ряд строим из фигур 7 клеток (фиолетовой) и 2 клетки (красной) длиной, сориентировав их так, чтобы «носики» фигур вошли в имеющиеся пустоты.
shkolnaiapora.ru

Leave A Comment