Угловой коэффициент прямой — формула вычисления, калькулятор, применение в геометрии и физике
Калькулятор углового коэффициента прямой может не только рассчитать коэффициент, но и найдет точки пересечения прямой с осями абсцисс и ординат (x и y), а также покажет решение и построит график прямой.
Содержание:
- калькулятор углового коэффициента прямой
- определение углового коэффициента прямой
- формула углового коэффициента прямой
- геометрический смысл углового коэффициента
- k>0
- k
- k=0
- k не определен (k=∞)
- угловой коэффициент параллельных прямых
- угловой коэффициент перпендикулярных прямых
- примеры расчета углового коэффициента прямой по заданным координатам точек
Определение углового коэффициента прямой
Угловой коэффициент прямой — это число, которое определяет наклон прямой относительно положительного направления оси OX. Численно он равен тангенсу угла (отсчитываемого против часовой стрелки) между положительным направлением оси OX и прямой.
Численно он равен тангенсу угла (отсчитываемого против часовой стрелки) между положительным направлением оси OX и прямой.
Угловой коэффициент прямой обозначается буковой k.
Угловой коэффициент показывает, как быстро прямая меняет свое положение по оси OX при изменении координаты y и является ключевым понятием в геометрии и физике, используемым для описания многих физических явлений, например, движения тела в пространстве или распространение света.
В геометрии, угловой коэффициент прямой используется для определения угла наклона прямой относительно оси абсцисс и для вычисления ее точек пересечения с осями координат. Также угловой коэффициент прямой используется для записи уравнения прямой в общем виде. Знание углового коэффициента прямой является необходимым при решении многих задач геометрии, таких как построение перпендикуляров и параллельных линий, определение углов между прямыми и плоскостями, а также решение задач на поиск расстояний между прямыми и плоскостями.
Формула углового коэффициента прямой
Формула вычисления углового коэффициента прямой определяется как отношение изменения координаты y к изменению координаты x между любыми двумя точками на прямой. Математически это можно записать следующим образом:
{k=\dfrac{y_b — y_a}{x_b — x_a} = \tg(\alpha)}
k — угловой коэффициент прямой,
xa, ya — координаты точки A,
xb, yb — координаты точки B
α — угол между осью OX и прямой (против часовой стрелки).
Если прямая задана уравнением в общем виде y = kx + b, то угловой коэффициент прямой равен коэффициенту при x, то есть k.
Геометрический смысл углового коэффициента прямой
Рассмотрим возможные значения углового коэффициента и какой геометрический смысл он несет.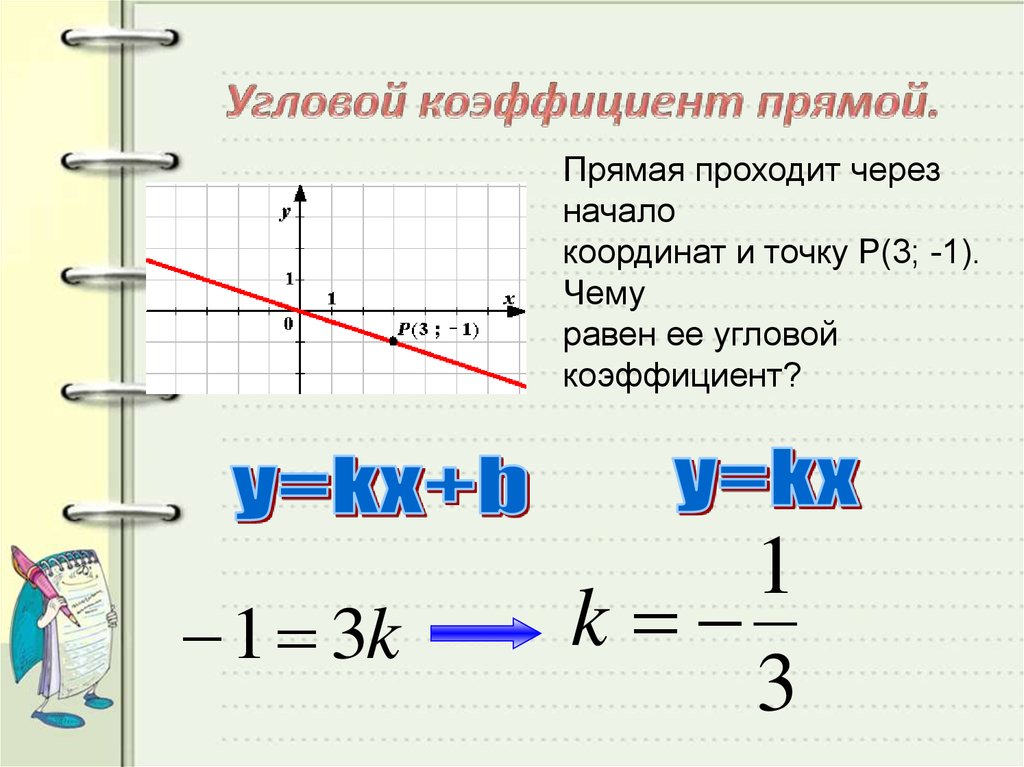
Угловой коэффициент прямой больше нуля
Если угловой коэффициент прямой больше нуля (k>0), то угол между осью OX и прямой является острым, а график прямой возрастающий. Обратное утверждение также справедливо — если график прямой возрастает, то ее угловой коэффициент больше нуля.
Угловой коэффициент прямой меньше нуля
Если угловой коэффициент прямой меньше нуля (k
Угловой коэффициент равен нулю
Если угловой коэффициент прямой равен нулю (k=0), то это значит, что прямая параллельна оси x.
Угловой коэффициент не определен (равен бесконечности)
Если угловой коэффициент прямой не определен (или можно сказать обращается в бесконечность) (k=∞), то это значит, что прямая параллельна оси y.
Угловой коэффициент параллельных прямых
Если прямые параллельны, то их угловые коэффициенты равны и наоборот — если у прямых равные угловые коэффициенты, то они параллельны друг другу.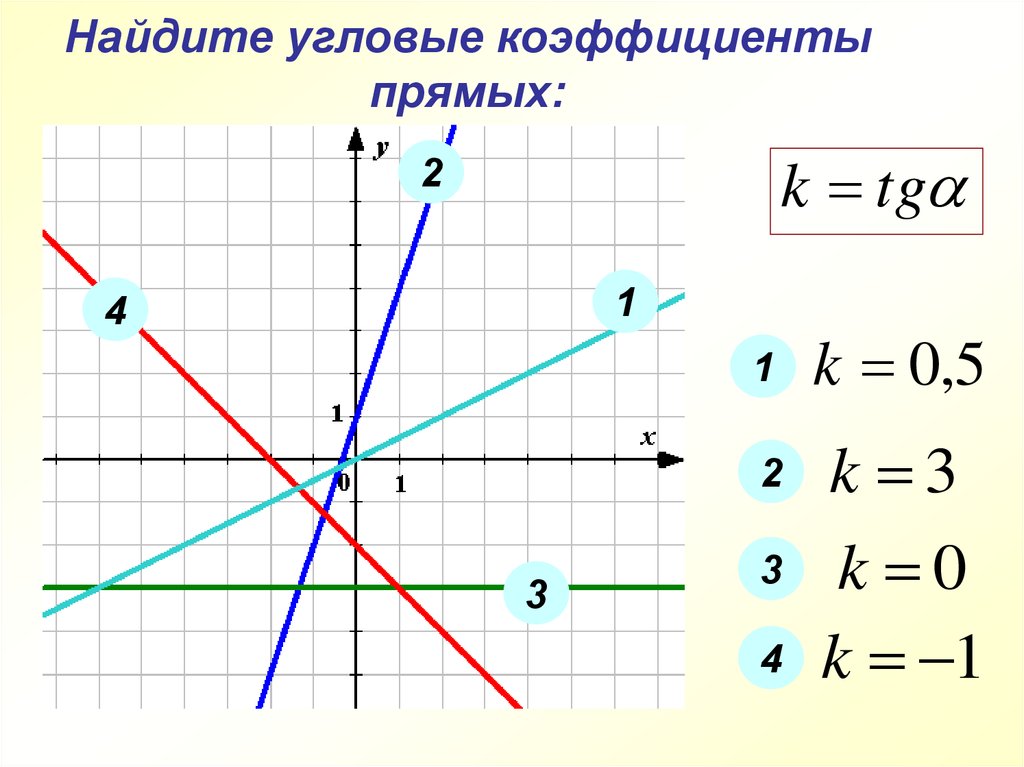
Угловой коэффициент перпендикулярных прямых
Если прямые перпендикулярны, то их угловые коэффициенты обратно пропорциональны и имеют противоположный знак.
Для примера рассмотрим две прямые, заданные угловыми коэффициентами:
y = k_{m} x + b_m
y = k_{n} x + b_n
Прямые будет перпендикулярны, если k_{m} = — \dfrac{1}{k_{n}}
Как рассчитать угловой коэффициент прямой по заданным координатам точек
Чтобы закрепить материал, рассмотрим решение задачи.
Задача 1
Найдите угловой коэффициент прямой, проходящей через точки A(5, -2) и B(-3, 1).
Решение
Воспользуемся формулой углового коэффициента прямой. Для начала найдем разницу между соответствующими координатами двух точек:
{\Delta x = x_b — x_a = -3 -5 -= -8}
{\Delta y = y_b — y_a = 1 — -(2) = 3}
Осталось применить формулу и поделить \Delta y на \Delta x:
k = \dfrac{\Delta y}{\Delta x} = \dfrac{3}{-8} = — \dfrac{3}{8} \approx -0.375
Это и есть угловой коэффициент прямой AB.
А если вы внимательно читали статью, то, учитывая, что полученный угловой коэффициент отрицательный, можно сказать, что прямая AB убывающая.
Ответ: k = — \dfrac{3}{8} \approx -0.375
Проверить ответ нам поможет калькулятор .
Калькулятор уклона
Калькулятор Использование
Наклон линии представляет собой ее вертикальное изменение, деленное на ее горизонтальное изменение, также известное как подъем относительно пробега. Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.
Наклон линии является мерой ее крутизны.
Решения для калькулятора уклона
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби. Калькулятор уклона показывает работу и дает следующие решения для уклона:
- Уклон м с двумя точками
- График линии для y = mx + b
- Форма уклона точки y — y 1 = m(x — x 1 )
- Форма пересечения уклона y = mx + b
- Стандартная форма Ax + By = C
- y-отрезок, когда x = 0
- x-пересечение, когда y = 0
Вам также будет предоставлена настраиваемая ссылка на
Калькулятор средней точки, который решит и покажет работу, чтобы найти среднюю точку и расстояние для заданных двух точек.
Как рассчитать уклон линии
Рассчитать уклон, м , используя формулу для уклона:
Формула уклона
\[ m = \dfrac {(y_{2} — y_{1})} {(x_{2} — x_{1})} \] \[ m = \dfrac{rise}{run} = \dfrac{ \Delta y}{\Delta x} = \dfrac{y_2 — y_1}{x_2 — x_1} \]
Здесь вам нужно знать координаты 2-х точек на прямой, (x 1 , y 1 ) и (x 2 , y 2 ).
Как найти наклон линии
- Найти разницу между координатами y, Δy — изменение y
- Найдите разницу между координатами x, Δx — это изменение x
- Разделите Δy на Δx, чтобы найти наклон
Δу = у 2 — у 1
Δх = х
м = Δy/Δx
Пример: Найдите уклон
Допустим, вы знаете две точки на прямой, и их координаты (2, 5) и (9, 19).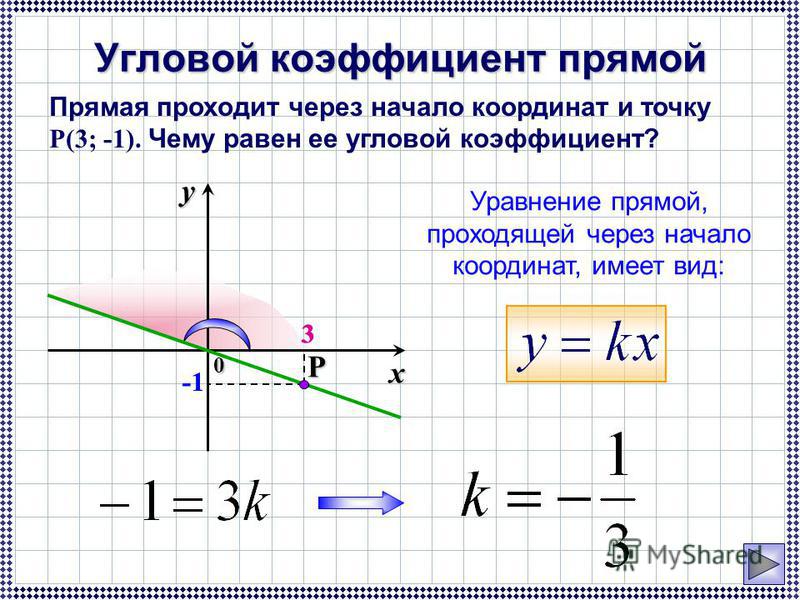 Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
- Разница между координатами y Δy равна
- Разница между координатами x Δx равна
- Разделите Δy на Δx, чтобы найти уклон м
Δу = у 2 — у 1
Δу = 19 — 5
Δy = 14
Δх = х 2 — х 1
Δx = 9 — 2
Δx = 7
\( m = \dfrac {14} {2} \)
\(m = 7 \)
Уравнения линии с наклоном
Существует 3 распространенных способа записи уравнений линии с наклоном:
- Точечный наклон форма
- Форма пересечения уклона
- Стандартная форма
Точечный уклон формы записывается как
y — y 1 = м (x — x 1 )
Используя координаты одной из точек на линии, вставьте значения в x1 и y1 точек, чтобы получить уравнение линии в форме точечного наклона.
Давайте используем точку из исходного примера выше (2, 5) и наклон, который мы вычислили как 7. Поместите эти значения в формат наклона точки, чтобы получить уравнение этой линии в форме наклона точки:
y — 5 = 7(x — 2)
Если вы упростите приведенное выше уравнение наклона точки, вы получите уравнение линии в форме пересечения наклона.
Форма пересечения уклона записывается как
y = м x + b
Возьмите уравнение формы уклона точки и умножьте его на 7 x и 7 на 2.
y — 5 = 7(x — 2) )
y — 5 = 7x — 14
Продолжайте работать над уравнением так, чтобы y было по одну сторону от знака равенства, а все остальное по другую сторону.
Добавьте 5 к обеим частям уравнения, чтобы получить уравнение в форме точки пересечения:
y = 7x — 9
Стандартная форма уравнения для линии записывается как
Ax + By = C
Вы также можете увидеть стандартную форму, записанную как Ax + By + C = 0 в некоторых ссылках.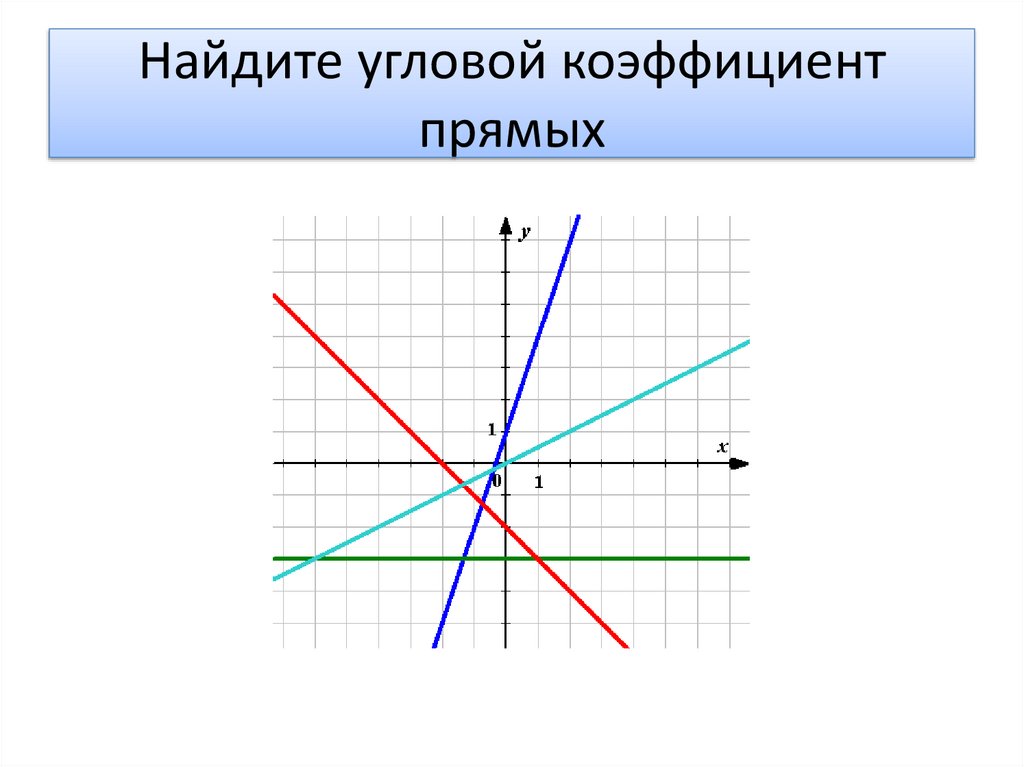
Используйте либо формулу формы точки наклона, либо формулу пересечения наклона и выполните математические вычисления, чтобы преобразовать уравнение в стандартную форму. Обратите внимание, что уравнение не должно включать дроби или десятичные знаки, а коэффициент x должен быть только положительным.
Форма пересечения наклона: y = 7x — 9
Вычтите y из обеих частей уравнения, чтобы получить 7x — y — 9 = 0
Добавьте 9 к обеим частям уравнения, чтобы получить 7x — y = 9
Наклон форма перехвата y = 7x — 9 становится 7x — y = 9, записанной в стандартной форме.
Найти наклон по уравнению
Если у вас есть уравнение для прямой, вы можете представить его в форме пересечения наклона. Коэффициент x будет наклоном.
Пример
У вас есть уравнение прямой, 6x — 2y = 12, и вам нужно найти наклон.
Ваша цель — преобразовать уравнение в формат пересечения наклона y = mx + b
- Начните с уравнения 6x — 2y = 12
- Добавьте 2y к обеим сторонам, чтобы получить 6x = 12 + 2y
- Вычтите 12 из обеих частей уравнения, чтобы получить 6x — 12 = 2y
- Вы хотите получить y в одной части уравнения, поэтому вам нужно разделить обе части на 2, чтобы получить y = 3x — 6
- Это форма пересечения наклона, y = 3x — 6.
 Наклон — это коэффициент x, поэтому в этом случае наклон = 3
Наклон — это коэффициент x, поэтому в этом случае наклон = 3
Как найти точку пересечения с осью y
Точка пересечения с осью y представляет собой значение y, когда x=0. Это точка пересечения прямой с осью Y.
Используя уравнение y = 3x — 6, установите x=0, чтобы найти точку пересечения с осью y.
y = 3(0) — 6
y = -6
Точка пересечения с осью y равна -6
Как найти точку пересечения с осью x =0. Это точка пересечения прямой с осью x.
Используя уравнение y = 3x — 6, установите y=0, чтобы найти точку пересечения по оси x.
0 = 3x — 6
3x = 6
x = 2
Х-отрезок равен 2
Наклон параллельных прямых
одинаковый наклон, и эти линии никогда не пересекутся.
Наклон перпендикулярных линий
Если известен наклон линии, любая линия, перпендикулярная к ней, будет иметь наклон, равный отрицательной обратной величине известного наклона.
Перпендикуляр означает, что линии образуют угол 90° при пересечении.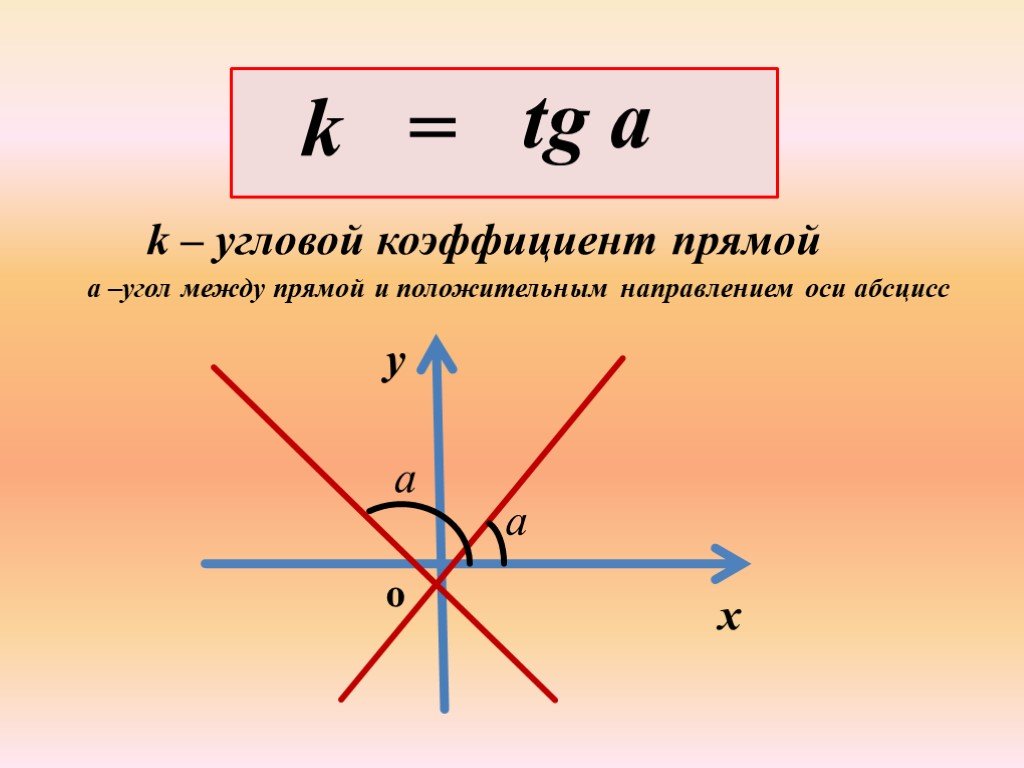
Допустим, у вас есть линия с наклоном -4. Каков наклон прямой, перпендикулярной к ней?
- Сначала возьмите отрицательный наклон вашей линии
-(-4) = 4 - Во-вторых, возьмите обратное число. 4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4.
- Линия, перпендикулярная исходной линии, имеет наклон 1/4.
Дальнейшее исследование
Брайан Маклоган (2014) Определение наклона между двумя точками в виде дробей, 10 июня. На https://www.youtube.com/watch?v=Hz_eapwVcrM
Калькулятор уклона
Создано Матеушем Мухой и Юлией Жулавинской
Отзыв от Богны Шик и Джека Боуотера
Последнее обновление: 21 декабря 2022 г.
Содержание:- Как найти уклон
- Формула уклона
- Другие связанные темы
- Часто задаваемые вопросы
Калькулятор уклона определяет уклон или градиент между двумя точками в декартовой системе координат. Наклон — это в основном величина наклона линии, которая может иметь положительное, отрицательное, нулевое или неопределенное значение. Прежде чем пользоваться калькулятором, наверное, стоит научиться находить уклон по формуле уклона. Чтобы найти уравнение прямой для любых двух точек, через которые проходит эта линия, используйте наш калькулятор формы пересечения наклона.
Наклон — это в основном величина наклона линии, которая может иметь положительное, отрицательное, нулевое или неопределенное значение. Прежде чем пользоваться калькулятором, наверное, стоит научиться находить уклон по формуле уклона. Чтобы найти уравнение прямой для любых двух точек, через которые проходит эта линия, используйте наш калькулятор формы пересечения наклона.
Как найти уклон
- Определите координаты (x1,y1)(x_1, y_1)(x1,y1) и (x2,y2)(x_2, y_2)(x2,y2). Мы будем использовать формулу для расчета наклона линии, проходящей через точки (3,8)(3, 8)(3,8) и (−2,10)(-2, 10)(−2,10) .
- Введите значения в формулу. Это дает нам (10-8)/(-2-3)(10-8)/(-2-3)(10-8)/(-2-3).
- Вычтите значения в скобках, чтобы получить 2/(-5)2/(-5)2/(-5).
- Упростите дробь, чтобы получить наклон −2/5–2/5–2/5.
- Проверьте результат с помощью калькулятора уклона.
Чтобы найти наклон линии, нам нужны две координаты на линии. Достаточно любых двух координат.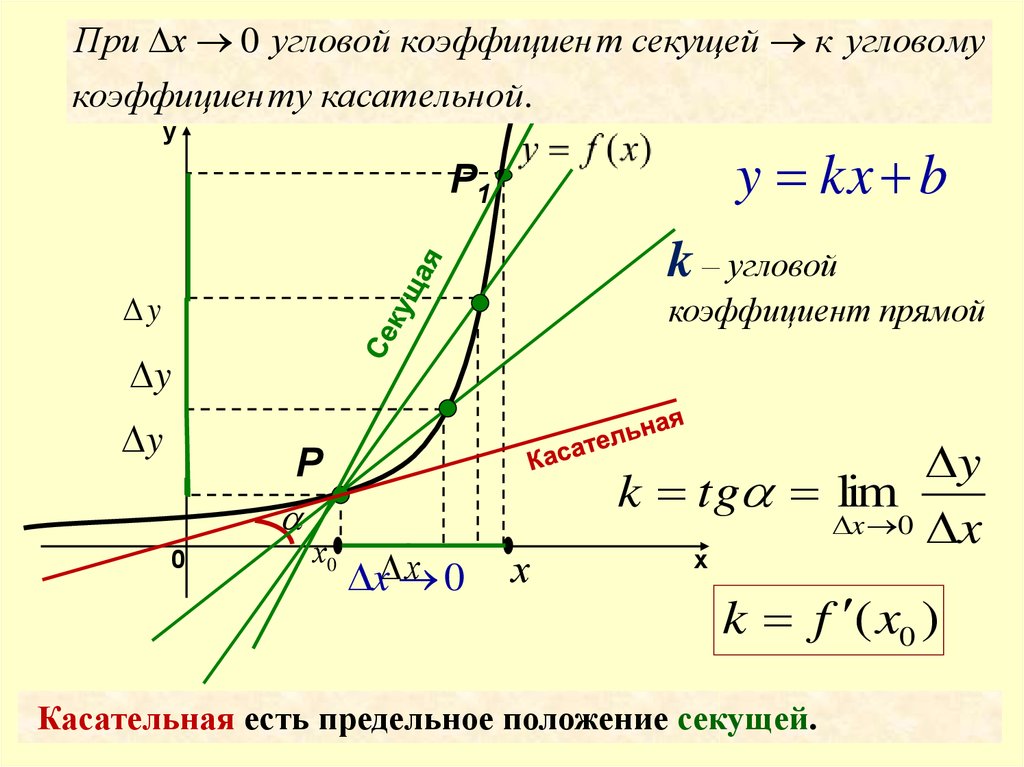 Мы в основном измеряем величину изменения координаты y, часто известную как подъем , деленную на изменение координаты x, известную как run . Вычисления по нахождению наклона просты и включают в себя не что иное, как базовое вычитание и деление.
Мы в основном измеряем величину изменения координаты y, часто известную как подъем , деленную на изменение координаты x, известную как run . Вычисления по нахождению наклона просты и включают в себя не что иное, как базовое вычитание и деление.
🙋 Чтобы найти градиент нелинейных функций, вы можете использовать калькулятор средней скорости изменения.
Формула наклона
наклон=y2−y1x2−x1\mathrm{slope} = \frac{y_2 — y_1}{x_2 — x_1}slope=x2−x1y2−y1
Обратите внимание, что наклон линии легко вычисляется вручную с использованием небольших целых чисел координат. Формула становится все более полезной по мере того, как координаты принимают большие значения или десятичные значения.
Стоит отметить, что любая горизонтальная линия имеет нулевой градиент, потому что горизонтальная линия имеет те же координаты y. Это приведет к нулю в числителе формулы наклона. С другой стороны, вертикальная линия будет иметь неопределенный наклон, поскольку координаты x всегда будут одинаковыми. Это приведет к ошибке деления на ноль при использовании формулы.
Это приведет к ошибке деления на ноль при использовании формулы.
Точно так же, как наклон можно вычислить, используя конечные точки сегмента, можно вычислить и среднюю точку. Середина — важное понятие в геометрии, особенно при вписании многоугольника внутрь другого многоугольника, когда его вершины касаются середины сторон большего многоугольника. Это можно получить с помощью калькулятора средней точки или просто взяв среднее значение каждой координаты x и среднее значение координаты y, чтобы сформировать новую координату.
Наклон линий важен для определения того, является ли треугольник прямоугольным. Если любые две стороны треугольника имеют наклоны, которые умножаются на -1, то треугольник является прямоугольным. Вычисления для этого можно выполнить вручную или с помощью калькулятора прямоугольного треугольника. Вы также можете использовать калькулятор расстояний, чтобы вычислить, какая сторона треугольника является самой длинной, что поможет определить, какие стороны должны образовывать прямой угол, если треугольник прямоугольный.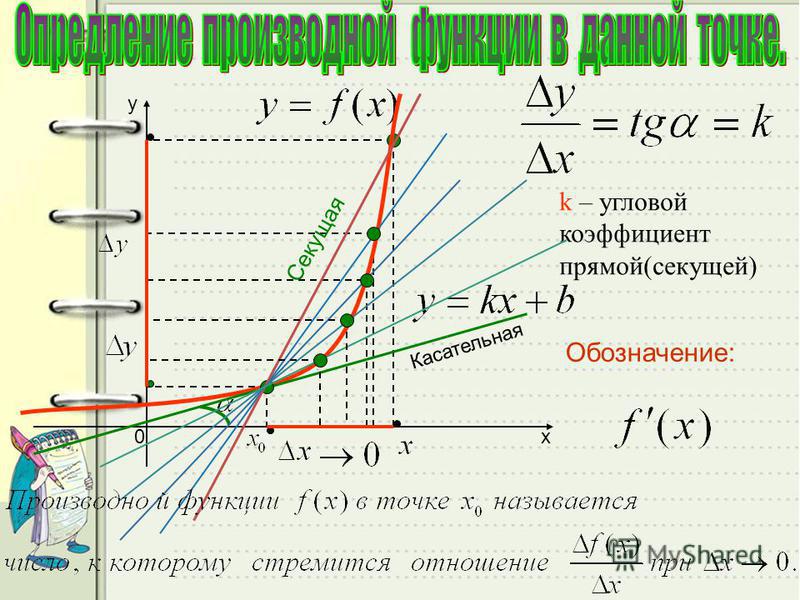
Знак перед градиентом, предоставленным калькулятором наклона, указывает, является ли линия возрастающей, убывающей, постоянной или неопределенной. Если график линии перемещается из нижнего левого угла в верхний правый, он увеличивается и, следовательно, является положительным. Если он уменьшается при движении из левого верхнего угла в правый нижний, то градиент отрицательный.
Часто задаваемые вопросы
Как найти наклон по уравнению?
Метод для нахождения наклона из уравнения зависит от формы уравнения перед вами. Если форма уравнения y = mx + c, то наклон (или градиент) просто m . Если уравнение не в этой форме, попробуйте изменить уравнение. Чтобы найти градиент других полиномов, вам нужно будет продифференцировать функцию по x .
Как рассчитать уклон холма?
- Используйте карту, чтобы определить расстояние между вершиной и основанием холма по прямой.
- Использование той же карты или GPS, найти высоту между вершиной и подошвой холма .
 Убедитесь, что точки, от которых вы измеряете, такие же, как и в шаге 1.
Убедитесь, что точки, от которых вы измеряете, такие же, как и в шаге 1. - Преобразуйте оба измерения в одни и те же единицы.
- Разделите разницу высот на расстояние между двумя точками.
- Это число представляет собой уклон холма, если он увеличивается линейно. Если это не так, повторите шаги, но там, где есть заметное изменение наклона.
Как рассчитать длину склона?
- Измерьте разницу между верхней и нижней частью уклона относительно осей x и y.
- Если вы можете измерить только изменение по оси x, умножьте это значение на градиент, чтобы найти изменение по оси y.
- Убедитесь, что единицы измерения для обоих значений одинаковы.
- Используйте теорему Пифагора, чтобы найти длину склона . Возведите в квадрат как изменение x, так и изменение y.
- Сложите два значения вместе.
- Найдите квадратный корень из суммы.
- Это новое значение представляет собой длину склона.

Что такое уклон 1 из 20?
Уклон 1/20 — это уклон, который увеличивается на 1 единицу за каждые 20 единиц, пройденных по горизонтали . Так, например, пандус длиной 200 футов и высотой 10 футов будет иметь уклон 1/20. Наклон 1/20 эквивалентен градиенту 1/20 (как ни странно) и образует угол 2,86° между собой и осью x.
Как найти наклон кривой?
Поскольку наклон кривой меняется в каждой точке, вы можете найти наклон кривой, продифференцировав уравнение по x и в полученном уравнении подставив x вместо точки, в которой вы хотите найти градиент.
Скорость изменения равна наклону?
Скорость изменения графика также является его наклоном , который также совпадает с градиентом. Скорость изменения можно найти, разделив изменение в направлении y (по вертикали) на изменение в направлении по оси x (горизонтально), если, конечно, оба числа выражены в одних и тех же единицах.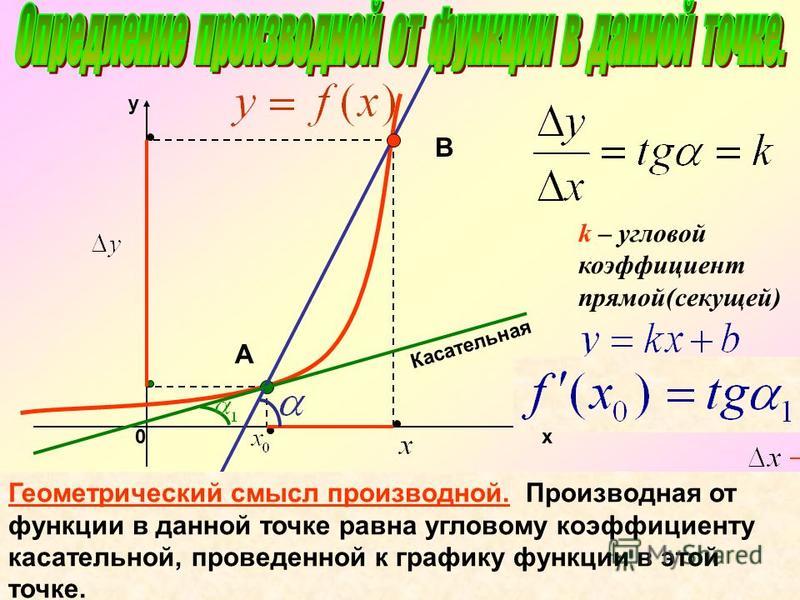 Скорость изменения особенно полезна, если вы хотите предсказать будущее предыдущего значения чего-либо , так как при изменении переменной x будет присутствовать соответствующее значение y (и наоборот).
Скорость изменения особенно полезна, если вы хотите предсказать будущее предыдущего значения чего-либо , так как при изменении переменной x будет присутствовать соответствующее значение y (и наоборот).
Где вы используете уклон в повседневной жизни?
Уклоны (или уклоны) имеют множество применений в повседневной жизни . Есть несколько очевидных физических примеров — у каждого холма есть склон, и чем круче холм, тем больше его уклон . Это может быть полезно, если вы смотрите на карту и хотите найти лучший холм для спуска на велосипеде. Вы тоже, наверное, спите под скатом, крыша то есть . Наклон крыши будет меняться в зависимости от стиля и места вашего проживания. Но, что более важно, если вы когда-нибудь захотите узнать, как что-то меняется со временем, вы в конечном итоге построите график с наклоном .
Что такое уклон 10%?
Уклон 10 % — это уклон, который увеличивается на 1 единицу за каждые 10 единиц, пройденных по горизонтали (10 %).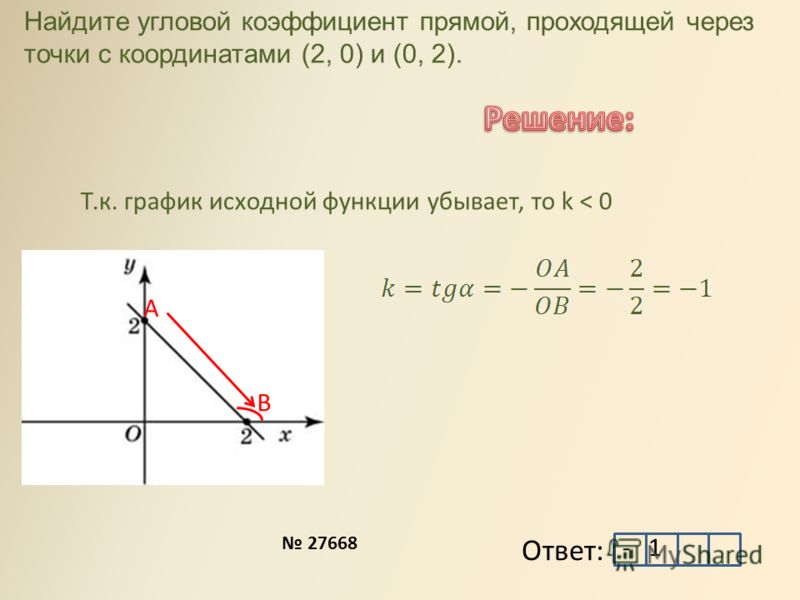 Например, крыша с уклоном 10% и шириной 20 м будет иметь высоту 2 м. Это то же самое, что и градиент 1/10 , и между линией и осью x образуется угол 5,71°.
Например, крыша с уклоном 10% и шириной 20 м будет иметь высоту 2 м. Это то же самое, что и градиент 1/10 , и между линией и осью x образуется угол 5,71°.
Как найти площадь под уклоном?
Чтобы найти площадь под уклоном, необходимо проинтегрировать уравнение и вычесть нижнюю границу площади из верхней границы. Для линейных уравнений:
- Запишите уравнение в виде
y = mx + c. - Напишите новую строку, в которой вы добавляете 1 к порядку x (например, x становится x 2 , х 2,5 становится х 3,5 ).
- Разделите m на новый номер заказа и поставьте его перед новым x.
- Умножьте c на x и добавьте это в новую строку.
- Решите эту новую строку дважды, где x — верхняя граница области, которую вы хотите найти, и где x — нижняя граница.
- Вычтите нижнюю границу из верхней.
- Поздравьте себя с достижением.
Какой градус наклона 5 к 1?
Наклон 5 к 1 — это уклон, который при каждом увеличении на 5 единиц по горизонтали увеличивается на 1 единицу .

 Наклон — это коэффициент x, поэтому в этом случае наклон = 3
Наклон — это коэффициент x, поэтому в этом случае наклон = 3 Убедитесь, что точки, от которых вы измеряете, такие же, как и в шаге 1.
Убедитесь, что точки, от которых вы измеряете, такие же, как и в шаге 1.
Leave A Comment