Решение неравенств второй степени с одной переменной. Метод интервалов 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 6.
Решение неравенств второй степени с одной переменной. Метод интервалов.
Неравенства вида
ax2 + bx + c > 0 и ax2 + bx + c
где x – переменная, a, b и c – некоторые числа и a ≠ 0, называют неравенствами второй степени с одной переменной.
Решение неравенства ax2 + bx + c > 0 или ax2 + bx + c y = ax2 + bx + c принимает положительные или отрицательные значения. Для этого достаточно проанализировать, как расположен график функции y = ax2 + bx + c в координатной плоскости: куда направлены ветви параболы – вверх или вниз, пересекает ли парабола ось 
Пример:
Решить неравенство: x2 + 2x — 48
Введем функцию y = x2 + 2x — 48.
Графиком этой функции является парабола, ветви которой направлены вверх, так как a = 1.
Выясним, как расположен график этой функции относительно оси x. Для этого решим квадратное уравнение x2 + 2x — 48 = 0.
Это уравнение имеет два корня:
x1 = -8 и x2 = 6.
Значит, парабола y
Ответ: x∈-8;6
Решим неравенство:
—x2 + 2x + 15
График функции y = —x2 + 2x + 15 – это парабола, ветви которой направлены вниз, так как a
Выясним, как расположен график функции y = —x2 + 2x + 15 в координатной плоскости, пересекает ли он ось x и в каких точках.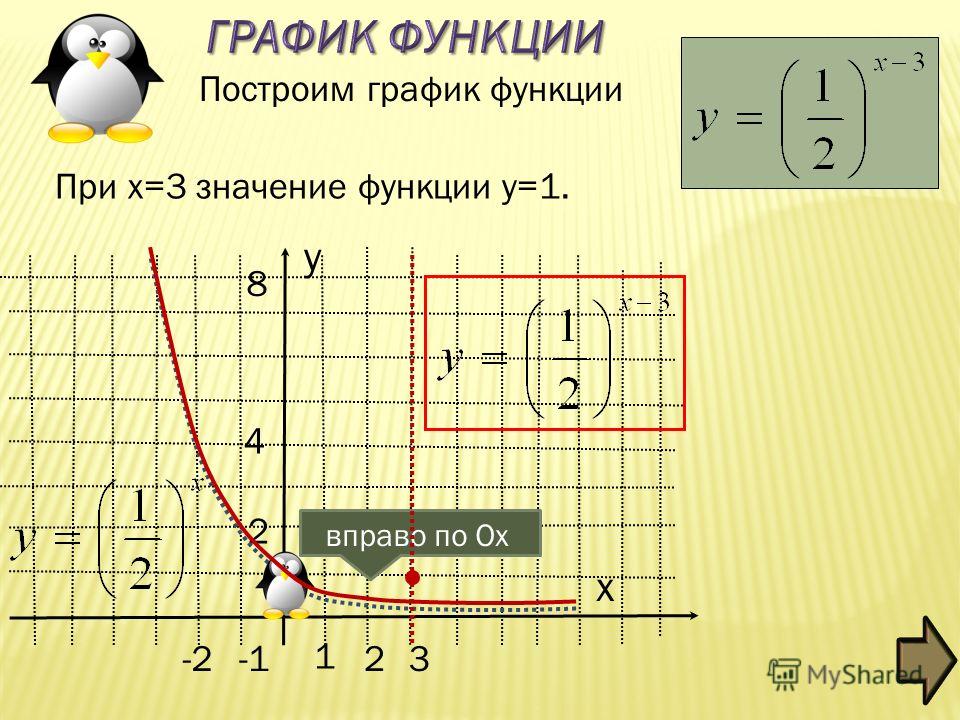
Для этого решим уравнение:
—x2 + 2x + 15 = 0
x1=-3; x2=5
Схематично изобразим эту параболу
Функция принимает отрицательные значения при x принадлежит -∞;-3 или 5;+∞.
Ответ: x∈-∞;-3∪5;+∞
Решим неравенство:
2x2 — 3x + 8 > 0
Графиком функции y = 2x2 — 3x + 8 является парабола, ветви которой направлены вверх, так как a > 0. Выясним, как располагается эта парабола относительно оси
2x2 — 3x + 8 = 0
D = 9 — 4 ∙ 2 ∙ 8 = -55
Данное уравнение не имеет корней, значит, парабола не пересекает ось x. Схематично покажем, как располагается эта парабола относительно оси x.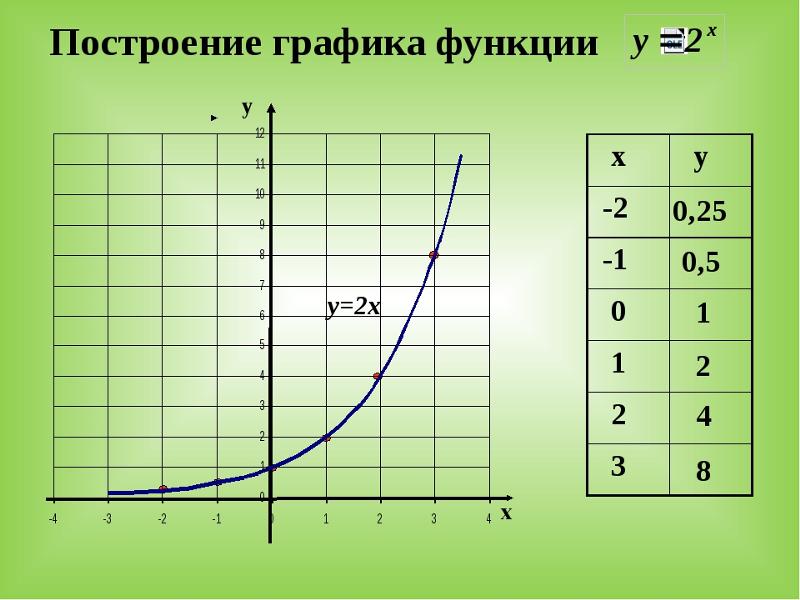
Из рисунка видно, что данная функция принимает положительные значения при любом значении x.
Ответ: -∞;+∞
Итак, для решения неравенств вида
ax2 + bx + c > 0 и ax2 + bx + c
- Выяснить имеет ли квадратный трехчлена ax2 + bx + c имеет ли трехчлен корни;
- Если трехчлен имеет корни, то отмечают их на оси x и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх, если a > 0 или вниз, если a a > 0 или в нижней полуплоскости при a
-
На оси x найти промежутки, для которых точки параболы расположены выше оси x (если решают неравенство ax2 + bx
Рассмотрим функцию
fx=x+1x-2x+3
Областью определения этой функции является множество всех чисел.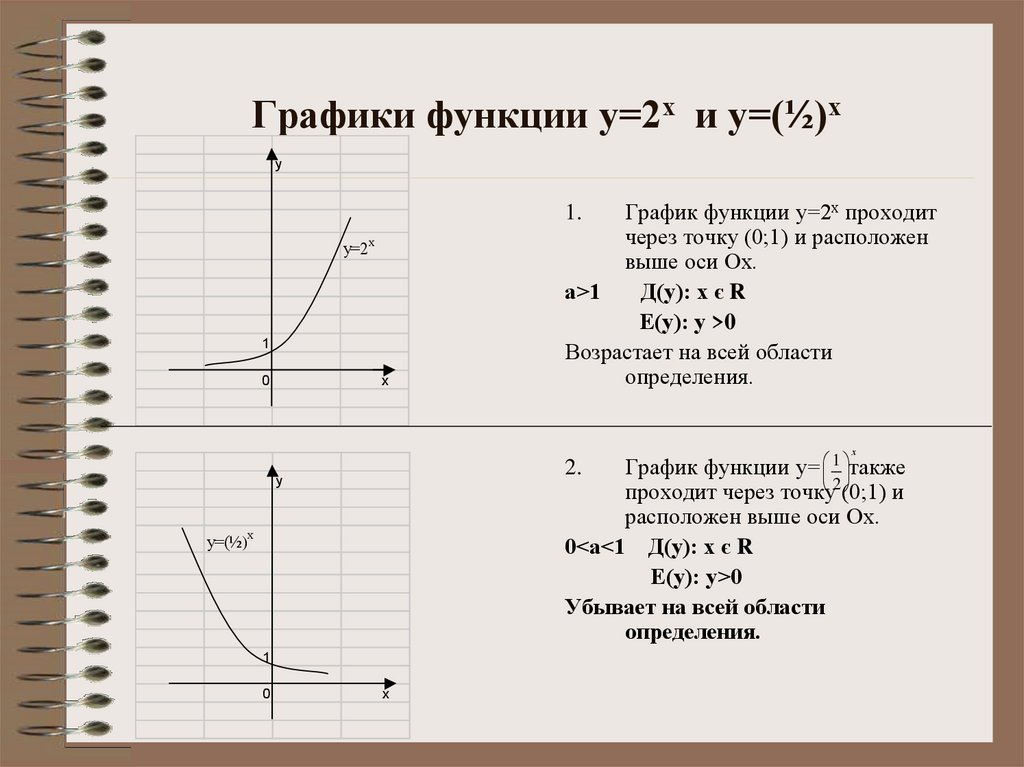 Точки -3, -1 и 2 нули функции, которые разбивают область определения на промежутки -∞;-3,-3;-1,-1;2,2;+∞. Выясним знак функции в каждом из указанных промежутков.
Точки -3, -1 и 2 нули функции, которые разбивают область определения на промежутки -∞;-3,-3;-1,-1;2,2;+∞. Выясним знак функции в каждом из указанных промежутков.
Выражение (x + 1)(x — 2)(x + 3) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице.
|
-∞;-3 |
-3;-1 |
-1;2 |
2;+∞ |
|
|
x + 3 |
— |
+ |
+ |
+ |
|
x + 1 |
— |
— |
+ |
+ |
|
x — 2 |
— |
— |
— |
+ |
Отсюда ясно, что:
Если x∈-∞;-3, то fx<0;
Если x∈-3;-1, то fx>0;
Если x∈-1;2, то fx<0;
Если x∈2;+∞, то fx>0;
Видно, что в каждом из промежутков
-∞;-3,-3;-1,-1;2,2;+∞ функция сохраняет знак, а при переходе через точки -3, -1 и 2 ее знак изменяется.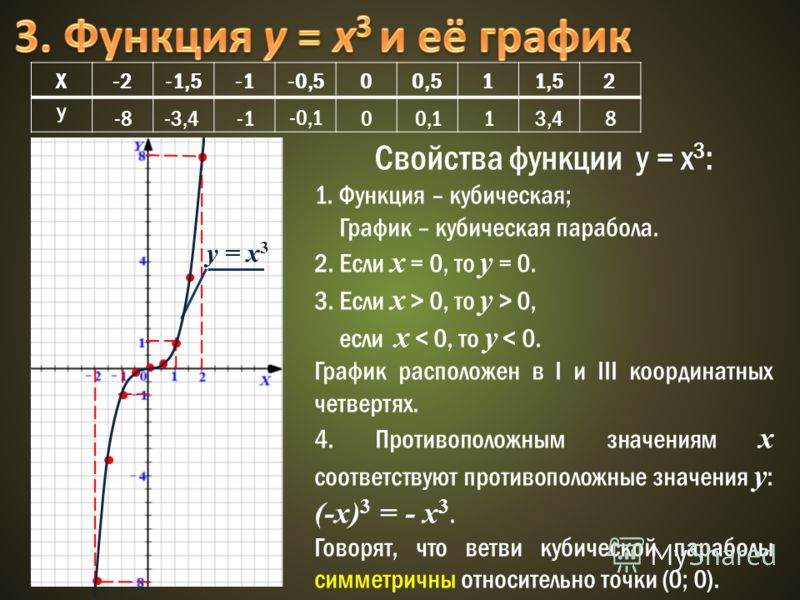
Вообще пусть функция задана формулой
fx=x-x1x-x2…x-xn, где x – переменная, а x1, x2, …, xn не равные друг другу числа. Числа x1, x2, …, xn являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через ноль знак изменяется.
Это свойство используется для решений неравенств вида:
x-x1x-x2…x-xn>0,
x-x1x-x2…x-xn<0.
x-5x+3x+7>0
Введем функцию fx=x-5x+3x+7
Найдем нули функции: -7, -3 и 5
Определим знак функции в каждом из этих промежутков. В крайнем правом промежутке функция положительна, а далее знаки чередуются.
Ответ: -7;-3∪5;+∞
Итак, чтобы решить неравенство методом интервалов, надо:
- Ввести функцию;
- Найти нули этой функции;
- Нанести нули функции на числовую прямую;
- Определить знак в каждом промежутке;
-
Посмотреть знак и выделить нужный интервал.

§ Построить график функции онлайн
←Вернуться в «Калькуляторы онлайн»
| y = | |||
| y = | |||
Здесь будет анализ функции… |
Инструкции
- Чтобы построить график функции онлайн:
- укажите функцию в поле выше в виде «y = x2 — 3»;
- нажмите кнопку «Построить график функции»;
- ожидайте результат анализа функции (точки пересечения с осями координат) и график функции под полем задания функции.
При необходимости вы можете построить одновременно графики двух функций онлайн. Для этого нажмите кнопку
«Добавить функцию».
Для этого нажмите кнопку
«Добавить функцию».
В случае построения двух графиков функции будут показаны их точки пересечения.
Таблица обозначений для задания функций
| Математическая операция | Символ | Пример использования |
|---|---|---|
| Десятичная дробь | Можно и через точку, и через запятую. | «2,789» или «2.879» |
| Сложение | «+» | x + 1 |
| Вычитание | «-» | x — 2.5 |
| Умножение | «*»(shift + 8) | 2 * x Коэффициент при «x» можно записывать без знака умножения. |
| Корень | Кнопка | 2 √(x — 2) — квадратный корень 3 √(2x — 1) — кубический корень |
| Синус | Кнопка | sin(x + 1) |
| Косинус | Кнопка | cos(x) |
| Тангенс | Кнопка | tg(2.5 — x) |
| Число π (пи) | Кнопка | sin(x + π) + 2 |
| Логарифм | Кнопка | log2(2x — 1,4) |
| Натуральный логарифм | Кнопка | ln(x) — 2 |
| Десятичный логарифм | Кнопка | lg(2. 3 — x) 3 — x) |
| Основание натурального логарифма (число Эйлера) | Кнопка | ex |
Важно!
Научиться строить график функции самостоятельно можно в уроке «Функция в математике».
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
20 апреля 2023 в 6:08
Илья Костромин
Профиль
Благодарили: 0
Сообщений: 1
y =
y= x +7
0 СпасибоОтветить
3-8
Домен и диапазон экспоненциальных и логарифмических функций
Напомним, что
домен
функции представляет собой набор входных или
Икс
-значения, для которых определена функция, а
диапазон
это набор всех выходных или
у
-значения, которые принимает функция.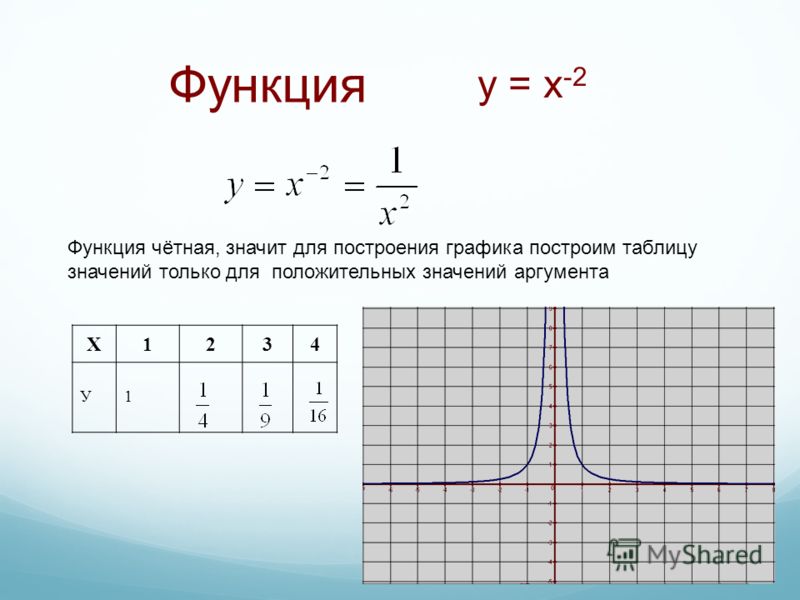
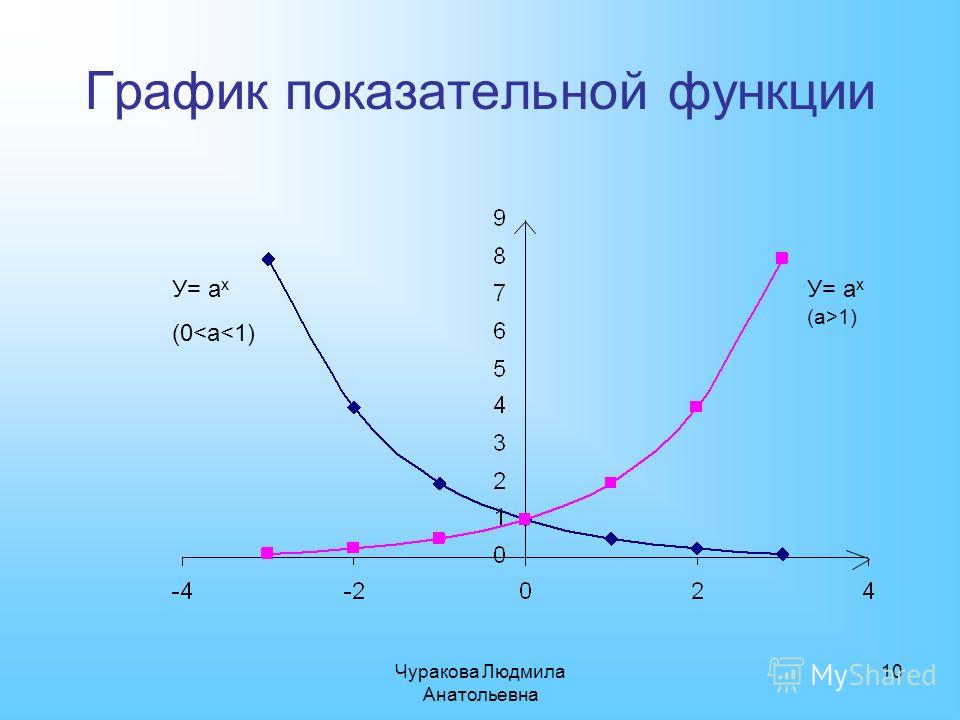
Простая экспоненциальная функция, например ф ( Икс ) «=» 2 Икс имеет своей областью всю реальную линию. Но его диапазон только положительный вещественные числа, у > 0 : ф ( Икс ) никогда не принимает отрицательное значение. Кроме того, он никогда не достигает 0 , хотя асимптотически приближается к Икс идет к − ∞ .
Если мы заменим Икс с − Икс чтобы получить уравнение г ( Икс ) «=» 2 − Икс , график отражается вокруг у -axis, но домен и диапазон не меняются:
Если мы поставим перед собой знак минус, чтобы получить уравнение
час
(
Икс
)
«=»
−
2
Икс
, график отражается вокруг
Икс
-ось. У нас все еще есть целая действительная линия в качестве нашего домена, но диапазон теперь состоит из отрицательных чисел,
у <
0
.
У нас все еще есть целая действительная линия в качестве нашего домена, но диапазон теперь состоит из отрицательных чисел,
у <
0
.
Теперь рассмотрим функцию ф ( Икс ) «=» ( − 2 ) Икс . Когда Икс «=» 1 2 , у должно быть комплексным числом, так что все усложняется. Для этого урока нам потребуется, чтобы наши базисы были положительными на данный момент, чтобы мы могли оставаться в реальном мире.
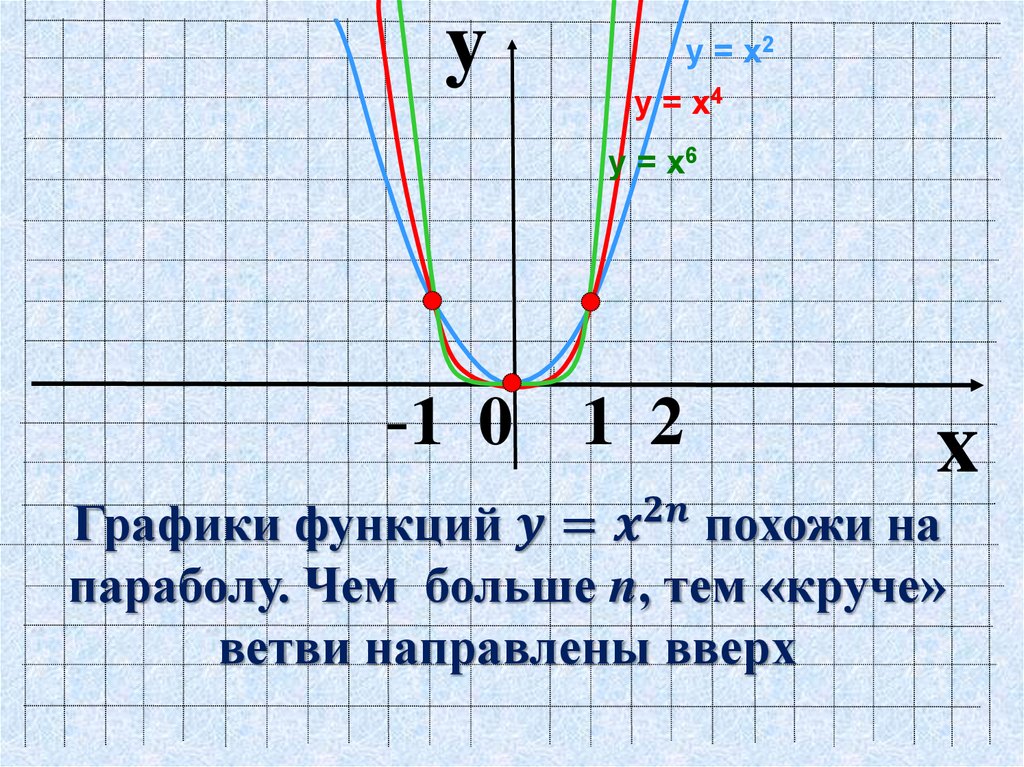
В общем случае график основной экспоненциальной функции
у
«=»
а
Икс
капли от
∞
к
0
когда
0 <
а
<
1
как
Икс
варьируется от
−
∞
к
∞
и поднимается из
0
к
∞
когда
а
> 1
.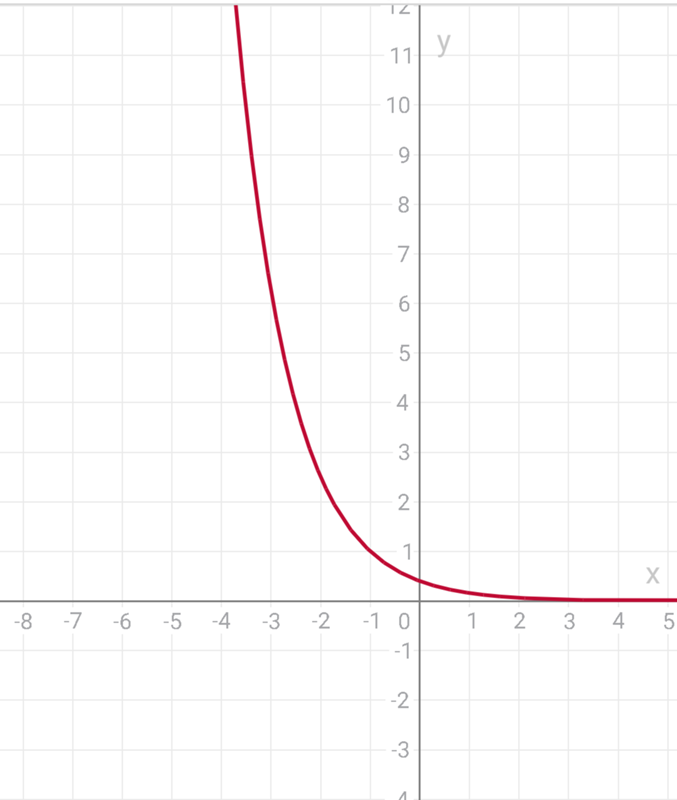
Экспоненциальная функция у «=» а Икс , можно сдвинуть к единицы по вертикали и час единицы по горизонтали с уравнением у «=» а ( Икс + час ) + к . Тогда область определения функции остается неизменной, а диапазон становится { у е ℝ | у > час } .
Пример 1:
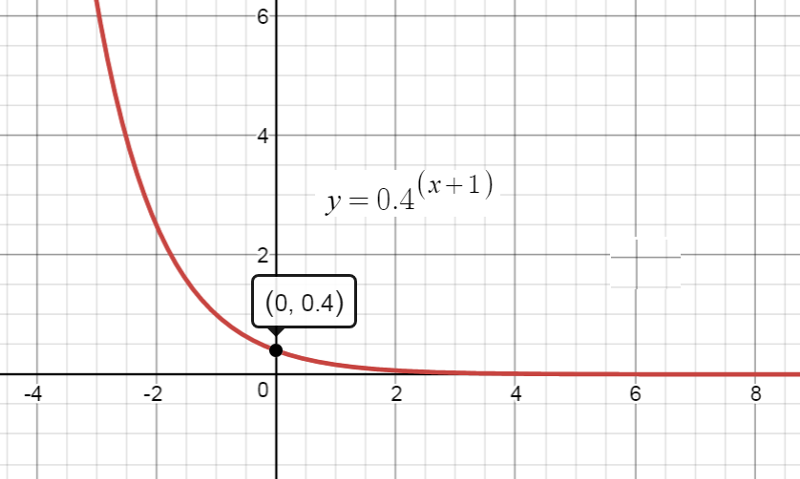
Найдите область определения и диапазон функции у «=» 3 Икс + 2 .
График функции на координатной плоскости.
График не что иное, как график у «=» 3 Икс переведено 2 единицы влево.
Функция определена для всех действительных чисел.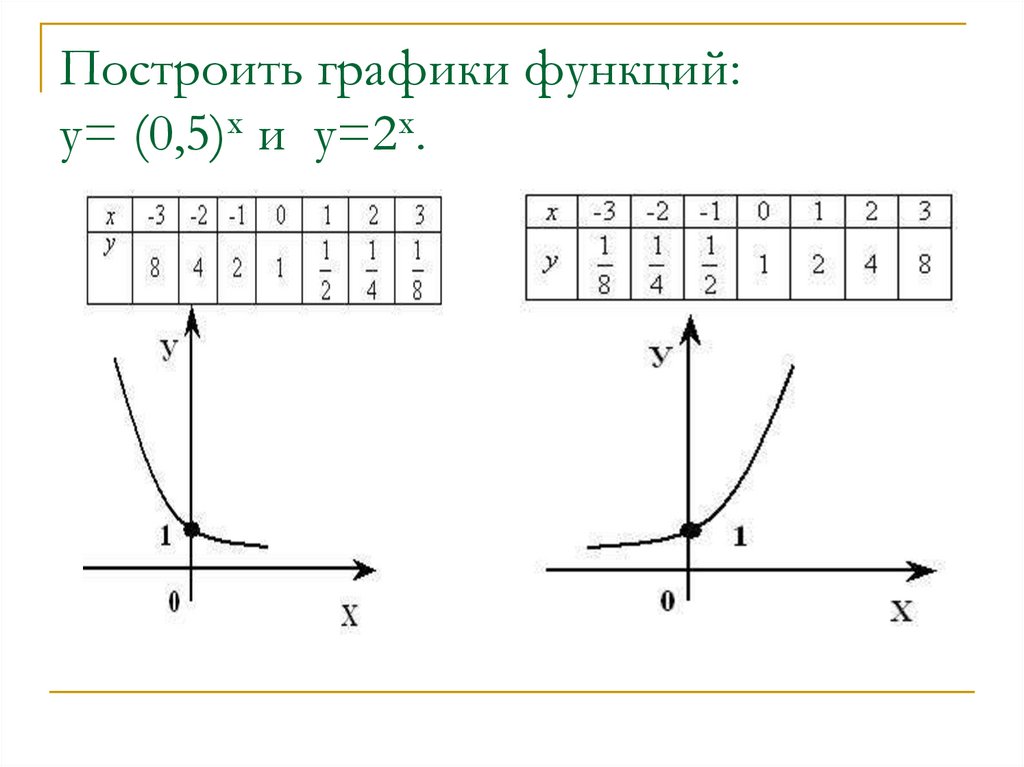 Итак, областью определения функции является множество действительных чисел.
Итак, областью определения функции является множество действительных чисел.
Как Икс как правило ∞ , значение функции также стремится к ∞ и в качестве Икс как правило − ∞ , функция приближается к Икс -ось, но никогда не касается ее.
Следовательно, диапазон функции представляет собой набор действительных положительных чисел или { Икс е ℝ | Икс > 0 } .
Пример 2:
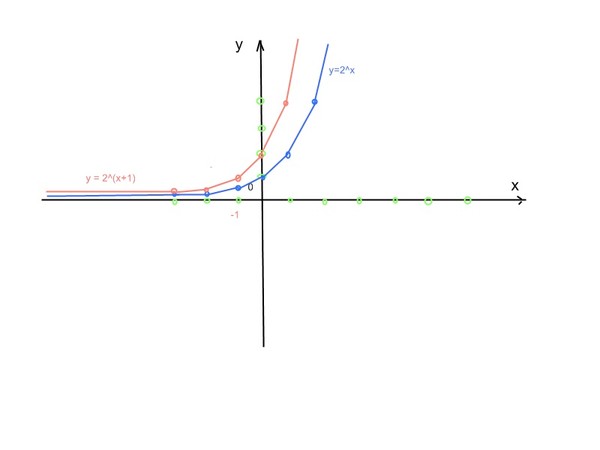
Найдите область определения и диапазон функции у «=» ( 1 4 ) 2 Икс .
График функции на координатной плоскости.
График не что иное, как график
у
«=»
(
1
4
)
Икс
сжатый в разы
2
.
Функция определена для всех действительных чисел. Итак, областью определения функции является множество действительных чисел.
Как Икс как правило ∞ , значение функции стремится к нулю, а график приближается Икс -ось, но никогда не касается ее.
Как Икс как правило − ∞ , функция также стремится к ∞ .
Следовательно, диапазон функции представляет собой набор действительных положительных чисел или { у е ℝ | у > 0 } .
Обратная экспоненциальная функция является логарифмической функцией.
Просто
логарифмическая функция
у
«=»
бревно
2
Икс
где
Икс
>
0
эквивалентна функции
Икс
«=»
2
у
. То есть,
у
«=»
бревно
2
Икс
является обратной функцией
у
«=»
2
Икс
.
То есть,
у
«=»
бревно
2
Икс
является обратной функцией
у
«=»
2
Икс
.
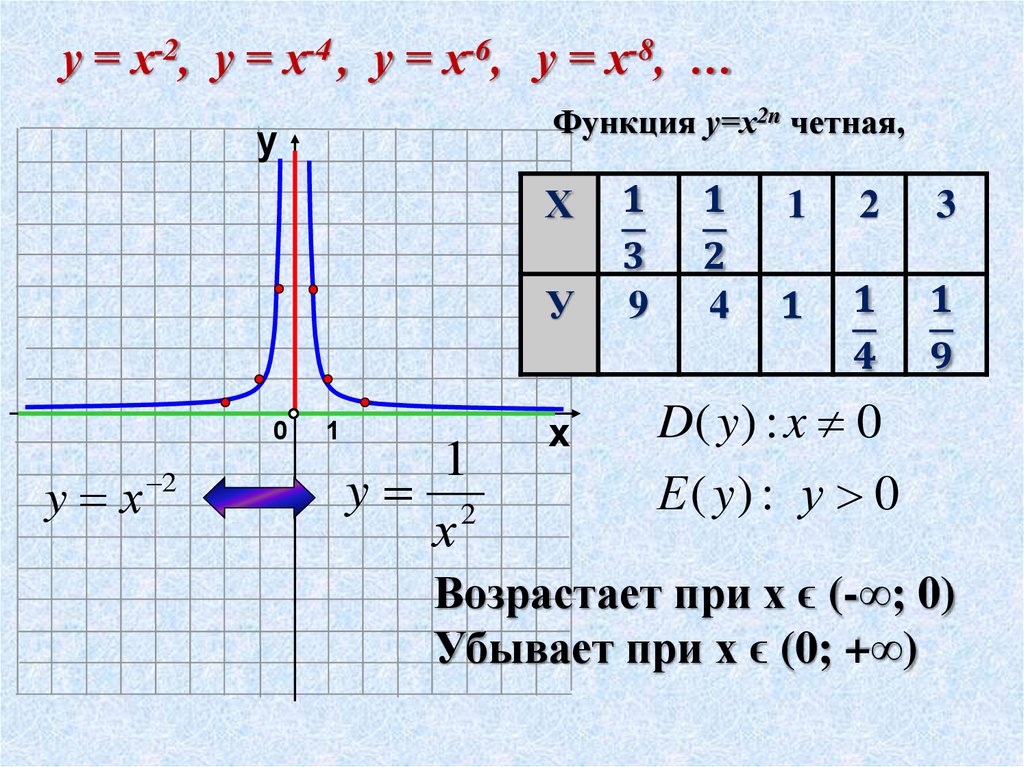
Функция у «=» бревно 2 Икс имеет область определения множества положительных действительных чисел и диапазон множества действительных чисел.
Помните, что, поскольку логарифмическая функция является обратной экспоненциальной функции, областью определения логарифмической функции является диапазон экспоненциальной функции, и наоборот.
В общем случае функция
у
«=»
бревно
б
Икс
где
б
,
Икс
>
0
и
б
≠
1
является непрерывной и однозначной функцией. Обратите внимание, что логарифмическая функция не определен для отрицательных чисел или для нуля. График функции приближается к
у
-ось как
Икс
как правило
∞
, но никогда не касается его.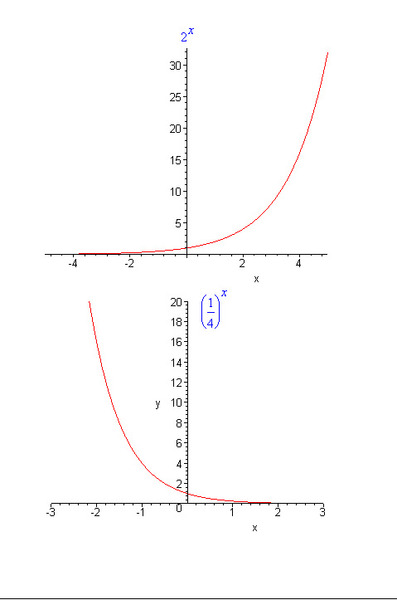
Следовательно, область определения логарифмической функции у «=» бревно б Икс — множество положительных действительных чисел, а диапазон — множество действительных чисел.
Функция возникает из − ∞ к ∞ как Икс увеличивается, если б > 1 и падает с ∞ к − ∞ как Икс увеличивается, если 0 < б < 1 .
Логарифмическая функция,
у
«=»
бревно
б
Икс
, можно сдвинуть
к
единицы по вертикали и
час
единицы по горизонтали с уравнением
у
«=»
бревно
б
(
Икс
+
час
)
+
к
. Тогда область определения функции становится
{
Икс
е
ℝ
|
Икс
>
−
час
}
. Однако ассортимент остается прежним.
Однако ассортимент остается прежним.
Пример 3:
Найдите область определения и диапазон функции у «=» бревно ( Икс ) − 3 .
Начертите функцию на координатной плоскости. Помните, что если основание не показано, то под основанием понимается 10 .
График не что иное, как график у «=» бревно ( Икс ) переведено 3 единиц вниз.
Функция определена только для положительных действительных чисел. Итак, область определения функции — это множество положительных действительных чисел или { Икс е ℝ | Икс > 0 } .
Функция принимает все действительные значения из
−
∞
к
∞
.
Таким образом, диапазон функции представляет собой множество действительных чисел.
Пример 4:
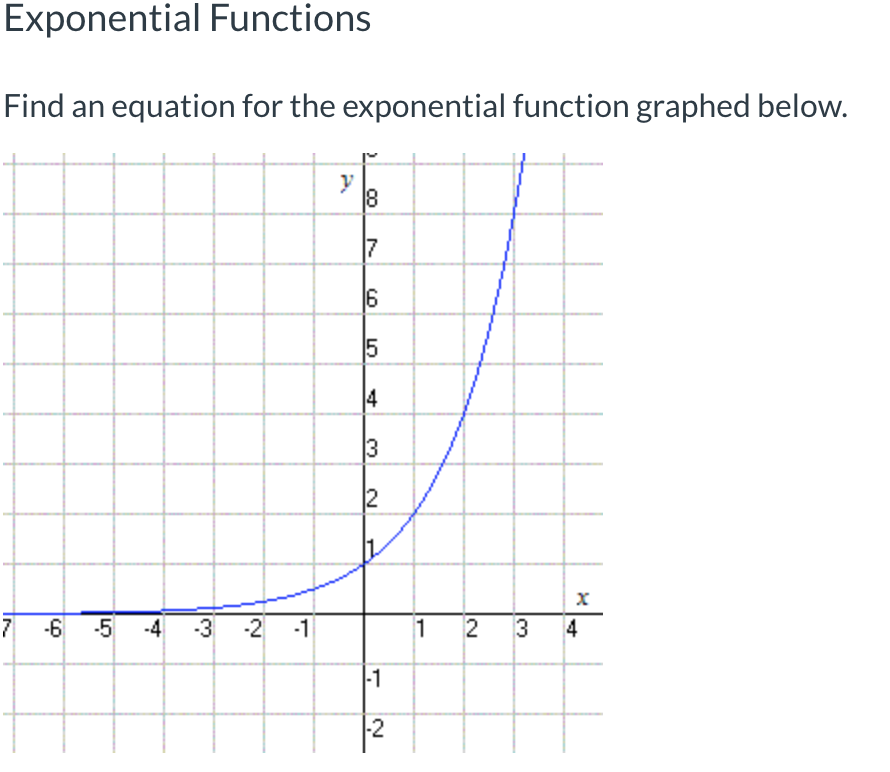
Найдите область определения и диапазон функции у «=» бревно 3 ( Икс − 2 ) + 4 .
График функции на координатной плоскости.
График не что иное, как график у «=» бревно 3 ( Икс ) переведено 2 единицы вправо и 4 единиц вверх.
Как
Икс
как правило
2
, функция приближается к прямой
Икс
«=»
2
но никогда не прикасается к нему. Как
Икс
как правило
∞
значение функции также стремится к
∞
. То есть функция определена для действительных чисел, больших, чем
2
.


 (2)».
(2)».
Leave A Comment