Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
задача для 5 класса. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Помогите пожалуйста квадратный участок со стороной 90 м, ограждённый сеткой, делят на 4 участка прямоугольной формы.1) хватит ли 200 погонных метров
Решено
в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?
Решено
какой цифрой оканчивается значение 2017 в степени 2016
Пользуйтесь нашим приложением
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
В треугольнике ABC угол A равен 45 градусов, угол B равен 60 градусов, BC= 6√6. 5
5
Оцените значение выражения 5а, если 1< а < 3
Пользуйтесь нашим приложением
Площадь конуса
Освойте 7 столпов успеха в школе
Улучшите свои оценки и снизьте стресс
Common Core Standard 8.G.9
4
5 3 Наклонный конус
Правый конус
Нажмите на картинку, чтобы узнать площадь и объем калькулятора конуса.
Калькулятор найдет площадь вместе с радиусом, высотой или наклонной высотой конуса, если задано два значения.
Калькулятор также рассчитает объем конуса.
Усеченный конус
Усеченный конус — это твердое тело, подобное цилиндру, за исключением того, что круглые основания не равны по размеру. Вы могли бы описать форму как абажур.
Думайте об этом как о конусе с частью, содержащей удаленную вершину.
Если разрез параллелен основанию, то это усеченный конус 92)
Итак… Чтобы найти площадь поверхности конуса , выполните следующие действия.
- Найдите площадь боковой поверхности конуса, используя:
- πрадиус x высота наклона конуса
- Найдите площадь основания конуса, используя: 7 709 908105
- 0078 πрадиус в квадрате
- Добавьте боковую область плюс базовую область
Что такое конус в геометрии?
Конус представляет собой трехмерную геометрическую фигуру. Основание конуса имеет круглую форму.
Конус имеет только одну вершину.
Два распространенных типа конусов: правый конус и наклонный конус
Вершина правого конуса расположена над центром конуса основания.
Вершина косого конуса не расположена над центром основания конуса
Площадь = боковая площадь конуса + площадь основания конуса 0006
Наклонная высота равна =√h3 +r2
h = высота r = радиус
Площадь поверхности конуса Пример задачи
Найдите площадь поверхности конуса радиус 6 92
60 π + 36π=96π единиц в квадрате s
Вам также могут понравиться….
Геометрия Формулы
Площадь поверхности призмы
Площадь поверхности цилиндра
Площадь поверхности конуса
| 1. | Какова площадь поверхности конуса? |
| 2. | Площадь поверхности конуса Формула |
| 3. | Изогнутая поверхность конуса |
| 4. | Расчет площади поверхности конуса |
| 5. | Часто задаваемые вопросы о площади поверхности конуса |
Какова площадь поверхности конуса?
Площадь, занимаемая поверхностью/границей конуса, называется площадью поверхности конуса. Она всегда измеряется в квадратных единицах. Складывание множества треугольников и вращение их вокруг оси дает форму конуса. Поскольку он имеет плоское основание, он имеет общую площадь поверхности, а также площадь изогнутой поверхности. Мы можем классифицировать конус как прямой круговой конус или наклонный конус. Вершина в прямом круглом конусе обычно находится вертикально над центром основания, тогда как вершина конуса в наклонном конусе не находится вертикально над центром основания.
Она всегда измеряется в квадратных единицах. Складывание множества треугольников и вращение их вокруг оси дает форму конуса. Поскольку он имеет плоское основание, он имеет общую площадь поверхности, а также площадь изогнутой поверхности. Мы можем классифицировать конус как прямой круговой конус или наклонный конус. Вершина в прямом круглом конусе обычно находится вертикально над центром основания, тогда как вершина конуса в наклонном конусе не находится вертикально над центром основания.
Площадь поверхности конуса Формула
Поскольку конус имеет криволинейную поверхность, мы можем выразить площадь его криволинейной поверхности, а также общую площадь поверхности. Конус имеет два вида площади поверхности:
- Общая площадь поверхности
- Изогнутая поверхность
Если радиус основания конуса равен «r», а наклонная высота конуса равна «l», площадь поверхности конуса определяется как:
- Общая площадь поверхности, T = πr(r + л) квадратных единиц
- Площадь криволинейной поверхности, S = πrl квадратных единиц
Применяя теорему Пифагора о конусе, мы можем найти связь между площадью поверхности конуса и его высотой. Мы знаем, h 2 + r 2 = l 2 , где h — высота конуса, r — радиус основания, а l — наклонная высота конуса.
Мы знаем, h 2 + r 2 = l 2 , где h — высота конуса, r — радиус основания, а l — наклонная высота конуса.
⇒ l = √(h 2 + r 2 )
Таким образом,
- Общая площадь поверхности по высоте может быть определена как T = πr(r + l) = T = πr(r + √(ч 2 + р 2 )).
- Площадь искривленной поверхности конуса по высоте может быть выражена как S = πrl = πr(√(h 2 + r 2 )).
Изогнутая поверхность конуса
Мы обсудили формулу для нахождения площади криволинейной поверхности конуса, теперь давайте разберемся в ее значении. Как и другие трехмерные фигуры, конус также имеет как плоские, так и криволинейные поверхности. Площадь изогнутой поверхности конуса относится только к изогнутой части конуса, отличной от круглого плоского основания. Чтобы найти площадь криволинейной поверхности конуса, мы умножаем радиус и наклонную высоту конуса на pi(π). Выведем формулу площади криволинейной поверхности конуса ниже.
Выведем формулу площади криволинейной поверхности конуса ниже.
Площадь криволинейной поверхности конуса Формула
Площадь криволинейной поверхности конуса может быть определена путем нахождения площади сектора по формуле
Площадь сектора (в пересчете на длину дуги) = (длина дуги × радиус)/ 2 = ((2πr) × l)/2 = πrl.
∴ Площадь криволинейной поверхности конуса, S = πrl единиц 2 .
Расчет площади поверхности конуса
Возьмем конус высотой «h», радиусом основания «r» и высотой наклона «l». Чтобы определить площадь поверхности образования конуса, мы вырезаем конус из центра, который выглядит как сектор круга (плоская форма).
Общая площадь поверхности конуса = площадь основания конуса + площадь изогнутой поверхности конуса
⇒ Общая площадь поверхности конуса = πr 2 + πrl = πr (r + l).
∴ Полная площадь поверхности конуса, T = πr (r + l) ед. криволинейная поверхность конуса.
Пример: Найдите общую площадь поверхности и площадь криволинейной поверхности конуса, радиус которого равен 7 дюймам, а наклонная высота равна 3 дюймам. (Используйте π = 22/7).
Мы знаем, что площадь полной поверхности конуса равна πr (r + l), а площадь боковой поверхности конуса равна πrl. Учитывая, что: r = 7 дюймов, l = 3 дюйма и π = 22/7. Таким образом, общая площадь поверхности конуса T = πr (r + l) = (22/7) × 7 × (7 + 3) = (22/7) × 7 × 10 = 22 × 10 = 220 в 2 .
∴ Общая площадь поверхности конуса 220 2 .
Площадь криволинейной поверхности конуса, S = πrl = (22/7) × 7 × 3 = 66 в 2 . ∴ Площадь изогнутой поверхности конуса составляет 66 дюймов 2 .
Давайте рассмотрим еще несколько примеров площади поверхности конуса для более глубокого понимания.
Часто задаваемые вопросы о площади поверхности конуса
Какова площадь поверхности конуса?
Мера площади, занимаемой поверхностью конуса, называется площадью поверхности конуса. Существует два типа площади поверхности конуса, которые можно разделить на общую площадь поверхности и площадь криволинейной поверхности конуса.
Существует два типа площади поверхности конуса, которые можно разделить на общую площадь поверхности и площадь криволинейной поверхности конуса.
Как найти площадь поверхности конуса?
Площадь поверхности конуса можно найти, выполнив следующие шаги:
- Шаг 1: Определите заданные значения радиуса, наклонной высоты и высоты конуса.
- Шаг 2: Используйте соответствующую формулу для расчета площади поверхности. Если необходимо найти общую площадь поверхности конуса, используйте формулу πr (r + l) квадратных единиц, а если нужно найти площадь криволинейной поверхности конуса, используйте формулу πrl квадратных единиц.
- Шаг 3: Упростите и запишите ответ в квадратных единицах.
Какова площадь криволинейной поверхности конуса?
Площадь криволинейной поверхности конуса известна как площадь криволинейной поверхности конуса. Формула для расчета площади криволинейной поверхности конуса: πrl, где «r» — радиус основания, а «l» — наклонная высота конуса. При этом мы не рассматриваем площадь основания конуса, имеющего форму круга.
При этом мы не рассматриваем площадь основания конуса, имеющего форму круга.
Какова площадь криволинейной поверхности прямоугольного конуса?
Прямой круговой конус определяется как конус, осью которого является линия, соединяющая вершину и середину кругового основания. Таким образом, площадь криволинейной поверхности прямого круглого конуса определяется как πrl, где «r» — радиус основания, а «l» — наклонная высота. С точки зрения высоты, площадь криволинейной поверхности прямого круглого конуса определяется как πr(√(h 2 + r 2 )) где «h» — высота правильного круглого конуса.
Как найти площадь поверхности конуса с наклонной высотой и диаметром?
Общая площадь поверхности конуса с наклонной высотой и диаметром конуса может быть найдена по формуле T = π(D/2) ((D/2) + l), где D — диаметр, а l — наклонная высота. Площадь криволинейной поверхности конуса с наклонной высотой и диаметром можно найти по формуле S = π(D/2)l, где D — диаметр, а l — наклонная высота.
Как найти полную площадь поверхности конуса?
Полную площадь поверхности конуса можно найти, выполнив следующие шаги:
- Шаг 1: Проверьте значения, указанные в вопросе.
- Шаг 2: Подставьте значения радиуса и наклонной высоты в формулу πr (r + l). В случае, если наклонная высота не указана, мы запишем значение наклонной высоты через высоту конуса «h», подставив l = √(h 2 + r 2 ), что дает значение, T = πr(r + √(h 2 + r 2 )) где «r» — радиус конуса, а «h» — высота конуса.
- Шаг 3: Теперь найдите значение общей площади поверхности.
- Шаг 4: Запишите окончательный ответ в квадратных единицах.
Как найти площадь криволинейной поверхности конуса?
Площадь криволинейной поверхности конуса можно найти, используя следующие шаги:
- Шаг 1: Запишите значения, указанные в вопросе.

- Шаг 2: Подставьте значения радиуса и наклонной высоты заданного вопроса в формулу πrl. В случае, если наклонная высота не указана, мы запишем значение наклонной высоты через высоту конуса «h», подставив l = √(h 2 + r 2 ), что дает значение S = πr√(h 2 + r 2 ), где «r» — радиус конуса, а «h» — высота конуса.
- Шаг 3: Теперь найдите значение площади криволинейной поверхности и запишите ответ в квадратных единицах.
Что произойдет с площадью поверхности конуса, если наклонную высоту и радиус основания удвоить?
Площадь поверхности конуса зависит от радиуса основания и его наклонной высоты. Таким образом, общая площадь поверхности и площадь криволинейной поверхности конуса увеличиваются в четыре раза, когда наклонная высота и радиус основания удваиваются как:

 04.17
04.17 04.19
04.19 Мы можем найти площадь поверхности конуса двумя способами — полной площадью поверхности и площадью криволинейной поверхности конуса.
Мы можем найти площадь поверхности конуса двумя способами — полной площадью поверхности и площадью криволинейной поверхности конуса.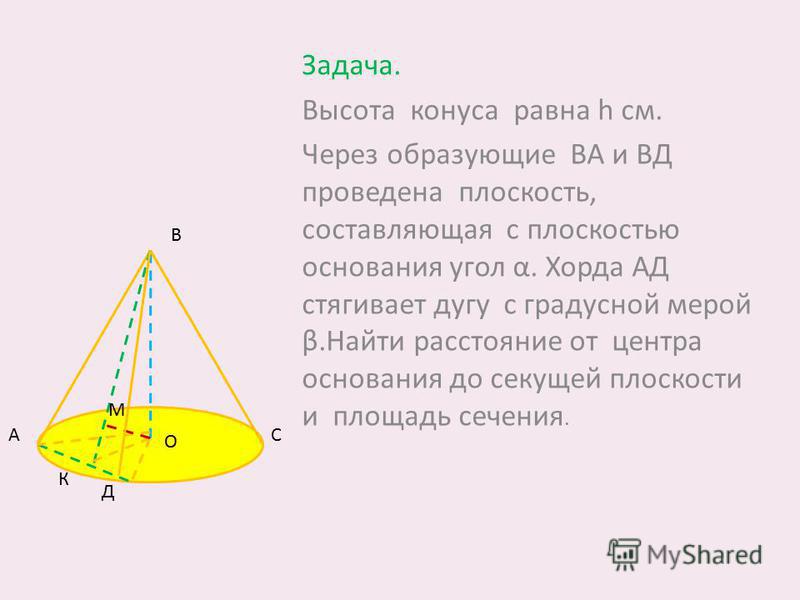

Leave A Comment