Трапеция. Конспект занятия в системе дополнительного образования.
Сценарий занятия творческой мастерской «Математика»
(весенняя сессия)
Тема: «Трапеция в задачах ОГЭ»
Чернышев Э.Н., педагог дополнительного образования
Цель занятия: сформировать условия для овладения обучающимися опытом преобразования зависимостей между элементами трапеции и их измеряемыми значениями.
Ход занятия.
1.Вступительное слово учителя.
Известно, какую большую роль играет геометрия в науке и образовании. На протяжении всей истории человечества она служила источником развития не только математики, но и многих других наук. Именно в ней появились первые теоремы и доказательства. Сами законы математического мышления формировались с помощью геометрии.
Многие
геометрические задачи способствовали появлению новых научных направлений. Наоборот,
решение многих научных проблем получено с использованием геометрических
методов.
Понятие трапеции вводится в среднем звене и рассматривается на всём протяжении изучения геометрии, используется не только в школьном курсе геометрии, но так же является одним из базовых понятий курсов высшего образования, такие как высшая математика, линейная алгебра, численные методы, экономика, программирование, физика, теоретическая механика, сопротивление металлов т.д.
Изучение геометрической фигуры трапеция полезно тем, что при решении задач на этой фигуре закрепляются знания, полученные ранее (свойства треугольников, подобие треугольников, свойства параллельных прямых и т.д.)
Не случайно, что в прототипах номер 26 заданий ОГЭ почти четверть всех задач посвящено трапеции.
2.Обзор теоретического материала (формируется в ходе работы творческих групп).
Понятие
трапеции формировалось длительного периода времени. Сначала трапецией называли
любой четырёхугольник, не являющийся параллелограммом. Именно в таком смысле
термин «трапеция» использовал Евклид в своих «Началах». В ХVIII
веке понятие трапеции приобретает современное значение.
В ХVIII
веке понятие трапеции приобретает современное значение.
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, как минимум две противоположные стороны которого параллельны. Две параллельные стороны называются основаниями трапеции, а две другие — это боковые стороны. Средняя линия — отрезок, соединяющий середины боковых сторон.
Элементы трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
· Параллельные стороны называются основаниями трапеции.
· Две другие стороны называются боковыми сторонами.
· Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Виды трапеций. Трапеция, у которой боковые стороны равны, называется
· Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Общие свойства
· Средняя линия трапеции параллельна основаниям и равна их полусумме.
· Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии.
· (Обобщённая теорема Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
· В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
· Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен (среднее гармоническое), где и — основания трапеции (формула Буракова).
·
Точка пересечения диагоналей
трапеции, точка пересечения продолжений её боковых сторон и середины оснований
лежат на одной прямой.
· Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
· Треугольники, лежащие на основаниях при пересечении диагоналей подобны.
· Треугольники, лежащие на боковых сторонах, равновеликие.
· Если отношение оснований равно , то отношение площадей треугольников, лежащих на основаниях, равно .
Свойства и признаки равнобокой трапеции.
· Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
· Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований
· Углы при любом основании равны.
· Длины диагоналей равны.
·
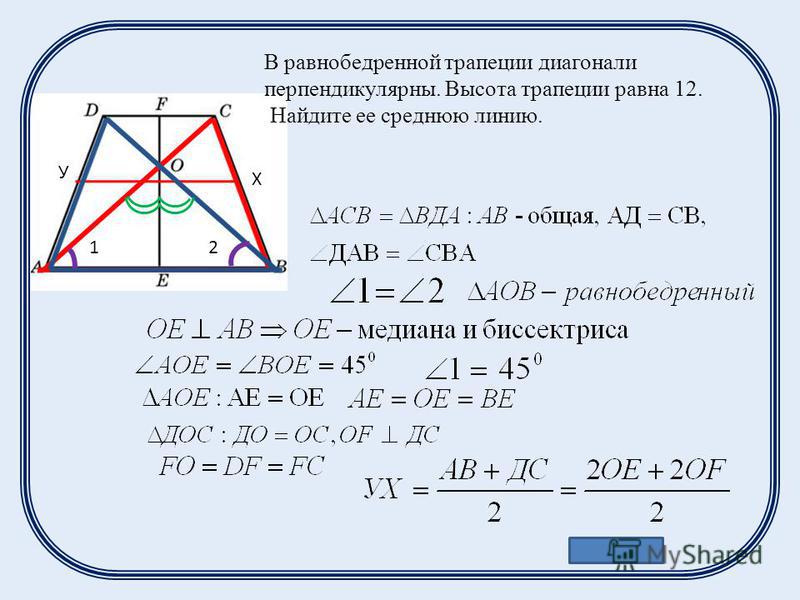
Если в равнобедренной
трапеции диагонали перпендикулярны, то высота равна полусумме оснований.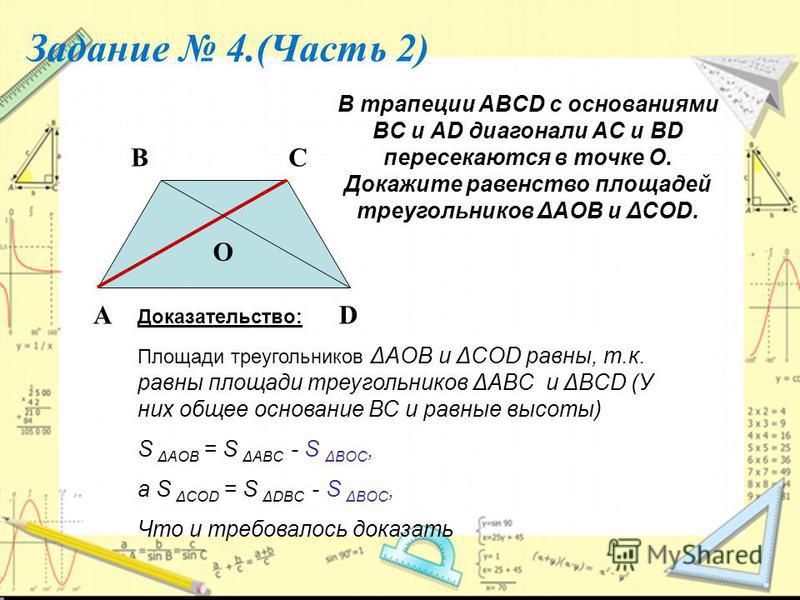
Вписанная и описанная окружность.
· Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
· В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
· Если трапеция равнобедренная, то около неё можно описать окружность.
· Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , — то .
Площадь.
Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.
· В случае, если и — основания и — высота, формула площади:
· В случае, если — средняя линия и — высота, формула площади:
* Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:
3. Решение задач (по группам).
Решение задач (по группам).
Группы предсчтавляют и «защищают» решения».
Задача № 1. |
|
| |||||
| В равнобедренную трапецию, периметр которой равен 120, а площадь равна 540, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания. |
| ||||
| ||||||
Решение задачи: SABCD=EF*(AD+BC)/2=540PABCD=AB+BC+CD+AD=120 AB=CD (так как трапеция равнобедренная).  Чтобы окружность можно было вписать в трапецию должно выполняться
условие — суммы противоположных сторон трапеции должны быть равны, т.е. Чтобы окружность можно было вписать в трапецию должно выполняться
условие — суммы противоположных сторон трапеции должны быть равны, т.е.AD+BC=AB+CD AD+BC=2AB (т.к. AB=CD) Тогда: P AB=30 Значит, AD+BC=2*30=60 SABCD=EF*(AD+BC)/2=EF*60/2=EF*30=540 EF=18 Проведем высоту BH, как показано на рисунке. BH=EF=18, так как BEFH — прямоугольник. AH=(AD-BC)/2 По теореме Пифагора: AB2=BH2+AH2 302=182+AH2 900=324+AH2 576=AH2 24=AH=(AD-BC)/2 48=AD-BC (1), вспомним, что AD+BC=60 (2), сложим (1) и (2) 108=2AD 54/6=KF/KE 9=(EF-KE)/KE (вспомним, что EF=18) 9KE=18-KE 10KE=18 KE=1,8 Ответ: KE=1,8 | ||||||
| Задача
№ 2. |
| ||||
В трапеции боковая сторона перпендикулярна основанию . Окружность проходит через точки и и касается прямой в точке . Найдите расстояние от точки до прямой , если , . |
В трапеции АВСД продлим стороны AB и
CD до пересечения в точке S. Прямая EK будет перпендикулярна стороне CD, так
как точка K проекция точки E на прямую CD. M — ,будет проекцией точки C на
прямую AD.
Если угол ∠CAD = α, а CD=x, так как MD=4-3=1, то:
cosα=MD/DC = 1/x
Из подобия треугольников SBC и SAD
находим, что SC = 3x. Поэтому:
SE2=SD*SC=12x2
Значит можно найти
SE=2x√3; EK=SE*cos∠SEM=SE*cos∠SDA=SE*cosα=2x√3 / x = 2√3
Ответ: ЕК= 2√3
Задача
№ 3. |
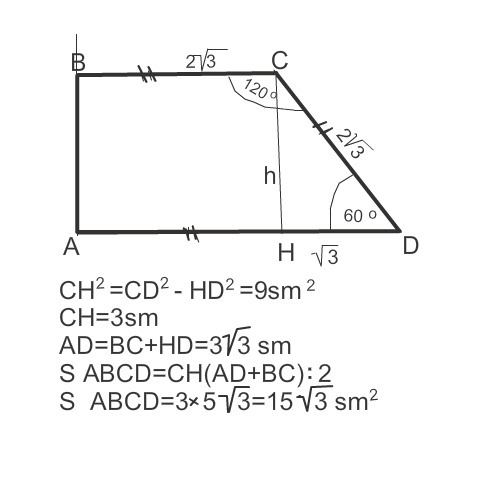
Боковые стороны и трапеции равны соответственно 8 и 10, а основание равно 2. Биссектриса угла проходит через середину стороны . Найдите площадь трапеции. |
5, а это значит, что нижнее основание равно 2+ AD/2=5, 2+ AD=10, AD=8 – тогда полусумма оснований будет равна 5.
Проведем высоты трапеции. Высоты отсекут от нижнего основания трапеции отрезки AM и ND, которые мы обозначим a и b. Тогда высоту трапеции можно записать для прямоугольного треугольника ABM:
h2=82-a2
Высоту можно записать и в треугольнике CND:
h2=102-b2
Приравняем данные два выражения: 82-a2=102-b2
Это выражение можно переписать так: b2-a2=102-82
А теперь разложим правую и левую части как разность квадратов:
(b+a)(b-a)=(10+8)(10-8)=18*2=36
Сумму отрезков a и b легко определить как разность оснований трапеции: a+b=8-2=6
Подставим данную сумму в предыдущее уравнение: 6(b-a)=36, или b-a=6
Составим систему: b+a=6
b-a =6
Сложив два уравнения системы, найдем: 2b=12, b=6.
Теперь можно найти высоту трапеции и ее площадь: h2=100-36 = 64 h=8.
S=.(2+8)*8=40
Ответ: 40
.
Задача № 4. |
Основания трапеции относятся как 1:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции? Решение: Треугольники AOD и BOC –подобны по двум углам.
Посмотрим на рисунок. Для начала предположим, что средняя линия NM=11, а вторая линия, соединяющая середины оснований HS=10. В
условии этой задачи самое важное – это сумма углов при основании. Если
заметить, что сумма этих углов равна 90 градусам – догадаться, как решается задача,
совсем просто. Достроим нашу трапецию до треугольника. Треугольник AOD –
прямоугольный (по теореме о сумме углов треугольника). Треугольники AOD, KLO, BOC подобны
(по двум углам, так как углы при основаниях этих треугольников – соответственные,
а прямые BC, KL , AD – параллельны по условию). Ответ: 1,21 | |||||
Задача № 6. |
Найдите площадь трапеции, диагонали которой равны 3 и 4, а средняя линия равна 2,5. |
D”
Для того, чтобы решить эту задачу, перенесем диагональ BD вправо на длину верхнего основания трапеции ВС, образовав таким образом треугольник ACD’:
Сторона АС нашего
треугольника является диагональю трапеции и равна 3, сторона СD’ – это вторая
диагональ, равная 4. Основание треугольника AD’- сумма длин оснований трапеции,
а так как нам известна средняя линия, то можно узнать и сумму оснований: 2,5*2=5. Таким образом, в
треугольнике ACD’ мы знаем длины всех его сторон.
Основание треугольника AD’- сумма длин оснований трапеции,
а так как нам известна средняя линия, то можно узнать и сумму оснований: 2,5*2=5. Таким образом, в
треугольнике ACD’ мы знаем длины всех его сторон.
Теперь вернемся к цели задачи: надо определить площадь трапеции. Она равна произведению полусуммы оснований на высоту трапеции. Но площадь треугольника ACD’ равна половине произведения основания на высоту, а высота у него такая же, как и у трапеции, и половина основания – ни что иное, как средняя линия трапеции, или полусумма ее оснований! То есть искомая площадь трапеции и площадь треугольника ACD’ равны. Осталось найти площадь треугольника ACD’, т.к. 32+42=52, т по теореме обратной теореме Пифагора треугольник ACD’ прямоугольный. S=.4*3=6 или по формуле Герона:
. Здесь p – полупериметр, в нашем случае половина периметра равна р=(5+4+3):2=6 Тогда: S=6 Ответ: 6.
Задача № 7. | ||
В трапеции основания и равны соответственно 36 и 12, а сумма углов при основании равна . Найдите радиус окружности, проходящей через точки и и касающейся прямой , если . | ||
Из
того, что сумма углов при основании АД равна 90º, следует, что продолжение АВ и
СД пересекаются под углом 90º.
Достроим трапецию до прямоугольного треугольника АЕД
треугольники ВЕС и АЕД — подобны.
∠ Е в них — общий,ВС||АД,∠ ЕСВ=∠ЕДА
по свойству углов при пересечении параллельных прямых секущей.
Коэффициент подобия АД:ВС=36:12=3
Тогда АЕ:ВЕ=3
АЕ=АВ+ВЕ
(АВ+ВЕ):ВЕ=3
(10+ВЕ):ВЕ=3
10+ВЕ=3ВЕ
2ВЕ=10, ВЕ=5
Пусть точка касания окружности и прямой СД будет F
Соединим центр О окружности с вершиной В трапеции и точкой касания М.
Так как углы ОFE и АEF прямые, ОF и АE
— параллелльны.
Рассмотрим треугольник АОВ.Его стороны АО и ОВ, являясь радиусами
окружности, равны.
Треугольник АОВ — равнобедренный.
Проведем в нем высоту ОK.Эта высота — и медиана ( треугольник ведь
равнобедренный).Следовательно, KВ
=АВ/2=10/2=5.
Рассмотрим четырехугольник KEFО.Это
прямоугольник с равными сторонами KE=FО.FО
— радиус окружности.
КE=KВ+ВE=5+5=10
FО=КE=10
Радиус окружности равен 10.
4.Выводы (формируются и защищаются группами).
Проанализировав все решённые задачи, я пришёл к такому выводу.
Чтобы понять, как решать задачи с трапецией, полезно запомнить три основных пути решения.
I. Провести две высоты
.
А) Четырехугольник BCKF — прямоугольник (так как у него все углы прямые). Следовательно, FK=BC.
AD=AF+FK+KD, отсюда AD=AF+BC+KD.
Треугольники ABF и DCK — прямоугольные.
(Следует учесть и другой вариант:
Ib.
В этом случае AD=AF+FD=AF+FK-DK=AF+BC-DK.)
Б). Если трапеция равнобедренная, решение задачи упрощается:
В этом случае прямоугольные
треугольники ABF и DCK равны, например, по катету и гипотенузе (AB=CD по
условию, BF=CK как высоты трапеции). Из равенства треугольников следует
равенство соответствующих сторон:
Из равенства треугольников следует
равенство соответствующих сторон:
AF=KD=(AD-FK):2=(AD-BC):2.
II. Провести прямую, параллельную боковой стороне.
IIa. BM∥CD. Так как BC∥AD (как основания трапеции), то BCDM — параллелограмм. Следовательно, MD=BC, BM=CD, AM=AD-BC.
IIb. В частности, для равнобедренной трапеции
BM∥CD. Так как CD=AB, то и BM=AB. То есть получаем равнобедренный треугольник ABM и параллелограмм BCDM.
III. Продолжить боковые стороны и получить треугольник.
Прямые AB и CD пересекаются в точке P.
Треугольники APD и BPC подобны по двум углам (угол P — общий, ∠PAD= ∠PBC как соответственные при BC∥AD и секущей AP).
Следовательно, их стороны пропорциональны:
Эти три подхода к решению задач на трапецию — основные, именно их я использовал при решении задач.
Эту работу можно применять
в качестве учебного материала на уроках геометрии, на консультациях при
подготовке к экзаменам.
ЗАКЛЮЧИТЕЛЬНОЕ СЛОВО
Творческая мастерская «Математика» занималась исследованием одного из древнейших геометрических объектов – трапеции. Работая по группам, участники мастерской смогли составить не только подробное описание известных им свойств трапеции, но и овладеть способами решения задач из второй части ОГЭ по математике. В этих задачах что только не происходит с трапецией: в нее вписывается окружность, основания делятся прямой в определенной пропорции, диагонали делят среднюю линию и высоты… Эти замечательные «приключения» трапеции стали открытием для многих ребят, ведь они раньше думали: ну что там, в этой трапеции может еще быть неизвестного ? Оказалось, — может. А решение сложных задач из ОГЭ имеет еще один практический смысл, — чем больше баллов, тем выше шанс попасть в профильный математический класс и посвятить свой труд совершенствованию науки и техническому прогрессу во благо процветания и безопасности России !
1.
2.Приведите пример числа-палиндрома, которое делится на 55. Сколько существует пятизначных чисел-палиндромов, делящихся на 55 ? Найти 13-е по величине число-палиндром, которое делится на 55.
3.Решить неравенство
4.Через точку пересечения диагоналей трапеции АВСД проведена прямая МЕ, параллельная основаниям АД и ВС. Найти отношение площадей трапеций МВСЕ и АМЕД, если одно из оснований трапеции в три раза больше другого.
5.Периметр равнобедренной трапеции равен 200, а площадь 1500. Найти расстояние от точки пересечения диагоналей до меньшего основания, если в данную трапецию можно вписать окружность.
6. В трапеции боковая сторона перпендикулярна основанию . Окружность проходит через точки и и касается прямой в точке . Найдите расстояние от точки до прямой , если , .
7. Боковые стороны и трапеции равны соответственно 8 и 10, а основание равно 2. Биссектриса угла проходит через середину стороны . Найдите площадь трапеции.
1.
2. Приведите
пример числа-палиндрома, которое делится на 55. Сколько существует пятизначных
чисел-палиндромов, делящихся на 55 ? Найти 13-е по величине число-палиндром,
которое делится на 55.
Приведите
пример числа-палиндрома, которое делится на 55. Сколько существует пятизначных
чисел-палиндромов, делящихся на 55 ? Найти 13-е по величине число-палиндром,
которое делится на 55.
3.Решить неравенство
4.Через точку пересечения диагоналей трапеции АВСД проведена прямая МЕ, параллельная основаниям АД и ВС. Найти отношение площадей трапеций МВСЕ и АМЕД, если одно из оснований трапеции в три раза больше другого.
5.Периметр равнобедренной трапеции равен 200, а площадь 1500. Найти расстояние от точки пересечения диагоналей до меньшего основания, если в данную трапецию можно вписать окружность.
6. В трапеции боковая сторона перпендикулярна основанию . Окружность проходит через точки и и касается прямой в точке . Найдите расстояние от точки до прямой , если , .
7. Боковые стороны и трапеции равны соответственно 8 и 10, а основание равно 2. Биссектриса угла проходит через середину стороны . Найдите площадь трапеции.
Простая физика — EASY-PHYSIC
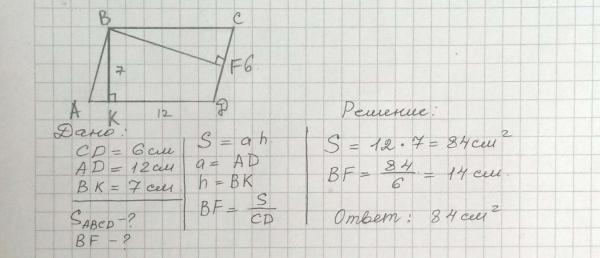
1. Биссектрисы углов А и В при боковой стороне АВ трапеции АВСD пересекаются в точке F. Найдите АВ, если .
Биссектрисы углов А и В при боковой стороне АВ трапеции АВСD пересекаются в точке F. Найдите АВ, если .
Задача 1
Сумма углов при боковой стороне трапеции, как известно, равна . Каждая из биссектрис разделит свой угол пополам, поэтому сумма углов FBA и BAF будет равна , и значит, треугольник BAF — прямоугольный, и его гипотенузу АВ можно определить по теореме Пифагора:
Ответ: 26.
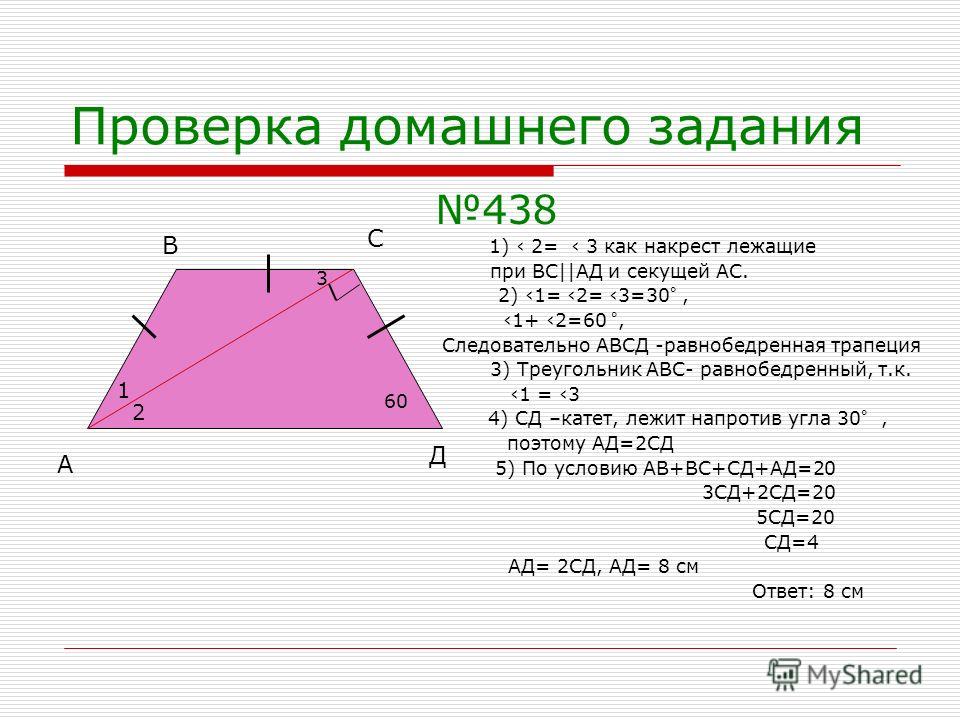
2. Боковые стороны AB и CD трапеции ABCD равны соответственно 36 и 39, а основание ВС равно 12. Биссектриса угла ADC проходит через середину стороны АВ. Найдите площадь трапеции.
Задача 2
Так как по условию АК=КB=18, то точка К — один из концов средней линии. Проведем среднюю линию трапеции. Тогда L — середина CD, и CL=LD=19,5. Образовался треугольник KLD, который является равнобедренным: биссектриса KD разделит угол ADC пополам, а углы KLD и KAD равны как накрестлежащие. Тогда средняя линия этой трапеции равна 19,5, а это значит, что нижнее основание равно 27 — тогда полусумма оснований будет равна 19,5.
Проведем высоты трапеции. Высоты отсекут от нижнего основания трапеции отрезки AM и ND, которые мы обозначим a и b. Тогда высоту трапеции можно записать для прямоугольного треугольника ABM:
Высоту можно записать и в треугольнике CND:
Приравняем данные два выражения:
Это выражение можно переписать так:
А теперь разложим правую и левую части как разность квадратов:
Сумму отрезков a и b легко определить как разность оснований трапеции:
Подставим данную сумму в предыдущее уравнение: , или .
Составим систему:
Сложив два уравнения системы, найдем: , .
Теперь можно найти высоту трапеции и ее площадь: , .
.
Ответ: 702.
3. Найдите площадь трапеции, диагонали которой равны 15 и 9, а средняя линия равна 6.
Задача 3
Для того, чтобы решить эту задачу, сделаем «финт ушами»: перенесем диагональ BD вправо на длину верхнего основания трапеции ВС, образовав таким образом треугольник ACD’:
Сторона АС нашего треугольника является диагональю трапеции и равна 15, сторона СD’ — это вторая диагональ, равная 9.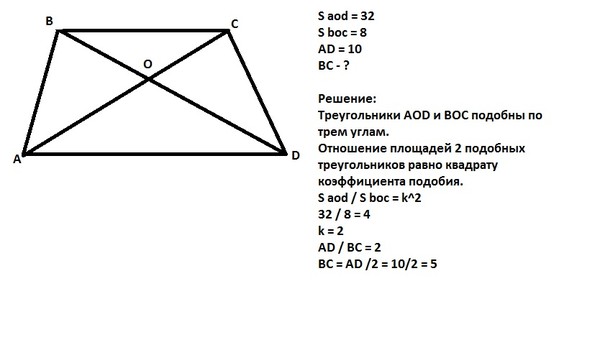 Основание треугольника AD’- сумма длин оснований трапеции, а так как нам известна средняя линия, то можно узнать и сумму оснований: . Таким образом, в треугольнике ACD’ мы знаем длины всех его сторон.
Основание треугольника AD’- сумма длин оснований трапеции, а так как нам известна средняя линия, то можно узнать и сумму оснований: . Таким образом, в треугольнике ACD’ мы знаем длины всех его сторон.
Теперь вернемся к цели задачи: надо определить площадь трапеции. Она равна произведению полусуммы оснований на высоту трапеции. Но площадь треугольника ACD’ равна половине произведения основания на высоту, а высота у него такая же, как и у трапеции, и половина основания — ни что иное, как средняя линия трапеции, или полусумма ее оснований! То есть искомая площадь трапеции и площадь треугольника ACD’ равны. Осталось найти площадь треугольника ACD’, для этого воспользуемся формулой Герона:
. Здесь p — полупериметр, в нашем случае половина периметра равна
Тогда:
Ответ: 54.
4. Биссектрисы углов А и В при боковой стороне АВ трапеции АВСD пересекаются в точке F. Биссектрисы углов С и D при боковой стороне CD пересекаются в точке G. Найдите FG, если основания равны 16 и 30, боковые стороны 13 и 15.
Задача 4
Как уже было пояснено в задаче 1, треугольники ABF и CDG — прямоугольные, это нам пригодится попозже. А сейчас рассмотрим треугольник ABM. Он равнобедренный, так как угол ABM равен углу MBC по условию, а угол AMB равен углу MBC как накрестлежащий. Аналогично и треугольник CDN также является равнобедренным по тем же соображениям. Тогда AM=AB=13, CD=DN=15, а отрезок . Так как треугольник ABM равнобедренный, а треугольник ABF — прямоугольный, то отрезок AF является высотой, а также и медианой треугольника ABM и делит его сторону BM пополам: BF=FM. Так же DG является высотой и медианой треугольника CDN, и делит NC пополам: NG=CG. Тогда можно заметить, что FG — средняя линия трапеции BMNC, и тогда она равна полусумме оснований:
Ответ: 9.
5. Биссектрисы углов А и В при боковой стороне АВ трапеции АВСD пересекаются в точке E. Биссектрисы углов С и D при боковой стороне CD пересекаются в точке F. Найдите EF, если средняя линия равна 21, боковые стороны 13 и 15.
Задача 5
Решение этой задачи похоже на решение предыдущей. Опять биссектрисы отсекут равнобедренные треугольники ABM и CDN: AM=AB=13, CD=DN=15. Так как треугольник ABM равнобедренный, а треугольник ABE — прямоугольный, то отрезок AE является биссектрисой, высотой, а также и медианой треугольника ABM и делит его сторону BM пополам: BE=EM. Так же DG является биссектрисой, высотой и медианой треугольника CDN, и делит NC пополам: NF=CF. Тогда KE — средняя линия треугольника ABM, и равна половине основания: , а FT — средняя линия треугольника NCD: .
Найдем EF:
6. Углы при одном из оснований трапеции АВСD равны 53 и 37 градусов, а отрезки, соединяющие середины противоположных сторон трапеции, равны 6 и 2. Найдите основания трапеции.
Посмотрим на рисунок. Для начала предположим, что средняя линия NM=6, а вторая линия, соединяющая середины оснований HS=2.
Задача 6
В условии этой задачи самое важное — это сумма углов при основании.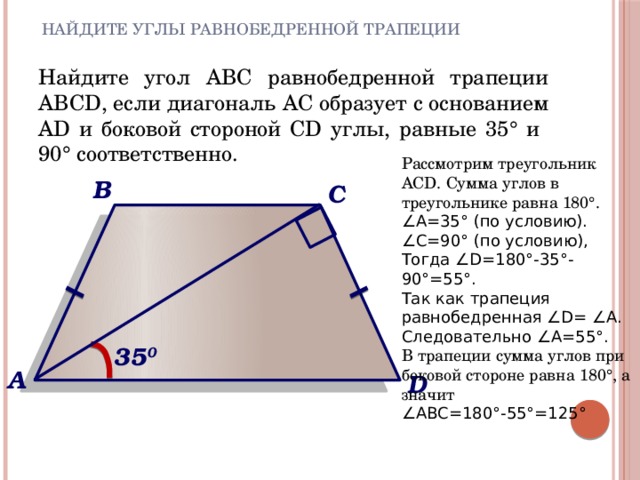 Если заметить, что сумма этих углов равна 90 градусам — догадаться, как решается задача, совсем просто. Достроим нашу трапецию до треугольника. Треугольник ATD — прямоугольный (по теореме о сумме углов треугольника). Треугольники ATD, NMT, BTC подобны (по двум углам, так как углы при основаниях этих треугольников — соответственные, а прямые BC, NM, AD — параллельны по условию). Так как треугольник ATD — прямоугольный, то, если описать около него окружность, то ее центр будет лежать на середине гипотенузы AD, в точке H, AD — диаметр этой окружности. Поэтому, если провести медиану к гипотенузе AD из вершины T, то она будет равна радиусу окружности и половине AD: . Тогда треугольники ATH, NOT, BST — равнобедренные. Кроме того, ОТ — медиана треугольника NMT и разделит его основание пополам: . Если же OT=3, то . (Отрезок SO равен 1, так как OM — средняя линия трапеции HSCD, и разделит HS пополам). Так как , то BC=4, и тогда из теоремы о средней линии AD=8.
Если заметить, что сумма этих углов равна 90 градусам — догадаться, как решается задача, совсем просто. Достроим нашу трапецию до треугольника. Треугольник ATD — прямоугольный (по теореме о сумме углов треугольника). Треугольники ATD, NMT, BTC подобны (по двум углам, так как углы при основаниях этих треугольников — соответственные, а прямые BC, NM, AD — параллельны по условию). Так как треугольник ATD — прямоугольный, то, если описать около него окружность, то ее центр будет лежать на середине гипотенузы AD, в точке H, AD — диаметр этой окружности. Поэтому, если провести медиану к гипотенузе AD из вершины T, то она будет равна радиусу окружности и половине AD: . Тогда треугольники ATH, NOT, BST — равнобедренные. Кроме того, ОТ — медиана треугольника NMT и разделит его основание пополам: . Если же OT=3, то . (Отрезок SO равен 1, так как OM — средняя линия трапеции HSCD, и разделит HS пополам). Так как , то BC=4, и тогда из теоремы о средней линии AD=8.
Если немного подумать, то понятно, что ситуация, когда отрезок HS=6, а NM=2 — невозможна.
Ответ: 4, 8.
В трапеции ABCD, AB || DC, AB = a см и DC = b см. Если M и N — середины непараллельных сторон AD и BC соответственно, то найдите отношение ar(DCNM) и ar(MNBA).
Вопрос
Обновлено:22/08/2019
NCERT EXEMPLAR-Площади параллелограммов и треугольников-Площади параллелограммов и треугольников
20 видеоРЕКЛАМА
Текст Решение
2 02 (3а+б):( а+3б)
С
(а+3б):(3а+б)
D
(2a+b):(3a+b)
Ответ
Правильный ответ B
Решение
Дано, AB = a см, DC = b см и AB|| ОКРУГ КОЛУМБИЯ.
Кроме того, E и F являются серединами AD и BC соответственно.
Таким образом, расстояние между CD, EF и AB, EF будет таким же, скажем, h.
Соедините BD, которые пересекают EF в точке M.
Теперь в ΔABD точка E является средней точкой AD и EM || AB
Итак, M является серединой BD
и EM=12AB [по теореме о средней точке] . ..(i)
..(i)
Аналогично в ΔCBD MF=12CD …(ii)
При добавлении, уравнения (i) и (ii), мы получаем
EM+MF=12AB+12CD
⇒ EF=12(AB+CD)=12(a+b)
Теперь площадь трапеции ABFE=12(сумма параллельных сторон) ×(расстояние между параллельными сторонами)
=12(a+12(a+b))×h=14(3a+b)h
Теперь площадь трапеции EFCD =12[b+12(a+b)]× h=14(3b+a)h
∴ Требуемое соотношение=Площадь ABFEAплощадь EFCD=14(3a+b)h24(3b+a)H
=(3a+b)(a+3b)или (3a+b) ):(a+3b)
Ответить
Пошаговое решение от экспертов, которое поможет вам в решении сомнений и получении отличных оценок на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Похожие видео
ABCD — трапеция, в которой AB |DC, AB=16см и DC=24см. Если E и Fare соответственно, то середины AD и BC доказывают, что ar(ABFE)=(9)/(11)ar(EFCD)
7362230
В трапеции ABCD,AB |DC,AB=acm и DC= млрд куб. Если M и N — середины непараллельных сторон AD и BC соответственно, то найдите отношение ar(DCNM) и ar(MNBA).
Если M и N — середины непараллельных сторон AD и BC соответственно, то найдите отношение ar(DCNM) и ar(MNBA).
7362253
ABCD — трапеция, в которой AB∣∣DC, DC = 30 см и AB = 50 см. Если X и Y являются серединами AD и BC соответственно, докажите, что
ar(DCYX)=79ar(XYBA).
26522243
ABCD – трапеция, у которой AB∣∣DC, DC = 30 см и AB = 50 см. Если X и Y являются серединами AD и BC соответственно, докажите, что
ar(DCYX)=79ar(XYBA).
642505502
ABCD — трапеция, параллельные стороны которой AB=acm и DC=bcm равны E, а F — середины параллельных сторон. Соотношение ar (ABFE) и ar (EFCD) равно
642856980
ABCD — трапеция, в которой AB∣∣DC. M и N — середины AD и BC соответственно. Если AB = 12 см, а MN = 14 см, найдите CD.
642908926
На приведенном ниже рисунке изображена трапеция ABCD. M и N — середины непараллельных сторон AD и BC соответственно. Найти:
МН, если АВ = 11 см и ВС = 8 см.
644269169
На приведенном ниже рисунке изображена трапеция ABCD. M и N — середины непараллельных сторон AD и BC соответственно. Найти:
AB, если DC = 20 см и MN = 27 см
644269170
На приведенном ниже рисунке изображена трапеция ABCD. M и N — середины непараллельных сторон AD и BC соответственно. Найти:
ДС, если МН = 15 см и АВ = 23 см.
644269171
В трапеции ABCD, как показано, AB // DC, AD = DC = BC = 20 см и ∠A=60∘. Найти:
(i) длина AB
644442927
В трапеции ABCD, AB//DC. M — середина AD, N — середина BC.
Если AB = 8 см и DC = 11 см, найдите MN.
644443133
В трапеции ABCD, AB//DC. M — середина AD, N — середина BC.
Если AB = 5,7 см и MN = 6,2 см, найти DC.
644443134
В трапеции ABCD, AB || DC, AB = a см и DC = b см. Если M и N — середины непараллельных сторон AD и BC соответственно, то найдите отношение ar(DCNM) и ar(MNBA).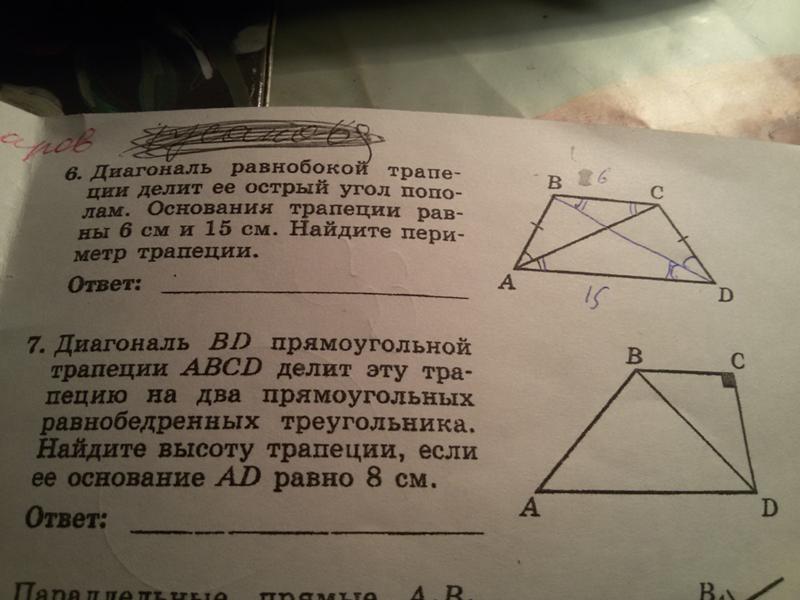


 Так как
треугольник AOD – прямоугольный, то, если описать около него
окружность, то ее центр будет лежать на середине гипотенузы AD, в точке M, AD –
диаметр этой окружности. Поэтому, если провести медиану к гипотенузе AD из
вершины O, то она будет равна радиусу окружности и половине AD: AM=MD=MO. Тогда треугольники AOM, KNO, BSO –
равнобедренные. Кроме того, NО – медиана треугольника KLO и
разделит его основание пополам: NK=NL=NO=5,5.
Если же ON=5,5, то SO=ON-NS=0,5. (Отрезок SN равен 5, так как NL – средняя
линия трапеции MSCD, и разделит MS пополам). Так как BS=SC=SO=0,5, то BC=1, и тогда из теоремы о средней линии
AD=21.
Так как
треугольник AOD – прямоугольный, то, если описать около него
окружность, то ее центр будет лежать на середине гипотенузы AD, в точке M, AD –
диаметр этой окружности. Поэтому, если провести медиану к гипотенузе AD из
вершины O, то она будет равна радиусу окружности и половине AD: AM=MD=MO. Тогда треугольники AOM, KNO, BSO –
равнобедренные. Кроме того, NО – медиана треугольника KLO и
разделит его основание пополам: NK=NL=NO=5,5.
Если же ON=5,5, то SO=ON-NS=0,5. (Отрезок SN равен 5, так как NL – средняя
линия трапеции MSCD, и разделит MS пополам). Так как BS=SC=SO=0,5, то BC=1, и тогда из теоремы о средней линии
AD=21.
Leave A Comment