Модуль ускорения свободного падения на планете а в 4 раза больше: Ускорение свободного падения — урок. Физика, 9 класс.

Ускорение свободного падения на Земле и на Луне

☰

Все тела притягиваются друг к другу — это закон всемирного тяготения. Силы, с которыми тела притягиваются вычисляются по формуле:

F = G × m₁m₂ ÷ R²

Здесь G — это гравитационная постоянная, равная 6,67 × 10^-11 Н · м²/кг². Она численно равна силе, с которой одно тело массой 1 кг притягивает другое тело с массой 1 кг, находящееся от него на расстоянии 1 м. Как мы видим, это очень маленькая сила. Поэтому мы замечаем притяжение только к очень массивным телам, космического масштаба.

Если размеры одного тела несоизмеримо меньше размеров другого тела и оно находится на поверхности второго тела или на высоте намного меньше радиуса второго тела, то за расстояние между телами принимается радиус второго тела. (Притяжение всегда идет к центру тела.)

В результате действия закона всемирного тяготения планеты и другие космические тела притягивают к себе другие тела.

Эта сила притяжения называется силой тяжести. Под ее действием падающим телам сообщается ускорение свободного падения (g). Сила тяжести вычисляется по формуле:

F = mg

Подставим вместо F в первую формулу значение F из второй. При этом пусть m₁ — это масса падающего на Землю тела. Обозначим ее как m. А m₂ — это масса Земли. Обозначим ее как M. Тогда получим:

mg = G × mM ÷ R²

Разделим обе части формулы на m (массу падающего тела):

g = G × M ÷ R²

Мы видим, что ускорение свободного падения зависит от массы и радиуса планеты. Чем больше ее масса, тем сильнее она притягивает тела и тем больше на ней ускорение свободного падения. Чем больше радиус планеты, тем дальше от ее центра находится притягиваемое тело и тем меньше будет ускорение свободного падения.

Таким образом, чтобы сравнить ускорение свободного падения на Земле и Луне, надо сравнить отношения их масс к квадратам их радиусов. Но чтобы найти само ускорение свободного падения, надо еще умножить на гравитационную постоянную.

Масса Земли приблизительно равна 6 × 10²⁴ кг, а ее радиус приблизительно равен 6400 км (6,4 × 10⁶ м). Поэтому ускорение свободного падения на Земле приблизительно будет равно:

g = 6,67 × 10^-11 Н × м²/кг² × 6 × 1024 кг ÷ (6,4 × 106 м)² ≈ 0,977 × 10¹ ≈ 9,8 Н/кг (м/c²)

Масса Луны примерно равна 7,5 × 10²² кг, а ее радиус примерно равен 1750 км. Поэтому ускорение свободного падения на Луне приблизительно будет равно:

g = 6,67 × 10^-11 Н × м²/кг² × 7,5 × 10²² кг ÷ (1,75 × 10⁶ м)² ≈ 16,335 10^-1 ≈ 1,6 Н/кг (м/с²)

Отношение ускорений свободного падения на Земле и Луне равно 9,8 : 1,6 ≈ 6 : 1. Значит, сила притяжения тела с массой m на Луне будет примерно в 6 раз меньше, чем на Земле.

Формула ускорения свободного падения в физике

Формула ускорения свободного падения в физике

Гравитационное поле и ускорение свободного падения

Гравитационные взаимодействия тел можно описывать, применяя понятие гравитационного поля. Считают, что передача любых взаимодействий между телами реализуется при помощи полей, которые создают рассматриваемые тела. Одно из тел не оказывает непосредственного действия на другое тело, но оно создает в окружающем его пространстве гравитационное поле, особый вид материи, которая и оказывает воздействие на второе тело. Наглядной картины поля дать нельзя, понятие физического поля относят к основным понятиям, которые невозможно определить, используя другие более простые понятия. Можно только определить свойства поля.

Гравитационное поле может создавать силу. Поле зависит только от тела, которое его создает и не зависит от тела, на которое оно действует. Силовой характеристикой гравитационного поля является его напряжённость, которую обозначают $\overline{g}$. 2}\left(2\right).\]

Из формулы (2) следует, что $g$ зависит от расстояния ($r$) от источника поля до точки, в которой поле рассматривается. В таком поле движение происходит по законам Кеплера.

Гравитационные поля удовлетворяют принципу суперпозиции. Напряженность поля, которая создается несколькими телами, равна векторной сумме напряженностей полей, которые порождаются каждым телом отдельно. Принцип суперпозиции выполняется, поскольку гравитационное поле, создаваемое какой-либо массой, не зависит от присутствия других масс. Принцип суперпозиции дает возможность рассчитывать гравитационные поля, которые созданы телами, отличающимися от точечных (размеры которых следует учитывать).

Ускорение при свободном падении

Если тело около поверхности Земли движется только под воздействием силы тяжести ($\overline{F}$), говорят, что оно свободно падает. Ускорение свободного падения обозначают буквой $g$. В соответствии со вторым законом Ньютона это ускорение равно:

\[\overline{g}=\frac{\overline{F}}{m}\left(3\right),\]

где $m$ — масса свободно падающего тела. 2}\frac{3}{4\pi }\frac{g_0}{\gamma R}=g_0\frac{R-h}{R}\to h=R\left(1-\frac{g}{g_0}\right)=0,7R.\]

Ответ. $h=R\left(1-\frac{g}{g_0}\right)=0,7R$

Читать дальше: формула центростремительного ускорения.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Гравитация | План урока MINDSTORMS EV3

ARROW_LEFTARROW_LEFTПлан модуля

Урок 1 из 1

Базовый набор MINDSTORMS® EV3

Модуль обучения свободному падению выделяет уравнение времени-расстояния, когда объект ускоряется.

ЧАСЫ

90-120 мин.

КИРПИЧ

Промежуточный.

ВЫПУСКНИК

6-8 классы

Connect

(5 минут)

Свободное падение описывает состояние, в котором такие предметы, как камни, монеты или падающие фрукты, падают на землю под действием силы тяжести.

Интересные соображения включают :
расстояние, пройденное объектом при свободном падении,
время падения объекта до удара о землю,
скорость, с которой объект падает, и
скорость ускорения объекта.

Следующий эксперимент включает в себя строительство падающей башни, оснащенной соответствующими датчиками для наблюдения за гравитационными явлениями, воздействующими на стальной шар при свободном падении.

Примечания по предварительным соображениям
Объясните, почему опасно сидеть под деревом, полным спелых яблок.
Яблоки могут упасть на землю, и невозможно среагировать достаточно быстро, чтобы убраться с дороги.

Объясните, зачем человеку, прыгающему с большой высоты из самолета, нужен парашют.
Потому что иначе они упадут слишком быстро и будут раздавлены при ударе.

Перечислите повседневные события, в которых гравитация играет роль.
Все, что падает, проточная вода, движение/бег по поверхности земли и т.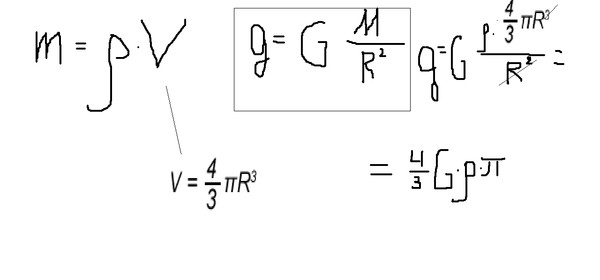 д.

Построить

(20 минут)

Заметки по строительству
Убедитесь, что учащиеся правильно построили падающую башню, а также правильно загрузили предоставленную программу.

ПРОСМОТРЕТЬ ИНСТРУКЦИЮ ПО СБОРКЕ

Загрузить программу «10»

ЗАГРУЗИТЬ ОБРАЗЕЦ ПРОГРАММЫ 23 КБ, требуется программное обеспечение EV3 Desktop

Contemplate

(20 минут17 примечаний)

при использовании модели
Датчик касания установлен на задняя часть башни падения. Он используется для запуска эксперимента с падением.
: Захват автоматически закрывается для следующего эксперимента.
Дисплей модуля EV3 показывает время падения.

• Убедитесь, что модель построена правильно.
• Правильно поместите модель на твердую и ровную поверхность.
• Убедитесь, что башня не трясется при выпуске мяча.
• Датчик касания также можно держать и использовать в качестве ручного пульта дистанционного управления, если это необходимо. Это позволяет избежать сотрясения башни, что может привести к недействительным тестам.

Эксперимент – измерение

1. Старт программы «10»
2. Поместите мяч в закрытый захват.
3. Начните тест с помощью бесплатного датчика касания на падающей башне.

Вот что происходит:
Мяч падает на датчик касания в нижней части башни.
Время падения отображается на дисплее.
Захват закрывается, и теперь вы можете повторить эксперимент.
Неверные тесты приводят к сердитому лицу.
Проведите эксперимент не менее трех раз.
Запишите в таблицу номера экспериментов и время падения. Расширьте таблицу, если это необходимо.

Убедитесь, что учащиеся провели эксперимент несколько раз, и занесите свои результаты в предоставленную таблицу.
Сообщите учащимся, что записанные ими результаты измерений будут использоваться в последующих заданиях.

Продолжить

(15 минут)

Анализ
Вы знаете расстояние падения d и время падения t.

1. Используя измеренное время падения, рассчитайте среднюю скорость v падающего мяча.
2. Введите результаты в таблицу.
   Напоминаем: v = d/t.
   Согласно закону падения тел : d = 0,5 * g * t².
   г — естественная постоянная, обозначающая ускорение свободного падения.
3. Решите уравнение закона падения тел для g.
4. Рассчитайте ускорение свободного падения (g) на основе измеренных значений ваших экспериментов.
5. Введите рассчитанные значения g в таблицу.

Предложите учащимся выполнить дополнительные расчеты с использованием измеренных значений.
Расчетная скорость является средней скоростью, а не скоростью удара.
Различные измеренные значения приводят к различным значениям ускорения свободного падения. Сообщите учащимся о возможных ошибках измерения.
Сообщите учащимся, что установленное значение ускорения свободного падения на Земле предполагает свободное падение в идеальном вакууме.

Обзор
Кратко подведите итоги вашего эксперимента. Сообщите о том, что вы узнали.

• Предыстория и вопрос (тема)
• Ответы (связывание)
• Выводы
• Как это связано с повседневной жизнью (где мы видим или используем то, что наблюдали в повседневной жизни?)

Поддержка учителей

4

Учащиеся знают

Как определить гравитационную постоянную
Существуют законы гравитации, применимые ко всем объектам

Учащиеся умеют
Записывать измеренные значения
Анализировать измеренные значения
Интерпретировать результаты
Понимать взаимосвязь между используемыми материалами и их влияние на результаты

Навыки, связанные с экспериментом
Получение ускорения свободного падения из экспериментов

Введение в EV3 ScienceEV3 Science Curriculum GridAcceleration of Gravity Вопросы учащихсяAcceleration of Gravity Вопросы учащихся с ответамиAcceleration of Gravity дополнительная информация

0

Материалы для учащихся

Рабочий лист для учащихся

Загрузите, просмотрите или поделитесь в виде онлайн-страницы HTML или PDF-файла для печати.

Посмотреть онлайн

Гравитация | Физика | Visionlearning

• Закладка
• Глоссарий терминов

Что заставляет предметы падать на Землю? Почему планеты вращаются вокруг Солнца? Что удерживает галактики вместе? Если бы вы отправились на другую планету, почему бы изменился ваш вес?

Все эти вопросы относятся к одному аспекту физики: гравитации. При всем его влиянии на нашу повседневную жизнь, при всем его контроле над космосом и при всей нашей способности описывать и моделировать его эффекты, мы не понимаем реальных механизмов гравитационной силы. Из четырех фундаментальных взаимодействий, идентифицированных физиками — сильной ядерной, электрослабой, электростатической и гравитационной — гравитационная сила изучена меньше всего. Физики сегодня стремятся к «теории Великого объединения», в которой все четыре эти силы объединены в одну физическую модель, описывающую поведение всего во Вселенной. В данный момент беспокойной силой является гравитационная сила, сила, которая сопротивляется объединению.

Несмотря на тайну механизмов гравитации, физикам удалось довольно подробно описать поведение объектов под действием гравитации. Исаак Ньютон, английский ученый и математик семнадцатого по восемнадцатый век (среди прочего), был первым, кто предложил математическую модель для описания гравитационного притяжения между объектами. Альберт Эйнштейн опирался на эту модель в двадцатом веке и разработал более полное описание гравитации в своей общей теории относительности. В этом модуле мы рассмотрим ньютоновское описание гравитации и некоторые экспериментальные подтверждения его теории, которые появились спустя много лет после того, как он предложил свою первоначальную идею.

Яблоко

Независимо от того, действительно ли Исаак Ньютон сидел под яблоней, размышляя о природе гравитации, тот факт, что объекты падают на поверхность Земли, был хорошо известен задолго до Ньютона. У каждого есть опыт работы с гравитацией и ее воздействием вблизи поверхности Земли, и наш интуитивный взгляд на мир включает в себя понимание того, что то, что поднимается, должно опускаться.

Галилео Галилей (1564–1642) продемонстрировал, что все объекты падают на поверхность Земли с одинаковым ускорением, и что это ускорение не зависит от массы падающего объекта (см. Концептуальное моделирование Пизанская башня, эксперимент ниже). . Исаак Ньютон, без сомнения, был знаком с этой концепцией, и в конце концов он сформулировал широкую и далеко идущую теорию гравитации. Теория Ньютона будет охватывать не только поведение яблока вблизи поверхности Земли, но и движение гораздо более крупных тел на достаточно большом расстоянии от Земли.

Планеты

Ранние представления о Вселенной были «геоцентрическими» — они помещали Землю в центр Вселенной, а планеты и звезды двигались вокруг Земли. Эта птолемеевская модель Вселенной доминировала в научной мысли на протяжении многих столетий, пока работы таких внимательных астрономов, как Тихо Браге, Николай Коперник, Галилео Галилей и Иоганн Кеплер, не вытеснили этот взгляд на космос. «Коперниканская революция» поместила Солнце в центр Солнечной системы, а планеты, включая Землю, на орбиты вокруг Солнца. Этот значительный сдвиг в восприятии заложил основу для того, чтобы Исаак Ньютон начал думать о гравитации, поскольку она связана с движением планет.

Рисунок 1: Изображение Солнечной системы © Вектомарт/Shutterstock

Ранняя теория объединения

Точно так же, как современные физики ищут способы объединить фундаментальные силы, Исаак Ньютон также стремился объединить два, казалось бы, несовместимых явления: движение объектов, падающих на Землю, и движение планет, вращающихся вокруг Солнца. Открытие Исаака Ньютона заключалось не в том, что яблоки падают на Землю из-за гравитации; дело в том, что планеты постоянно падают к солнцу по одной и той же причине: гравитации!

Ньютон основывался на работах первых астрономов, в частности Иоганна Кеплера, который в 1596 и 1619 годах опубликовал свои законы движения планет. Одним из центральных наблюдений Кеплера было то, что планеты движутся по эллиптическим орбитам вокруг Солнца. Ньютон расширил кеплеровское описание движения планет до теории гравитации.

Проверка понимания

Какой самый важный вклад Ньютона в наше понимание гравитации?

• а. Яблоки падают на землю под действием силы тяжести.
• b.Планеты притягиваются к Солнцу из-за гравитации.

Закон всемирного тяготения Ньютона

Существенной особенностью закона всемирного тяготения Ньютона является то, что сила притяжения между двумя объектами обратно пропорциональна квадрату расстояния между ними. Такая связь известна как связь «обратный квадрат». Ньютон вывел это соотношение из утверждения Кеплера о том, что планеты движутся по эллиптическим орбитам. Чтобы понять это, рассмотрим свет, исходящий от поверхности Солнца. Свет имеет некоторую интенсивность на поверхности солнца. По мере удаления света от солнца его интенсивность уменьшается. Интенсивность света на любом расстоянии от солнца равна силе источника, деленной на площадь поверхности сферы, окружающей солнце на этом радиусе.

Когда расстояние от солнца ( r ) удваивается, площадь сферы, окружающей солнце, увеличивается в четыре раза. Таким образом, интенсивность солнечного света обратно пропорциональна квадрату расстояния от Солнца. Ньютон представил гравитационную силу равно излучаемой во всех направлениях от центрального тела, точно так же, как солнечный свет в предыдущем примере. Ньютон понял, что его гравитационная модель должна иметь форму отношения обратных квадратов. Такая модель предсказывает, что орбиты объектов вокруг центрального тела будут представлять собой конические сечения, и годы астрономических наблюдений подтвердили это. Хотя эту идею чаще всего приписывают Исааку Ньютону, английский математик Роберт Гук утверждал, что он создал идею отношения обратных квадратов. Тем не менее, Ньютон в конце концов опубликовал свою теорию гравитации и в результате прославился.

Соотношение, которое придумал Ньютон, выглядит так:

F=Gm1m2r2

, где F — сила тяжести (в единицах, которые теперь называются ньютонами), m ₁ и m ₂ — массы двух объектов в килограммах (например, Солнце и Земля), r — расстояние, разделяющее центры масс объектов, а G — «гравитационная постоянная». Уравнение показывает, что сила тяжести прямо пропорциональна произведению двух масс, но обратно пропорциональна квадрату расстояния между центрами этих двух масс. Чтобы понять формулу, имейте в виду, что сила тяжести уменьшается с увеличением расстояния (обратная зависимость). Расстояние ( r ) возводится в квадрат из-за соотношения между увеличением расстояния и увеличением площади, на которую действует сила (точно так же, как лучи света распространяются по мере удаления от солнца). Наконец, поскольку обе массы действуют под действием гравитации, значение имеет произведение их масс, а не просто одна масса.

Это соотношение стало известно как закон всемирного тяготения Ньютона. Оно «универсально», потому что все объекты во вселенной притягиваются ко всем другим объектам во вселенной в соответствии с этим отношением. Два человека, сидящие друг напротив друга в комнате, на самом деле притягиваются гравитацией. Как мы знаем из повседневного опыта, объекты размером с человека не врезаются друг в друга под действием этой силы, но она существует, даже если она очень мала. Хотя Ньютон правильно определил эту связь между силой, массой и расстоянием, он смог только оценить значение гравитационной постоянной между этими величинами. Миру пришлось бы ждать более столетия экспериментального измерения константы пропорциональности: Г .

Контрольная точка понимания

Чем дальше два объекта друг от друга, тем сильнее гравитационное притяжение между ними.

• правда
• б.ложь

Измерение массы Земли: эксперимент Кавендиша

В 1797 и 1798 годах Генри Кавендиш намеревался подтвердить теорию Ньютона и определить константу пропорциональности в законе всемирного тяготения Ньютона. Его гениальный эксперимент, основанный на работе Джона Мичелла, увенчался успехом в обоих направлениях. Для этого Кавендиш создал «крутильные весы», которые состояли из двух масс на обоих концах стержня, подвешенного к потолку на тонкой проволоке (см. рис. 2).

Рисунок 2 : Торсионные весы, разработанные Мичеллом и Кавендишем для определить константу пропорциональности в законе всемирного тяготения Ньютона.

К проводу было прикреплено зеркало, от которого отражался луч света. Кавендиш приблизил третью массу к одной из масс на крутильных весах. Поскольку третья масса притягивала один из концов крутильных весов, весь прибор, включая зеркало, слегка вращался, и пучок света отклонялся. Тщательно измерив угловое отклонение луча света, Кавендиш смог определить степень притяжения известной массы к введенной массе. Кавендиш не только подтвердил теорию Ньютона, но и определил значение гравитационной постоянной с точностью около 1 процента.

G=6,674×10−11 Нм2кг2

Кавендиш удачно назвал свое исследование «Измерение массы Земли». Поскольку он определил значение G , он мог сделать несколько простых вычислений, чтобы определить массу Земли. По второму закону Ньютона сила между объектом и Землей равна произведению ускорения ( a ) на массу объекта ( м ):

Галилей определил ускорение свободного падения ( g ) всех объектов вблизи поверхности Земли в начале 1600-х годов как g=9,8 мс2.

Следовательно, приравняв это уравнение к закону всемирного тяготения Ньютона, описанному выше, Кавендиш нашел:

F=mg=GmmErE2

, где m — масса объекта, m _E — масса Земли, а r _E — радиус Земли. Решение для массы Земли дает следующий результат:

mE=grE2G=(9,8 мс2)(6,38×106 м)26,67×10−11 Нм2кг2

мЭ=5,98×1024 кг

Кавендиш с большой точностью определил массу Земли. Мы также можем использовать это соотношение для расчета силы притяжения между двумя людьми в комнате. Для этого нам просто нужно использовать закон всемирного тяготения Ньютона с гравитационной постоянной Кавендиша. Предположим, что два человека имеют массу 75 и 100 кг соответственно и находятся на расстоянии 5 метров друг от друга. Сила притяжения между ними равна:

F=(6,67×10−11 Нм2кг2)⋅(75кг)⋅(100кг)(5м)2

F=2.00×10−8N

Несмотря на маленькую силу, она все же есть!

Заключение

Закон всемирного тяготения Ньютона приобретал все большее значение, когда ученые осознавали его полезность в предсказании орбит планет и других тел в космосе. В 1705 году сэр Эдмунд Галлей, тщательно изучив кометы, правильно предсказал, что знаменитая комета 1682 года вернется 76 лет спустя, в декабре 1758 года. Галлей использовал закон Ньютона, чтобы предсказать поведение кометы, вращающейся вокруг Солнца. С появлением точного значения Кавендиша для гравитационной постоянной ученые получили возможность использовать закон Ньютона для еще большего числа целей. В 1845 году Джон Коуч Адамс и Урбен Леверье предсказали существование новой, еще невидимой планеты, основываясь на небольших расхождениях между предсказаниями и наблюдениями за положением Урана. В 1846 году немецкий астроном Иоганн Галле подтвердил их предсказания и официально открыл новую планету Нептун.

Хотя закон всемирного тяготения Ньютона остается очень полезным и сегодня, Альберт Эйнштейн продемонстрировал в 1915 году, что закон верен только приблизительно и что он не работает, когда гравитация становится чрезвычайно сильной. Тем не менее, гравитационная постоянная Ньютона играет важную роль в общей теории относительности, альтернативной Эйнштейном закону Ньютона. Значение G было предметом больших споров даже в последние годы, и ученые все еще пытаются определить очень точное значение этой самой неуловимой из фундаментальных физических констант.