mopg[1] — Стр 3
16. В остроугольном треугольнике ABC проведены высоты CH и Ah2 . Известно, что AC = 2 и площадь круга, описанного
около треугольника HBh2 , равна π3 . Найти угол между высотой
CH и стороной BC . (Ответ: 30o ).
17.Дан треугольник со сторонами 4, 8, 9. Найти длину биссектрисы, проведенной к большей стороне. (Ответ: 14 ).
18.Биссектриса AD равнобедренного треугольника ABC делит его на треугольники ABD и ACD площадью 4см2 и 2см2 соответственно. Найти стороны треугольника, если AC — его ос-
нование. (Ответ: | 2 6 | , | 4 6 | , | 4 6 | ). | |
4 15 | 4 15 | 4 15 | |||||
|
|
|
|
19. В равнобедренном треугольнике ABC (AB = BC) проведена биссектриса AD . Площади треугольников ABD и ADC равны S1 и S2 . Найти длину основания треугольника. (От-
В равнобедренном треугольнике ABC (AB = BC) проведена биссектриса AD . Площади треугольников ABD и ADC равны S1 и S2 . Найти длину основания треугольника. (От-
вет: 2 S(22 (S1 + S2 ))2 ). 4S12 − S22
20.Доказать, что если биссектриса одного из углов треугольника равна произведению заключающих ее сторон, деленному на их сумму, то этот угол равен 120°.
21.В равнобедренном треугольнике угол при основании равен 72°, а биссектриса этого угла имеет длину, равную m. Найти
длины сторон треугольника. (Ответ: m, m( 5 +1) , m( 5 +1) ).
2 2
22. В равнобедренном треугольнике угол при вершине равен 36°, а биссектриса угла при основании равна 20 . Найти длины сторон треугольника. (Ответ: 2 5,5 + 5,5 + 5 ).
23.Медиана ВМ треугольника АВС равна его высоте АН. Найдите угол МВС. (Ответ: 30° или 150°).
24.Высоты треугольника ABC пересекаются в точке Н. Известно, что СН = АВ. Найдите угол АСВ. (Ответ: 45° или 135º).
25.Точки А1, B1, C1 , — основания высот треугольника ABC.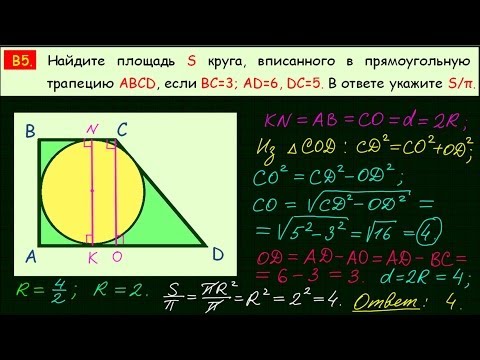 Углы треугольника А1B1C1 равны 90°, 60° и 30°. Найдите углы треугольника ABC. (Ответ: 45°, 75°,60° или 135°, 15°, 30°, или 120°, 15°, 45° или 105°, 30°, 45°).
Углы треугольника А1B1C1 равны 90°, 60° и 30°. Найдите углы треугольника ABC. (Ответ: 45°, 75°,60° или 135°, 15°, 30°, или 120°, 15°, 45° или 105°, 30°, 45°).
26.Точки D и E – основания высот непрямоугольного треугольника АВС, проведенных из вершин А и С соответственно.
Известно, | что | DE | = k, BC = a, AB = b . Найдите сторону АС. | |
AC | ||||
|
|
| ||
(Ответ: | a2 +b2 −2abk или a2 +b2 + 2abk ). | |||
27. Углы при вершинах А и С треугольника ABC равны 45° и 60° соответственно; AM, BN и СК — высоты треугольника. Най-
ти отношение MN : KN. (Ответ: 23 ).
28. В треугольнике АВС проведены высоты АА1, ВB1 и СC1.
Известно, что угол BAC =120o и АА1=6.
29. Высоты треугольника АВС пересекаются в точке Н . Известно, что отрезок СН равен радиусу окружности, описанной около треугольника АВС. Найдите угол АСВ . (Ответ: 60° или 120º).
30.Отрезки, соединяющие основания высот остроугольного треугольника, равны 5, 12 и 13. Найти площадь треугольника.
(Ответ: 195).
31.Найти площадь прямоугольного треугольника, если известны радиусы R и r описанного и вписанного в него кругов.
(Ответ: R2 + 2Rr ).
32.В равнобедренном треугольнике АВС с основанием АВ вершины А,С и точка пересечения высот расположены на одной окружности радиуса 5. Найти площадь треугольника АВС, если АС=6. (Ответ:432/25).
33.В треугольнике АВС биссектриса AD делит сторону ВС в отношении BD:CD=2:1. В каком отношении медиана СЕ делит эту биссектрису? (Ответ: 3:1).
34.В треугольнике АВС площадью 40 см2 биссектриса AD делит сторону ВС на отрезки BD и DC, причем BD:DC=3:2. Бис-
сектриса AD пересекает медиану ВК в точке Е. Найти площадь четырехугольника EDCK. (Ответ:11 см2).
Найти площадь четырехугольника EDCK. (Ответ:11 см2).
35.В треугольнике АВС биссектриса АН делит медиану ВЕ в отношении ВК:КЕ=2, а угол АСВ равен 45о. Найти отношение площади треугольника ВСЕ к площади описанного около этого
треугольника круга. (Ответ: 54π ).
36. Продолжения медиан АМ и ВК треугольника АВС пересекают описанную около него окружность в точках E и F соответственно, причем AE:AM=2:1, BF:BK=3:2. Найти углы тре-
угольника АВС. (Ответ: π2 ,arctg2, π2 −arctg2 ).
37. Большее основание трапеции в два раза больше ее меньшего основания. Через точку пересечения диагоналей проведена
42
прямая, параллельная основаниям. Найти отношение высоты каждой из двух полученных трапеций к высоте данной трапе-
ции. (Ответ: 1:3, 2:3).
38.Диагонали равнобедренной трапеции взаимно перпендикулярны , а ее площадь равна а2. Определить высоту трапеции. (Ответ: а).
39.Вычислить площадь равнобедренной трапеции, если ее
высота равна h, а боковая сторона видна из центра описаннй ок-
ружности под углом 60о. (Ответ: h3 3 ).
(Ответ: h3 3 ).
40.Сумма квадратов параллельных сторон трапеции равна
228.Определить длину отрезка, параллельного этим сторонам и делящего площадь трапеции пополам. (Ответ: 12).
41.Найти среднюю линию равнобедренной трапеции с высотой h, если боковая сторона видна из центра описанной окруж-
ности под углом 120°. (Ответ: h43 ).
42.Центр окружности, описанной около равнобедренной трапеции делит ее высоту в отношении 3:4 (считая от большего основания. Найти основания трапеции, если ее средняя линия равна высоте, а радиус окружности равен 10. (Ответ: 12 и 16).
43.Четырехугольник АВСD вписан в окружность. Известно,
что BD=7, CD=8, DC<4, BAD =120o . Определить угол CAD. (Ответ: arccos(−1/ 7)).
44.Четырехугольник АВСD вписан в окружность. Известно,
что AB=7, AC=5, BC<5, ADС =135o . Определить угол ADB.
(Ответ: arccos(−1/ 5 2)).
43
45. Центр окружности, вписанной в прямоугольную трапецию, удален от концов ее боковой стороны на расстояния 3см и
9см.
46.Центр круга, вписанного в прямоугольную трапецию, отстоит от концов боковой стороны на 1 и 2. Найти площадь тра-
пеции. (Ответ:3,6).
47.Основания трапеции равны 4 и 16. Найти радиусы окружностей, вписанной в трапецию и описанной около нее, если из-
вестно, что эти окружности существуют. (Ответ: 4 и 5 441 ).
48. Равнобедренная трапеция ABCD с основаниями AD и BC описана около окружности с центром О. Найти площадь трапе-
ции, если АВ=4, ВО=1. (Ответ: 2 15 ).
49. Дан вписанный четырехугольник с взаимно перпендикулярными диагоналями. Докажите, что ломаная, проходящая через центр описанной окружности и две противоположные вершины четырехугольника делит его на две равновеликие части.
50. В окружности радиуса R проведены две пересекающиеся перпендикулярные хорды AB и CD. Доказать, что
AC2 + BD2 = 4R2 .
51. Боковая сторона неравнобедренной трапеции равна 12 и образует с ее основанием угол 60°. Основания трапеции равны 16 и 40. Найти длину отрезка, соединяющего середины основа-
Основания трапеции равны 16 и 40. Найти длину отрезка, соединяющего середины основа-
ний. (Ответ: 12 или 6 13 ).
52. Сумма внутренних углов при основании AD трапеции ABCD равна 135°. В трапецию вписана окружность, причем бо-
44
ковая сторона AВ делится точкой касания на отрезки длины 2
и 4 2 . Определить длину боковой стороны CD трапеции. (От-
вет: 40 или 40/7).
53.Косинус угла между боковыми сторонами AD и BC трапеции ABCD равен 0,8. В трапецию вписана окружность, причем сторона AD делится точкой касания на отрезки длины 1 и 4. Определить длину боковой стороны BC трапеции. (Ответ: 4 или
100/7).
54.Диагонали выпуклого четырёхугольника равны а и b, а отрезки, соединяющие середины противоположных сторон, равны между собой. Найти площадь четырёхугольника.
(Ответ: ab2 ).
55. Доказать следующие соотношения:
а) | ra +rb +rc = 4R +r ; b) S = rra rbrc ; | ||||||||||||||||
c) | 1 | = | 1 | + | 1 | + | 1 | ; | 1 | = | 1 | + | 1 | − | 1 |
| |
r | r | r | r | r | h | h | h | ||||||||||
|
|
|
|
|
|
|
| ||||||||||
|
|
| a |
| b |
| c |
| a |
| b |
| c |
| a | ||
где: a, b и c – стороны треугольника;
ha , hb , hc — высоты, проведенные из вершин треугольника к сто-
ронам a, b и c соответственно;
ra , rb , rc — радиусы вневписанных окружностей, касающихся сторон a, b и c соответственно;
R– радиус описанной окружности; r – радиус вписанной окружности;
S– площадь треугольника;
56. Вписанная окружность треугольника ABC касается стороны BC в точке K, а вневписанная — в точке L. Доказать, что CK=BL=(a+b-c)/2, где a, b, c – длины сторон треугольника.
Вписанная окружность треугольника ABC касается стороны BC в точке K, а вневписанная — в точке L. Доказать, что CK=BL=(a+b-c)/2, где a, b, c – длины сторон треугольника.
45
57.Доказать, что в прямоугольном треугольнике с гипотенузой с rc = r +ra +rb .
58.Доказать, что сторона BC треугольника ABC видна из центра O вписанной окружности под углом 90°+ A/ 2 , а из цен-
тра Ia вневписанной окружности под углом 90°− A/ 2 .
59. Вневписанная окружность треугольника АВС касается его стороны ВС в точке К, а продолжения стороны АВ — в точке L. Другая вневписанная окружность касается продолжений сторон АВ и ВС в точках М и N соответственно. Доказать, что прямая KL параллельна, а прямая MN перпендикулярна биссектрисе угла В треугольника.
60. В треугольнике ABC угол C прямой. Докажите, что rc = a +2b +c .
61. Радиус окружности, описанной около остроугольного треугольника ABC, равен 1. Известно, что на этой окружности лежит центр другой окружности, проходящей через вершины A, C и точку пересечения высот треугольника ABC. Найдите AC.
Найдите AC.
(Ответ: 3 ).
62. В выпуклом четырехугольнике ABCD известно, что
CBD = 58o, ABD = 44o, ADC = 78o . Найти угол CAD. (Ответ: 58°).
46
Литература
1.Александров А.Д. Геометрия: учебное пособие для 8 кл. с углубленным изучением математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. – М.: Просвещение, 2002. – 240с.
2.Александров А.Д. Геометрия: учебное пособие для 9 кл. с углубленным изучением математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. – М.: Просвещение, 2004. – 240с.
3.Атанасян Л.С. Геометрия, 7 – 9: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2009. – 384с.
4.Атанасян Л.С. Геометрия: доп. главы к шк. учеб. 8 кл.: учебное пособие для учащихся шк. и кл. с углубленным изучением математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев
идр. – М.: Просвещение, 1996. – 205с.
5.Атанасян Л.С. Геометрия: доп. главы к шк. учеб. 9 кл.: учебное пособие для учащихся шк. и кл. с углубленным изучением математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев
и кл. с углубленным изучением математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев
идр. – М.: Просвещение, 1997.
6.Белоносов М.В. Задачи вступительных экзаменов по математике: учебное пособие / М.В. Белоносов, М.В. Фокин. − Новосибирск: Изд-во Новосиб. Ун-та: Сиб. Унив. изд-во, 2002.
– 215с.
7.Гордин Р.К. ЕГЭ 2010. Математика. Задача С4 / Гордин Р.К.: под ред. А.Л. Семенова и И.В. Ященко. – М. МЦНМО. 2010 — 148 с.
8.Готман Э.Г. Задача одна – решения разные. Геометрические задачи / Э.Г. Готман, С. Залман. – М.: Просвещение, 2000. – 224с.
9.Готман Э.Г. Задачи по планиметрии и методы их решения / Э.Г. Готман. – М.: Просвещение, 1996. – 241с.
10.Егерев В.К. Сборник задач по математике для поступающих в вузы: учебное пособие / В.К.Егерев, В.В. Зайцев и др.; под ред. Сканави М.И. – М.: Издательский Дом ОНИКС: Альянс-
В, 2003. – 608с.
47
11.Зив Б.Г. Задачи по геометрии для 7 – 11 классов./ Б.Г. Зив, В.М. Мейлер, А.П. Баханский. – М. : Просвещение, 2009. – 271с.
: Просвещение, 2009. – 271с.
12.Куланин Е.Д. 3000 конкурсных задач по математике. / Е.Д. Куланин, В.П. Норин, С.Н. Федин, Ю.А. Шевченко. – Изд. 5- е испр. – М.: Айрис-пресс, 2003. — 624с.
13.Понарин Я. П. Элементарная геометрия: В 2 т. Т. 1: Планиметрия, преобразования плоскости./ Я.П. Понарин. – М.:
МЦНМО, 2004. – 312с.
14.Прасолов В. В. Задачи по планиметрии / В.В. Просолов. –
Изд. 4-е, допол. – М.: МЦНМО, 2001. – 584 с
15.Сборник задач по математике для поступающих в вузы / под ред. Прилепко А.И. – М.: Высшая школа, 1989. – 271с.
16.Шарыгин И.Ф. Математика. 2200 задач по геометрии для школьников и поступающих в вузы / И.Ф. Шарыгин. – М.:
Дрофа, 1999. – 304с.
17.Шарыгин И.Ф. Стандарт по математике: 500 геометрических задач: кн. для учителя / И.Ф. Шарыгин. – М.: Просвещение, 2005. – 205с.
Методическое пособие
Осипенко Лариса Анатольевна Стацевичуте Елена Эдмундовна
Опорные задачи в планиметрии
Серия «Университетский лицей»
Компьютерный набор авторов
МОУ Лицей ИГУ г. Иркутска Г. Иркутск, ул. Курчатова, 13а
Иркутска Г. Иркутск, ул. Курчатова, 13а
Тел./факс (3952) 41-05-35 e-mail: [email protected]
Подписано в печать 02.06.10. Формат 60х84 1/16 Бумага офисная. Печать DUPLO.
Заказ 8. Тираж 200 экз. Усл. печ .л. 3,0
УНИВЕРСИТЕТСКИЙ ЛИЦЕЙ
Вып.1 О.В.Кузьмин. Принцип Дирихле.
Вып.2 Э.А. Маричева. Практикум к курсу «Биология человека». Вып.3 Э.Ф. Дубинина, Л.Н. Шеметова. Компьютерная графика.
Вып.4 Э.Ф. Дубинина, Л.Н. Шеметова. Компьютерная графика. CorelDRAW Вып.5 Л.А. Осипенко. Комбинации сферы и многогранников. Задачи и упражнения.
Вып. 6 Р.М. Островская, В.И. Чемерилова В.И. Решаем задачи по генетике. Том 1.
Вып. 7 Р.М. Островская, В.И. Чемерилова В.И. Решаем задачи по генетике. Том 2.
Вып.8 Л.А. Осипенко, Е.Э. Стацевичуте. Опорные задачи планиметрии.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
24.04.2019710.66 Кб1Logika-OZO.doc
- #
27.
 08.2019248.83 Кб2m340.doc
08.2019248.83 Кб2m340.doc - #
10.09.2019168.45 Кб1Metodicheskie_ukazania_k_kursovomu_proektirovan…doc
- #
14.04.2019145.09 Кб8MMPI.docx
- #
16.09.2019364.54 Кб0MODEL.DOC
- #
31.05.2015438.45 Кб34mopg[1].pdf
- #
30.05.201556.82 Кб51Moy_referat Готовый.docx
- #
31.05.2015167.35 Кб9N 1-ФКЗ о военных судах.rtf
- #
20.09.2019534.79 Кб24Nauki_o_Zemle.docx
- #
27.11.201927.27 Кб1Non verbal Communication.docx
- #
26.03.20161.8 Mб930Novye_bilety_GOS.docx
Страница не найдена (ошибка 404)
- Родителям и ученикам
- Полезная информация
- Безопасность
- Информационная безопасность
- Вакантные места для приема (перевода) обучающихся
- Помощь в трудной ситуации
- Будущим первоклассникам
- Правила приема, перевода, отчисления
- Детям с ограниченными возможностями здоровья
- Мероприятия
- Платные образовательные услуги
- Новости
- Каникулы
- Оценка качества подготовки обучающихся
- Секции и кружки
- Олимпиады и конференции
- Стипендии и меры поддержки обучающихся
- Услуги и сервисы
- Безопасность
- Опросы
- Полезная информация
- Наша школа
- О школе
- Администрация
- Педагогический состав
- Профильные направления
- Экономика, право
- IT-классы
- математика
- Наши классы
- Достижения и победы
- Доска почета
- Педагогам и сотрудникам
- Электронный журнал
- Образовательные ресурсы
- Профессиональные стандарты
- Аттестация педагогических работников
- Повышение квалификации
- Профсоюзная организация
- Вакансии
- Функциональная грамотность
- Внедрение системы (целевой модели) наставничества
- Персоны
- Независимая оценка качества образования
- Независимая оценка качества условий образовательной деятельности
- Независимая оценка качества подготовки обучающихся
- Часто задаваемые вопросы
- Контакты
Математическая задача: Круг и квадрат
Дан квадрат ABCD со стороной 100 мм. Вычислите радиус окружности, проходящей через вершины B, C и центр стороны AD.
Вычислите радиус окружности, проходящей через вершины B, C и центр стороны AD.
Правильный ответ:
r = 62,5 ммПошаговое объяснение:
a=100 мм r2 = x2 + (a/2)2 r+x=a r2 = (r−a)2 + (a/2)2 r2 = r2 − 2⋅ ra + a2 + (a/2)2 2⋅ r⋅ a = a2 + (a/2)2 r = 2⋅ aa2+(a/2)2 r= 85⋅a=85⋅ 100=85⋅ 100=8500=2125 мм=62,5 мм
Вы нашли ошибку или неточность? Не стесняйтесь
пишите нам. Спасибо!
Советы для связанных онлайн-калькуляторов
Вам нужна помощь в вычислении корней квадратного уравнения?
У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?
Вы хотите преобразовать единицы длины?
См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.
Для решения данной задачи по математике необходимо знать следующие знания:
- алгебра
- квадратное уравнение
- уравнение
- выражение переменной из формулы
- 3
- выражение переменной из формулы
- 3 9000 7
- Теорема Пифагора
- прямоугольный треугольник
- круг
- треугольник
- квадрат
Единицы физических величин:
- длина
Уровень задачи:
- Практика для 14-летних
- Старшая школа
Мы рекомендуем вам посмотреть это учебное видео по этой математической задаче: видео1 видео2
- 0AB2 построенный квадрат со стороной 12 см.
 В этом квадрате он рассыпал четверть круга с центром в точке В, проходящую через точку А, и полуокружность l с центром в центре стороны ВС и прошел точку В. Он все равно построил бы круг-й
В этом квадрате он рассыпал четверть круга с центром в точке В, проходящую через точку А, и полуокружность l с центром в центре стороны ВС и прошел точку В. Он все равно построил бы круг-й - Рассчитать 70814
Длины сторон AB и AD прямоугольника ABCD относятся как 3:4. Окружность k диаметром 10 см описывает прямоугольник. Вычислите длины сторон данного прямоугольника. - Цилиндрический 46021
Рассчитайте энергию магнитного поля цилиндрической катушки с 400 витками, длиной 0,4 м и радиусом 20 мм. Через катушку проходит ток силой 3А. (µo = 4π 10-7 H. M-1) - Уравнение 2604
Данным треугольником является ABC: A [-3; -1] Б [5; 3] С [1; 5] Напишите уравнение прямой, проходящей через вершину C параллельно стороне AB. - Прямоугольник — параллелограмм
Прямоугольник описан окружностью радиусом 5 см. Короткая сторона прямоугольника равна 6 см. Вычислите периметр параллелограмма ABCD, вершины которого являются серединами сторон прямоугольника.
- Четырехугольник 78874
Дан четырехугольник ABCD, вписанный в окружность, диагональ АС которого равна диаметру окружности. Расстояние между точкой В и диаметром 15 см, а между точкой D и диаметром 18 см. Вычислить радиус окружности и перим - Квадратные круги
Вычислите длину описанного и вписанного круга до квадрата ABCD со стороной 5см. - Два круга
Даны два круга с одинаковым радиусом, r = 1. Центр второго круга лежит на окружности первого. Чему равна площадь квадрата, вписанного в пересечение данных окружностей? - Вычислить 2577
Вычислить длину хорды окружности, которая находится на расстоянии 2,5 см от центра окружности. Радиус 6,5 см. - Цилиндрический 4411
В блоке высотой 50 см с квадратным основанием с длиной ребра 20 см просверлено цилиндрическое отверстие диаметром 12 см. Ось этого отверстия проходит через центр основания прямоугольного параллелепипеда. Вычислите объем и площадь поверхности - Трапеция MO-5-Z8
ABCD представляет собой трапецию, в которой лаймовый сегмент CE разделен на треугольник и параллелограмм. Точка F — середина СЕ, прямая DF проходит через центр отрезка ВЕ, а площадь треугольника СДЕ равна 3 см². Определить площадь трапеции
Точка F — середина СЕ, прямая DF проходит через центр отрезка ВЕ, а площадь треугольника СДЕ равна 3 см². Определить площадь трапеции - Построить 30121
Точка B является вершиной прямоугольника ABCD. Диагональ BD этого прямоугольника лежит на прямой p. Точка X — внутренняя точка стороны AD прямоугольника ABCD, а точка Y — внутренняя точка стороны CD. Постройте недостающие вершины D, A и C прямоугольника AB - Увеличенный периметр
Квадрат и окружность проходят через две соседние вершины квадрата (концы стороны a) и центр противоположной стороны (c). Какая из плоских фигур имеет больший периметр? - Хорда окружности
Рассчитайте длину хорды окружности радиусом r = 10 см, длина которой равна расстоянию от центра окружности. - Построение ромба
Постройте ромб ABCD, если его диагональ AC=9 см, а сторона AB = 6 см. Впишите в него окружность, касаясь всех сторон. - Квадраты рекурсии
В квадрат ABCD вписал квадрат так, что его вершины лежат в центрах сторон квадрата ABCD. Процедура вписывания квадрата повторяется таким образом. Длина стороны квадрата ABCD равна а = 22 см. Вычислите: а) сумму пери
Процедура вписывания квадрата повторяется таким образом. Длина стороны квадрата ABCD равна а = 22 см. Вычислите: а) сумму пери - Уравнение окружности
Найдите уравнение окружности, вписанной в ромб ABCD, где A[1, -2], B[8, -3] и C[9, 4].
Глоссарий по геометрии
Глоссарий по геометрии- остроугольный треугольник
- треугольник, все углы которого меньше 90° o
- смежная ветвь
- катет прямоугольного треугольника рядом с опорным углом
- высота
- отрезок треугольника, соединяющий вершину с линией, содержащей противоположную сторону и перпендикулярной этой стороне
- высота треугольника
- отрезок, проведенный или опущенный перпендикулярно вершине треугольника к линии, содержащей противоположную сторону, высоту треугольника
- Биссектриса угла
- луч, делящий угол на две равные части
- угол наклона
- угол, измеренный ниже определенной контрольной точки (обычно линии визирования)
- угол места
- угол, измеренный над определенной опорной точкой (обычно линией прямой видимости)
- вершина
- вершина пирамиды, противоположная основанию пирамиды
- апофема
- длина перпендикуляра от центра правильного многоугольника до его края
- дуга
- изогнутая линия, являющаяся частью круга, частью окружности круга
- длина дуги
- мера расстояния по криволинейной линии окружности, отрезок окружности
- участок
- количество квадратных единиц, необходимое для покрытия заданной плоской поверхности
- аксиома
- утверждение, которое принимается за истинное
- база
- конгруэнтные многоугольники, параллельные друг другу на вершине и дне призмы
- биссектриса
- разделить на две равные части; разделительная линия называется биссектриса
- центральный уголок
- угол, который пересекает окружность в двух точках и вершина которого является центром окружности
- хорда
- отрезок с двумя концами, лежащими на окружности
- окружность
- периметр круга; С = 2 π r или C = d π , где C = окружность, r = радиус и d = диаметр
- составная фигура
- фигура, состоящая из двух или более геометрических фигур
- предположение
- обоснованная догадка; предложение, которое либо истинно, либо ложно
- вывод
- часть «q» условного оператора, следующая за словом «then», часть, которую необходимо доказать
- условный оператор
- утверждение, записанное в форме если «p», то «q»
- конус
- трехмерная фигура, имеющая одно круглое основание и одну вершину
- конгруэнтно
- фигуры имеют одинаковую форму и размер, углы и стороны имеют одинаковые размеры
- конгруэнтных треугольников
- треугольников с соответствующими сторонами одинаковой длины и соответствующими внутренними углами одинаковой меры
- предположение
- утверждение, которое считается верным и требует доказательства
- противоречивое заявление
- утверждение, заменяющее и отрицающее гипотезу и заключение исходного утверждения
- обратный оператор
- утверждение, заменяющее гипотезу и заключение исходного утверждения
- следствие
- утверждение, непосредственно вытекающее из теоремы; мини-теорема
- соответствующие детали
- стороны и углы, которые совпадают и имеют одинаковую форму и размер (конгруэнтны)
- контрпример
- пример, подтверждающий ложность гипотезы
- перекрестное умножение
- продукты средств и крайностей
- сечение
- плоская фигура, которая получается при пересечении трехмерного твердого тела плоскостью
- куб
- прямоугольная призма, все стороны которой равны, а все грани квадратные
- цилиндр
- трехмерная геометрическая фигура с двумя конгруэнтными параллельными круглыми основаниями
- дедуктивное рассуждение
- рассуждение, которое приводит к заключению, используя факты, определения, теоремы, постулаты или свойства
- знаменатель
- нижнее число в дроби
- диагональ
- сегмент внутри многоугольника, соединяющий несмежные вершины
- диаметр
- отрезок, проходящий через центр окружности, причем обе его конечные точки лежат на окружности или сфере
- расширение
- преобразование, которое увеличивает или уменьшает фигуру
- размеры
- используется для описания размера и формы объекта
- край
- пересечение граней в объемной фигуре
- расширение
- результат расширения с масштабным коэффициентом больше 1
- равноугольный
- все углы многоугольника равны или равны
- равносторонний
- все стороны многоугольника имеют одинаковую длину или равные размеры
- Формула Эйлера
- количество вершин плюс количество граней минус количество ребер равно 2
- Теорема Эйлера
- соотношение между числом граней, ребер и вершин в многограннике: V − E + F = 2
- внешний уголок
- удлините каждую сторону правильного многоугольника, как показано ниже, ни одна вершина не будет иметь более одного внешнего угла
- лицо
- плоская поверхность объемной фигуры
- геометрические свойства
- атрибуты или характеристики геометрической фигуры, которые поддерживаются определениями, постулатами или теоремами
- большие круги
- круг на поверхности сферы, центр которого совпадает с центром сферы
- высота
- для цилиндра: длина сегмента, перпендикулярного обоим основаниям;
для конуса: длина отрезка, перпендикулярного основанию и заканчивающегося в точке конуса - гипотенуза
- сторона, противоположная прямому углу прямоугольного треугольника; это самая длинная сторона прямоугольного треугольника
- гипотеза
- часть «p» условного оператора, следующая за словом «if», данная информация
- изображение
- фигурка из трансформации
- угол в комплекте
- угол между двумя соседними сторонами многоугольника; отрезки, представляющие соседние стороны, входят в состав лучей, образующих угол
- индуктивное рассуждение 90 131 рассуждение, которое приходит к выводу путем обобщения утверждения на основе наблюдения за закономерностями 90 134
- вписанный угол
- угол, который пересекает окружность в двух точках и вершина которого лежит на окружности
- вписанный многоугольник
- многоугольник, все вершины которого лежат на окружности
- вписанный квадрат
- квадрат, вершины которого лежат на окружности
- перехваченная дуга
- дуга окружности, лежащая внутри вписанного угла
- внутренние углы
- углов, расположенных внутри треугольника, по одному в каждой вершине
- обратный оператор
- утверждение, отрицающее как гипотезу, так и заключение исходного утверждения
- неправильный многоугольник
- многоугольник, стороны которого не конгруэнтны друг другу
- изометрический
- представление трехмерных фигур так, чтобы можно было наблюдать три стороны фигуры
- равнобедренный треугольник
- треугольник, в котором две стороны имеют одинаковую длину
- оправдать 90 131 для предоставления уважительной причины, возможно, с использованием постулатов, теорем, следствий или определений 90 134
- боковая часть
- стороны:
боковая поверхность цилиндра прямоугольник
боковая поверхность конуса круглого сечения - боковой край
- пересекающиеся ребра боковых граней твердого тела
- ножки
- стороны, прилегающие к прямому углу в прямоугольном треугольнике
- строка
- удерживает местоположение и не имеет толщины, длины или ширины; он не имеет меры ни в каком направлении
- сегмент линии
- часть одной линии с двумя конечными точками и всеми точками между ними
- линейная пара
- внутренний угол, соединенный с внешним углом, имеющим одну и ту же сторону
- медиана треугольника
- отрезок с концами, являющимися вершиной треугольника и серединой противоположной стороны
- малая дуга
- кратчайшее расстояние от одной точки на окружности до другой точки на окружности
- несколько
- произведение числа и любого целого числа
- отрицание
- утверждение, образованное вставкой слова «не» для изменения значения гипотезы или вывода на противоположное значение
- нетто
- двухмерное изображение трехмерной фигуры, которое можно сложить, чтобы сформировать фигуру
- числитель
- первое число в дроби
- наклонный конус
- конус, у которого высота не перпендикулярна основанию
- наклонный цилиндр
- цилиндр, основания которого не выровнены
- косая призма
- призма, основания которой не выровнены должным образом
- тупоугольный треугольник
- треугольник с одним углом больше 90° o но меньше 180° o (тупой угол
- противоположная нога
- катет прямоугольного треугольника, противоположный опорному углу
- орфографический
- представление трехмерных фигур с использованием двухмерных перспектив, таких как вид спереди, сбоку или сверху
- идеальный квадрат
- произведение квадрата целого числа или целого числа во второй степени
- перпендикулярно
- две линии или отрезки, пересекающиеся и образующие 90 o углы
- самолет
- имеет длину и ширину, но не толщину и высоту; плоская поверхность, простирающаяся бесконечно во всех направлениях по своей длине и ширине
- точка
- удерживает местоположение и не имеет толщины, длины или ширины; он не имеет меры ни в каком направлении
- точка касания
- точка пересечения касательной с окружностью
- полигон
- Замкнутая плоская фигура, образованная тремя или более отрезками, пересекающимися в своих концах
- многогранник
- объемная фигура, стороны которой являются многоугольниками
- постулат
- утверждение, которое принимается за истинное без доказательства
- прообраз
- исходное изображение до преобразования
- призма
- Трехмерное твердое тело с двумя параллельными и конгруэнтными основаниями, названное в честь формы основания
- пропорциональный
- имеющий постоянное соотношение всех соответствующих сторон между двумя фигурами
- пирамида
- объемная фигура с многоугольником в основании и треугольниками в качестве сторон
- Теорема Пифагора
- в прямоугольном треугольнике, где a и b — длины катетов и c — длина гипотенузы, а a 2 + b
- 2 = 2 2
- Пифагорейская тройка
- набор из трех целых чисел, удовлетворяющих теореме Пифагора
- радиус
- расстояние от центра круга до любой точки на окружности круга или для правильного многоугольника длина от центра до вершины
- отношение
- дробь
- скорость изменения
- отношение изменения выходного значения к изменению входного значения функции
- прямоугольная призма
- трехмерный объект с шестью гранями, представляющими собой прямоугольники
- переходник
- результат расширения с масштабным коэффициентом менее 1
- опорный угол
- один из двух острых углов прямоугольного треугольника, являющийся точкой отсчета
- отражение
- преобразование фигуры, перевернутой через линию
- правильный многоугольник
- замкнутая фигура, у которой все углы и все стороны равны
- правильная пирамида
- многогранник с многоугольным основанием и треугольниками в качестве сторон, высота пересекает основание под прямым углом и вершину
- прямой угол
- угол, длина которого равна 90° o
- правый конус
- трехмерная фигура, имеющая одно круглое основание, одну вершину и высоту, пересекающую основание под прямым углом
- правый цилиндр
- трехмерная геометрическая фигура, имеющая два конгруэнтных и параллельных основания, а высота перпендикулярна обоим основаниям
- правая призма
- многогранник, состоящий из двух параллельных конгруэнтных граней, называемых основаниями
- прямоугольный треугольник
- треугольник, содержащий один внутренний угол с величиной 90 o (т.


 08.2019248.83 Кб2m340.doc
08.2019248.83 Кб2m340.doc В этом квадрате он рассыпал четверть круга с центром в точке В, проходящую через точку А, и полуокружность l с центром в центре стороны ВС и прошел точку В. Он все равно построил бы круг-й
В этом квадрате он рассыпал четверть круга с центром в точке В, проходящую через точку А, и полуокружность l с центром в центре стороны ВС и прошел точку В. Он все равно построил бы круг-й
 Точка F — середина СЕ, прямая DF проходит через центр отрезка ВЕ, а площадь треугольника СДЕ равна 3 см². Определить площадь трапеции
Точка F — середина СЕ, прямая DF проходит через центр отрезка ВЕ, а площадь треугольника СДЕ равна 3 см². Определить площадь трапеции Процедура вписывания квадрата повторяется таким образом. Длина стороны квадрата ABCD равна а = 22 см. Вычислите: а) сумму пери
Процедура вписывания квадрата повторяется таким образом. Длина стороны квадрата ABCD равна а = 22 см. Вычислите: а) сумму пери
Leave A Comment