Средняя линия прямоугольного треугольника – формула
4.4
Средняя оценка: 4.4
Всего получено оценок: 190.
4.4
Средняя оценка: 4.4
Всего получено оценок: 190.
Средняя линия прямоугольного треугольника – это прекрасная возможность для составителей задач. Большая часть обучающихся знают, что такое средняя линия и умело используют ее свойства в решении. Но как только этот отрезок появляется на чертеже прямоугольного треугольника, то сразу впадают в ступор из-за некоторой необычности рисунка, поэтому разберемся в теме подробнее.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Что такое прямоугольный треугольник?
В общем случае, треугольник это фигура, состоящая из трех сторон и трех углов. В зависимости от величин углов, входящих в состав треугольника выделяют:
- Остроугольные треугольники, все углы которых меньше 90 градусов.

- Прямоугольные треугольники, один из углов которых равен 90 градусам.
Прямоугольные треугольники интересны специальными формулами, которые значительно упрощают решение. Но средняя линия прямоугольного треугольника ни чем не отличается от средней линии произвольного. Почему задачи с этим отрезком вызывают затруднения?
Только из-за необычности чертежа Рис. 1. Средние линии прямоугольного треугольника.Средняя линия
Что такое средняя линия? Это один из характеризующих отрезков любого треугольника. Средняя линия соединяет середины смежных сторон многоугольника.
Средняя линия есть не только у треугольника. Она существует у каждой выпуклой фигуры. При этом свойства средних линий треугольников не всегда совпадают с свойствами средних линий трапеций. Поэтому будьте аккуратны, у каждой фигуры есть свои свойства и признаки.
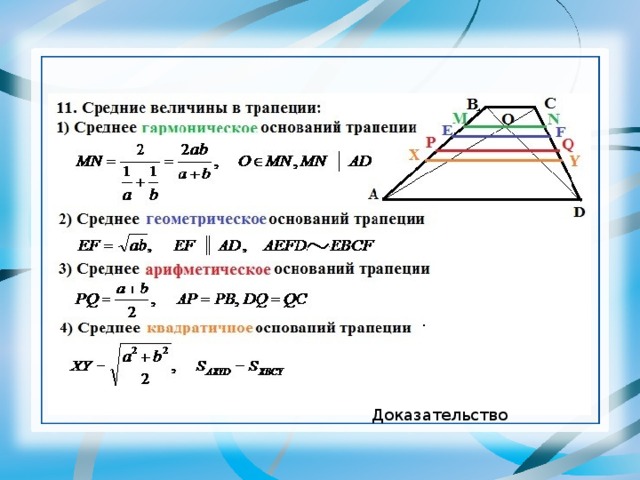
Свойства средней линии
Свойств у средней линии не так много, но все они более чем интересны.
- Средняя линия всегда параллельна стороне, через которую она не проходит. Иначе говорят, что средняя линия параллельна основанию. Так проще запомнить это свойство, но немного страдает формулировка. Дело в том, что в любом треугольнике можно провести 3 средних линии, а основание только одно, поэтому будьте аккуратнее в формулировках.
- Средняя линия равна половине основания. А вернее не основания, а стороны, которую средняя линия не пересекает. Это и есть формула средней линии любого треугольника, в том числе и прямоугольного.
- Средняя линия отсекает треугольник подобный изначальному с коэффициентом подобия 1:2
Если формулировка «Средняя линия параллельна основанию» не совсем правильная, то почему же ее применяют в учебнике? Дело в том, что любое свойство должно быть коротким и ясным для простоты запоминания. Поэтому и сокращают некоторые высказывания.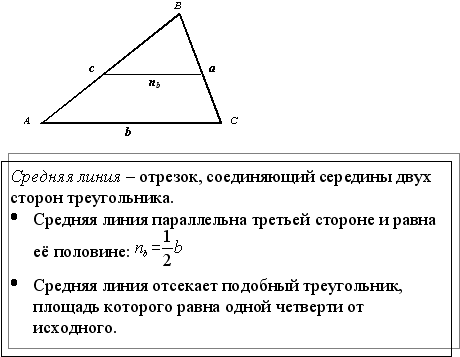
Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними.
$$S=5*5*0,5=12,5$$
В большом треугольнике 4 малых, а в прямоугольнике 2 малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольнику, нужно умножить площадь прямоугольника на 2.
$S=12,5*2=25$ – ответ получен.
Что мы узнали?
Мы узнали, что такое средняя линия прямоугольного треугольника. Поговорили о свойствах средней линии и решили небольшую задачу для закрепления материала.
Тест по теме
Доска почёта
Милана Швецова
5/10
Виктория Белоносова
10/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 190.
А какая ваша оценка?
Средняя линия выпуклого четырехугольника: свойства, определение
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Геометрия Что такое средняя линия четырехугольника
ru Математика Геометрия Что такое средняя линия четырехугольника
В данной публикации мы рассмотрим определение и основные свойства средних линий выпуклого четырехугольника касательно точки их пересечения, соотношения с диагоналями и т.д.
Примечание: далее мы будем рассматривать только выпуклую фигуру.
- Определение средней линии четырехугольника
- Свойства средней линии четырехугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
Определение средней линии четырехугольника
Отрезок, соединяющий середины противоположных сторон четырехугольника (т.е. не пересекающий их), называется его

- EF – средняя линия, соединяющая середины AB и CD; AE=EB, CF=FD.
- GH – средняя линия, сеодиняющая середины BC и AD; BG=GC, AH=HD.
Свойства средней линии четырехугольника
Свойство 1
Средние линии четырехугольника пересекаются и в точке пересечения делятся пополам.
- EF и GH (средние линии) пересекаются в точке O;
- EO=OF, GO=OH.
Свойство 2
Точка пересечения средних линий четырехугольника является серединой отрезка, соединяющего середины его диагоналей.
- K – середина диагонали AC;
- L – середина диагонали BD;
- KL проходит через точку O, соединяя K и L.
Свойство 3
Середины сторон четырехугольника являются вершинами параллелограмма, который называется параллелограммом Вариньона.
Центром образованного таким образом параллелограмма и точкой пересечения его диагоналей является середина средних линий исходного четырехугольника, т.е. точка их пересечения – O.
Примечание: Площадь параллелограмма равняется половине площади четырехугольника.
Свойство 4
Если углы между диагоналями четырехугольника и его средней линией равны, значит диагонали имеют одинаковую длину.
- EF – средняя линия;
- AC и BD
- ∠ELC = ∠BMF = α, следовательно AC=BD.
Свойство 5
Средняя линия четырехугольника меньше или равна полусумме непересекающих ее сторон (при условии, что данные стороны параллельны).
EF – средняя линия, не пересекающаяся со сторонами AD и BC.
Иначе говоря, средняя линия четырехугольника равняется половине суммы не пересекающих ее сторон тогда и только тогда, когда данный четырехугольник является трапецией. В этом случае рассматриваемые стороны являются основаниями фигуры.
В этом случае рассматриваемые стороны являются основаниями фигуры.
Свойство 6
Для вектора средней линии произвольного четырехугольника выполняется следующее равенство:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
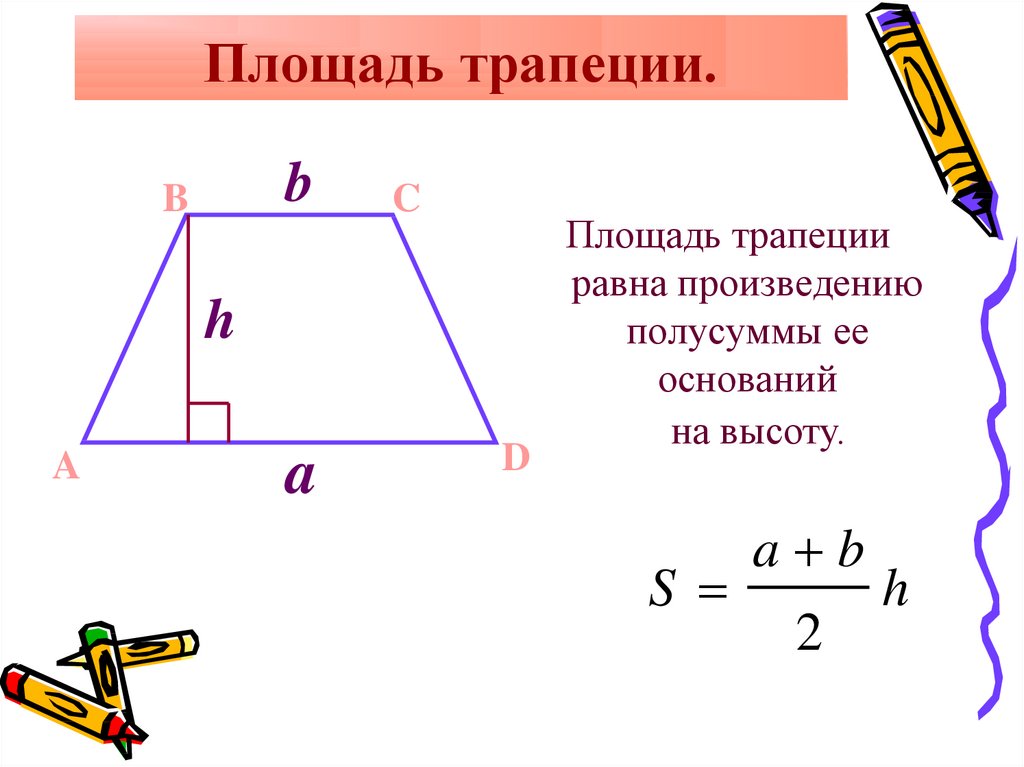
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
math — Найдите углы повернутого прямоугольника, зная его центральную точку и поворот
спросил
Изменено 1 год, 6 месяцев назад
Просмотрено 14 тысяч раз
Может ли кто-нибудь дать мне алгоритм, который находит положение всех четырех углов прямоугольника, если я знаю его центральную точку (в глобальном координатном пространстве), ширину и высоту, а также его вращение вокруг этой центральной точки?
уточнение редактировать:
Ширина и высота, о которых я говорю, — это длина сторон прямоугольника.
- математика
1
Верхний правый угол имеет координаты w/2, h/2 относительно центра. После поворота его абсолютные координаты равны
x = cx + w/2 * Cos(Phi) - h/2 * Sin(Phi) y = cy + w/2 * Sin(Phi) + h/2 * Cos(Phi)
3
Координаты каждой вершины:
Центральная точка = (center.x, center.y) Угол = угол Высота = высота Ширина = ширина ВЕРХНЯЯ ПРАВАЯ ВЕРШИНА: Top_Right.x = center.x + ((ширина / 2) * cos (угол)) - ((высота / 2) * sin (угол)) Top_Right.y = center.y + ((ширина / 2) * sin (угол)) + ((высота / 2) * cos (угол)) ВЕРХНЯЯ ЛЕВАЯ ВЕРШИНА: Top_Left.x = center.x - ((ширина / 2) * cos (угол)) - ((высота / 2) * sin (угол)) Top_Left.y = center.y - ((ширина / 2) * sin (угол)) + ((высота / 2) * cos (угол)) НИЖНЯЯ ЛЕВАЯ ВЕРШИНА: Bot_Left.x = center.x - ((ширина / 2) * cos (угол)) + ((высота / 2) * sin (угол)) Bot_Left.y = center.y - ((ширина / 2) * sin (угол)) - ((высота / 2) * cos (угол)) НИЖНЯЯ ПРАВАЯ ВЕРШИНА: Bot_Right.x = center.x + ((ширина / 2) * cos (угол)) + ((высота / 2) * sin (угол)) Bot_Right.y = center.y + ((ширина / 2) * sin (угол)) - ((высота / 2) * cos (угол))
Этот алгоритм представляет собой сжатую версию этих 3 шагов:
Шаг 1: Центрируйте прямоугольник вокруг начала координат
Шаг 2: Примените матрицу поворота к каждой вершине
Шаг 3: Переместите повернутый прямоугольник в правильное положение, добавив центральную точку к каждой координате
Более подробно это объясняется здесь https://math.stackexchange.com/questions/126967/rotating-a-rectangle-via-a-rotation-matrix
3
Если вам нужны все углы, возможно, будет быстрее создать два перпендикулярных вектора из центра прямоугольника к обеим его сторонам, а затем сложить/вычесть эти векторы в/из центра прямоугольника, чтобы сформировать точки.
Это может быть быстрее, так как вам не нужно повторно вызывать функции sin() и cos() (вы делаете это только один раз для каждой).
Если предположить, что у нас есть библиотека Vector (для более чистого кода — помогает только с векторной арифметикой), вот код на Python:
def get_corners_from_rectangle (центр: вектор, угол: плавающий, размеры: вектор):
# создаем (нормализованные) перпендикулярные векторы
v1 = вектор (cos (угол), sin (угол))
v2 = Vector(-v1[1], v1[0]) # повернуть на 90°
# масштабируем их соответствующим образом по размерам
v1 *= размеры[0] / 2
v2 *= размеры[1] / 2
# возвращаем углы, перемещая центр прямоугольника по векторам
возвращаться [
центр + v1 + v2,
центр - v1 + v2,
центр - v1 - v2,
центр + v1 - v2,
]
Код Python с матрицами:
импортировать numpy как np импортировать математику импортировать matplotlib.pyplot как plt из matplotlib.patches импортировать прямоугольник, круг #центр прямоугольника Х = 2698,77 Y = 1283,01 центр = np.массив ([[X], [Y]]) angle_deg = 83,5694 #угловой прямоугольник угол = math.radians (угол_градус) # размер прямоугольника ширина = 2022,23 рост = 1978,78 R_lt = np.array([[np.cos(угол),-np.sin(угол)],[-np.sin(угол),-np.cos(угол)]]) A = np.dot(R_lt,np.array([[ширина/2], [высота/2]])) + центр R_rt = np.array([[np.cos(угол),np.sin(угол)],[-np.sin(угол),np.cos(угол)]]) B = np.dot(R_rt,np.array([[ширина/2], [высота/2]])) + центр R_rb = np.array([[-np.cos(угол),np.sin(угол)],[np.sin(угол),np.cos(угол)]]) C = np.dot(R_rb,np.array([[ширина/2], [высота/2]])) + центр R_lb = np.array([[-np.cos(угол),-np.sin(угол)],[np.sin(угол),-np.cos(угол)]]) D = np.dot(R_lb,np.array([[ширина/2], [высота/2]])) + центр углы = [A,B,C,D]
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Как найти площадь прямоугольника
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 Следующая →
Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Прямоугольники » Как найти площадь прямоугольника
Периметр прямоугольника равен .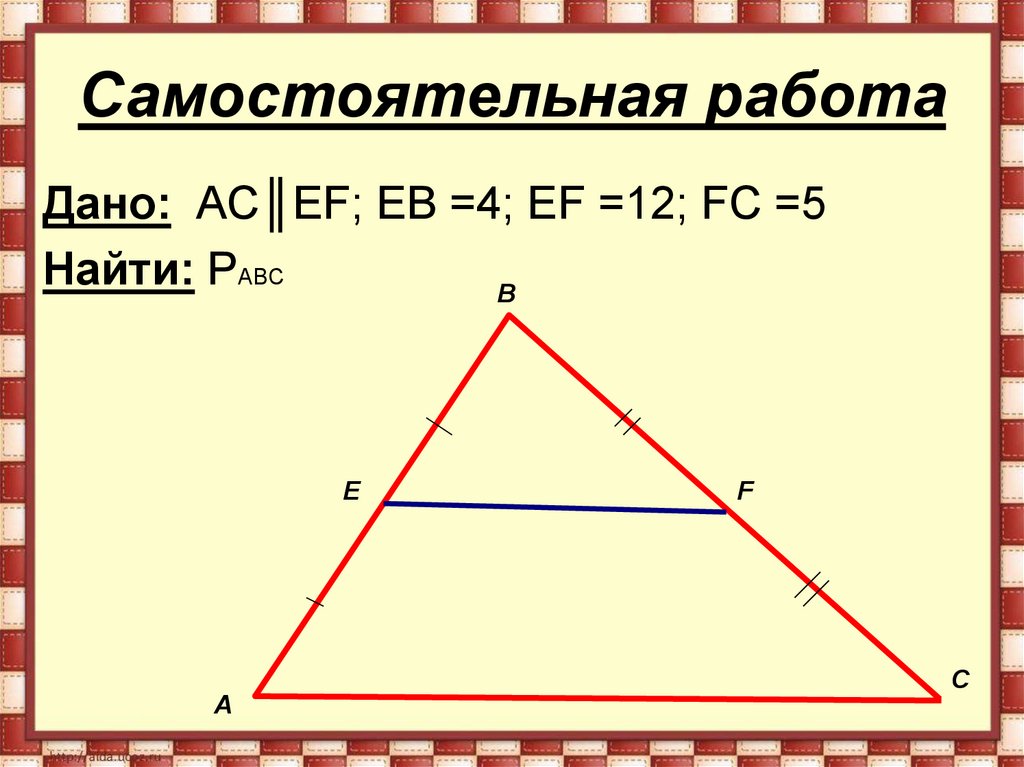 Длина на десять метров больше ширины. Чему равна площадь прямоугольника?
Длина на десять метров больше ширины. Чему равна площадь прямоугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Для прямоугольника общее уравнение для периметра и площади: где длина, а ширина.
Пусть = ширина и = длина
Итак, уравнение для решения становится таким образом, что ширина равна, а длина равна .
Таким образом, площадь равна
Сообщить об ошибке
Какой из следующих данных , а не будет достаточно, чтобы найти площадь прямоугольника?
Возможные ответы:
Длины одной пары противоположных сторон.
Длины одной пары смежных сторон.
Длины одной стороны и диагонали.
Периметр и длина одной стороны.
Все остальные варианты перечисляют информацию, которой будет достаточно.
Правильный ответ:
Длины одной пары противоположных сторон.
Объяснение:
Площадь прямоугольника можно вычислить, умножив длины двух соседних сторон. Все приведенные варианты содержат достаточную информацию, за одним исключением. Мы изучаем каждый из вариантов.
Длины одной пары смежных сторон: Этот выбор неверен, как прямо указано выше.
Периметр и длина одной стороны: Используя формулу периметра, вы можете найти длину соседней стороны, что делает этот выбор неверным.
Длины одной стороны и диагонали: используя теорему Пифагора, вы можете найти длину соседней стороны, что делает этот выбор неверным.
Длины одной пары противоположных сторон: это не дает вам возможности узнать длины смежных сторон. Это правильный выбор.
Сообщить об ошибке
Найдите площадь многоугольника.
Возможные ответы:
Правильный ответ:
Объяснение:
Проведение вертикальной линии в конце стороны длины делит фигуру на прямоугольник и прямоугольный треугольник.
Сумма площадей двух фигур составляет площадь многоугольника. Умножьте длину прямоугольника на его ширину, чтобы найти площадь прямоугольника, и используйте формулу, где – основание, а – высота треугольника, чтобы найти площадь треугольника. Сложение их вместе дает ответ.
Сообщить об ошибке
Одна сторона прямоугольника 7 дюймов, а другая 9 дюймов. Чему равна площадь прямоугольника в дюймах?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти площадь прямоугольника, умножьте его ширину на высоту. Если мы знаем две стороны прямоугольника разной длины, то у нас есть и высота, и ширина.
Сообщить об ошибке
Какова площадь прямоугольника на диаграмме?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь прямоугольника находится путем умножения длины на ширину.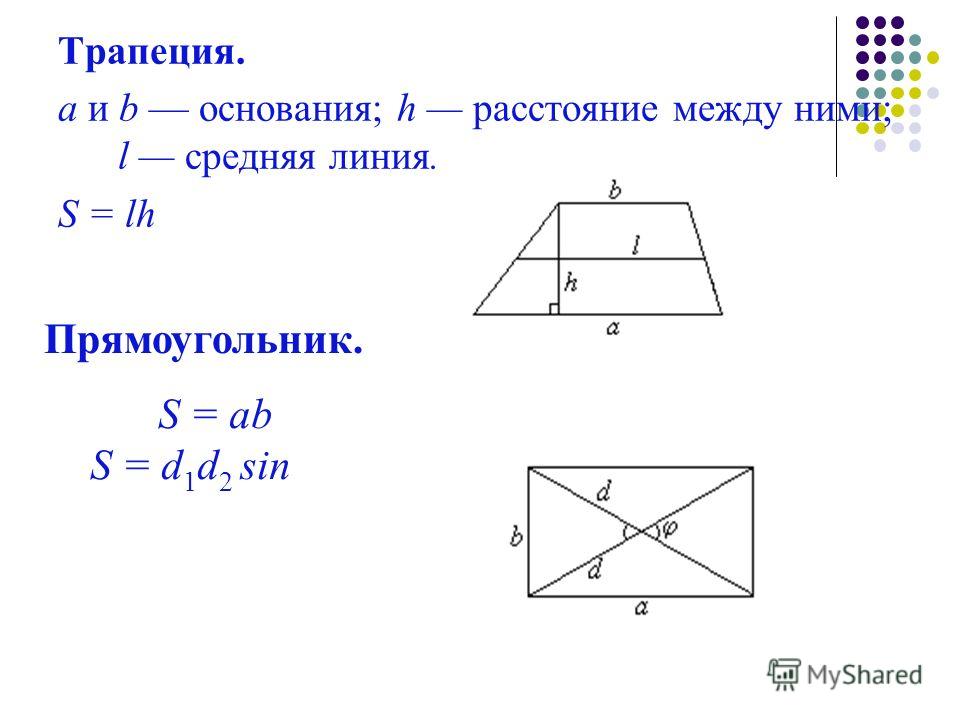
Длина 12 см, ширина 7 см.
Следовательно, площадь 84 см 2 .
Сообщить об ошибке
Какова площадь прямоугольника, длина и ширина которого равны дюймам и дюймам соответственно?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь любого прямоугольника с длиной и шириной:
Сообщить об ошибке
Какова площадь прямоугольника, имеющего длину и ширину ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольника:
Теперь подставьте данные длину и ширину, чтобы найти площадь.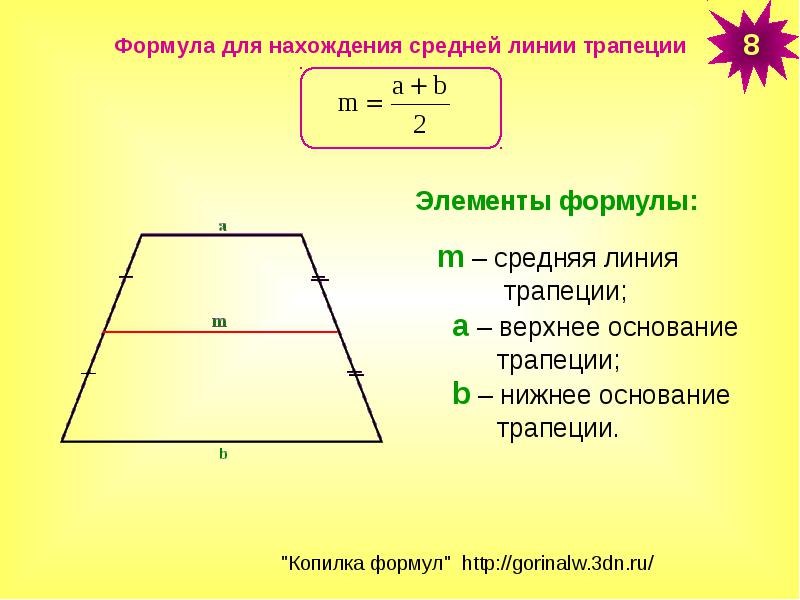
Сообщить об ошибке
Какова площадь прямоугольника, имеющего длину и ширину ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольника:
Теперь подставьте данные длину и ширину, чтобы найти площадь.
Сообщить об ошибке
Какова площадь прямоугольника, имеющего длину и ширину ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольника:
Теперь подставьте данные длину и ширину, чтобы найти площадь.
Сообщить об ошибке
Какова площадь прямоугольника, имеющего длину и ширину ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните, как найти площадь прямоугольника:
Теперь подставьте данные длину и ширину, чтобы найти площадь.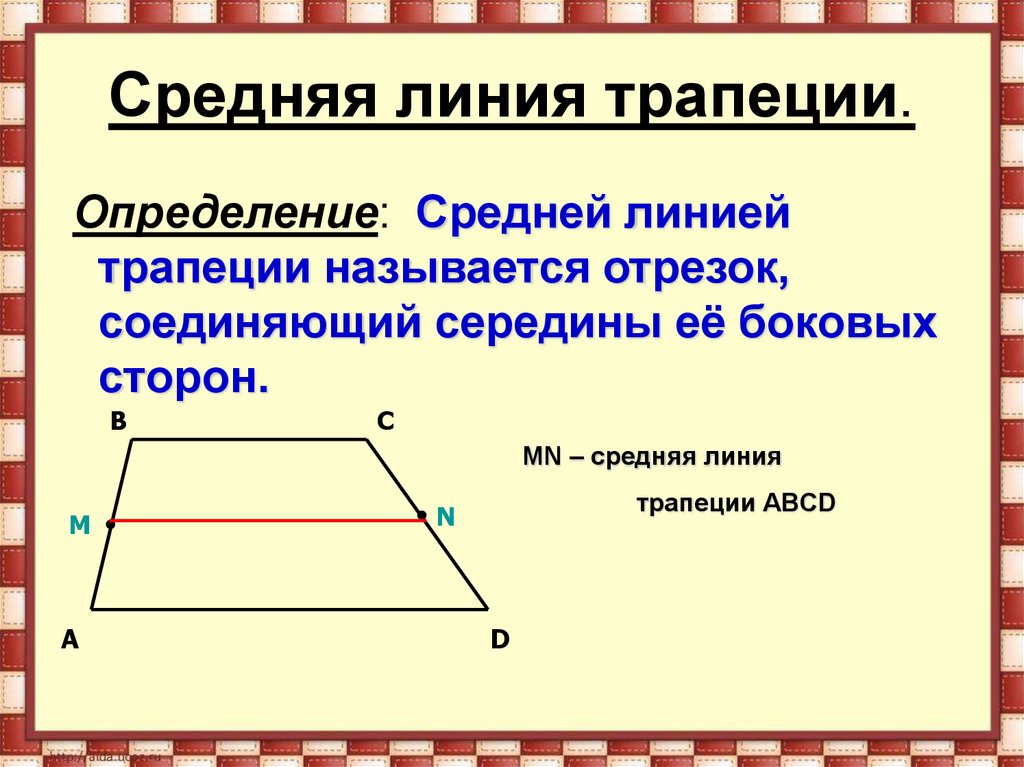


 y = center.y - ((ширина / 2) * sin (угол)) - ((высота / 2) * cos (угол))
НИЖНЯЯ ПРАВАЯ ВЕРШИНА:
Bot_Right.x = center.x + ((ширина / 2) * cos (угол)) + ((высота / 2) * sin (угол))
Bot_Right.y = center.y + ((ширина / 2) * sin (угол)) - ((высота / 2) * cos (угол))
y = center.y - ((ширина / 2) * sin (угол)) - ((высота / 2) * cos (угол))
НИЖНЯЯ ПРАВАЯ ВЕРШИНА:
Bot_Right.x = center.x + ((ширина / 2) * cos (угол)) + ((высота / 2) * sin (угол))
Bot_Right.y = center.y + ((ширина / 2) * sin (угол)) - ((высота / 2) * cos (угол))
 массив ([[X], [Y]])
angle_deg = 83,5694 #угловой прямоугольник
угол = math.radians (угол_градус)
# размер прямоугольника
ширина = 2022,23
рост = 1978,78
R_lt = np.array([[np.cos(угол),-np.sin(угол)],[-np.sin(угол),-np.cos(угол)]])
A = np.dot(R_lt,np.array([[ширина/2], [высота/2]])) + центр
R_rt = np.array([[np.cos(угол),np.sin(угол)],[-np.sin(угол),np.cos(угол)]])
B = np.dot(R_rt,np.array([[ширина/2], [высота/2]])) + центр
R_rb = np.array([[-np.cos(угол),np.sin(угол)],[np.sin(угол),np.cos(угол)]])
C = np.dot(R_rb,np.array([[ширина/2], [высота/2]])) + центр
R_lb = np.array([[-np.cos(угол),-np.sin(угол)],[np.sin(угол),-np.cos(угол)]])
D = np.dot(R_lb,np.array([[ширина/2], [высота/2]])) + центр
углы = [A,B,C,D]
массив ([[X], [Y]])
angle_deg = 83,5694 #угловой прямоугольник
угол = math.radians (угол_градус)
# размер прямоугольника
ширина = 2022,23
рост = 1978,78
R_lt = np.array([[np.cos(угол),-np.sin(угол)],[-np.sin(угол),-np.cos(угол)]])
A = np.dot(R_lt,np.array([[ширина/2], [высота/2]])) + центр
R_rt = np.array([[np.cos(угол),np.sin(угол)],[-np.sin(угол),np.cos(угол)]])
B = np.dot(R_rt,np.array([[ширина/2], [высота/2]])) + центр
R_rb = np.array([[-np.cos(угол),np.sin(угол)],[np.sin(угол),np.cos(угол)]])
C = np.dot(R_rb,np.array([[ширина/2], [высота/2]])) + центр
R_lb = np.array([[-np.cos(угол),-np.sin(угол)],[np.sin(угол),-np.cos(угол)]])
D = np.dot(R_lb,np.array([[ширина/2], [высота/2]])) + центр
углы = [A,B,C,D]
Leave A Comment