Как найти площадь ромба? Формулы через периметр и угол, через высоту и сторону / Справочник :: Бингоскул
Как найти площадь ромба? Формулы через периметр и угол, через высоту и сторонудобавить в закладки удалить из закладок
Содержание:
Параллелограмм с равными сторонами называется ромбом. Он обладает рядом особенностей, присущих разным четырёхугольникам. Часто встречается в геральдике, орнаментах резных изделий и на вышивке. Рассмотрим, как найти площадь ромба: по его периметру, сторонам, зная угол между ними. Научимся вычислять высоту геометрической фигуры через её периметр и площадь.
Площадь через сторону с высотой
Поверхность правильного четырёхугольника вычисляется как произведение стороны (они все равны) на высоту геометрической фигуры – опущенный с любой вершины перпендикуляр.
S = AD*BE.
Найти площадь, зная диагонали
Вторая формула подразумевает, что известны длины диагоналей геометрической фигуры или есть возможность вычислить их, например, по формуле Пифагора. Поверхность равна половине произведения одной диагонали ромба на другую.
Поверхность равна половине произведения одной диагонали ромба на другую.
S = ½*AC*DB.
Площадь через сторону и угол
Когда есть информация о величине стороны четырёхугольника и значении одного из его внутренних углов, поверхность вычисляется как произведение квадрата стороны на синус угла между ними.
S = AD2 * sinα = a2 * sinα.
AD или a – случайная сторона, можно брать любую – они одинаковы.
Α – величина угла между соседними сторонами четырёхугольника.
Площадь ромба через периметр и угол
Дан периметр P = 50 см, стороны образуют острый угол, равный 30°. Нужно вычислить площадь 4-угольника. Делается это в несколько шагов.
Периметр – сумма четырёх сторон: P = 4a, отсюда: a = P/4 = 50/4 = 12,5 см.
Задействуем рассмотренную выше формулу: S = a2 * sin α.
Подставляем значения: S = 12,52 * sin 30° = 156,25 * 0,5 = 78,125 см2. 2 } { 16 } * 0.5 = 250016*0.5 = 78,125 см 2.
2 } { 16 } * 0.5 = 250016*0.5 = 78,125 см 2.
Высота через площадь с периметром
Найти высоту ромба, зная его площадь (S) и периметр (P) несложно. Рассмотрим на примере, когда S = 16 см2, P = 16 см.
Начинаем логическое мышление. Из формулы вычисления поверхности S = h * a выразим высоту: h = S/a.
Сторону, зная периметр – сумму всех четырёх, вычислить просто: разделить его на четыре: a = P/4.
Подставим значения и получим a = P/4 = 16/4 = 4 см.
Заменим известные величины в формуле h = S/a = 16/4 = 4.
Данная фигура является квадратом, только у него длина стороны равна опущенной на неё высоте при прочих заданных условиях.
Найти площадь рассматриваемого 4-угольника несложно. Даже если исходные данные нельзя поставить в известную формулу, нужную информацию легко вычислить, например, используя формулу Пифагора и свойства ромба.
Поделитесь в социальных сетях:
25 декабря 2021, 18:29
Геометрия
Could not load xLike class!
формула через диагонали, сторону и угол (или высоту)
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Геометрия Нахождение площади ромба: формула и примеры
ru Математика Геометрия Нахождение площади ромба: формула и примеры
Ромб – это геометрическая фигура; параллелограмм, имеющие 4 равные стороны.
- Формула вычисления площади
- По длине стороны и высоте
- По длине стороны и углу
- По длинам диагоналей
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h
По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 ⋅ sin α
По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
S = 1/2 ⋅ d1 ⋅ d2
Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 10 см ⋅ 8 см = 80 см
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 ⋅ sin 30° = 36 см2 ⋅ 1/2 = 18 см2.
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Калькулятор площади ромба— Формула | Периметр
Калькулятор площади ромба является полезным математическим инструментом для вычисления площади, высоты , угла и других параметров ромба . Поскольку существует много способов найти площадь, ниже мы перечислили формулы и другую важную информацию о площади ромба, его использовании и характеристиках.
Поскольку существует много способов найти площадь, ниже мы перечислили формулы и другую важную информацию о площади ромба, его использовании и характеристиках.
Ромб и его свойства
Ромб по определению в Евклидовом геометрия, представляет собой особый параллелограмм, у которого противоположные стороны равны , а параллельны . Ромб может быть квадратным и иметь форму ромба , если он имеет два острых и тупых угла. Ромб обладает многими свойствами, наиболее важными из которых являются:
- Все стороны ромба равны .
- Противоположные стороны параллельны.
- Сумма смежных углов равна 180 градусам.
- Ромб не имеет описанной окружности.
- Если одна из сторон ромба равна меньшей диагонали , образуются два конгруэнтных равносторонних треугольников.

Формула площади ромба
В зависимости от параметров ромба можно использовать различные формулы для расчета площади, а именно:
Формула с использованием основания и высоты
Площадь = высота * основание
Пример: если длина стороны ромба 6 см, а высота 10 см, формула будет: 92, где «А» — внутренний угол.
Периметр ромба
Периметр ромба равен сумме его сторон . Ромб – это четырехугольник, у которого все четыре стороны равны. Он рассчитывается путем суммирования длин всех сторон. Поскольку все четыре стороны ромба равны, формула для периметра P = 4 \cdot s, где «s» — сторона ромба
Как найти площадь ромба?
Делаем ромб со сторонами s с четырьмя углами A, B, C, D. мы можем соединить диагонали d1 и d2, каждая из которых имеет противоположный угол. Высота определяется путем проведения перпендикулярной линии с одной стороны на другую.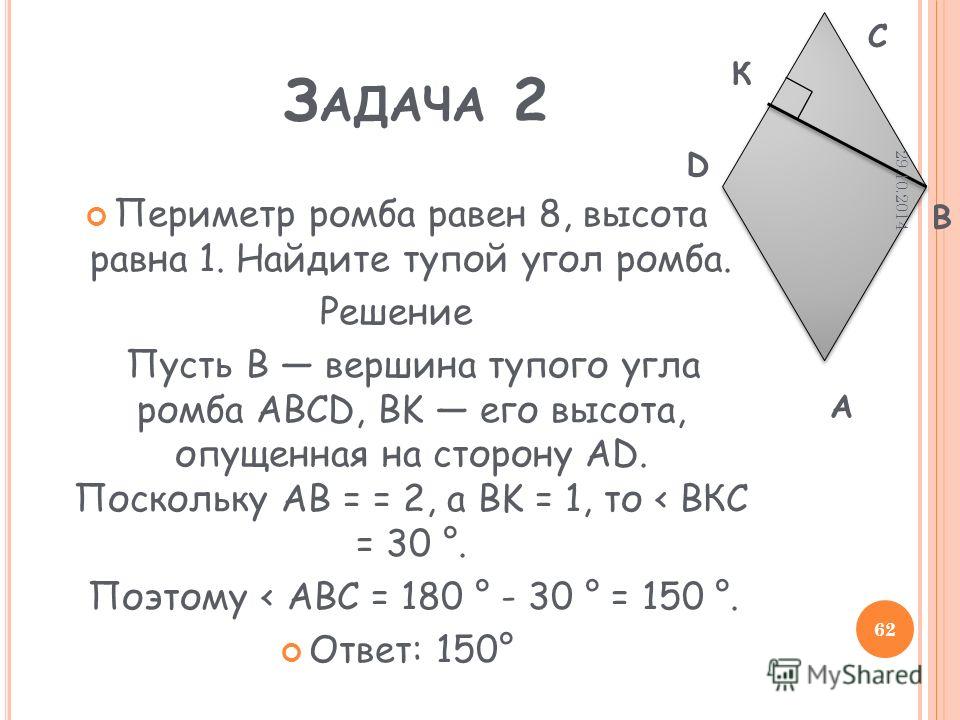
У нашего ромба четыре равные стороны AB, BC, CD, DA и четыре угла, где противоположные равны \угол a=\угол c \, и \, \угол b=\угол d. Диагонали d1 и d2 равны по длине только в квадратах. Высота h — это длина от одной стороны до противоположной, когда ромб лежит двумя сторонами горизонтально (плоско).
Если вы знаете длины любой стороны, поскольку они равны, вы знаете длину всех сторон. То же самое и с углом. Чтобы найти площадь, нужно знать высоту ромба. В нашем калькуляторе для нахождения площади ромба есть все параметры, поэтому его легко вычислить.
Является ли квадрат ромбом? Или ромб — это параллелограмм?
Ответ на оба вопроса положительный. Единственным условием для ромба является то, что у него должны быть равны все стороны, поэтому каждый квадрат является ромбом. Кроме того, ромб является параллелограммом, так как у него должны быть две пары параллельных сторон, чтобы его можно было назвать таковым. Параллелограмм является ромбом только в одном случае — параллелограммом, имеющим четыре равные стороны, но ромб всегда является параллелограммом.
Часто задаваемые вопросы
Все ли квадраты ромбы?
Да, все квадраты — ромбы, потому что ромб — это параллелограмм, у которого четыре равные стороны, а квадрат — это и тоже четыре равных угла. Итак, согласно этим определениям, квадрат есть ромб; однако не все ромбы являются квадратами.
Все ли ромбы параллелограммы?
Все ромбы являются параллелограммами, но не все параллелограммы являются ромбами, потому что у них должны быть равны только противоположные стороны, в отличие от ромбов, у которых все стороны должны быть одинаковой длины.
Диагонали ромба равны?
Нет, диагонали ромба в большинстве случаев различны по длине, где одна длиннее другой, за исключением случая квадрата, где диагонали равны.
Все ли стороны ромба равны? 92, где s — сторона, а квадрат стороны — площадь квадрата.
Можно ли найти площадь ромба, зная только его периметр?
В большинстве случаев вам потребуются дополнительные характеристики данного ромба, такие как высота или диагональ. Тем не менее, в случае квадрата периметр равен сумме четырех сторон, P=4\cdot s. Итак, имея это в виду, единственный ромб, который можно вычислить только с периметром, — это квадрат.
Тем не менее, в случае квадрата периметр равен сумме четырех сторон, P=4\cdot s. Итак, имея это в виду, единственный ромб, который можно вычислить только с периметром, — это квадрат.
Как найти длину диагонали ромба
Все дополнительные ресурсы по геометрии
6 Диагностические тесты 57 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Расширенная справка по геометрии » Плоская геометрия » Четырехугольники » ромбы » Как найти длину диагонали ромба
Предположим, что четырехугольник — ромб. Если периметр и длина диагонали , какова длина диагонали ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти значение диагонали, мы должны сначала узнать некоторые важные свойства ромбов.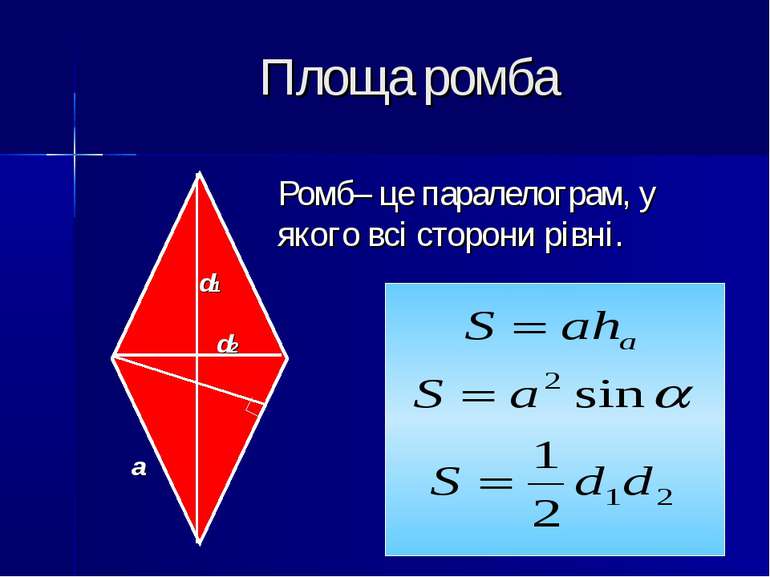 Поскольку периметр равен , а ромб по определению имеет четыре стороны одинаковой длины, длина каждой стороны ромба равна . Диагонали ромбов также образуют четыре прямоугольных треугольника с гипотенузами, равными длине стороны ромба, и катетами, равными половине длин диагоналей. Поэтому мы можем использовать теорему Пифагора, чтобы найти половину неизвестной диагонали:
Поскольку периметр равен , а ромб по определению имеет четыре стороны одинаковой длины, длина каждой стороны ромба равна . Диагонали ромбов также образуют четыре прямоугольных треугольника с гипотенузами, равными длине стороны ромба, и катетами, равными половине длин диагоналей. Поэтому мы можем использовать теорему Пифагора, чтобы найти половину неизвестной диагонали:
, где — длина стороны ромба, — половина известной диагонали, а — половина неизвестной диагонали. Таким образом, мы можем найти:
, следовательно, равно . Поскольку представляет половину неизвестной диагонали, нам нужно умножить на , чтобы найти полную длину диагонали .
Следовательно, длина диагонали равна
Сообщить об ошибке
Предположим, что четырехугольник является ромбом. Если площадь равна квадратным единицам, а длина диагонали равна единицам, то какова длина диагонали?
Возможные ответы:
Объяснение:
Эта задача основана на знании уравнения площади ромба, , где – площадь, а и – длины отдельных диагоналей. Мы можем подставить известные нам значения в уравнение, чтобы получить:
Мы можем подставить известные нам значения в уравнение, чтобы получить:
Таким образом, наш окончательный ответ состоит в том, что диагональ
Сообщить об ошибке
Если площадь ромба , а длина одной из диагоналей , то какова длина другой диагонали?
Возможные ответы:
Правильный ответ:
Пояснение:
Площадь ромба указана ниже.
Подставить заданную площадь и диагональ. Найдите другую диагональ.
Сообщить об ошибке
Если площадь ромба , а длина диагонали , то какова длина другой диагонали?
Возможные ответы:
Правильный ответ:
Пояснение:
Площадь ромба указана ниже.
Сообщить об ошибке
Площадь ромба . Длина одной диагонали в два раза больше другой диагонали. Какова длина меньшей диагонали?
Возможные ответы:
Правильный ответ:
Объяснение:
Пусть меньшая диагональ будет , а длинная диагональ будет . Более длинный размер в два раза длиннее другой диагонали. Напишите выражение для этого.
Напишите площадь ромба.
Поскольку мы вычисляем более короткую диагональ, лучше всего составить уравнение в терминах , чтобы мы могли найти более короткую диагональ. Подставьте площадь и выражение для решения .
Сообщить об ошибке
является ромбом со стороной . Диагональ имеет длину . Найдите длину диагонали .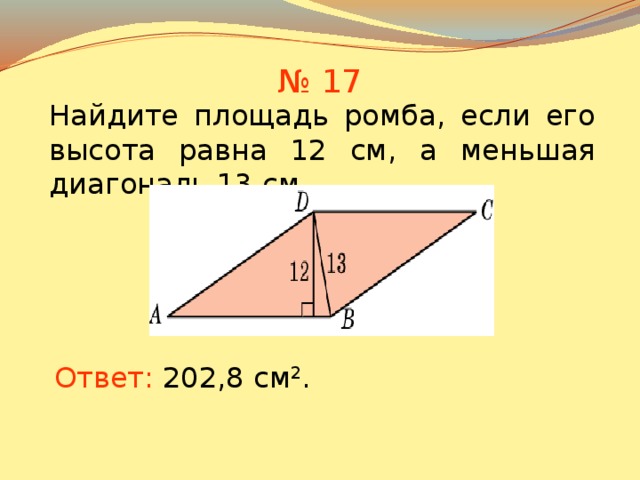
Возможные ответы:
Правильный ответ:
Пояснение:
Ромб – это четырехугольник с четырьмя сторонами одинаковой длины. Диагонали ромбов делят друг друга пополам под прямым углом.
Таким образом, мы можем рассмотреть прямоугольный треугольник, чтобы найти длину диагонали. Из задачи известно, что стороны равны и . Поскольку диагонали делят друг друга пополам, мы знаем:
Использование теоремы Pythagorean,
Отчет о ошибке
— Rhombus. и . Находить .
Возможные ответы:
Правильный ответ:
Пояснение:
Ромб – это четырехугольник с четырьмя сторонами одинаковой длины.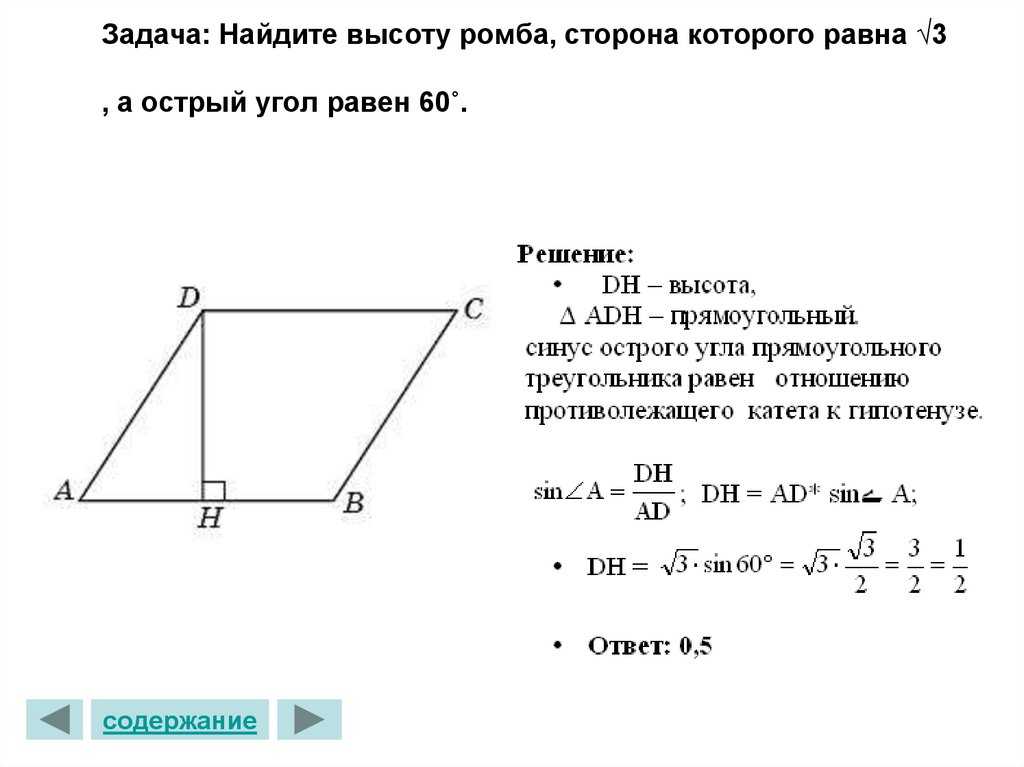 Диагонали ромбов делят друг друга пополам под прямым углом.
Диагонали ромбов делят друг друга пополам под прямым углом.
Таким образом, мы можем рассмотреть прямоугольный треугольник, чтобы найти длину диагонали. Из задачи известно, что стороны равны и . Поскольку диагональ разбивает друг друга, мы знаем:
с использованием теоремы Pythagorean,
. Отчет о ошибке
. и . Находить .
Возможные ответы:
Правильный ответ:
Пояснение:
Ромб – это четырехугольник с четырьмя сторонами одинаковой длины. Диагонали ромбов делят друг друга пополам под прямым углом.
Таким образом, мы можем рассмотреть прямоугольный треугольник, чтобы найти длину диагонали.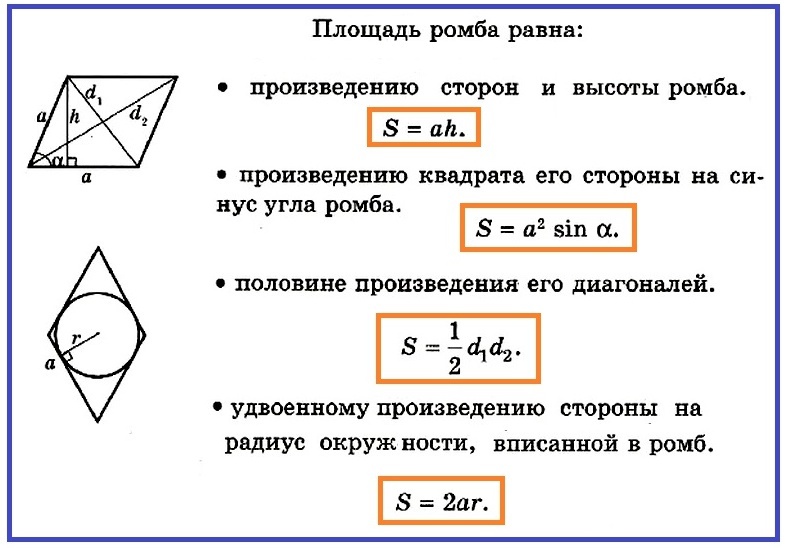 Из задачи известно, что стороны равны и . Поскольку диагонали делят друг друга пополам, мы знаем:
Из задачи известно, что стороны равны и . Поскольку диагонали делят друг друга пополам, мы знаем:
Используя теорему Пифагора,
Сообщить об ошибке
является ромбом. , , и . Находить .
Возможные ответы:
Правильный ответ:
Пояснение:
Ромб – это четырехугольник с четырьмя сторонами одинаковой длины. Диагонали ромбов делят друг друга пополам под прямым углом.
Таким образом, мы можем рассмотреть прямоугольный треугольник и использовать теорему Пифагора для решения . Из задачи:
Because the diagonals bisect each other, we know:
Using the Pythagorean Theorem,
Using the quadratic formula,
С этим уравнением мы получаем два решения:
Для этой задачи справедливо только положительное решение.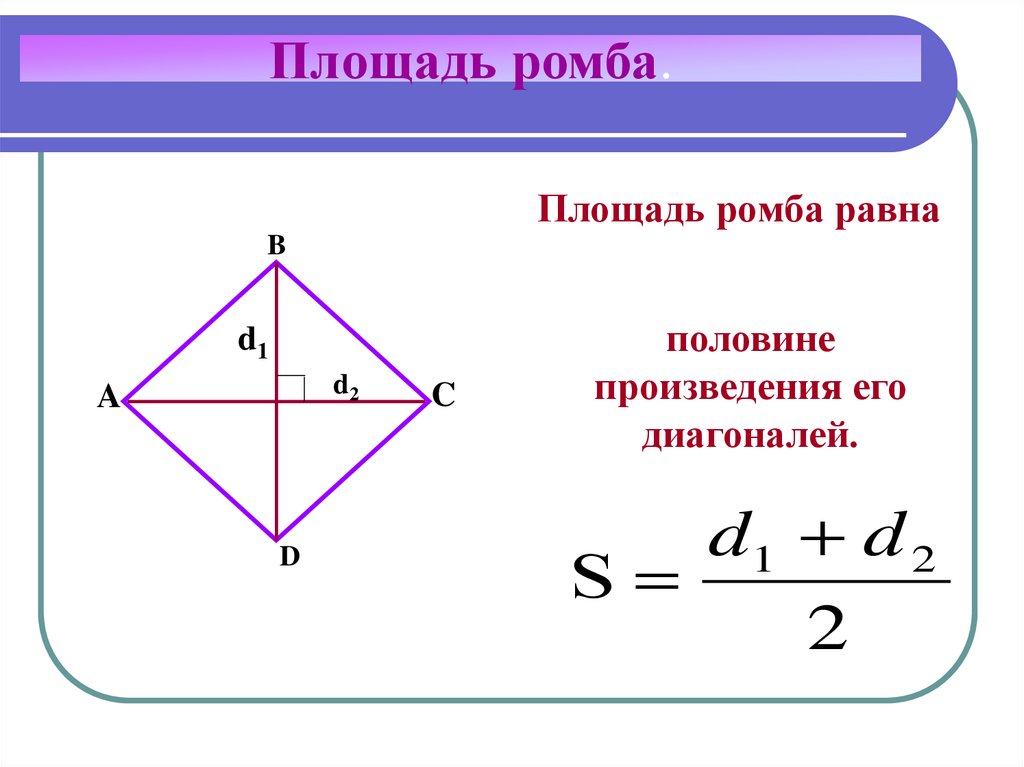

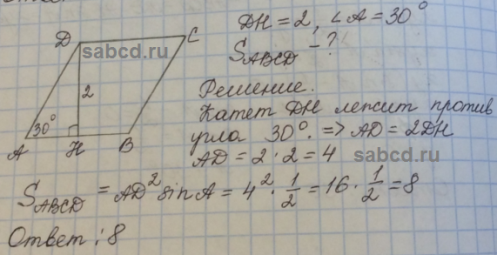
Leave A Comment