Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Конусом называется фигура, полученная
при вращении прямоугольного
треугольника вокруг оси, содержащей его
катет.
Sбок rl
Sполн r rl
2
1
1 2
V Sоснh r h
3
3
21.10.2021
1
Площади подобных фигур относятся
как коэффициент подобия в квадрате.
Объемы подобных фигур относятся
как коэффициент подобия в кубе.

21.10.2021
2
Площади боковых
поверхностей
подобных
цилиндров и
конусов относятся
как квадраты
радиусов или высот,
а объемы – как кубы
радиусов или высот.
2
2
s r
h
2 2
S R
H
3
3
v r
h
3 3
V R
H

4. Площадь боковой поверхности конуса равна 48π, а площадь основания равна 36π. Найдите длину образующей конуса.

21.10.2021
4
Площадь боковой поверхности конуса равна 48π, а площадь боковой
поверхности усеченного конуса с такими же основанием и углом
наклона образующей к плоскости основания равна 36π. Найдите
высоту усеченного конуса, если высота исходного конуса равна 10.
21.10.2021
5
• Высота конуса равна 15, а диаметр
основания – 16. Найдите образующую
конуса.
21.10.2021
6
. Длина окружности основания конуса равна
образующая равна Найдите площадь боковой поверхности конуса.
• Длина окружности основания конуса
равна 5, образующая равна 8. Найдите
площадь боковой поверхности конуса.
21.10.2021
7
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в раз?
• Во сколько раз увеличится площадь
боковой поверхности конуса, если его
образующую увеличить в 9 раз?
21.10.2021
8
Во сколько раз увеличится объем конуса, если
радиус его основания увеличится в 17 раз,
а высота останется прежней?
21.10.2021
9
• Площадь полной поверхности конуса
равна 148. Параллельно основанию конуса
проведено сечение, делящее высоту
пополам. Найдите площадь полной
поверхности отсеченного конуса.
21.10.2021
10
Найдите объем V конуса, образующая которого равна 2 и
V
0
наклонена к плоскости основания под углом 30 . В ответе укажите
.
А
Vкон.
S r
О
3
300
1
V
из АОС
1
S осн h
3
С
So
Vкон.
OC
cos 30
AC
0
3 OC
2
2
OC 3
2
3 3
2
1
3 1
3
Высота конуса равна 6, образующая равна 10. Найдите его объем,
деленный на .
А
Vкон.
So r
6
10
О
V
1
Sо h
3
S o 8 64
2
Vкон.
8
С
128
2
128
1
64 6 128
3
Конус получается при вращении равнобедренного прямоугольного
треугольника АВС вокруг катета, равного 6. Найдите его объем,
деленный на .
Vкон.
А
1
Sо h
3
So r 2
6
S o 6 36
1
Vкон. 36 6 72
3
2
В
С
V
72
72
Объем конуса равен 16. Через середину высоты параллельно
основанию конуса проведено сечение, которое является
основанием меньшего конуса с той же вершиной. Найдите
объем меньшего конуса.
Решение:
1
k
2
Конусы подобны
Vм 1
Vб
2
3
Vм
1
16 1
Vм
2
16
8
8
Ответ: 2
Во сколько раз уменьшится объем конуса, если его высота
уменьшится в 3 раза, а радиус основания останется
прежним?
Решение:
3h
r
h
r
1 2
V1 r 3 h
3
1 2
V2 r h
3
Составим отношение:
1
r 2 3h
V1
3
3
в три раза
1
V2
1
r 2 h
3
Ответ: 3
Чунин Павел 11«А»
Во сколько раз уменьшится объем конуса, если его высоту
уменьшить в 5 раз?
1
Sо h
5
V1
3
V2 1 S 1 h 1
о
3 5
V1
h
1
V = SoH
3
1
h
5
О
V2
r
Во сколько раз увеличится объем конуса, если радиус его
основания увеличится в 1,5 раза, а высота останется
прежней?
h
h
r
1,5 r
Решение:
1 2
V1 r h
3
1
V2 ( 1,5 r )2 h
3
Составим отношение:
1
r 2 h
3
V1
1
в 2,25 раза
1
V2
2 ,25 r 2 h 2 ,25
3
Ответ: 2 ,
2 5
Во сколько раз увеличится площадь боковой поверхности
конуса, если его образующая увеличится в 3 раза, а радиус
основания останется прежним?
Решение:
Sбок 1 rl
3l
Sбок 2 r 3l
l
r
r
Составим отношение:
Sбок 1
rl
1
Sбок 2
r 3 l
3
Ответ: 3
в три раза
Во сколько раз увеличится объём конуса, если радиус его основания
увеличить в 8 раз, а высоту оставить прежней?
21. 10.2021
19
Площадь боковой поверхности конуса в два раза больше
площади основания. Найдите угол между образующей
конуса и плоскостью основания.
21.10.2021
20

21. Площадь основания конуса равна 36 π, высота – 10. Найти площадь осевого сечения этого конуса.

21.10.2021
21
Площадь полной поверхности конуса равна 12. Параллельно
основанию конуса проведено сечение, делящее высоту
пополам. Найдите площадь полной поверхности отсеченного
конуса.
Решение:
k
Конусы подобны
Sм
1
Sб
2
Sм
1
12
4
Ответ: 3
Sм
1
2
2
12 1
3
4

23. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.

21.10.2021
23
Конус и цилиндр имеют общее основание и общую высоту
(конус вписан в цилиндр). Вычислите объём конуса, если объём
цилиндра равен 150.
Решение:
Vц r 2 h
h
h
1 2
Vк r h
3
r
Составим отношение:
Vц
r 2 h
1
3
150
3
Vк 150 1 50
1 2
1
Vк
1
Vк
1
3
r h
3
3
Ответ: 5 0

25.

Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конусаравен 25.
Решение:
Vк
1
R 2 h
3
Vц R 2 h
Составим отношение объема конуса к объему цилиндра.
1
R2 h
Vк
1
3
2
Vц
R h
3
25
1
Vц
3
25 3
Vц
75
1
Ответ:
21.10.2021
7 5
25

26. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Причем радиус основания равен высоте. Найдите

площадь боковой поверхности цилиндра, если площадь
боковой поверхности конуса равна 7√2.
21.10.2021

27. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса

равен 57.
21.10.2021
Площадь основания конуса равна 48. Плоскость,
параллельная плоскости основания конуса, делит
его высоту на отрезки длиной 15 и 45 считая от
вершины. Найдите площадь сечения конуса этой
плоскостью.
21.10.2021
28
Площадь полной поверхности конуса равна 50.
Параллельно основанию конуса проведено сечение,
делящее высоту в отношении 3:2, считая от вершины
конуса. Найдите площадь полной поверхности
отсечённого конуса.
21.10.2021
29
В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/2 высоты. Объём жидкости равен 70 мл. Сколько
миллилитров жидкости нужно долить, чтобы полностью
наполнить сосуд?
Решение:
k
Конусы подобны
Vм 1
Vб
2
1
2
3
70 8
70
1
Vб
560
1
Vб
8
Долить нужно: Vб Vv 560 70 490
Ответ: 4 9 0
В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/2 высоты. Объём жидкости равен 54 мл. Сколько
миллилитров жидкости нужно долить, чтобы полностью
наполнить сосуд?
В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/2 высоты. Объём жидкости равен 25
мл.Сколько миллилитров жидкости нужно долить, чтобы
полностью наполнить сосуд?
В сосуде, имеющем форму конуса, уровень жидкости
достигает 2/3 высоты. Объём жидкости равен 16
мл.Сколько миллилитров жидкости нужно долить, чтобы
полностью наполнить сосуд?

English     Русский Правила

Формулы объема цилиндра, шара, конуса — площадь поверхности и основания

Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.

Например, такой важный факт:

Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз.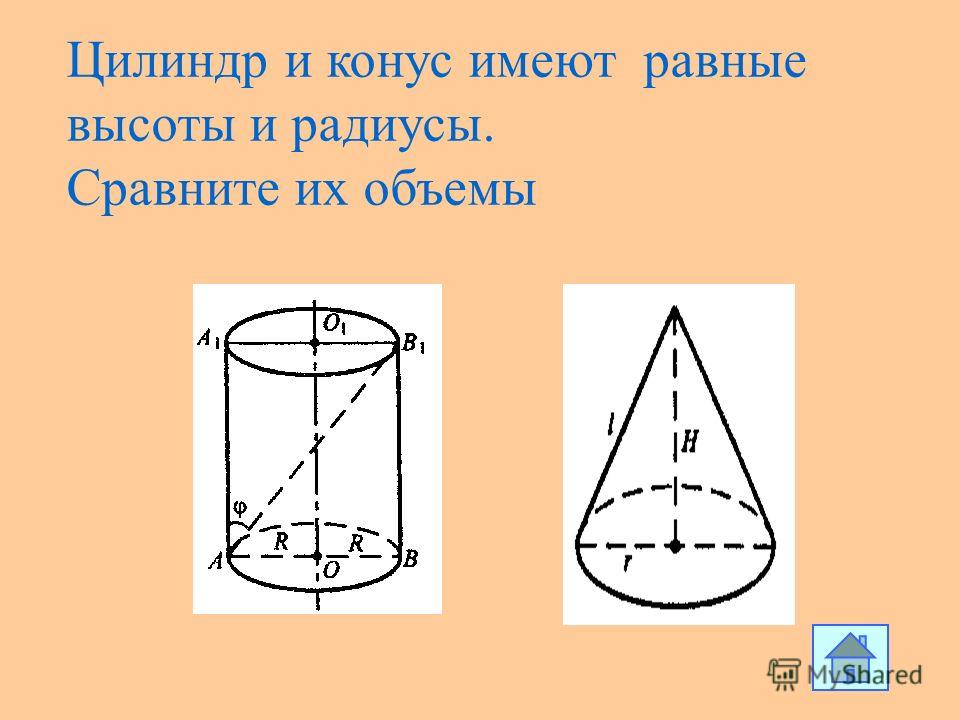

 

(ведь , ).

Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.

1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.

Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.

2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.

Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться! Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.

Мы тоже расскажем о ней.

Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Формулы объема и площади поверхности. Цилиндр, конус и шар» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 08.04.2023

Сферы, конусы и цилиндры – Окружности и Пи – Матигон

В предыдущих разделах мы изучали свойства окружностей на плоской поверхности. Но наш мир на самом деле трехмерен, поэтому давайте посмотрим на некоторые трехмерные тела, основанные на окружностях:

Цилиндр состоит из двух конгруэнтных параллельных окружностей, соединенных изогнутой поверхностью.

Конус имеет круглое основание, соединенное с одной точкой (называемой вершиной).

Каждая точка на поверхности 9Сфера 0005 находится на таком же расстоянии от своего центра.

Обратите внимание, что определение сферы почти такое же, как определение а, за исключением трех измерений!

Цилиндры

Здесь вы можете увидеть цилиндрический Газометр в Оберхаузене, Германия. Он использовался для хранения природного газа, который использовался в качестве топлива на близлежащих заводах и электростанциях. Газометр имеет высоту 120 м, а его основание и потолок представляют собой два больших круга радиусом 35 м. Есть два важных вопроса, на которые инженеры, возможно, захотят ответить:

  • Сколько природного газа можно хранить? Это цилиндр.
  • Сколько стали нужно для изготовления Газометра? Это (приблизительно) размер цилиндра.

Попробуем найти формулы для обоих результатов!

Газометр Оберхаузен

Объем цилиндра

Верх и низ цилиндра представляют собой две конгруэнтные окружности, называемые основаниями . Высота h цилиндра есть перпендикулярное расстояние между этими основаниями, а 0005 радиус r цилиндра — это просто радиус круглых оснований.

Мы можем аппроксимировать цилиндр, используя ${n}-стороннюю призму . По мере увеличения количества сторон призма все больше и больше становится похожей на цилиндр:

Хотя цилиндр технически не является призмой, у них много общих свойств. В обоих случаях мы можем найти объем, умножив площадь их основания на их высоту . Это означает, что цилиндр радиусом r и высота h имеет объем

V=

Помните, что радиус и высота должны использовать одни и те же единицы измерения. Например, если r и h оба в см, то объем будет в .

В приведенных выше примерах два основания цилиндра всегда находились непосредственно друг над другом : это называется правым цилиндром . Если основания не находятся прямо друг над другом, у нас есть косой цилиндр . Основания по-прежнему параллельны, но стороны как бы «наклоняются» под углом, не равным 90°.

Пизанская башня в Италии — это не совсем косой цилиндр.

Объем косого цилиндра оказывается точно таким же, как у прямого цилиндра с тем же радиусом и высотой. Это связано с принципом Кавальери , названным в честь итальянского математика Бонавентуры Кавальери: если два твердых тела имеют одинаковую площадь поперечного сечения на каждой высоте, то они будут иметь одинаковый объем.

Представьте, что вы разрезаете цилиндр на множество тонких дисков. Затем мы можем сдвинуть эти диски горизонтально, чтобы получить наклонный цилиндр. Объем отдельных дисков не меняется, когда вы делаете его наклонным, поэтому общий объем также остается постоянным:

Площадь поверхности цилиндра

Чтобы найти площадь поверхности цилиндра, мы должны «развернуть» его в плоскую сетку. Вы можете попробовать это сами, например, сняв этикетку с банки с едой.

Их два, один вверху и один внизу цилиндра. Изогнутая сторона на самом деле большая.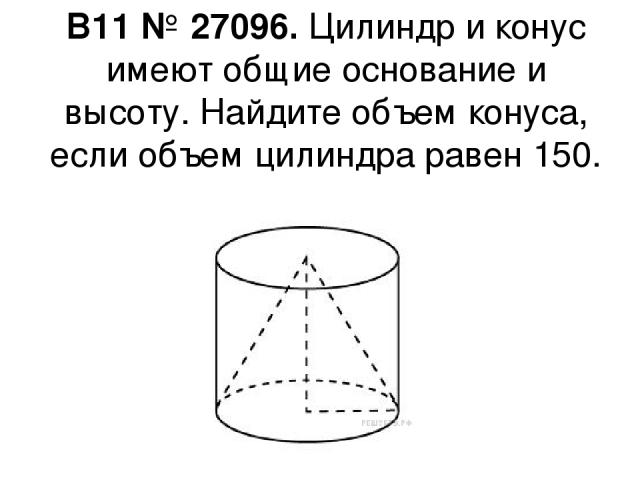

  • Каждый из двух кругов имеет площадь .
  • Высота прямоугольника и ширина прямоугольника такие же, как у кругов: .

Это означает, что общая площадь поверхности цилиндра с радиусом r и высотой h равна

A=.

Цилиндры можно найти повсюду в нашем мире — от банок с газировкой до туалетной бумаги или водопроводных труб. Можете ли вы вспомнить какие-либо другие примеры?

Газометр выше имел радиус 35 м и высоту 120 м. Теперь мы можем подсчитать, что его объем примерно равен м3, а площадь поверхности примерно м2.

Конусы

Конус представляет собой трехмерное твердое тело с круглым основанием . Его сторона «сужается вверх», как показано на диаграмме, и заканчивается в одной точке, называемой вершиной .

Радиус конуса — это радиус круглого основания, а высота конуса — это расстояние по перпендикуляру от основания до вершины.

Как и другие формы, которые мы встречали ранее, конусы повсюду вокруг нас: рожки для мороженого, дорожные конусы, некоторые крыши и даже рождественские елки. Что еще вы можете придумать?

Объем конуса

Ранее мы нашли объем цилиндра, аппроксимируя его с помощью призмы. Точно так же мы можем найти объем конуса, аппроксимируя его с помощью пирамиды .

Здесь вы видите ${n}-стороннюю пирамиду. По мере увеличения количества сторон пирамида все больше и больше становится похожей на конус. На самом деле, мы могли бы думать о конусе как о пирамиде с бесконечно многими сторонами!

Это также означает, что мы также можем использовать уравнение для объема: V=13база×высота. Основанием конуса является круг, поэтому объем конуса радиусом r и высота h равна

V=

Обратите внимание на сходство с уравнением для объема цилиндра. Представьте себе, что вокруг конуса нарисован цилиндр с тем же основанием и высотой — это называется описанным цилиндром . Теперь конус будет занимать в точности объем цилиндра:

Примечание: Вы можете подумать, что бесконечное множество крошечных сторон в качестве приближения немного «неточно». Математики долго пытались найти более простой способ вычисления объема конуса. В 1900, великий математик Давид Гильберт даже назвал ее одной из 23 самых важных нерешенных проблем математики! Сегодня мы знаем, что это на самом деле невозможно.

Как и цилиндр, конус не обязательно должен быть «прямым». Если вершина находится прямо над центром основания, у нас есть правый конус . В противном случае мы называем его косым конусом .

И снова мы можем использовать принцип Кавальери, чтобы показать, что все наклонные конусы имеют одинаковый объем, если они имеют одинаковое основание и высоту.

Площадь поверхности конуса

Найти площадь поверхности конуса немного сложнее. Как и прежде, мы можем распутать конус в свою сеть. Переместите ползунок, чтобы увидеть, что произойдет: в этом случае мы получим один кружок и один .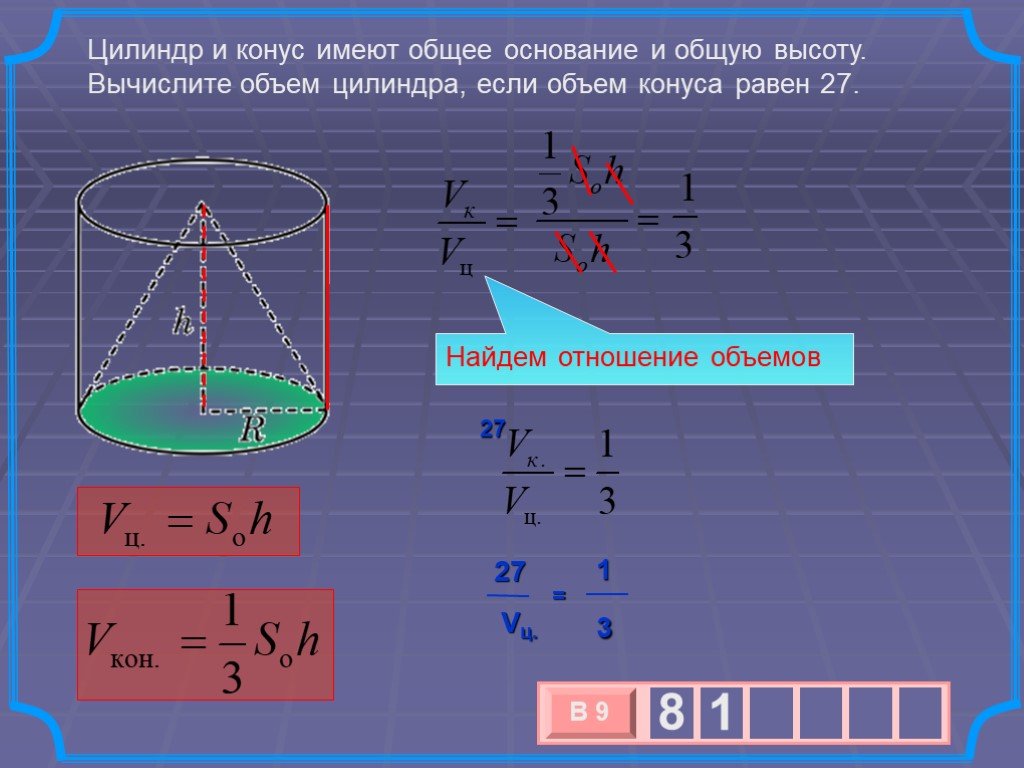

Теперь нам просто нужно сложить площади обоих этих компонентов. Основание — это круг с радиусом r , поэтому его площадь равна

ABase=.

Радиус сектора равен расстоянию от края конуса до его вершины. Это называется наклонной высотой s конуса, а не такой же, как обычная высота h . Мы можем найти наклонную высоту с помощью Пифагора:

Длина дуги сектора такая же, как у основания: 2πr. Now we can find the area of ​​the sector using the formula we derived in a previous section:

ASector = ACircle×arccircumference
=

Finally, we just нужно сложить площадь основание и площадь сектора , чтобы получить общую поверхность конуса:

A=

Сферы

Сфера представляет собой трехмерное тело, состоящее из всех точек, находящихся на одинаковом расстоянии из заданного центра C .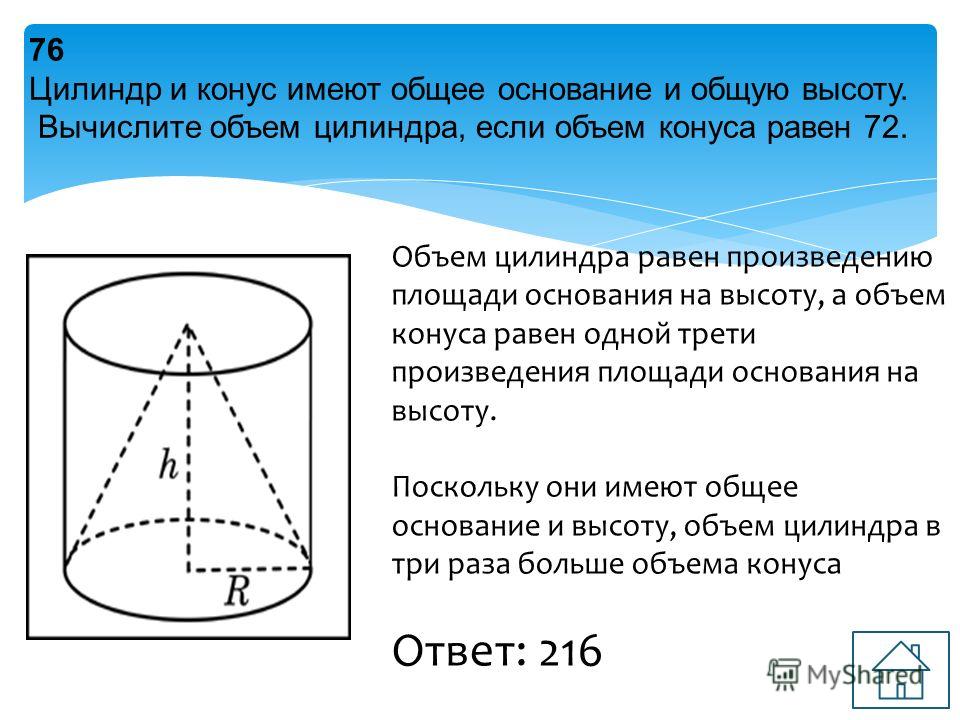 Это расстояние называется радиусом r сферы.

Сферу можно представить как «трехмерный круг». Так же, как круг, сфера также имеет диаметр d , который является длиной радиуса, а также хорд и секущих.

В предыдущем разделе вы узнали, как греческий математик Эратосфен вычислил радиус Земли по тени от полюса — он составил 6 371 км. Теперь попробуем найти общий объем и площадь поверхности Земли.

Объем сферы

Чтобы найти объем сферы, мы снова должны использовать принцип Кавальери. Начнем с полушария — сферы, разрезанной пополам по экватору. Также нам понадобится цилиндр такого же радиуса и высоты, как у полусферы, но с «вырезанным» посередине перевернутым конусом.

При перемещении ползунка ниже вы можете увидеть поперечное сечение обеих этих фигур на определенной высоте над основанием:

Попробуем найти площадь поперечного сечения обоих этих тел на высоте h над основанием.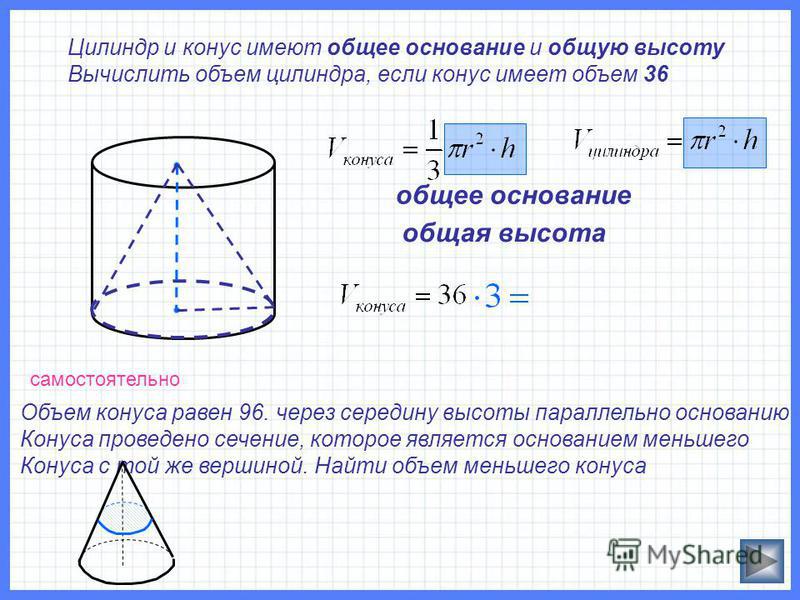

Сечение полушария всегда равно .

Радиус поперечного сечения x является частью прямоугольного треугольника, поэтому мы можем использовать Пифагор:

r2=h3+x2.

Теперь площадь поперечного сечения равна

Поперечное сечение вырезанного цилиндра всегда равно .

Радиус отверстия ч . We can find the area of ​​the ring by subtracting the area of ​​the hole from the area of ​​the larger circle:

A = πr2−πh3
= πr2−h3

Похоже, что оба тела имеют одинаковую площадь поперечного сечения на каждом уровне. По принципу Кавальери оба тела должны иметь одинаковые ! Мы можем найти объем полушария, вычитая объем цилиндра и объем конуса:

VHemisphere = VCylinder−VCone
=

A sphere consists of hemispheres, which means that its volume must be

V=43πr3.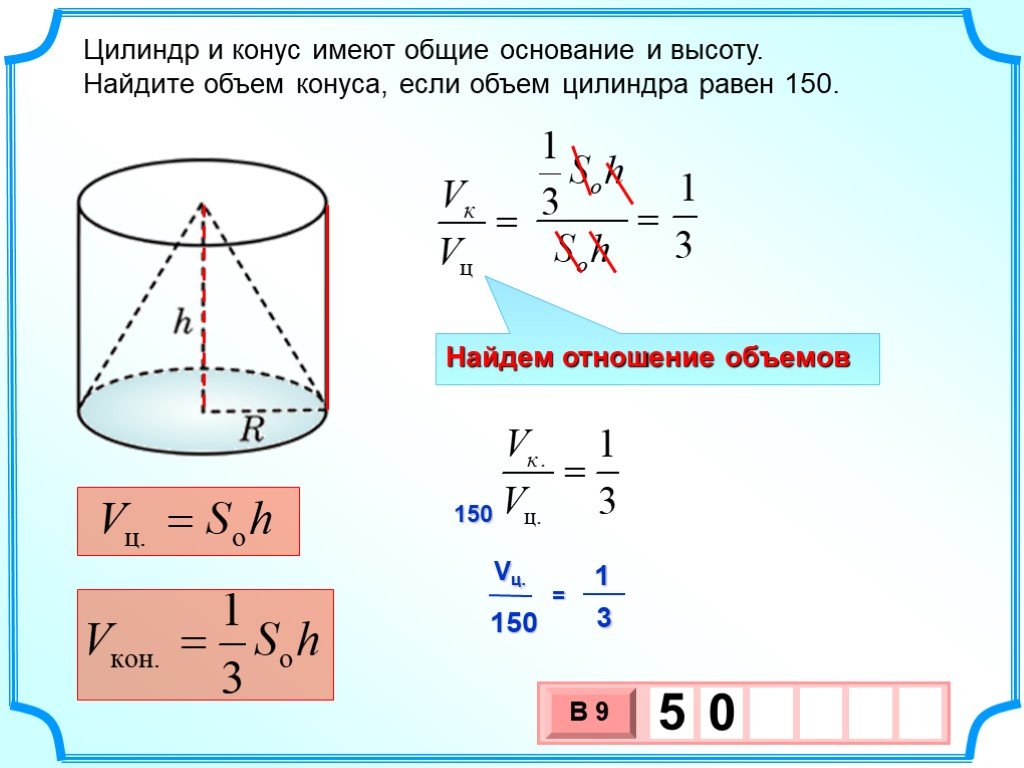

Земля (приблизительно) представляет собой сферу с радиусом 6 371 км. Следовательно, его объем равен

V =
= 1 км3

Средняя плотность Земли составляет 5510 кг/м3. Это означает, что его общая масса равна

Масса=Объем×Плотность≈6×1024 кг

Это 6 с 24 нулями!

Если вы сравните уравнения для объема цилиндра, конуса и сферы, вы можете заметить одно из самых удовлетворительных соотношений в геометрии. Представьте, что у нас есть цилиндр, высота которого равна диаметру его основания. Теперь мы можем идеально разместить конус и сферу внутри него:

+

Этот конус имеет радиус r и высоту 2r. Его объем

=

Радиус этой сферы равен r. Его объем

Этот цилиндр имеет радиус r и высоту 2r. Его объем равен

. Обратите внимание, если мы возьмем объем конуса и сферы, мы получим в точности объем цилиндра!

Площадь поверхности сферы

Найти формулу площади поверхности сферы очень сложно.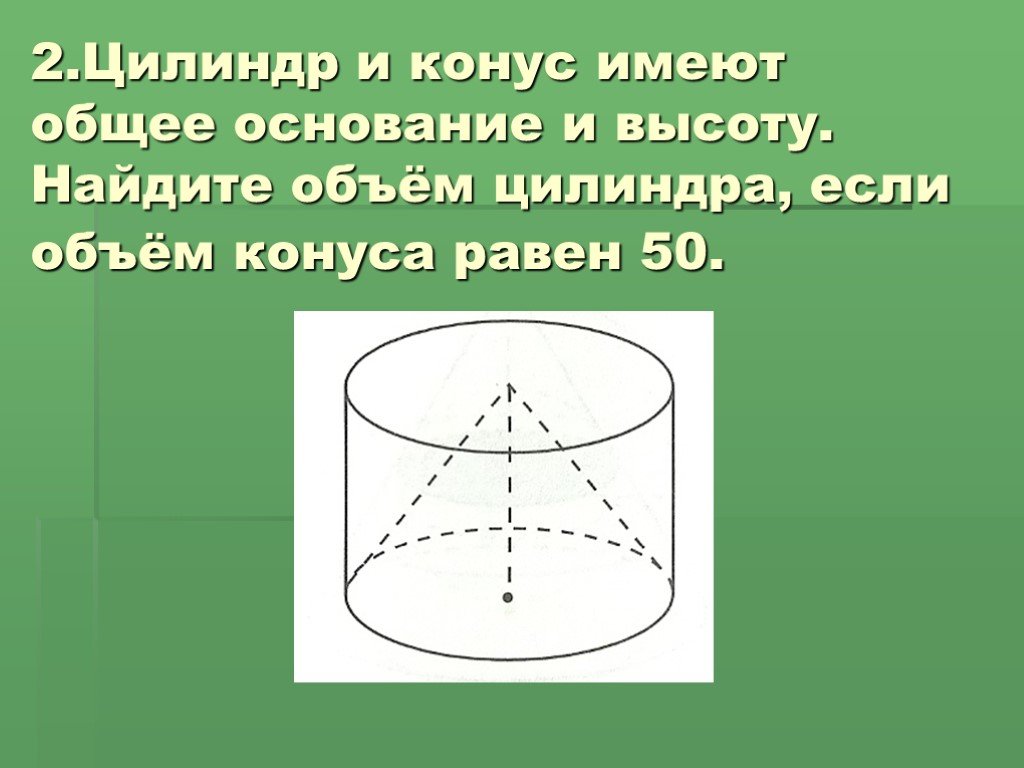 Одна из причин заключается в том, что мы не можем открыть и «сгладить» поверхность сферы, как мы делали раньше для конусов и цилиндров.

Это особая проблема при попытке создать карты. Земля имеет изогнутую трехмерную поверхность, но каждая печатная карта должна быть плоской и двухмерной. Это означает, что географам приходится хитрить: растягивать или сжимать определенные области.

Здесь вы можете увидеть несколько разных типов карт, называемых проекциями . Попробуйте переместить красный квадрат и посмотрите, как эта область на самом деле выглядит на глобусе:

Меркатор

Цилиндрический

Robinson

Mollweide

Когда вы перемещаете квадрат по карте, обратите внимание, как размер и форма реальной области меняются на трехмерном глобусе.

Чтобы найти площадь поверхности сферы, мы можем еще раз аппроксимировать ее, используя другую форму — например, многогранник с множеством граней. По мере увеличения количества граней многогранник начинает все больше и больше походить на сферу.

СКОРО: Доказательство площади поверхности сферы

Геометрия: цилиндры и конусы

В определении призмы основания должны быть конгруэнтными многоугольниками. Если основания представляют собой конгруэнтные замкнутые кривые (например, круг), то у вас есть цилиндр . Я нарисовал цилиндр с круглым основанием на рис. 21.4. Основание этого цилиндра представляет собой окружность, поэтому у него нет вершин. Большинство цилиндров, с которыми вы сталкиваетесь, имеют круги для формы основания, и они называются круглыми цилиндрами . Но иметь круглую основу — это просто вежливость. Это не требование.

Рисунок 21.4 Круглый цилиндр.

Когда вы думаете о цилиндре, на ум сразу же приходит форма консервной банки. Эти типы цилиндров классифицируются как правильные круговые цилиндры.

Ослабление ограничений на основания призменных цилиндров. Ослабление ограничений на форму основания пирамиды приведет к созданию конуса.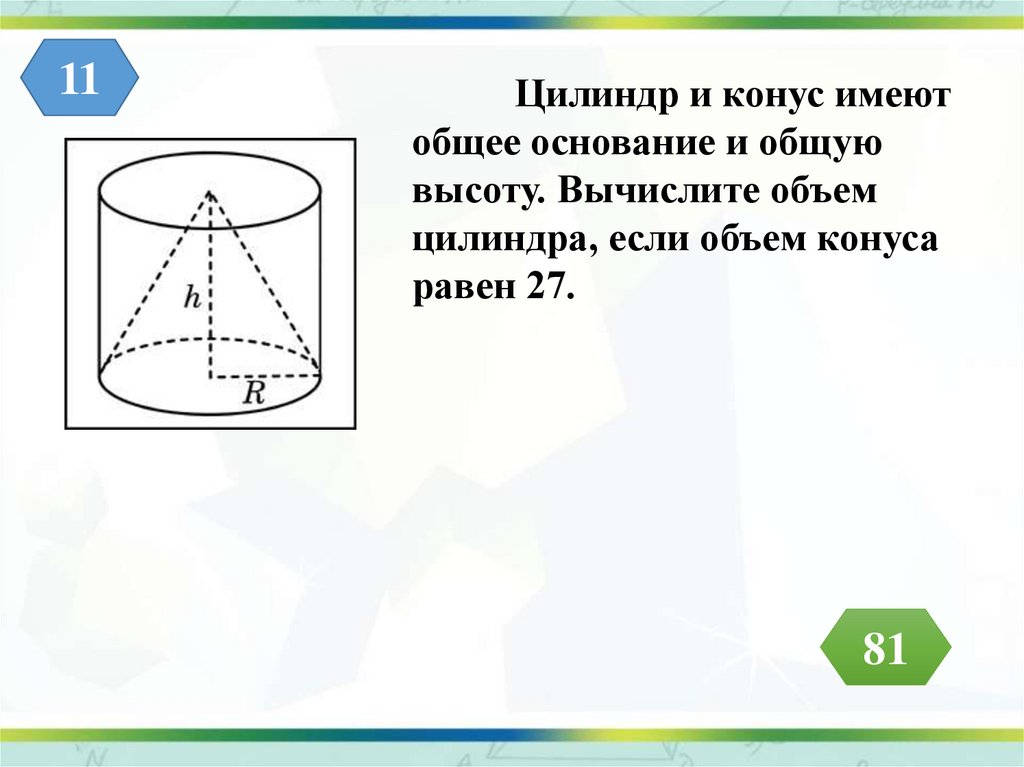 Постройте конус так же, как вы строили пирамиду. Начните с замкнутой кривой, лежащей в плоскости, которая будет служить основание конуса, и точка, которая будет служить вершиной конуса. Конус представляет собой твердое тело, образованное внутренней частью этой замкнутой кривой вместе с поверхностью, образованной при соединении каждой точки замкнутой кривой с вершиной с помощью отрезков прямой.

Solid Facts

Цилиндр представляет собой тело, образованное двумя конгруэнтными замкнутыми кривыми в параллельных плоскостях вместе с поверхностью, образованной отрезками, соединяющими соответствующие точки двух кривых. А круглый цилиндр представляет собой цилиндр с круглым основанием.

Название конуса основано на форме его основания. На рис. 21.5 показан круглый конус. Круглые конусы попадают в одну из двух категорий: прямые круглые конусы и наклонные круглые конусы. Прямой круглый конус представляет собой круглый конус, в котором отрезок, соединяющий вершину конуса с центром круглого основания, перпендикулярен плоскости основания.

Наклонный круглый конус представляет собой круглый конус, в котором отрезок, соединяющий вершину конуса с центром круглого основания, не перпендикулярен плоскости основания.

Рисунок 21.5 Круглый конус.

Solid Facts

Конус представляет собой твердое тело, образованное внутренней частью плоской замкнутой кривой вместе с поверхностью, образованной при соединении каждой точки замкнутой кривой с некомпланарной точкой с помощью отрезков прямой.

Основание конуса представляет собой плоскую замкнутую кривую конуса.

Вершина конуса — это некомпланарная точка, соединенная с каждой точкой основания.

A Прямой круглый конус представляет собой круглый конус, в котором отрезок, соединяющий вершину конуса с центром круглого основания, перпендикулярен плоскости основания.

Наклонный круглый конус представляет собой круглый конус, в котором отрезок, соединяющий вершину конуса с центром круглого основания, не перпендикулярен плоскости основания.