В равносторонний треугольник вписана окружность со стороной 8 см: В равносторонний треугольник со стороной 8 см вписана окружность. Найдите радиус окружности.

8 класс. Геометрия. Окружность. Вписанная и описанная окружность. — Вписанная окружность.

Комментарии преподавателя

Впи­сан­ная окруж­ность

Нач­нем с на­по­ми­на­ния важ­ных опор­ных фак­тов, и пер­вый факт – это ка­са­ние пря­мой и окруж­но­сти.

За­да­на окруж­ность с цен­тром О и ра­ди­у­сом r (см. Рис. 1). А – общая точка пря­мой и окруж­но­сти. Если такая точка един­ствен­ная, то пря­мая р – ка­са­тель­ная к окруж­но­сти. Ра­ди­ус ОА, про­ве­ден­ный в точку ка­са­ния, пер­пен­ди­ку­ля­рен ка­са­тель­ной р.

Спра­вед­ли­во об­рат­ное: если А – общая точка пря­мой и окруж­но­сти, и ра­ди­ус, про­ве­ден­ный в эту точку, пер­пен­ди­ку­ля­рен пря­мой, то общая точка един­ствен­ная, и пря­мая р – ка­са­тель­ная.

Рис. 1

Рас­смот­рим ка­са­ние окруж­но­сти сто­ро­на­ми угла (см. Рис. 2).

Пом­ним, что бис­сек­три­са угла – это гео­мет­ри­че­ское место точек, рав­но­уда­лен­ных от сто­рон дан­но­го угла.

Точка О лежит на бис­сек­три­се: пер­пен­ди­ку­ляр ОА к пря­мой а, ОВ – к пря­мой В, .

По­стро­им окруж­ность ра­ди­у­сом ОА.

Рис. 2

Утвер­жда­ем, что окруж­ность ка­са­ет­ся пря­мой а, т.к. А – общая точка пря­мой а и окруж­но­сти, и она един­ствен­ная (ра­ди­ус ОА пер­пен­ди­ку­ля­рен пря­мой). Ана­ло­гич­но пря­мая b ка­са­ет­ся окруж­но­сти.

Таким об­ра­зом, имеем окруж­ность, впи­сан­ную в угол.

Мно­го­уголь­ник имеет несколь­ко углов и несколь­ко сто­рон, мы го­то­вы дать опре­де­ле­ние впи­сан­ной в него окруж­но­сти.

Окруж­ность на­зы­ва­ет­ся впи­сан­ной в мно­го­уголь­ник, если ка­са­ет­ся всех его сто­рон.

Мы будем рас­смат­ри­вать толь­ко вы­пук­лые мно­го­уголь­ни­ки, рас­смот­рим при­мер – окруж­ность впи­са­на в вы­пук­лый че­ты­рех­уголь­ник:

Как по­лу­чить центр и ра­ди­ус впи­сан­ной окруж­но­сти?

Мы знаем, что точка О – центр, лежит на бис­сек­три­се угла А, впи­са­на в угол А, ана­ло­гич­но точка О лежит на бис­сек­три­се каж­до­го угла и впи­са­на в каж­дый угол.

Таким об­ра­зом, все бис­сек­три­сы че­ты­рех­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке – точке О.

Стро­им бис­сек­три­сы, на их пе­ре­се­че­нии по­лу­ча­ем центр окруж­но­сти. Из точки О опус­ка­ем пер­пен­ди­ку­ля­ры к сто­ро­нам

Рис. 3

че­ты­рех­уголь­ни­ка в точки K, L, M, N. Ка­са­тель­ные, про­ве­ден­ные к окруж­но­сти из одной точки, равны между собой, таким об­ра­зом, из каж­дой вер­ши­ны вы­хо­дит пара рав­ных ка­са­тель­ных – , , , .

В опи­сан­ном че­ты­рех­уголь­ни­ке суммы про­ти­во­по­лож­ных сто­рон равны.

Дано: окруж­ность с цен­тром О впи­са­на в че­ты­рех­уголь­ник ABCD. Че­ты­рех­уголь­ник ABCD опи­сан около окруж­но­сти. Таким об­ра­зом, опи­сан­ный че­ты­рех­уголь­ник – это такой че­ты­рех­уголь­ник, в ко­то­рый можно впи­сать окруж­ность (см. Рис. 4)_.

До­ка­зать: 

Рис. 4

До­ка­за­тель­ство:

За­пи­шем ра­вен­ство через от­рез­ки ка­са­тель­ных:

; ; ; ;

;

Рас­кро­ем скоб­ки:

;

Таким об­ра­зом, суммы про­ти­во­по­лож­ных сто­рон че­ты­рех­уголь­ни­ка, опи­сан­но­го около окруж­но­сти, равны, что и тре­бо­ва­лось до­ка­зать.

Итак, если в че­ты­рех­уголь­ник можно впи­сать окруж­ность, то суммы его про­ти­во­по­лож­ных сто­рон равны.

Спра­вед­ли­ва об­рат­ная тео­ре­ма.

Тео­ре­ма

Если суммы про­ти­во­по­лож­ных сто­рон вы­пук­ло­го че­ты­рех­уголь­ни­ка равны, в него можно впи­сать окруж­ность.

Это важ­ная тео­ре­ма, так как центр впи­сан­ной окруж­но­сти на­хо­дит­ся на пе­ре­се­че­нии бис­сек­трис. От­сю­да, если суммы про­ти­во­по­лож­ных сто­рон че­ты­рех­уголь­ни­ка равны, его бис­сек­три­сы пе­ре­се­кут­ся в одной точке.

Дан­ную тео­ре­му мы до­ка­зы­вать не будем.

Пря­мую и об­рат­ную тео­ре­мы можно объ­еди­нить.

Тео­ре­ма

В вы­пук­лый че­ты­рех­уголь­ник можно впи­сать окруж­ность тогда и толь­ко тогда, когда суммы его про­ти­во­по­лож­ных сто­рон равны.

При­ве­дем кон­крет­ные при­ме­ры че­ты­рех­уголь­ни­ков, в ко­то­рые можно впи­сать окруж­ность и в ко­то­рые нель­зя впи­сать окруж­ность.

Ромб

У ромба все сто­ро­ны равны, от­сю­да суммы про­ти­во­по­лож­ных сто­рон равны, зна­чит, в ромб можно впи­сать окруж­ность (см. Рис. 5). Кроме того, мы знаем, что диа­го­на­ли ромба пер­пен­ди­ку­ляр­ны и делят углы ромба по­по­лам. Зна­чит, каж­дая диа­го­наль – это бис­сек­три­са, бис­сек­три­сы всех че­ты­рех углов пе­ре­сек­лись в одной точке – точке О. О – центр впи­сан­ной окруж­но­сти.

Рис. 5

Квад­рат

Квад­рат – част­ный слу­чай ромба, в него также можно впи­сать окруж­ность (см. Рис. 6).

Рис. 6

Пря­мо­уголь­ник

В пря­мо­уголь­ник нель­зя впи­сать окруж­ность (см. Рис. 7), это оче­вид­но из ри­сун­ка – суммы про­ти­во­по­лож­ных сто­рон не равны, т.к. про­ти­во­по­лож­ные сто­ро­ны равны между собой, а со­сед­ние не равны:

Рис. 7

В любой тре­уголь­ник можно впи­сать окруж­ность, и толь­ко одну (см. Рис. 8).

Рис. 8

До­ка­за­тель­ство:

Мы знаем, что все бис­сек­три­сы тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке – пусть в точке О. Про­ве­дем бис­сек­три­сы АО, ВО, СО. Точка их пе­ре­се­че­ния О рав­но­уда­ле­на от сто­рон тре­уголь­ни­ка. Она рав­но­уда­ле­на от сто­рон угла  – АС и АВ, так как при­над­ле­жит бис­сек­три­се этого угла. Ана­ло­гич­но она рав­но­уда­ле­на от сто­рон углов  и , таким об­ра­зом, от трех сто­рон тре­уголь­ни­ка.

Опу­стим пер­пен­ди­ку­ля­ры из точки О на сто­ро­ны тре­уголь­ни­ка – ОМ на сто­ро­ну АС, OL – на ВС, ОК – на АВ. Эти пер­пен­ди­ку­ля­ры и будут рас­сто­я­ни­я­ми от точки О до сто­рон тре­уголь­ни­ка, и они равны:

.

Обо­зна­чим рас­сто­я­ние от точки О до сто­рон тре­уголь­ни­ка за r и рас­смот­рим окруж­ность с цен­тром в точке О и ра­ди­у­сом r.

Окруж­ность ка­са­ет­ся пря­мой АВ, т.к. имеет с ней общую точку К, и ра­ди­ус ОК, про­ве­ден­ный в эту точку, пер­пен­ди­ку­ля­рен пря­мой АВ. Ана­ло­гич­но окруж­ность ка­са­ет­ся пря­мых АС и ВС. Таким об­ра­зом, окруж­ность ка­са­ет­ся всех тех сто­рон тре­уголь­ни­ка, зна­чит, она впи­са­на в тре­уголь­ник.

До­ка­жем, что дан­ная впи­сан­ная окруж­ность един­ствен­ная. Если бы была вто­рая окруж­ность, ее центр был бы рав­но­уда­лен от всех сто­рон тре­уголь­ни­ка и лежал бы на пе­ре­се­че­нии всех бис­сек­трис.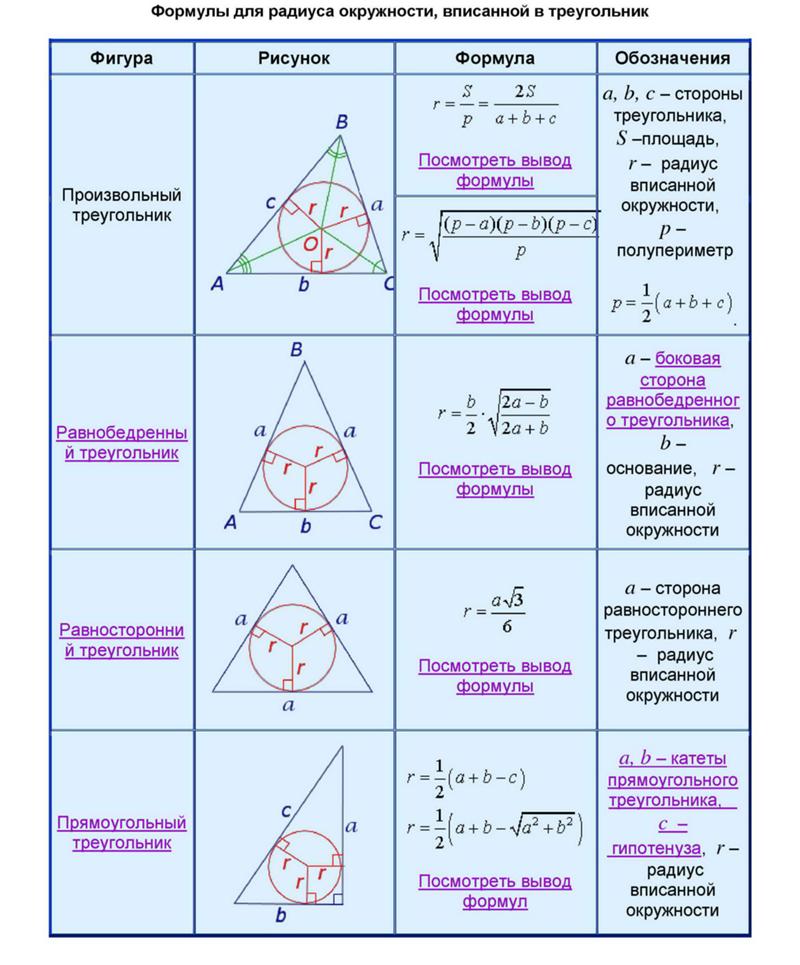 Но все бис­сек­три­сы пе­ре­се­ка­ют­ся в един­ствен­ной точке – точке О, таким об­ра­зом, и впи­сан­ная окруж­ность в тре­уголь­ник един­ствен­ная.

Итак, мы озна­ко­ми­лись с по­ня­ти­ем впи­сан­ной окруж­но­сти и до­ка­за­ли неко­то­рые важ­ные тео­ре­мы. В сле­ду­ю­щем уроке мы рас­смот­рим опи­сан­ную окруж­ность.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/okruzhnost/vpisannaya-okruzhnost

http://www.youtube.com/watch?v=anExTX9sEkQ

http://insuredsecured.com/images/560873dbaa6f5.jpg

http://otvet.imgsmail.ru/download/d8fc62f744e584d0d24aeaf99f0b82df_i-149.jpg

http://auto.ur.ru/img/books_covers/1007081838.jpg

 

Задачи обучающего характера по теме ВПИСАННАЯ ОКРУЖНОСТЬ

Вписанная Окружность

(задачи Обучающего характера)

Геометрия, 8 класс

К учебнику Л.С.Атанасяна

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Площадь описанного многоугольника

В

r

r

С

О

r

r

А

Д

Задача 1.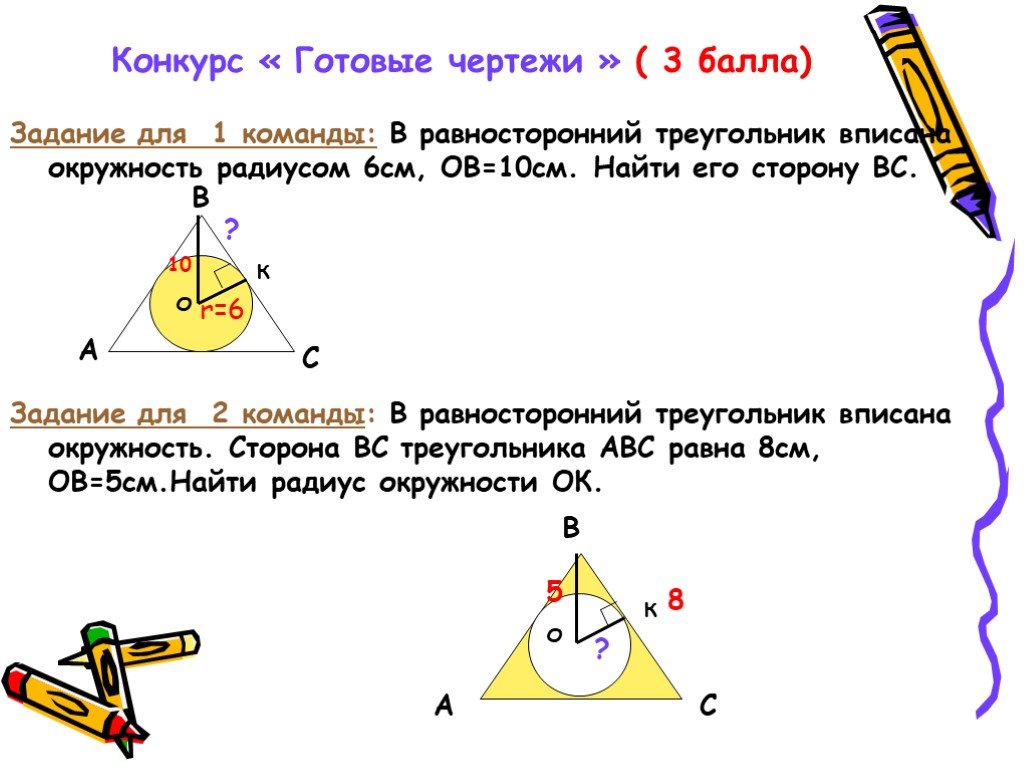

В равносторонний треугольник вписана окружность радиусом 4 см. Найдите сторону треугольника.

В

О – точка пересечения

биссектрис АР и ВК

P

О

ОК – радиус вписанной

окружности, ОК = 4.

4

К

С

А

2 способ

АС — ?

АО =

АК = …

АС = …

Задача 2.

В равносторонний треугольник со стороной 8 см вписана окружность. Найдите радиус окружности

В

АВ = ВС = АС = 8.

О – точка пересечения

P

биссектрис АР и ВК

8

О

ОК – радиус вписанной

окружности

ОК — ?

К

С

А

АК = 4

ОК = х

АО = 2х

Задача 3.

В прямоугольном треугольнике АВС ( ∠С = 90 0 ) АВ = 10 см, радиус вписанной окружности равен 2 см. Найдите площадь треугольника.

А

х

О – точка пересечения биссектрис

М

х

К, М, Р – точки касания

10 — х

О

К

ОК = ОМ = ОР = 2 см, АВ = 10 см

2

Р

АС = х + 2

ВС = 2 + 10 — х = 12 — х

В

10 — х

2

С

По теореме Пифагора

АС = 4 + 2 = 6

АС = 6 + 2 = 8

(х + 2) 2 + (12 – х) 2 = 10 2

ВС = 12 – 4 = 8

ВС = 12 – 6 = 6

х 2 – 10 х + 24 = 0

х 1 = 4, х 2 = 6

или

Задача 4.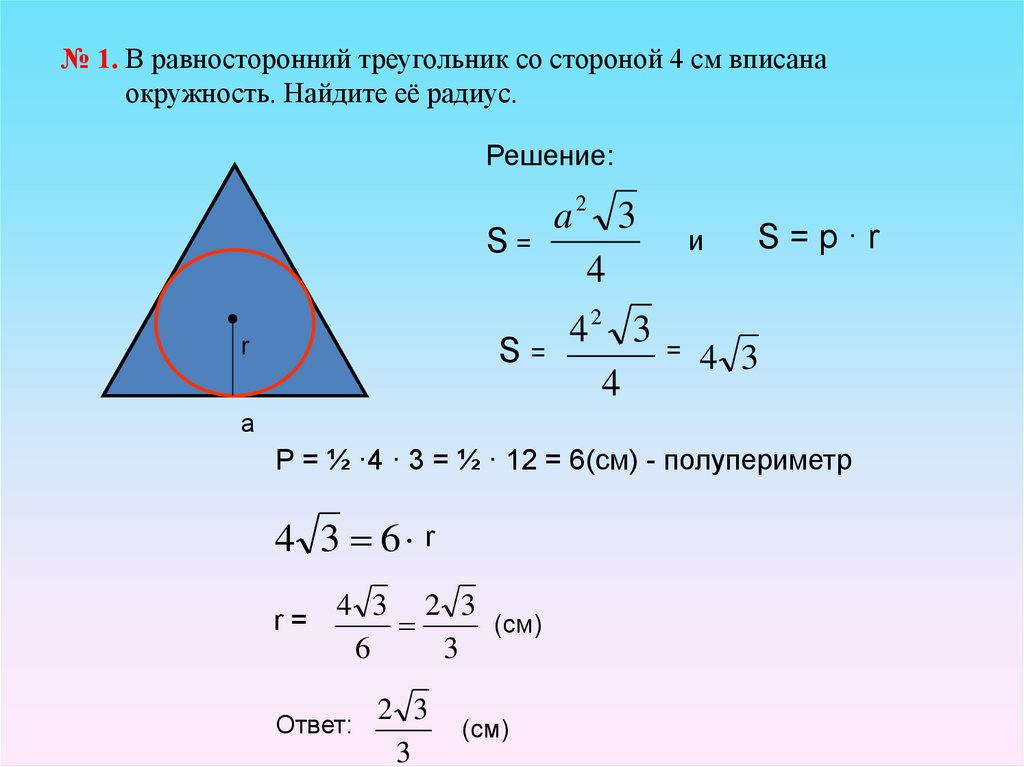

В прямоугольном треугольнике АВС ( ∠С = 90 0 ) АС + ВС = 17 см, радиус вписанной окружности равен 2 см. Найдите площадь треугольника.

А

х-2

О – точка пересечения биссектрис

М

х-2

К, М, Р – точки касания

15 — х

О

К

ОК = ОМ = ОР = 2 см, АС + ВС = 17 см

2

АС = х

ВС = 17 — х

Р

В

15 — х

2

С

АВ = х – 2 +15 – х = 13

По теореме Пифагора

АС = 12

АС = 5

х 2 + (17 – х) 2 = 13 2

ВС = 17 – 12 = 5

ВС = 17 – 5 = 12

х 2 – 17 х + 60 = 0

х 1 = 12, х 2 = 5

или

Задача 5.

В прямоугольном треугольнике один из углов равен 30 0 , радиус вписанной в него окружности равен 5 см. Найдите площадь треугольника.

А

х-5

О – точка пересечения биссектрис

М

х-5

К, М, Р – точки касания

х+5

О

К

ОК = ОМ = ОР = 5 см, ∠В = 30 0

5

30 0

АВ = 2 х

АС = х

Р

В

С

5

х+5

СВ = 5 + х + 5 = х + 10

По теореме Пифагора

х 2 + (х + 10) 2 = (2х) 2

х 2 – 10 х — 50 = 0

Задача 6.

В прямоугольном треугольнике один из углов равен 60 0 , радиус вписанной в него окружности равен 4 см. Найдите площадь треугольника.

А

х+4

О – точка пересечения биссектрис

М

х+4

К, М, Р – точки касания

х-4

О

К

ОК = ОМ = ОР = 4 см, ∠В = 60 0

4

60 0

АВ = 2 х

ВС = х

Р

В

С

4

х-4

АС = 4 + х + 4 = х + 8

По теореме Пифагора

х 2 + (х + 8) 2 = (2х) 2

х 2 – 8 х — 32 = 0

Задача 7.

Четырехугольник АВСД описан около окружности. Найдите стороны АВ и СД, если ВС = 6 см, АД = 9 см, АВ в два раза больше, чем СД.

B

6

AB + CD = BC + AD

C

2х

х

2х + х = 6 + 9

х = 5

A

9

D

СД = 5 см

АВ = 10 см

Задача 8.

х

х

В

С

С

В

О

х

D

10

А

10

А

D

х + 20

К

Н

BC + AD = AB + CD

х + х + 20 = 18 + 18

х = 8

СD = 18

ВС = 8

ВС = 8 + 20 = 28

Задача 9.

х

х

В

С

В

С

О

24

24

х

D

А

48 – х

Н

К

24-х

А

24-х

D

BC + AD = AB + CD = 48

АВ = СD = 24

ВС = 12

АD = 48 – 12 = 36

Расстояния от центра вписанной в прямоуголь-ную трапецию окружности до концов большей боковой стороны равны 6 см и 8 см.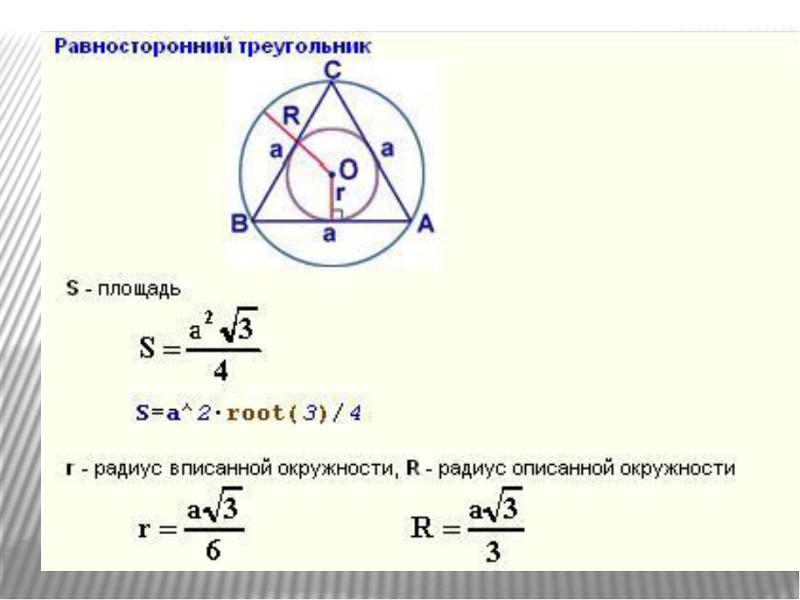 Найдите площадь трапеции.

Задача 10.

N

К, N, H – точки касания

С

В

6

К

О – точка пересечения биссектрис

О

СО, DО –биссектрисы углов С и D

8

∠ ВСD + ∠АDС = 180 0 , ∠ОСD + ∠ОDС = 90 0

D

Н

А

∠ CОD = 90 0

CD = 10

OH⏊AD, ON⏊BC, OH = ON = OK = 4,8

OK⏊CD

NH = AB = 9,6

BC + AD = AB + CD = 9,6 + 10 = 19,6

Расстояния от центра вписанной в равнобедренную трапецию окружности до концов боковой стороны равны 9 см и 12 см. Найдите площадь трапеции.

Задача 11.

N

К, N, H – точки касания

С

В

9

К

О – точка пересечения биссектрис

О

СО, DО –биссектрисы углов С и D

12

∠ ВСD + ∠АDС = 180 0 , ∠ОСD + ∠ОDС = 90 0

D

Н

А

∠ CОD = 90 0

CD = АВ = 15

OH⏊AD, ON⏊BC, OH = ON = OK = 7,2

OK⏊CD

NH = 14,4

BC + AD = AB + CD = 15 + 15 = 30

{2}-\frac{22 \times 16}{21} \)

\( \Large =\frac{\sqrt{3}}{4} \times 64-16,76=16\sqrt{3}-16,76 \)

Часть решенных вопросов и ответов на вопросы об измерении : >> Способности >> Измерение

Комментарии

---

Похожие вопросы

1). В треугольном поле со сторонами 30 м, 72 м и 78 м длина высоты до стороны, равной 72 м, равна: А). 25 м Б). 28 м С). 30 м Д). 35 м — Просмотреть ответ

2). Если периметр прямоугольного равнобедренного треугольника равен \((4\sqrt{2}+4)\) см, длина гипотенузы равна ; 9{2} \) А). 4 см Б). 6 см С). 8 см Д). 10 см — Просмотреть ответ

8). Периметр (в метрах) полукруга: численно равен его площади (в квадратных метрах). Длина его диаметра равна \(\Large\left(Возьмите \pi=\frac{22}{7}\right) \) А). \( \Large 3\frac{3}{11} \) метров Б). \( \Large 5\frac{6}{11} \) метров С). \( \Large 6\frac{6}{11} \) метров 9{2} \) — Просмотреть ответ

10). Если треугольник с основанием 8 см имеет ту же площадь, что и круг с радиусом 8 см, то соответствующая высота (в см) треугольника равна А). \(12 \пи\) Б). \(20 \пи\) С). \(16 \пи\) Д). \(32 \пи\) — Просмотреть ответ

Равносторонний треугольник со стороной 6 см вписан в окружность Найдите радиус окружности…

Перейти к

• Круговое упражнение 15.1
• Круговое упражнение 15.2

• Рациональные и иррациональные числа
• Сложные проценты
• Расширения
• Факторизация
• Одновременные линейные уравнения
• Задачи на одновременные линейные уравнения
• Квадратные уравнения
• Индексы
• Логарифмы
• Треугольники
• Теорема о средней точке
• Теорема Пифагора
• Прямолинейные фигуры
• Теоремы о площади
• Круг
• Измерение
• Тригонометрические отношения
• Тригонометрические отношения и стандартные углы
• Координатная геометрия
• Статистика

Главная > ML Aggarwal Solutions Класс 9Математика > Глава 15 — Круг > Круговое упражнение 15. 1 > Вопрос 8

Вопрос 8 Круг Упражнение 15.1

В окружность вписан равносторонний треугольник со стороной 6 см. Найдите радиус круга

.

Ответ:

ABC — равносторонний треугольник, вписанный в окружность

с центром O. Соедините OB и OC,

Из A нарисуйте AD ⊥ BC, который пройдет

через центр O окружности. 9{2}-6 в 3 р\\ &\text { (D — середина ВС) }\\ &6 \sqrt{3} r=36\\ &R=36 / 6 \sqrt{3}=6 / \sqrt{3} \times \sqrt{3} / \sqrt{3}=6 \sqrt{3} / 3=2 \sqrt{3} \mathrm{ см}\\ &\text { Радиус }=2 \sqrt{3} \mathrm{см} \end{выровнено}

Связанные вопросы

Вычислите длину хорды, которая находится на расстоянии 12 см от центра окружности радиуса…

Хорда длиной 8 см проходит на расстоянии 3 см от центра окружности.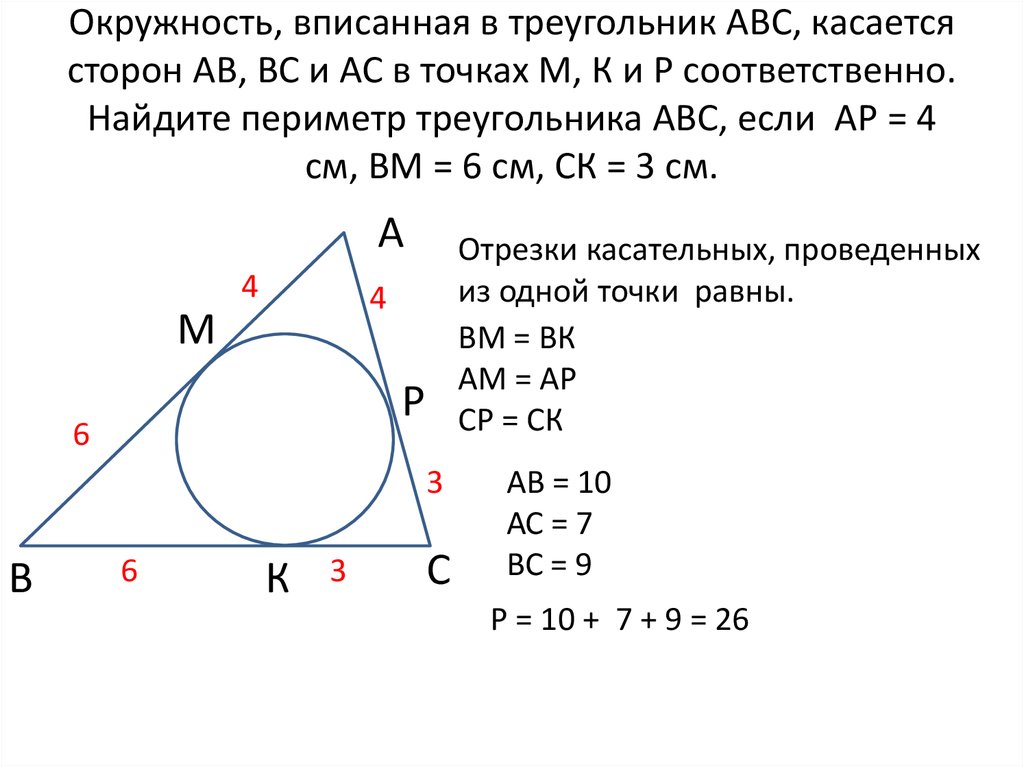 Вычислите радиус…

Вычислите длину хорды, которая проходит на расстоянии 6 см от центра окружности диаметром…

Хорда длиной 16 см проходит на расстоянии 6 см от центра окружности. Найдите длину т…

В окружности радиусом 5 см AB и CD проходят две параллельные хорды длиной 8 см и 6 см соответственно….

а) На приведенном ниже рисунке О — центр окружности. AB и CD — две хорды окружности…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение по кругу 15.