2

методы умножения, примеры с объяснением

Известно, что знак корня  является квадратным корнем из некоторого числа. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.

Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:

  • без множителей;
  • с множителями;
  • с разными показателями.

Метод умножения корней без множителей

Алгоритм действий:

Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.

Пример

Пример 1: 18×2=?

Пример 2: 10×5=?

Пример 3: 33×93=?

Далее необходимо перемножить числа под корнем.

 

Пример

Пример 1: 18×2=36

Пример 2: 10×5=50

Пример 3: 33×93=273

Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:

Пример

Пример 1: 36=6. 36 — квадратный корень из шести (6×6=36).

Пример 2: 50=(25×2)=(5×5)×2=52. Число 50 раскладываем на произведение 25 и 2. Корень из 25 — 5, поэтому выносим 5 из-под знака корня и упрощаем выражение.

Пример 3: 273=3. Кубический корень из 27 равен 3: 3×3×3=27.

Метод умножения показателей с множителями

Алгоритм действий:

Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:

Пример

Пример 1: 32×10=3?3×1=3

Пример 2: 43×36=12?4×3=12

Умножить числа под знаком корня.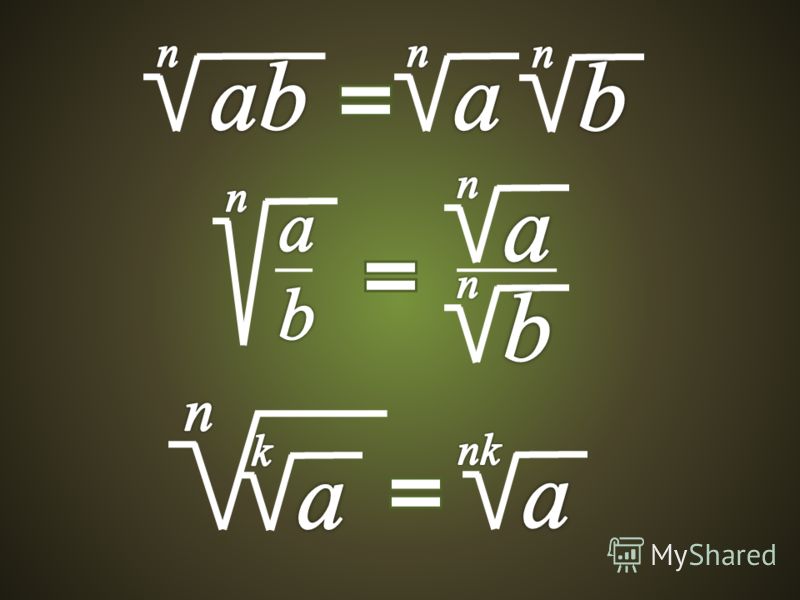 Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:

Пример

Пример 1: 32×10=3(2×10)=320

Пример 2: 43×36=12(3×6)=1218

Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:

Пример

Пример 1: 320=3(4×5)=3(2×2)×5=(3×2)5=65

Пример 2: 1218=12(9×2)=12(3×3)×2=(12×3)2=362

Метод умножения корней с разными показателями

Алгоритм действий:

Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.

Пример

Необходимо найти НОК показателей для следующего выражения: 

53×22

Показатели равны 3 и 2. Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3, и на 2). Для умножения корней необходим показатель 6.

Записать каждое выражение с новым показателем:

56×26

Найти числа, на которые нужно умножить показатели, чтобы получить НОК.

В выражении 53 необходимо умножить 3 на 2, чтобы получить 6. А в выражении 22 — наоборот, необходимо умножить на 3, чтобы получить 6.

Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге. Для первого выражения 5 нужно возвести в степень 2, а втором — 2 в степень 3:

2→56=5263→26=236

Возвести в степень выражения и записать результат под знаком корня:

526=(5×5)6=256236=(2×2×2)6=86

Перемножить числа под корнем:

(8×25)6

Записать результат:

(8×25)6=2006

По возможности необходимо упростить выражение, но в данном случае оно не упрощается.

Автор: Ирина Мальцевская

Преподаватель математики и информатики.