Проверочная работа « 8 задание БАЗА ЕГЭ математика»

8 задание

 БАЗА ЕГЭ математика

1 вариант

1. Второй закон Ньютона можно записать в виде F = ma , где F — сила (в ньютонах), действующая на тело, m — его масса (в килограммах), a — ускорение, с которым движется тело (в м/с2 ). Найдите m (в килограммах), если F = 296 Н и a = 37 м/с2.

2. Площадь трапеции S в м2 можно вычислить по формуле   где   — основания трапеции,   — высота (в метрах). Пользуясь этой формулой, найдите S, если a = 5, b = 3 и h = 6.

3. Работа постоянного тока (в джоулях) вычисляется по формуле  где U — напряжение (в вольтах), R — сопротивление (в омах), t — время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 18 c, U = 7 В и R = 14 Ом.

4. Среднее квадратичное трёх чисел   и  вычисляется по формуле  Найдите среднее квадратичное чисел  и 

5. Длина биссектрисы lc, проведённой к стороне c треугольника со сторонами a, b и c, вычисляется по формуле  Найдите длину биссектрисы lc, если a = 3, b = 9, 

6. Площадь поверхности прямоугольного параллелепипеда с рёбрами  и  вычисляется по формуле  Найдите площадь поверхности прямоугольного параллелепипеда с рёбрами  и 

7. Работа постоянного тока (в джоулях) вычисляется по формуле  где  — напряжение (в вольтах),  — сопротивление (в омах),  — время (в секундах). Пользуясь этой формулой, найдите  (в джоулях), если  с,  В и  Ом.

8. Площадь треугольника можно вычислить по формуле  где a, b и c — стороны треугольника, а R — радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите площадь S, если a = 4, b = 13, c = 15 и 

9.  Площадь треугольника со сторонами    можно найти по формуле Герона  где  Найдите площадь треугольника со сторонами   

10. Теорему косинусов можно записать в виде  где   и  — стороны треугольника, а  — угол между сторонами  и  Пользуясь этой формулой, найдите величину  если  и 

 

8 задание

 БАЗА ЕГЭ математика

2 вариант

1. Среднее квадратичное трёх чисел  и  вычисляется по формуле  Найдите среднее квадратичное чисел   и 

2. Площадь треугольника вычисляется по формуле  где b и с — две стороны треугольника, а  — угол между ними. Пользуясь этой формулой, найдите величину  если b = 5, с = 6 и S = 6.

3. Среднее квадратичное трёх чисел   и  вычисляется по формуле  Найдите среднее квадратичное чисел  и 

4. Мощность постоянного тока (в ваттах) вычисляется по формуле  где 

I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если R = 5 Ом и I = 7 А.

5. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле  где  — длительность поездки, выраженная в минутах  Пользуясь этой формулой, рассчитайте стоимость 15-минутной поездки. Ответ укажите в рублях.

6. Количество теплоты (в джоулях), полученное однородным телом при нагревании, вычисляется по формуле  где c — удельная теплоёмкость  m — масса тела (в кг), 

t1 — начальная температура тела (в кельвинах), а t2 — конечная температура тела (в кельвинах). Пользуясь этой формулой, найдите Q если t2 = 657 К,  m = 4 кг и t1 = 653 К.

7. Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле  Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты 62,5 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2 .

8. Среднее гармоническое трёх чисел  и  вычисляется по формуле  Найдите среднее гармоническое чисел  и 

9. Площадь треугольника можно вычислить по формуле  где a, b и c — стороны треугольника, а R — радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите площадь S, если a = 10, b = 9, c = 17 и 

10. Площадь четырёхугольника можно вычислить по формуле  где  и  — длины диагоналей четырёхугольника,  — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали  если   а 

 

8 задание

 ПРОФИЛЬ ЕГЭ математика

3 вариант

1. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле  где  — число шагов,  — длина шага. Какое расстояние прошёл человек, если  см,  ? Ответ выразите в километрах.

2. Второй закон Ньютона можно записать в виде F = ma , где F — сила (в ньютонах), действующая на тело, m — его масса (в килограммах), a — ускорение, с которым движется тело (в м/с2 ). Найдите m (в килограммах), если F = 319 Н и a = 29 м/с2.

3. Сумма углов правильного выпуклого многоугольника вычисляется по формуле  где n — количество его углов. Пользуясь этой формулой, найдите 

n, если  = 6π.

4. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле  где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если  см,  Ответ дайте в метрах.

5. Площадь трапеции    можно вычислить по формуле   где   — основания трапеции,   — высота (в метрах). Пользуясь этой формулой, найдите высоту   если основания трапеции равны    и   а её площадь  

6. Работа постоянного тока (в джоулях) вычисляется по формуле  где  — напряжение (в вольтах),  — сопротивление (в омах),  — время (в секундах). Пользуясь этой формулой, найдите  (в джоулях), если  с,  В и  Ом.

7. Мощность постоянного тока (в ваттах) вычисляется по формуле  где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если R = 16 Ом и I = 5,5 А.

8. Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле  Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты 3,6 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2 .

9. 

Среднее квадратичное трёх чисел   и  вычисляется по формуле  Найдите среднее квадратичное чисел  и 

10. Площадь поверхности прямоугольного параллелепипеда с рёбрами  и  вычисляется по формуле  Найдите площадь поверхности прямоугольного параллелепипеда с рёбрами  и 

 

8 задание

 ПРОФИЛЬ ЕГЭ математика

4 вариант

1. Среднее квадратичное трёх чисел   и  вычисляется по формуле  Найдите среднее квадратичное чисел  и 

2. Количество теплоты (в джоулях), полученное однородным телом при нагревании, вычисляется по формуле  где c — удельная теплоёмкость  m — масса тела (в кг), t1 — начальная температура тела (в кельвинах), а t

2 — конечная температура тела (в кельвинах). Пользуясь этой формулой, найдите Q (в джоулях), если t2 = 366 К, c = 500  m = 4 кг и t1 = 359 К.

3. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите R (в омах), если P = 144 Вт и I = 4 А.

4. Теорему косинусов можно записать в виде  где   и  — стороны треугольника, а  — угол между сторонами  и  Пользуясь этой формулой, найдите величину  если  и 

5. Площадь четырёхугольника можно вычислить по формуле  где  и  — длины диагоналей четырёхугольника,  — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали  если   а 

6. Количество теплоты (в джоулях), полученное однородным телом при нагревании, вычисляется по формуле  где c — удельная теплоёмкость  m — масса тела (в кг), t1 — начальная температура тела (в кельвинах), а t2 — конечная температура тела (в кельвинах).

Пользуясь этой формулой, найдите Q если t2 = 412 К,  m = 3 кг и t1 = 407 К.

7. Закон Гука можно записать в виде  где F — сила (в ньютонах), с которой растягивают пружину, x — абсолютное удлинение пружины (в метрах), а k — коэффициент упругости. Пользуясь этой формулой, найдите x (в метрах), если  Н и  Н/м.

8. Площадь прямоугольника равняется произведению половины квадрата диагонали и синуса угла между диагоналями. Найдите площадь прямоугольника, если длина диагонали равняется 4, а синус угла между диагоналями равен 

9. Площадь трапеции S в м2 можно вычислить по формуле   где   — основания трапеции,   — высота (в метрах). Пользуясь этой формулой, найдите S, если a = 4, b = 9 и h = 2.

10. Второй закон Ньютона можно записать в виде  где F — сила (в ньютонах), с которой растягивают пружину, m — его масса (в килограммах), a — ускорение, с которым движется тело (в м/с2).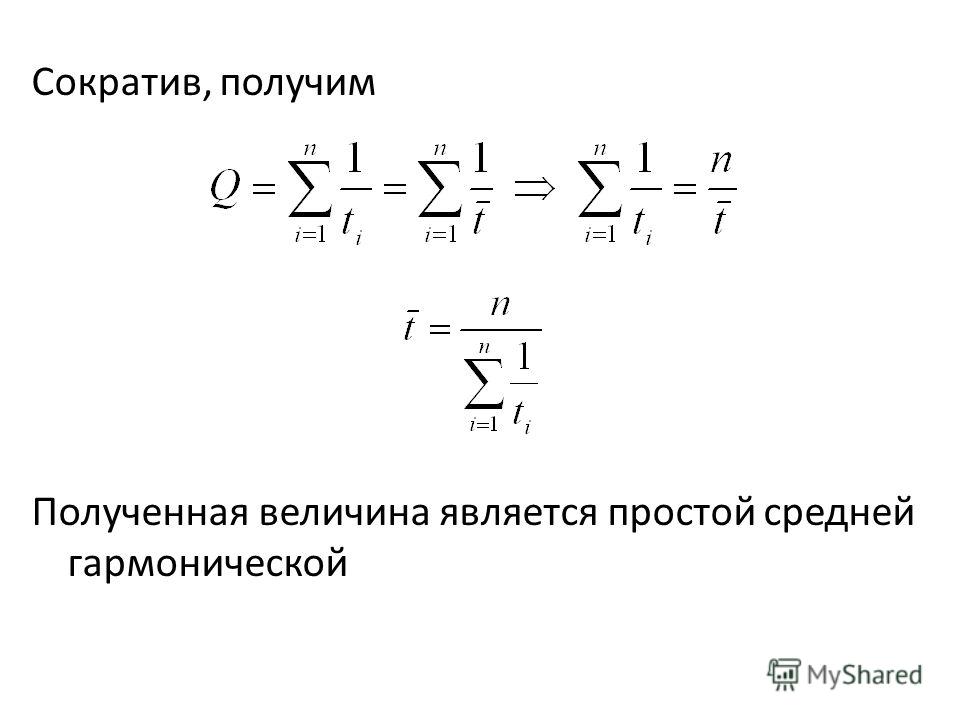 Пользуясь этой формулой, найдите m (в килограммах), если  Н и  м/с2.

 

 

 

Ответы

8 задание

 ПРОФИЛЬ ЕГЭ математика

1 вариант

№ п/п

№ задания

Ответ

1

512236

8

2

507929

24

3

510325

63

4

511728

10

5

509649

3

6

511648

142

7

511768

25

8

514503

24

9

506387

66

10

510255

0,5

 

8 задание

 ПРОФИЛЬ ЕГЭ математика

2 вариант

№ п/п

№ задания

Ответ

1

506737

10

2

520468

0,4

3

511728

10

4

520712

245

5

506427

1610

6

510700

8000

7

512752

35

8

506879

0,2

9

514383

36

10

506819

9

 

8 задание

 ПРОФИЛЬ ЕГЭ математика

3 вариант

№ п/п

№ задания

Ответ

1

506630

0,7

2

514027

11

3

512412

8

4

513078

600

5

506299

4

6

522312

48

7

511474

484

8

512772

8,4

9

511588

4

10

511648

142

 

8 задание

 ПРОФИЛЬ ЕГЭ математика

4 вариант

№ п/п

№ задания

Ответ

1

511628

6

2

509609

14000

3

514737

9

4

510235

0,5

5

506467

19

6

510720

4500

7

512356

17

8

511957

4

9

507952

13

10

512376

9

 

 

 

 

 

 

 

Базовый уровень ЕГЭ 2015 с WolframAlpha

2015 БАЗОВЫЙ УРОВЕНЬ 04 

ТРЕБОВАНИЯ
Уметь выполнять вычисления и преобразования
1. 2   Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования
ЭЛЕМЕНТЫ СОДЕРЖАНИЯ 

1.4.1  Преобразования выражений, включающих арифметические операции
1.4.2  Преобразования выражений, включающих операцию возведения в степень

 

01 ЦЕЛЬСИЙ И ФАРЕНГЕЙТ

Чтобы перевести температуру из шкалы Цельсии в шкалу Фаренгейта, пользуются формулой tF = 1.8 tC + 32 , где tC — температура в градусах по шкале Цельсия,
tF — температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует −1 градус по шкале Цельсия?

02 ФАРЕНГЕЙТ И ЦЕЛЬСИЙ

Перевести температуру из шкалы Фаренгейта в шкалу Цельсия позволяет формула
tC = 5 ( tF  ̶  32 ) / 9 , где tC — температура в градусах по шкале Цельсия,
tF — температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Цельсия соответствует 68 градусов по шкале Фаренгейта?

03 СТОИМОСТЬ КОЛОДЦА

В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 6000 + 4100 n, где n — число колец, установленных при копании колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 5 колец. Ответ укажите в рублях.

04 ДОСРОЧНЫЙ СТОИМОСТЬ ПОЕЗДКИ

В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле C = 150 +11 (t  − 5), где t — длительность поездки, выраженная в минутах (t > 5). Пользуясь этой формулой, рассчитайте стоимость 15-минутной поездки. Ответ укажите в рублях.

05 ДЛИНА ШАГА

Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = n l, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 80 см, n = 1600? Ответ дайте в метрах.


06 ЗАКОН ГУКА

Закон Гука можно записать в виде f = k x, где f — сила (в ньютонах), с которой сжимают пружину, x — абсолютное удлинение (сжатии) пружины (в метрах), a k — коэффициент упругости. Пользуясь этой формулой, найдите x (в метрах), если  f  = 35 Н и k = 7 Н/м.

07 ЗАКОН НЬЮТОНА

Второй закон Ньютона можно записать в виде f = m a, где где f — сила (в ньютонах), действующая на тело, m — его масса (в килограммах), a — ускорение, с которым движется тело (в м/c2). Найдите m (в килограммах), если f = 195 Н и a = 39 м/c2 .

08 ВЫСОТА

Найдите h из равенства Е = mgh, если g = 9. 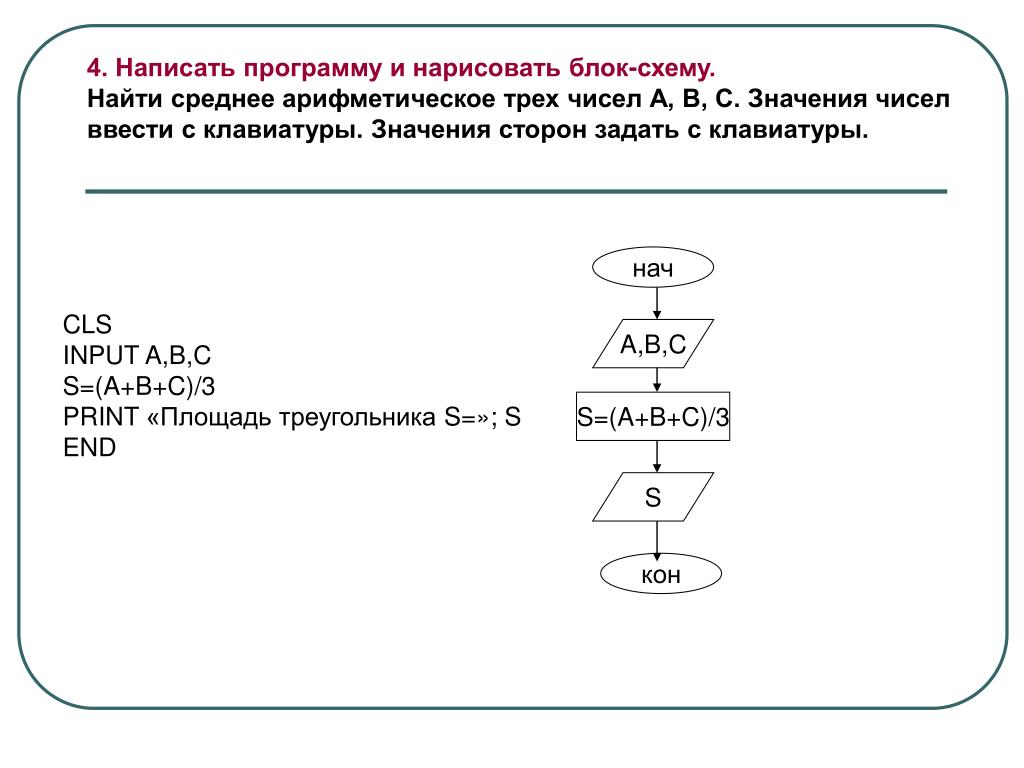8, m = 5, а Е = 4.9.

09 МАССА

Найдите m из равенства E = m v2/2, если v = 3 и Е = 54 .


10 УСКОРЕНИЕ ТЕЛА

Ускорение тела (в м/c2) при равномерном движении по окружности можно вычислить по формуле α = ω2 R, где ω — угловая скорость вращения (в c-1), a R — радиус окружности (в метрах). Пользуясь этой формулой, найдите а (в м/c2),
если R = 4 м и  ω = 7 c-1 .

11 КИНЕТИЧЕСКАЯ ЭНЕРГИЯ

Кинетическая энергия тела (в джоулях) вычисляется по формуле E = m v2/2 , где m — масса тела (в килограммах), a v — его скорость (в м/с). Пользуясь этой формулой, найдите Е (в джоулях), если v = 4 м/с и m = 10 кг.

12 ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

Потенциальная энергия тела (в джоулях) в поле тяготения Земли вблизи поверхности вычисляется по формуле Е = m g h где где m — масса тела (в килограммах) , g — гравитационная постоянная, a h — высота (в метрах), на которой находится это тело, относительно условного нуля. Пользуясь этой формулой, найдите m (в килограммах), если g = 9.8 м/c2 , h = 2 м, а Е = 98 Дж.

13 КОЛИЧЕСТВО ТЕПЛОТЫ

Количество теплоты (в джоулях), полученное однородным телом при нагревании, вычисляется по формуле Q = c m ( t2  ̶  t1 ), где c — удельная теплоемкость ( в Дж/(кг·К)), m — масса тела (в кг), t1 — начальная температура тела (в кельвинах), а t2 — конечная температура тела (в кельвинах). Пользуясь этой формулой, найдите Q (в джоулях), если t2 = 509 К, с = 400 Дж/(кг·К) , m = 2 кг и t1 = 505 К.

14 МОЩНОСТЬ ТОКА И НАПРЯЖЕНИЕ

Мощность постоянного тока, (в ваттах) вычисляется по формуле P = U 2/ R, где U — напряжение (в вольтах), R — сопротивление (в омах). 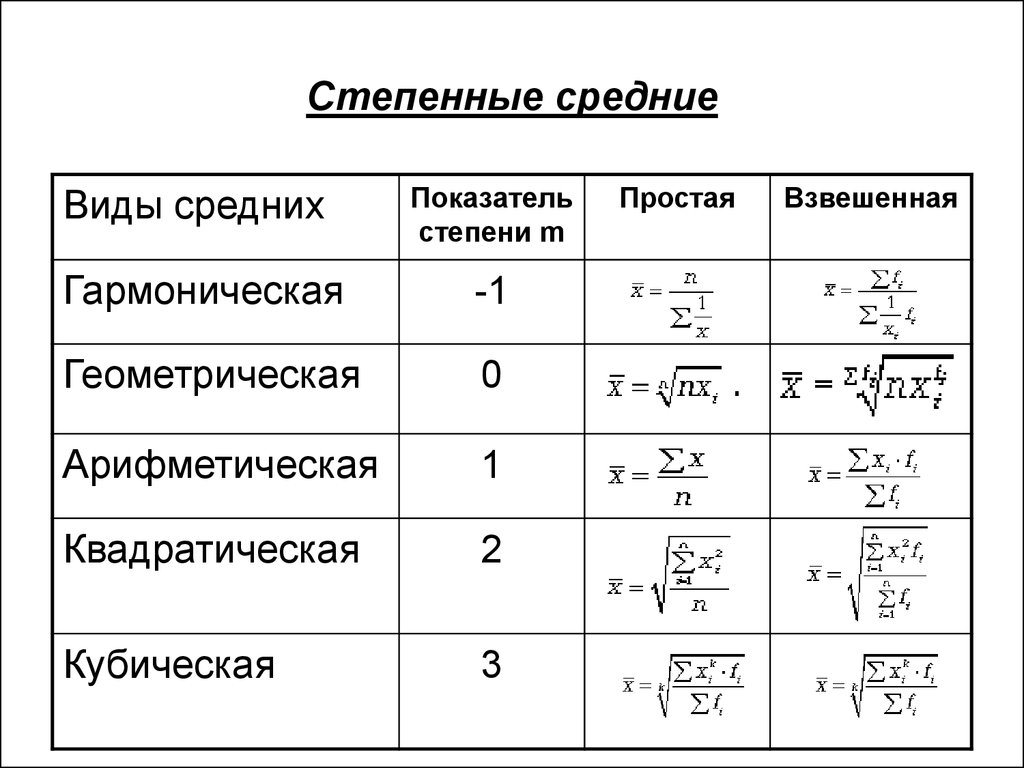Пользуясь этой формулой, найдите Р (в ваттах), если R = 7 Ом и U = 14 А.


15 МОЩНОСТЬ И СИЛА ТОКА

Мощность постоянного тока, (в ваттах) вычисляется по формуле P = I 2R , где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите Р (в ваттах), если R = 12 Ом и I = 3.5 А.

16 МОЩНОСТЬ ТОКА И СОПРОТИВЛЕНИЕ

Мощность постоянного тока (в ваттах) вычисляется по формуле P = I 2R, где  I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 96 Вт, а сила тока равна 4 А.


17 РАБОТА ПОСТОЯННОГО ТОКА И САМ ТОК

Работа постоянного тока (в джоулях) вычисляется по формуле A = I 2R t , где I — сила тока (в амперах), R — сопротивление (в омах), t — время (в секундах). 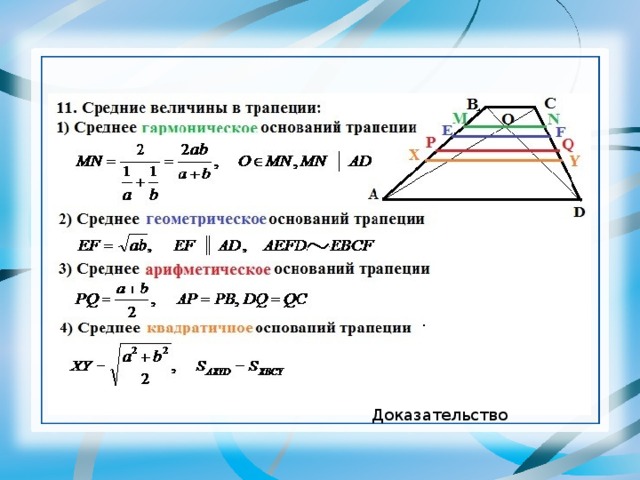Пользуясь этой формулой, найдите А (в джоулях), если t = 2 c, I = 6 А и R = 5 Ом.


18 РАБОТА ПОСТОЯННОГО ТОКА И НАПРЯЖЕНИЕ

Работа постоянного тока (в джоулях) вычисляется по формуле A = U 2t /R  , где U — напряжение (в вольтах), R — сопротивление (в омах), t — время (в секундах). Пользуясь этой формулой, найдите А (в джоулях), если t = 8 c, U = 6 В и R = 2 Ом.


19 СУММА ДЕЛИТЕЛЕЙ

Если p1, p2, p3 — различные простые числа, то сумма всех делителей числа p1· p2· p3 равна ( p1 + 1) ( p2 + 1) ( p3 + 1 ). Найдите сумму всех делителей числа 130 = 2·5·13.

20 СУММА КВАДРАТОВ ЧИСЕЛ

Известно, что 12 + 22 + 32 + . .. + n2 = n ( n + 1 ) (2 n + 1) / 6 .
Найдите сумму  12 + 22 + 32 + … + 302.

21 СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ

Среднее геометрическое трёх чисел a, b и с вычисляется по формуле g = ( a b c )1/3. Найдите среднее геометрическое чисел 2, 4, 27.

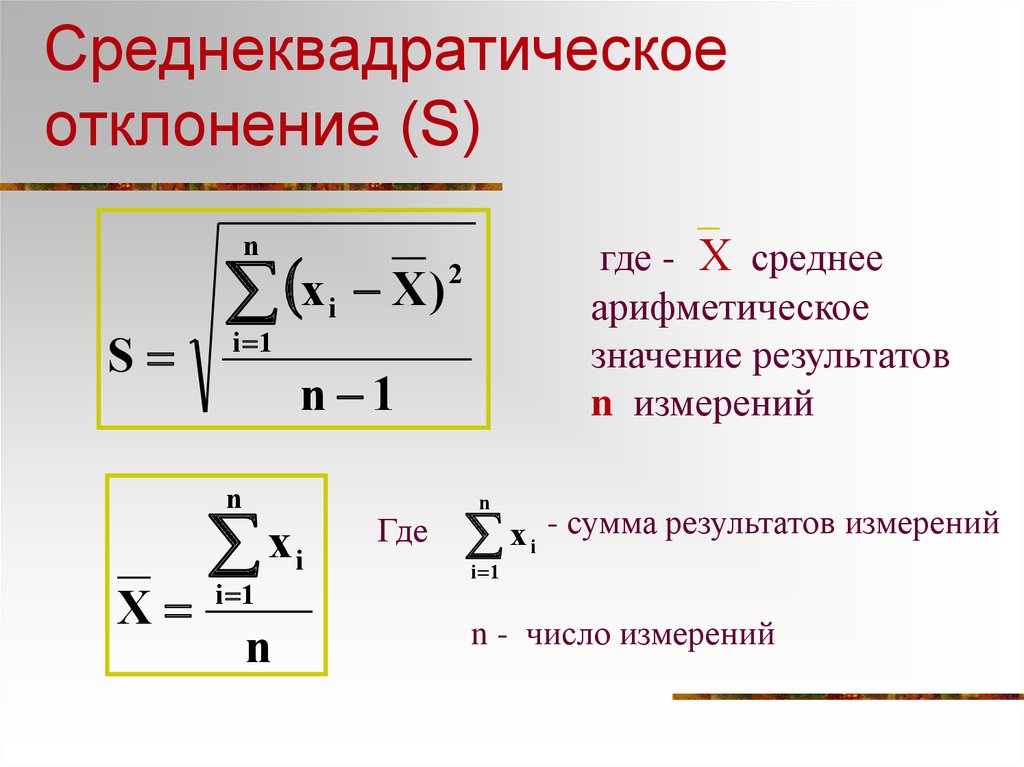
22 СРЕДНЕЕ КВАДРАТИЧНОЕ

Среднее квадратичное трёх чисел a, b и с вычисляется по формуле
 q = (( a2 + b2 + c2 )/3)1/2 . Найдите среднее квадратичное чисел 21/2, 3 и 17.

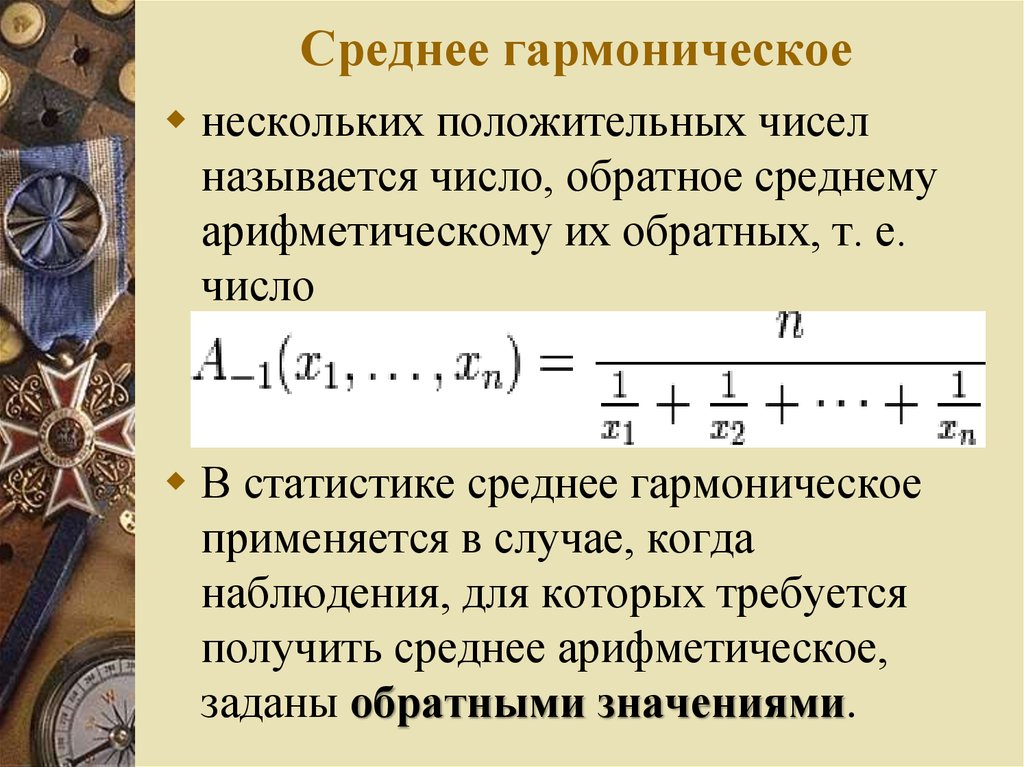
23 СРЕДНЕЕ ГАРМОНИЧЕСКОЕ

Среднее гармоническое трёх чисел a, b и с вычисляется по формуле
h = (( a ̶ 1 + b ̶ 1 + c ̶ 1 )/3) ̶ 1. Найдите среднее гармоническое чисел 1/4, 1/7, 1.

24 ПЛОЩАДЬ ТРЕУГОЛЬНИКА И СТОРОНА

Площадь треугольника можно вычислить по формуле S = a b c /(4 R), где a, b и c — стороны треугольника, а R — радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите b, если a = 12, c = 13, S = 30, R = 13/2.  

25 ПЛОЩАДЬ ТРЕУГОЛЬНИКА

Площадь треугольника можно вычислить по формуле S = a b c /(4 R), где a, b и c — стороны треугольника, а R — радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите S, если a = 4, b = 13, c = 15, R = 65/8.  

26 ПЛОЩАДЬ ТРЕУГОЛЬНИКА И ПОЛУПЕРИМЕТР

Площадь треугольника можно вычислить по формуле S = ( a + b + c ) r / 2, где a, b и c — стороны треугольника, а r — радиус окружности, вписанной в этот треугольник. Пользуясь этой формулой, найдите b, если a = 7, c = 9, S = 12·51/2, r = 51/2.

27 ПЛОЩАДЬ ТРЕУГОЛЬНИКА И СИНУС

Площадь треугольника вычисляется по формуле S = ½  b c sin α, где b и c — стороны треугольника, а α — угол между ними. Пользуясь этой формулой, найдите величину sin α, если b = 5, c = 16, S = 12.

28 ПЛОЩАДЬ ТРЕУГОЛЬНИКА ПО СТОРОНАМ И УГЛУ

Площадь треугольника вычисляется по формуле S = ½  b c sin α, где b и c — стороны треугольника, а α — угол между ними. Пользуясь этой формулой, найдите площадь S, если b = 18, c = 16, sin α = 1/3.

29 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА

Площадь прямоугольника вычисляется по формуле S = ½  d 2 sin α,
где d — диагональ, α — угол между диагоналями.
Пользуясь этой формулой, найдите S, если d = 5 и sin α = 2/5.

30 ПЛОЩАДЬ ТРАПЕЦИИ

Площвдь трапеции вычисляется по формуле s = ½ (a + b ) h, где a и b — основания трапеции, h — её высота. Пользуясь этой формулой, найдите s, если a = 3, b = 8 и h = 4.

31 ПЛОЩАДЬ ЧЕТЫРЁХУГОЛЬНИКА

Площадь четырёхугольника можно вычислить по формуле S = ½  d1· d2 sin α, где d1, d2 — длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите площадь S, если d1= 4, d2 = 7, sin α = 2/7.

32 ПЛОЩАДЬ ЧЕТЫРЁХУГОЛЬНИКА

Площадь четырёхугольника можно вычислить по формуле S = ½  d1· d2 sin α, где d1, d2 — длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если S = 4, d2 = 7, sin α = 2/7.

33 ПЛОЩАДЬ ПАРАЛЛЕЛЕПИПЕДА

Площадь поверхности прямоугольного параллелепипеда с рёбрами a, b и с можно найти по формуле S = 2 (ab + ac + bc). Найдите площадь поверхности прямоугольного параллелепипеда с рёбрами 3, 4 и 6.

34 ОБЪЁМ ПАРАЛЛЕЛЕПИПЕДА

Объём прямоугольного параллелепипеда вычисляется по формуле V = a b c , где а, b и с — длины трёх его рёбер, выходящих из одной вершины. Пользуясь этой формулой, найдите a, если V = 27, b = 3 и c = 4.5.

35 МЕДИАНА ТРЕУГОЛЬНИКА

Длина медианы mc ,  проведенной к стороне треугольника со сторонами a, b и c, вычисляется по формуле mc  = ½ (2a2 + 2b2  ̶  c2)1/2 .
Найдите длину медианы mc , если a = 31/2, b = 71/2, c = 2.

36 ФОРМУЛА ГЕРОНА

Площадь треугольника со сторонами a, b, с можно найти по формуле Герона
S = ( p ( p  ̶  a ) ( p  ̶  b ) ( p  ̶  c ))1/2, где  p = ½ ( a + b + c ).
Найдите площадь треугольника со сторонами 4, 13, 15.

37 ТЕОРЕМА СИНУСОВ И СТОРОНА

Теорему синусов можно записать в виде a / sin α = b / sin β, где a и b — две стороны треугольника, а α и β — углы треугольника, лежащие против них соответственно. Пользуясь этой формулой, найдите a, если b = 15, sin α = 1/5, sin β = 1/4.  

38 ТЕОРЕМА СИНУСОВ И УГОЛ

Теорему синусов можно записать в виде a / sin α = b / sin β, где a и b — две стороны треугольника, а α и β — углы треугольника, лежащие против них соответственно. Пользуясь этой формулой, найдите величину sin α, если a = 13, b = 5, sin β = 1/26.  

39 ТЕОРЕМА КОСИНУСОВ

Теорему косинусов можно записать в виде cos γ = ( a2 + b2 ̶  c2 )/(2ab), где a, b и c — стороны треугольника, а γ — угол между сторонами a и b. Пользуясь этой формулой, найдите величину cos γ, если a = 5, b = 6 и c = 7.


40 РАДИУС ОПИСАННОЙ ОКРУЖНОСТИ

Радиус окружности, описанной около треугольника, можно вычислить по формуле

R  = a / (2 sin α), где a — сторона, а α — противолежащий ей угол треугольника. Пользуясь этой формулой, найдите a, если R = 12 и sin α = 2/3

41 РАДИУС ОПИСАННОЙ ОКРУЖНОСТИ

Радиус окружности, описанной около треугольника, можно вычислить по формуле

R  = a / (2 sin α), где a — сторона, а α — противолежащий ей угол треугольника. Пользуясь этой формулой, найдите R, если a = 8 и sin α = 1/7


42 РАДИУС ВПИСАННОЙ ОКРУЖНОСТИ

Радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле r = ½ ( a + b  ̶  c ) , где a и b — катеты, а c — гипотенуза. Пользуясь этой формулой, найдите c, если a = 6, b = 8 и r = 2.

43 СУММА УГЛОВ МНОГОУГОЛЬНИКА

Сумма углов правильного выпуклого многоугольника вычисляется по формуле
Σ = ( n  ̶  2 ) π, где n — количество его углов. Пользуясь этой формулой, найдите n, если
Σ = 14 π.

44 ДЛИНА БИССЕКТРИСЫ

Длина биссектрисы lc , проведённой к стороне с треугольника со сторонами a, b и с, вычисляется по формуле lc = ( a b (( a + b)2  ̶  c2 ))1/2/( a + b ). Треугольник имеет стороны 4, 5·71/2, 16 . Найдите биссектрису  lc , если a = 2, b = 4, c = 3·21/2 .

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

05 

РЕШЕНИЕ

06 

РЕШЕНИЕ

07 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

05 

РЕШЕНИЕ

06 

РЕШЕНИЕ

07 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

05 

РЕШЕНИЕ

06 

РЕШЕНИЕ

07 

РЕШЕНИЕ

08 

РЕШЕНИЕ

09 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

05 

РЕШЕНИЕ

06 

РЕШЕНИЕ

01 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

05 

РЕШЕНИЕ

06 

РЕШЕНИЕ

07 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

05 

РЕШЕНИЕ

06 

РЕШЕНИЕ

07 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

05 

РЕШЕНИЕ

06 

РЕШЕНИЕ

07 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

05 

РЕШЕНИЕ

06 

РЕШЕНИЕ

07 

РЕШЕНИЕ

08 

РЕШЕНИЕ

09 

РЕШЕНИЕ

10 

РЕШЕНИЕ

11 

РЕШЕНИЕ

12 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

01 

РЕШЕНИЕ

02 

РЕШЕНИЕ

03 

РЕШЕНИЕ

04 

РЕШЕНИЕ

05 

РЕШЕНИЕ

06 

РЕШЕНИЕ

07 

РЕШЕНИЕ

 

Калькулятор среднего гармонического

Используйте этот калькулятор среднего гармонического, чтобы легко вычислить среднее гармонического набора чисел.

    Быстрая навигация:

  1. Что такое среднее гармоническое?
  2. Формула среднего гармонического
  3. Расчет среднего гармонического
  4. Формула взвешенного среднего гармонического
  5. Как вычислить среднее гармоническое двух чисел
  6. Среднее гармоническое трех чисел
  7. Пример использования в финансах
  8. Пример использования в физике
  9. Применение в геометрии
  10. Применение калькулятора среднего гармонического в других науках

    Что такое среднее гармоническое?

Гармоническое среднее (архаичное: субпротивоположное среднее) — это специализированное среднее значение набора чисел. Это одно из трех пифагорейских средних, обеспечивающее наиболее точное среднее значение. Среднее гармоническое вычислить сложнее, чем арифметическое, хотя на первый взгляд они могут показаться похожими. Разница между ними заключается в том, что среднее гармоническое вычисляет обратную величину среднего арифметического обратных величин.

Среднее гармоническое в основном используется в ситуациях, связанных с количественными данными, например, при нахождении среднего значения скоростей или отношений , из-за того, что на него серьезно не влияют колебания.

    Формула среднего гармонического

Формула для расчета среднего гармонического набора ненулевых положительных чисел: где n — количество элементов, а X 1 … X 2

9 числа от 1 до н.

Проще говоря, все, что вам нужно сделать, это разделить количество предметов в наборе на сумму их обратных величин. Приведенная выше формула — это то, что мы используем в этом калькуляторе среднего гармонического.

    Вычисление среднего гармонического

Если вам дан набор чисел: 3, 12, 20, 24, и вы должны найти их среднее гармоническое, первое, что вам нужно сделать, это найти общий знаменатель. Это пригодится, когда вы сложите обратные величины. В этом случае все числа делятся на 120. Затем найдите сумму обратных чисел:

1/3 + 1/12 + 1/20 + 1/24 = 40/120 + 10/120 + 6/120 + 5/120 = 61/120.

Поскольку в наборе 4 предмета, ваш окончательный расчет должен быть следующим:

4/(61/120) = 4 x 120/61 = 7,87 гармоническое среднее в наборе чисел, если одно из них равно 0.

Наш калькулятор гармонического среднего вычисляет за вас! Вам просто нужно записать числовой набор данных, разделяя элементы запятой и пробелом.

    Формула взвешенного среднего гармонического

Средневзвешенное гармоническое значение является обратной величиной средневзвешенного обратного значения набора данных весов, соответствующего набору чисел. Он рассчитывается по формуле:

    Как вычислить среднее гармоническое двух чисел

В особых случаях, когда набор состоит только из двух чисел, можно вычислить среднее гармоническое по следующей формуле: . Даже в этом простом случае может быть полезно обратиться к калькулятору, если числа большие или дробные.

Среднее гармоническое находится по отношению к среднему арифметическому (A = (X 1 + X 2 )/2) и среднему геометрическому (G = √X 1 x X 2 ) в следующем образом:

H = G 2 /A

Поскольку в наборе действительных неотрицательных чисел арифметическое всегда больше среднего геометрического, мы можем заключить, что при n = 2 среднее гармоническое всегда будет меньше по значению или равен среднему геометрическому (H ≤ G).

Еще одним свойством пифагорейских средних является то, что среднее геометрическое двух чисел равно среднему геометрическому их среднего арифметического и среднего гармонического (G = √A x H).

    Среднее гармоническое трех чисел

Три действительных неотрицательных числа A, G и H являются соответственно средним геометрическим и гармоническим средним трех действительных неотрицательных чисел тогда и только тогда, когда это неравенство верно :

    Пример использования в финансах

При усреднении множителей, где цена находится в числителе, рекомендуется обращаться к взвешенному среднему гармоническому. Например, если вы хотите рассчитать соотношение цена-прибыль с помощью средневзвешенного арифметического, результаты будут смещены вверх, поскольку больший вес придается более высоким точкам данных. Однако взвешенное среднее гармоническое присваивает равный вес всем точкам данных [1] , что дает наиболее точное среднее значение.

Допустим, вам нужно рассчитать фондовый индекс P/E для 3 компаний. Первая имеет рыночную капитализацию в 10 миллиардов долларов и прибыль в 1 миллиард долларов; у второго рыночная капитализация составляет 27 миллиардов долларов, а прибыль — 3 миллиарда долларов; наконец, третья компания имеет рыночную капитализацию в 100 миллионов долларов и прибыль в 2 миллиона долларов. Вы вычисляете коэффициент P/E первой, второй и третьей компании, равный соответственно 10, 9 и 50. Индекс, который вам нужно рассчитать, состоит из трех акций: 60% инвестированы в первую компанию, 25% во второй и 15% вложили в третью. Его отношение P/E, найденное с использованием среднего гармонического взвешенного значения, составляет:

P/E = (0,6 + 0,25 + 0,15)/ 0,6/10 + 0,25/9 + 0,15/50 = 1/ 0,09 = 11,1 х 10 + 0,25 х 9 + 0,15 х 50 = 15,75

Очевидно, средневзвешенное арифметическое завышает показатель, что дает вам неверную информацию.

    Пример использования в физике

Если вы хотите измерить среднюю скорость транспортного средства, движущегося туда и обратно, используя среднее гармоническое, вы получите наиболее точное число. Допустим, расстояние от А до Б равно 120 км. Известно, что автомобиль проехал из точки А в точку В со скоростью 80 км/ч, а обратно из В в А со скоростью 60 км/ч. Уравнение для нахождения средней скорости:

Средняя скорость = общее расстояние/общее время

Средняя скорость = 2 x 120/(120/80 + 120/60) = 240/3,5 = 68,6 км/ч .

    Приложения в геометрии

Существует несколько теорем относительно использования среднего гармонического в геометрии:

  • В каждом треугольнике среднее гармоническое трех высот равно 1/3 радиуса ( r ) вписанной окружности;
  • В прямоугольном треугольнике с высотой ( h ) до прямого угла от гипотенузы и катетами a и b , среднее гармоническое a 2 и b 2 6 равно вдвое больше h 2 [2] [3] ;
  • Если m и n стороны двух вписанных квадратов в прямоугольном треугольнике, то среднее гармоническое квадрата гипотенузы c 2 и m 2 вдвое больше, чем n 2 ;
  • Если точка D лежит на малой дуге BC описанной окружности равностороннего треугольника ABC, она находится на расстоянии 90 107 м 90 108 от B и на расстоянии 90 107 n 90 108 от C.   Пересечение AD и BC находится в расстояние o от D. Следовательно, среднее гармоническое м и n в два раза больше, чем o [4] ;
  • Полуширокая прямая кишка в эллипсе К равна среднему гармоническому минимального и максимального расстояний К от фокуса;
  • В трапеции ABCD, стороны которой параллельны AB и CD, диагонали AC и BD пересекаются в точке E. Если точка F лежит на AD, а точка G лежит на BC, так что FEG параллельна AB и CD, то FG равно среднему гармоническому AB и CD.

Вы можете использовать этот калькулятор для решения любой из вышеперечисленных задач.

В популярной задаче о перекрещенных лестницах , показанной ниже, где две лестницы параллельны друг другу, одна поднимается на высоту A , другой на высоте B . Две лестницы пересекаются на высоте 90 107 H 90 108 от земли. В этом случае среднее гармоническое A и B в два раза больше, чем H .


    Применение калькулятора гармонического среднего в других науках

Учитывая тот факт, что гармоническое среднее является наиболее точным, неудивительно, что оно нашло применение во многих науках. Например, в информатика среднее гармоническое используется для расчета совокупного балла для оценки производительности машин, алгоритмов и систем.

Это среднее значение полезно для определения точной плотности и массы частиц в химических анализах и ядерно-физических испытаниях .

В биологии, точнее в популяционной генетике , гармоническое среднее является средством расчета влияния флуктуаций на размер поколения.

Студенты и исследователи этих научных дисциплин часто обращаются к калькулятору среднего гармонического при решении задач в своей области.

    Ссылки

[1] Мэтьюз, Г. (2004) «Мнения о справедливости: распространенные ошибки и упущения». В Справочник по оценке бизнеса и анализу интеллектуальной собственности . Макгроу Хилл.

[2] Роджер Воулс. (1999) «Целые решения a -2 + b -2 = d -2 «, Mathematical Gazette, 83 , с. 269-271.

[3] Richinick, J. (2008) «Перевернутая теорема Пифагора» Mathematical Gazette, 92 , с. 313-317.

[4] Позаментье, А.С. и Салкинд, К.Т. (1996) «Сложные задачи геометрии». Нью-Йорк: Dover Publications.

Среднее гармоническое Определение: формула и примеры

Что такое среднее гармоническое?

Среднее гармоническое — это тип среднего численного значения. Он рассчитывается путем деления количества наблюдений или записей в серии на обратную величину каждого числа в серии. Таким образом, среднее гармоническое является обратной величиной среднего арифметического обратных величин.

Например, чтобы вычислить среднее гармоническое 1, 4 и 4, вы должны разделить количество наблюдений на обратную величину каждого числа следующим образом:

3 ( 1 1 + 1 4 + 1 4 ) «=» 3 1,5 «=» 2 \frac{3}{\left(\frac{1}{1}\ +\ \frac{1}{4}\ +\ \frac{1}{4}\right)}\ =\ \frac{3 {1,5}\ =\ 2 (11​ + 41​ + 41​)3​ = 1,53​ = 2

Среднее гармоническое используется, в частности, в финансах и техническом анализе рынков.

Основные выводы

  • Среднее гармоническое является обратной величиной среднего арифметического обратных величин.
  • Гармонические средние используются в финансах для усреднения данных, таких как мультипликаторы цен.
  • Гармонические средства также могут использоваться рыночными техниками для определения таких моделей, как последовательности Фибоначчи.

Основы гармонического среднего

Гармоническое среднее помогает находить отношения мультипликативных или делителей между дробями, не беспокоясь об общих знаменателях. Гармонические средние часто используются для усреднения таких вещей, как скорости (например, средняя скорость движения с учетом продолжительности нескольких поездок).

Взвешенное среднее гармоническое используется в финансах для усреднения множителей, таких как отношение цены к прибыли (P/E), потому что оно придает равный вес каждой точке данных. Использование взвешенного среднего арифметического для усреднения этих отношений придаст больший вес высоким точкам данных, чем низким точкам данных, потому что отношения P/E не нормализованы по цене, в то время как доходы уравниваются.

Гармоническое среднее — это взвешенное гармоническое среднее, где веса равны 1. Взвешенное гармоническое среднее x 9n_{i=1}\frac{w_i}{x_i}}} ∑i=1n​xi​wi​​∑i=1n​wi​​

Обратная величина числа n равна просто 1 / n.

Среднее гармоническое против. Среднее арифметическое и среднее геометрическое

Другие способы расчета средних значений включают простое среднее арифметическое и среднее геометрическое. В совокупности эти три типа среднего (гармоническое, арифметическое и геометрическое) известны как пифагорейские средние. Различия между тремя типами пифагорейского среднего делают их подходящими для различных целей.

Среднее арифметическое — это сумма ряда чисел, деленная на количество этого ряда чисел. Если бы вас попросили найти классовое (арифметическое) среднее тестовых результатов, вы бы просто сложили все результаты тестов студентов, а затем разделили эту сумму на количество студентов. Например, если пять студентов сдавали экзамен и их баллы были 60 %, 70 %, 80 %, 90 % и 100 %, среднее арифметическое значение класса будет 80 %.

Среднее геометрическое — это среднее значение набора продуктов, расчет которого обычно используется для определения результатов эффективности инвестиций или портфеля. Технически это определяется как « nth  корневой продукт n  чисел.» Среднее геометрическое должно использоваться при работе с процентами, которые получены из значений, в то время как стандартное среднее арифметическое работает с самими значениями.

Среднее гармоническое лучше всего использовать для дробей, таких как доли или кратные.

Пример гармонического среднего

В качестве примера возьмем две фирмы. Рыночная капитализация одного из них составляет 100 миллиардов долларов, а прибыль — 4 миллиарда долларов (цена/прибыль 25), а рыночная капитализация другого — 1 миллиард долларов, а прибыль — 4 миллиона долларов (цена/прибыль 250). В индексе, составленном из двух акций, 10% вложено в первую и 90% вложено во вторую, коэффициент P/E индекса составляет:

Использование WAM: P/E «=» 0,1 × 25 + 0,9 × 250 «=» 227,5 Использование WHM: P/E «=» 0,1 + 0,9 0,1 25 + 0,9 250 ≈ 131,6 где: ВАМ «=» средневзвешенное арифметическое Цена/прибыль «=» соотношение цены и прибыли WHM «=» средневзвешенное гармоническое значение \begin{aligned}&\text{Используя WAM:\ P/E}\ =\ 0,1 \times25+0,9\times250\ =\ 227,5\\\\&\text{Используя WHM:\ P/E}\ =\ \frac{0,1\ +\ 0,9}{\frac{0,1}{25}\ +\ \frac{0,9}{250}}\ \приблизительно\ 131,6\\&\textbf{где:}\\&\text{WAM}=\text{средневзвешенное арифметическое}\\&\text{P/E}=\text{цена отношение к прибыли}\\&\text{WHM}=\text{средневзвешенное гармоническое}\end{выровнено} ​Используя WAM: P/E = 0,1 × 25+0,9 × 250 = 227,5 Используя WHM: P/E = 250,1 + 2500,9 0,1 + 0,9 ≈ 131,6, где: WAM = средневзвешенное арифметическое P/E = цена-к -коэффициент прибылиWHM=взвешенное гармоническое среднее​

Как видно, взвешенное среднее арифметическое значительно завышает среднее отношение цены к прибыли.

Преимущества и недостатки среднего гармонического

Среднее гармоническое эффективно, потому что оно включает в себя все записи в ряду, и его невозможно вычислить, если какой-либо элемент запрещен. Использование среднего гармонического также позволяет придать более значительный вес меньшим значениям в ряду, а также может быть рассчитано для ряда, включающего отрицательные значения. По сравнению со средним арифметическим и средним геометрическим среднее гармоническое дает более прямую кривую.

Однако у использования среднего гармонического есть и несколько недостатков. Прежде всего, поскольку для этого требуется использовать обратные числа в ряду, вычисление среднего гармонического может быть сложным и трудоемким. Кроме того, из-за невозможности найти обратную величину нуля невозможно вычислить среднее гармоническое, если ряд содержит нулевое значение. Наконец, любые экстремальные значения в верхней или нижней части ряда оказывают сильное влияние на результаты среднего гармонического.

В чем разница между средним гармоническим и средним арифметическим?

Среднее гармоническое вычисляется путем деления числа наблюдений или записей в ряду на обратную величину каждого числа в ряду. Напротив, среднее арифметическое — это просто сумма ряда чисел, деленная на количество чисел в этом ряду. Среднее гармоническое равно обратной величине среднего арифметического обратных величин.

Когда следует использовать среднее гармоническое?

Среднее гармоническое лучше всего использовать для дробей, таких как доли или кратные. Гармонические средние используются в финансах для усреднения данных, таких как мультипликаторы цен, такие как отношение цены к прибыли (P/E). Специалисты по рынку могут также использовать гармонические средства для определения моделей, таких как последовательности Фибоначчи.

Каковы преимущества использования гармонического среднего?

Среднее гармоническое обязательно включает все записи в ряду и позволяет придавать более значительный вес меньшим значениям.