Импульс тела, силы. Изменение и направление вектора, единицы измерения. Связь с законом Ньютона. Примеры
Тестирование онлайн
Импульс тела, импульс силы. Основные понятия
Импульс тела, импульс силы
Импульс тела
Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.
Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.
Импульс это векторная величина, которая определяется по формуле
Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.
Направление вектора импульса всегда совпадает с направлением вектора скорости.
Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

Импульс силы
Это векторная величина, которая определяется по формуле
Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.
Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.
Изменение импульса тела
Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание!
Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.
1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.
Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.
2) Изменение импульса тела изображено на рисунке
3) Из второго закона Ньютона
Главное запомнить
1) Формулы импульса тела, импульса силы;
3) Находить изменение импульса тела
Импульс силы численно равен площади фигуры под графиком F(t).
Если же сила непостоянная во времени, например линейно увеличивается F=kt, то импульс этой силы равен площади треугольника. Можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину за тот же промежуток времени
Средняя равнодействующая сила
fizmat.by
Импульс тела. Импульс силы. Закон сохранения импульса | LAMPA
Закон сохранения импульса
Импульс вводился не случайно. Оказывается, импульс тела никуда не девается — он сохраняется. Мы предлагаем вам убедиться в этом. Рассмотрим простой случай — столкновение двух шаров.
То, что будет происходить между этими двумя шарами, можно изобразить на рисунке. При этом можно выделить три этапа:
- ситуация «до» (до столкновения)
- само столкновение
- ситуация «после» (после столкновения).
«До»: шары летели навстречу друг к другу; «после»: шары разлетелись после столкновения; столкновение: шары действовали друг на друга.
Нам интересен момент столкновения. Первый шар действует на второй с силой F⃗21\vec{F}_{21}F⃗21, а второй шар действует на первый с силой F⃗12\vec{F}_{12}F⃗12. По 3-му закону Ньютона эти силы равны друг другу по модулю и противоположны по направлению:
F⃗21=−F⃗12\vec{F}_{21}=-\vec{F}_{12}F⃗21=−F⃗12.
Домножим это равенство на длительность столкновения Δt\Delta tΔt:
F⃗21⋅Δt=−F⃗12⋅Δt\vec{F}_{21}\cdot\Delta t=-\vec{F}_{12}\cdot\Delta tF⃗21⋅Δt=−F⃗12⋅Δt.
У нас получились импульсы сил, действующие на каждое из тел. Мы помним, импульс силы равен изменению импульса тела. Можем записать:
Δp⃗2=−Δp⃗1\Delta\vec{p}_2=-\Delta\vec{p}_1Δp⃗2=−Δp⃗1.
Распишем изменение импульсов тел. Буквой VVV будем обозначать скорости до столкновения, а буквой UUU — скорости после столкновения.
m2(U⃗2−V⃗2)=−m1(U⃗1−V⃗1)m_2(\vec{U}_2-\vec{V}_2)=-m_1(\vec{U}_1-\vec{V}_1)m2(U⃗2−V⃗2)=−m1(U⃗1−V⃗1).
Если отбросить знак «минус», то изменения импульсов тел равны друг другу. Можно заметить интересную вещь: если два тела разной массы сталкиваются, то скорость более легкого тела (с меньшей массой) в результате столкновения изменится сильнее.
Продолжаем наши преобразования:
m2U⃗2−m2V⃗2=−(m1U⃗1−m1V⃗1)m_2\vec{U}_2-m_2\vec{V}_2=-(m_1\vec{U}_1-m_1\vec{V}_1)m2U⃗2−m2V⃗2=−(m1U⃗1−m1V⃗1),
m2U⃗2−m2V⃗2=−m1U⃗1+m1V⃗1m_2\vec{U}_2-m_2\vec{V}_2=-m_1\vec{U}_1+m_1\vec{V}_1m2U⃗2−m2V⃗2=−m1U⃗1+m1V⃗1,
m2U⃗2+m1U⃗1=m2V⃗2+m1V⃗1m_2\vec{U}_2+m_1\vec{U}_1=m_2\vec{V}_2+m_1\vec{V}_1m2U⃗2+m1U⃗1=m2V⃗2+m1V⃗1.
Что получилось? Получился закон сохранения импульса.
Закон сохранения импульса. Векторная сумма импульсов тел до взаимодействия равна векторной сумме импульсов тел после взаимодействия:
векторная сумма того, что было «до» = векторная сумма того, что стало «после».
Небольшое дополнение. Мы рассматривали ситуацию, в которой не было никаких внешних сил: никто «извне» не действовал на шары. Закон сохранения импульса справедлив для случая, когда внешние силы не действуют на систему тел или же действие внешних сил скомпенсировано. Такие системы тел называются замкнутыми.
Порешаем задачки.
Условие
Одинаковые шары движутся с одинаковыми по модулю скоростями в направлениях, указанных стрелками на рисунке, и абсолютно неупруго соударяются.
Как будет направлен импульс шаров после их столкновения?
- ↙\swarrow↙
- ←\leftarrow←
- ↓\downarrow↓
- ↖\nwarrow↖
(Источник: ЕГЭ-2014. Физика. Досрочный этап. Вариант 1)
Решение
Начнем с того, что поясним, что такое «неупругий удар». Неупругий удар или столкновение — это столкновение, которое приводит к «слипанию» соударяющихся тел. При неупругом ударе не выполняется закон сохранения механической энергии. Но об этом в следующих темах. В этой задаче для нас важно то, что после соударения тела будут двигаться вместе — «слипнутся».
В задаче говорится о том, что было «до», а спрашивается про то, что стало «после». Даны направления скоростей. Очень похоже на то, что это задача на закон сохранения импульса. Что мы знаем из него? Мы знаем, что в замкнутой системе тел векторная сумма импульсов тел «до» соударения равна векторной сумме импульсов тел «после»:
m1U⃗1+m2U⃗2=m1V⃗1+m2V⃗2m_1\vec{U}_1+m_2\vec{U}_2=m_1\vec{V}_1+m_2\vec{V}_2m1U⃗1+m2U⃗2=m1V⃗1+m2V⃗2.
В нашем случае m1=m2=mm_1=m_2=mm1=m2=m, а после столкновения шары «слипаются», поэтому закон сохранения импульса примет вид
mU⃗1+mU⃗2=2mV⃗m\vec{U}_1+m\vec{U}_2=2m\vec{V}mU⃗1+mU⃗2=2mV⃗,
где V⃗\vec{V}V⃗ — скорость совместного движения шаров после столкновения, а U⃗1\vec{U}_1U⃗1 и U⃗2\vec{U}_2U⃗2 — скорости шаров до столкновения. Направление импульса шаров после столкновения, о котором спрашивается в задаче, — это направление вектора 2mV⃗2m\vec{V}2mV⃗.
Как его найти? Направление вектора в правой части равенства совпадает с направлением вектора в левой части равенства. Попробуем сложить импульсы шаров до столкновения, чтобы получить векторную сумму импульсов и определить ее направление.
Направления импульсов до столкновения нам известны (направления импульсов совпадают с направлениями скоростей, а они указаны на рисунке). Так как шары были одинаковыми и двигались с одинаковыми скоростями, модули импульсов шаров были равны. Складываем векторы импульсов по правилу параллелограмма.
Видно, что суммарный импульс направлен влево. По закону сохранения импульса в ситуации «после» суммарный импульс будет направлен точно так же. Значит, подходит ответ 2).
Ответ. 2) ←\leftarrow←
Решим еще одну задачу.
Условие
Мальчик массой 505050 кг находится на тележке массой 505050 кг, движущейся по гладкой горизонтальной дороге со скоростью 111 м/с. Каким станет модуль скорости тележки, если мальчик прыгнет с нее со скоростью 222 м/с относительно дороги в направлении, противоположном первоначальному направлению движения тележки? Ответ выразите в м/с.
(Источник: ЕГЭ-2013. Физика. Реальный экзамен)
Решение
Шаг 1. Мы думаем, что вы согласитесь с тем, что без рисунка непросто представить, что именно происходит в этой задаче. Давайте сделаем рисунок. У нас на рисунке будут изображены две ситуации: ситуация «до» и ситуация «после». На рисунке кроме самих предметов нужно также указать направление скоростей и ось, на которую мы будем проецировать эти скорости. Должно получиться что-то вроде этого:
Шаг 2. Отлично! Теперь можно записать закон сохранения импульса в векторной форме.
lampa.io
Импульс силы | Все формулы
Импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени.
Векторную величину Ft, равную произведению силы на время ее действия, называют импульсом силы. Векторную величину р=mv, равную произведению массы тела на его скорость, называют импульсом тела.
Формула для нахождения импульса тела вытекает из всем извесного Второго закона Ньютона
А ускорение найдем через разность скоростей на время.
Отсюда и получается, что импульс силы
Из импульса силы вытекает закон сохранения импульса
Так же есть:
Импульс тела
В Формуле мы использовали :
— Импульс силы
— Сила приложенная к телу
— Время действия силы
— Конечная скорость тела
— Начальная скорость тела
xn--b1agsdjmeuf9e.xn--p1ai
Импульс тела | Все формулы
Импульс тела — это физическая векторная величина, равная произведению массы тела на его скорость
Каждое тело, которое имеет массу и скорость, так же имеет и импульс.
Пусть на тело массой в течение некоторого малого промежутка времени Δt действовала сила F. Под действием этой силы скорость тела изменилась на . Следовательно, тело на промежутке Δt двигалось с ускорением
На основе Второго закон Ньютона
А если немного преобразовать, то у нас получится:
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела . А физическая величина, равная произведению силы на время ее действия, называется импульсом силы .
Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с)
В Формуле мы использовали :
— Импульс тела
— Масса тела
— Скорость тела
Импульс тела и закон сохранения импульса
ОПРЕДЕЛЕНИЕЕдиница измерения импульса в системе СИ: кг • м/с .
Импульс системы тел равен векторной сумме импульсов всех тел, входящих в систему:
ОПРЕДЕЛЕНИЕ
Импульс силы – это величина, равная произведению силы на время ее действия, т.е. величина .
Закон сохранения импульса
Если на систему взаимодействующих тел действуют дополнительно внешние силы, например, силы трения, то в этом случае справедливо соотношение, которое иногда называют законом изменения импульса:
- изменение импульса системы тел равно векторной сумме импульсов всех внешних сил, действующих на систему:
Для замкнутой системы (при отсутствии внешних сил) справедлив закон сохранения импульса:
- импульс замкнутой системы есть величина постоянная:
Действием закона сохранения импульса можно объяснить явление отдачи при стрельбе из винтовки или при артиллерийской стрельбе. Также действие закона сохранения импульса лежит в основе принципа работы всех реактивных двигателей.
При решении физических задач законом сохранения импульса пользуются, когда знание всех деталей движения не требуется, а важен результат взаимодействия тел. Такими задачами, к примеру, являются задачи о соударении или столкновении тел. Законом сохранения импульса пользуются при рассмотрении движения тел переменной массы таких, как ракеты-носители. Большую часть массы такой ракеты составляет топливо. На активном участке полета это топливо выгорает, и масса ракеты на этом участке траектории быстро уменьшается. Также закон сохранения импульса необходим в случаях, когда неприменимо понятие «ускорения». Трудно себе представить ситуацию, когда неподвижное тело приобретает некоторую скорость мгновенно. В обычной практике тела всегда разгоняются и набирают скорость постепенно. Однако при движении электронов и других субатомных частиц изменение их состояния происходит скачком без пребывания в промежуточных состояниях. В таких случаях классическое понятие «ускорения» применять нельзя.
Примеры решения задач
ПРИМЕР 1| Задание | Снаряд массой 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с, попадает в вагон с песком массой 10 т и застревает в нем. Какую скорость получит вагон, если он двигался со скоростью 36 км/ч в направлении, противоположном движению снаряда? |
| Решение | Система вагон+снаряд является замкнутой, поэтому в данном случае можно применить закон сохранения импульса.
Выполним рисунок, указав состояние тел до и после взаимодействия. При взаимодействии снаряда и вагона имеет место неупругий удар. Закон сохранения импульса в этом случае запишется в виде:
Выбирая направление оси совпадающим с направлением движения вагона, запишем проекцию этого уравнения на координатную ось:
откуда скорость вагона после попадания в него снаряда:
Переводим единицы в систему СИ: т кг. км/ч м/с Вычислим:
|
| Ответ | После попадания снаряда вагон будет двигаться со скоростью 5 м/с. |
| Задание | Снаряд массой m=10 кг обладал скоростью v=200 м/с в верхней точке траектории. В этой точке он разорвался на две части. Меньшая часть массой m |
| Решение | Траектория движения снаряда – парабола. Скорость тела всегда направлена по касательной к траектории. В верхней точке траектории скорость снаряда параллельна оси .
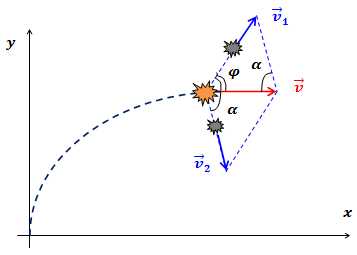
Запишем закон сохранения импульса:
или
Перейдем от векторов к скалярным величинам. Для этого возведем обе части векторного равенства в квадрат и воспользуемся формулами для скалярного произведения векторов:
Учитывая, что , а также что , находим скорость второго осколка:
Подставив в полученную формулу численные значения физических величин, вычислим:
Направление полета большей части снаряда определим, воспользовавшись теоремой синусов:
откуда
Подставив в формулу численные значения, получим:
|
| Ответ | Большая часть снаряда полетит со скоростью 249 м/с вниз под углом к горизонтальному направлению. |
| Задание | Масса поезда 3000 т. Коэффициент трения 0,02. Какова должна быть сила тяги паровоза, чтобы поезд набрал скорость 60 км/ч через 2 мин после начала движения. |
| Решение | Так как на поезд действует сила трения (внешняя сила), систему нельзя считать замкнутой, и закон сохранения импульса в данном случае не выполняется.
Воспользуемся законом изменения импульса:
Так как сила трения всегда направлена в сторону, противоположную движению тела, в проекцию уравнения на ось координат (направление оси совпадает с направлением движения поезда) импульс силы трения войдет со знаком «минус»:
или
На горизонтальном участке сила трения:
поэтому можно записать:
откуда находим силу тяги паровоза:
Переводим единицы в систему СИ: т кг. км/ч м/с мин с Ускорение свободного падения м/с . Вычислим:
|
| Ответ | Сила тяги паровоза должна составлять Н. |
ru.solverbook.com
Модуль силы, скорости, импульса. Что это?!
В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!
Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.
Сила и модуль силы
В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.
Что такое модуль силы?
Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.
Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.
Модуль равнодействующих двух сил определяется по формулам:
- F=F1 + F2 (в случае сил с одинаковым направлением)
- F=F1 — F2 (силы с разным направлением)
Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.
Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).
Что это модуль скорости?

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.
Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.
Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:
v = S/t = (x — x0)/t.
Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.
Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:
- Вычисляется скорость v21 на базе закона сложения скоростей v2 = v21 + v1, а значит v21 = v2 – v1.
- Определяется модуль скорости тела согласно теореме Пифагора.
Модуль импульса и модуль оси
Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.
Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
14. Импульс. Закон сохранения импульса.
Импульс тела (или количество движения) − это векторная физическая величина, равная произведению массы тела на его скорость.
Единица измерения импульса в СИ – кг*м/с
Закон сохранения импульса: если сумма внешних сил, действующих на точки системы, равна нулю, то сумма импульсов всех точек системы остается величиной постоянной.
15. Энергия. Кинетическая и потенциальная энергия. Теорема об изменении кинетической энергии. Закон сохранения энергии в механики.
Работа − это количественная характеристика процесса обмена энергией между взаимодействующими телами.
Кинетическая энергия − это энергия тела, обусловленная его механическим движением
Теорема об изменении кинетической энергии:
Потенциальная энергия − часть общей механической энергии системы, зависящей от взаимного расположения материальных точек системы и их положения во внешнем силовом поле.
К1 + П1 = К2 + П2 = const (1)
Величину E = К + П называют полной механической энергией системы.
Из соотношения (1) следует закон сохранения полной механической энергии: полная механическая энергия системы, на материальные точки которой действуют только консервативные силы, с течением времени не изменяется:
E = const.
16. Момент импульса материальной точки относительно некоторого центра. Чему равен модуль вектора момента импульса? Что называется плечом импульса? Момент импульса в си.
Момент импульса − векторная величина, равная векторному произведению радиус-вектора точки, проведенного из центра на ее импульс .
Модуль вектора момента импульса относительно центра или оси − есть скалярная величина, равная произведению им-пульса p на плечо импульса d относительно этой оси.
Модуль вектора момента импульса равен:
где d − плечо импульса относительно точки О.
Плечо импульса − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой направлен импульс.
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
17. Как определяется направление вектора момента импульса.
Направление момента импульса совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к импульсу, и он перпендикулярен как вектор , так и вектору.
18. Момент силы материальной точки относительно некоторого центра.
Момент силы — векторная величина, равная векторному произведению радиус-вектора точки, проведенному из полюса в точку приложения силы, на силу:
19. Формула для определения модуля вектора момента силы. Плечо силы. Момент силы в СИ.
Модуль вектора момента силы равен:
где d = r sin α − плечо силы относительно точки О.
Плечо силы − это расстояние, измеряемое по перпендикуляру от оси вращения до линии, вдоль которой действует сила.
Момент силы измеряется в ньютон-метрах. 1 Н·м
20. Как определяется направление вектора момента силы.
Направление момента силы совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора к силе, и он перпендикулярен как вектору, так и вектору
21. Момент инерции тела относительно данной оси. Физический смысл момента инерции. Момент инерции в СИ
Моментом инерции твердого тела относительно данной оси называется физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси:
[I] = 1 кг · м2
Физический смысл момента инерции можно определить из выражения:
Момент инерции тела является мерой инерции тела при вращательном движении.
22. Теорема Штейнера. Правило аддитивности для момента инерции.
Теорема Штейнера: момент инерции тела Iz относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:
Правило аддитивности: сумма моментов инерции частей системы относительно оси равен моменту инерции системы относительно данной оси:
23. Формула для расчета работы силы при вращении тела.
24. Основное уравнение динамики вращательного движения относительно точки. Закон сохранения момента импульса.
Уравнение динамики вращательного движения относительно точки (или иначе закон изменения момента импульса механической системы)
Производная по времени от момента импульса системы относительно точки равна сумме моментов внешних сил относительно этой точки.
Закон сохранения момента импульса: если момент внешних сил действующих на механическую систему относительно центра оси равен нулю, то момент импульса системы остаётся величиной постоянной.
25. Основное уравнение динамики вращательного движения относительно неподвижной оси. Закон сохранения проекции момента импульса.
Основное уравнение динамики вращательного движения относительно неподвижной оси:
Закон сохранения проекции момента импульса:
Если проекцию моментов внешних сил относительно оси z равна нулю, то момент импульса тела относительно этой оси остаётся величиной постоянной.
26. Кинетическая энергия тела вращающегося вокруг неподвижной оси. Кинетическая энергия тела при плоском движении.
27. Свободные гармонические колебания и их характеристики( смещение, амплитуда, частота и период колебаний, циклическая частота фаз и начальная фаза колебаний).
Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени.
Периодические колебания − значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени.
Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид:


28. Дать определение частоты обращения тела. Дайте определение периода обращения тела.
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения — это время, за которое совершается один оборот. Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения.
29.Характеристики колебательной системы. Коэффициент затухания и логарифмический декремент затухания. Время релаксации. Добротность колебательной системы.
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать.


30. Уравнение состояния идеального газа(Клапейрона – Менделеева).
Уравнением состояния идеального газа или уравнение Менделеева − Клапейрона.
31. Внутренняя энергия идеального газа. Дать определение числа степеней свободы молекулы газа. Работа газа при изменении его объёма.
Число степеней свободы − это число независимых координат (переменных), которые полностью определяют положение системы в пространстве.
Молекулу одноатомного газа рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения. Молекула двухатомного газа рассматривается как совокупность двух материальных точек,
связанных недеформированной связью. Эта система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Трехатомная молекула имеет шесть степеней свободы: три поступательные и три вращательные. Столько же степеней свободы будут иметь и многоатомные молекулы (четырех, пяти и т. д.).
studfiles.net

Leave A Comment