Площадь боковой поверхности призмы
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-08-31
Площадь боковой поверхности призмы. Здравствуйте! В этой публикации мы с вами разберём группу задач по стереометрии. Рассмотрим комбинацию тел – призмы и цилиндра. На данный момент эта статья завершает всю серию статей связанных с рассмотрением типов заданий по стереометрии.
Если в банке заданий будут появляться новые, то, конечно же, будут и дополнения на блоге в будущем. Но и того что уже есть вполне достаточно, чтобы вы могли научиться решать все задачи с кратким ответом в составе экзамена. Материала хватит на годы вперёд (программа по математике статична).
Представленные задания связаны с вычислением площади боковой поверхности призмы. Отмечу, что ниже рассматривается прямая призма (и соответственно прямой цилиндр).
Без знания всяких формул, мы понимаем, что боковая поверхность призмы это все её боковые грани. У прямой призмы боковые грани это прямоугольники.
У прямой призмы боковые грани это прямоугольники.
Площадь боковой поверхности такой призмы равна сумме площадей всех её боковых граней (то есть прямоугольников). Если речь идёт о правильной призме, в которую вписан цилиндр, то понятно, что все грани этой призмы являются РАВНЫМИ прямоугольниками.
Формально площадь боковой поверхности правильной призмы можно отразить так:
27064. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Боковая поверхность данной призмы состоит из четырёх равных по площади прямоугольников. Высота грани равна 1, ребро основания призмы равно 2 (это два радиуса цилиндра), следовательно площадь боковой грани равна:
Площадь боковой поверхности:
Ответ: 8
73023. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √0,12, а высота равна 3.
Площадь боковой поверхности данной призмы равна сумме площадей трёх боковых граней (прямоугольников). Для нахождения площади боковой грани необходимо знать её высоту и длину ребра основания. Высота равна трём. Найдём длину ребра основания. Рассмотрим проекцию (вид сверху):
Имеем правильный треугольник в который вписана окружность с радиусом √0,12. Из прямоугольного треугольника АОС можем найти АС. А затем и AD (AD=2АС). По определению тангенса:
Значит AD=2АС=1,2.Таким образом, площадь боковой поверхности равна:
Ответ: 3,6
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √75, а высота равна 1.
Искомая площадь равна сумме площадей всех боковых граней. У правильной шестиугольной призмы боковые грани это равные прямоугольники.
Для нахождения площади грани необходимо знать её высоту и длину ребра основания. Высота известна, она равна 1.
Найдём длину ребра основания. Рассмотрим проекцию (вид сверху):
Имеем правильный шестиугольник, в который вписана окружность радиуса √75.
Рассмотрим прямоугольный треугольник АВО. Нам известен катет ОВ (это радиус цилиндра). ещё можем определить угол АОВ, он равен 300 (треугольник АОС равносторонний, ОВ –биссектриса).
Воспользуемся определением тангенса в прямоугольном треугольнике:
АС=2АВ, так как ОВ является медианой, то есть делит АС пополам, значит АС=10.
Таким образом, площадь боковой грани равна 1∙10=10 и площадь боковой поверхности:
Ответ: 60
76485. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 8√3, а высота равна 6.
Площадь боковой поверхности указанной призмы из трёх равных по площади граней (прямоугольников). Чтобы найти площадь требуется знать длину ребра основания призмы (высота нам известна). Если рассматривать проекцию (вид сверху), то имеем правильный треугольник вписанный в окружность. Сторона этого треугольника выражается через радиус как:
Сторона этого треугольника выражается через радиус как:
Подробности этой взаимосвязи изложены здесь. Значит она будет равна
Тогда площадь боковой грани равна: 24∙6=144. А искомая площадь:
Ответ: 432
245354. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Всё просто. Имеем четыре равных по площади боковые грани, следовательно площадь одной грани равна 48:4=12. Так как радиус основания цилиндра равен 2, то ребро основания призмы будет рано 4 – оно равно диаметру цилиндра (это два радиуса). Нам известна площадь грани и одно ребро, второе являющееся высотой будет равно 12:4=3.
Ответ: 3
27065. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Посмотреть решение
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Посмотреть решение
27170. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.
Посмотреть решение
Как видите задачки на раз-два. На этом всё! Успеха вам!
С уважением, Александр.
Делитесь информацией в социальных сетях.
Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2Площадь
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Площадь боковой поверхности треугольной призмы Калькулятор
✖Сторона A основания треугольной призмы — это длина стороны A основания трех ребер основания треугольной призмы.ⓘ Сторона A основания треугольной призмы [Sa] | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Сторона B основания треугольной призмы — это длина стороны B основания трех основных ребер треугольной призмы. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Сторона С основания треугольной призмы — это длина стороны С основания трех ребер основания треугольной призмы. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Высота треугольной призмы — это длина прямой линии, соединяющей любую точку основания с вершиной треугольной призмы. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Площадь боковой поверхности треугольной призмы — это количество плоскостей, заключенных между всеми боковыми поверхностями (то есть верхняя и нижняя грани исключены) треугольной призмы. |
|
⎘ копия |
👎
Формула
сбросить
👍
Площадь боковой поверхности треугольной призмы Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Сторона A основания треугольной призмы: 10 метр —> 10 метр Конверсия не требуется
Сторона B основания треугольной призмы: 12 метр —> 12 метр Конверсия не требуется
Сторона C основания треугольной призмы: 12 метр —> 12 метр Конверсия не требуется
Высота треугольной призмы: 25 метр —> 25 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
850 Квадратный метр —> Конверсия не требуется
< 8 Площадь треугольной призмы Калькуляторы
Общая площадь поверхности треугольной призмы
Идти Общая площадь поверхности треугольной призмы = (Сторона A основания треугольной призмы+Сторона B основания треугольной призмы+Сторона C основания треугольной призмы)*Высота треугольной призмы+1/2*sqrt((Сторона A основания треугольной призмы+Сторона B основания треугольной призмы+Сторона C основания треугольной призмы)*(Сторона A основания треугольной призмы+Сторона B основания треугольной призмы-Сторона C основания треугольной призмы)*(Сторона B основания треугольной призмы+Сторона C основания треугольной призмы-Сторона A основания треугольной призмы)*(Сторона C основания треугольной призмы+Сторона A основания треугольной призмы-Сторона B основания треугольной призмы))
Площадь основания треугольной призмы
Идти Площадь основания треугольной призмы = 1/4*sqrt((Сторона A основания треугольной призмы+Сторона B основания треугольной призмы+Сторона C основания треугольной призмы)*(Сторона A основания треугольной призмы+Сторона B основания треугольной призмы-Сторона C основания треугольной призмы)*(Сторона B основания треугольной призмы+Сторона C основания треугольной призмы-Сторона A основания треугольной призмы)*(Сторона C основания треугольной призмы+Сторона A основания треугольной призмы-Сторона B основания треугольной призмы))
Верхняя площадь треугольной призмы с учетом сторон
Идти
Верхняя площадь треугольной призмы = 0.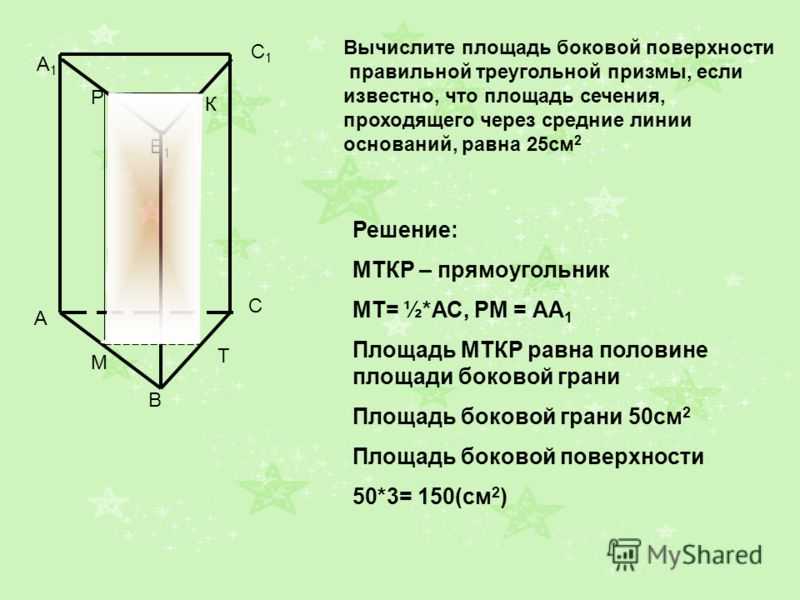 25*sqrt((Сторона A основания треугольной призмы+Сторона B основания треугольной призмы+Сторона C основания треугольной призмы)*(Сторона B основания треугольной призмы+Сторона C основания треугольной призмы-Сторона A основания треугольной призмы)*(Сторона B основания треугольной призмы+Сторона A основания треугольной призмы-Сторона C основания треугольной призмы)*(Сторона C основания треугольной призмы+Сторона A основания треугольной призмы-Сторона B основания треугольной призмы))
25*sqrt((Сторона A основания треугольной призмы+Сторона B основания треугольной призмы+Сторона C основания треугольной призмы)*(Сторона B основания треугольной призмы+Сторона C основания треугольной призмы-Сторона A основания треугольной призмы)*(Сторона B основания треугольной призмы+Сторона A основания треугольной призмы-Сторона C основания треугольной призмы)*(Сторона C основания треугольной призмы+Сторона A основания треугольной призмы-Сторона B основания треугольной призмы))
Общая площадь поверхности треугольной призмы с учетом площади основания
Идти Общая площадь поверхности треугольной призмы = 2*Площадь основания треугольной призмы+Высота треугольной призмы*(Сторона A основания треугольной призмы+Сторона B основания треугольной призмы+Сторона C основания треугольной призмы)
Площадь боковой поверхности треугольной призмы
Идти Площадь боковой поверхности треугольной призмы = (Сторона A основания треугольной призмы+Сторона B основания треугольной призмы+Сторона C основания треугольной призмы)*Высота треугольной призмы
Площадь основания треугольной призмы с заданной высотой на стороне A основания
Идти Площадь основания треугольной призмы = (1/2)*Сторона A основания треугольной призмы*Высота на стороне A основания треугольной призмы
Площадь основания треугольной призмы при заданном объеме
Идти Площадь основания треугольной призмы = Объем треугольной призмы/Высота треугольной призмы
Верхняя площадь треугольной призмы с учетом объема и высоты
Идти Верхняя площадь треугольной призмы = Объем треугольной призмы/Высота треугольной призмы
Площадь боковой поверхности треугольной призмы формула
Площадь боковой поверхности треугольной призмы = (Сторона A основания треугольной призмы+Сторона B основания треугольной призмы+Сторона C основания треугольной призмы)*Высота треугольной призмы
LSA = (Sa+Sb+Sc)*h
Что такое треугольная призма?
Треугольная призма представляет собой многогранник (трехмерная форма), состоящий из двух треугольных оснований и трех прямоугольных сторон. Как и в других призмах, здесь два основания параллельны и конгруэнтны друг другу. Всего у него 5 граней, 6 вершин и 9 ребер. Треугольная призма представляет собой пятигранник с девятью различными сетками.
Как и в других призмах, здесь два основания параллельны и конгруэнтны друг другу. Всего у него 5 граней, 6 вершин и 9 ребер. Треугольная призма представляет собой пятигранник с девятью различными сетками.
Share
Copied!
Боковая площадь треугольной призмы
LearnPracticeDownload
Треугольная призма представляет собой трехмерную фигуру с двумя треугольными основаниями и тремя прямоугольными сторонами. Два основания параллельны и конгруэнтны друг другу. Всего у него 5 граней, 6 вершин и 9 ребер. Ребра и вершины обоих оснований соединены друг с другом тремя прямоугольными сторонами. Обратите внимание, что все три стороны основания (треугольника) не обязательно должны быть одинаковыми. Таким образом, основания/ширины всех трех боковых граней (прямоугольников) неодинаковы, но их высоты/длины одинаковы. Мы будем использовать эти факты, чтобы найти боковую площадь треугольной призмы. Но что понимается под боковой площадью треугольной призмы? Давайте изучим это вместе с его формулой, несколькими решенными примерами и практическими вопросами.
Но что понимается под боковой площадью треугольной призмы? Давайте изучим это вместе с его формулой, несколькими решенными примерами и практическими вопросами.
| 1. | Что такое боковая площадь треугольной призмы? |
| 2. | Боковая площадь треугольной призмы Формула |
| 3. | Как найти боковую площадь треугольной призмы? |
| 4. | Часто задаваемые вопросы о боковой области треугольной призмы |
Что такое боковая площадь треугольной призмы?
Слово «боковой» означает «принадлежащий стороне». Боковая площадь треугольной призмы равна сумме площадей ее боковых граней (которые представляют собой 3 прямоугольника). т. е. это общая площадь поверхности за вычетом площадей двух оснований. Она также известна как площадь боковой поверхности (LSA). Для его расчета задействованы два измерения, поэтому мы измеряем его в квадратных единицах.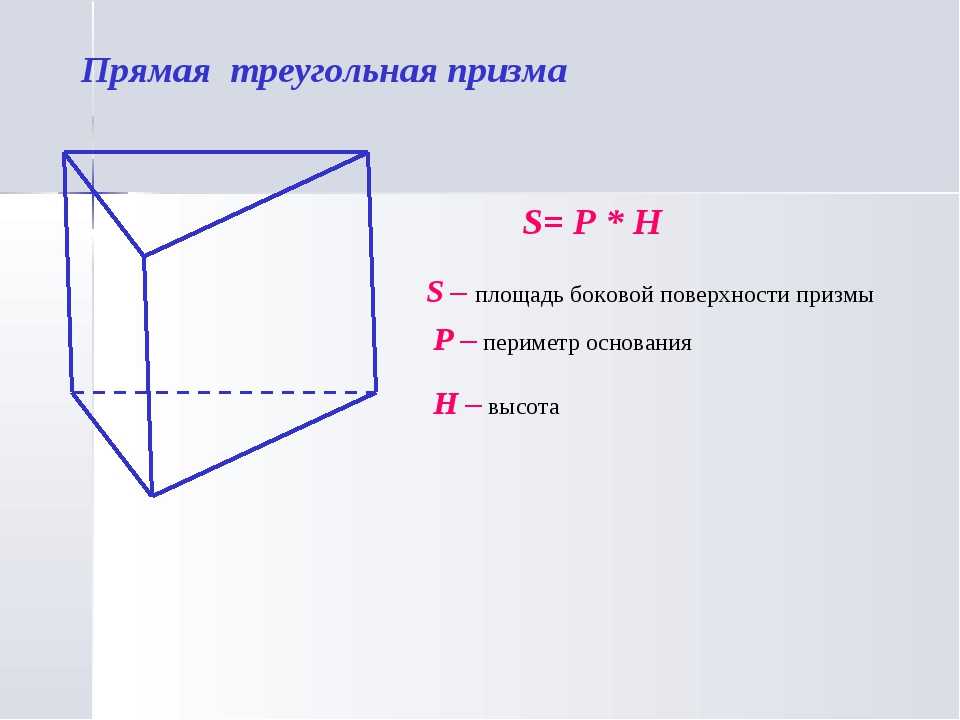
Боковая площадь треугольной призмы Формула
Площадь боковой поверхности треугольной призмы равна сумме всех трех площадей. Таким образом, формула площади поперечного сечения треугольной призмы
Площадь боковой поверхности треугольной призмы (LSA) = ah + bh + ch (или) (a + b + c) h.
Мы знаем, что (a + b + c) — это периметр основания (треугольника). Следовательно,
Площадь боковой поверхности треугольной призмы (LSA) = периметр основания × высота призмы
Как найти формулу площади боковой поверхности треугольной призмы?
Мы знаем, что треугольная призма имеет 3 боковые грани, каждая из которых представляет собой прямоугольник. Посмотрим, каковы размеры этих прямоугольников.
- Один размер каждого из этих прямоугольников совпадает с одним из размеров базового треугольника.
- Другой размер каждого из трех прямоугольников одинаков (равен высоте призмы).

Рассмотрим треугольную призму, высота которой равна «h». Предположим, что длины сторон каждого из треугольных оснований равны a, b и c. Тогда размеры:
- Одна прямоугольная грань равна ‘a’ и ‘h’. Следовательно, его площадь = ah.
- Вторая прямоугольная грань — «b» и «h». Следовательно, его площадь = bh.
- Третья прямоугольная грань — «c» и «h». Отсюда его площадь = ch.
Решенные примеры на боковой поверхности треугольной призмы
Пример 1: Найдите площадь боковой поверхности треугольной призмы, высота которой равна 10 см, а размеры каждого из ее оснований равны 3 см, 6 см и 7 см.
Решение:
Размеры каждой базы:
a = 3 см
b = 6 см
c = 7 см
Высота треугольной призмы = 10 см.
Таким образом, площадь боковой поверхности треугольной призмы = (a + b + c) h
= (3 + 6 + 7) 10
= (16) 10
= 160 см 2
7 90 Ответ: Площадь боковой поверхности данной треугольной призмы = 160 см 2 .

Пример 2: Периметр треугольной призмы равен 108 единицам, а площадь ее боковой поверхности равна 756 единицам. Найдите высоту призмы.
Раствор
Периметр треугольной призмы = 108 единиц.
LSA треугольной призмы = 756 ед.
Предположим, что его высота равна h.
Мы знаем, что LSA треугольной призмы = Периметр призмы × Высота
756 = 108 h
Разделив обе стороны на 108,
7 = h
Ответ: 7 Высота данной призмы единицы измерения.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы о боковой поверхности треугольной призмы
Что такое боковые грани треугольной призмы?
Боковые грани треугольной призмы представляют собой прямоугольники.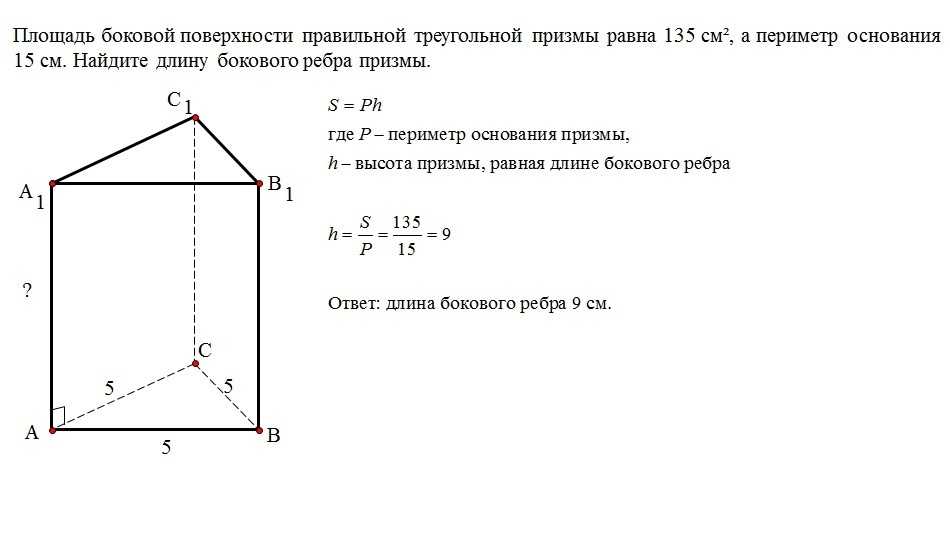 Все эти прямоугольники имеют одинаковую высоту. Основание каждого из этих прямоугольников совпадает с одной стороной треугольного основания.
Все эти прямоугольники имеют одинаковую высоту. Основание каждого из этих прямоугольников совпадает с одной стороной треугольного основания.
Чем боковая грань треугольной призмы отличается от основания?
«Основания» треугольной призмы — это треугольники (конгруэнтные и параллельные), лежащие на вершине и дне призмы, тогда как «боковые грани» — это боковые грани (все грани, кроме «оснований») что прямоугольники.
Какой многоугольник является боковой гранью треугольной призмы?
Каждая боковая грань (боковая грань) треугольной призмы представляет собой прямоугольник. Треугольная призма имеет 3 боковые грани, которые являются прямоугольниками.
Что означает площадь боковой поверхности треугольной призмы?
Площадь боковой поверхности треугольной призмы равна сумме площадей всех ее боковых граней, которые представляют собой 3 прямоугольника. Боковая площадь призмы высотой h, где размеры треугольных оснований равны a, b и c, равна (a + b + c) h.
По какой формуле можно найти площадь боковой поверхности треугольной призмы?
Известно, что площадь любой призмы равна сумме площадей ее боковых граней. Таким образом, площадь боковой поверхности треугольной призмы равна сумме боковых граней, то есть трех прямоугольных граней. Формула для нахождения боковой площади треугольной призмы: (a + b + c) h или Ph.
Как найти площадь боковой поверхности прямоугольной призмы?
Площадь боковой поверхности правой треугольной призмы (ППП) = ah + bh + ch (или) (a + b + c) h, где a, b и c — основания прямоугольных граней, а h — общая высота или общая высота призмы. Кроме того, (a + b + c) — это периметр основания (треугольника). Таким образом, можно сделать вывод, что площадь боковой поверхности треугольной призмы = Периметр основания × Высота призмы. Чтобы найти площадь поперечного сечения, подставьте соответствующие значения в формулу и добавьте единицу к полученному конечному значению.
Как рассчитать боковую площадь треугольной призмы?
Чтобы вычислить площадь поперечного сечения треугольной призмы, выполните шаги, указанные ниже:
- Шаг 1: Определите размеры треугольного основания (основания трех прямоугольных граней) и найдите периметр, P = a + b + в.

- Шаг 2: Определите высоту призмы, h.
- Шаг 3: Подставьте значения заданных размеров в формулу LSA = (a + b + c) h или Ph.
- Шаг 4: Запишите конечное значение в соответствующих квадратных единицах.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Рабочий лист площади поверхности
Рабочие листы по математике и наглядная программа
Видео с вопросами: Определение площади боковой поверхности треугольной призмы квадратный сантиметр.
Боковая площадь – площадь поверхности сторон, исключая верх и низ. Так что здесь это не верх и низ, потому что низ на самом деле не является основанием. Он не лежит на дне. Это треугольная призма.
Призма состоит из прямоугольников и двух оснований. А основания — это то, что отличает призму. Итак, здесь у нас есть треугольники в качестве наших оснований. Так она становится треугольной призмой. Таким образом, боковая площадь будет площадью сторон, за исключением вершины и низа, которые являются основаниями, треугольниками.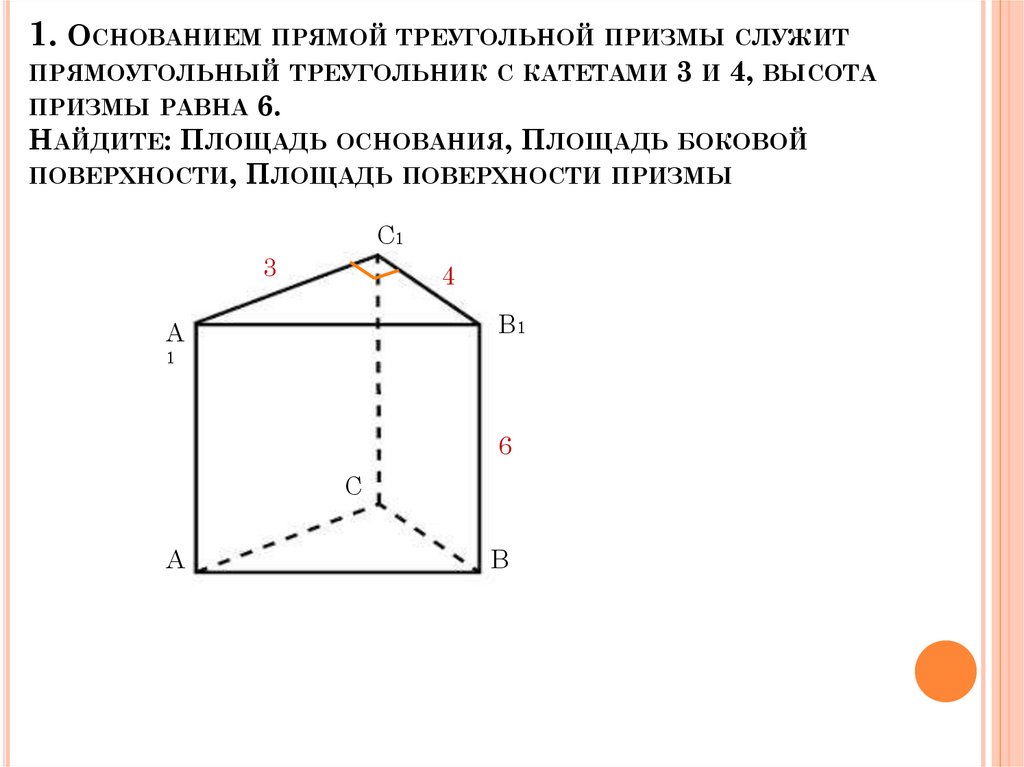
Итак, площадь, которую нам нужно найти, будет прямоугольником 10 на 16, потому что мы знаем, что его длина равна 16. Нам также нужно найти площадь этого прямоугольника. И это 16 на — мы на самом деле не знаем эту длину. Но мы знаем, что у нас есть прямоугольный треугольник со сторонами 10 и 15. Поэтому мы можем использовать теорему Пифагора, чтобы найти его.
10 и 15 будут ногами. И мы можем назвать гипотенузу 𝑥, потому что теорема Пифагора утверждает, что квадрат самой длинной стороны, той, что находится напротив угла 90 градусов, равен сумме квадратов более коротких сторон, 10 и 15. Таким образом, 100 плюс 225 будет 325.
Теперь нам нужно извлечь квадратный корень из обеих сторон, что примерно равно 18.03. Итак, мы можем пойти дальше и обозначить это на нашей диаграмме. Итак, здесь мы распознали два прямоугольника, площадь которых нам нужно найти, чтобы найти нашу боковую площадь. Есть еще один прямоугольник, тот, что внизу. А это 15 на 16. Итак, давайте выпишем все области, которые нам нужно найти.
Первый прямоугольник был 10 на 16. И мы находим площадь прямоугольника, умножив длину на ширину, то есть 10 умножить на 16. Наш следующий прямоугольник будет 16 на 18,03. Так что мы умножим их. И, наконец, у нас есть прямоугольник 15 на 16. Поэтому нам нужно умножить, а затем сложить их вместе. Итак, у нас есть 160 плюс 288,48 плюс 240, что дает нам 688,48.
Однако он говорит округлить до ближайшего квадратного сантиметра. Итак, мы смотрим здесь на четверку. Поскольку четыре меньше пяти, эта восьмерка останется восьмеркой, в результате чего получится 688 сантиметров в квадрате, потому что это площадь. Так и должно быть квадратных сантиметров.
Теперь есть еще один способ решить эту задачу. Мы могли бы использовать формулу площади поперечного сечения, которая представляет собой произведение периметра основания на высоту самой призмы. Итак, основания были треугольниками. Итак, чтобы найти периметр, нам нужно сложить все стороны. Итак, у нас есть 10 плюс 15 плюс 18,03, что дает нам 43,03.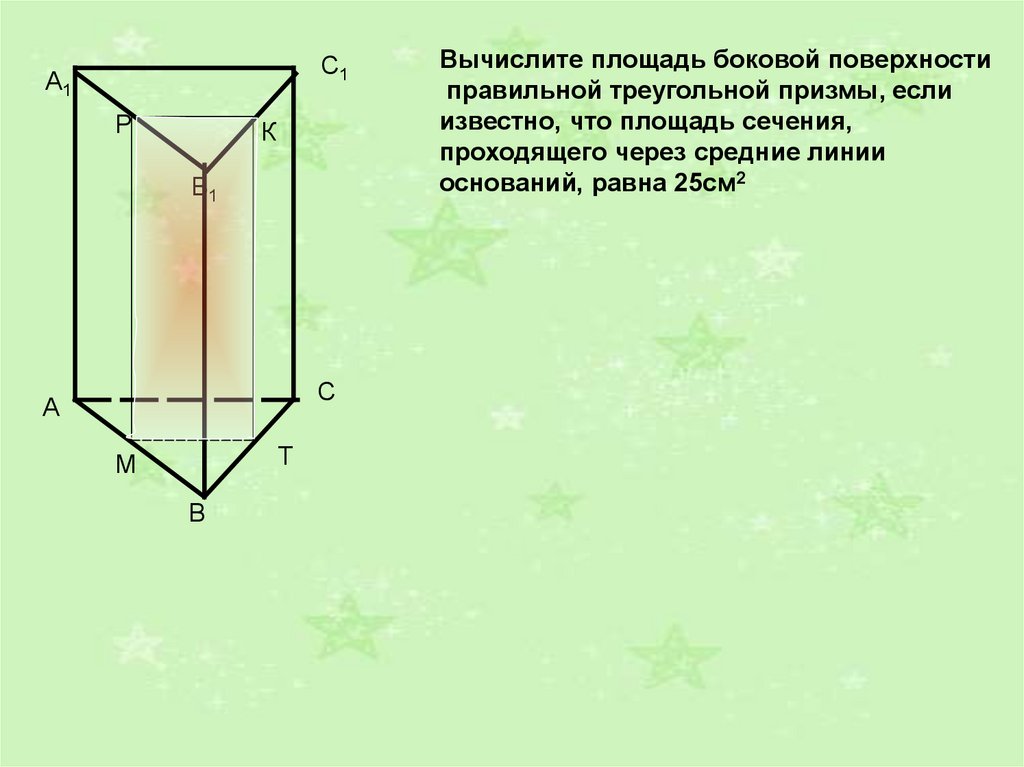

 ⓘ Сторона B основания треугольной призмы [Sb]
ⓘ Сторона B основания треугольной призмы [Sb]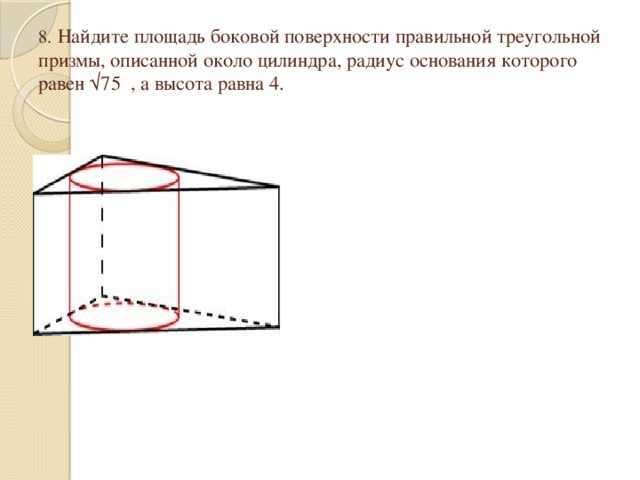 ⓘ Сторона C основания треугольной призмы [Sc]
ⓘ Сторона C основания треугольной призмы [Sc] ⓘ Высота треугольной призмы [h]
ⓘ Высота треугольной призмы [h]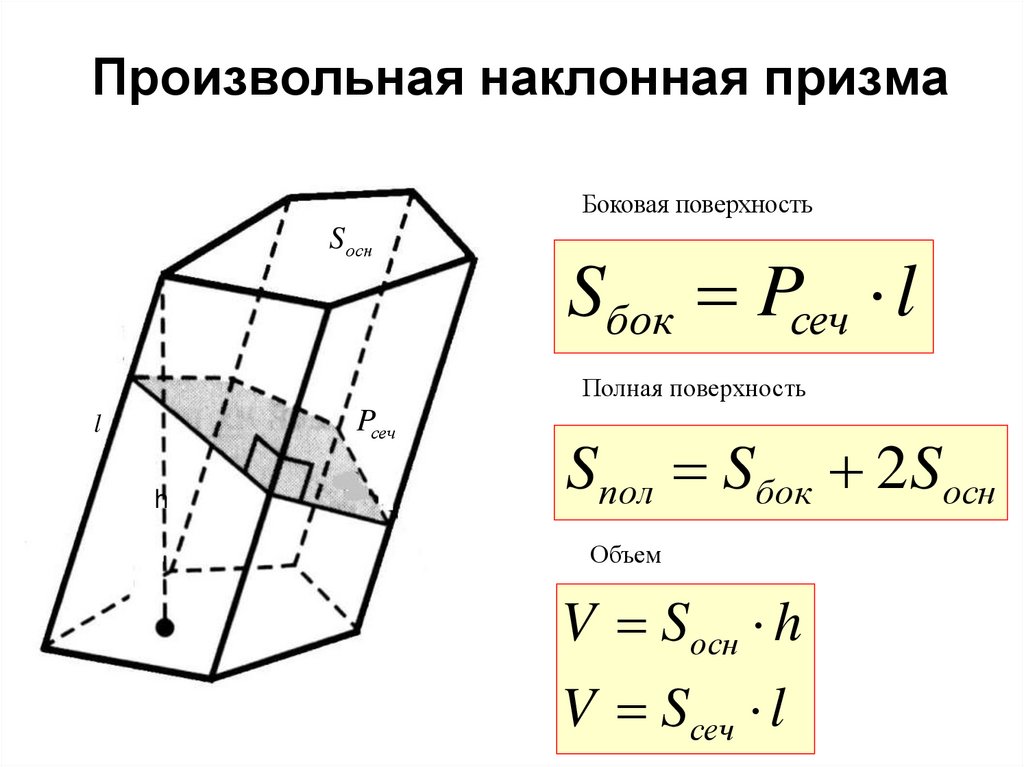 ⓘ Площадь боковой поверхности треугольной призмы [LSA]
ⓘ Площадь боковой поверхности треугольной призмы [LSA]



Leave A Comment