Гипотенуза в прямоугольном треугольнике — как её найти, зная катеты?

Гипотенуза — сторона в прямоугольном треугольнике, находящаяся напротив прямого угла. Две других стороны — катеты. В прямоугольном треугольнике гипотенуза всегда длиннее катетов.

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов (формула: c² = a² + b², где c — гипотенуза, a и b — катеты). Очень часто для вычисления гипотенузы используется именно эта теорема.

Как найти гипотенузу, зная катеты?

Если известны оба катета (две другие стороны прямоугольного треугольника), можно применить Теорему Пифагора.

Теорема Пифагора — в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Формула: c² = a² + b² (при c — гипотенуза, a и b — катеты).

Например:

Один катет равен 3 см, другой — 4 см. Таким образом, а = 3, b = 4, подставляем в формулу:

c² = 3² + 4² <=> c² = 9 + 16 <=> c² = 25 <=> c = √25 <=> c = 5.

Ответ: длина гипотенузы 5 см (или x = 5).

Как найти
катет в прямоугольном треугольнике

По той же формуле можно найти и длину одного неизвестного катета, нужно только немного её изменить:

Начальная формула: c² = a² + b² (при c — гипотенуза, a и b — катеты), и найти катет можно по этой:

(c — гипотенуза, a и b — катеты)

Например: Один катет равен 3 см, а гипотенуза — 5 см. Нужно узнать длину второго катета.

Применяем формулу b = √c² — a² ⇔

b = √5² — 3² ⇔ b = √25 — 9 ⇔ b = √16 ⇔ b = 4.

Как найти гипотенузу, зная катет и угол?

Если есть противолежащий катет — теорема синусов

Если в условии задачи дан угол и противолежащий катет, то ищем гипотенузу по Теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов.

Примечание: гипотенуза есть только в прямоугольном треугольнике, однако теорему синусов можно применять к любым треугольникам (не только к прямоугольным).

Формула:

Например:

Известна одна сторона треугольника 𝐴𝐶 = √2 и ∠β = 45º.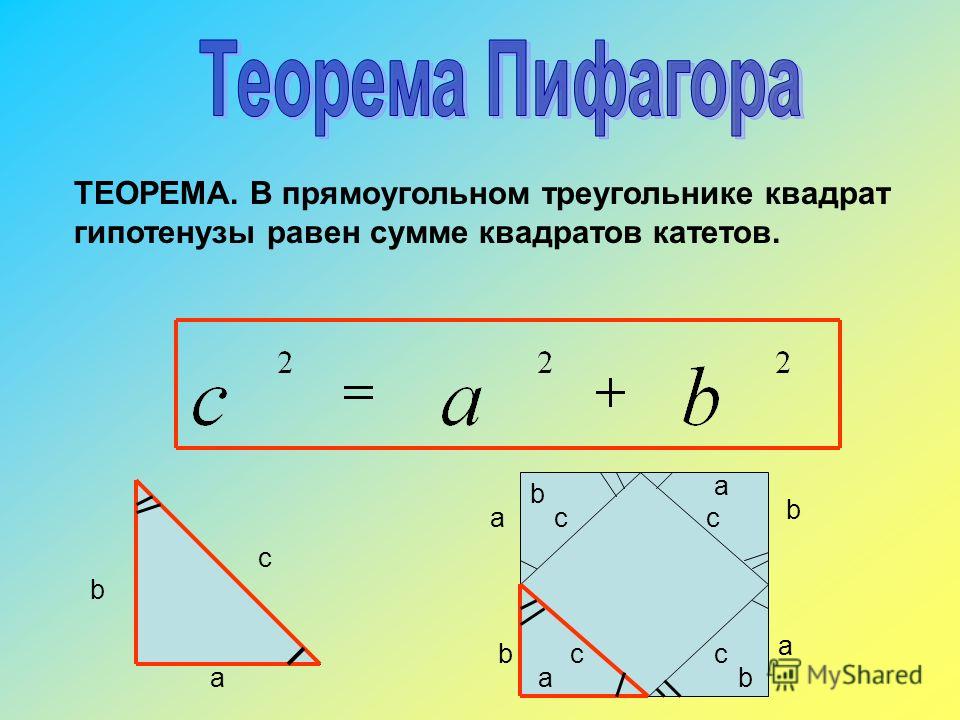

∠α = 90º (т.к. мы ищем гипотенузу, то второй угол в треугольнике прямой, значит имеет 90º).

Так как во всех треугольниках сумма всех углов равна 180º, то можем узнать оставшийся ∠c.

Значит: ∠c = 180º — (90º + 45º) = 45º.

Подставляем в формулу (a/sinα = b/sinβ = c/sinγ) известные:

BC/sin90º = AC/sin45º = AB/sin45º

В таблице вы найдёте значения для синуса:

sin 45º√2/2
sin 60º√3/2
sin 90º1

В условии задачи нам дано: 𝐴𝐶 = √2, значит:

BC/sin90º = √2/sin45º = AB/sin45º

Подставляем значения синуса из таблицы:

BC/1 = √2/(√2/2) = AB/(√2/2) (забудем на время про катет AB) ⇔

BC = √2/(√2/2) ⇔ BC = 2 (гипотенуза равна 2)

Если хотите вычислить катет, уже зная другой катет и гипотенузу:

AB/(√2/2) = 2 ⇔ AB = √2

Ответ: гипотенуза BC равна 2 см, а катет AB √2 см.

Если есть прилежащий катет — по косинусу

Если в условии задачи дан угол и прилежащий катет, то ищем гипотенузу по косинусу (в прямоугольном треугольнике, косинус острого угла (cos) — это отношение прилежащего катета (b) к гипотенузе(c), таким образом cos a = b/c, из этого получается c = b / cos α).

Т.е. гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α.

Например:

Известна одна сторона треугольника AB = 1 и ∠β = 45º. Нужно вычислить гипотенузу (BC).

Помним, что гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α. Т.е.: BC = AB / cosβ ⇔ BC = 1/ cos 45º.

Смотрим в таблице, чему равен cos 45º.

BC = 1/ (√2/2) = √2

Ответ: гипотенуза BC равна √2 см.

Как найти гипотенузу равнобедренного треугольника

В равнобедренном треугольнике есть гипотенуза только в том случае, если он одновременно и прямоугольный, т.к. гипотенуза есть только в прямоугольных треугольниках (и его основание будет гипотенузой).

Чтобы найти такую гипотенузу, нужно любой из двух одинаковых катетов возвести в квадрат, умножить на 2 и посчитать квадратный корень: b = √2a² (где b — гипотенуза, а — катет). Это следствие из теоремы Пифагора.

Например:

Катет равнобедренного треугольника равен 7см. Нужно найти гипотенузу.

Формула b = √2a². Подставляем:

b = √2*7² = √2*49 ≈ √98 ≈ 9.899

Если забудете эту формулу, можно использовать уже знакомую формулу Пифагора для гипотенузы (c² = a² + b²):

c² = a² + b²

c² = 7² + 7²

c² = 49 + 49

c² = 98

c = √98

c ≈ 9.899

Ответ: гипотенуза равна 9.899.

Узнайте больше про Теорему Пифагора, Теорему косинусов, а также, что такое Тангенс и Аксиома.

8 класс. Геометрия. Теорема Пифагора. — Теорема Пифагора.

Комментарии преподавателя

Если один из углов тре­уголь­ни­ка пря­мой и во вто­ром тре­уголь­ни­ке тоже один из углов пря­мой, то эти углы равны друг другу. И если сто­ро­ны, за­клю­ча­ю­щие пря­мые углы (а сто­ро­ны, ко­то­рые за­клю­ча­ют пря­мые углы, на­зы­ва­ют­ся ка­те­та­ми), равны, то равны и сами пря­мо­уголь­ные тре­уголь­ни­ки. Но это, в свою оче­редь, озна­ча­ет, что если мы знаем два ка­те­та пря­мо­уголь­но­го тре­уголь­ни­ка, то ги­по­те­ну­за опре­де­ле­на одним един­ствен­ным об­ра­зом, ко­то­рый мы и рас­смот­рим.

Еще в Древ­нем Егип­те было из­вест­но, что если взять пря­мо­уголь­ный тре­уголь­ник, ка­те­ты ко­то­ро­го равны 3 и 4 еди­ни­цы, то ги­по­те­ну­за обя­за­тель­но будет равна 5 еди­ни­цам.

Еги­пет­ский тре­уголь­ник — otvet.mail.ru

В Древ­нем Егип­те часто поль­зо­ва­лись таким тре­уголь­ни­ком. Он на­зы­ва­ет­ся еги­пет­ским тре­уголь­ни­ком. Это самый ма­лень­кий из пря­мо­уголь­ных тре­уголь­ни­ков с це­лы­ми сто­ро­на­ми. Вы мо­же­те сло­жить пря­мо­уголь­ные тре­уголь­ни­ки с по­мо­щью спи­чек и уви­деть, что если хотя бы ка­кой-ни­будь из ка­те­тов будет мень­шим чис­лом, то ги­по­те­ну­за обя­за­тель­но не будет целым чис­лом.

—————————————————

Мы го­то­вы сфор­му­ли­ро­вать тео­ре­му Пи­фа­го­ра и за­пи­сать фор­му­лу, ко­то­рая поз­во­лит вы­чис­лить ги­по­те­ну­зу пря­мо­уголь­но­го тре­уголь­ни­ка, если из­вест­ны ка­те­ты этого пря­мо­уголь­но­го тре­уголь­ни­ка:

В пря­мо­уголь­ном тре­уголь­ни­ке квад­рат ги­по­те­ну­зы равен сумме квад­ра­тов ка­те­тов.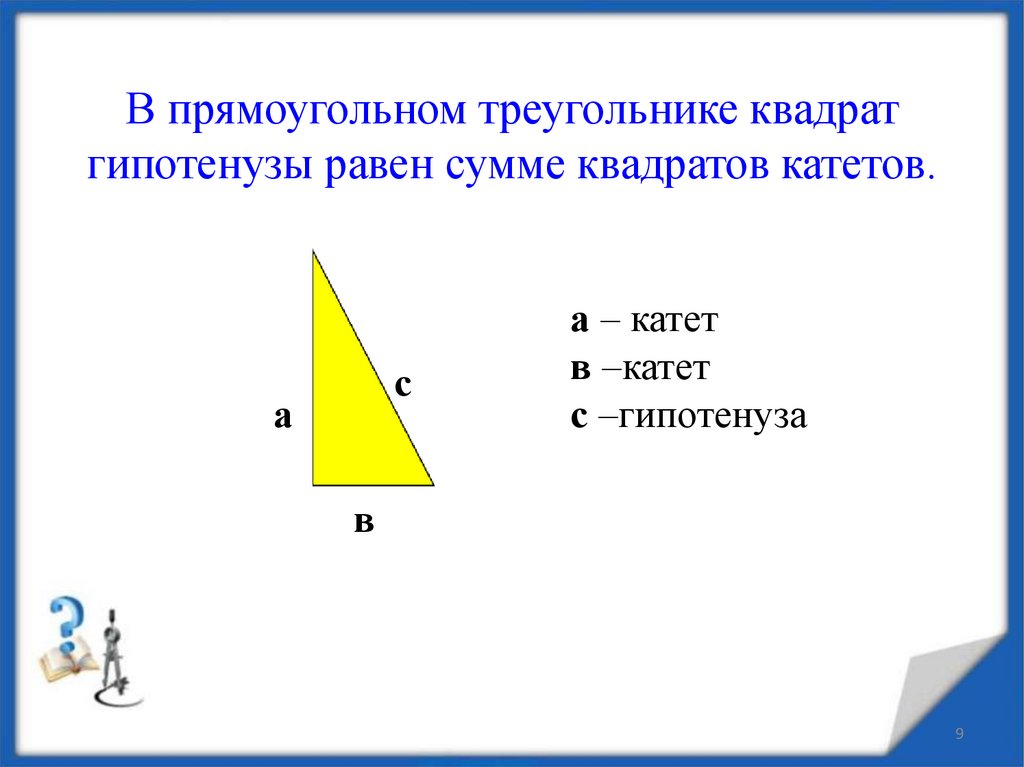

Пря­мо­уголь­ный тре­уголь­ник — sovetclub.ru

 – эта фор­му­ла и на­зы­ва­ет­ся тео­ре­мой Пи­фа­го­ра 

Тео­ре­ма Пи­фа­го­ра фор­му­ла

 —  в пря­мо­уголь­ном тре­уголь­ни­ке квад­рат ги­по­те­ну­зы равен сумме квад­ра­тов ка­те­тов.

——————————————

До­ка­жем тео­ре­му Пи­фа­го­ра.

За­да­ча № 1. Дано: пря­мо­уголь­ный тре­уголь­ник АВС, в ко­то­ром угол С – пря­мой (90 °). Катет ВС = a, катет АС = b, ги­по­те­ну­за АВ = с 

До­ка­зать: 

Ил­лю­стра­ция к тео­ре­ме Пи­фа­го­ра

Ре­ше­ние.

В фор­му­ле, ко­то­рую нам необ­хо­ди­мо до­ка­зать, фи­гу­ри­ру­ют квад­ра­ты трех ве­ли­чин: квад­ра­ты с, а и b. В гео­мет­рии мы стал­ки­ва­ем­ся с квад­ра­та­ми длин от­рез­ков, когда счи­та­ем пло­ща­ди фигур. Но и, на­вер­ное, самая про­стая фи­гу­ра, пло­щадь ко­то­ро­го можем по­счи­тать – квад­рат. Со­от­ветс­вен­но, пер­вая мысль – до­стро­ить эту кар­тин­ку до квад­ра­тов. До­стро­им тре­уголь­ник АВС до квад­ра­та со сто­ро­ной а+b.

Для этого про­дол­жим катет АС на длину ка­те­та ВС (+ а), а ВС на длину ка­те­та АС (+ b) 

Ри Ил­лю­стра­ция к тео­ре­ме

До­стро­им по­лу­чив­шу­ю­ся кар­тин­ку до пря­мо­уголь­ни­ка 

 Ил­лю­стра­ция к тео­ре­ме

У этого пря­мо­уголь­ни­ка смеж­ные сто­оро­ны равны (а+b). Зна­чит, этот пря­мо­уголь­ник обя­за­тель­но яв­ля­ет­ся квад­ра­том. Обо­зна­чим по­лу­чив­ши­е­ся точки бук­ва­ми. По­лу­чим квад­рат СDEF.

Все сто­ро­ны этого ква­дар­та равны (а + b). Со­от­вет­ствен­но, сто­ро­ны DE и EF тоже можем раз­де­лить на от­рез­ки а и b. Обо­зна­чим эти точки бук­ва­ми G и H. Со­еди­ним точку А с точ­кой G, точку G с точ­кой Н, точку Н с точ­кой В 

Ил­лю­стра­ция к тео­ре­ме

Квад­рат СDEF ока­зал­ся раз­ре­зан­ным на 5 фигур: 4 тре­уголь­ни­ка по углам и 1 че­ты­рех­уголь­ник в цен­тре. Если этот че­ты­рех­уголь­ник ока­жет­ся квад­ра­том, то это будет удоб­но для нас. Но это сна­ча­ла нужно до­ка­зать.

Вы­яс­ним, что мы знаем про по­лу­чив­шу­ю­ся фи­гу­ру. Все 4 тре­уголь­ни­ка обя­за­тель­но яв­ля­ют­ся пря­мо­уголь­ны­ми,по­то­му что каж­дый из них со­дер­жит один из углов квад­ра­та (Ð С = Ð D = Ð Е = Ð F = 90°). Ка­те­ты в этих тре­уголь­ни­ках равны а и b. Зна­чит, все эти тре­уголь­ни­ки равны друг другу (по двум сто­ро­нам и углу между ними). А если все эти тре­уголь­ни­ки равны друг другу, то равны все их со­от­ветс­вен­ные эле­мен­ты. На­при­мер, все ги­по­те­ну­зы у них обя­за­тель­но равны 

 Ил­лю­стра­ция к тео­ре­ме

Зна­чит, че­ты­рех­уголь­ник АGНВ – ромб. Че­ты­рех­уголь­ник, у ко­то­ро­го все сто­ро­ны равны, на­зы­ва­ет­ся ромб. Мы до­ка­за­ли, что все сто­ро­ны равны, АG = GН = НВ = ВА = с. АGНВ – ромб.

Ги­по­те­ну­за не един­ствен­ное, что равно у наших тре­уголь­ни­ков. Еще у них равны все ост­рые углы.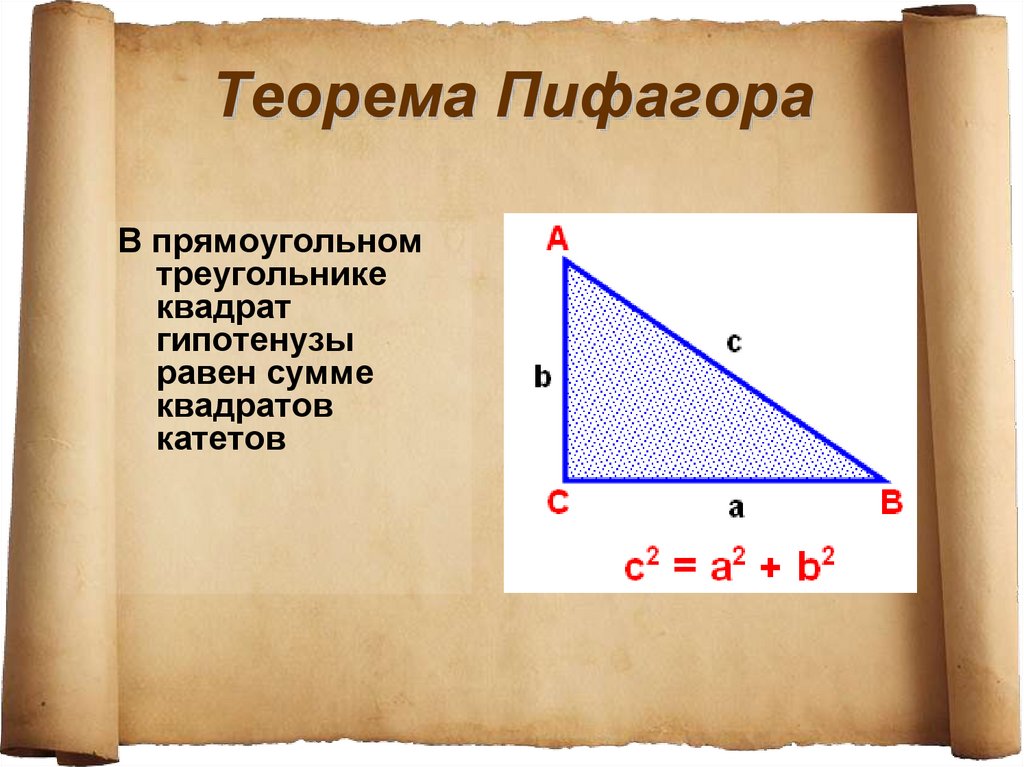 От­ме­тим это на кар­тин­ке. Во-пер­вых, равны Ð САВ = Ð DGA = Ð EHG = Ð FBH. Зе­ле­ным цве­том обо­зна­чим эти углы, ве­ли­чи­ной α. И такие углы тоже равны: Ð СВА = Ð DAG = Ð EGH = Ð FHB. Крас­ным цве­том обо­зна­чим углы ве­ли­чи­ной b

 Ил­лю­стра­ция к тео­ре­ме

На нашей кар­тин­ке от­ме­че­но очень много углов, но не все. Остал­ся, на­при­мер, не от­ме­чен­ным Ð GАВ. Вы­чис­лим его.

Эти три угла вме­сте, Ð DAG, ÐGAB, Ð CAB, со­став­ля­ют раз­вер­ну­тый угол. Со­от­вет­ствен­но:

Ð GАВ = 180° — Ð CAB — Ð DAG = 180 ° — α — b.

Пре­об­ра­зу­ем эту фор­му­лу сле­ду­ю­щим об­ра­зом:

Ð GАВ = 180° — (α + b).

У нас по­лу­чи­лась сумма (α + b). Что такое сумма (α + b)? Это сумма ост­рых углов пря­мо­уголь­но­го тре­уголь­ни­ка. В пря­мо­уголь­ном тре­уголь­ни­ке сумма ост­рых углов равна 90°. По­это­му по­лу­ча­ет­ся:

Ð GАВ = 180° — (α + b) = 180° — 90° = 90°. То есть Ð GАВ – пря­мой. А зна­чит наш ромб АGНВ яв­ля­ет­ся квад­ра­том. Если в ромбе один из углов пря­мой, то этот ромб обя­за­тель­но квад­рат.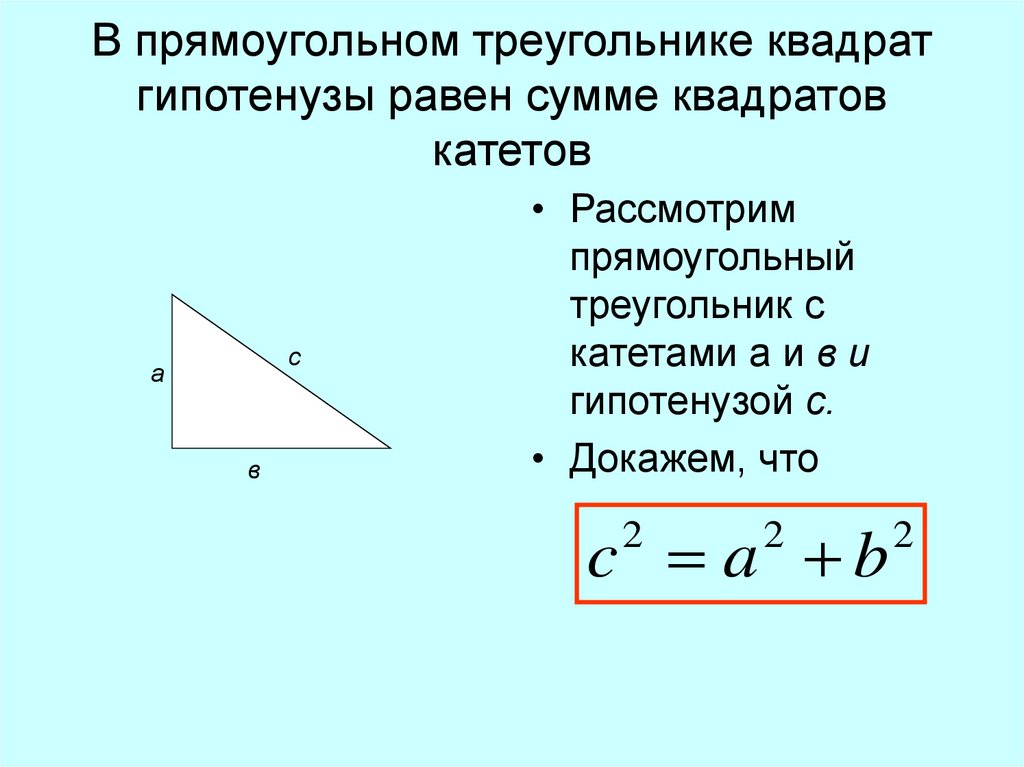

Мы по­лу­чи­ли: боль­шой квад­рат СDEF, квад­рат мень­ше АGНВ. Можно на­чи­нать за­пи­сы­вать пло­ща­ди.

С одной сто­ро­ны, СDEF – квад­рат и его пло­щадь можно по­счи­тать как квад­рат сто­ро­ны:

С дру­гой сто­ро­ны, этот квад­рат со­сто­ит из 5 фигур: 4 тре­уголь­ни­ков и квад­ра­та в цен­тре. Пло­щадь квад­ра­та в цен­тре равнас2, а че­ты­ре тре­уголь­ни­ка равны друг другу и пло­щадь каж­до­го из них – по­ло­ви­на про­из­ве­де­ния ка­те­тов.

Пло­щадь че­ты­рех­уголь­ни­ка СDEF не за­ви­сит от того, каким об­ра­зом мы с вами ее счи­та­ем. Она все­гда одна и та же. Со­от­вет­ствен­но, мы можем при­рав­нять наши ра­вен­ства, но сна­ча­ла их надо пре­об­ра­зо­вать.

В пер­вом ра­вен­стве рас­кры­ва­ем квад­рат суммы:

Во вто­ром слу­чае:

Пер­вое вы­ра­же­ние равно вто­ро­му.

И там, и там есть 2аb. От них легко от­ка­зать­ся – со­кра­тим их. И по­лу­чим:

То есть в нашем пря­мо­уголь­ном тре­уголь­ни­ке квад­рат ги­по­те­ну­зы равен сумме квад­ра­тов ка­те­тов.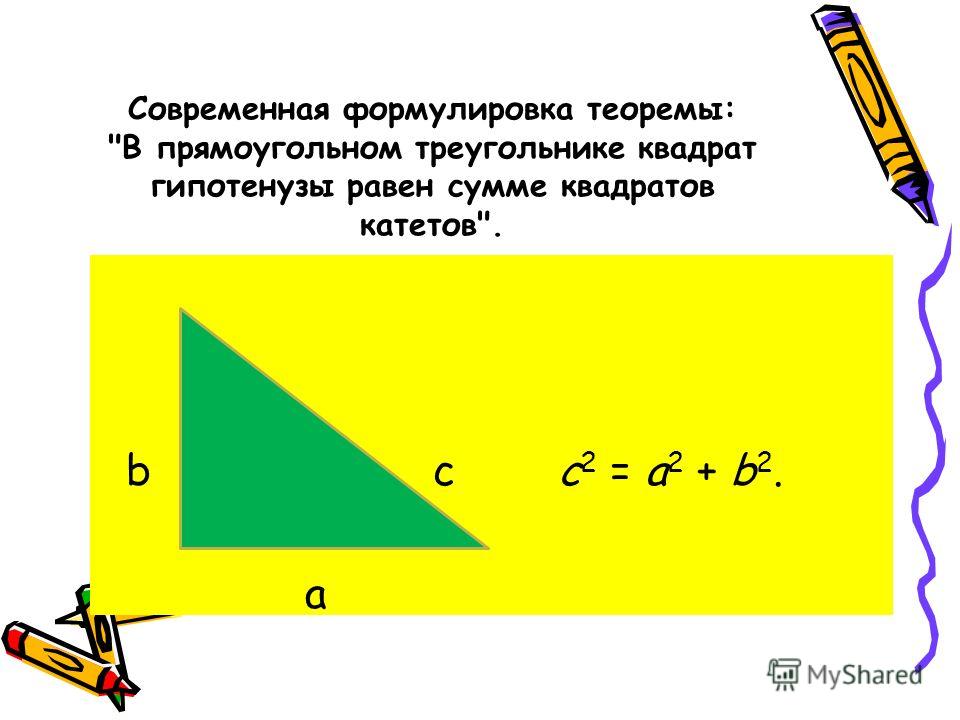 Что и тре­бо­ва­лось до­ка­зать.

Это до­ка­за­тель­ство – не един­ствен­ное до­ка­за­тель­ство тео­ре­мы Пи­фа­го­ра. У нее очень много до­ка­за­тельств. Тео­ре­ма Пи­фа­го­ра за­не­се­на даже в Книгу ре­кор­дов Гин­не­са за счет того, что у нее так много до­ка­за­тельств. Ин­те­рес­ным яв­ля­ет­ся тот факт, что мно­гие из них почти не тре­бу­ют ал­геб­ры. Вот, на­при­мер, в Древ­ней Индии ис­поль­зо­ва­ли такой спо­соб до­ка­за­тель­ства.

———————————————

Ри­со­ва­ли 2 оди­на­ко­вых квад­ра­та. Один такой, как у нас уже был на­ри­со­ван (№1). И вто­рой тоже со сто­ро­ной (а + b). Такой же квад­рат, но раз­ре­за­ли его немно­го по-дру­го­му (№2) 

 

                                     №1                                                                              №2

Ил­лю­стра­ция к тео­ре­ме

Сна­ча­ла его раз­ре­за­ли на 4 фи­гу­ры: 2 квад­ра­та. Один со сто­ро­ной а, вто­рой со сто­ро­ной b.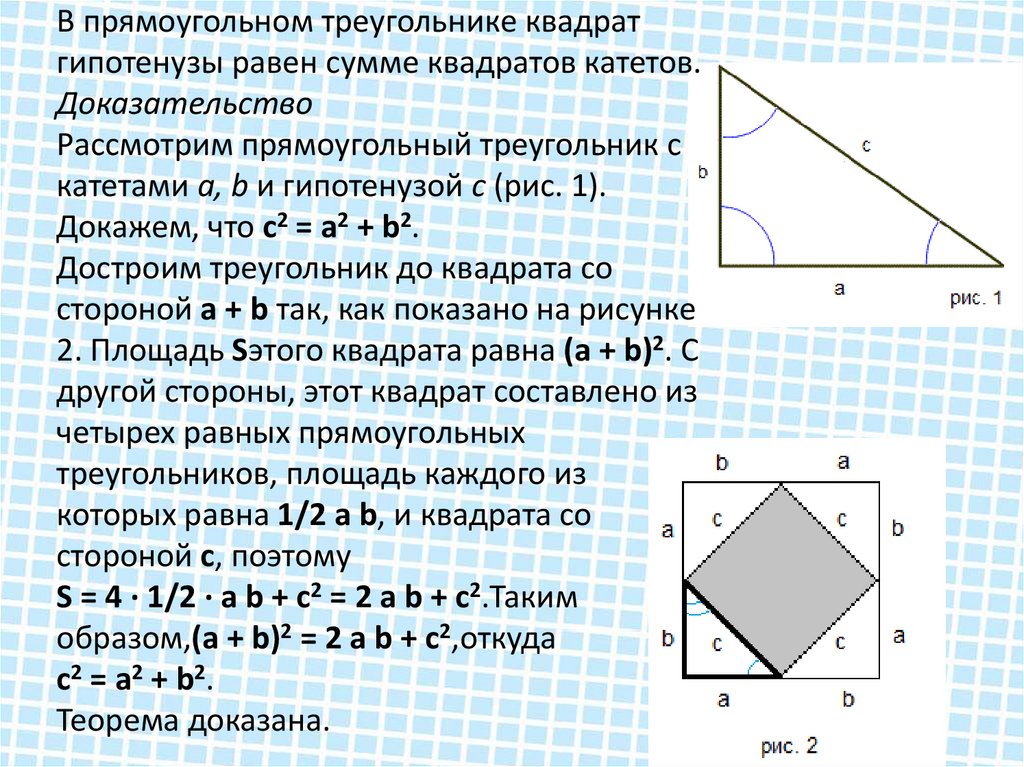 Со­от­вет­ствен­но, по углам оста­ва­лись пря­мо­уголь­ни­ки со сто­ро­на­ми а и b. А даль­ше каж­дый из этих пря­мо­уголь­ни­ков со сто­ро­на­ми а и b раз­ре­за­ли по­по­лам на 2 тре­уголь­ни­ка.

Те­перь по­лу­ча­ет­ся 2 оди­на­ко­вых квад­ра­та, по-раз­но­му раз­ре­зан­ных. И в этих оди­на­ко­вых квад­ра­тах есть оди­на­ко­вые фи­гу­ры. Даже в одном и том же по­ло­же­нии. Их ра­вен­ство вы­де­ле­но оди­на­ко­вы­ми цве­та­ми на ри­сун­ках

Ил­лю­стра­ция к тео­ре­ме

Если у каж­дой кар­тин­ке вы­ре­зать эти тре­уголь­ни­ки, то на одной кар­тин­ке оста­ет­ся квад­рат со сто­ро­ной с и пло­ща­дью с2; а на дру­гой кар­тин­ке оста­ет­ся 2 квад­ра­та со сто­ро­на­ми а и b, сумма пло­ща­дей этих квад­ра­тов – это а2 + b2.

Такое до­ка­за­тель­ство ис­поль­зо­ва­ли в Древ­ней Индии.

————————————————————————————————————

Также есть дру­гое до­ка­за­тель­ство, бла­го­да­ря ко­то­ро­му стало из­вест­но про «пи­фа­го­ро­вы штаны, ко­то­рые во все сто­ро­ны равны». По­смот­ри­те на кар­тин­ку 

Ил­лю­стра­ция к тео­ре­ме

На ка­те­тах пря­мо­уголь­но­го тре­уголь­ни­ка по­стро­е­ны квад­ра­ты. На ги­по­те­ну­зе тоже по­стро­ен квад­рат. Его вы­ре­за­ли, и оста­лось пу­стое место (для удоб­ства окра­шен в зе­ле­ный цвет). Квад­ра­ты, ко­то­рые об­ра­зо­ва­ны на ка­те­тах, раз­ре­за­ны на 5 ку­соч­ков. По­про­бу­ем сло­жить из этих ку­соч­ков квад­рат на ги­по­те­ну­зе. (Из двух ма­лень­ких квад­ра­тов по­стро­и­ли боль­шой на ги­по­те­ну­зе. Каж­дый ку­со­чек со своей окрас­кой по­ка­зы­ва­ет рас­по­ло­же­ние в боль­шом квад­ра­те.)

Ил­лю­стра­ция к тео­ре­ме

————————————————————

Мы видим, что квад­рат, по­стро­ен­ный на ги­по­те­ну­зе, со­бран из ку­соч­ков квад­ра­тов, по­стро­ен­ных на ка­те­тах. То есть пло­щадь этого квад­ра­та с2 равна сумме пло­ща­дей этих квад­ра­тов а2 + b2.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/fakultativ/formulirovka-i-dokazatelstvo-teoremy-pifagora

http://www. youtube.com/watch?v=529Rj_xaS9Q

http://www.youtube.com/watch?v=GnfAViieGII

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/94-test-po-geometrii-8-klass-tema-teorema-pifagora-variant-1.html

http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/95-test-po-geometrii-8-klass-tema-teorema-pifagora-variant-2.html

http://uchkollektor39.ru/uploads/images/items/5397b07a6344d4655e9aee3c8d38dc9d.jpg

http://volna.org/wp-content/uploads/2014/11/volna_org_tieoriema_pifaghora3.zip

Теорема Пифагора — Формула, Доказательство, Примеры

Теорема Пифагора , также называемая теоремой Пифагора, объясняет взаимосвязь между тремя сторонами прямоугольного треугольника. По теореме Пифагора квадрат гипотенузы равен сумме квадратов двух других сторон треугольника. Давайте узнаем больше о теореме Пифагора, формуле

теоремы Пифагора и доказательстве теоремы Пифагора вместе с примерами.

1. Что такое теорема Пифагора?
2. История теоремы Пифагора
3. Теорема Пифагора Формула
4. Доказательство теоремы Пифагора
5. Теорема Пифагора Треугольники
6. Теорема Пифагора Квадраты
7. Приложения теоремы Пифагора
8. Часто задаваемые вопросы по теореме Пифагора

Что такое Теорема Пифагора?

Теорема Пифагора утверждает, что если треугольник прямоугольный, то квадрат гипотенузы равен сумме квадратов двух других сторон. Обратите внимание на следующий треугольник ABC, в котором имеем ВС 2 = АВ 2 + АС 2 . Здесь АВ — основание, АС — высота (высота), ВС — гипотенуза.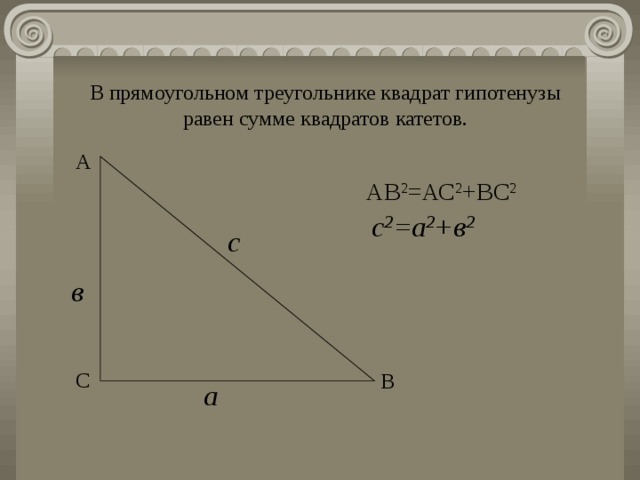 Следует отметить, что гипотенуза является наибольшей стороной прямоугольного треугольника.

Уравнение теоремы Пифагора

Уравнение теоремы Пифагора выражается следующим образом: две другие ноги. Следовательно, любой треугольник с одним углом, равным 90 градусов дает треугольник Пифагора, и уравнение Пифагора может быть применено к треугольнику.

История теоремы Пифагора

Теорема Пифагора была введена греческим математиком Пифагором Самосским. Он был древнегреческим философом, который сформировал группу математиков, которые религиозно работали над числами и жили как монахи. Хотя эту теорему ввел Пифагор, есть свидетельства того, что она существовала и в других цивилизациях за 1000 лет до рождения Пифагора. Самые старые известные свидетельства встречаются между 20 и 16 веками до нашей эры в старовавилонский период.

Теорема Пифагора Формула

Формула теоремы Пифагора утверждает, что в прямоугольном треугольнике ABC квадрат гипотенузы равен сумме квадратов двух других катетов. Если АВ и АС — стороны, а ВС — гипотенуза треугольника, то: ВС 2 = АВ 2 + АС 2 ​. В этом случае АВ — основание, АС — высота или высота, а ВС — гипотенуза.

Другой способ понять формулу теоремы Пифагора — использовать следующий рисунок, который показывает, что площадь квадрата, образованного самой длинной стороной прямоугольного треугольника (гипотенузой), равна сумме площадей квадратов, образованных две другие стороны прямоугольного треугольника.

В прямоугольном треугольнике формула теоремы Пифагора выражается как: треугольник

  • «a» и «b» — две другие ноги.

    • Доказательство теоремы Пифагора

    Теорему Пифагора можно доказать разными способами. Одними из наиболее распространенных и широко используемых методов являются алгебраический метод и метод подобных треугольников. Давайте посмотрим на оба этих метода по отдельности, чтобы понять доказательство этой теоремы.

    Доказательство формулы теоремы Пифагора с использованием алгебраического метода

    Доказательство теоремы Пифагора может быть получено с использованием алгебраического метода.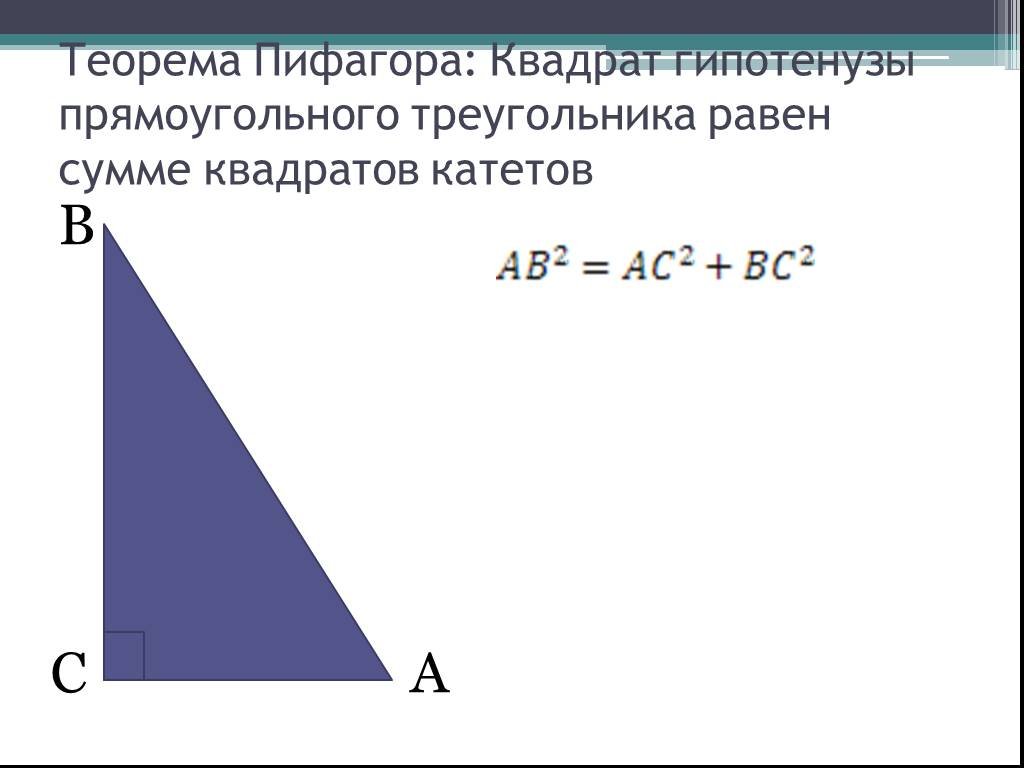

    Например, давайте использовать значения a, b и c, как показано на следующем рисунке, и выполнить шаги, указанные ниже:

    • Шаг 1: Этот метод также известен как «доказательство перестановкой». Возьмем 4 конгруэнтных прямоугольных треугольника со сторонами «а» и «b» и гипотенузой «с». Расположите их так, чтобы гипотенузы всех треугольников образовывали наклонный квадрат. Видно, что в квадрате PQRS длина сторон равна «a + b». Четыре прямоугольных треугольника имеют основание «b», высоту «a» и гипотенузу «c».
    • Шаг 2: 4 треугольника образуют внутренний квадрат WXYZ, как показано, с четырьмя сторонами «с».
    • Шаг 3: Площадь квадрата WXYZ при расположении четырех треугольников равна c
      2       .
    • Шаг 4: Площадь квадрата PQRS со стороной (a + b) = площадь 4 треугольников + площадь квадрата WXYZ со стороной «c». Это означает (a + b) 2 = [4 × 1/2 × (a × b)] + c 2 . Это приводит к a 2 + b 2 + 2ab = 2ab + c 2 . Следовательно, a 2 + b 2 = c 2 . Таким образом, формула теоремы Пифагора доказана.

    Формула теоремы Пифагора Доказательство с использованием подобных треугольников

    Два треугольника называются подобными, если их соответствующие углы имеют одинаковую меру и их соответствующие стороны находятся в одном и том же отношении. Кроме того, если углы имеют одинаковую меру, то, используя закон синусов, мы можем сказать, что соответствующие стороны также будут в том же отношении. Следовательно, соответствующие углы в подобных треугольниках приводят нас к равным отношениям длин сторон.

    Вывод теоремы Пифагора Формула

    Рассмотрим прямоугольный треугольник ABC с прямым углом в точке B. Проведите перпендикуляр BD, пересекающий AC в точке D.

    А (общий)

  • ∠ADB = ∠ABC (оба угла прямые)

    • Таким образом, 4ABD ∼ 4ACB (по критерию подобия AA)

    Аналогично можно доказать 4BCD ∼ △ACB.

    Таким образом, △ABD ∼ △ACB, Следовательно, AD/AB = AB/AC. Мы можем сказать, что AD × AC = AB 2 .

    Аналогично, △BCD ∼ △ACB. Следовательно, CD/BC = BC/AC. Мы также можем сказать, что CD × AC = BC 2 .

    Сложив эти 2 уравнения, мы получим AB 2 + BC 2 = (AD × AC) + (CD × AC)

    AB 2 + BC 2

    =AC(AD +DC)

    7

    7

    7

    7

    7

    AB 2 + BC 2 =AC 2

    Отсюда доказано.

    Теорема Пифагора Треугольники

    Прямоугольные треугольники подчиняются правилу теоремы Пифагора и называются треугольниками по теореме Пифагора. Три стороны такого треугольника в совокупности называются тройками Пифагора. Все треугольники по теореме Пифагора следуют теореме Пифагора, которая гласит, что квадрат гипотенузы равен сумме двух сторон прямоугольного треугольника. Это можно выразить как c 2 = а 2 + б 2 ; где «с» — гипотенуза, а «а» и «b» — катеты треугольника.

    Теорема Пифагора Квадраты

    Согласно теореме Пифагора, площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на двух других сторонах. Эти квадраты известны как квадраты Пифагора.

    Приложения теоремы Пифагора

    Применение теоремы Пифагора можно увидеть в нашей повседневной жизни. Вот некоторые из приложений теоремы Пифагора.

    • Машиностроение и строительство

    Большинство архитекторов используют технику теоремы Пифагора для нахождения неизвестных размеров. Когда известна длина или ширина, очень легко вычислить диаметр конкретного сектора. Он в основном используется в двух измерениях в инженерных областях.

    • Распознавание лиц в камерах наблюдения

    Функция распознавания лиц в камерах безопасности использует концепцию теоремы Пифагора, то есть расстояние между камерой безопасности и местоположением человека отмечается и хорошо проецируется через объектив с использованием концепции.

    • Изделия из дерева и дизайн интерьера

    Концепция Пифагора применяется в дизайне интерьеров и архитектуре домов и зданий.

    • Навигация

    Люди, путешествующие по морю, используют эту технику, чтобы найти кратчайшее расстояние и маршрут, чтобы добраться до нужных им мест.

    ☛ Статьи по теме

    • Формулы прямоугольного треугольника
    • Теорема о катете гипотенузы
    • Подобные треугольники
    • Теорема Пифагора Рабочие листы

    Cuemath — одна из ведущих мировых обучающих платформ по математике, которая предлагает онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.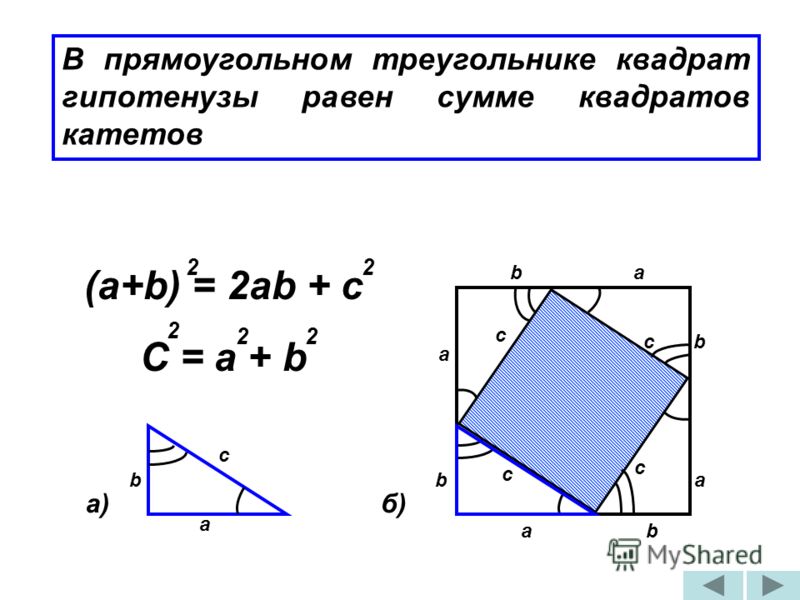

    Часто задаваемые вопросы по теореме Пифагора

    Что такое теорема Пифагора в математике?

    Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Эта теорема может быть выражена как c 2 = a 2 + b 2 ; где «с» — гипотенуза, а «а» и «b» — катеты треугольника. Эти треугольники также известны как треугольники теоремы Пифагора.

    Что такое обратная теорема Пифагора?

    Теорема Пифагора, обратная: если сумма квадратов любых двух сторон треугольника равна квадрату третьей (наибольшей) стороны, то треугольник называется прямоугольным.

    В чем польза формулы теоремы Пифагора?

    Теорема Пифагора работает только для прямоугольных треугольников. Когда известны любые два значения, мы можем применить теорему Пифагора и вычислить неизвестные стороны треугольника. Есть и другие реальные приложения теоремы Пифагора, например, в области навигации, инженерии и архитектуры.

    Какая польза от теоремы Пифагора?

    Теорема Пифагора используется в различных областях. Ниже приведены некоторые из его применений.

    • Архитектура, строительство и судоходство.
    • Для вычисления расстояния между точками на плоскости.
    • Для расчета периметра, площади поверхности, объема геометрических фигур и т.д.

    Можно ли применить формулу теоремы Пифагора к любому треугольнику?

    Нет, теорему Пифагора можно применить только к прямоугольному треугольнику, поскольку теорема Пифагора выражает отношение между сторонами треугольника, где квадрат двух катетов равен квадрату третьей стороны, которая является гипотенузой. .

    Как решить теорему Пифагора?

    Теорему Пифагора можно использовать для нахождения неизвестной стороны прямоугольного треугольника. Например, если два катета прямоугольного треугольника равны 4 единицам и 6 единицам, то гипотенузу (третью сторону) можно рассчитать по формуле c 2 = а 2 + б 2 ; где «с» — гипотенуза, а «а» и «b» — два катета. Подставляя значения в формулу, c 2 = a 2 + b 2 = c 2 = 4 2 + 6 2 = 16 + 36 = √52 = 7,2 единицы.

    Что такое формула теоремы Пифагора?

    Формула теоремы Пифагора выражается как Гипотенуза 2 = Основание 2 + Высота 2 . Это также пишется как c 2 = а 2 + б 2 ; где «с» — гипотенуза, а «а» и «b» — катеты прямоугольного треугольника. Используя формулу теоремы Пифагора, можно вычислить любую неизвестную сторону прямого угла, если известны две другие стороны.

    Почему важна теорема Пифагора?

    Теорема Пифагора важна, потому что она помогает вычислить неизвестную сторону прямоугольного треугольника. У него есть и другие реальные приложения в области архитектуры и инженерии, навигации и так далее.

    Как теорема Пифагора используется в навигации?

    Теорема Пифагора широко используется в аэронавигации и судовой навигации. Теорема Пифагора дает возможность штурману корабля рассчитать расстояние до точки в океане, например, если расстояние между двумя точками задано как 600 км к северу и 800 км к западу, требуемое расстояние можно рассчитать с помощью Пифагора. теорема.

    Когда используется теорема Пифагора?

    Теорема Пифагора используется, когда известны любые две стороны прямоугольного треугольника и необходимо вычислить третью сторону. Например, если перпендикуляр и основание прямоугольного треугольника даны как 12 единиц и 5 единиц соответственно, и нам нужно найти третью сторону (гипотенузу), мы можем вычислить ее, используя теорему, которая говорит, что гипотенуза 2 = перпендикулярно 2 + основание 2 . После подстановки значений в уравнение получаем гипотенузу 2 = 12 2 + 5 2 = 144 + 25 = 169. Итак, гипотенуза = √169 = 13 единиц.

    Какое пифагорейское свойство треугольников?

    Пифагоровость треугольников — еще один термин для теоремы Пифагора. Согласно свойству Пифагора, в прямоугольном треугольнике квадрат гипотенузы всегда равен сумме квадратов двух других сторон. Эта теорема выражается как c 2 = а 2 + б 2 ; где «с» — гипотенуза, а «а» и «b» — катеты треугольника.

    Теорема Пифагора

    Чтобы лучше понять некоторые проблемы, связанные с самолетами и движение необходимо использовать некоторые математические идеи из тригонометрия изучение треугольников. Давайте начнем с некоторых определений и терминологии, которые мы будем использовать на этом слайде. Начнем с прямоугольного треугольника . Прямоугольный треугольник – это трехсторонняя фигура, один из углов которой равен 90 градусов. Угол 90 градусов это называется прямым углом , и именно отсюда прямоугольный треугольник получил свое название. Определим сторону треугольника, противоположную от прямого угла к быть гипотенузой , h . Это самая длинная сторона из трех сторон прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов что означает «растягиваться», так как это самая длинная сторона. Мы собираемся пометить две другие стороны 92

    25 = 9 + 16

    Пифагор обобщил результат на любой прямоугольный треугольник. Есть много разных алгебраические и геометрические доказательства теоремы. Большинство из них начинаются с построение квадратов по эскизу базового прямоугольного треугольника. На фигуре у вверху этой страницы мы показываем квадраты, нарисованные на трех сторонах треугольника. Квадрат – это частный случай прямоугольника, у которого все стороны равны в длину. площадь A прямоугольника есть произведение сторон. Итак, для квадрата со стороной, равной 92 квадрата, нарисованного на стороне b .

    Вот интерактивная программа на Java, которая позволяет вам увидеть, что это отношение площадей верно:

    На этой странице показан интерактивный Java-апплет, демонстрирующий теорему Пифагора.

    Начнем с прямоугольного треугольника, на котором мы построили квадраты с двух сторон, одна красный и один синий. Мы собираемся разбить части этих двух квадратов и переместить их в область серого квадрата на гипотенузе. Мы не потеряем материал во время операция. Итак, если мы можем точно заполнить квадрат на гипотенузе, мы показали, что площади равны. Вы прорабатываете конструкцию, нажимая на кнопку кнопку с надписью «Далее». Вы можете вернуться «Назад» и повторить раздел или вернуться к началу, нажав «Сброс».

    Что он делает? Первый шаг вращает треугольник вниз на синий квадрат. Этот разрезает синий квадрат на три части, два треугольника и красный прямоугольник. Два треугольника точно такого же размера, как исходный треугольник. «Дно» исходного треугольника точно соответствует вертикальная сторона квадрата, потому что стороны квадрата равны. Красный прямоугольник имеет вертикальные стороны, равные основанию исходного треугольника, а его горизонтальные стороны равны разнице между «нижней» стороной и «вертикальная» сторона исходного треугольника. Используя терминологию из рисунка в верхней части этой страницы, размеры красного прямоугольника:

    вертикальная длина = b

    горизонтальная длина = b — a

    Следующим шагом будет перемещение красного прямоугольника рядом с Красной площадью. Прямоугольник выступает из верхней части красного квадрата. и два треугольника остаются в синем квадрате. Следующим шагом является перемещение одного из синие треугольники вертикально в квадрат гипотенузы. Он подходит точно вдоль стороны в квадрат гипотенузы, так как стороны квадрата равны. Следующим шагом является перемещение другой синий треугольник в квадрат гипотенузы. (Мы на полпути!) Следующий шаг состоит в том, чтобы сдвинуть форму исходного треугольника влево в красную область. Треугольник разрезает красную область на три части, два треугольника и маленький желтый квадрат. Исходный треугольник точно вписывается в эту область по двум причинам; вертикальные стороны одинаковы, а горизонтальная сторона красной области равна длина красного квадрата плюс горизонтальная длина красного прямоугольника, которую мы взолнованный.

    Related Posts

    Leave A Comment