Мгновенная и средняя скорость | Физика
1. Мгновенная скорость
В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.
На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.
Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.
Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).
Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).
Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы. А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.
Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.
Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.
Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.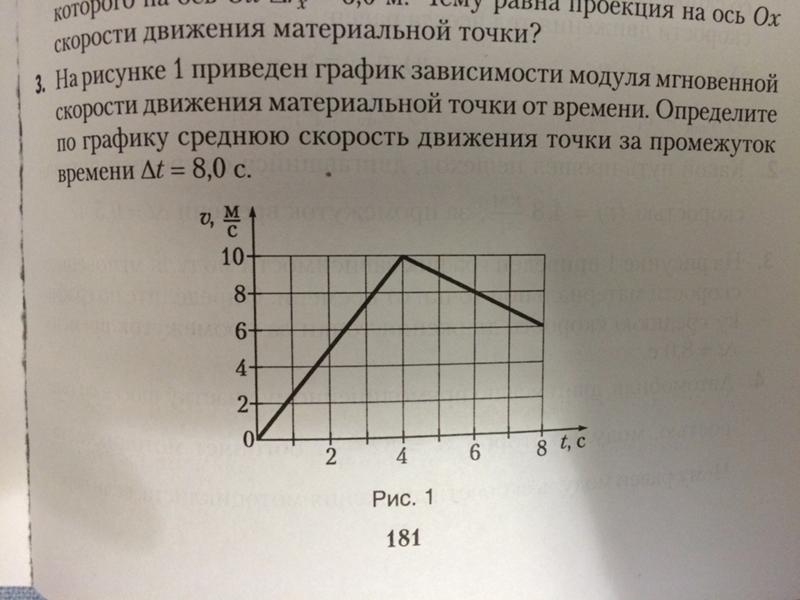
В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!
Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.
? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.
Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).
Как найти мгновенную скорость по графику зависимости координаты от времени
На рисунке 4.4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.
Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.
Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).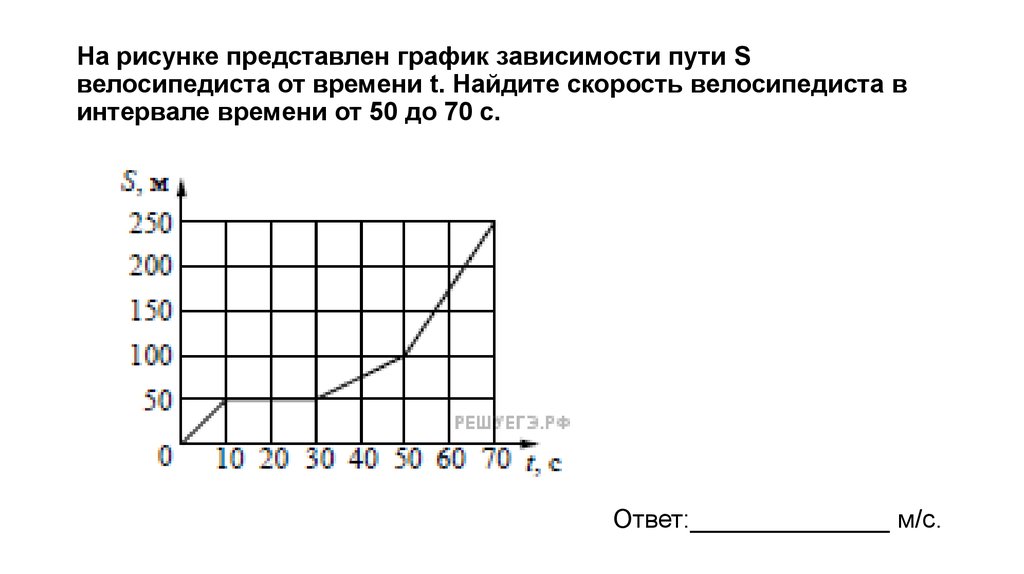
Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.
На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).
Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.
2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?
Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).
Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела. (Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.
(Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.
? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.
2. Средняя скорость
Во многих задачах используют среднюю скорость, связанную с пройденным путем:
vср = l/t. (1)
Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)
Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.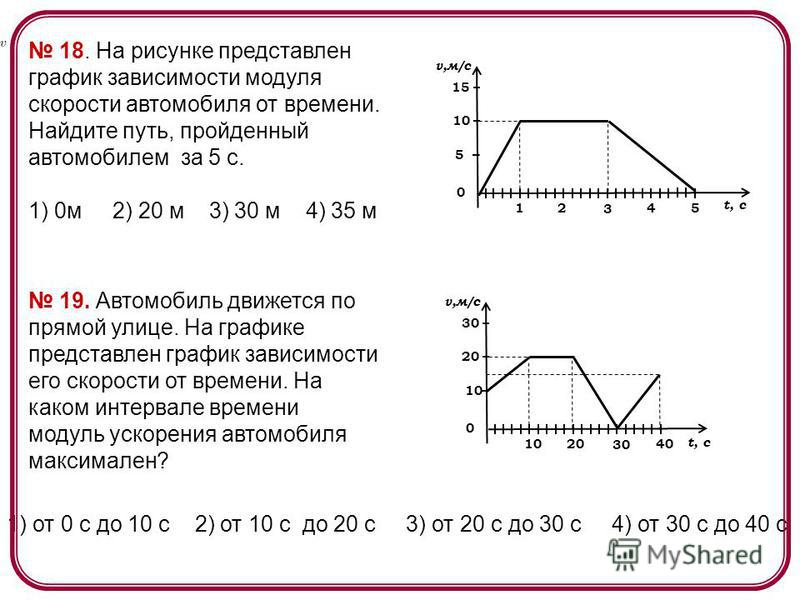
? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?
Средняя скорость на двух участках движения
Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:
vср = (l1 + l2)/(t1 + t2), (2)
где l1 и t1 – путь и время для первого участка, а l2 и t2 – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.
? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.
В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел.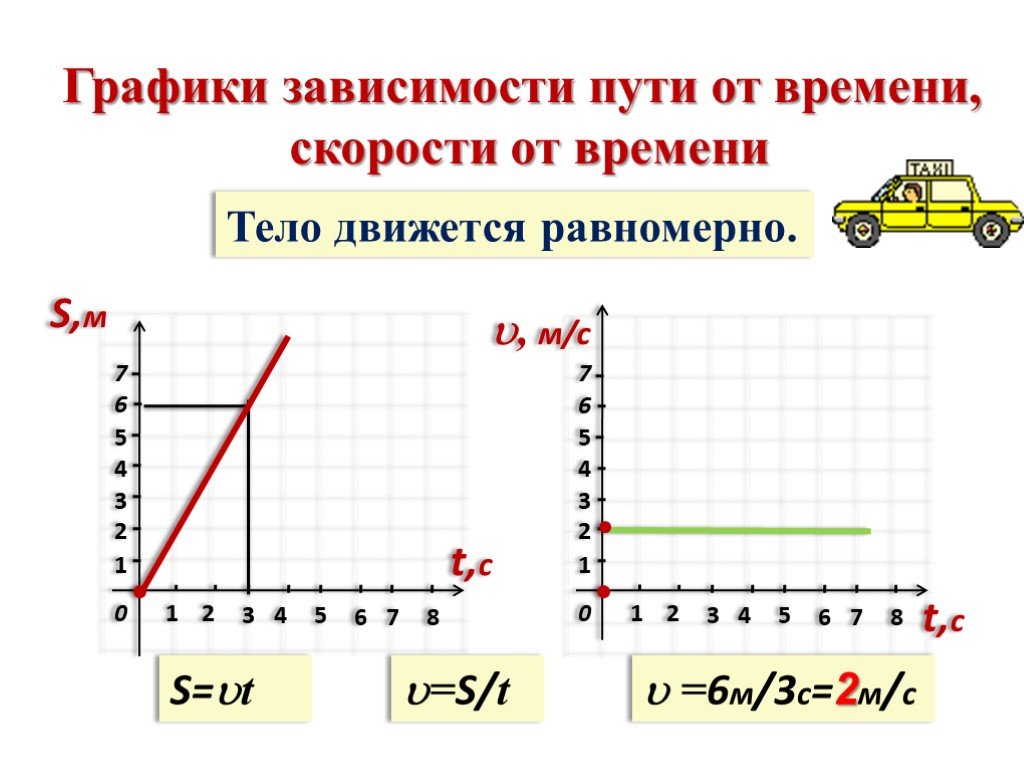 Всегда ли это справедливо? Рассмотрим следующий пример.
Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.
? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.
Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?
? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.
Обобщим рассмотренные выше ситуации.
Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.
Пусть первую половину всего времени движения тело двигалось со скоростью v1, а вторую половину – со скоростью v2.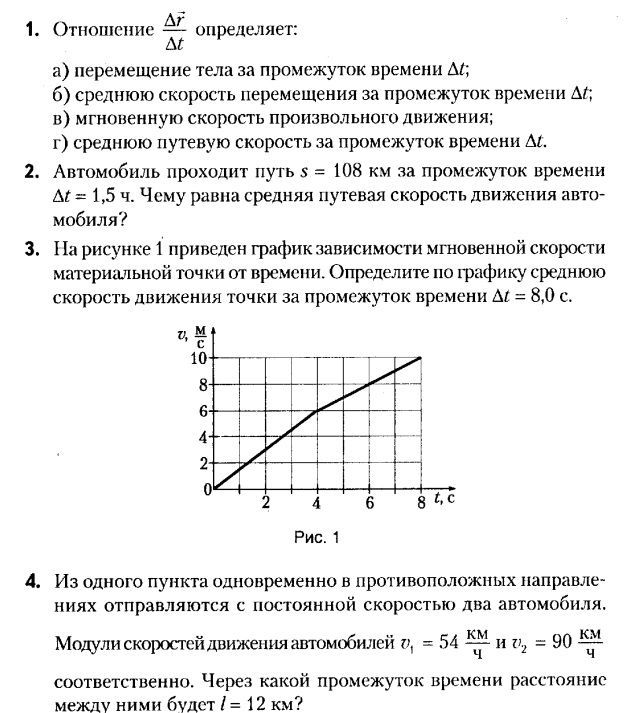 Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?
Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?
Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.
Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l1 и l2.
? 8. Выразите через v1, v2 и t:
a) l1 и l2; б) l; в) среднюю скорость.
Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.
Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.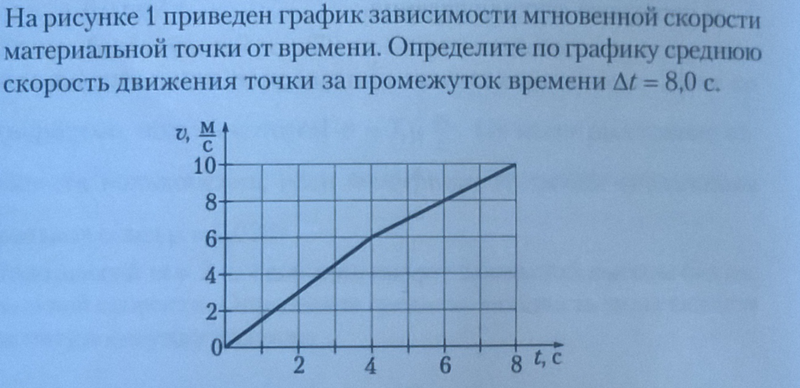
Пусть теперь первую половину всего пути тело двигалось со скоростью v1, а вторую половину – со скоростью v2. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t1 и t2.
? 9. Выразите через v1, v2 и l:
а) t1 и t2; б) t; в) среднюю скорость.
Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.
? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.
? 11. На первом участке пути тело двигалось со скоростью v1, а на втором – со скоростью v2. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v1 и v2?
Дополнительные вопросы и задания
12. Одну треть всего времени движения поезд ехал со скоростью v1, а оставшееся время – со скоростью v2.
а) Выразите пройденный поездом путь через v1, v2 и все время движения t.
б) Выразите среднюю скорость поезда через v1 и v2.
в) Найдите числовое значение средней скорости при v1 = 60 км/ч, v2 = 90 км/ч.
13. Автомобиль ехал три четверти всего пути со скоростью v1, а оставшийся участок пути – со скоростью v2.
а) Выразите все время движения автомобиля через v1, v2 и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v1 и v2.
в) Найдите числовое значение средней скорости при v1 = 80 км/ч, v2 = 100 км/ч.
14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?
15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.
16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t2.
а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.
б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за все время движения.
Средняя скорость-Скоростьв физике
| На главную
Теория
Задачи
Учёные
Интересные статьи
Шкала скоростей
Средняя скорость – не
самое сложное понятие в кинематике. Однако для многих учащихся простота этого
понятия оказывается обманчивой. 2. Как правильно рассчитать среднюю скорость тела, которое начало движение в пункте А, окончило его в пункте В, но по дороге из А в В поворачивало назад (может быть ни один раз!), а затем вновь продолжало движение к пункту В? В определении указано “…равная отношению пути, пройденного телом…”, значит, при расчете средней скорости определяющим является не расстояние между точками (пунктами) начала и окончания движения, а реальный путь, которое прошло тело. Пример 1. Найти среднюю скорость человека на пути от дома до
станции, расстояние между которыми l =800 м, если, пройдя четверть пути,
он вернулся домой (например, проверить, хорошо ли закрыта дверь) и через мин
продолжил путь на станцию. Решение. Началом движения человека, конечно, следует считать момент времени, когда он первый раз вышел из дома. Четверть пути составляет расстояние l1/4 =l : 4 =800 : 4 =200 м. При возвращении домой человек прошел путь 2l1/4 =400 м. После этого он вышел из дома второй раз и дошел до станции. Путь, пройденный человеком с начала движения, составит: S = 2l1/4 + l =400 + 800 =1200 м =1,2 км. Время t, которое затрачено на преодоление этого пути, складывается из времени пребывания дома и времени Т, в течение которого человек двигался по маршруту “из дома–к дому–на станцию”. Поскольку скорость движения человека постоянна ( 1,2 км : 4
км/ч =0,3 ч =18 мин. t =+ T = 2 + 18 =20 мин =1/3 ч. 1,2 км : ч =3,6 км/ч. Ответ: vср =3,6 км/ч. Среднюю скорость движения человек оценивает довольно часто, но судит о ней, глядя на часы. Торопящийся человек соотносит расстояние, которое ещё осталось преодолеть, и время, отпущенное ему на это, после чего делает вывод (хотя числовое значение средней скорости вряд ли при этом находится): “Ну, теперь можно идти помедленнее” или “Придется еще поднажать, иначе не успею”. Вернемся к рассмотренному примеру. Будем считать, что скорость v0 =4 км/ч выбрана человеком не случайно. проходя от дома до станции ежедневно, человек замечает, что расстояние l ==800 м, он проходит за время t0 =12 мин =0,2 ч: = 0,8 км : 0,2 ч =4 км/ч. По существу, это – средняя скорость,
поскольку доподлинно неизвестно, с какой скоростью человек идет в каждый момент
времени. Пример 2. Человек обычно доходит из дома до станции за время t0 =12 мин, проходя расстояние 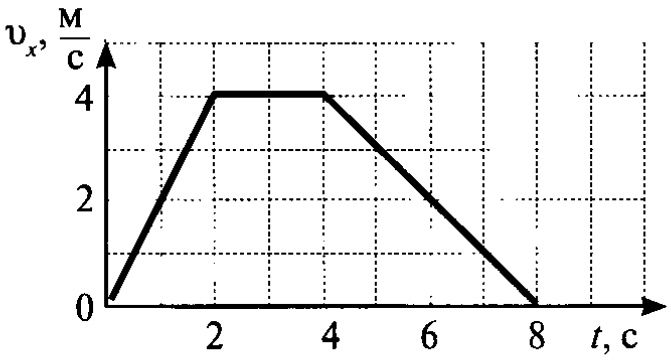 Решение. 1. Обычно человек двигается со скоростью м/мин =4 км/ч. 2. Пройдя с такой скоростью четверть пути, он затратил время : 4 км/ч =0,05 ч =3 мин. Значит, в его распоряжении осталось время 3. За время Т2 человек должен
преодолеть путь до дома, а затем снова до станции: ч, то есть со скоростью, не меньшей, чем 1 км : ч =км/ч =км/ч » 8,6 км/ч. Проверьте, что добежав до дома со скоростью км/ч, а
затем шагая со скоростью v2 =2v0 =8 км/ч,
человек придет на станцию вовремя. м/мин =100 м/мин =6 км/ч. Найденное значение vср в полтора раза выше, чем v0, и показывает, с какой начальной скоростью следует выходить человеку из дома, если он забывчив. На рис.1 показан график зависимости скорости человека от времени для примера 2 в случае, если человек бежит домой со скоростью v1 Подсчитаем среднее арифметическое для значений скорости v0, v1, v2: км/ч. Это значение не равно значению средней
скорости vср. Убедитесь в этом и не совершайте в дальнейшем
распространенную ошибку: не пытайтесь искать среднюю скорость как среднее
арифметическое значение (оно не имеет физического смысла!). Пример 3. Автомобиль проезжает первую треть пути равномерно со
скоростью v1 =108 км/ч, а остальные две трети пути – со
скоростью v2 =72 км/ч. Найти среднюю скорость автомобиля. км/ч. 1. Найдем время t1 движения
со скоростью v1, полагая, что весь путь равен L [км].
Из условия ясно, что 2. Время t 3. Итак, время на продолжение пути L составляет 4. По определению средней скорости км/ч. Ответ: средняя скорость vср =81 км/ч. Значение средней скорости совпадает со
средним арифметическим значением скорости только в одном частном случае,
когда тело двигается с различными скоростями так, что между последовательными
моментами изменения (переключения) скорости проходит одинаковое время Т. S =v1t1 + v2t2 + v3t3 + … +vntn =T(v1 + v2 + v3 + … +vn). Время t, за которое пройден путь, составляет t =t1 + t2 + t3 + … + tn =T*n. По определению: . Не запрещено для этого частного случая
двигаться со скоростью v0=0, т. Пример 4. Вертолет пролетает без остановок равномерно и прямолинейно над пунктами А, В, С (в указанном порядке) и возвращается в А. Пункты А, В, С являются как бы вершинами треугольника. Расстояние между А и В составляет LAB =150 км, между В и С LBC =200 км, между С и А LCA =100 км. Время, за которое вертолет пролетает от одного пункта до другого, составляет полчаса. Найти среднюю скорость движения вертолета на маршруте АВСА. Изменится ли средняя скорость, если LCA =200 км и всё расстояние вертолет преодолеет за 1 ч? Решение. 1. Находим скорость движения вертолета на каждом участке: км/ч; км/ч; км/ч. 2. Поскольку t =0,5 ч одинаково для всех участков движения, то км/ч. 3. Если расстояние LСА =200 км и tCA=1ч, то не меняется vCA=200 км/ч. Но в этом случае нельзя подсчитывать (для простоты) среднюю скорость как среднее арифметическое, так как tCА ? tAB ==tBC. км/ч. Ответ: 1) vcp1 =300 км/ч; 2) vcp2 =275 км/ч. Контрольные задания на эту тему
|
Скорость против скорости
Как расстояние и перемещение имеют совершенно разные значения (несмотря на их сходство), так и скорость и скорость. Скорость — это скалярная величина, которая относится к тому, «как быстро движется объект». Скорость можно рассматривать как скорость, с которой объект преодолевает расстояние. Быстро движущийся объект имеет высокую скорость и преодолевает относительно большое расстояние за короткий промежуток времени. Сравните это с медленно движущимся объектом с низкой скоростью; он покрывает относительно небольшое расстояние за то же время. Объект без движения имеет нулевую скорость.
Объект без движения имеет нулевую скорость.
Скорость как векторная величина
Скорость — это векторная величина, которая относится к «скорости, с которой объект меняет свое положение». Представьте себе человека, который быстро движется — один шаг вперед и один шаг назад — и всегда возвращается в исходное исходное положение. Хотя это может привести к безумной активности, это приведет к нулевой скорости. Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения. Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости. Если человек в движении хочет максимизировать свою скорость, то этот человек должен приложить все усилия, чтобы максимизировать величину, на которую он смещен от своего исходного положения. Каждый шаг должен быть направлен на то, чтобы продвинуть этого человека дальше от того, с чего он начал. Наверняка человек ни в коем случае не должен менять направления и начинать возвращаться в исходное положение.
Скорость является векторной величиной. Таким образом, скорость знает направление . При оценке скорости объекта необходимо следить за направлением. Было бы недостаточно сказать, что объект имеет скорость 55 миль в час. Необходимо включить информацию о направлении, чтобы полностью описать скорость объекта. Например, вы должны описать скорость объекта как 55 миль/ч, восток . Это одно из существенных различий между скоростью и скоростью. Скорость является скалярной величиной и не следить за направлением ; скорость является векторной величиной и знает направление .
Определение направления вектора скорости
Задача описания направления вектора скорости проста. Направление вектора скорости совпадает с направлением движения объекта. Не имеет значения, ускоряется объект или замедляется. Если объект движется вправо, то его скорость описывается как направленная вправо. Если объект движется вниз, то его скорость описывается как нисходящая. Таким образом, самолет, летящий на запад со скоростью 300 миль/час, имеет скорость 300 миль/час на запад. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент времени — это просто значение скорости с направлением.
Таким образом, самолет, летящий на запад со скоростью 300 миль/час, имеет скорость 300 миль/час на запад. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент времени — это просто значение скорости с направлением.
Расчет средней скорости и средней скорости
Когда объект движется, его скорость часто меняется. Например, во время обычной поездки в школу происходит много изменений скорости. Вместо того, чтобы измеритель скорости поддерживал устойчивые показания, стрелка постоянно движется вверх и вниз, отражая остановку и запуск, ускорение и замедление. В один момент машина может двигаться со скоростью 50 миль в час, а в другой момент она может остановиться (т. е. 0 миль в час). Тем не менее, во время поездки в школу человек может проехать в среднем 32 мили в час. Среднюю скорость во время всего движения можно рассматривать как среднее значение всех показаний спидометра.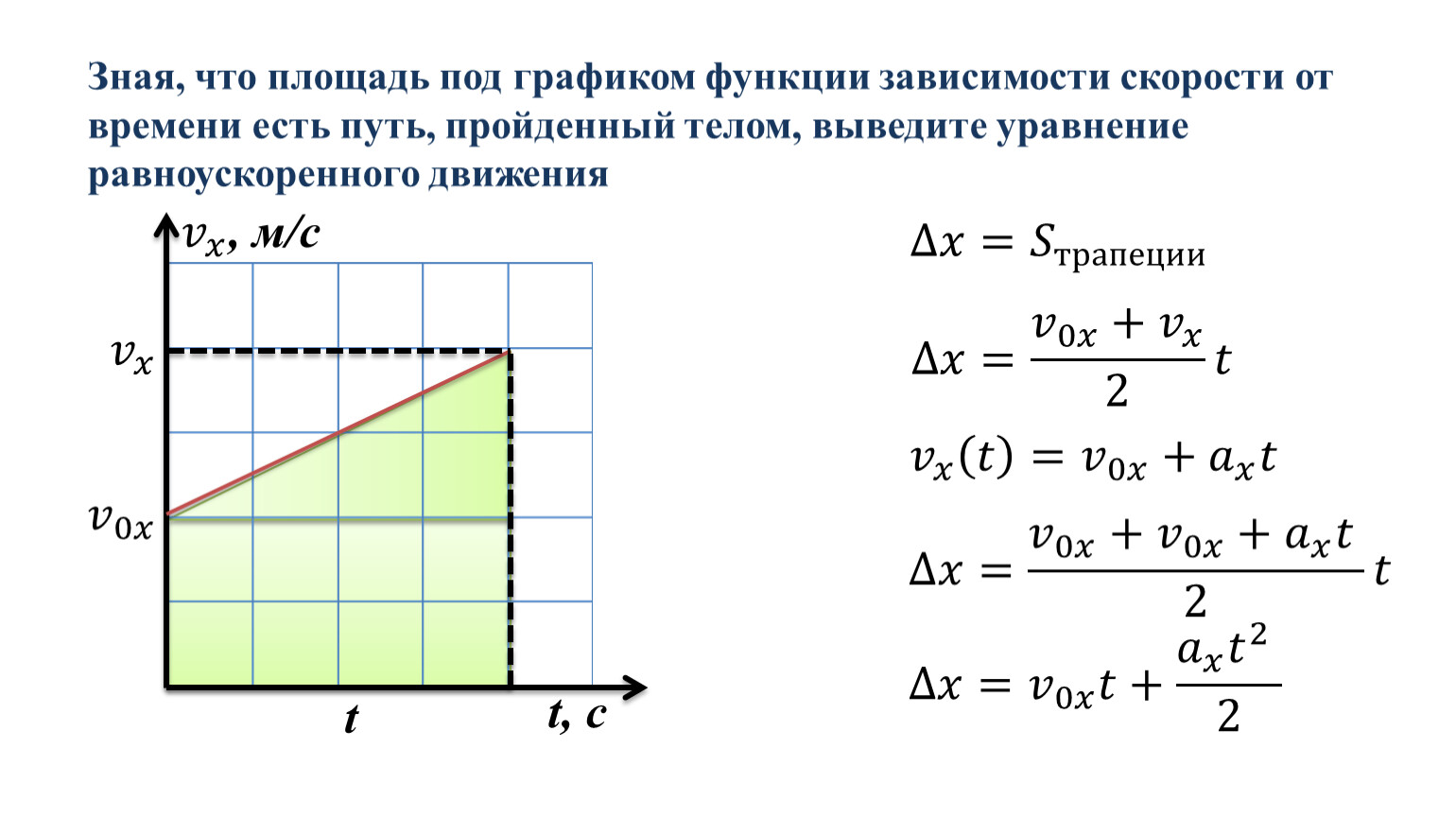 Если бы показания спидометра можно было собирать с интервалом в 1 секунду (или с интервалом в 0,1 секунды, или…), а затем усреднять вместе, можно было бы определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть короткий путь. Читай дальше.
Если бы показания спидометра можно было собирать с интервалом в 1 секунду (или с интервалом в 0,1 секунды, или…), а затем усреднять вместе, можно было бы определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть короткий путь. Читай дальше.
Средняя скорость во время движения часто рассчитывается по следующей формуле:
Средняя скорость, напротив, часто рассчитывается по этой формуле
Давайте начнем реализацию нашего понимания этих формул со следующей задачи:
В: Во время отпуска Лиза Карр преодолела в общей сложности 440 миль. Ее поездка заняла 8 часов. Какова была ее средняя скорость?
Чтобы вычислить ее среднюю скорость, мы просто делим пройденное расстояние на время в пути.
Это было просто! Лиза Карр в среднем разгонялась до 55 миль в час. Возможно, она не двигалась с постоянной скоростью 55 миль в час. Она, несомненно, была остановлена в какой-то момент времени (возможно, для перерыва в ванной или на обед), и, вероятно, в другие моменты времени она двигалась со скоростью 65 миль в час. Тем не менее, она развивала среднюю скорость 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.
Тем не менее, она развивала среднюю скорость 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.
Средняя скорость по сравнению с мгновенной скоростью
Поскольку движущийся объект часто меняет свою скорость во время движения, принято различать среднюю скорость и мгновенную скорость. Различие заключается в следующем.
- Мгновенная скорость — скорость в любой данный момент времени.
- Средняя скорость — среднее значение всех мгновенных скоростей; находится просто по соотношению расстояние/время.
Вы можете думать о мгновенной скорости как о скорости, которую показывает спидометр в любой данный момент времени, а о средней скорости как о среднем значении всех показаний спидометра в ходе поездки. Поскольку задача усреднения показаний спидометра была бы достаточно сложной (а может быть, и опасной), среднюю скорость чаще рассчитывают как отношение расстояния к времени.
Движущиеся объекты не всегда движутся с неустойчивой и меняющейся скоростью. Иногда объект будет двигаться с постоянной скоростью с постоянной скоростью. То есть объект будет преодолевать одно и то же расстояние каждый регулярный интервал времени. Например, бегун по пересеченной местности может бежать с постоянной скоростью 6 м/с по прямой в течение нескольких минут. Если ее скорость постоянна, то расстояние, пройденное за каждую секунду, одинаково. Бегун будет преодолевать расстояние 6 метров каждую секунду. Если бы мы могли измерять ее положение (расстояние от произвольной начальной точки) каждую секунду, то заметили бы, что положение меняется на 6 метров каждую секунду. Это будет резко контрастировать с объектом, который меняет свою скорость. Объект с изменяющейся скоростью будет перемещаться на разное расстояние каждую секунду. В приведенных ниже таблицах данных изображены объекты с постоянной и изменяющейся скоростью.
Теперь давайте снова рассмотрим движение этого учителя физики. Учитель физики проходит 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север. Все движение длилось 24 секунды. Определить среднюю скорость и среднюю скорость.
Учитель физики проходит 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север. Все движение длилось 24 секунды. Определить среднюю скорость и среднюю скорость.
Учитель физики прошел 12 метров за 24 секунды; таким образом, ее средняя скорость составила 0,50 м/с. Однако, поскольку ее перемещение равно 0 м, ее средняя скорость равна 0 м/с. Помните, что смещение относится к изменению положения, а скорость зависит от этого изменения положения. В этом случае движения учителя происходит изменение положения на 0 метров и, следовательно, средняя скорость равна 0 м/с.
Вот еще один пример, аналогичный тому, что мы видели ранее при обсуждении расстояния и смещения. На приведенной ниже диаграмме показано положение лыжника в разное время. В каждый из указанных моментов времени лыжник поворачивается и меняет направление движения. Другими словами, лыжник движется от A к B, затем C и D.
Используйте диаграмму, чтобы определить среднюю скорость и среднюю скорость лыжника в течение этих трех минут. Когда закончите, нажмите кнопку, чтобы просмотреть ответ.
Когда закончите, нажмите кнопку, чтобы просмотреть ответ.
В качестве последнего примера рассмотрим футбольного тренера, расхаживающего взад-вперед вдоль боковой линии. На приведенной ниже диаграмме показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в обратном направлении. Другими словами, тренер перемещается из позиции A в B, затем в C и затем в D.
Какова средняя скорость и средняя скорость тренера? Когда закончите, нажмите кнопку, чтобы просмотреть ответ.
В заключение, скорость и скорость являются кинематическими величинами, которые имеют совершенно разные определения. Скорость, будучи скалярной величиной, представляет собой скорость, с которой объект преодолевает расстояние. Средняя скорость — это расстояние (скалярная величина) за отношение времени. Скорость не знает направления . С другой стороны, скорость — векторная величина; это с учетом направления . Скорость – это скорость изменения положения. Средняя скорость — это смещение или изменение положения (векторная величина) за отношение времени.
Скорость – это скорость изменения положения. Средняя скорость — это смещение или изменение положения (векторная величина) за отношение времени.
Мы хотели бы предложить…
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактива Name That Motion Interactive. Он находится в разделе «Интерактивная физика» и позволяет учащемуся применять понятия скорости, скорости и ускорения.
Посетите назовите это движение.
Следующий раздел:
Перейти к следующему уроку:
2.3 Время, скорость и скорость – Физика колледжа
Резюме
- Объясните взаимосвязь между мгновенной скоростью, средней скоростью, мгновенной скоростью, средней скоростью, перемещением и временем.

- Вычислить скорость и скорость, зная начальное положение, начальное положение, конечное положение и конечное время.
- Построить график зависимости скорости от времени по графику зависимости положения от времени.
- Интерпретация графика зависимости скорости от времени.
Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как «Сколько времени занимает пеший забег?» и «Какова была скорость бегуна?» нельзя ответить без понимания других понятий. В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.
Как обсуждалось в Главе 1.2 Физические величины и единицы измерения, наиболее фундаментальные физические величины определяются тем, как они измеряются. Так обстоит дело со временем. Каждое измерение времени связано с измерением изменения некоторой физической величины. Это может быть цифра на цифровых часах, сердцебиение или положение Солнца на небе. В физике определение времени простое: время равно изменению или интервалу, в течение которого происходит изменение. Невозможно узнать, что время прошло, если что-то не изменится.
Это может быть цифра на цифровых часах, сердцебиение или положение Солнца на небе. В физике определение времени простое: время равно изменению или интервалу, в течение которого происходит изменение. Невозможно узнать, что время прошло, если что-то не изменится.
Количество времени или изменения калибруется путем сравнения со стандартом. Единицей времени в СИ является секунда, сокращенно с. Мы могли бы, например, заметить, что некий маятник совершает полный оборот каждые 0,75 с. Затем мы могли бы использовать маятник для измерения времени, считая его колебания или, конечно, подключив маятник к часовому механизму, который регистрирует время на циферблате. Это позволяет нам не только измерять количество времени, но и определять последовательность событий.
Как время связано с движением? Обычно нас интересует время, затраченное на определенное движение, например, сколько времени требуется пассажиру самолета, чтобы добраться от своего места до задней части самолета.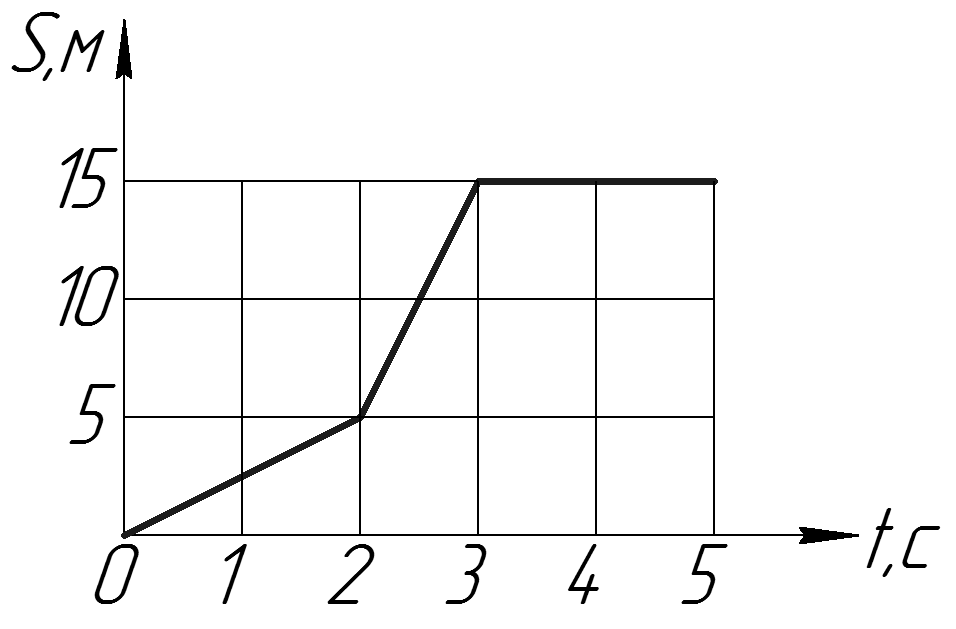 Чтобы найти прошедшее время, мы отмечаем время в начале и в конце движения и вычитаем два. Например, лекция может начаться в 11 часов утра. и закончить в 11:50, так что прошедшее время будет 50 мин. Прошедшее время [латекс]\жирныйсимвол{\Delta{t}}[/латекс] — разница между временем окончания и временем начала,
Чтобы найти прошедшее время, мы отмечаем время в начале и в конце движения и вычитаем два. Например, лекция может начаться в 11 часов утра. и закончить в 11:50, так что прошедшее время будет 50 мин. Прошедшее время [латекс]\жирныйсимвол{\Delta{t}}[/латекс] — разница между временем окончания и временем начала,
[латекс]\boldsymbol{\Delta{t}=t_f-t_0}[/латекс],
, где[latex]\boldsymbol{\Delta{t}}[/latex] — изменение времени или прошедшее время, [latex]\boldsymbol{t_f}[/latex] — время в конце движения, а [latex]\boldsymbol{t_0}[/latex] — время начала движения. (Как обычно, дельта-символ [латекс]\жирныйсимвол{\Дельта}[/латекс] означает изменение величины, следующей за ним.)
Жизнь проще, если время начала[latex]\boldsymbol{t_0}[/latex]принято равным нулю, как при использовании секундомера. Если бы мы использовали секундомер, он просто показывал бы ноль в начале лекции и 50 минут в конце. Если[латекс]\boldsymbol{t_0=0}[/латекс], то[латекс]\жирныйсимвол{\Delta{t}=t_f\equiv{t}}[/латекс].
В этом тексте для простоты
- движение начинается в момент времени, равный нулю[latex]\boldsymbol{(t_0=0)}[/latex]
- символ t используется для прошедшего времени, если не указано иное[latex]\boldsymbol{(\Delta{x}=t_f\equiv{t})}[/latex]
Ваше представление о скорости, вероятно, совпадает с ее научным определением. Вы знаете, что если у вас есть большое перемещение за небольшой промежуток времени, у вас будет большая скорость, и эта скорость имеет единицы измерения расстояния, деленные на время, такие как мили в час или километры в час.
СРЕДНЯЯ СКОРОСТЬ
Средняя скорость равна смещению (изменению положения), деленному на время движения ,
[латекс]\boldsymbol{\bar{v}=}[/latex][латекс]\boldsymbol{\frac {\Delta{x}}{\Delta{t}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{x_f-x_0}{t_f-t_0}} [/латекс],
, где[латекс]\жирныйсимвол{\бар{v}}[/латекс]является средней (обозначенной чертой над v) скоростью,[латекс]\жирныйсимвол{\Дельта{х}}[/латекс ] — изменение положения (или смещения), а [latex]\boldsymbol{x_f}[/latex]и[latex]\boldsymbol{x_0}[/latex] — конечная и начальная позиции в момент времени[latex]\boldsymbol {t_f}[/latex] и [latex]\boldsymbol{t_0}[/latex] соответственно. Если начальное время[latex]\boldsymbol{t_0}[/latex]принято равным нулю, то средняя скорость равна просто
Если начальное время[latex]\boldsymbol{t_0}[/latex]принято равным нулю, то средняя скорость равна просто
[латекс]\boldsymbol{\bar{v}=}[/латекс][латекс]\boldsymbol{\frac{\Delta{x}}{t}}[/латекс].
Обратите внимание, что это определение указывает, что скорость является вектором, потому что смещение является вектором . Она имеет как величину, так и направление. Единицей скорости в СИ является метр в секунду или м/с, но широко используются многие другие единицы, такие как км/ч, мили/ч (также пишется как миль/ч) и см/с. Предположим, например, что пассажиру самолета потребовалось 5 секунд, чтобы переместиться на -4 м (знак минус указывает, что перемещение происходит в направлении задней части самолета). Его средняя скорость будет
[латекс]\boldsymbol{\bar{v}=}[/латекс][латекс]\boldsymbol{\frac{\Delta{x}}{t}}[/латекс][латекс]\boldsymbol{=}[ /латекс][латекс]\boldsymbol{\frac{-4\textbf{м}}{5\textbf{s}}}[/латекс][латекс]\boldsymbol{=-0,8\:м/с}[/ латекс]
Знак минус указывает, что средняя скорость также направлена к задней части самолета.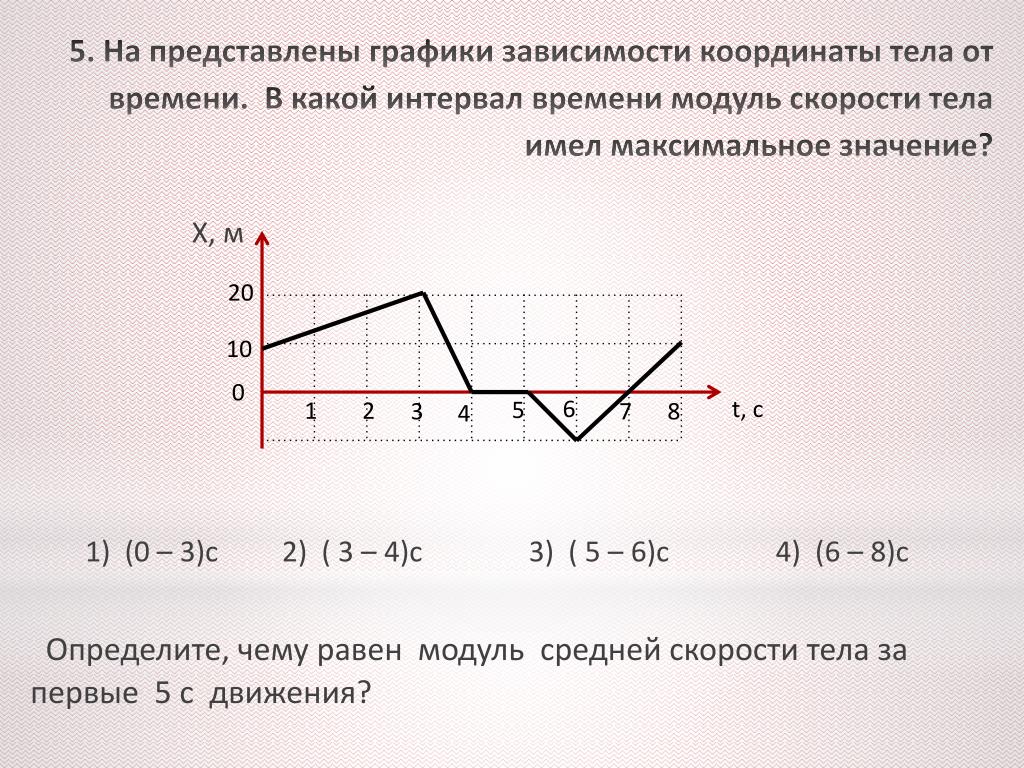
Однако средняя скорость объекта ничего не говорит нам о том, что происходит с ним между начальной и конечной точками. Например, по средней скорости мы не можем сказать, остановился ли пассажир самолета на мгновение или дал задний ход перед тем, как подойти к задней части самолета. Чтобы получить больше деталей, мы должны рассмотреть меньшие отрезки пути за меньшие промежутки времени.
Рисунок 2. Более подробная запись пассажира самолета, направляющегося к задней части самолета, показывающая небольшие сегменты его полета. Чем меньше временных интервалов, учитываемых в движении, тем детальнее информация. Когда мы доводим этот процесс до его логического завершения, остается бесконечно малый интервал. За такой интервал средняя скорость становится мгновенной скоростью или скоростью в конкретный момент времени . Автомобильный спидометр, например, показывает величину (но не направление) мгновенной скорости автомобиля. (Полиция выдает билеты на основе мгновенной скорости, но при расчете времени, которое потребуется, чтобы добраться из одного места в другое во время дорожного путешествия, вам необходимо использовать среднюю скорость.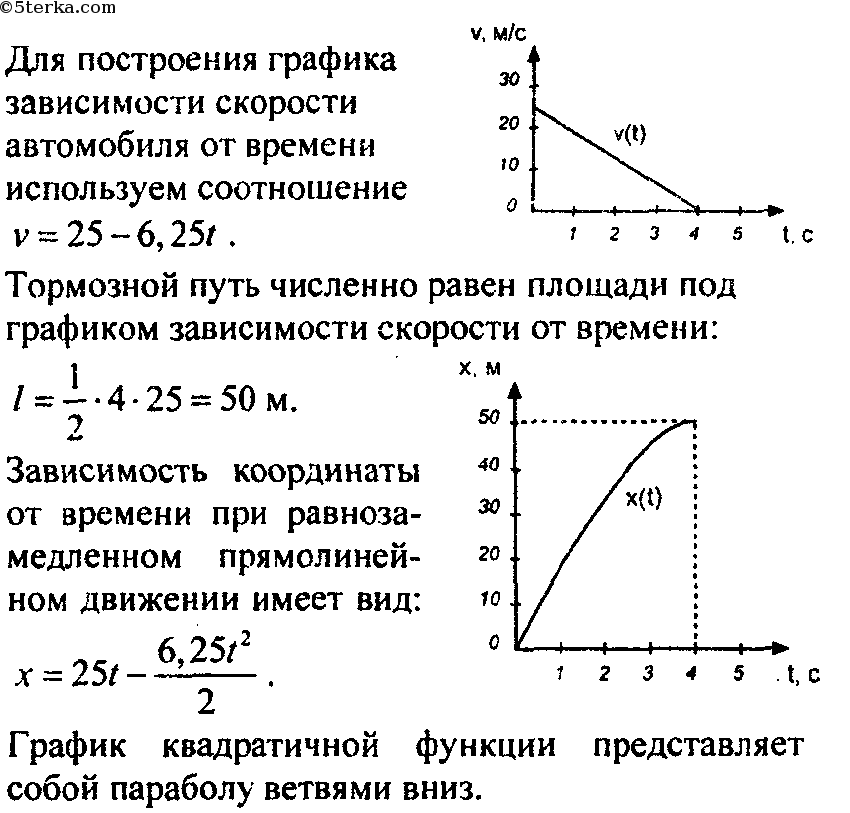 ) Мгновенная скорость [latex]\boldsymbol{v}[ /latex] — средняя скорость в конкретный момент времени (или за бесконечно малый интервал времени).
) Мгновенная скорость [latex]\boldsymbol{v}[ /latex] — средняя скорость в конкретный момент времени (или за бесконечно малый интервал времени).
Математически, нахождение мгновенной скорости,[latex]\boldsymbol{v}[/latex], в конкретный момент времени[latex]\boldsymbol{t}[/latex]может потребовать принятия предела, вычислительной операции, выходящей за рамки этого текст. Однако во многих случаях мы можем найти точные значения мгновенной скорости без вычислений.
В повседневном языке большинство людей используют термины «скорость» и «скорость» как синонимы. Однако в физике они не имеют одинакового значения и представляют собой разные понятия. Одним из основных отличий является то, что скорость не имеет направления. Таким образом, скорость является скаляром . Точно так же, как нам нужно различать мгновенную скорость и среднюю скорость, нам также необходимо различать мгновенную скорость и среднюю скорость.
Мгновенная скорость — величина мгновенной скорости. Например, предположим, что пассажир самолета в какой-то момент имел мгновенную скорость -3,0 м/с (минус означает направление к задней части самолета). При этом его мгновенная скорость была 3,0 м/с. Или предположим, что в какой-то момент во время похода по магазинам ваша мгновенная скорость составляет 40 км/ч строго на север. Ваша мгновенная скорость в этот момент будет 40 км/ч — та же величина, но без указания направления. Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, деленное на прошедшее время.
Например, предположим, что пассажир самолета в какой-то момент имел мгновенную скорость -3,0 м/с (минус означает направление к задней части самолета). При этом его мгновенная скорость была 3,0 м/с. Или предположим, что в какой-то момент во время похода по магазинам ваша мгновенная скорость составляет 40 км/ч строго на север. Ваша мгновенная скорость в этот момент будет 40 км/ч — та же величина, но без указания направления. Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, деленное на прошедшее время.
Мы заметили, что пройденное расстояние может быть больше, чем перемещение. Таким образом, средняя скорость может быть больше, чем средняя скорость, которая равна смещению, деленному на время. Например, если вы едете в магазин и через полчаса возвращаетесь домой, а одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км/ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение за кругосветное путешествие равно нулю. (Перемещение — это изменение положения и, таким образом, равно нулю для кругового рейса.) Таким образом, средняя скорость равна не просто величина средней скорости.
(Перемещение — это изменение положения и, таким образом, равно нулю для кругового рейса.) Таким образом, средняя скорость равна не просто величина средней скорости.
Другой способ визуализации движения объекта — использование графика. График зависимости положения или скорости от времени может быть очень полезен. Например, для этой поездки в магазин графики положения, скорости и зависимости скорости от времени показаны на рис. 4. (Обратите внимание, что эти графики изображают очень упрощенную модель поездки. Мы предполагаем, что скорость постоянна во время поездки, что нереально, учитывая, что мы, вероятно, остановимся у магазина. Но для простоты мы будем моделировать его без остановок или изменения скорости. Мы также предполагаем, что маршрут между магазином и домом — совершенно прямая линия.)
Мы также предполагаем, что маршрут между магазином и домом — совершенно прямая линия.)
УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: ИССЛЕДОВАНИЕ ДЛЯ ДОМА — ПОЛУЧЕНИЕ ЧУВСТВА СКОРОСТИ
Если вы провели много времени за рулем, вы, вероятно, хорошо чувствуете скорость от 10 до 70 миль в час. Но что это в метрах в секунду? Что мы имеем в виду, когда говорим, что что-то движется со скоростью 10 м/с? Чтобы лучше понять, что на самом деле означают эти значения, сделайте несколько наблюдений и расчетов самостоятельно:
- рассчитайте типичную скорость автомобиля в метрах в секунду
- оценивайте скорость бега трусцой и ходьбы, измеряя время самостоятельно; конвертировать измерения как в м/с, так и в мили/ч
- определить скорость муравья, улитки или падающего листа
- Время измеряется в единицах изменения, и его единицей СИ является секунда (с).
 Прошедшее время для события
Прошедшее время для события[латекс]\boldsymbol{\Delta{t}=t_f -t_0}[/латекс]
, где[latex]\boldsymbol{t_f}[/latex] — конечное время, а [latex]\boldsymbol{t_0}[/latex] — начальное время. Начальное время часто принимается равным нулю, как если бы оно измерялось секундомером; прошедшее время равно просто[латекс]\жирныйсимвол{т}[/латекс].
- Средняя скорость[латекс]\boldsymbol{\bar{v}}[/латекс]определяется как смещение, деленное на время в пути. В символах средняя скорость
[латекс]\boldsymbol{\bar{v} =}[/латекс][латекс]\boldsymbol{\frac{\Delta{x}}{\Delta{t}}}[/latex][латекс]\boldsymbol {=}[/латекс][латекс]\boldsymbol{\frac{x_f -x_0}{t_f — t_0}}[/латекс].
- Единицей скорости в системе СИ является м/с.
- Скорость является вектором и поэтому имеет направление.
- Мгновенная скорость[latex]\boldsymbol{v}[/latex] — это скорость в конкретный момент времени или средняя скорость за бесконечно малый интервал.
- Мгновенная скорость — величина мгновенной скорости.



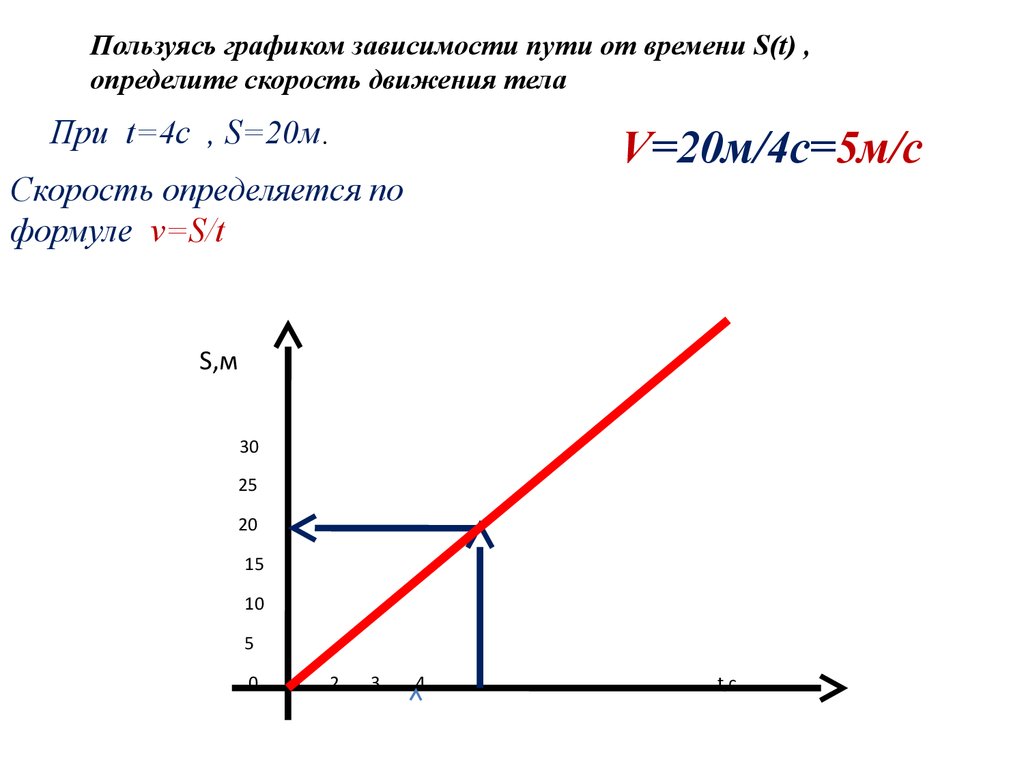
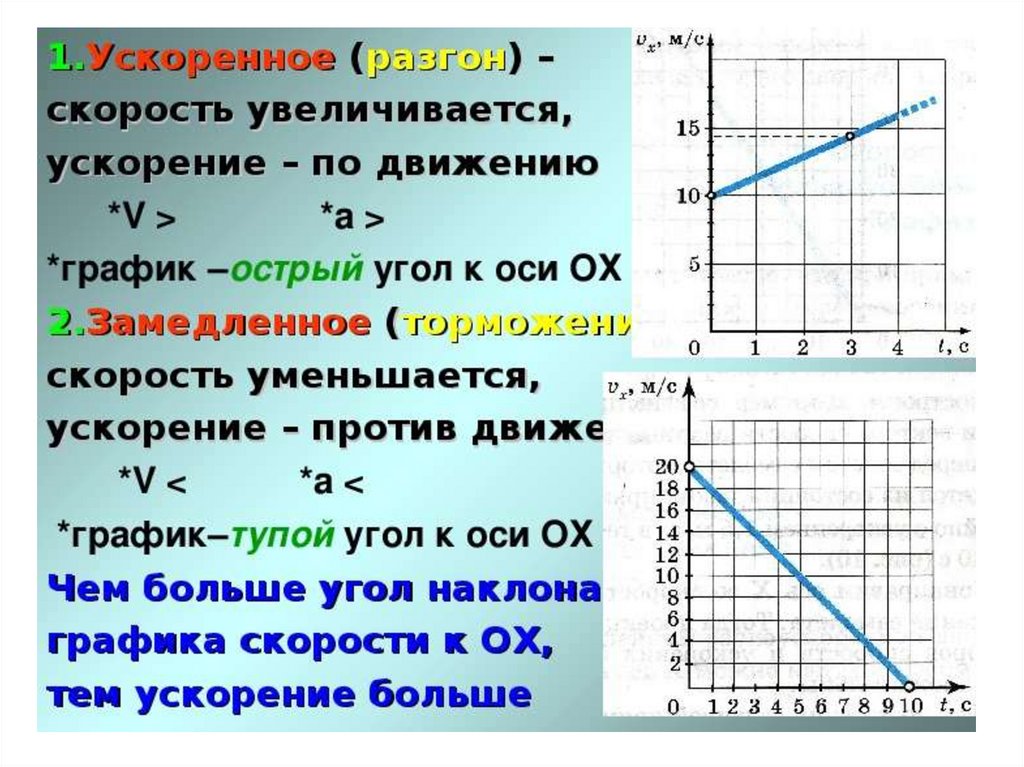 Скорость движения человека постоянна и равна
Скорость движения человека постоянна и равна 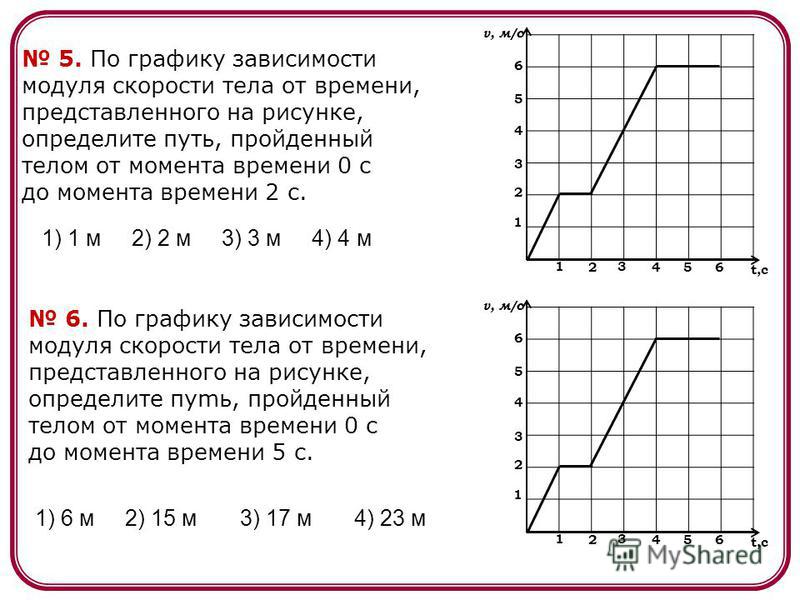
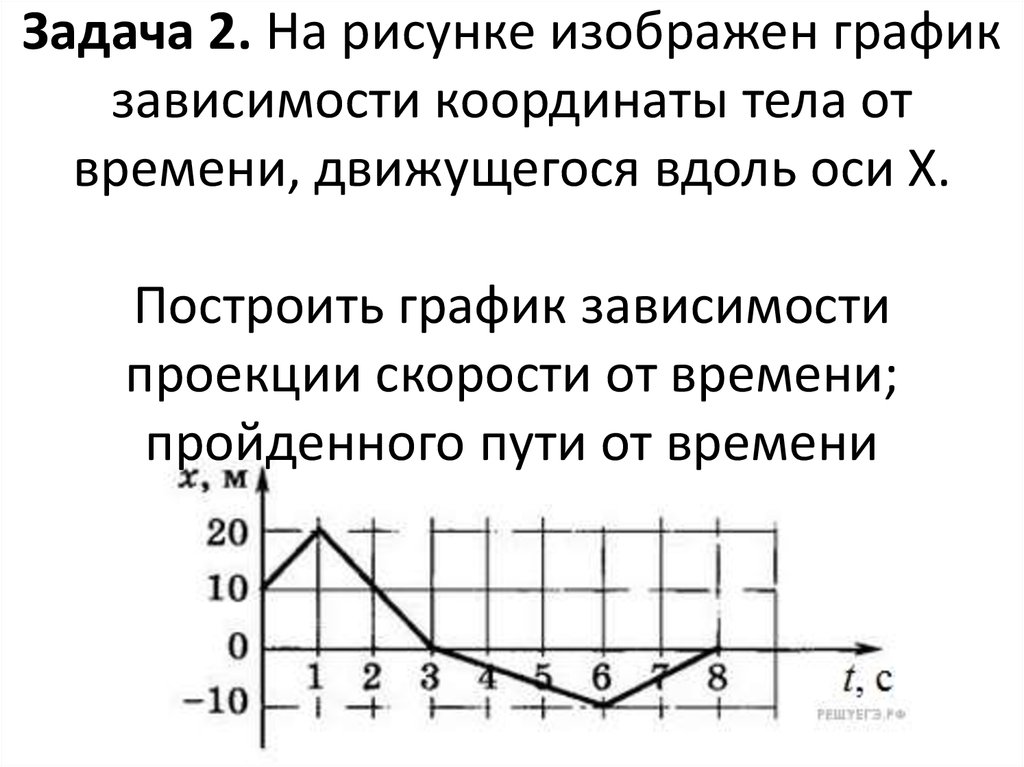
 Таким образом, тело двигается со скоростью
Таким образом, тело двигается со скоростью  е. делать остановки. Но время
остановки должно составлять t0 =T.
е. делать остановки. Но время
остановки должно составлять t0 =T.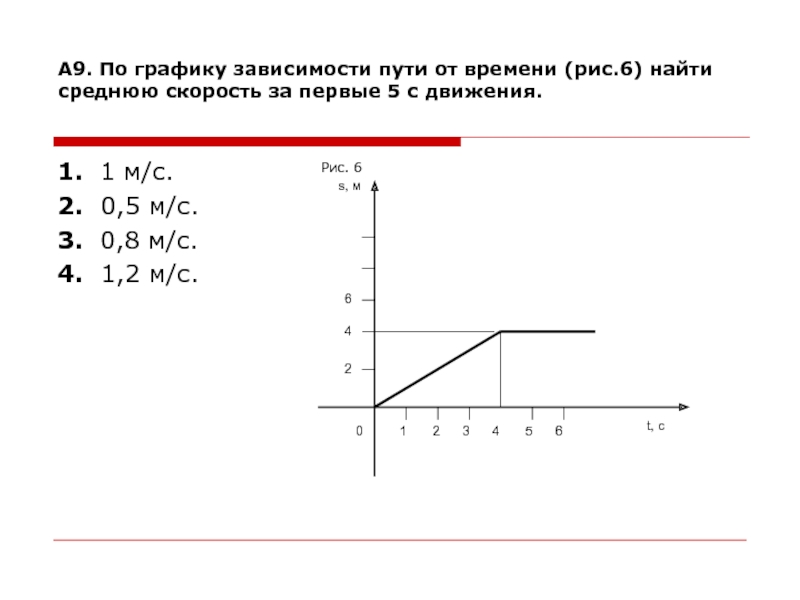

 Прошедшее время для события
Прошедшее время для события
Leave A Comment