Один из методов использования алгоритмов при решении задач по физике в профильных классах

На свете есть вещи важнее самых
замечательных открытий — это знание методов,
которыми эти открытия были сделаны.
Готфрид Лейбниц

Методы обучения предмету «Физика» очень многообразны. Одним из факторов понимания является умение решать задачи. Как без логического мышления, без научных знаний решить задачу. Решение задач это и труд, и собранность, и умение преодолеть себя, понять, что ты можешь. А вот научить этому — очень нелегкая задача учителя. Существует немало методов, которые бы привели наших учеников к успеху, и сегодня хотелось бы поделиться с вами одним из них. Этот метод позаимствован у учителей информатики, так как впервые учащиеся знакомятся с понятием АЛГОРИТМА в начале изучения курса информатики. Еще в 90г.г. был издан замечательный учебник «Основы информатики и вычислительной техники» под редакцией А. П.Ершова, он и дал нам инструмент — алгоритмический язык.[8]

Алгори́тм (лат. algorithmi — от имени среднеазиатского математика Аль-Хорезми) — конечная совокупность точно заданных правил решения некоторого класса задач или набор инструкций, описывающих порядок действий исполнителя для решения определённой задачи.

Используя законы логики и законы физики, возможно создать алгоритмы решения задач, то есть такие предписания, которые позволили бы на основе определенной системы элементарных действий безошибочно находить искомый результат. Ведь привитие обучающимся умений и навыков в выполнении действий по строго установленным правилам имеет общеобразовательное, воспитательное и практическое значение. Ученики приучаются к строгости в рассуждениях и действиях, подготавливаются к выполнению операций по инструкциям, что весьма важно в современном производстве, оснащенном сложными устройствами и приборами.

Составление алгоритмов для решения физических задач крайне затруднительно. Физические задачи весьма разнообразны. Их решение — это, прежде всего, творческий процесс. Кроме того, даже при составлении строгих предписаний для какого-либо узкого класса задач часто нельзя быть полностью уверенным в том, что каждый шаг или «элементарная» операция действительно является «элементарной», т.е. простой и очевидной для учащихся. Тем не менее перечни отдельных правил или предписаний алгоритмического типа при решении задач необходимы и существуют. [1]

Например: алгоритм решения задач на применение закона сохранения импульса. (Здесь идет такая ступенчатая нумерация действий).

  1. Выбрать систему отчета.
  2. Рассмотреть систему взаимодействующих тел
  3. Определить импульсы тел системы до и после взаимодействия.
  4. Применить закон сохранения импульса к системе взаимодействующих тел, записать его в векторной форме и в проекциях на координатную ось.
  5. Решить уравнение относительно искомой физической величины.
  6. Подставить числовые данные и записать ответ.

Или вот, например алгоритм решения задач по «Термодинамике»:

  1. Проанализировать условие задачи; проверить систему тел на замкнутость; определить, какие тела участвуют в теплообмене.
  2. Записать краткое условие задачи в единицах СИ.
  3. Определить для каждого тела, какие процессы с ним происходят при теплообмене.
  4. Записать для каждого процесса формулу для вычисления количества теплоты, выделенной или поглощенной.
  5. Составить уравнение теплового баланса.
  6. Вывести формулу для расчета искомой величины.
  7. Вычислить значение искомой величины.
  8. Проконтролировать размерность и ответ. Мы используем методику решения задач с помощью блок-схем по термодинамике. Блок-схема — распространённый тип схем (графических моделей), описывающих алгоритмы или процессы, в которых отдельные шаги изображаются в виде блоков различной формы, соединённых между собой линиями или стрелками, указывающими направление последовательности.

Основной идеей при использовании такого метода является наглядность.

Начало закладывается в 7 классе (А.В.Перышкин) [5] обеспечивается усвоение знаний о физических особенностях отдельных агрегатных состояний веществ.

В 8 классе (по А.В.Перышкину) [6] закладывается понимание и способность объяснять физические явления: конвекция, излучение, теплопроводность, изменение внутренней энергии тела в результате теплопередачи или работы внешних сил, определения удельной теплоемкости вещества, понимание смысла закона сохранения и превращения энергии в механических и тепловых процессах и умение применять его на практике, овладение способами выполнения расчетов для нахождения, удельной теплоемкости, количества теплоты, удельной теплоты сгорания топлива, удельной теплоты плавления, удельной теплоты парообразования и конденсации, КПД теплового двигателя, умение использовать полученные знания в повседневной жизни (экология, быт, охрана окружающей среды).[1]

Ну, а в десятом классе мы подходим к полноценному пониманию тепловых процессов т. е. познаём их более глубоко: модель идеального газа, абсолютная температура, температура как мера средней кинетической энергии теплового движения частиц, связь между давлением идеального газа и средней кинетической энергией теплового движения его молекул, уравнение состояния идеального газа, изопроцессы, границы применимости модели идеального газа, внутренняя энергия и способы ее изменения, первый закон термодинамики, расчет количества теплоты при изменении агрегатного состояния вещества, адиабатный процесс, второй закон термодинамики и его статистическое истолкование, принципы действия тепловых машин, КПД тепловой машины, проблемы энергетики и охрана окружающей среды. [7] В преддверии раздела термодинамики дается вот такая опорная схема связывающая различные законы и уравнения.

А теперь перейдем к первому закону термодинамики: Например:

Как можно изменить внутреннюю энергию? Существуют два способа.

  1. Совершение работы самим телом, или совершение работы над телом.
  2. Передача количества теплоты телу или наоборот, забираем у тела некоторое количество теплоты.

Первый закон термодинамики гласит: Изменение внутренней энергии происходит за счет совершения работы и передачи или отбора количества теплоты:

⁺₋ ΔU = ⁺₋ А + ⁺₋ Q

Применим первый закон термодинамики к изопроцессам с учетом блок-схем

Предварительно вводим обозначения:

Направление стрелки на блок — схеме показывает направление:

Количества теплоты от системы или к системе;

Работы совершаемой над газом или самим газом. [3]

Ниже приведена таблица, в которой расписано применение первого закона термодинамики к изопроцессам. Она интересна тем, что формула для закона сформулирована с учетом блок — схемы.[1]

Таблица №1. Первый закон термодинамики и его применение к изопроцессам.

В качестве примеров использования этой таблицы решим несколько задач.

Задача 1. При нагревании тела его внутренняя энергия увеличивается на ΔU= 600 Дж и он совершает работу А= 200 Дж. Какое количество теплоты сообщили телу?

Составим блок-схему данной задачи.

Значит, следуя схеме, напишем формулу первого закона термодинамики: все тепло, которое передано системе, идет на увеличение внутренней энергии и совершении газом работы.

Q = ΔU + A; Q = 600 Дж + 200 Дж = 800 Дж

Задача 2. Газу сообщают количество теплоты Q= 7 кДж. При этом η= 60 % подведенного тепла идет на увеличение внутренней энергии газа. Найти работу, совершаемую газом.

Газу передано количество теплоты, которое расходуется на увеличение его внутренней энергии и совершение им работы. Блок-схема этой задачи выглядит следующим образом:

Формула первого закона термодинамики выглядит так:

Q = ΔU + A т.

к. 60% от Q идет на увеличение внутренней энергии,

то запишем формулу: Q = 0.6 • Q + A 0.6 • Q = ΔU

Отсюда A = Q — 0,6 • Q = 0, 4 • Q = 0.4• 7000 Дж = 2800 Дж = 2,8 кДж

Задание № 7350. Газ в некотором процессе отдал количество теплоты 35кДж, а внутренняя энергия газа в этом процессе увеличилась на 10 кДж. Какую работу совершили над газом?

Составим блок-схему процесса.

Изменение внутренней энергии системы покажем стрелочкой [3]

Раз газ отдаёт отдает Q то на блок схеме стрелка вверх от термодинамической системы, а так как внешние силы совершают работу над газом то стрелочка к системе.

Решение:

Согласно первому началу термодинамики изменение энергии газа равно разнице между совершённой над ним работой внешних сил и отданным газом теплом. Следовательно, работа которую совершили над газом внешние силы равна 45 Дж.

Задание 11 №1110. В процессе эксперимента газ отдал окружающей среде количество теплоты, равное 3 кДж. При этом внутренняя энергия газа уменьшилась на 13 кДж. Следовательно, газ расширился. Какую работу он при этом совершил?

Составить блок-схему процесса.

(Отдал Q стрелка вверх от системы, совершил работу, стрелка от системы)

Решение:

Согласно первому началу термодинамики, тепло, переданное системе, идет на изменение внутренней энергии и совершение работы против внешних сил.

— ΔU = — Q — A отсюда находим работу газа А = ΔU — Q = 13 — 3= 10 кДж

Задание №10282. В процессе адиабатного сжатия двух молей идеального одноатомного газа внешние силы совершили работу А = 623,25 Дж. Определите изменение температуры данной порции газа в результате процесса.

Составить блок-схему процесса:

Совершение работы это стрелка от системы Q = 0

Решение:

В адиабатном процессе изменение внутренней энергии газа равно работе внешних сил. ΔU = A. Для идеального одноатомного газа ΔU= 3/2 R ΔT

В результате процесса Температура увеличилась на 25 градусов.

Задача №8003. В некотором процессе газ отдал окружающей среде количество теплоты, равное 10 кДж. При этом внутренняя энергия газа увеличилась на 30 кДж. Определите работу, которую совершили внешние силы, сжав газ.

Построим блок-схему процесса.

Внутренняя энергия увеличивается, следовательно, стрелочка вверх. Количество теплоты отдаём и стрелочка вверх от системы, Работу совершают над газом и стрелочка к системе.[4]

Решение:

Согласно первому началу термодинамики отданное окружающей среде количество теплоты, изменение внутренней энергии газа и работа внешних сил связаны соотношением. А = ΔU + Q = 40 кДж

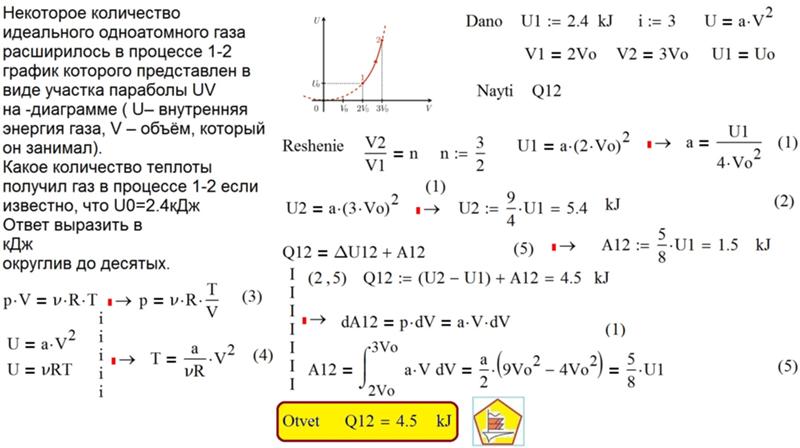
Задача 3. Один моль идеального одноатомного газа, находящегося при температуре + 27*С изобарно нагревают. При этом абсолютная температура этого газа увеличивается в 3 раза. Определите чему равно количество теплоты, сообщенное этому газу. Ответ выразите в джоулях.

Составим блок-схему процесса.

(Получил Q стрелка к системе, совершил работу, стрелка от системы)

Задача 4. Внутренняя энергия одного моля газообразного метана в 2.5 раз больше внутренней энергии такого же количества идеального одноатомного газа при той же температуре. Какое количество теплоты выделится при изобарном охлаждении 0.3 молей газообразного метана на 50К.

Составим блок-схему процесса.

Решение:

В изобарном процессе А = р ΔV = R ΔT

ΔT = -50К

Задача 5. В изохорном процессе идеальный одноатомный газ отдает некоторое количество теплоты. Определите, как при этом изменяются следующие физические величины: Давление газа, Температура газа.

Для каждой величины определите соответствующий характер изменения:

  1. Увеличивается;
  2. Уменьшается;
  3. Не изменяется
  4. Запишите в таблицу выбранные цифры для каждой физической величины.

Давление газа

Температура

Составим блок-схему процесса.

Решение:

В изохорном процессе объем газа постоянен, а значит газ не совершает работу. Если газ отдаёт некоторое количество теплоты, то его внутренняя энергия и температура уменьшается. Согласно уравнению Менделеева-Клапейрона уменьшение температуры приведёт к уменьшению давления.

Ответ: 2,2

Литература

  1. Милостивая Н.Ю., Баликоева А.Т., Гульчеева Р П., Джибилов Р.Б., учитель «Использование блок-схем при решении задач по физике (термодинамика)» Международная научно-практическая конференция «Наука, образование, общество: тенденции и перспективы развития», 2021.
  2. «Использование алгоритмических методов при обучении решению задач по физике. Механика» (Спб, ТОО Икар, 2002)).
  3. Милостивая Н.Ю. «Некоторые методы и приемы решения задач по термодинамике», «Первое сентября», 2011.
  4. Павлова М.В. «Использование алгоритма при решении задач по физике», «Первое сентября», 2011.
  5. Перышкин А. В. Физика 7 класс, Дрофа, 2021г.
  6. Перышкин А.В. Физика 8 класс, Дрофа, 2020г.
  7. Мякишев Г.Я. Физика 10 класс Москва «Просвещение», 2020г.
  8. Ершов Е.П. Основы информатики и вычислительной техники, Москва «Просвещение», 1985.

тест 10 класс работа газа и 1 начало термодинамики | Методическая разработка по физике (10 класс) на тему:

Вариант 1

1. При переходе из состояния 1 в состояние 3 газ совершает работу

   1) 2 кДж    2) 4 кДж        3) 6 кДж           4) 8 кДж  

2. В результате эксперимента по изучению циклического процесса, проводившегося с некоторым постоянным количеством одноатомного газа, который в условиях опыта можно было считать идеальным, получилась зависимость давления p от температуры T, показанная на графике. Выберите два утверждения, соответствующие результатам этого эксперимента, и запишите в таблицу цифры, под которыми указаны эти утверждения.

 

1) В процессе 2–3 газ не совершал работу.

2) В процессе 1–2 газ совершал положительную работу.

3) В процессе 2–3 газ совершал положительную работу.

4) В процессе 3–1 газ совершал положительную работу.

5) Изменение внутренней энергии газа на участке 1–2 было равно модулю изменения внутренней энергии газа на участке 3–1.              

3. Внешние силы совершили над идеальным газом работу 300 Дж, и при этом внутренняя энергия газа увеличилась на 500 Дж. Выберите верное утверждение, характеризующее этот процесс. В этом процессе газ

1) отдал количество теплоты 100 Дж  2) получил количество теплоты 200 Дж

3) отдал количество теплоты 400 Дж  4) получил количество теплоты 400 Дж

4. Каково изменение внутренней энергии газа, если ему передано количество теплоты 300 Дж, а внешние силы совершили над ним работу 500 Дж? (Ответ дайте в джоулях.)

Вариант 2

1. При переходе из состояния 1 в состояние 3 газ совершает работу

          1) 2 кДж     2) 4 кДж   3) 6 кДж         4) 8 кДж    

2.  В результате эксперимента по изучению циклического процесса, проводившегося с некоторым постоянным количеством одноатомного газа, который в условиях опыта можно было считать идеальным, получилась зависимость давления p от температуры T, показанная на графике. Выберите два утверждения, соответствующие результатам этого эксперимента, и запишите в таблицу цифры, под которыми указаны эти утверждения.

 

1) В процессе 1–2 газ совершал отрицательную работу.

2) В процессе 2–3 газ совершал отрицательную работу.

3) В процессе 3–1 газ совершал положительную работу.

4) Изменение внутренней энергии газа на участке 1–2 было меньше изменения внутренней энергии газа на участке 2–3.

5) В процессе 3–1 газ совершал отрицательную работу.    

     3. Постоянную массу газа в сосуде сжали, совершив работу 30 Дж. Внутренняя энергия газа при этом увеличилась на 25 Дж. Следовательно, газ

1) получил извне количество теплоты, равное 5 Дж

2) отдал окружающей среде количество теплоты, равное 5 Дж

3) получил извне количество теплоты, равное 55 Дж

4) отдал окружающей среде количество теплоты, равное 55 Дж

4.  В процессе эксперимента газ отдал окружающей среде количество теплоты, равное 3 кДж. При этом внутренняя энергия газа уменьшилась на 13 кДж. Следовательно, газ расширился. Какую работу он при этом совершил? (Ответ дайте в кДж.)

Вариант 3

1. При переходе из состояния 1 в состояние 3 газ совершает работу

 1) 2 кДж             2) 4 кДж            3) 6 кДж          4) 8 кДж    

2. В результате эксперимента по изучению циклического процесса, проводившегося с некоторым постоянным количеством одноатомного газа, который в условиях опыта можно было считать идеальным, получилась зависимость давления p от температуры T, показанная на графике. Выберите два утверждения, соответствующие результатам этого эксперимента, и запишите в таблицу цифры, под которыми указаны эти утверждения.

 

1) В процессе 2–3 газ совершал работу.

2) В процессе 1–2 газ совершал отрицательную работу.

3) В процессе 2–3 газ совершал отрицательную работу.

4) В процессе 3–1 газ совершал отрицательную работу.

5) Изменение внутренней энергии газа на участке 1–2 по модулю больше изменения внутренней энергии газа на участке 3–1.              

 3. Внешние силы совершили над газом работу 300 Дж, при этом внутренняя энергия газа увеличилась на 500 Дж. В этом процессе газ

1) Отдал количество теплоты 100 Дж  2) Получил количество теплоты 200 Дж

3) Отдал количество теплоты 400 Дж  4) Получил количество теплоты 400 Дж

4. Идеальный газ получил количество теплоты 100 Дж и при этом внутренняя энергия газа уменьшилась на 100 Дж. Какова работа, совершенная внешними силами над газом? (Ответ дайте в джоулях.)

Вариант 4

1. При переходе из состояния 1 в состояние 3 газ совершает работу

       1) 2 кДж            2) 4 кДж        3) 6 кДж           4) 8 кДж            

2. В результате эксперимента по изучению циклического процесса, проводившегося с некоторым постоянным количеством одноатомного газа, который в условиях опыта можно было считать идеальным, получилась зависимость давления p от температуры T, показанная на графике. Выберите два утверждения, соответствующие результатам этого эксперимента, и запишите в таблицу цифры, под которыми указаны эти утверждения.

 

1) В процессе 1–2 газ совершал положительную работу.

2) В процессе 2–3 газ совершал положительную работу.

3) В процессе 3–1 газ совершал отрицательную работу.

4) Изменение внутренней энергии газа на участке 1–2 было больше изменения внутренней энергии газа на участке 2–3.

5) В процессе 3–1 работа не совершалась.                

3. Газ сжали, совершив работу 38 Дж, и сообщили ему количество теплоты 238 Дж. Как изменилась внутренняя энергия газа?

1) увеличилась на 200 Дж  2) уменьшилась на 200 Дж 3) уменьшилась на 276 Дж  4) увеличилась на 276 Дж

4. В процессе эксперимента внутренняя энергия газа уменьшилась на 40 кДж, и он совершил работу 35 кДж. Какое количество теплоты (в кДж) газ отдал окружающей среде?

Плавление, кипячение и возгонка – Введение в химию – 1-е канадское издание

Глава 10. Твердые и жидкие вещества

  1. Опишите, что происходит во время изменения фазы.
  2. Рассчитайте изменение энергии, необходимое для фазового перехода.

Вещества могут менять фазу — часто из-за изменения температуры. При низких температурах большинство веществ твердые; при повышении температуры они становятся жидкими; при еще более высоких температурах они становятся газообразными.

Процесс превращения твердого тела в жидкость называется плавлением (более старый термин, который вы иногда можете встретить, это слияние ). Противоположный процесс, превращение жидкости в твердое тело, называется затвердеванием . Для любого чистого вещества температура, при которой происходит плавление, известная как точка плавления , является характеристикой этого вещества. Чтобы твердое тело превратилось в жидкость, требуется энергия. Каждое чистое вещество имеет определенное количество энергии, необходимое для перехода из твердого состояния в жидкое. Эта сумма называется энтальпия плавления (или теплота плавления)  вещества, представленная как Δ H плавка . Некоторые значения Δ H fus приведены в табл. 10.2 «Энтальпии плавления различных веществ»; предполагается, что эти значения относятся к температуре плавления вещества. Обратите внимание, что единицей измерения Δ H fus является килоджоуль на моль, поэтому нам нужно знать количество материала, чтобы знать, сколько энергии задействовано. Предохранитель Δ H всегда табулируется как положительное число. Однако его можно использовать как для процессов плавления, так и для процессов затвердевания, если помнить, что плавление всегда эндотермическое (поэтому Δ H будет положительным), а затвердевание всегда экзотермическое (поэтому Δ H будет отрицательный).

Таблица 10.2 Энтальпии плавления различных веществ
Вещество (точка плавления) Δ H сплав (кДж/моль)
Вода (0°C) 6. 01
Алюминий (660°C) 10,7
Бензол (5,5°C) 9,95
Этанол (-114,3°C) 5,02
Ртуть (-38,8°C) 2,29

Как изменится энергия, если 45,7 г H 2 O расплавятся при 0°C?

Решение

Δ H предохранитель H 2 O составляет 6,01 кДж/моль. Однако наше количество дано в граммах, а не в молях, поэтому первым шагом является преобразование граммов в моли с использованием молярной массы H 2 O, которая составляет 18,0 г/моль. Тогда мы можем использовать Δ H fus в качестве коэффициента преобразования. Поскольку вещество плавится, процесс эндотермический, поэтому изменение энергии будет иметь положительный знак.

Без знака число считается положительным.

Проверь себя

Как изменится энергия, если 108 г C 6 H 6 замерзнут при 5,5°C?

Ответ

−13,8 кДж

При плавлении энергия идет исключительно на изменение фазы вещества; это не касается изменения температуры вещества. Следовательно, плавление является изотермическим процессом, поскольку вещество остается при одной и той же температуре. Только когда все вещество расплавлено, дополнительная энергия идет на изменение его температуры.

Что происходит, когда твердое тело становится жидкостью? В твердом теле отдельные частицы застревают на месте, потому что межмолекулярные силы не могут быть преодолены за счет энергии частиц. Когда подается больше энергии (например, за счет повышения температуры), наступает момент, когда частицы имеют достаточно энергии, чтобы двигаться, но недостаточно энергии, чтобы разделиться. Это жидкая фаза: частицы все еще находятся в контакте, но могут двигаться вокруг друг друга. Это объясняет, почему жидкости могут принимать форму своих сосудов: частицы перемещаются и под действием гравитации заполняют наименьший возможный объем (если только жидкость не находится в среде с невесомостью — см. рис. 10.16 «Жидкости и гравитация»). .

Рисунок 10.16 «Жидкости и гравитация». а) Жидкость заполняет дно своего сосуда, когда она стягивается вниз под действием силы тяжести, и частицы скользят друг по другу. б) Жидкость плавает в условиях невесомости. Частицы все еще скользят друг по другу, потому что они находятся в жидкой фазе, но теперь нет гравитации, которая могла бы тянуть их вниз.

Фазовый переход между жидкостью и газом имеет некоторое сходство с фазовым переходом между твердым телом и жидкостью. При определенной температуре частицы жидкости обладают достаточной энергией, чтобы превратиться в газ. Процесс превращения жидкости в газ называется кипение (или испарение) , а процесс превращения газа в жидкость называется конденсацией . Однако, в отличие от процесса конверсии твердого тела в жидкость, на процесс конверсии жидкость/газ заметно влияет окружающее давление на жидкость, поскольку давление сильно влияет на газы. Это означает, что температура, при которой жидкость становится газом, точка кипения , может изменяться в зависимости от окружающего давления. Поэтому мы определяем нормальную температуру кипения  как температура, при которой жидкость превращается в газ, когда окружающее давление составляет ровно 1 атм или 760 торр. Если не указано иное, предполагается, что точка кипения соответствует давлению в 1 атм.

Подобно фазовому переходу твердое тело/жидкость, фазовый переход жидкость/газ требует энергии. Количество энергии, необходимое для преобразования жидкости в газ, называется энтальпией парообразования (или теплотой парообразования), представленной как Δ H пар . Некоторые Δ H vap значения приведены в таблице 10.3 «Энтальпии испарения различных веществ»; предполагается, что эти значения относятся к нормальной температуре кипения вещества, которая также приведена в таблице. Единицей для Δ H vap также является килоджоуль на моль, поэтому нам нужно знать количество материала, чтобы знать, сколько энергии задействовано. Δ H vap также всегда указывается в таблице как положительное число. Его можно использовать как для процессов кипения, так и для процессов конденсации, если помнить, что кипение всегда эндотермическое (поэтому Δ H будет положительным), в то время как конденсация всегда экзотермическая (поэтому Δ H будет отрицательным).

Таблица 10.3 Энтальпии испарения различных веществ
Вещество (нормальная температура кипения) Δ H пар (кДж/моль)
Вода (100°C) 40,68
Бром (59,5°C) 15,4
Бензол (80,1°С) 30,8
Этанол (78,3°C) 38,6
Ртуть (357°C) 59,23

Как изменится энергия при конденсации 66,7 г Br 2 (г) в жидкость при 59,5°С?

Раствор

Δ H vap Br 2 составляет 15,4 кДж/моль. Несмотря на то, что это процесс конденсации, мы все же можем использовать числовое значение Δ H vap до тех пор, пока мы понимаем, что должны отводить энергию, поэтому значение Δ H будет отрицательным. Чтобы определить величину изменения энергии, мы должны сначала перевести количество Br 2 в моли. Тогда мы можем использовать Δ H vap в качестве коэффициента преобразования.

Поскольку процесс экзотермический, фактическое значение будет отрицательным: Δ H = −6,43 кДж.

Проверь себя

Как изменится энергия при 822 г C 2 H 5 OH(ℓ) кипятить при нормальной температуре кипения 78,3°C?

Ответ

689 кДж

Как и при плавлении, при кипении энергия идет исключительно на изменение фазы вещества; это не касается изменения температуры вещества. Так что кипение тоже изотермический процесс. Только когда все вещество закипит, дополнительная энергия идет на изменение его температуры.

Что происходит, когда жидкость становится газом? Мы уже установили, что жидкость состоит из частиц, находящихся в контакте друг с другом. Когда жидкость становится газом, частицы отделяются друг от друга, и каждая частица движется в пространстве своим путем. Именно так газы стремятся заполнить свои сосуды. Действительно, в газовой фазе большую часть объема занимает пустое пространство; только одна тысячная объема фактически занята веществом (см. рис. 10.17 «Жидкости и газы»). Именно это свойство газов объясняет, почему они могут сжиматься, что и рассматривается в главе 6 «Газы».

Рисунок 10.17 Жидкости и газы. В (а) частицы представляют собой жидкость; частицы находятся в контакте, но также могут перемещаться друг вокруг друга. В (b) частицы представляют собой газ, и большая часть объема на самом деле представляет собой пустое пространство. Частицы не в масштабе; на самом деле точки, представляющие частицы, будут примерно в одну тысячную меньше, чем изображено.

При некоторых обстоятельствах твердая фаза может перейти непосредственно в газовую фазу, минуя жидкую фазу, а газ может сразу стать твердым. Переход твердого состояния в газообразное называется 9.0015 сублимация , а обратный процесс называется осаждением . Сублимация изотермическая, как и другие фазовые переходы. Во время сублимации происходит измеримое изменение энергии; это изменение энергии называется энтальпией сублимации , представленной как Δ H к югу от . Соотношение между Δ H sub и другими изменениями энтальпии выглядит следующим образом:

Δ H суб = Δ H предохранитель + Δ H пар

Таким образом, Δ H sub не всегда указывается в таблице, поскольку его можно просто рассчитать из Δ H fus и Δ H vap .

Есть несколько распространенных примеров сублимации. Известный продукт — сухой лед — на самом деле является твердым CO 2 . Сухой лед является сухим, потому что он возгоняется, при этом твердая фаза минует жидкую фазу и переходит прямо в газовую фазу. Сублимация происходит при температуре -77°С, поэтому с ней нужно обращаться осторожно. Если вы когда-нибудь замечали, что кубики льда в морозильной камере со временем становятся меньше, то это потому, что твердая вода очень медленно сублимирует. «Ожог от заморозки» на самом деле не ожог; это происходит, когда некоторые продукты, такие как мясо, медленно теряют содержание твердой воды из-за сублимации. Еда по-прежнему хороша, но выглядит неаппетитно. Снижение температуры морозильной камеры замедлит сублимацию твердой воды.

Химические уравнения могут использоваться для описания фазового перехода. В таких случаях крайне важно использовать фазовые метки на веществах. Например, химическое уравнение таяния льда для получения жидкой воды выглядит следующим образом:

H 2 O(s) → H 2 O(ℓ)

Химических изменений не происходит; однако происходит физическое изменение.

График зависимости температуры от количества подведенного тепла известен как кривая нагрева (см. рис. 10.18). Они обычно используются, чтобы визуально показать взаимосвязь между фазовыми переходами и энтальпией для данного вещества.

Рисунок 10.18 «Общая диаграмма кривой нагрева».

На рис. 10.18 [1] твердое тело приобретает кинетическую энергию и, следовательно, повышается температура по мере добавления тепла. В точке плавления добавленное тепло используется для разрушения межмолекулярных сил притяжения твердого тела вместо увеличения кинетической энергии, и поэтому температура остается постоянной. После того, как все твердое вещество расплавится, снова подведенное тепло идет на увеличение кинетической энергии (и температуры) молекул жидкости до точки кипения. В точке кипения, опять же, добавленное тепло используется для разрушения межмолекулярных сил притяжения вместо обеспечения кинетической энергии, и температура остается постоянной до тех пор, пока вся жидкость не превратится в газ.

  • Фазовые превращения могут происходить между любыми двумя фазами материи.
  • Все фазовые переходы происходят с одновременным изменением энергии.
  • Все фазовые переходы изотермические.
  1. В чем разница между плавление и затвердевание ?
  2. В чем разница между кипящим и конденсационным ?
  3. Опишите молекулярные изменения, когда твердое тело становится жидкостью.
  4. Опишите молекулярные изменения, когда жидкость превращается в газ.
  5. Как изменится энергия, если 78,0 г ртути расплавятся при температуре -38,8°C?
  6. Как изменится энергия при затвердевании 30,8 г алюминия при 660°С?
  7. Как изменится энергия при кипении 111 г Br 2 при 59,5°С?
  8. Как изменится энергия при конденсации 98,6 г H 2 O при 100°C?
  9. Каждое из следующих утверждений неверно. Перепишите их так, чтобы они были правильными.
    1. Изменение температуры во время фазового перехода.
    2. Процесс превращения жидкости в газ называется сублимацией.
  10. Каждое из следующих утверждений неверно. Перепишите их так, чтобы они были правильными.
    1. Объем газа содержит только около 10% материи, а остальное — пустое пространство.
    2. Δ H sub равно Δ H vap .
  11. Напишите химическое уравнение плавления элементарного натрия.
  12. Напишите химическое уравнение затвердевания бензола (C 6 H 6 ).
  13. Напишите химическое уравнение сублимации CO 2 .
  14. Напишите химическое уравнение кипения пропанола (C 3 H 7 OH).
  15. Что такое Δ H sub из H 2 O? (Подсказка: см. Таблицу 10.2 «Энтальпии плавления различных веществ» и Таблицу 10.3 «Энтальпии испарения различных веществ».)
  16. Δ H sub I 2 составляет 60,46 кДж/моль, а его Δ H vap составляет 41,71 кДж/моль. Что такое Δ H fus I 2 ?
  1. Плавление — это фазовый переход от твердого к жидкому, тогда как затвердевание — это фазовый переход от жидкого к твердому.
  1. Молекулы имеют достаточно энергии, чтобы двигаться относительно друг друга, но недостаточно, чтобы полностью отделиться друг от друга.
  1. 890 Дж
  1. 10,7 кДж
    1. Температура не изменяется при изменении фазы.
    2. Процесс превращения жидкости в газ называется кипением; процесс превращения твердого тела в газ называется сублимацией.
  1. Na(s) → Na(ℓ)
  1. CO 2 (s) → CO 2 (g)
  1. 46,69 кДж/моль

Атрибуция СМИ

  • «Стакан воды» © 2005 г. Дерека Дженсена под лицензией Public Domain
  • «Клейтон Андерсон в невесомости» © 2010 НАСА находится под лицензией Public Domain
  1. Предоставлено UC Davis Chemwiki\CC-BY-NC-SA-3. 0 ↵

Глава 11: Горение (обновлено 31.05.10)

Глава 11: Горение (обновлено 31.05.10)

Глава 11: Возгорание
(Спасибо к Дэвид Bayless за помощь в написании этот раздел)

Введение — до этого точка теплоты Q во всех задачах и примерах была либо заданной значение или было получено из отношения первого закона. Однако в различных тепловые двигатели, газовые турбины и паровые электростанции полученный в результате процессов сжигания с использованием либо твердого топлива (например, уголь или дрова). жидкое топливо (например, бензин, керосин или дизельное топливо), или газообразное топливо (например, природный газ или пропан).

В этой главе мы познакомимся с химией и термодинамика горения универсальных углеводородных топлив — (C х Н у ), в котором окислителем является кислород, содержащийся в атмосферном воздухе. Обратите внимание, что мы не будем рассматривать сжигание твердого топлива или сложные смеси и смеси углеводородов, входящие в состав бензин, керосин или дизельное топливо.

Атмосферный воздух содержит примерно 21% кислорода (O 2 ) по объему. Остальные 79% «других газов» в основном азот (N 2 ), т.е. будем считать, что воздух состоит из 21 % кислорода и 79 % азота. объем. Таким образом, каждый моль кислорода, необходимый для окисления углеводорода, в сопровождении 79/21 = 3,76 моль азота. Используя эту комбинацию молекулярная масса воздуха становится 29 [кг/кмоль]. Обратите внимание, что это предполагается, что азот обычно не подвергается никакому химическому воздействию. реакция.

Процесс горения — Основной процесс горения можно описать топливом (т. углеводород) плюс окислитель (воздух или кислород), называемый Реагенты , которые подвергаются химическому процессу с выделением тепла с образованием Продукты сгорания так, чтобы масса сохранялась. в простейший процесс горения, известный как Стехиометрический Сгорание , весь углерод в топливе образует двуокись углерода (CO 2 ) и весь водород образует воду (H 2 O) в продуктах, поэтому химическую реакцию можно записать так:


где z известен как стехиометрический коэффициент для окислителя (воздуха) 90 548

Обратите внимание, что эта реакция дает пять неизвестных: z, a, b, c, d, поэтому нам нужно решить пять уравнений. стехиометрический сжигание предполагает, что в продуктах нет избыточного кислорода, поэтому d = 0. Остальные четыре уравнения получаем из балансировки числа атомов каждого элемента в реагентах (углерод, водород, кислород и азот) с количеством атомов этих элементов в продукты. Это означает, что ни один атом не разрушается и не теряется в реакция горения.

  Элемент

Сумма в реагентах

90 554 = 90 005

  Сумма в продуктах

  Сокращенное уравнение

 Углерод (C)

х

 

 а

а = х

Водород (H)

 и

 

 2b

 б = у/2

Кислород (O)

 2z

 

 2а+б

z = а + b/2

Азот (N)

 2(3,76)z

 

 2с

 c = 3,76z

Обратите внимание, что образовавшаяся вода может находиться в виде пара или жидкой фазы в зависимости от температуры и давления продукты горения.

В качестве примера рассмотрим стехиометрическое горение метана (СН 4 ) в атмосферном воздухе. Приравнивание моляра коэффициенты реагентов и продуктов получаем:

Теоретическое соотношение воздух-топливо и воздух-топливо -The минимальное количество воздуха, обеспечивающее полное сгорание топлива называется Теоретическая Air (также называемый Стехиометрический воздух ). В этом случае продукты не содержат кислорода. Если мы поставляем меньше, чем теоретический воздух, тогда продукты могут содержать углерод монооксида (CO), поэтому нормальная практика заключается в подаче более теоретический воздух, чтобы предотвратить это явление. это Превышение Air приведет к появлению кислорода в продукты.

Стандартная мера количества воздуха, используемого в процесс сгорания Air-Fuel Соотношение 90 510 (AF), определяемое следующим образом: 90 005

Таким образом, рассматривая только реагенты метана сгорания с теоретическим воздухом, представленным выше, получаем:

Решенная проблема 11. 1 — В этой задачи мы хотим разработать уравнение горения и определить соотношение воздух-топливо для полного сгорания н-бутана (C 4 Н 10 ) с а) теоретическим воздухом и б) 50% избытком воздуха.


Анализ продуктов сгорания — Горение всегда происходит при повышенных температурах и будем считать, что все продукты сгорания (включая воду пар) ведут себя как идеальные газы. Так как газ у них разный. постоянных, удобно использовать уравнение состояния идеального газа в через универсальную газовую постоянную следующим образом:

При анализе продуктов сгорания имеется интересны несколько пунктов:

  • 1) Что такое объемный процент конкретных продуктов, в частности двуокиси углерода (CO 2 ) и углерод монооксид (СО)?

  • 2) Что такое роса точка водяного пара в продуктах сгорания? Это требует оценка парциального давления паровой составляющей водяного пара продукты.

  • 3) Имеются экспериментальные методы объемного анализ продуктов сгорания, как правило, делается на Сухой Основа , что дает объемный процент всех компонентов, кроме водяного пара. Это позволяет простой метод определения фактического соотношения воздух-топливо и избытка используемого воздуха в процессе горения.

Для идеальных газов мы находим, что мольная доля y i i-го компонента в смеси газов при удельном давлении P а температура T равна объемной доле этого компонента.
Так как из молярного отношения идеального газа: P.V = N.R у .Т, у нас есть:

Кроме того, поскольку сумма объемов компонентов V i должны равняться общему объему V, имеем:

Используя аналогичный подход, мы определяем частичную давление компонента с использованием закона парциальных давлений Дальтона:

Решенная проблема 11. 2 — В эта проблема Пропан (C 3 H 8 ) сжигается с 61% избыточного воздуха, который поступает в камеру сгорания при 25°С. Предполагая полное сгорание и полное давление 1 атм. (101,32 кПа), определите а) соотношение воздух-топливо [кг воздуха/кг топлива], б) объемный процент двуокиси углерода в продуктах, и c) температура точки росы продуктов.

Решенная проблема 11.3 — В эта проблема Этан (C 2 H 6 ) сжигается атмосферным воздухом, а объемный анализ сухие продукты сгорания дают следующее: 10% CO 2 , 1% CO, 3% O 2 и 86% N 2 . Развивать уравнение горения, и определить а) процент избытка воздух, б) соотношение воздух-топливо, и в) точка росы сгорания продукты.


Первый закон анализа горения — Основной целью горения является получение тепла за счет изменения энтальпии от реагентов к продуктам. Из первого закона уравнение в контрольном объеме без учета кинетической и потенциальной энергии изменения и при условии, что работа не выполняется, мы имеем:

, где суммирование ведется по всем продукты (p) и реагенты (r). N относится к количеству молей каждого компонента, а h [кДж/кмоль] относится к молярной энтальпии каждый компонент.

Поскольку существует ряд различных веществ нам необходимо установить общее эталонное состояние для оценки энтальпии, обычно выбирают 25 ° C и 1 атм, что обычно обозначается верхним индексом о. Проф. С. Бхаттачарджи из Государственный университет Сан-Диего разработал экспертную веб-систему в < www.thermofluids.net > называется ТЕСТ ( Т он E эксперт S система для T (гермодинамика) в который он включил набор таблиц свойств идеального газа, основанных на на энтальпии h или = 0 по этой общей ссылке. Мы адаптировали некоторые из этих таблиц специально для этого раздела, и их можно найти в по следующей ссылке:

Горение Таблицы молярной энтальпии

В качестве примера снова рассмотрим полное сгорание метана (CH 4 ) с теоретическим воздухом:

Обратите внимание, что в реагентах и ​​продуктах В приведенном выше примере у нас есть основные элементы O 2 и N 2 как а также соединения CH 4 , CO 2 и H 2 O. Когда соединение образуется, изменение энтальпии называется Энтальпия пласта , обозначаемый h f o , и для нашего примера:

Вещество

Формула

hfo [кДж/кмоль]

Углекислый газ

СО 2 (г)

-393 520

Водяной пар

Н 2 О(г)

-241 820

Вода

Н 2 О(л)

-285 820

Метан

CH 4 (г)

-74 850

где (g) относится к газу и (l) относится к жидкость.

Знак минус означает, что процесс Экзотермический , т. е. при образовании соединения выделяется тепло. Обратите внимание, что энтальпия образования основных элементов O 2 и N 2 составляет нуль.

Сначала рассмотрим случай, когда имеется достаточно теплообмен таким образом, что и реагенты, и продукты находятся в 25°C и давление 1 атм, и что водный продукт является жидким. С заметного изменения энтальпии нет, уравнение энергии принимает вид:

Это тепло (Qcv) называется энтальпией . Горения или Отопление Значение топлива. Если продукты содержат жидкую воду, то это Высшее Теплота сгорания (как в нашем примере), однако, если продукт содержит водяной пар, то это Нижний Теплотворная способность топлива. энтальпия сгорания – это наибольшее количество тепла, которое может быть выделяется данным топливом.

Адиабатическая температура пламени — Противоположная крайность приведенного выше примера, в котором мы оценивали энтальпией сгорания является случай адиабатического процесса, в котором тепло не выделяется. Это приводит к значительной температуре увеличение продуктов сгорания (обозначается Адиабатическая Температура пламени ), которая может быть уменьшается за счет увеличения соотношения воздух-топливо.

Решенная проблема 11.4 — Определить адиабатическая температура пламени для полного сгорания Метан ( CH 4 ) с 250% теоретического воздуха в адиабатическом контрольном объеме.

Это уравнение может быть решено только итеративным метод проб и ошибок с использованием таблиц Sensible Энтальпия против температуры для всех четырех составные части продукции — СО 2 , Н 2 О, О 2 , и N 2 . Быстрый приближение к адиабатической температуре пламени может быть получено с помощью при условии, что продукты полностью состоят из воздуха. Этот подход был представил нас Поттер и Somerton в их Schaum’s Краткое изложение термодинамики для инженеров , в котором они предполагали, что все продукты будут N 2 . Мы находим более удобным использовать воздух, предполагая репрезентативное значение Конкретный Теплоемкость воздуха : С р, 1000К = 1,142 [кДж/кг.К].

Таким образом, суммируя все моли продуктов, мы имеем:

Использование таблиц Sensible Энтальпия против температуры мы оценили энтальпии всех четырех продуктов при температуре 1280К. Этот в результате общая энтальпия составила 802 410 [кДж/кмоль топлива], что составляет очень близко к требуемому значению, что оправдывает такой подход.

Проблема 11.5 — — Определить адиабатическую температуру пламени. полное сгорание пропана ( C 3 H 8 ) с 250% теоретического воздуха в адиабатическом контрольном объеме [T = 1300К].

__________________________________________________________________________________________


Инженерная термодинамика, Израиль Уриэли находится под лицензией Creative Commons Attribution-Noncommercial-Share Alike 3.