диагоналей, углов, оснований, высоты и тд
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Свойства равнобедренной (равнобокой) трапеции
В данной публикации мы рассмотрим определение и основные свойства равнобедренной трапеции.
Напомним, трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны, т.е. AB = CD.
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Свойство 7
Свойство 1
Углы при любом из оснований равнобедренной трапеции равны.
- ∠DAB = ∠ADC = α
- ∠ABC = ∠DCB = β
Свойство 2
Сумма противоположных углов трапеции равняется 180°.
Для рисунка выше: α + β = 180°.
Свойство 3
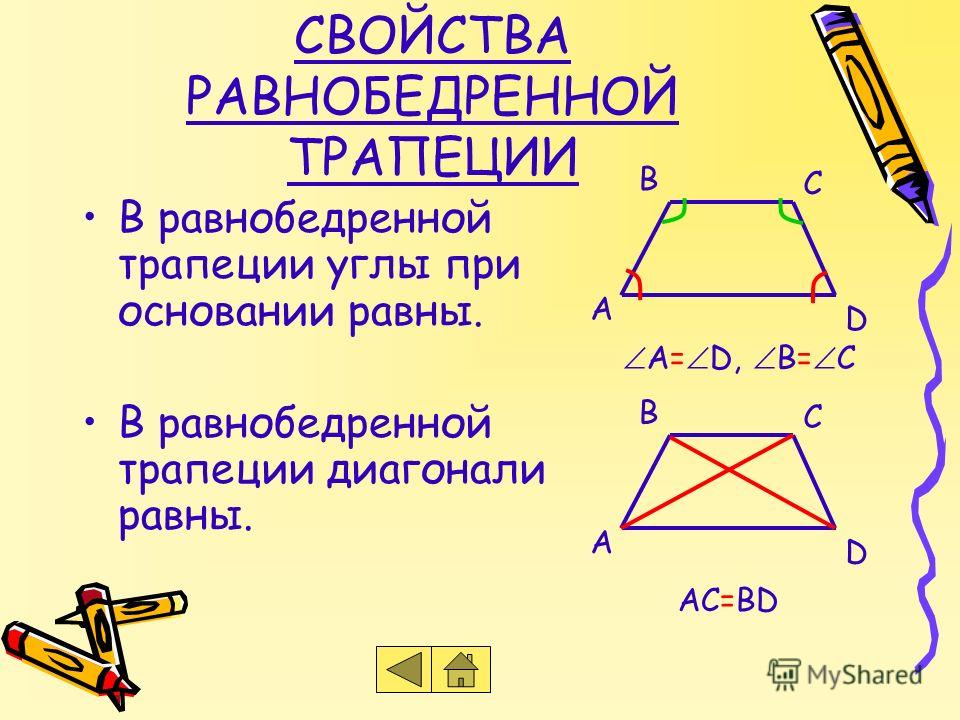
Диагонали равнобедренной трапеции имеют одинаковую длину.
AC = BD = d
Свойство 4
Высота равнобедренной трапеции BE, опущенная на основание большей длины AD, делит его на два отрезка: первый равняется половине суммы оснований, второй – половине их разности.
Свойство 5
Отрезок MN, соединяющий середины оснований равнобокой трапеции, перпендикулярен этим основаниям.
Прямая, проходящая через середины оснований равнобедренной трапеции, называется ее осью симметрии.
Свойство 6
Вокруг любой равнобедренной трапеции можно описать окружность.
Свойство 7
Если сумма оснований равнобокой трапеции равно удвоенной длине ее боковой стороны, в нее можно вписать окружность.
Радиус такой окружности равняется половине высоты трапеции, т.е. R = h/2.
Примечание: остальные свойства, которые применимы ко всем видам трапеций, приведены в нашей публикации – “Что такое трапеция: определение, виды, свойства”.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Четырехугольники |
| Основные определения и свойства трапеций |
| Свойства и признаки равнобедренных трапеций |
Основные определения и свойства трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Трапеция | Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции | |
| Определение | Диагонали трапеции | Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции | |
| Определение | Высота трапеции | Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение | |
| Свойство | Точка пересечения диагоналей | Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве | |
| Определение | Средняя линия трапеции | Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции | |
| Свойство | Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство | ||
| Свойство | Биссектрисы углов при боковой стороне трапеции | Биссектрисы углов при боковой стороне трапеции перпендикулярны |
| Определение: трапеция | |
Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции | |
| Определение: диагонали трапеции | |
| Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции | |
| Определение: высота трапеции | |
| Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение | |
| Свойство: точка пересечения диагоналей | |
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве | |
| Определение: средняя линия трапеции | |
| Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции | |
| Свойство: средняя линия трапеции | |
Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство | |
| Свойство: биссектрисы углов при боковой стороне трапеции | |
| Биссектрисы углов при боковой стороне трапеции перпендикулярны | |
| Трапеция |
Определение: Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции |
| Диагонали трапеции |
Определение: Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Высота трапеции |
Определение: Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Точка пересечения диагоналей |
Свойство: Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве |
| Средняя линия трапеции |
Определение: Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции Свойство: Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство |
| Биссектрисы углов при боковой стороне трапеции |
Свойство: Биссектрисы углов при боковой стороне трапеции перпендикулярны |
Подробнее со свойствами средней линии трапеции можно ознакомиться в разделе нашего справочника «Средняя линия трапеции».
В разделе нашего справочника «Типы четырёхугольников» представлена схема классификации трапеций. В том же разделе представлена таблица, в которой описаны всевозможные типы трапеций.
Свойства и признаки равнобедренных трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренная трапеция | Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. | |
| Свойство | Равенство углов при основании | Если трапеция является равнобедренной, то углы при каждом из её оснований равны. | |
| Признак | Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. | ||
| Свойство | Равенство диагоналей | Если трапеция является равнобедренной, то её диагонали равны. | |
| Признак | Если у трапеции диагонали равны, то она является равнобедренной | ||
| Свойство | Углы, которые диагонали образуют с основаниями | Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. | |
| Признак | Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. | ||
| Свойство | Описанная окружность | Если трапеция является равнобедренной, то около неё можно описать окружность. | |
| Признак | Если около трапеции можно описать окружность, то она является равнобедренной. | ||
| Свойство | Высоты трапеции | Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
| Определение: Равнобедренная трапеция | |
Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. | |
| Свойство: равенство углов при основании | |
| Если трапеция является равнобедренной, то углы при каждом из её оснований равны. | |
| Признак: равенство углов при основании | |
| Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. | |
| Свойство: равенство диагоналей | |
| Если трапеция является равнобедренной, то её диагонали равны. | |
| Признак: равенство диагоналей | |
| Если у трапеции диагонали равны, то она является равнобедренной | |
| Свойство: углы, которые диагонали образуют с основаниями | |
| Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. | |
| Признак: углы, которые диагонали образуют с основаниями | |
Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. | |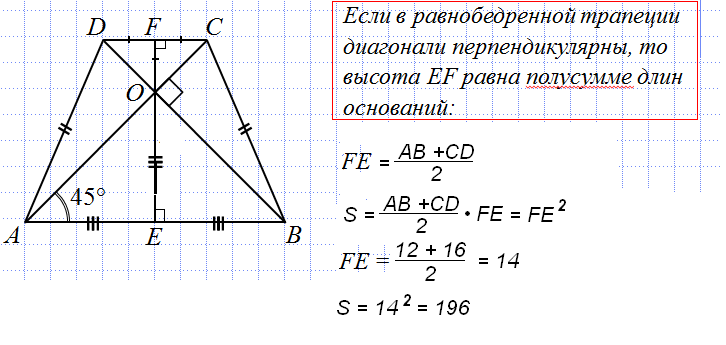
| Свойство: описанная окружность | |
| Если трапеция является равнобедренной, то около неё можно описать окружность. | |
| Признак: описанная окружность | |
| Если около трапеции можно описать окружность, то она является равнобедренной. | |
| Свойство: высоты трапеции | |
| Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований | |
| Равнобедренная трапеция |
Определение: Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Равенство углов при основании |
Свойство: Если трапеция является равнобедренной, то углы при каждом из её оснований равны. Признак: Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. |
| Равенство диагоналей |
Свойство: Если трапеция является равнобедренной, то её диагонали равны. Признак: Если у трапеции диагонали равны, то она является равнобедренной. |
| Углы, которые диагонали образуют с основаниями |
Свойство: Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. Признак: Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. |
| Описанная окружность |
Свойство: Если трапеция является равнобедренной, то около неё можно описать окружность. Признак: Если около трапеции можно описать окружность, то она является равнобедренной. |
| Высоты трапеции |
Свойство: Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Q5 Две диагонали равнобедренной трапеции равны x см и 3x 8 см Найдите значение x…
Перейти к
- Упражнение 27 (А)
- Упражнение 27(Б)
- Система счисления (закрепление чувства числа)
- Числа в Индии и международной системе (со сравнением)
- Место Значение
- Натуральные числа и целые числа (включая шаблоны)
- Номер строки
- HCF и LCM
- Игра с числами
- Соотношение
- Доля (включая словесные задачи)
- Унитарный метод
- Фракции
- Процент (Процент)
- Представление о скорости, расстоянии и времени
- Основные понятия (алгебра)
- Основные операции (связанные с алгебраическими выражениями)
- Замена (включая использование скобок в качестве группирующих символов)
- Обрамление алгебраических выражений (включая вычисление)
- Основные понятия (геометрия)
- Углы (с их типами)
- Свойства углов и линий (включая параллельные линии)
- четырехугольник
- Полигоны
- Круг
- Повторное упражнение по симметрии (включая построения по симметрии)
- Распознавание твердых тел
- Периметр и площадь плоских фигур
- Обработка данных (включая пиктограмму и гистограмму)
Главная > Селина Солюшнс Класс 6 Математика > Глава 27 — Четырехугольник > Упражнение 27(Б) > Вопрос 5
Вопрос 5 Упражнение 27(B)
В5) Две диагонали равнобедренной трапеции равны x см и (3x – 8) см.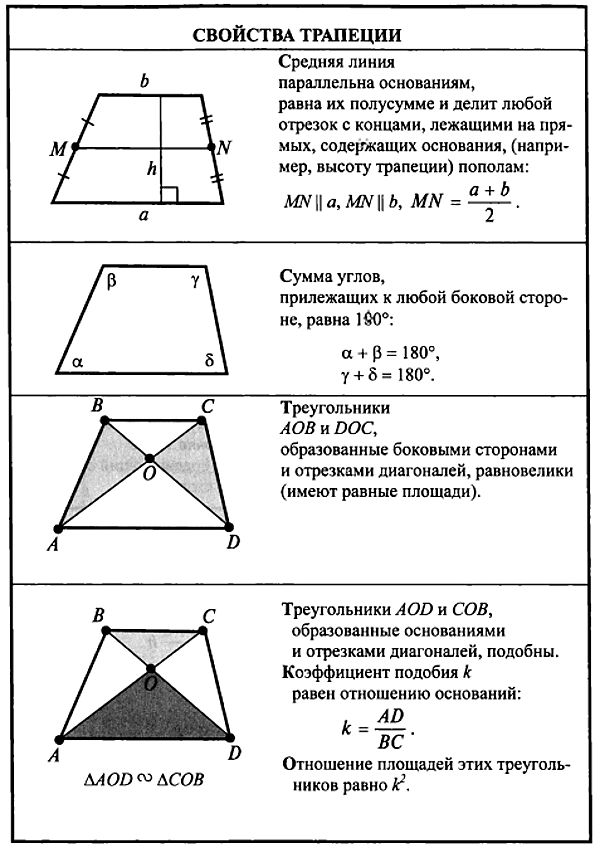
Найдите значение х.
Ответ:
Решение:
Диагонали равнобедренной трапеции имеют одинаковую длину
3x — 8 = x
3x — x = 8 см
2x = 8 см
x = 4 см x
- .
Стенограмма видео
Надеюсь, у вас все хорошо. Добро пожаловать, чтобы возглавить наши вопросы и ответы, которые Лидо делает еще раз с другим вопросом. Хорошо, на ESPN такого рода, так что это больница в определенный день, есть 15 весов. Тогда у нас есть уравнения. Мы рассмотрим их один за другим. Хорошо. Так что первое переставляем колеса в порядке убывания что разумнее делать так что самое высокое у нас это 3.1.
Белый рыцарь дважды 2,8 дважды два целых семь десятых. Итак, мы напишем дважды. Итак, две целых шесть десятых месяца два целых пять десятых. Да, так что мы можем видеть ключ 3.1, тогда мы определили самый низкий.
Солист ждать снова
Ясно по убыванию можно сказать 2,1. Итак, у нас были данные о 16 младенцах. Итак, 15 детей. Сколько демонов ребенок 2.5 детей по данным у нас есть и так и уходите тогда и увидимся в нашем следующем видео. Будьте здоровы и продолжайте тренироваться. Пока
Связанные вопросы
Q1) В трапеции ABCD сторона AB параллельна стороне DC. Если ∠A = 78° и ∠C = 120°, найдите углы B и…
Q2) В трапеции ABCD сторона AB параллельна стороне DC. Если ∠A = x° и ∠D = (3x – 20)°; найди ва…
Q3) Углы A, B, C и D трапеции ABCD относятся как 3 : 4 : 5 : 6.Le. ∠А : ∠Б : ∠С : ∠…
Q4) В равнобедренной трапеции одна пара противоположных сторон ….. друг к другу, а другая пара …
Q6) Угол А равнобедренной трапеции равен 115°; Найдите углы В, С и D.
Q7) Два противоположных угла параллелограмма равны 100° каждый. Найдите два других противоположных угла…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 27(A)
Упражнение 27(B)
Главы
Система счисления (Закрепление чувства числа)
Оценка
Числа в Индии и международной системе (с сравнением)
Значение места
Натуральные числа и целые числа (включая шаблоны)
Отрицательные числа и целые числа
Числовые линии
HCF и LCM
играют с номерами
Setss и LCM
.
Соотношение
Доля (включая задачи со словами)
Унитарный метод
Дроби
Десятичные дроби
Проценты (проценты)
Представление о скорости, расстоянии и времени
Основные понятия (алгебра)
Основные операции (относящиеся к алгебраическим выражениям)
Подстановка (включая использование скобок в качестве группирующих символов)
Обрамление алгебраических выражений (включая вычисление)
23 Линейные) Уравнения (включая текстовые задачи)
Основные понятия (геометрия)
Углы (с их типами)
Свойства углов и прямых (включая параллельные прямые)
Треугольники (включая типы, свойства и строительство)
Кваровнопочечные
Полигоны
Круг
Упражнения по симметрии (включая конструкции на симметрии)
Распознавание твердых веществ
Периметр и область плоскости
. (включая пиктограмму и гистограмму)
Среднее и медиана
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd.
Все права защищены. доказательство может быть полезным.
Студенты несколько минут работали в одиночку, размышляя о том, что было дано и что могло подразумеваться. Затем они работали со своей командой, чтобы обсудить свои идеи и приступить к планированию доказательства.
У некоторых было хорошее начало.
Некоторые явно практиковали поиск и использование структуры .
Некоторые застряли.
Я разговаривал с несколькими группами, выслушивая их план, задавая несколько вопросов, чтобы они не застряли.
И тут у меня достала цветная бумага, на которой нужно написать доказательство команды.
Часы тикали, но я думал, что они наверняка смогут обменяться доказательствами с другой командой для обратной связи в течение нескольких минут.
Я разговаривал с другой группой. Они отражали ∆ABC относительно линии AC.
Каким будет изображение ∆ABC относительно линии AC?
Ответ? ∆ACD.
Конечно, это неправильно. Кажется настолько очевидным, что ∆ABC не конгруэнтно ∆ACD. И мне также интересно, как это поможет нам доказать, что AC=BD, поскольку BD не находится ни в одном из этих треугольников. Но вот где эта команда студентов. Теперь у меня есть возможность поддержать их продуктивную борьбу , или я могу остановить продуктивную борьбу, дав им свое объяснение.
Мой выбор? Ножницы. и бумага. И еще время.
Что произойдет, если отразить ∆ABD относительно линии AC?
О! Треугольники не равны.
Итак, существуют ли конгруэнтные треугольники, которые могут привести нас к диагоналям?
∆ABC конгруэнтно ∆BAD.
Откуда вы знаете?
Отражение.
О чем?
Этот карандаш!
Так что же важно в линии, которую проводит карандаш?
Это линия симметрии трапеции.
Проходит через средние точки.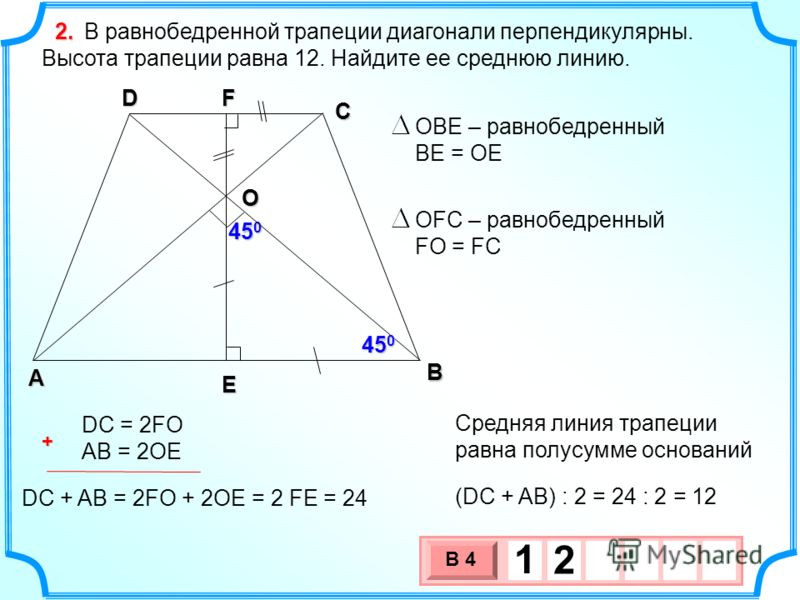
(Один из членов команды использовал программу динамической геометрии, чтобы отразить ∆ABC во время нашего разговора, но у меня нет фотографий ее работы.)
Таким образом, план был для команды написать свои доказательства на цветной бумаге, а затем обменяться мнениями с другими командами. Отличная идея, правда? Итак, как поступить, когда осталось 15 минут? Действовать в соответствии с планом и позволить им давать обратную связь без обсуждения всем классом? Или устроить обсуждение всего класса, чтобы соединить студенческую работу? Потому что, как оказалось, нет двух команд, доказывающих конгруэнтность диагоналей одинаково. Я выбрал последнее.
Я попросил первую команду поделиться своей работой.
Их доказательство нуждается в доработке. Но у них есть хорошая идея.
Они доказали, что ∆AMD≅∆BMC делает соответствующие стороны конгруэнтными, поэтому с помощью подстановки и постулата сложения отрезков мы можем показать, что диагонали конгруэнтны.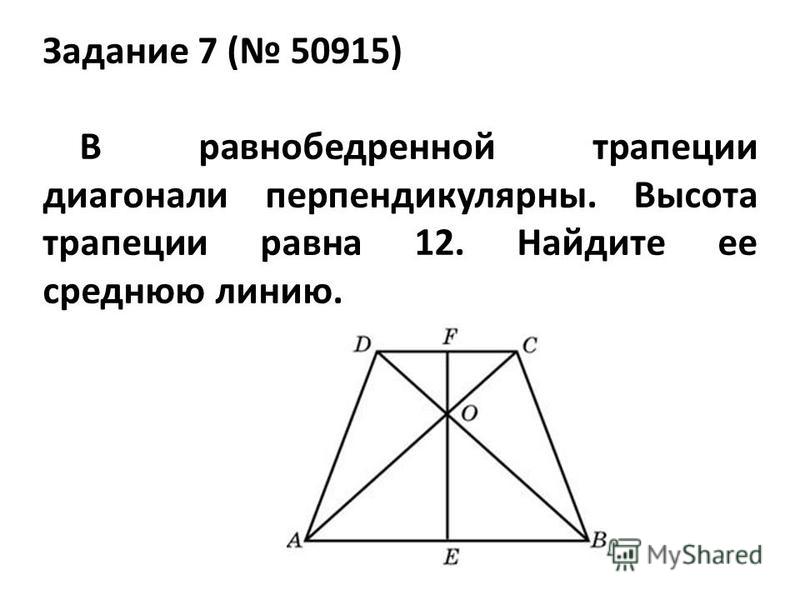
Затем я попросил команду поделиться тем, кто доказал ∆ABC≅∆BAD, используя размышления о линии, содержащей середины оснований. Их письменное доказательство тоже нуждается в доработке. Но у них была хорошая идея.
Другая команда доказала ∆ACD≅∆BDC.
Другая команда построила биссектрисы оснований. Так как основания параллельны, то прямая, перпендикулярная одному из них, будет перпендикулярна и другому. Я не уверен, что они нашли причину, по которой серединные перпендикуляры должны быть параллельными. Они могли бы использовать ∆AZD≅∆BZC, чтобы показать это. Вместо этого они использовали точку Z на обеих серединных перпендикулярах (они знают, что любая точка на серединном перпендикуляре отрезка равноудалена от концов отрезка), чтобы сделать вывод, что ∆AZB и ∆DZC равнобедренные, а затем использовали сложение отрезков. Постулат и замена, чтобы показать, что диагонали конгруэнтны. Не идеально. Но хорошее начало.
Обсуждение Принципов действий NCTM по поддерживает продуктивную борьбу в изучении математики говорит: «Учителя иногда воспринимают разочарование учеников или отсутствие немедленных успехов как индикаторы того, что они каким-то образом подвели своих учеников.
Leave A Comment