Решение задач. Конус 11 класс онлайн-подготовка на Ростелеком Лицей
Задача 1
Рис. 1. Иллюстрация к задаче
Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса (см. рис. 1).
Решение
Рис. 2. Подобные треугольники
Заметим, что у отсеченного конуса высота в два раза меньше высоты исходного. Рассмотрим осевое сечение большего и увидим, что треугольники подобны с коэффициентом 2 (см. рис. 2).
Значит, и образующая, и радиус также в два раза меньше.
По формуле , если мы уменьшим радиус и образующую вдвое, то правая часть уменьшится вчетверо, значит, ответ 3.
Ответ: 3.
Задача 2
Длина окружности основания конуса равна 3, а образующая равна 2. Найти площадь боковой поверхности конуса.
Решение
Ответ: 3.
Задача 3
Рис. 3. – искомый угол
Площадь боковой поверхности конуса в два раза больше площади его основания. Найти угол между образующей конуса и плоскостью его основания. Ответ дайте в градусах (см. рис. 3).
Решение
Значит, .
Теперь рассмотрим осевое сечение, проведем высоту (ось). Получим прямоугольный треугольник, в котором катет (радиус основания) вдвое меньше гипотенузы, значит, угол при радиусе равен 60 градусам (см. рис. 4).
Рис. 4. Иллюстрация к задаче
Ответ: 60 градусов.
Задача 4
Рис. 5. Сечение конуса
Рис. 6. Фигура в основании конуса
Радиус основания конуса равен 6, а его высота равна 8. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 4 (см. рис. 5). Найдите расстояние от центра основания конуса до плоскости сечения.
Решение
Рассмотрим основание конуса. Так как хорда в плоскости сечения равна 4, а радиус равен 6, имеем равнобедренный треугольник, высота которого по теореме Пифагора равна (см. рис. 6).
Так как хорда в плоскости сечения равна 4, а радиус равен 6, имеем равнобедренный треугольник, высота которого по теореме Пифагора равна (см. рис. 6).
Рис. 7. Конечный рисунок
Рассмотрим треугольник ( – вершина конуса). Докажем, что высота этого треугольника и есть искомое расстояние. Во-первых, по построению. Во-вторых, плоскость (т.к. перпендикулярно и ), а значит, .
Следовательно, – искомое расстояние. По теореме Пифагора . А тогда .
Ответ: .
Задача 5
Рис. 8. Вращаемый треугольник
Рис. 9. Тело, полученное при вращении равнобедренного треугольника
Равнобедренный треугольник, боковая сторона которого равна , а угол при основании равен , вращается вокруг своего основания (см. рис. 8). Найти площадь поверхности полученного при вращении тела (см. рис. 9).
Решение
Рис. 10. Два равных конуса
Если провести в треугольнике высоту из вершины, то получается два прямоугольных треугольника, вращая которые мы получаем два равных конуса, прилегающих друг к другу основаниями (см. рис. 10).
рис. 10).
Значит, площадь поверхности искомого тела равна удвоенной площади боковой поверхности любого из конусов. Таким образом, нам надо найти радиус основания и образующую конуса (см. рис. 11).
Рис. 11. Иллюстрация к последнему шагу
Радиус основания конуса равен высоте исходного треугольника, а образующая – боковой стороне. Очевидно, высота равна , а значит, , таким образом, окончательный ответ: .
Ответ: .
Заключение
Сегодня мы решили несколько задач с площадями боковой и полной поверхностей конуса.
Список рекомендованной литературы
- Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. — М.: Просвещение, 2009. — 255 с.
- Геометрия 11 класс, А.В. Погорелов, М.: Просвещение, 2002
- Рабочая тетрадь по геометрии 11 класс, В.Ф. Бутузов, Ю.А. Глазков
Рекомендованные ссылки на ресурсы сети Интернет
- Egemaximum.
 ru (Источник).
ru (Источник). - Matematikalegko.ru (Источник).
- 2mb.ru (Источник).
Домашнее задание
- Найдите угол при вершине осевого сечения конуса, если образующая конуса в два раза больше его высоты.
- Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 4 раза?
С.р.конус решение задач
Вариант 1. База задание
1.) Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
2.) Высота конуса равна 36, образующая равна 45. Найдите площадь его полной поверхности, деленную на .
3.) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 11 раз?
4.) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 10 раз?
5. ) Высота конуса равна 48, а диаметр основания — 72. Найдите образующую конуса
) Высота конуса равна 48, а диаметр основания — 72. Найдите образующую конуса
6.) Высота конуса равна 60, а длина образующей — 87. Найдите диаметр основания конуса.
7.) Диаметр основания конуса равен 126, а длина образующей — 87. Найдите высоту конуса.
Вариант 1. Профиль
1.) Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
2.) Площадь основания конуса равна , высота — 15. Найдите площадь осевого сечения конуса.
3.) Высота конуса равна 40, а длина образующей — 50. Найдите площадь осевого сечения этого конуса.
4.) Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
5.) Радиусы оснований усеченного конуса равны 3 см и 6 см, а высота равна 4 см. Найдите площадь осевого сечения и боковой поверхности усеченного конуса.
Найдите площадь осевого сечения и боковой поверхности усеченного конуса.
Вариант 2 База
1.) Длина окружности основания конуса равна 6, образующая равна 2. Найдите площадь боковой поверхности конуса.
2.) Высота конуса равна 21, образующая равна 35. Найдите площадь его полной поверхности, деленную на .
3.) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 9 раз?
4.) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 2 раза?
5. ) Высота конуса равна 30, а диаметр основания — 32. Найдите образующую конуса.
6. ) Высота конуса равна 48, а длина образующей — 52. Найдите диаметр основания конуса.
7.) Диаметр основания конуса равен 40, а длина образующей — 52. Найдите высоту конуса.
Вариант 2 Профиль
1.) Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
2.) Площадь основания конуса равна , высота — 9. Найдите площадь осевого сечения конуса.
3.) Высота конуса равна 32, а длина образующей — 40. Найдите площадь осевого сечения этого конуса.
4) Площадь полной поверхности конуса равна 84. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
5. ) Радиусы оснований усеченного конуса 12 см и 6 см, высота его равна 8 см. Найдите образующую усеченного конуса, площадь осевого сечения, площадь боковой и полной поверхности усеченного конуса.
Вариант 3 База
1.) Длина окружности основания конуса равна 5, образующая равна 8. Найдите площадь боковой поверхности конуса.
2. ) Высота конуса равна 24, образующая равна 26. Найдите площадь его полной поверхности, деленную на .
3. ) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 22 раза?
4. ) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 40 раз?
) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 40 раз?
5. ) Высота конуса равна 96, а диаметр основания – 56. Найдите образующую конуса.
6. ) Высота конуса равна 30, а длина образующей — 34. Найдите диаметр основания конуса.
7. ) Диаметр основания конуса равен 120, а длина образующей — 65. Найдите высоту конуса.
Вариант 3 Профиль
1.) Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
2. ) Площадь основания конуса равна 36π, высота — 3. Найдите площадь осевого сечения конуса.
3.) Высота конуса равна 24, а длина образующей — 25. Найдите площадь осевого сечения этого конуса.
4) Площадь полной поверхности конуса равна 148. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Найдите площадь полной поверхности отсеченного конуса.
5.) Радиусы оснований усеченного конуса равны 3 см и 6 см, а высота равна 4 см. Найдите площадь осевого сечения и боковой поверхности усеченного конуса.
Вариант 4 База
1.) Длина окружности основания конуса равна 7, образующая равна 8. Найдите площадь боковой поверхности конуса.
2.) Высота конуса равна 40, образующая равна 50. Найдите площадь его полной поверхности, деленную на .
3.) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 35 раз?
4. ) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 28 раз?
5. ) Высота конуса равна 57, а диаметр основания – 152. Найдите образующую конуса.
6. ) Высота конуса равна 64, а длина образующей — 80. Найдите диаметр основания конуса
7. ) Диаметр основания конуса равен 96, а длина образующей — 80.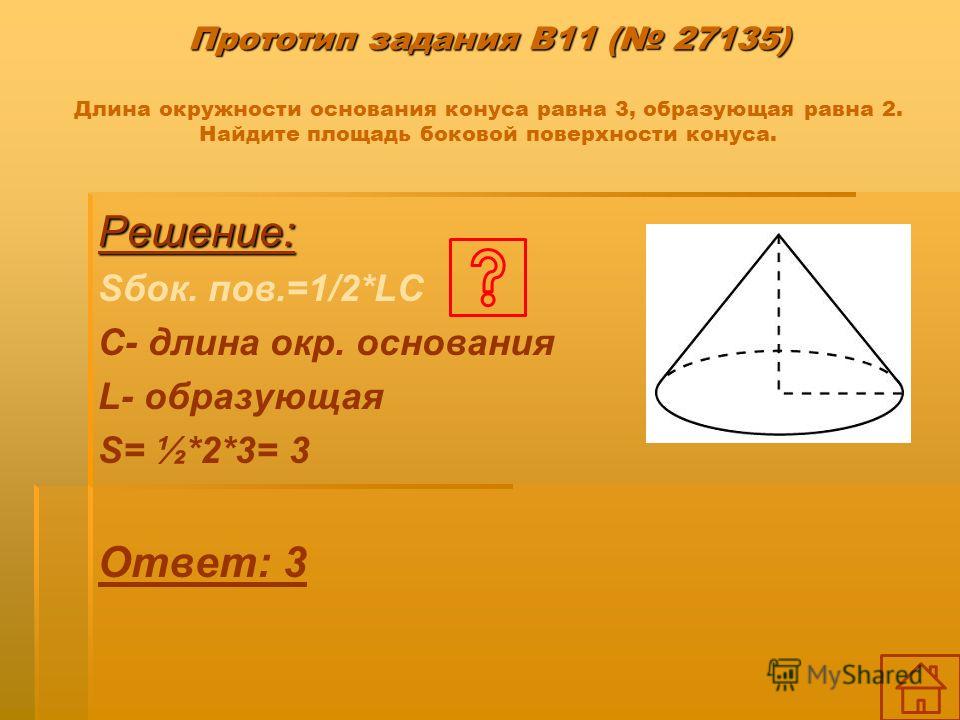 Найдите высоту конуса.
Найдите высоту конуса.
Вариант 4 Профиль
1.) Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
2.) Площадь основания конуса равна , высота — 10. Найдите площадь осевого сечения конуса.
3.) Высота конуса равна 16, а длина образующей — 20. Найдите площадь осевого сечения этого конуса.
4) Площадь полной поверхности конуса равна 36. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
5.) Радиусы оснований усеченного конуса 12 см и 6 см, высота его равна 8 см. Найдите образующую усеченного конуса, площадь осевого сечения, площадь боковой и полной поверхности усеченного конуса.
Вариант 5 База задание 13
1.Длина окружности основания конуса равна 2, образующая равна 5. Найдите площадь боковой поверхности конуса.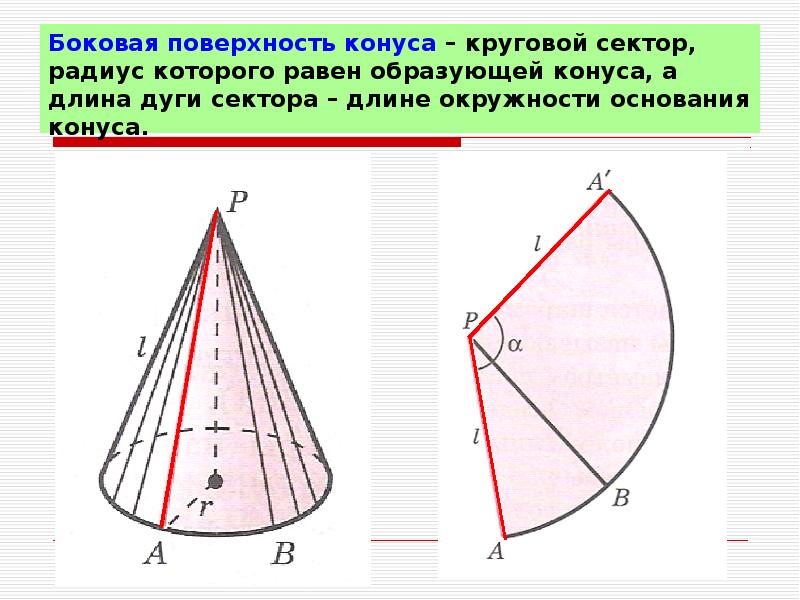
2. Высота конуса равна 28, образующая равна 35. Найдите площадь его полной поверхности, деленную на .
3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 40 раз?
4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 15 раз?
5. Высота конуса равна 15, а диаметр основания – 16. Найдите образующую конуса.
6. Высота конуса равна 96, а длина образующей — 100. Найдите диаметр основания конуса.
7. Диаметр основания конуса равен 56, а длина образующей — 100. Найдите высоту конуса.
Проф. Задание 8
1. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
2.Площадь основания конуса равна , высота — 2. Найдите площадь осевого сечения конуса.
3. Высота конуса равна 36, а длина образующей — 39.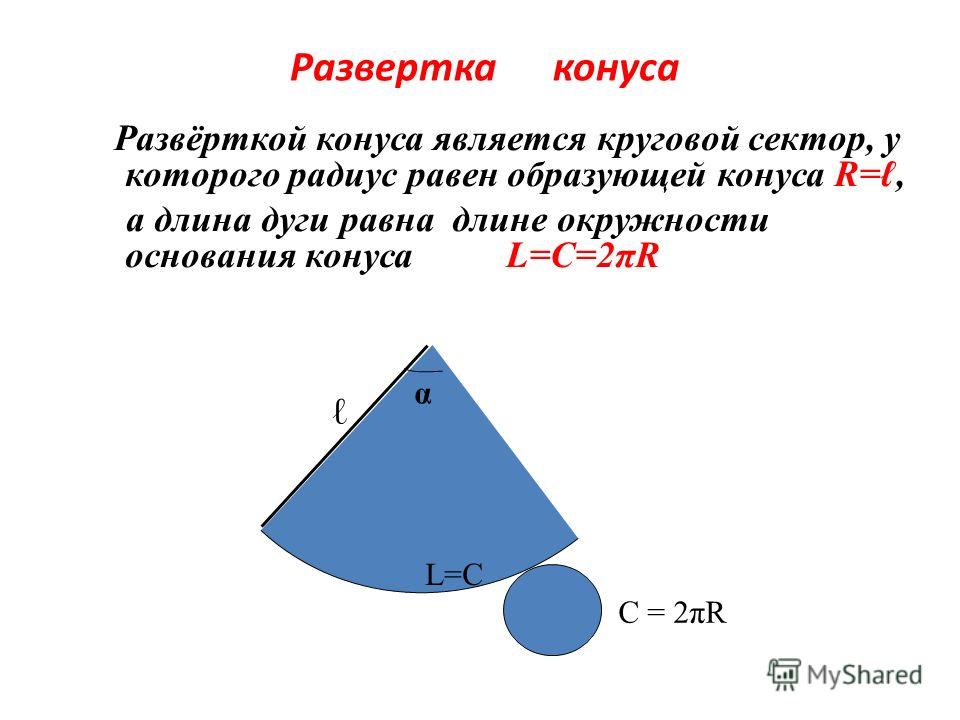 Найдите площадь осевого сечения этого конуса.
Найдите площадь осевого сечения этого конуса.
4)* Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Вариант 6 База задание 13
1.Длина окружности основания конуса равна 3, образующая равна 8. Найдите площадь боковой поверхности конуса.
2. Высота конуса равна 15, образующая равна 17. Найдите площадь его полной поверхности, деленную на .
3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 20 раз?
4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 19 раз?
5. Высота конуса равна 21, а диаметр основания – 144. Найдите образующую конуса.
6. Высота конуса равна 57, а длина образующей — 95. Найдите диаметр основания конуса.
7. Диаметр основания конуса равен 152, а длина образующей — 95. Найдите высоту конуса.
Найдите высоту конуса.
Проф. Задание 8
1.Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
2. Площадь основания конуса равна , высота — 8. Найдите площадь осевого сечения конуса.
3.Высота конуса равна 28, а длина образующей — 35. Найдите площадь осевого сечения этого конуса.
4)*Площадь полной поверхности конуса равна 84. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Вариант 7. База задание 13
1.Длина окружности основания конуса равна 4, образующая равна 6. Найдите площадь боковой поверхности конуса.
2. Высота конуса равна 20, образующая равна 25. Найдите площадь его полной поверхности, деленную на .
3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз?
4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 8 раз?
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 8 раз?
5. Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса.
6. Высота конуса равна 21, а длина образующей — 75. Найдите диаметр основания конуса.
7. Диаметр основания конуса равен 144, а длина образующей — 75. Найдите высоту конуса.
Проф. Задание 8
1.Площадь боковой поверхности конуса в раз больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
2.Площадь основания конуса равна , высота — 20. Найдите площадь осевого сечения конуса.
3.Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
4)* Площадь полной поверхности конуса равна 148. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
1. Осевое сечение конуса – равносторонний треугольник. Площадь боковой поверхности конуса равна
5см2. Найти площадь полной поверхности.
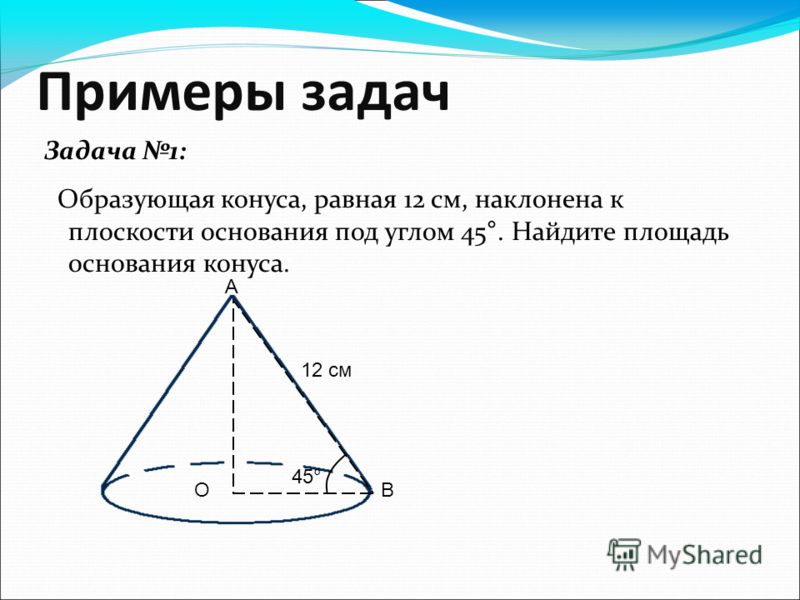
2. Образующая конуса наклонена к плоскости основания под углом 300, а высота конуса равна 12 см.
Найдите площадь боковой поверхности конуса.
3. Радиусы оснований усеченного конуса равны 3 см и 6 см, а высота равна 4 см. Найдите площадь
осевого сечения и боковой поверхности усеченного конуса.
4. Радиусы оснований усеченного конуса 12 см и 6 см, высота его равна 8 см. Найдите образующую
усеченного конуса, площадь осевого сечения, площадь боковой и полной поверхности усеченного
конуса.
5. Высота конуса равна 2 √3 см. Найдите площадь осевого сечения конуса, если оно является
правильным треугольником.
6.Прямоугольная трапеция вращается вокруг стороны АВ, угол А равен 90 градусов, угол Д равен 30 градусов, высота ДН, проведенная из вершины Д равна 7 см, ВС = 10 см. Найти площадь боковой и полной поверхности получившегося тела вращения.
Калькулятор площади поверхности конуса
Калькулятор площади поверхности конуса поможет вам вычислить площадь поверхности любого правильного конуса . В тексте ниже мы покажем вам площадь поверхности формулы конуса и как ее получить. Воспользовавшись нашим калькулятором и прочитав эту статью, вы будете очень уверены в том, как найти площадь поверхности конуса.
Для какого типа конуса подходит этот калькулятор?
Прежде чем мы объясним, как использовать наш калькулятор площади поверхности конуса, давайте сначала определим, на каком типе конуса вы можете его использовать. Общая форма конуса состоит из круглого или овального основания и вершины (или кончика) над основанием, соединенной с периметром базовой формы.
Этот калькулятор предназначен для конкретного типа конуса, называемого правым конусом (как показано на схеме над калькулятором). Он имеет круглое основание , а вершина находится прямо над центром основания. Следовательно, угол между основанием и воображаемой линией между основанием и вершиной равен 90°90\градус90°, обычно известный как прямой угол .
Следовательно, угол между основанием и воображаемой линией между основанием и вершиной равен 90°90\градус90°, обычно известный как прямой угол .
Этот инструмент нельзя использовать для наклонных конусов , у которых вершина не в центре. Для тех, кто знаком с расширенным исчислением, вы можете узнать больше о вычислении площади поверхности наклонного конуса, прочитав это обсуждение проблемы.
Как использовать калькулятор площади поверхности конуса
Калькулятор очень прост в использовании. Давайте рассмотрим это шаг за шагом:
Введите значение радиуса круглого основания. Помните, что радиус равен половине диаметра окружности. Вы можете выбрать разные единицы длины в зависимости от проблемы или выполненного измерения. Вместо можно ввести окружность круглого основания.
Введите высоту конуса или наклонную высоту
 Высота равна перпендикулярному расстоянию между вершиной конуса и центром круглого основания. Наклонная высота — это расстояние между кончиком и внешним краем (периметром) основания.
Высота равна перпендикулярному расстоянию между вершиной конуса и центром круглого основания. Наклонная высота — это расстояние между кончиком и внешним краем (периметром) основания.
Имейте в виду, что высота конуса должна быть на больше нуля и что высота наклона (если вы его вводите) должен быть на длиннее радиуса основания.
- Затем будет отображаться площадь поверхности
Как вычислить площадь поверхности конуса по формуле
Чтобы лучше понять, как работает этот калькулятор, мы рассмотрим формулу площади поверхности конуса и 92Abase=π⋅r2
где:
- AbaseA_{\text{base}}Abase — площадь поверхности основания конуса;
- π\piπ — отношение длины окружности к диаметру круга; и
- rrr — Радиус окружности.

Позже мы добавим это уравнение площади основания к уравнению, которое мы выведем для боковой площади прямого конуса.
Представьте конус без основания, сделанный из бумаги. Вы потом раскатываете, так лежит квартира на столе . У вас получится форма, как на схеме выше. Это часть (или сектор) большего круга, радиус которого (l) равен наклонной высоте конуса . Длина дуги сектора ( c ) эквивалентна окружности основания конуса.
Объединив уравнение, используемое для расчета площади сектора с точки зрения радиуса и угла, с уравнением длины дуги сектора, мы можем записать площадь сектора как:
Alat=12⋅c⋅lA_{\text{lat}} = \frac{1}{2}\cdot c\cdot lAlat=21⋅c⋅l
где:
- AlatA_{\text {lat}}Alat — Боковая площадь конуса
- ccc — Длина дуги сектора и, следовательно, длина окружности конуса
- lll — Радиус сектора и наклонная высота конуса
Теперь, используя формулу для длины окружности c=2⋅π⋅rc = 2\cdot\pi\cdot rc=2⋅π⋅r, приведенное выше уравнение можно переписать в терминах радиуса основания конуса: 92}\right)A=π⋅r⋅(r+h3+r2
)
где:
- hhh — перпендикулярная высота конуса.
 2
\end{split}A=π⋅r⋅(r+h3+r2 92
\end{split}A=π⋅r⋅(r+l)=π⋅5⋅(5+15)=314,16 in2
2
\end{split}A=π⋅r⋅(r+h3+r2 92
\end{split}A=π⋅r⋅(r+l)=π⋅5⋅(5+15)=314,16 in2Теперь вы знаете, как найти площадь поверхности конуса, и уравнения, лежащие в основе это площадь поверхности конуса калькулятор.
Если вам нужно рассчитать площадь поверхности других трехмерных геометрических фигур, почему бы не попробовать наш калькулятор площади поверхности?
Часто задаваемые вопросы
Как найти площадь боковой поверхности конуса данной высоты?
Чтобы определить площадь боковой поверхности конуса по его перпендикулярной высоте и радиусу, необходимо:
Вычислить квадраты высоты и радиуса и сложить их вместе.
Извлеките квадратный корень из результата шага 1.
Умножить на радиус.
Умножить на π ≈ 3,14 .
Вот оно! В результате вы получите площадь боковой поверхности вашего конуса.
Какова площадь поверхности конуса высотой 4 и радиусом 3?
Ответ 113.
 1 . Чтобы получить этот результат, вам нужно применить формулу A = πr(r + √(h² + r²)) с r = 3 и h = 4 . Помните, что ответ в квадратных единицах.
1 . Чтобы получить этот результат, вам нужно применить формулу A = πr(r + √(h² + r²)) с r = 3 и h = 4 . Помните, что ответ в квадратных единицах.Все о прямых круглых конусах
Прямой круглый конус представляет собой трехмерную фигуру с круглым основанием. Поверхность конуса порождается линией (образующей), проходящей через неподвижную точку на окружности основания и движущейся по плоскости, не пересекающей основание. Если плоскость пересекает окружность, то получается косой круговой конус. Пересечение плоскости с боковой поверхностью конуса называется направляющей конуса. Точка пересечения образующей и директрисы называется вершиной конуса. Наклонная высота — это перпендикулярное расстояние между направляющей и образующей в любой точке на их линиях пересечения с боковой поверхностью. Высота — это перпендикулярное расстояние между директрисой и плоскостью основания.
 Линия, соединяющая любую точку окружности с любой точкой этой плоскости, будет частью поверхности искомого конуса; такая линия называется образующей конуса. Если мы проведем через V любую другую плоскость, она вырежет другую часть этой поверхности; все точки, общие для этой плоскости и поверхности твердого тела, лежат на двух окружностях, одна в плоскости, а другая на поверхности, как показано в (а) на рисунке 2. Но если мы возьмем еще одну плоскость через V, скажем, под углом θ к первой плоскости как показано на (b), это снова вырежет какую-то другую часть поверхности; общие точки теперь лежат на двух окружностях, но также и на двух эллипсах, как видно из рисунка 3.92, где b теперь представляет собой длину большой полуоси. В отличие от эллипса или окружности может быть более одного значения наклонной высоты, соответствующих заданным значениям h и b (и, следовательно, r1 и r2).
Линия, соединяющая любую точку окружности с любой точкой этой плоскости, будет частью поверхности искомого конуса; такая линия называется образующей конуса. Если мы проведем через V любую другую плоскость, она вырежет другую часть этой поверхности; все точки, общие для этой плоскости и поверхности твердого тела, лежат на двух окружностях, одна в плоскости, а другая на поверхности, как показано в (а) на рисунке 2. Но если мы возьмем еще одну плоскость через V, скажем, под углом θ к первой плоскости как показано на (b), это снова вырежет какую-то другую часть поверхности; общие точки теперь лежат на двух окружностях, но также и на двух эллипсах, как видно из рисунка 3.92, где b теперь представляет собой длину большой полуоси. В отличие от эллипса или окружности может быть более одного значения наклонной высоты, соответствующих заданным значениям h и b (и, следовательно, r1 и r2).В заключение, помните, что прямой круглый конус имеет круглое основание, а наклонный круглый конус имеет некруглое основание.
 Если вы когда-нибудь застревали, пытаясь вспомнить, что есть что, просто подумайте о «правом» и «наклонном» — слово «правый» состоит из пяти букв, как и «круглый», а «наклонный» состоит из семи букв, как и «некруглый». .» Теперь вы больше никогда их не перепутаете!
Если вы когда-нибудь застревали, пытаясь вспомнить, что есть что, просто подумайте о «правом» и «наклонном» — слово «правый» состоит из пяти букв, как и «круглый», а «наклонный» состоит из семи букв, как и «некруглый». .» Теперь вы больше никогда их не перепутаете!Каковы свойства прямого кругового конуса?
Прямоугольные конусы обладают рядом интересных свойств. Они осесимметричны относительно своей оси, что означает, что они выглядят одинаково независимо от того, как вы их вращаете. Они также имеют круглое основание, что означает, что их поперечные сечения всегда являются кругами. Наконец, у них есть точка на вершине, которая является точкой, наиболее удаленной от их основания.
Как образуется правильный круговой конус?
Прямой круговой конус образуется, когда плоскость пересекает цилиндр таким образом, что пересечение представляет собой окружность. Окружность может быть как верхней, так и нижней частью цилиндра, а плоскость может пересекать цилиндр под любым углом.


 ru (Источник).
ru (Источник). Высота равна перпендикулярному расстоянию между вершиной конуса и центром круглого основания. Наклонная высота — это расстояние между кончиком и внешним краем (периметром) основания.
Высота равна перпендикулярному расстоянию между вершиной конуса и центром круглого основания. Наклонная высота — это расстояние между кончиком и внешним краем (периметром) основания.
 2
\end{split}A=π⋅r⋅(r+h3+r2 92
\end{split}A=π⋅r⋅(r+l)=π⋅5⋅(5+15)=314,16 in2
2
\end{split}A=π⋅r⋅(r+h3+r2 92
\end{split}A=π⋅r⋅(r+l)=π⋅5⋅(5+15)=314,16 in2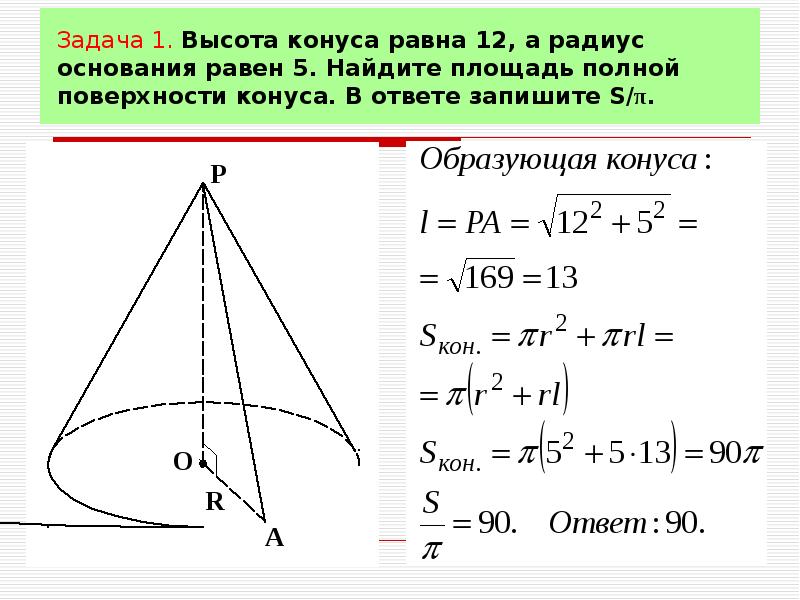 1 . Чтобы получить этот результат, вам нужно применить формулу A = πr(r + √(h² + r²)) с r = 3 и h = 4 . Помните, что ответ в квадратных единицах.
1 . Чтобы получить этот результат, вам нужно применить формулу A = πr(r + √(h² + r²)) с r = 3 и h = 4 . Помните, что ответ в квадратных единицах. Линия, соединяющая любую точку окружности с любой точкой этой плоскости, будет частью поверхности искомого конуса; такая линия называется образующей конуса. Если мы проведем через V любую другую плоскость, она вырежет другую часть этой поверхности; все точки, общие для этой плоскости и поверхности твердого тела, лежат на двух окружностях, одна в плоскости, а другая на поверхности, как показано в (а) на рисунке 2. Но если мы возьмем еще одну плоскость через V, скажем, под углом θ к первой плоскости как показано на (b), это снова вырежет какую-то другую часть поверхности; общие точки теперь лежат на двух окружностях, но также и на двух эллипсах, как видно из рисунка 3.92, где b теперь представляет собой длину большой полуоси. В отличие от эллипса или окружности может быть более одного значения наклонной высоты, соответствующих заданным значениям h и b (и, следовательно, r1 и r2).
Линия, соединяющая любую точку окружности с любой точкой этой плоскости, будет частью поверхности искомого конуса; такая линия называется образующей конуса. Если мы проведем через V любую другую плоскость, она вырежет другую часть этой поверхности; все точки, общие для этой плоскости и поверхности твердого тела, лежат на двух окружностях, одна в плоскости, а другая на поверхности, как показано в (а) на рисунке 2. Но если мы возьмем еще одну плоскость через V, скажем, под углом θ к первой плоскости как показано на (b), это снова вырежет какую-то другую часть поверхности; общие точки теперь лежат на двух окружностях, но также и на двух эллипсах, как видно из рисунка 3.92, где b теперь представляет собой длину большой полуоси. В отличие от эллипса или окружности может быть более одного значения наклонной высоты, соответствующих заданным значениям h и b (и, следовательно, r1 и r2).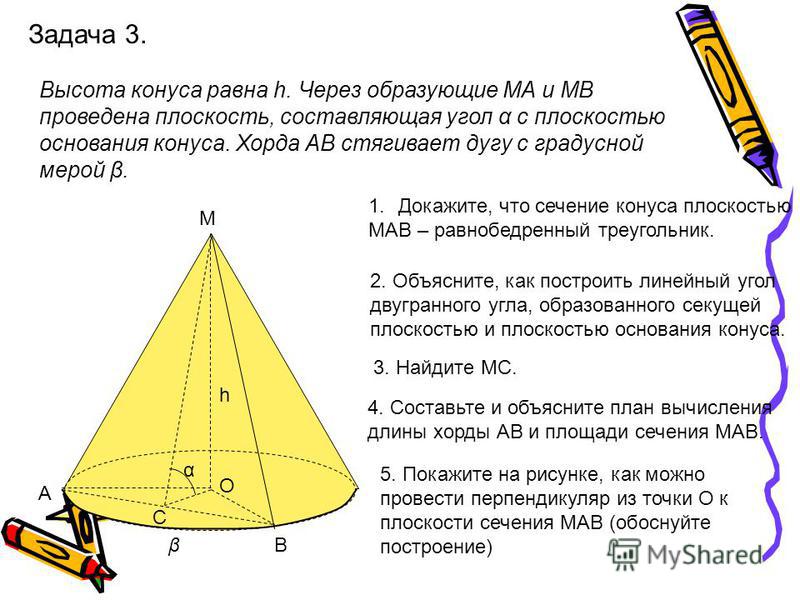 Если вы когда-нибудь застревали, пытаясь вспомнить, что есть что, просто подумайте о «правом» и «наклонном» — слово «правый» состоит из пяти букв, как и «круглый», а «наклонный» состоит из семи букв, как и «некруглый». .» Теперь вы больше никогда их не перепутаете!
Если вы когда-нибудь застревали, пытаясь вспомнить, что есть что, просто подумайте о «правом» и «наклонном» — слово «правый» состоит из пяти букв, как и «круглый», а «наклонный» состоит из семи букв, как и «некруглый». .» Теперь вы больше никогда их не перепутаете!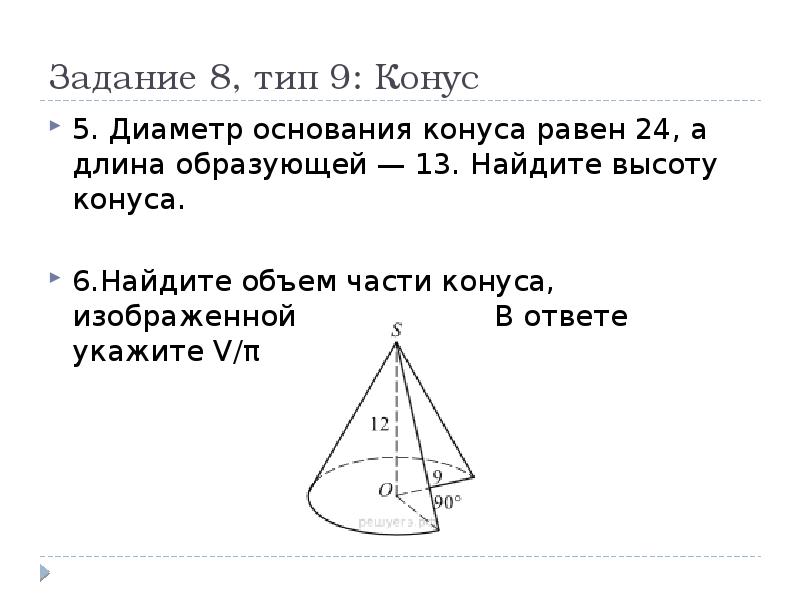
Leave A Comment