Медиана треугольника делит его на два равновеликих треугольника: Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Справочник по математике

Геометрия (Планиметрия)

Треугольники

      Определение. Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Рис.1

      Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

      На рисунке 1 медианой является отрезок BD.

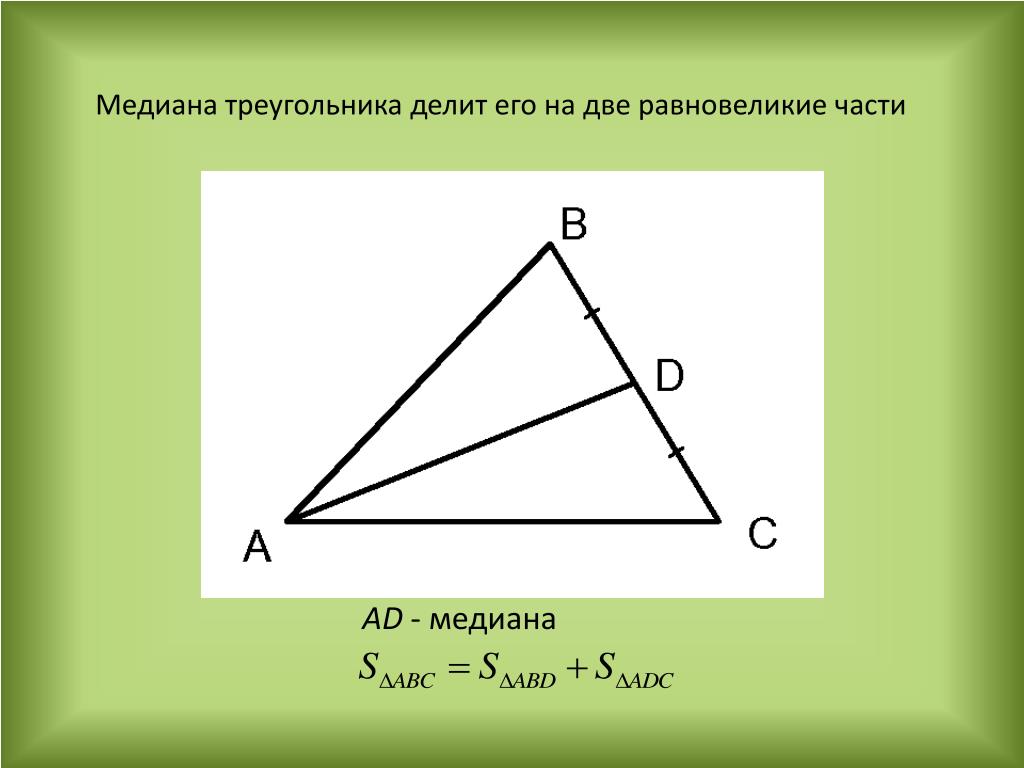
      Утверждение 1. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).

      Доказательство. Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

Рис.2

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

      Поскольку отрезок BD является медианой, то

что и требовалось доказать.

      Утверждение 2. Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1, считая от вершины треугольника.

      Доказательство. Рассмотрим две любых медианы треугольника, например, медианы AD и CE, и обозначим точку их пересечения буквой O (рис. 3).

Рис.3

      Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Рис.4

      Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Рис.5

      Сторона ED этого четырёхугольника является средней линией в треугольнике ABC. Следовательно,

      Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC. Следовательно,

откуда вытекает, что стороны ED и FG четырёхугольника FEDG равны и параллельны. Следовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммом, а у параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополам (рис.6).

Рис.6

      Таким образом,

| FO | = | OD | ,       | GO | = | OE | .

      Следовательно,

| AF | = | FO | = | OD | ,       | CG | = | GO | = | OE | .

      Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении   2 : 1, считая от вершины треугольника.

      Доказательство завершено.

      Следствие. Все три медианы треугольника пересекаются в одной точке.

      Доказательство. Рассмотрим медиану AD треугольника ABC и точку O, которая делит эту медиану в отношении   2 : 1, считая от вершины A (рис.7).

Рис.7

      Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

      Определение. Точку пересечения медиан треугольника называют центроидом треугольника.

      Утверждение 3. Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Рис.8

      Доказательство. Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC, равна  площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Рис.9

      Тогда

      В силу утверждения 1,

что и требовалось доказать.

      Утверждение 4. Длина медианы треугольника (рис. 10) вычисляется по формуле:

Рис.10

      Доказательство. Воспользуемся теоремой косинусов, примененной к треугольникам DBC и ABD:

      Складывая эти равенства, получим:

что и требовалось доказать.

      Следствие. Длины медиан и длины сторон треугольника связаны формулой

      Доказательство. В силу утверждения 4 справедливы равенства:

      Складывая эти равенства, получим:

что и требовалось доказать.

      Утверждение 5. В параллелограммепараллелограмме сумма квадратов диагоналей равна сумме квадратов сторон.

      Доказательство. Рассмотрим рисунок 11.

Рис.11

      Поскольку AO – медиана треугольника ABD, а DO – медиана треугольника ADC, то, в силу утверждения 4, справедливы равенства:

      Следовательно,

d₁² = 2a² + 2b² – d₂²,

d₂² = 2a² + 2b² – d₁².

      Складывая эти равенства, получим

что и требовалось доказать.

      Утверждение 6. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы (рис. 12).

Рис. 12

      Доказательство. Продолжим медиану CO за точку O до точки D так, чтобы было выполнено равенство CO = OD, и соединим полученную точку D с точками A и B (рис. 13).

Рис.13

      Получим четырехугольник ADBC, диагонали которого в точке пересечения делятся пополам. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма заключаем, что четырехугольник ADBC является параллелограммом, а поскольку полученный параллелограмм содержит прямой угол C, то и все его углы прямые, следовательно, четырехугольник ADBC – прямоугольникпрямоугольник. Поскольку диагонали прямоугольника равны, получаем равенства:

что и требовалось доказать.

      Следствие. Середина гипотенузы прямоугольного треугольника является центром описанной около треугольника окружности (рис. 14).

Рис.14

      Утверждение 7. Рассмотрим в пространстве или на плоскости декартову систему координат с началом в точке O и произвольный треугольник ABC. Если обозначить буквой M точку пересечения медиан этого треугольника (рис.15), то будет справедливо равенство

Рис.15

      Доказательство. По свойствам векторов

      Далее получаем

что и требовалось доказать.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

что это такое в геометрии, ее свойства, как построить и найти

Определение медианы в треугольнике

Определение 1

Медиана — важное понятие в геометрии. Это отрезок, проведенный из вершины треугольника, и делящий противоположную сторону пополам. Это «говорящее» название, оно произошло от латинского слова mediāna, что значит «середина».

На чертеже медиана выглядит так:

Красная линия — медиана. Для ΔABС отрезок АD — медиана к стороне BС, при этом BD=DC. Для ΔMNK NO — медиана из ∠MNK к NK, MO=OK. Равенство отрезков на рисунке обозначают одинаковым количеством черточек. Сколько медиан у треугольника? Их столько же, сколько и сторон, то есть три.

 Характерные особенности медианы

Медиана обладает многими свойствами, ниже их краткое перечисление. Некоторые из них будут рассмотрены подробнее.

1. Медиана треугольника делит его на два равновеликих треугольника: S▵ACD=S▵BDC  , S▵MNO=S▵ONK
2. Все медианы треугольника пересекаются в одной точке и разбивают его на 6 треугольников одной площади.
3. Медиана, проведенная из прямого угла прямоугольного треугольника, равна половине гипотенузы: CD=½AB=AD=BD.
4. У правильного или равностороннего треугольника медиана является одновременно биссектрисой и высотой, проведенными из того же угла.
5. У равнобедренного треугольника совпадают медиана, биссектриса и высота, которые проводятся к основанию.
6. Для нахождения длины медианы треугольника используется следующая формула: BD=12a2+12c2-14b2, где BD — медиана, а a, b и c — стороны треугольника.

Формулы и соотношения связанные с медианой

Пересечение медиан треугольника

Теорема 1

Медианы треугольника пересекаются в одной точке, которая делит их в отношении 2:1 от вершины.

Доказательство:

Строим медианы AD и CM треугольника ABC, пересекающиеся в точке О.

Найдем середины L и H отрезков ОA и ОC, и рассмотрим четырехугольник DHLM.

Его стороны MD и HL параллельны и равны как средние линии ΔABC и ΔAOC с общей стороной AC.

Из этого делаем вывод, что DHLM — параллелограмм.

Поскольку точка пересечения делит диагонали параллелограмма пополам, то OD = ОL.

L — середина отрезка ОA ⇒ AL = LO = ОD. Значит, AО:ОD = 2:1. Также CО:ОM = 2:1.

Остается доказать, что третья медиана BK проходит через точку О.

Пусть медианы BK и AD пересекаются в точке O1. Тогда по доказанному AO1:O1D=2:1.

Учитывая, что и AO:OD=2:1, заключаем, что точки O1 и О делят отрезок AD в одном и том же отношении.

А это значит, что точка O1 совпадает с точкой О.

Из этого сделаем окончательный вывод: медиана BK проходит через точку О пересечения медиан AD и CM.

Теорема о трех медианах и шести равновеликих треугольниках

 Теорема 2

Три медианы треугольника пересекаются в одной точке и делят его на 6 треугольников с равной площадью.

Доказательство:

Докажем, что S▵AOM=S▵MOB=S▵BOD=S▵DOC=S▵COK=S▵KOA

1. Построим медианы ΔABС.
2. Из вершины B опустим перпендикуляр BP на медиану AD и рассмотрим ΔBDO. S▵BOD=½OD·BP,OD=13AD по свойству медиан треугольника ⇒ S▵BOD=12·13AD·BP.
3. Следующим шагом рассмотрим ΔABD. S▵ABD=½AD·BP.
4. Из пунктов 2 и 3 следует, что S▵BOD=13S▵ABD.
5. AD — медиана ΔABC, ⇒ S▵ABD=S▵ADC,а S▵ABC=S▵ABD+S▵ADC=2S▵ABD,а S▵ABD=½S▵ABC.
6. Из двух предыдущих пунктов следует, что S▵BOD=16S▵ABC.
7. Аналогично доказываем, что S▵COD=16S▵ABC, S▵COK=16S▵ABC, S▵KOA=16S▵ABC, S▵AOM=16S▵ABC, S▵MOB=16S▵ABC.

Пример нахождения и построения медианы

Для того чтобы узнать длину медианы, нужно знать:

• длины всех сторон треугольника;
• либо периметр и две стороны.

Задача

Дан ΔABC с известными сторонами АВ=9 см, СВ=8 см, АС=13 см. Необходимо вычислить длину медианы, построенной к наибольшей стороне.

Решение: чтобы найти длину медианы, используют дополнительные построения. Продлим медиану BO ΔABC и построим параллелограмм. Отрезок BO равен ½ диагонали получившегося параллелограмма. Согласно теореме о диагоналях параллелограмма, сумма квадратов его диагоналей равна удвоенной сумме квадратов его сторон.

2(a2+b2)=d12+d22;

2(82+92)+132+x2;

290=169+x2;

x2=121;

x=11.

Медиана равна половине найденной диагонали, 11:2=5,5 (см).

Ответ: 5,5 см.

Докажите, что медиана треугольника делит его на два равновеликих треугольника.

Последняя обновленная дата: 27 марта 2023 г.

•

Общее представление: 207,7K

•

Просмотр сегодня: 1,83K

Ответ

Проверено

207,7K+ виды

HINT: на досту. медиану данного треугольника. Мы используем определение медианы. Тогда у нас будет два треугольника с общей вершиной и основаниями одинаковой длины. Найдите площадь одного треугольника и докажите, что он равен площади другого.

Полное пошаговое решение:

Пусть ABC — треугольник.
Пусть AD — одна из его медиан.

∆ABD и ∆ADC имеют общую вершину A.

Следовательно, основания BD и DC равны (поскольку AD — медиана).

Теперь проведите линию AE перпендикулярно BC, AE ⊥ BC.

Мы знаем, что площадь треугольника с основанием b и высотой h равна = $\dfrac{1}{2} \times {\text{b}} \times {\text{h}}$

Теперь площадь треугольник ∆ABD = $\dfrac{1}{2} \times {\text{base}}$× высота ∆ABD
                                        = $\dfrac{1}{2} \times {\text{BD}} \times {\text{AE}}$
                                 } {2 dfrac s } {2} d \times {\text{AE}}$ — (Поскольку BD = DC)

Но DC и AE являются основанием и высотой ∆ACD соответственно.

Площадь ∆ACD = $\dfrac{1}{2}$× основание DC × высота ∆ACD {AE}}$

Следовательно, площадь (∆ABD) = площадь (∆ACD)
Следовательно, медиана треугольника делит его на два равновеликих треугольника.

Примечание. Ключевым моментом в таких задачах является начертить фигуру и включить в нее медиану. Это превращает фигуру в два треугольника с общей вершиной и равными основаниями.
Нахождение площади одного треугольника и использование условия равных оснований дает нам доказательство.
(В геометрии медиана треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны, таким образом делящий эту сторону пополам.)

Недавно обновленные страницы

Если пружина имеет период T и разрезана на n равных 11 класс физики CBSE

Планета движется вокруг Солнца по почти круговой орбите 11 класс физики CBSE

В любом треугольнике AB2 BC4 CA3 и D является средней точкой класса 11 по математике JEE_Main

В треугольнике ABC 2asin dfracAB+C2 равен IIT Класс 11 по математике JEE_Main

сторона a sqrt 3 + 1rmcm и угол 11 класс математики JEE_Main

Если пружина имеет период T и разрезана на n равных частей 11 класса физики CBSE

Планета движется вокруг Солнца по почти круговой орбите 11 класса физики CBSE

В любом треугольнике AB2 BC4 CA3 и D является серединой класс 11 maths JEE_Main

В треугольнике ABC 2asin dfracAB+C2 равен IIT Отборочный класс 11 maths JEE_Main

Если в треугольнике ABCangle A 45circ угол C 60circ, то класс 11 maths JEE_Main

Если в треугольнике rmABC сторона a sqrt + 1rmcm и угловой класс 11 по математике JEE_Main

Тенденции сомнений

Докажите, что медиана делит треугольник на два треугольника равной площади.

Вопрос

Вопрос

---

Теорема ICSE-Area-Exercies 16 (c)

21 видео

Реклама

AB Padhai Karo Bina Ads KE

Khareedo DN Pro и Dekho Sari Videos Bina Kisi Ad ad ki rukaavat ruaavat ruaavat rukaavat ruaavat rukaavat rukaavat rukaavat rukaavat rukaavat rukaavat rukaavat rukaavat ru

Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.

Расшифровка

привет, бхаи, что медиана делит треугольник на два треугольника равной площади, так что, как вы можете видеть на экране, мы взяли треугольник ABC и его медиану, так что город наездников является средой, и, как мы знаем, если медиана делит сторону треугольника на две равные части, так что рынок состоит из двух равных частей, поэтому теперь рассмотрим a b c много этой стороны, поскольку a и высота треугольника будут равны, так что это самый важный термин для решения вопроса сейчас пойдем

вычисление площади треугольника находится в космосе, поэтому давайте возьмем площадь треугольника, площадь треугольника 8, а половина — это BD, а высота — это последняя формула, это уравнение как уравнение номер один, теперь учитывая, что площадь треугольника треугольника ADP в это может быть уравнение

, чтобы теперь рассмотреть общий треугольник, площадь которого треугольника ABC должна быть равна половине Pinto BC в общую площадь треугольника. Теперь возьмите это, что у нас есть, и решите его, добавив один конец этого приведет к тому, что площадь треугольника составит площадь треугольника Pintu

BD в в в в последнее в общее это будет половина в дыру в дыру в это впадина но мы знаем что она равна TC потому что медиана этой стороны треугольника на две равные части так что мы можем принять ее за половину в Чинту было бы так, что это приводит к уравнению 3, площадь которого треугольника ABC и треугольника и

доказывает, что медиана треугольника делит треугольник на два треугольника равной площади, я надеюсь, что вопрос верен, я надеюсь, что вы все божье решение, спасибо

---

সংশ্লিষ্ট ভিডিও

Покажите, что медиана треугольника делит его на два равновеликих треугольника.

Показать, что медиана треугольника делит его на два равновеликих треугольника.

1414780

Медиана делит треугольник на две треугольники одной и той же области

2970448

सिद कीजिए कि किसी त Вивра की म म म chvin выполняет क क व व Вивра में क chytrainध म व chytrainध म व व Вивра त व chytrainन में व Вивра तпере
ज्ञात है: ΔABC जिसकी माध्यिका AD है।
सिद्ध करना है : «क्षे».