описание, свойства, значение, отличие от графика функции
Содержание:
- График производной функции — описание
- Свойства графика
- Знак производной на интервалах возрастания
- Знак производной на интервалах убывания
- Производная и угловой коэффициент касательной
- В каких точках производная равна нулю
- Примеры производной на графике функции
- График производной функции — описание
- Свойства графика
- Знак производной на интервалах возрастания
- Знак производной на интервалах убывания
- Производная и угловой коэффициент касательной
- В каких точках производная равна нулю
- Примеры производной на графике функции
График производной функции — описание
Производная функции — это скорость изменения у при изменении х.
При этом одна и та же функция может иметь разное значение производной в разных точках. Обозначается производная следующим образом: \(f'(x)\).
Зависимость производной функции от скорости изменения y заключается в том, что они прямо пропорциональны. Значение производной может быть как больше, так и меньше нуля. Производную функции используют для нахождения точек максимума и минимума функций, а также промежутков их возрастания и убывания.
При помощи вычисления производной и приравнивания её к нулю, возможно найти точки, разбивающие числовую ось на интервалы. Знак производной будет определяться на каждом из найденных интервалов, что позволит сделать в дальнейшем сделать вывод о возрастании или убывании функции.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Производная функции \(f(x)\) в точке \(x_0\) эквивалентна тангенсу угла наклона касательной к графику функции в \(x_0\).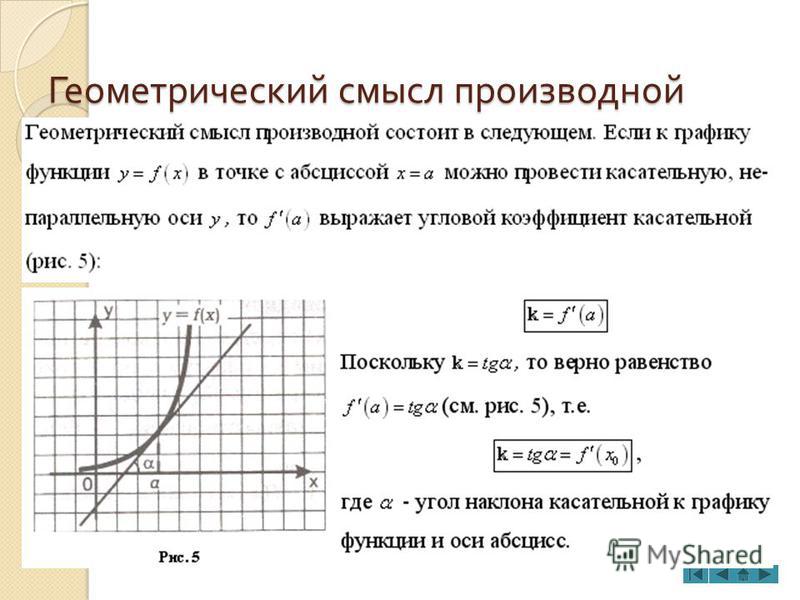
\(f'(x_0)\;=\;tg\alpha\)
Свойства графика
- Производная будет положительной на интервалах возрастания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает положительным значением, график функции возрастает в обозначенном интервале.
- Производная будет отрицательной на интервалах убывания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает отрицательным значением, график функции убывает в обозначенном интервале.
- В точке х производная будет равняться угловому коэффициенту касательной к графику функции в обозначенной точке.
- Производная равняется нулю в точках максимума и минимума функции, в тех же случаях параллельности касательной к графику функции и оси \(ОХ\).
Знак производной на интервалах возрастания
Определим, какая функция называется возвращающей.
\(y = f(x)\) будет возрастать на интервале \(X\), если для любых \(x_1\;\in\;X\) и \(x_2\;\in\;X\), где \(x_2\;>\;x_1\), справедливо неравенство \(f(x_2)\;\geq\;f(x_1)\).
В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть иметь вид \(f(x_1) < f(x_2)\), функция \(y = f(x)\) будет называться
На интервалах возрастания производная будет иметь положительный знак. То есть при подстановке значения из интервала в производную, получившееся число будет положительным.
В тех случаях, когда производная функции \(y = f(x)\) положительна для любого x из интервала \(X\), функция возрастает на \(X\).
Знак производной на интервалах убывания
Определим, какая функция называется убывающей.
\(y = f(x)\) будет убывать на интервале \(X\), если для любых \(x_1\;\in\;X\) и \(x_2\;\in\;X\), где \(x_2\;>\;x_1\) справедливо неравенство \(f(x_2)\;\leq\;f(x_1).\)
В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть имеет вид \(f(x_1) < f(x_2)\), функция \(y = f(x)\) будет называться строго убывающей на интервале \((a, b)\).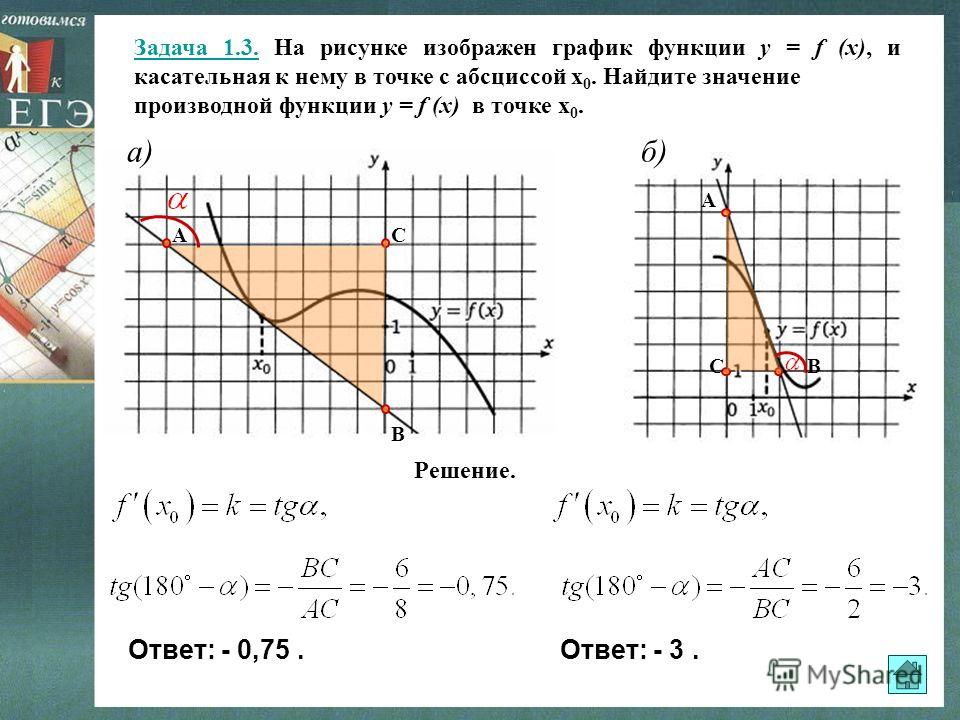
На интервалах убывания производная будет иметь отрицательный знак. То есть при подстановке значения из интервала в производную, получившееся число будет отрицательным.
В тех случаях, когда производная функции \(y = f(x)\) отрицательна для любого x из интервала \(X\), функция убывает на \(X\).
Производная и угловой коэффициент касательной
Касательная — прямая, которая имеет на определенном участке единственную общую точку с графиком.
В случае, когда при \(x_1\;\rightarrow\;x_0\) имеется предельное положение секущей графика функции \(y = f(x)\), оно будет носить название касательной к графику функции \(y = f(x)\) в точке \(A\;=\;((x_0;\;f(x_0))\). А значение производной в точке касания \(x_0\) будет эквивалентно угловому коэффициенту касательной.
Угловой коэффициент касательной равен значению производной в точке касания \(x_0\). И в соответствии с тем, что касательная параллельна прямой \(y = -x\), ее угловой коэффициент равен -1.
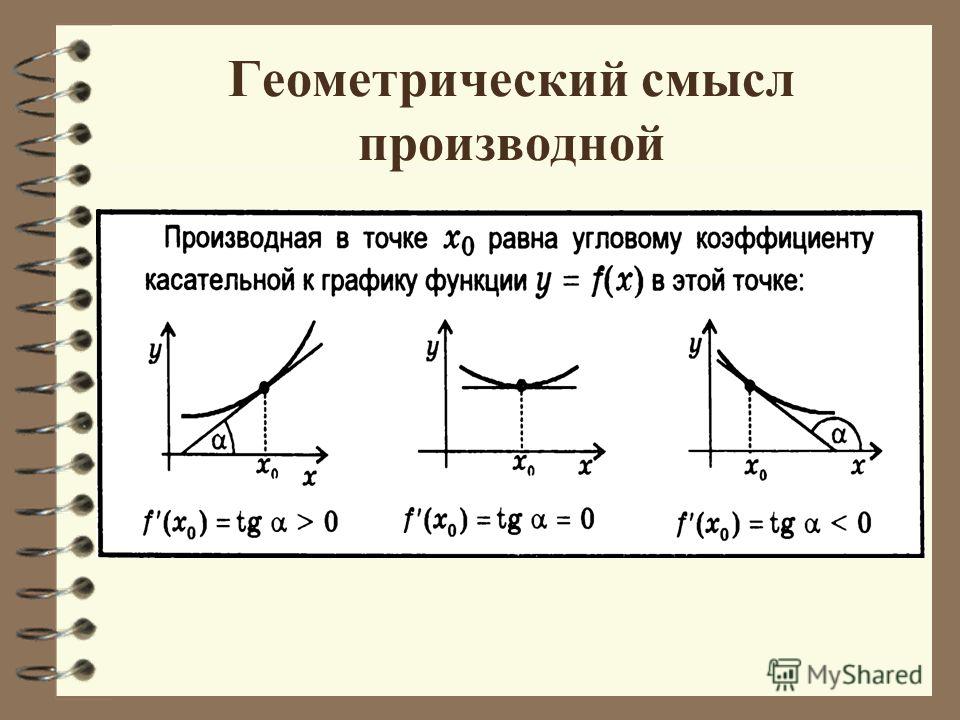
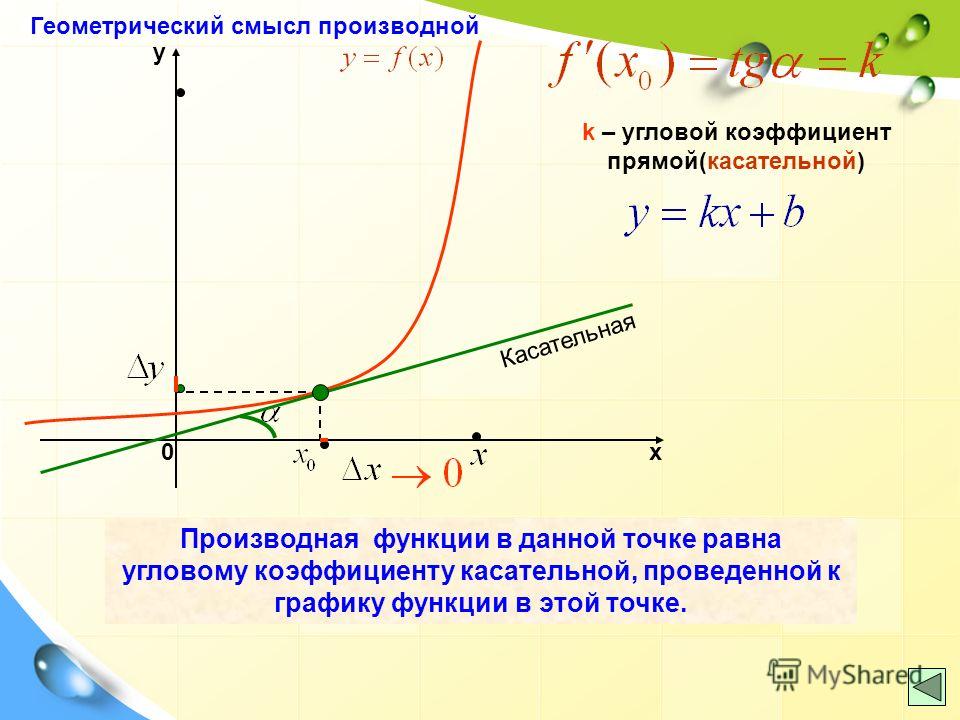
Геометрический смысл производной состоит в том, что производная в точке \(x_0\) равна угловому коэффициенту касательной к графику функции \(y = f(x)\) в этой точке.
Формула уравнения касательной к графику функции \(y = f(x)\) в точке \(x_0\) выглядит следующим образом:
\(y\;=\;f(x_0)\;+\;f'(x_0)(x\;-\;x_0)\)
Рассмотрим рисунок графика функции \(y = f(x)\). Очевидно, что для каждой из точек \(A\) и \(B\) графика функции справедливо следующее разностное отношение:
\(\frac{f(x_0+\triangle x)}{f(x_0)\triangle x}=tg\alpha\)
Здесь \(\alpha\) — угол между прямой и осью \(ОХ\), а предел разностного отношения эквивалентен угловому коэффициенту касательной в точке \(A\).
Зафиксируем точку \(A\) и будем продвигать точку \(B\) в направлении к ней. Тогда \(\triangle x\) бесконечно уменьшается и приближается к 0, а секущая \(АВ\) приближается к касательной \(АС\).
Пример
Необходимо записать уравнение касательной к графику функции \(y=x+e^{-2x}\), если эта функция параллельна прямой \(y = -x.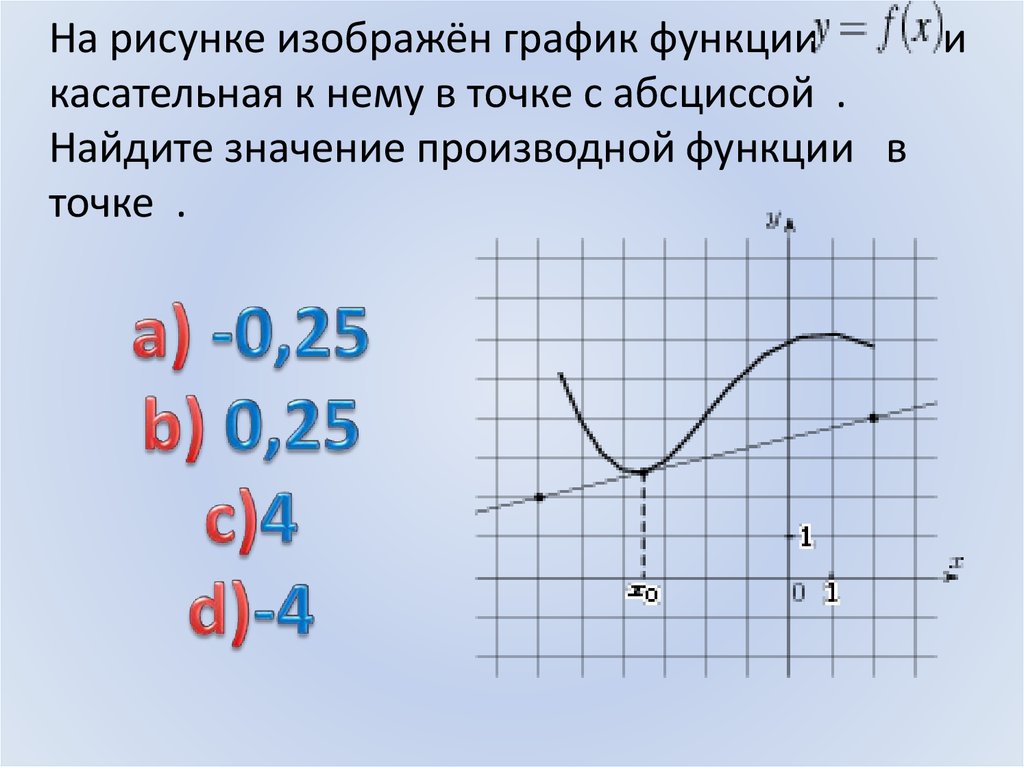
{-2x_0}\;=\;1\\-2x\;=\;0\\x_0\;=\;0\)
Используем уравнение касательной
\(y\;=\;f(x_0)\;+f'(x_0)(x\;-\;x_0)\\x_0\;=\;0;\;f'(x_0)\;=\;-1;\;f(x_0)\;=\;1\\y\;=\;1\;-\;1(x-0)\;=\;1\;-\;x\)
В каких точках производная равна нулю
Производная будет эквивалентна нулю в точках минимума, максимума и перегиба, при параллельной оси \(ОX\) касательной. Рассмотрим следующий рисунок:
Очевидно, что в точках \(C\) и \(D\) касательная горизонтальна, тогда тангенс угла ее наклона будет равняться 0. Отсюда можно сделать вывод, что и производная равна 0. Точка C здесь будет являться точкой максимума. В этой точке возрастание функции изменяется на убывание, как меняется и знак производной — с плюса на минус. Точка \(D\) здесь — точка минимума. В это случае также происходят изменения, но в обратном порядке.
Примечание
Важно отметить, что производная может не существовать в точке максимума. Такое происходит, если на графике изображен резкий излом, к которому невозможно провести касательную.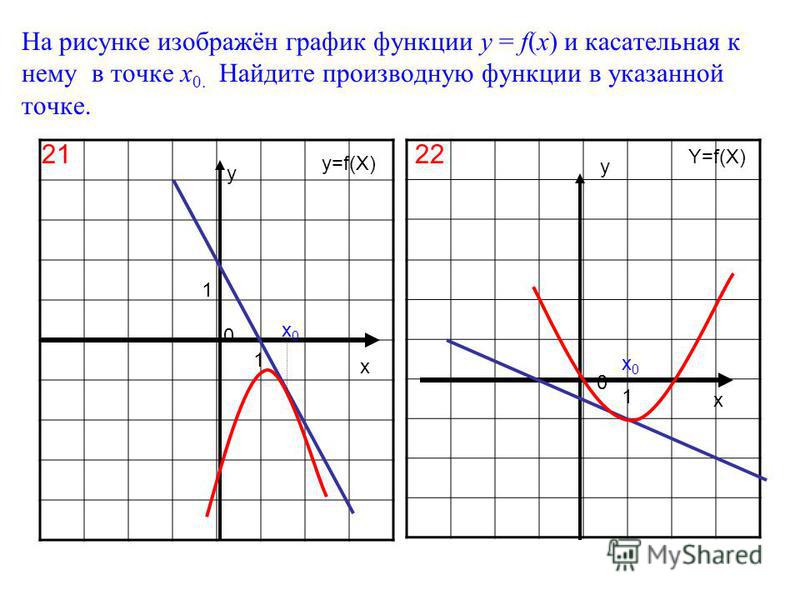
Рассмотрим еще одно изображение функции:
В данном случае производная будет эквивалентна нулю в точке перегиба, так как в точке \(E\) касательная к функции параллельна оси \(ОX\). В этом случае знак производной не будет изменяться, потому что до точки перегиба и после функция возрастает. Знак был и остается положительным.
Пример
Рассмотрим рисунок, на котором начерчен график функции \(y = f(x)\). График определен на интервале (−3; 9). Необходимо определить количество точек, где производная функции \(f(x)\) эквивалентна 0.
На данном рисунке очевидно, что производная функции f(x) эквивалентна нулю в точках максимума и минимума, то есть в точках −2; −1; 1; 4 и 6. Таким образом производная равна нулю в 5 точках.
Примеры производной на графике функции
Задача №1
Рассмотрим рисунок.
Рисунок изображает график производной функции \(f(x)\).
Функция определена на интервале (-10; 2). Необходимо найти, в скольких точках касательная к графику функции \(f(x)\) будет параллельна прямой \(y = -2x — 11\) или совпадать с ней.
Решение
Используем правило о значении производной, которое в точке касания эквивалентно угловому коэффициенту касательной. Тогда, зная, что касательная параллельна прямой \(y = -2x — 11\) или идентична с ней, можно утверждать, что угловые коэффициенты равны \(-2\).
Теперь необходимо найти число точек, в которых \(f'(x)\;=\;-2\). Искомое значение соответствует числу точек, где график производной пересекается с прямой \(y = -2\). На заданном интервале 5 таких точек.
Ответ: 5.
Задача №2
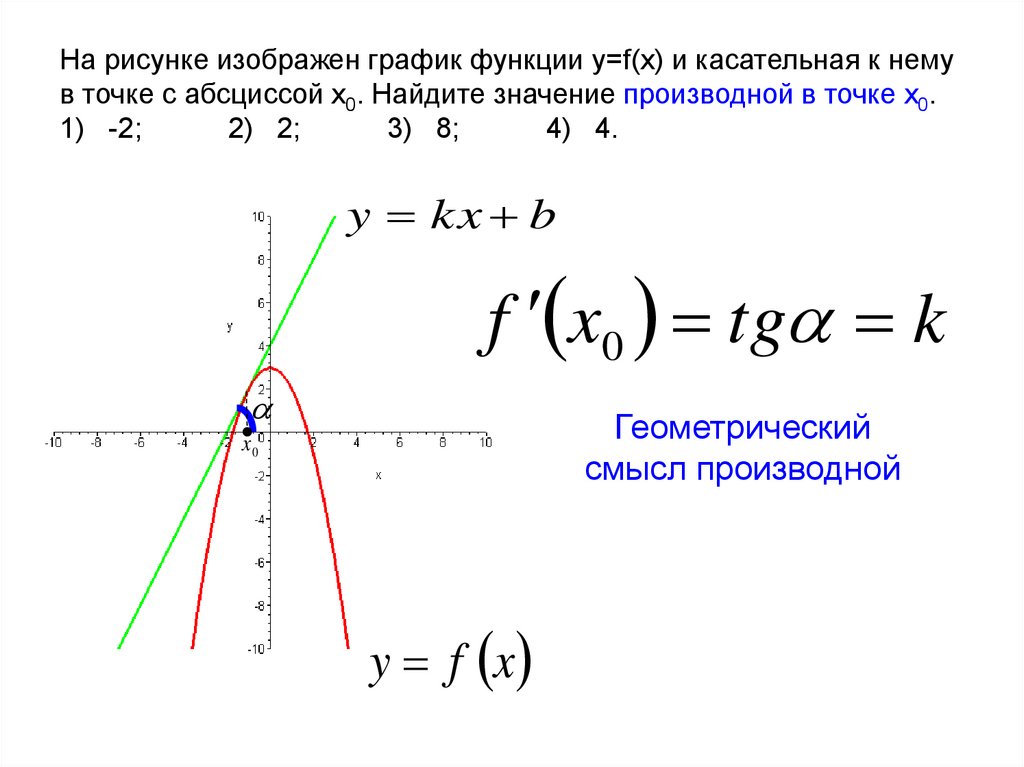
Первый рисунок изображает график функции \(y = f(x)\) и касательную к нему в точке с абсциссой \(x_0\). Необходимо установить значение производной функции \(f(x)\) в точке \(x_0\).
Решение
Используем правило, гласящее, что угловой коэффициент касательной эквивалентен значению производной в точке касания, который в свою очередь эквивалентен тангенсу угла наклона данной касательной к оси абсцисс.
На втором рисунке показано, что решить задачу можно с помощью построения треугольника, вершины которого соответствуют точкам A (1; 2), B (1; -4), C(-2; -4). Тогда угол наклона касательной к оси абсцисс можно найти через угол \(ACB\), которому он будет равен:
\(y'(x_0)\;=\;tg\angle ABC\;=\;\frac{AB}{BC}\;=\;\frac{2+4}{1+2}\;=\;2\)
Ответ: 2.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
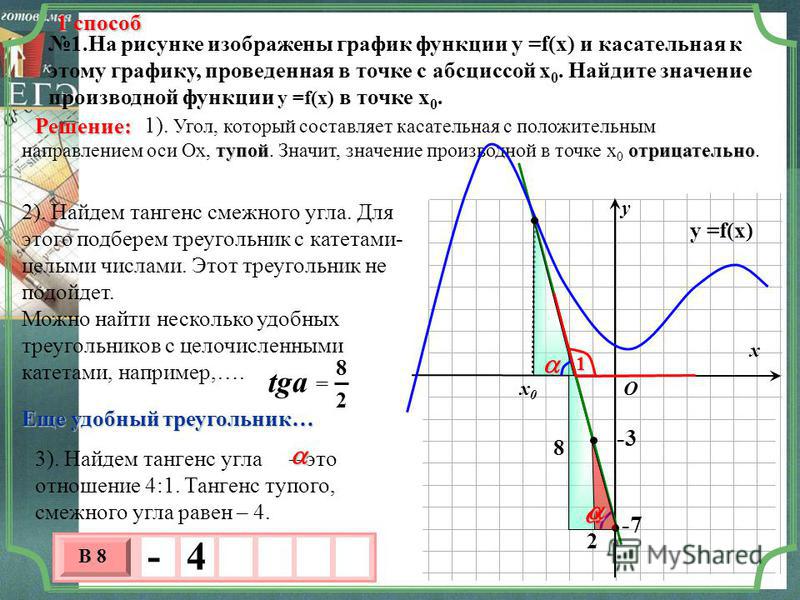
На рисунке изображены график функции и касательная
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2012-10-15
Данная статья является продолжением двух предыдущих. В статье «Геометрический смысл производной. Часть 1!» была изложена теория и рассмотрен один из способов нахождения производной по данному графику функции и касательной, проведенной в определённой точке графика.
Там же я обещал вам рассмотреть ещё один способ решения подобных задач. Напомню, что задания такого типа входят в состав экзамена по математике. В статье «Уравнение прямой, проведённой через две заданные точки» мы рассмотрели формулу, благодаря которой находится уравнение прямой.
Представленная в указанных статьях теория необходима, так как тот способ, который представлен ниже, непосредственно с ней связан. Итак, кратко:
1.
Из курса алгебры известно, что уравнение прямой имеет вид:
где k – угловой коэффициент прямой.
То есть производная функции y = f(x) в точке x0 равна угловому коэффициенту касательной:
2. Уравнение прямой, проходящей через две заданные точки имеет вид:
После подстановки координат в данное уравнение оно приводится к виду:
Таким образом, в случае, когда даны две точки, через которые проходит касательная (прямая) к графику функции, необходимо найти уравнение этой прямой.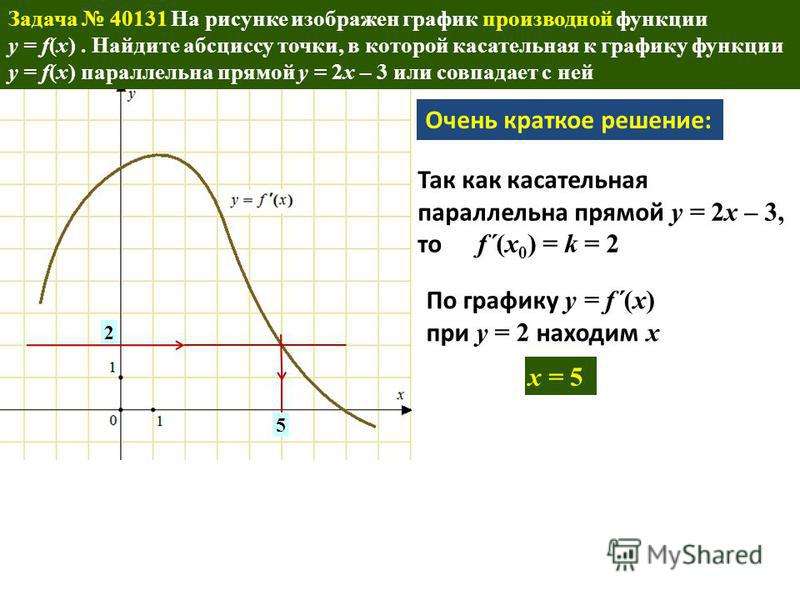
Решением задачи будет являться коэффициент k (он равен производной).
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой xо. Найдите значение производной функции f(x) в точке xо.
Как уже сказано, значение производной функции f(x) в точке xо равно коэффициенту k из уравнения прямой y=kx+b.
Во всех подобных задачах будут даны две точки, через которые проходит касательная, в данном случае это (–6;–2) и (–1; 8). Подставляем координаты в формулу уравнения прямой:
Настоятельно рекомендую вам сделать проверку (подставьте координаты обеих точек в уравнение). Цена ошибки как вы знаете – это потерянный бал на ЕГЭ.
Проверка:
– 2 = 2 (–6) + 10 → – 2 = – 2 Верно
8 = 2 (–1) + 10 → 8 = 8 Верно
Уравнение прямой найдено верно.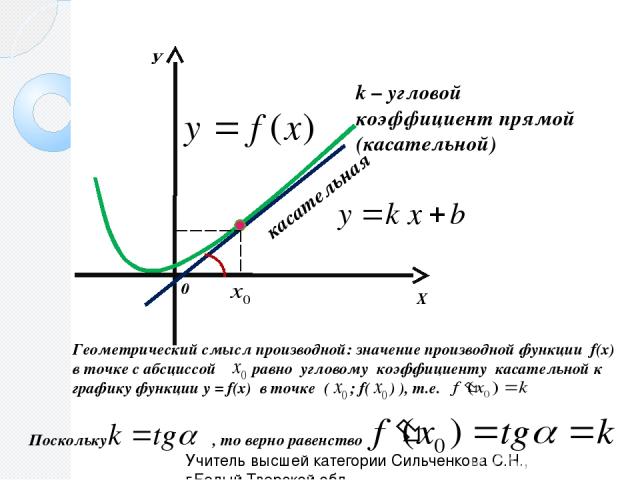
Если вы знаете другие способы нахождения уравнения прямой, то используйте (их, кстати, около шести).
Таким образом, f ′(x) = k = 2.
Как видите, вычисления просты.
Ответ: 2
Вывод: если вы видите перед собой подобную задачу, где на координатной плоскости обозначены две точки, через которые проведена касательная, то:
1. Определите координаты точек. Точки могут быть и не обозначены (не выделены), но на координатной сетке будет отчётливо видно, как (через какие точки) проходит прямая.
2. Найдите уравнение прямой (касательной) по представленной формуле или другим способом.
3. Проверьте полученное уравнение, подставив в него координаты точек.
4. Запишите ответ (коэффициент k).
На этом всё. Будет полезный материал в следующей статье!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Производная Графики | ЕГЭ-№7Производная
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Производная как функция – Дифференциальное исчисление
Цели обучения
- Определить производную функцию заданной функции.
- Постройте производную функцию по графику заданной функции.
- Укажите связь между производными и непрерывностью.
- Опишите три условия, при которых функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы продифференцируем функцию положения в данный момент времени, мы получим скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке даст ценную информацию о поведении функции. Однако процесс нахождения производной даже при нескольких значениях с использованием методов из предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная. Мы можем формально определить производную функцию следующим образом.
Определение
Позвольте быть функцией. Производная функция , обозначенная как , является функцией, область определения которой состоит из тех значений таких, что существует следующий предел:
.
Говорят, что функция дифференцируема в , если существует
. В более общем смысле говорят, что функция дифференцируема на , если она дифференцируема в каждой точке открытого множества, а дифференцируемая функция — это функция, которая существует в своей области определения.
В следующих нескольких примерах мы используем (Рисунок) для нахождения производной функции.
Нахождение производной функции квадратного корня
Нахождение производной функции .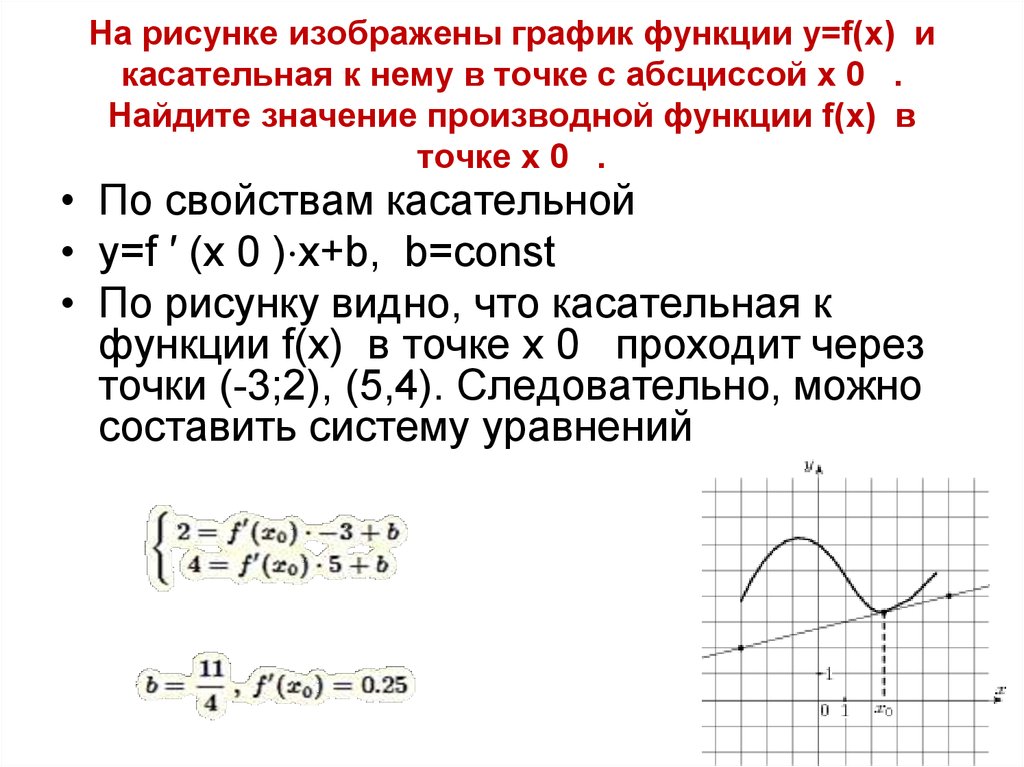
Решение
Начните непосредственно с определения производной функции. Используйте (рисунок).
Нахождение производной квадратичной функции
Нахождение производной функции .
Решение
Выполните ту же процедуру здесь, но без умножения на сопряженное.
Найдите производную от .
Решение
Мы используем различные обозначения для выражения производной функции. На (рис.) показано, что если , то . Если бы мы представили эту функцию в виде , мы могли бы выразить производную как или . Мы могли бы передать ту же информацию письменно. Таким образом, для функции каждое из следующих обозначений представляет собой производную от :
.
Вместо we may also use Использование обозначений (называемых обозначениями Лейбница) довольно распространено в технике и физике. Чтобы лучше понять эти обозначения, вспомним, что производная функции в точке — это предел наклона секущих по мере приближения секущих к касательной.
Наклоны этих секущих часто выражаются в виде где — разность значений, соответствующая разнице значений, которые выражаются как ((рисунок)). Таким образом, производная, которую можно рассматривать как мгновенную скорость изменения по отношению к , выражается как
.
Рис. 1. Производная выражается как .Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы могли бы построить график. Учитывая оба, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку дает скорость изменения функции (или наклон касательной к ).
На (рис.) мы обнаружили, что для . Если мы изобразим эти функции на тех же осях, что и на (рис.), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями. Во-первых, мы замечаем, что увеличивается по всей своей области, а это означает, что наклоны его касательных линий во всех точках положительны. Следовательно, мы ожидаем для всех значений в своей области определения.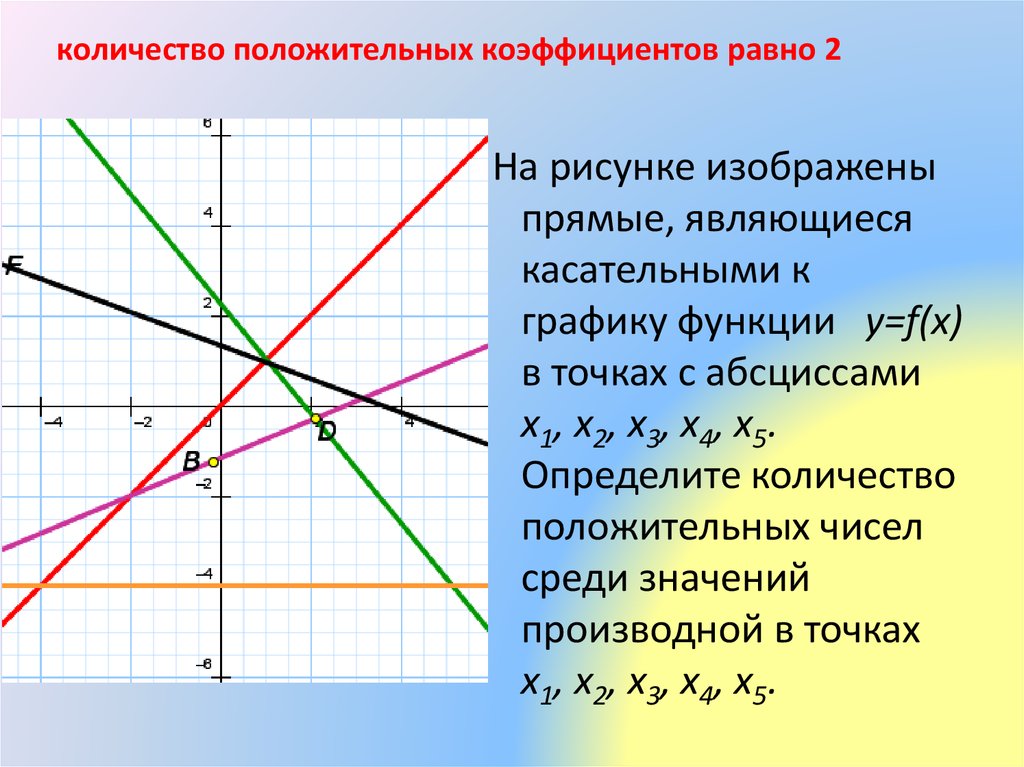
Более того, по мере увеличения наклоны касательных к уменьшаются, и мы ожидаем увидеть соответствующее уменьшение . Мы также замечаем, что это не определено и что , соответствующее вертикальной касательной к точке 0,
На (Рисунок) мы обнаружили, что для . Графики этих функций представлены на (рис.). Обратите внимание, что уменьшается для . Для этих же значений . При значениях возрастает и . Кроме того, имеет горизонтальную касательную в и .
Рис. 3. Производная, где функция убывает, а где возрастает. Производная равна нулю там, где функция имеет горизонтальный тангенс.Рисование производной с помощью функции
Используйте следующий график для построения графика .
Решение
Решение показано на следующем графике. Обратите внимание, что увеличивается и на . Кроме того, уменьшается и дальше и дальше. Также обратите внимание, что имеет горизонтальные касательные в точках -2 и 3, а также .
Нарисуйте график . На каком интервале находится график над осью -?
Раствор
Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Сначала рассмотрим связь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в точке, не обязательно должна быть дифференцируемой в этой точке. На самом деле функция может быть непрерывной в точке и не быть дифференцируемой в этой точке по одной из нескольких причин.
Дифференцируемость подразумевает непрерывность
Позвольте быть функцией и находиться в своей области определения. Если дифференцируема при , то непрерывна при .
Доказательство
Если дифференцируем при , то существует и
.
Мы хотим показать, что at является непрерывным, показав, что . Таким образом,
Поэтому, поскольку определено и , мы заключаем, что непрерывно в .
Мы только что доказали, что дифференцируемость влечет непрерывность, но теперь мы рассмотрим, влечет ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, рассмотрим функцию . Эта функция всюду непрерывна; однако не определено. Это наблюдение приводит нас к мысли, что непрерывность не влечет дифференцируемости. Давайте исследовать дальше. Для ,
.
Это ограничение не существует, потому что
.
См. (рисунок).
Рис. 4. Функция непрерывна в 0, но не дифференцируема в 0.Рассмотрим некоторые дополнительные ситуации, в которых непрерывная функция не может быть дифференцируема. Рассмотрим функцию:
.
Таким образом не существует. Беглый взгляд на график проясняет ситуацию. Функция имеет вертикальную касательную в точке 0 ((Рисунок)).
Рис. 5. Функция имеет вертикальную касательную в точке . Он непрерывен в точке 0, но не дифференцируем в точке 0,9.
0016 Функция также имеет производную, которая демонстрирует интересное поведение при 0. Мы видим, что.
Этого предела не существует, в основном потому, что наклоны секущих постоянно меняют направление по мере приближения к нулю ((Рисунок)).
Рис. 6. Функция не дифференцируема в точке 0.Итого:
- Заметим, что если функция не является непрерывной, она не может быть дифференцируемой, поскольку каждая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она может не быть дифференцируемой.
- Мы видели, что это не дифференцируемо в 0, потому что предел наклона касательных линий слева и справа не был одинаковым. Визуально это вылилось в острый угол на графике функции в 0. Отсюда делаем вывод, что для того, чтобы быть дифференцируемой в точке, функция должна быть в этой точке «гладкой».
- Как мы видели на примере , функция не может быть дифференцируема в точке, где есть вертикальная касательная.
- Как мы видели, функция может не быть дифференцируемой в какой-то точке и более сложными способами.
Кусочная функция, которая является непрерывной и дифференцируемой
Компания по производству игрушек хочет разработать траекторию для игрушечной машинки, которая начинается с параболической кривой, а затем переходит в прямую линию ((Рисунок)). Функция, описывающая дорожку, должна иметь вид , где и указаны в дюймах. Чтобы автомобиль двигался по трассе плавно, функция должна быть и непрерывной, и дифференцируемой при -10. Найдите значения и , которые делают и непрерывным и дифференцируемым.
Рис. 7. Для плавного движения автомобиля по трассе функция должна быть одновременно непрерывной и дифференцируемой.Решение
Чтобы функция была непрерывной при . Таким образом, поскольку
и , мы должны иметь . Эквивалентно имеем .
Чтобы функция была дифференцируемой при -10, должно существовать
. Поскольку определяется по разным правилам справа и слева, мы должны вычислить этот предел справа и слева, а затем приравнять их друг к другу:
У нас также есть
Это дает нам .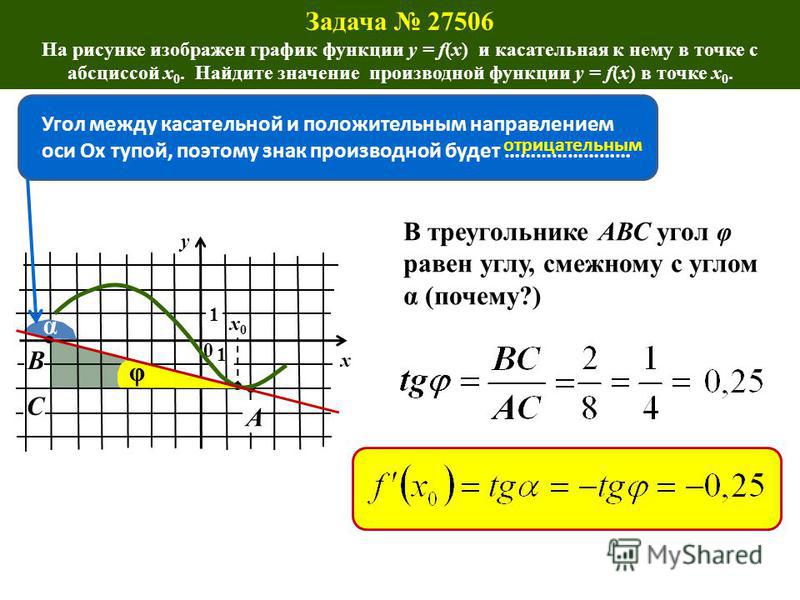
Таким образом и .
Найдите значения и, которые делают непрерывными и дифференцируемыми в 3.
Решение
и
Производная функции сама по себе является функцией, поэтому мы можем найти производную производной. Например, производная функции положения — это скорость изменения положения или скорость. Производная скорости — это скорость изменения скорости, то есть ускорение. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать брать производные, чтобы получить третью производную, четвертую производную и так далее. В совокупности они обозначаются как
.
Интересно отметить, что нотация for может рассматриваться как попытка выразиться более компактно. Аналогично, .
Нахождение второй производной
Для , найти .
Решение
Первая находка.
Затем найдите производную от .
Найти для .
Решение
Определение ускорения
Положение частицы вдоль координатной оси во времени (в секундах) определяется выражением (в метрах). Найдите функцию, описывающую его ускорение во времени.
Решение
Поскольку и , начнем с нахождения производной от :
Далее,
Таким образом, .
Для , найти .
Раствор
Ключевые понятия
- Производной функции называется функция, значение которой равно .
- График производной функции связан с графиком . Где имеет касательную с положительным наклоном, . Где есть касательная с отрицательным наклоном, . Где имеет горизонтальную касательную, .
- Если функция дифференцируема в некоторой точке, то она в этой точке непрерывна. Функция не является дифференцируемой в точке, если она не является непрерывной в этой точке, если она имеет в этой точке вертикальную касательную или если график имеет острый угол или точку возврата.
- Производные высшего порядка — это производные от производных, от второй производной до производной.
- Производная функция
В следующих упражнениях используйте определение производной, чтобы найти .
1.
2.
Раствор
-3
3.
4.
.0016
5.6.
Solution
7.
8.
Solution
9.
10.
Solution
В следующих упражнениях используйте график для построения графика его производной .
11.
12.
Раствор
13.
14.
Решение
Для следующих упражнений заданный предел представляет собой производную функции при . Найти и .
15.
16.
.0045 РешениеДля следующих функций
- нарисуйте график и
- используют определение производной, чтобы показать, что функция не является дифференцируемой при .
21.
22.
Раствор
а.
б.
23.
24.
Раствор
а.
б. .
Для следующих графиков
- определить, для каких значений существует, но не является непрерывным при , и
- определить, при каких значениях функция непрерывна, но не дифференцируема при .
25.
26.
Раствор
а. , б.
27. Используйте график для оценки a. , б. , с. , д. и е. , если они существуют.
Для следующих функций используйте для поиска .
28.
Решение
0
29.
30.
Раствор
для следующих упражнений, использование. Использование. Определите функцию, затем используйте калькулятор для построения графика.
31.0026
Раствор
35. [T]
36. [T]
Решение
. На следующих Arpressions, на следующих разражениях. заданных ситуаций. Обязательно укажите единицы измерения.
37. обозначает численность населения города в определенное время в годах.
38. обозначает общую сумму денег (в тысячах долларов), потраченную посетителями на уступки в парке развлечений.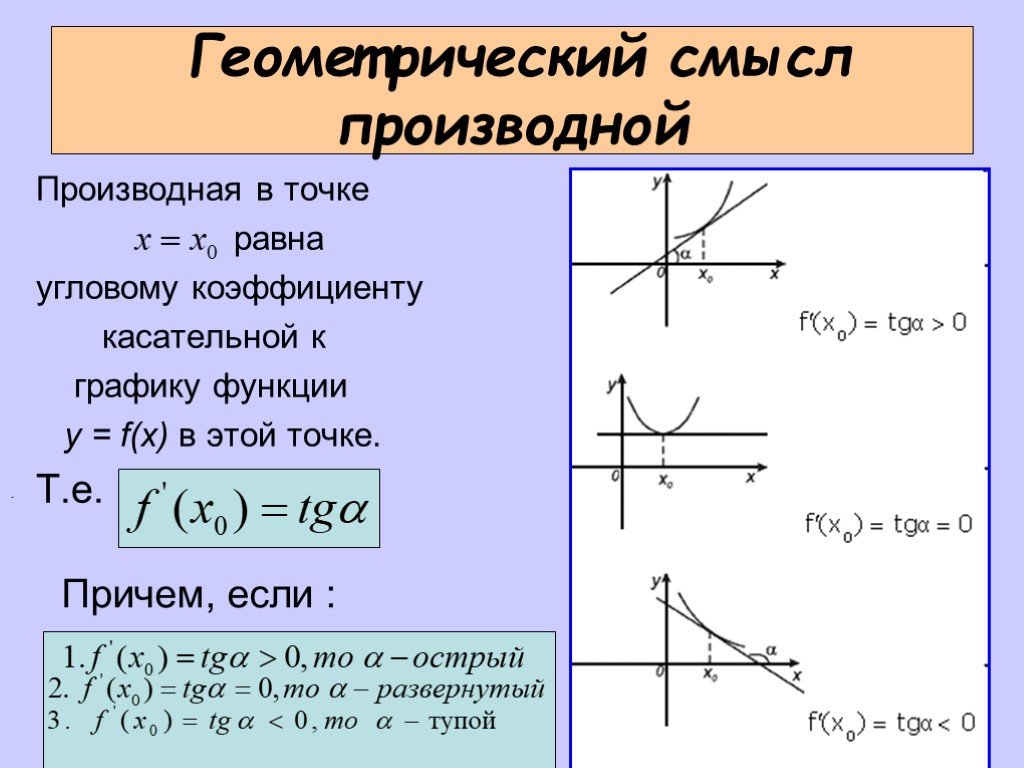
Раствор
а. Средняя ставка, по которой клиенты тратят на уступки, в тысячах на одного клиента.
б. Коэффициент (в тысячах на клиента), по которому клиенты потратили деньги на уступки, в тысячах на клиента.
39. обозначает общую стоимость (в тысячах долларов) производства радиочасов.
40. обозначает оценку (в процентах), полученную за тест с учетом часов обучения.
Раствор
а. Средняя оценка, полученная за тест при среднем времени обучения между двумя суммами.
б. Скорость (в процентных пунктах в час), с которой оценка за тест повысилась или понизилась за заданное среднее время обучения в часах.
41. обозначает стоимость (в долларах) учебника по социологии в университетских книжных магазинах США с 1990 года.
42. обозначает атмосферное давление на высоте футов.
Решение
а. Среднее изменение атмосферного давления между двумя разными высотами.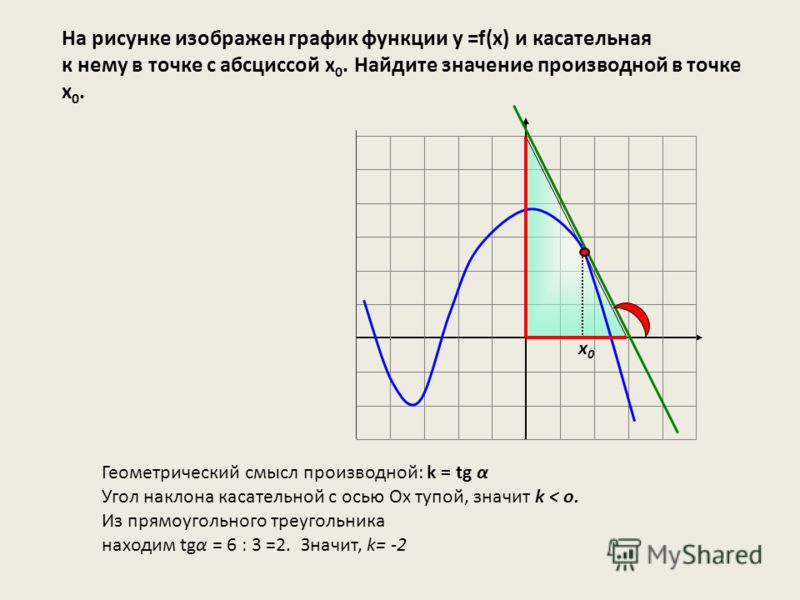
б. Скорость (торр на фут), с которой атмосферное давление увеличивается или уменьшается в футах.
43. Нарисуйте график функции со всеми следующими свойствами:
- для
- на
- и
- и
- не существует.
44. Предположим, что температура в градусах Фаренгейта на высоте в футах над землей равна .
- Дайте физическую интерпретацию в единицах измерения .
- Если мы знаем то объясним физический смысл.
Раствор
а. Скорость (в градусах на фут), с которой температура повышается или понижается на данной высоте.
б. Скорость изменения температуры при изменении высоты на высоте 1000 футов составляет -0,1 градуса на фут.
45. Предположим, что общая прибыль компании составляет тысячу долларов при продаже единиц товара.
- Что означает мера и каковы единицы измерения?
- Что измеряет и каковы единицы измерения?
- Предположим, что . Как приблизительно изменится прибыль, если количество проданных товаров увеличится с 30 до 31?
Как приблизительно изменится прибыль, если количество проданных товаров увеличится с 30 до 31?46. График на следующем рисунке моделирует количество людей, заболевших гриппом через несколько недель после его первоначальной вспышки в городе с населением 50 000 человек.
- Опишите, что представляет собой и как оно ведет себя при увеличении.
- Что говорит нам производная о том, как этот город пострадал от вспышки гриппа?
Раствор
а. Скорость, с которой число людей, заболевших гриппом, меняется через несколько недель после первоначальной вспышки.
б. Скорость резко возрастает до третьей недели, после чего замедляется, а затем становится постоянной.
В следующих упражнениях используйте следующую таблицу, в которой показана высота ракеты Saturn V для миссии Apollo 11 через несколько секунд после запуска.
The first column header is Time (seconds) and the second column is Height (meters). Under the first column are the values 0, 1, 2, 3, 4, and 5. Under the second column are the values 0, 2, 4, 13, 25, and 32.»>47. Каков физический смысл ? Что такое единицы?
48. [Т] Постройте таблицу значений и график на одном и том же графике. ( Подсказка: для внутренних точек, оцените как левый предел, так и правый предел и усредните их.)
Решение
The first row is a header row and it labels each column. The first column header is Time (seconds) and the second column is h’(t) (m/s). Under the first column are the values 0, 1, 2, 3, 4, and 5. Under the second column are the values 2, 2, 5.5, 10.5, 9.5, and 7.»>49. [T] Наилучшая линейная аппроксимация данных определяется выражением , где высота ракеты (в метрах) и время, прошедшее с момента взлета. Из этого уравнения определите . График с заданными данными и на отдельной координатной плоскости график .
50. [T] Наилучшее квадратичное соответствие данным определяется выражением , где высота ракеты (в метрах) и время, прошедшее с момента взлета.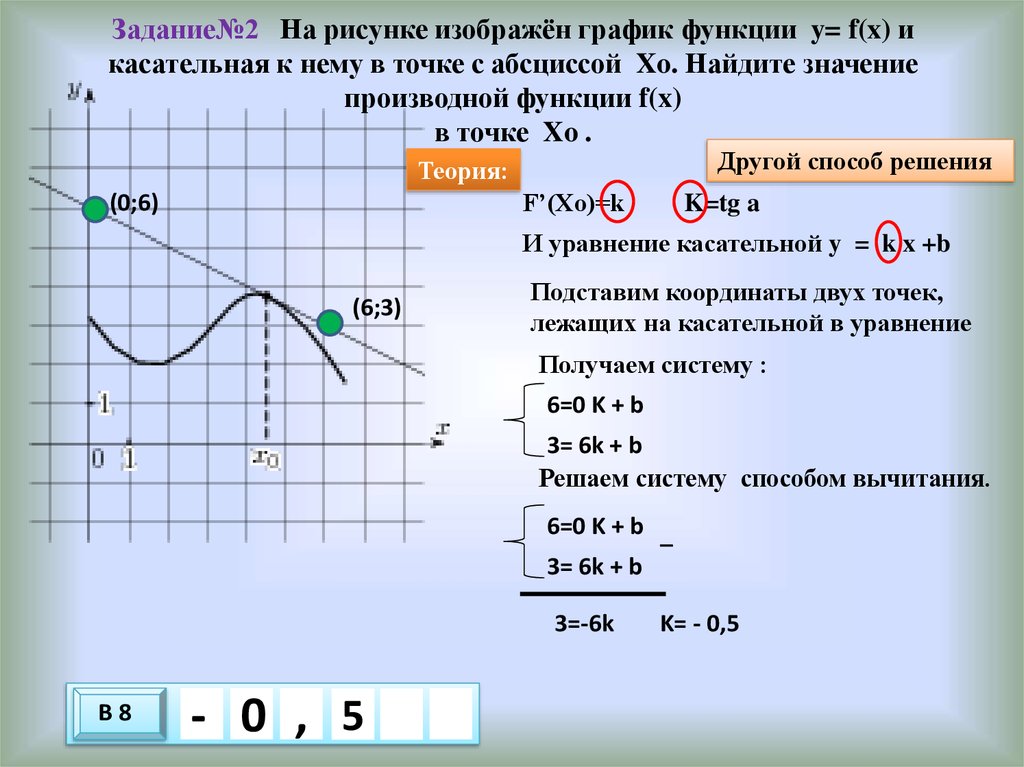
Из этого уравнения определите . График с заданными данными и на отдельной координатной плоскости график .
Решение
51. [T] Наилучшая кубическая аппроксимация данных определяется выражением , где высота ракеты (в м) и время, прошедшее с момента взлета. Из этого уравнения определите . График с заданными данными и на отдельной координатной плоскости график . Линейная, квадратичная или кубическая функция лучше всего соответствует данным?
52. Используя наилучшую линейную, квадратичную и кубическую аппроксимацию данных, определите, что такое , и . Каков физический смысл , и , и каковы их единицы?
Решение
, и представляют собой ускорение ракеты в метрах в секунду в квадрате ( ).
Глоссарий
- производная функция
- дает производную функции в каждой точке области определения исходной функции, для которой определена производная
- дифференцируемый в
- функция, для которой существует, дифференцируема в
- дифференцируемый на
- функция, для которой существует для каждого в открытом множестве, дифференцируема на
- дифференцируемая функция
- функция, для которой существует, является дифференцируемой функцией
- производная высшего порядка
- производная производной от второй производной до й производной называется производной высшего порядка
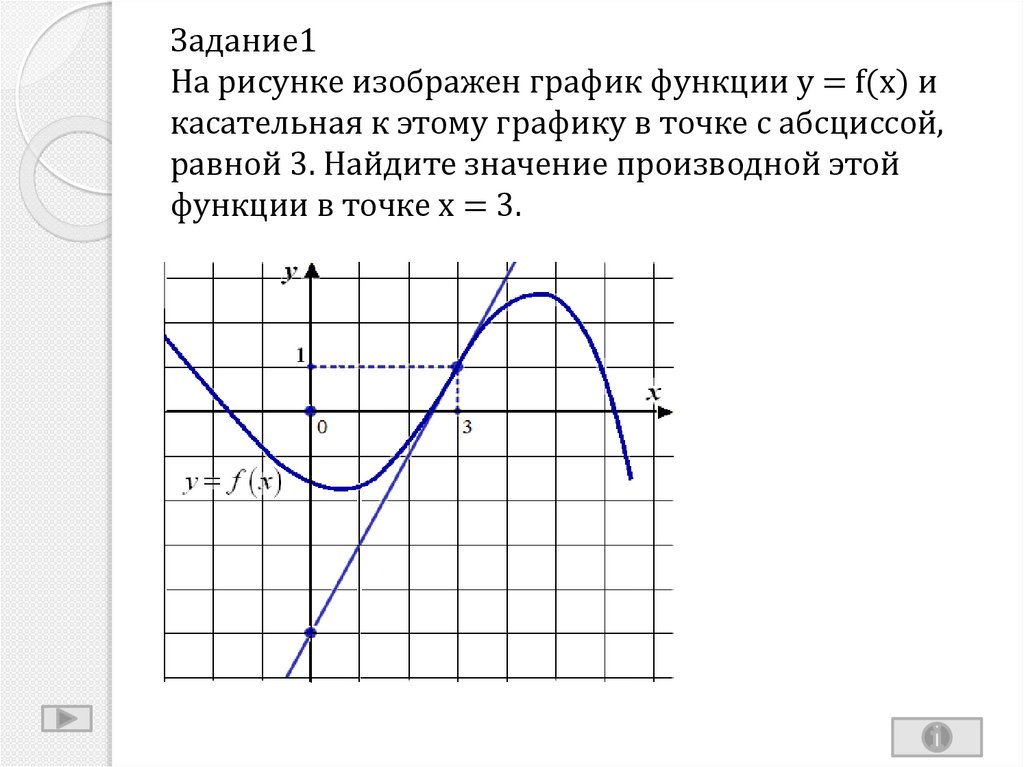Производная функции
ti.com/images/online_courses/t3/calculus/images/pd/GlossaryBackground.gif»>
Leave A Comment