Теоретическая механика (Голубева О.В.)
Теоретическая механика (Голубева О.В.)
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИЗА § 2. Вектор-функция Часть I. КИНЕМАТИКА § 1. Предмет теоретической механики и ее основные понятия § 2. Уравнение движения точки и ее траектория § 3. Скорость точки § 4.  Ускорение точки Ускорение точки§ 5. Проекции ускорения на естественные оси § 6. Частные случаи движепия точки. Физический смысл тангенциального и нормального ускорения точки § 7. Уравнения движения точки в криволинейных координатах. Проекция скорости и ускорения на осн криволинейных координат ГЛАВА 2. КИНЕМАТИКА НЕСВОБОДНОЙ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК § 2. Ограничения на скорость и ускорение, налагаемые геометрическими связями § 3. Число степеней свободы системы. Обобщенные координаты уравнения движения системы, обобщенные скорости ГЛАВА 3. КИНЕМАТИКА ТВЕРДОГО ТЕЛА ИЛИ НЕИЗМЕНЯЕМОЙ СРЕДЫ § 1. Уравнения движения абсолютно твердого тела § 2. Поступательное движение твердого тела § 3. Вращение твердого тела вокруг неподвижной оси § 4. Вращение тела около неподвижной точки. Теорема Даламбера § 5. Общий случай движения свободного твердого тела. Теорема Шаля Б. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ И ТВЕРДОГО ТЕЛА ГЛАВА 4 ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ 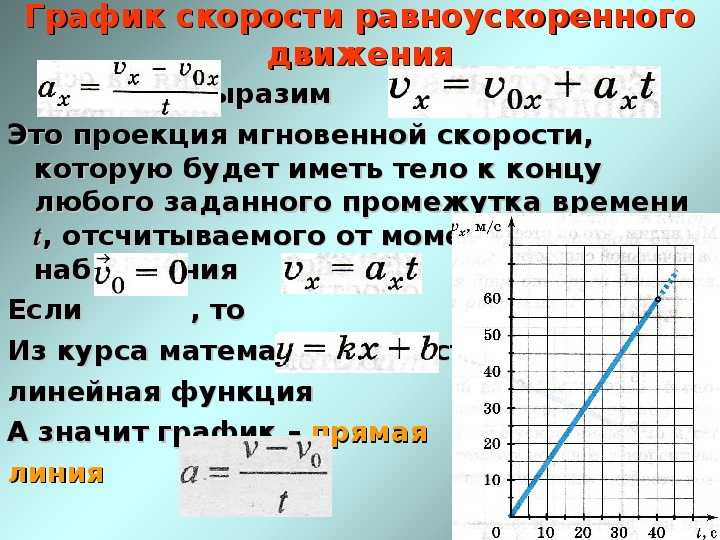 Сложение скоростей Сложение скоростей§ 3. Сложение ускорений ГЛАВА 5. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 2. Сложение вращений § 3. Плоскопараллельное движение твердого тела § 4. Кривошипно-шатупный механизм Часть II. КИНЕТИКА § 1. Вектор силы § 2. Тяжелая масса тел § 3. Закон инерции. Инерциальные системы координат § 1. Основной закон механики (второй закон Ньютона). Инертная масса. Принцип независимости действия сил § 5. Закон равенства действия и противодействия (третий закон Ньютона) Б. ДИНАМИКА ТОЧКИ § 1. Динамика точки и ее две основные задачи § 3. Дифференциальные уравнения движения § 4. Определение уравнения движения точки по заданной силе § 5. Определение силы по заданному уравнению движения § 6. Интегрирование дифференциальных уравнений движения точки в случае сил частного вида ГЛАВА 8. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 1. Уравнение движелия материальной точки в неинерциальной системе координат § 2. 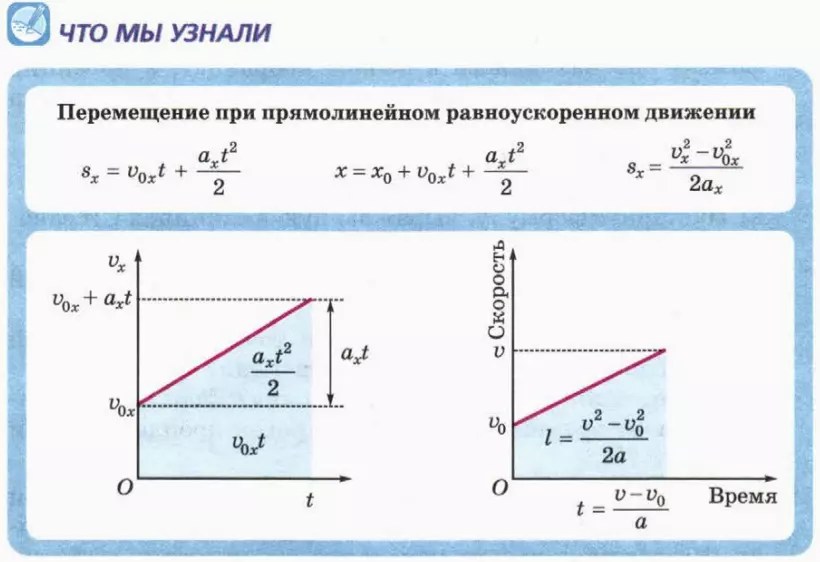 Координатные системы, связанные с Землей Координатные системы, связанные с Землей§ 3. Отклонение падающих тел от вертикали ГЛАВА 9. ДВИЖЕНИЕ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ § 1. Характерные особенности движения точки иод действием центральной силы § 3. Закон всемирного тяготения § 4. Задача двух тел § 5. Движение электрона в поле ионизированного атома (центральная отталкивающая сила) Б. СТАТИКА ГЛАВА 10. СТАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 2. Активные силы и силы реакции связей § 3. Система сходящихся сил § 4. Система параллельных сил § 5. Центр тяжести и центр масс § 6. Момент силы относительно точки и относительно оси § 7. Свойства пары сил § 8. Приведение произвольной системы сил § 9. Равновесие произвольной системы сил, действующих на твердое тело § 10. Раваовесне системы материальных точек ГЛАВА 11. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ В ИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ И ИХ ПЕРВЫЕ ИНТЕГРАЛЫ § 2.  Принцип Даламбера. Основные уравнения диижения системы Принцип Даламбера. Основные уравнения диижения системы§ 3. Теорема о количестве движения системы § 4. Теорема импульсов § 5. Теорема о количестве движения центра инерции системы и примеры ее применения § 6. Теорема о кинетическом моменте ГЛАВА 12. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ § 1. Теорема о количестве движения в неинерциальной системе координат § 2. Теорема о кинетическом моменте в неинерциальной системе координат § 4. Уравнения движения в расчетной системе координат Д. КОНСЕРВАТИВНЫЕ СИЛЫ ГЛАВА 13. РАБОТА СИЛЫ. ПОТЕНЦИАЛЬНОЕ ПОЛЕ § 2. Силовое поле и его частный случай — потенциальное поле § 3. Работа внутренних сил, действующих в системе ГЛАВА 14. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ § 1. Теорема о кинетической энергии и закон сохранения механической энергии точки § 2. Теорема о кинетической энергии системы § 3. Формула Кенига § 4.  Е. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА § 1. Кинетический момент твердого тела в частных случаях его движения § 2. Вычисление моментов инерции относительно параллельных осей § 3. Эдлипсоид инерции ГЛАВА 16. ДИНАМИКА ПРОСТЕЙШИХ ВИДОВ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 2. Вращение твердого тела вокруг неподвижной оси § 3. Физический и математический маятники ГЛАВА 17. ДИНАМИКА ТЕЛА, ВРАЩАЮЩЕГОСЯ ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТЕЛА § 1. Кинематические уравнения Эйлера Углы Эйлера § 2. Динамические уравнения Эйлера § 3. Постановка задачи о движении твердого тела вокруг неподвижной точки § 4. Регулярная прецессия гироскопа § 6. Общий случай движения твердого тела Ж. ПРИМЕНЕНИЕ ОСНОВНЫХ УРАВНЕНИЙ ДИНАМИКИ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ВОПРОСАМ МЕХАНИКИ ГЛАВА 18. ДВИЖЕНИЕ ТОЧКИ ПЕРЕМЕННОЙ МАССЫ § 2. Примеры применения уравнения Мещерского. Задачи Циолковского ГЛАВА 19.  УДАР УДАР§ 1. Основное уравнение теории удара § 2. Гипотеза Ньютона § 3. Абсолютно упругий удар точки о сферу § 4. Прямое центральное соударение двух тел З. ДИНАМИКА СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ (АНАЛИТИЧЕСКАЯ МЕХАНИКА) ГЛАВА 20. ЗАДАЧА О ДВИЖЕНИИ СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ § 3. Идеальные связи (основной постулат аналитической механики) § 4. Уравнения Лагранжа первого рода ГЛАВА 21. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА § 2. Уравнения Лагранжа второго рода § 3. Уравнения Лагранжа второго рода, как уравнения движения точки в 3n-мерном пространстве § 4. Уравнения Лагранжа второто рода для частных случаев сил, действующих на систему § 5. Первые интегралы уравнений движения ГЛАВА 22. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА § 2. Канонические уравнения Гамильтона 3. Первые интегралы канонических уравнений § 4. Скобки Пуассона § 5. Метод Рауса ГЛАВА 23. ОБЩИЕ ПРИНЦИПЫ МЕХАНИКИ § 2. 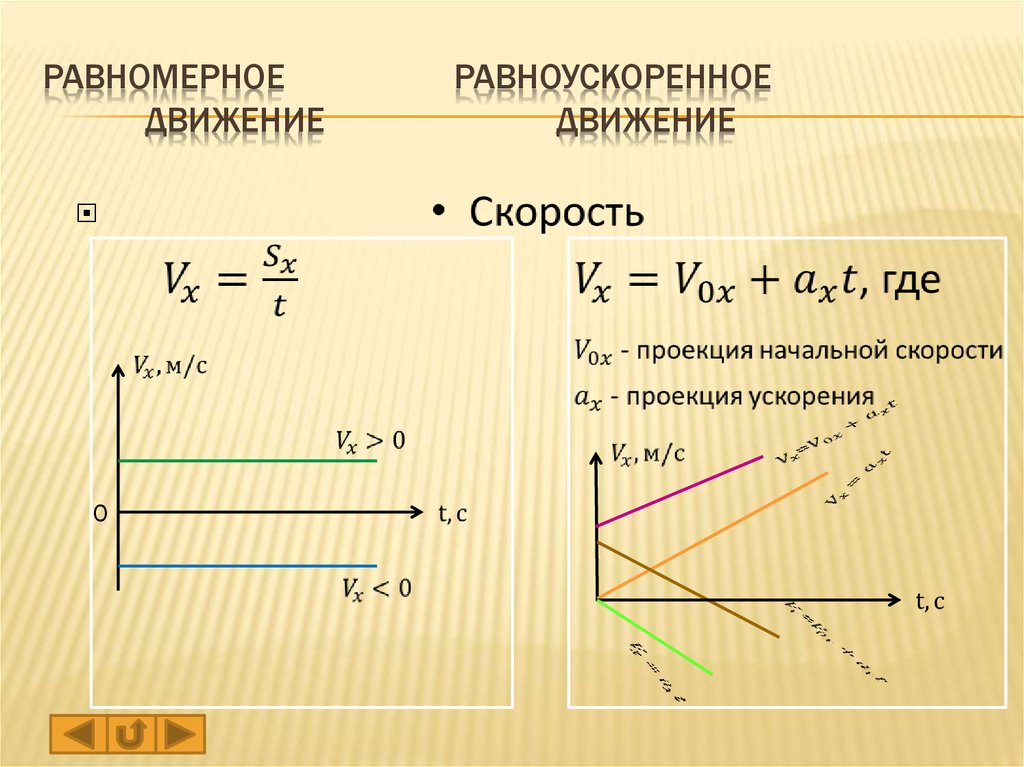 § 3. Вариационный интегральный принцип Гамильтона — Остроградского И. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ ГЛАВА 24. ПРЯМОЛИНЕЙНОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ § 2. Свободные колебания точки при наличии сопротивления среды § 3. Вынужденные колебания точки § 4. Резонанс ГЛАВА 25. ОБЩИЕ УРАВНЕНИЯ МАЛЫХ КОЛЕБАНИЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ § 2. Устойчивое равновесие консервативной системы § 3. Уравнения малых колебаний механических систем § 4. Малые колебания системы с одной степенью свободы § 2. Собственные колебания системы § 3. Главные координаты § 4. Вынужденные колебания системы с двумя степенями свободы § 5. Двойной математический маятник Часть III. УРАВНЕНИЯ МЕХАНИЧЕСКИХ ДВИЖЕНИИ ТОЧЕК СО СКОРОСТЯМИ, БЛИЗКИМИ К СКОРОСТИ СВЕТА (ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ) ГЛАВА 27.  ВВЕДЕНИЕ В СПЕЦИАЛЬНУЮ ТЕОРИЮ ОТНОСИТЕЛЬНОСТИ ВВЕДЕНИЕ В СПЕЦИАЛЬНУЮ ТЕОРИЮ ОТНОСИТЕЛЬНОСТИ§ 2. Элементарные сведения об ортогональных преобразованиях ГЛАВА 28. СВОЙСТВА ПРОСТРАНСТВА И ВРЕМЕНИ ПРИ СКОРОСТЯХ ТОЧЕК, СРАВНИМЫХ СО СКОРОСТЬЮ СВЕТА (ПЕРВЫЙ ЗАКОН НЬЮТОНА В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ) § 1. Порвый закон Ньютона и свойства пространства и времени ньютонианской маханики § 2. Преобразования Лоренца § 3. Свойства пространства и времени при относительном движении координатных систем, сравнимых со скоростью света § 4. Преобразование скорости и ускорения (теорема сложения скоростей Эйнштейна) ГЛАВА 29. ВТОРОЙ ЗАКОН НЬЮТОНА В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. Второй закон Ньютона в специальной теории относительности § 3. Уравнение энергии в специальной теории относительности § 4. Закон взаимной связи массы и энергии ГЛАВА 30. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. Уравнения движения механических систем ГЛАВА 31. РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ.  РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ§ 1. Релятивистские уравнения движения точки в криволинейных координатах § 2. Релятивистские уравнения движения связных механических систем |
Проекции скорости и ускорения
Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме.
Векторы начальной скорости и ускорениямогут иметь различные направления, поэтому переход от векторной записи уравнений к алгебраической может оказаться весьма трудоемким.
Известно, что проекция суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось.
Поэтому для
нахождения проекции
вектора скоростина произвольную ось OX нужно найти
алгебраическую сумму проекций векторовина ту же ось. Проекцию вектора на ось считают положительной, если от проекции начала к проекции конца вектора нужно идти по направлению оси, и отрицательной в противоположном случае. | |
График скорости
Из уравнения следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось OX равна нулю, то прямая проходит через начало координат.
Основные виды движения
аn = 0, a = 0 – прямолинейное равномерное движение;
аn = 0, a = const – прямолинейное равнопеременное движение;
аn = 0, a 0 – прямолинейное с переменным ускорением;
аn = const, a = 0 – равномерное по окружности
аn = const, a = const – равнопеременное по окружности
аn const, a const – криволинейное с переменным ускорением.

Вращательное движение твердого тела.
Вращательное движение твердого тела относительно неподвижной оси – движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
Равномерное движение по окружности
Рассмотрим наиболее простой вид вращательного движения, и уделим особое внимание центростремительному ускорению.
При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости изменяется в процессе движения.
За
интервал времени ∆t тело проходит путь
.
Этот путь равен длине дугиAB. Векторы скоростей
ив точкахA и B направлены
по касательным к окружности в этих
точках, а угол между векторами
иравен углу между радиусамиOA и OB. |
Из подобия треугольников OAB и BCD следует
Если интервал времени ∆t мал, то мал и угол . При малых значениях угла длина хорды AB примерно равна длине дуги AB, т.е. . Т.к.,, то получаем
.
Поскольку , то получаем
Период и частота
Промежуток времени,
за который тело совершает полный оборот
при движении по окружности, называется периодам
обращения (Т). Т.к. длина окружности равна 2R,
период обращения при равномерном
движении тела со скоростью v
по окружности радиусом R равняется:
Т.к. длина окружности равна 2R,
период обращения при равномерном
движении тела со скоростью v
по окружности радиусом R равняется:
Величина, обратная периоду обращения, называется частотой. Частота показывает, сколько оборотов по окружности совершает тело в единицу времени:
(с-1)
Вычисление ускорения свободного падения на самолете
Вы когда-нибудь задумывались, почему, когда тело подбрасывают вверх, оно возвращается вниз с большей скоростью? Это связано с ускорением, вызванным силой тяжести. Вблизи земной поверхности гравитационная сила почти не ощущается, но она меняется на больших расстояниях от земли. Гравитация — это сила, действующая между двумя объектами определенной массы и стремящаяся притянуть их к центру Земли.
Ускорение имеет как величину, так и направление, поэтому оно является векторной величиной. Ускорение называют изменением скорости в единицу времени и обозначают буквой «а». Единицей ускорения в СИ является (м/с2) или ньютон на килограмм (Н/кг).
Ускорение называют изменением скорости в единицу времени и обозначают буквой «а». Единицей ускорения в СИ является (м/с2) или ньютон на килограмм (Н/кг).
Это ускорение зависит от различных факторов; масса тела объекта (м), расстояние объекта от центра масс (r) и универсальная гравитационная постоянная (G), которая составляет 6,673*10-11 Нм2 кг2. Эти факторы связаны, как указано в уравнении; g=GM/r2…….. (i)
, здесь g представляет собой ускорение свободного падения.
Факторы, влияющие на ускорение под действием силы тяжести
Масса прямо пропорциональна силе тяжести; таким образом, чем тяжелее объект, тем большее гравитационное притяжение он будет испытывать. Гравитационная сила обратно пропорциональна квадрату расстояния между телами. Таким образом, чем больше расстояние разделения, тем слабее эффект гравитационного притяжения. Когда два объекта удаляются друг от друга, гравитационная сила между ними уменьшается.
Рассмотрим тела, которые находятся на расстоянии 2 м от центра масс и весят 5 кг и 3 кг соответственно. При подстановке с использованием приведенного выше уравнения видно, что ускорение свободного падения на массе 5 кг составляет 1,25G м/с2, а на массе 3 кг — 0,75G м/с2. Это доказывает, что масса напрямую влияет на гравитационное ускорение, испытываемое телом, т. Е. Чем тяжелее масса, тем выше ощущаемое гравитационное ускорение.
При подстановке с использованием приведенного выше уравнения видно, что ускорение свободного падения на массе 5 кг составляет 1,25G м/с2, а на массе 3 кг — 0,75G м/с2. Это доказывает, что масса напрямую влияет на гравитационное ускорение, испытываемое телом, т. Е. Чем тяжелее масса, тем выше ощущаемое гравитационное ускорение.
Высота также является фактором, влияющим на ускорение под действием силы тяжести. Высота обратно пропорциональна ускорению, которое уменьшается с увеличением высоты. На бесконечном расстоянии от земли значение становится равным нулю. Это можно вычислить по следующему уравнению;
gh=g(1+h/R)-2……. (ii)
gh – ускорение свободного падения на определенной высоте, «h» – высота над поверхностью земли, а «R» – радиус Земли.
Примеры
Предположим, что Луна имеет радиус 1,64 * 106 м и массу 7,24 * 1022 кг. Подставив это, значения в уравнении (i) выше,
I) идентифицируют «r» и «M», поскольку универсальная гравитационная постоянная (G) постоянна. В этом случае
В этом случае
r = 1,64 * 106 м и М = 7,24 * 1022 кг
G = 6,673 * 10 -11 Нм2 кг2
II) Подставив это значение в уравнение (i) выше
Умножьте «G» и «M», чтобы получить
= 4,831 * 10 12
III) Разделите вычисленное выше значение на r2
r2 =2,689 * 10 12 м2
г = 1,796 мс-2
Следовательно, значение ускорения свободного падения в данном случае равно 1,796 мс-2.
Как рассчитать ускорение свободного падения на плоскости
При расчете ускорения тела, движущегося на плоскости, учитываются несколько величин. Этими величинами являются перемещение, скорость и скорость. Смещение — это расстояние, пройденное в определенном направлении, обозначается буквой «S», а единицей СИ является метр (м). Скорость — это расстояние, пройденное за единицу времени, а единица СИ — метры в секунду (м/с или мс-1). Это скалярная величина.
Скорость представляет собой изменение смещения в единицу времени и является векторной величиной.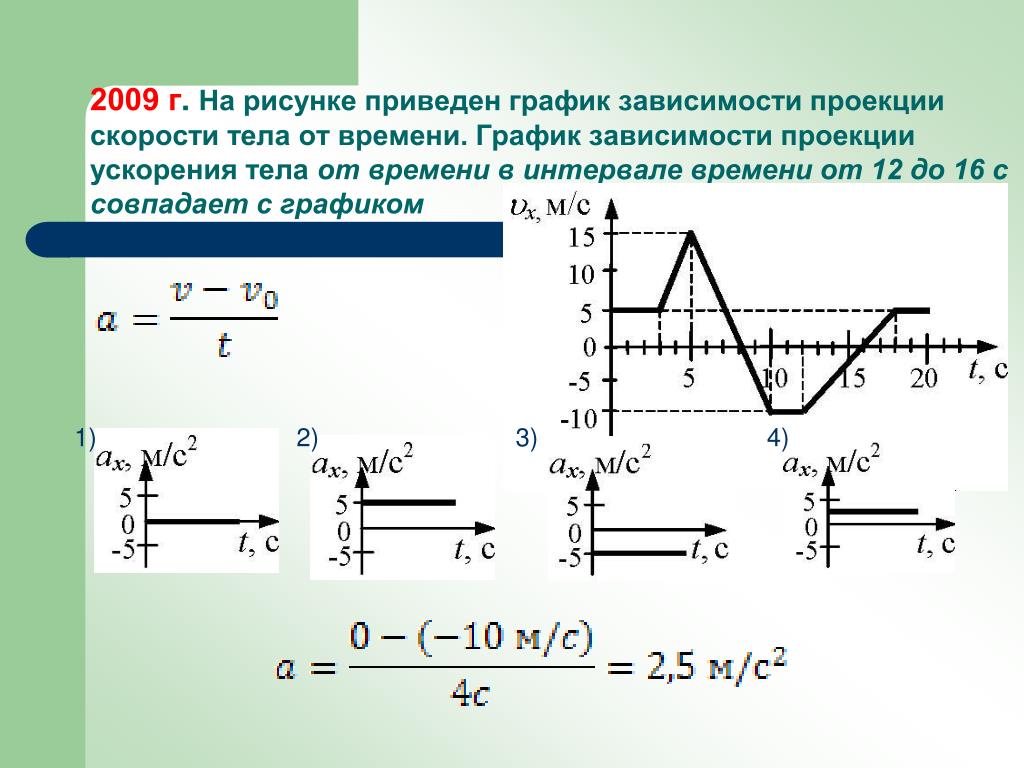 Единицей скорости в системе СИ является (м/с).
Единицей скорости в системе СИ является (м/с).
Начальная скорость обычно обозначается (u), а конечная скорость обозначается (v). При вычислении ускорения тела необходимо точно отметить две скорости, включая общее время.
Прикладные уравнения кинематики
Для равноускоренного движения на плоскости. Применяются следующие три кинематических уравнения.
v=u+ at…… (iii)
s=ut +1/2 at2… (iv)
v2 =u2 +2as…… (v)
Всегда наблюдается в нашей повседневной жизни что листья на дереве всегда падают на землю сами по себе. Почему они не остаются в воздухе или, что еще лучше, не движутся вверх, к небу? Или, вернее, почему камень, брошенный вверх, падает обратно на землю? Это явление связано с силой гравитации, которая вызывает свободное падение тел и предметов.
Непроизвольное движение объекта к земле с ускоренной скоростью под действием силы гравитации называется свободным падением. Это ускорение теоретически оценивается в 90,8 м/с2, но для расчетов и точности используемая сила тяжести округлена до 10 м/с2.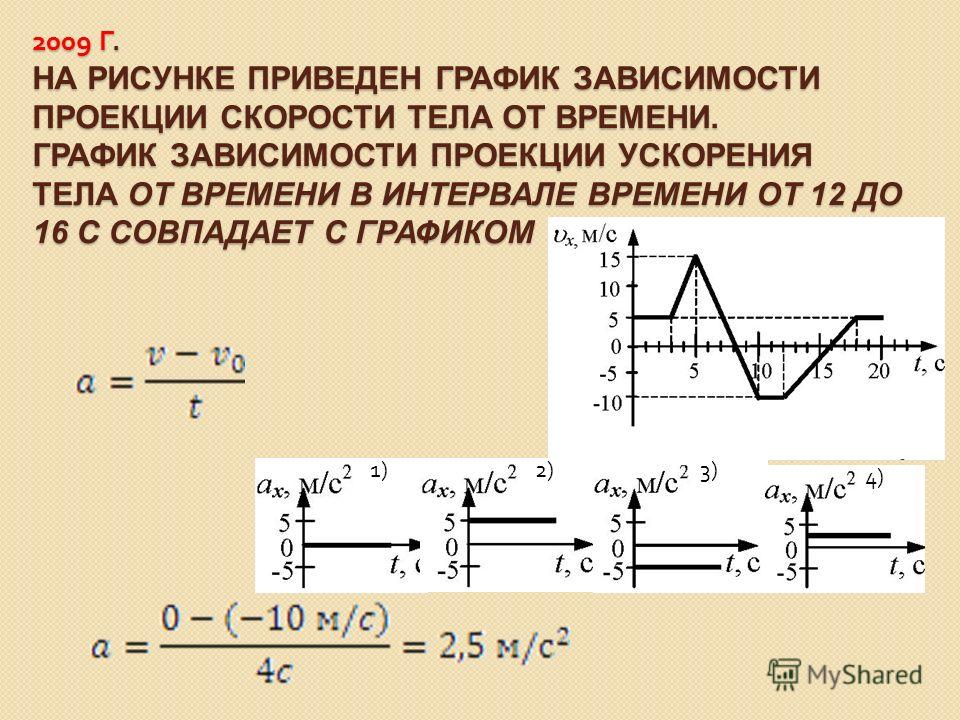
При попытке найти ускорение силы тяжести для свободного падения применяются приведенные выше кинематические уравнения, но в этом случае ускорение «а» заменяется силой тяжести, «поскольку это сила, вызывающая увеличение скорости. то есть
V= u+gt …. (vi)
S= ut +1/2 gt 2…. (vii)
V2 =u2 +2gs…… (viii)
Вертикальные проекции
В вертикальных проекциях тело движется против силы тяжести, и поэтому происходит замедление. В этом случае сила гравитации отрицательна.
Во время вертикальной проекции существует максимальная высота, которую можно достичь в определенное время. На этой высоте конечная скорость всегда равна нулю, поскольку движущееся тело должно остановиться, прежде чем оно начнет падать обратно на землю. Применяя соответствующие уравнения, из уравнения (vi)
V=u+gt… будет V= u-gt…..поскольку v=0, то u=gt и, таким образом, t=u/g… это показывает время, затраченное на объект для достижения максимальной высоты.
Из уравнения (viii)
V2= u2 +2gs… будет v2 =u2 -2gs в случае вертикальной проекции.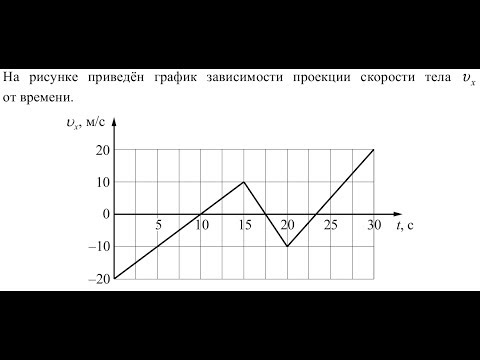
Поскольку v=0…тогда u2=2gHmax….. т.е. заменяется на максимальную высоту (Hmax). Это по-прежнему одно и то же, поскольку оба они представляют смещение. Следовательно, максимальная достигнутая высота может быть рассчитана с помощью уравнения… Hmax =u2/2g
Время полета снаряда в два раза больше времени, необходимого для достижения максимальной высоты, таким образом, t=2u/g. В случаях здесь и объект возвращается в исходное положение, полное перемещение равно нулю. Таким образом, уравнение (viii) становится v2=u2…. поэтому v=u.
Примеры
Рассмотрим камень, брошенный вертикально вверх со скоростью 20 м/с.
I) время достижения максимальной высоты составит;
U=20 г=10 …. таким образом, T=20/10 время, необходимое для достижения максимальной высоты, равно 2 секундам
II) Время полета в два раза больше времени, необходимого для достижения максимальной высоты, следовательно,
4 секунды — это время полета
III) максимальная достигнутая высота
Hmax =u2/2g (400/20), следовательно, максимальная достигнутая высота в данном случае составляет 20 м.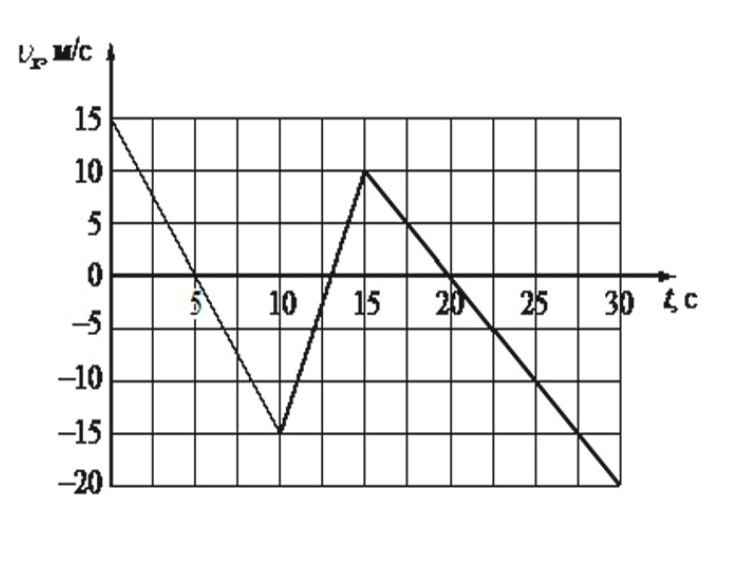
IV)Скорость, с которой камень падает на землю, равна его начальной скорости при условии отсутствия сопротивления воздуха. Таким образом, скорость будет 20 м/с.
Сделанные проекции также могут быть горизонтальными. Путь, пройденный во время горизонтальной проекции, известен как траектория. Максимальное горизонтальное расстояние, пройденное в данный момент времени, известное как дальность (R). Ускорение равно нулю на максимальном горизонтальном расстоянии; таким образом, из уравнения s=ut -1/2gt2 дальность R= ut, а вертикальное перемещение будет h=1/2gt2.
Заключение
Гравитационная сила отвечает за ускорение, наблюдаемое при движении объекта по мере его движения к земле. Тело при свободном падении всегда ускоряется со скоростью 9,8 м/с2.
Будьте первым, кто оставит комментарий ниже.
домашнее задание и упражнения — Как найти ускорение катушки, притянутой силой, и ее работу?
спросил 92$ , где $\gamma$ — числовой коэффициент, а $$ — внешний радиус катушки. Радиус слоя намотанной нити равен $r$. Катушку без скольжения тянут за нить с постоянной силой $F$, направленной под углом $\alpha$ к горизонту. Найти:
Радиус слоя намотанной нити равен $r$. Катушку без скольжения тянут за нить с постоянной силой $F$, направленной под углом $\alpha$ к горизонту. Найти:
Я уже сделал первую часть, как показано на картинке ниже:
Я получил $a=\frac{F(r-R\cos\alpha)}{Rm(\gamma+1)}$, но согласно моей книге ответ $a=\frac{F(\cos \alpha-\frac{r}{R})}{m(1+\gamma)}$. Я не понимаю, почему знаки разные, что я делаю не так?
Я не очень хорошо разбираюсь во второй части, может подскажете? Надеюсь, вы можете мне помочь.
- домашние задания и упражнения
- динамика вращения
- крутящий момент
$\endgroup$
$\begingroup$
Решение приведено выше. Другой – от вращения в момент, когда шпуля касается земли. Пусть для простоты $\alpha = 0$:
кинетическое соотношение: $a_{||} = R \frac{d \omega}{dt}$ 92\frac{d \omega}{dt}$
Так что: $a_{||} = \frac{1- \frac{r}{R}}{\gamma + 1} \frac{F}{ м}$
$\endgroup$
$\begingroup$
Необходимо соблюдать осторожность при применении правила правой руки для определения направления крутящих моментов и углового ускорения.




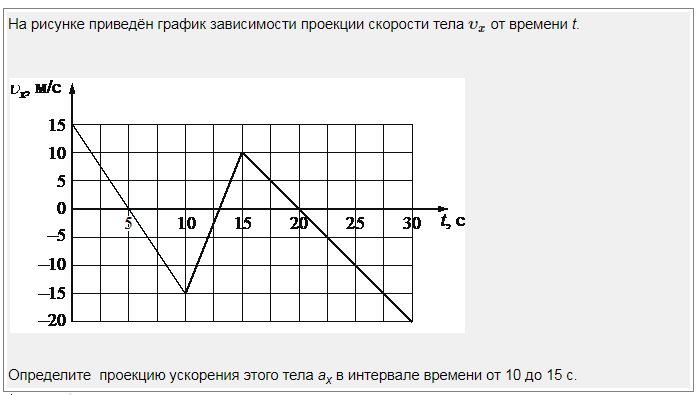 Найдем разность векторов
и определим отношение изменения
скорости к∆t:
Найдем разность векторов
и определим отношение изменения
скорости к∆t:
Leave A Comment