Matematika_v5 — Стр 3
заштрихованной фигуры.
188. Прототип задания B5 (№ 315124)
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.
189. Прототип задания B5 (№ 315132)
На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.
190. Прототип задания B5 (№ 315133)
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?
193. Прототип задания B5 (№ 319057)
Площадь параллелограмма ABCD равна 176. Точка E – середина стороны CD. Найдите площадь треугольника ADE.
194. Прототип задания B5 (№ 319058)
Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABDE.
195. Прототип задания B5 (№ 324460)
На клетчатой бумаге с размером клетки 1 × 1 отмечены точки A и B. Найдите длину отрезка AB.
196. Прототип задания B5 (№ 324461)
На клетчатой бумаге с размером клетки 1 × 1 изображён угол.
197. Прототип задания B5 (№ 324462)
На клетчатой бумаге с размером клетки 1 × 1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB.
198. Прототип задания B5 (№ 324463)
На клетчатой бумаге с размером клетки 1 × 1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.
191. Прототип задания B5 (№ 317338)
Площадь параллелограмма ABCD равна 189. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
192. Прототип задания B5 (№ 319056)
Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма.
21
199. Прототип задания B5 (№ 324464)
На клетчатой бумаге с размером клетки 1 × 1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе.
200. Прототип задания B5 (№ 324465)
На клетчатой бумаге с размером клетки 1 × 1 отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC.
Найдите расстояние от точки A до прямой BC.
201. Прототип задания B5 (№ 324466)
На клетчатой бумаге с размером клетки 1 × 1 изображён треугольник. Найдите радиус описанной около него окружности.
|
|
|
|
|
| Ответы: |
|
|
|
|
|
1 | 1 | 35 | 6 | 69 | 8 | 103 | 24 | 137 | 2 | 171 | 5 |
2 | 1 | 36 | 6 | 70 | 5 | 104 | 42 | 138 | 4,5 | 172 | 3 |
3 | 6 | 37 | 6 | 71 | 2 | 105 | 65 | 139 | 6 | 173 | 1 |
4 | 6 | 38 | 6 | 72 | 1 | 106 | 21 | 140 | 8 | 174 | 1,5 |
5 | 12 | 39 | 8 | 73 | 5 | 107 | 31 | 141 | 6 | 175 | 2,5 |
6 | 6 | 40 | 24 | 74 | 4 | 108 | 40 | 142 | 2 | 176 | 1 |
7 | 7,5 | 41 | 1 | 75 | 3 | 109 | 56 | 143 | 18 | 177 | 1 |
8 | 10,5 | 42 | 50 | 76 | 20 | 110 | 49 | 144 | 6 | 178 | 3 |
9 | 12 | 43 | 6 | 77 | 6 | 111 | 82 | 145 | 6 | 179 | 3 |
10 | 28 | 44 | 18 | 78 | 36 | 112 | 120 | 146 | 22 | 180 | 1 |
11 | 10 | 45 | 14 | 79 | 40 | 60 | 147 | 4 | 181 | 2 | |
12 | 10 | 46 | 13 | 80 | 10 | 114 | 30 | 148 | 10 | 182 | 4 |
13 | 12 | 47 | 2 | 81 | 45 | 115 | 4 | 149 | 2 | 183 | 1 |
14 | 12,5 | 48 | 6 | 82 | 62 | 116 | 3 | 150 | 52 | 184 | 4,5 |
15 | 6 | 49 | 4 | 83 | 104 | 117 | 5 | 151 | 7 | 185 | 3 |
16 | 17,5 | 50 | 5 | 84 | 31 | 118 | 10 | 152 | 14 | 186 | 153 |
17 | 15 | 51 | 12 | 85 | 116 | 119 | 5 | 153 | 24 | 187 | 3 |
18 | 14 | 52 | 9 | 86 | 64 | 120 | 20 | 154 | 2,5 | 188 | 7 |
19 | 32,5 | 53 | -4 | 87 | 69 | 121 | 20 | 155 | 2,5 | 189 | 24 |
20 | 10 | 54 | 8 | 88 | 41 | 122 | 10 | 156 | 2 | 190 | 96 |
21 | 12 | 55 | 2 | 89 | 38 | 123 | 23 | 157 | 2 | 191 | 141,75 |
22 | 12 | 56 | 6 | 90 | 74 | 124 | 10 | 158 | 5 | 192 | 76,5 |
23 | 12 | 57 | 8 | 91 | 52 | 125 | 12 | 159 | 2,5 | 193 | 44 |
24 | 12 | 58 | 2 | 92 | 48 | 126 | 9 | 160 | 3 | 194 | 9 |
25 | 12 | 59 | 2 | 93 | 32 | 127 | 4 | 161 | 1 | 195 | 17 |
26 | 25,5 | 60 | 6 | 94 | 108 | 128 | 3 | 162 | 3 | 196 | 135 |
27 | 54 | 61 | 10 | 95 | 130 | 129 | 40 | 163 | 2 | 197 | 2 |
28 | 68 | 62 | 8 | 96 | 119 | 130 | 30 | 164 | 198 | 3 | |
29 | 20 | 63 | 5 | 97 | 61 | 131 | 40 | 165 | 2,5 | 199 | 4,5 |
30 | 30 | 64 | 8 | 98 | 45 | 132 | 5 | 166 | 2,5 | 200 | 4 |
31 | 9 | 65 | 2 | 99 | 116 | 133 | 2 | 167 | 5 | 201 | 2,5 |
32 | 35 | 66 | 3 | 100 | 36 | 134 | 6 | 168 | 5 |
|
|
33 | 6 | 67 | 1,2 | 101 | 37 | 135 | 3 | 169 | 3 |
|
|
34 | 14 | 68 | -6 | 102 | 16 | 136 | 58 | 170 | 4 |
|
|
http://semenova-klass. moy.su/
moy.su/
22
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
13.02.2015131.46 Кб9MATAN_SMERT__33.docx
- #
12.03.2016825.21 Кб26matem2014gia4proba.pdf
- #
12.03.2016981.11 Кб8matem2015-04-22proba2varianta_copy.pdf
- #
04.08.2019249.14 Кб0Matematika.docx
- #
12.03.2016167.18 Кб670MATEMATIKA_11_kl_Fevral_2016_copy.pdf
- #
13.02.20151.2 Mб23Matematika_v5.pdf
- #
19.09.2019382.46 Кб3material (4).doc
- #
03.05.20151.13 Mб28math-bio.pdf
- #
13.02.2015616.49 Кб364matlog2011.pdf
- #
13.02.20152.14 Mб234Matmetodyvbiologii2012 (1).
 doc
doc - #
13.02.20151.29 Mб18may07015.pdf
Question
Question
RD SHARMA ENGLISH-ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММОВ И ТРЕУГОЛЬНИКОВ-Все вопросы
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
Стенограмма
вопрос вопрос говорит, что пусть ABCD является параллелограммом площадью 124 см квадрат, если p и F являются серединами сторон ab и CD соответственно, то найдите площадь параллелограмма, если известно, что ABCD является параллелограммом, площадь которого равна us это середина a b а F это середина CD нам нужно найти площадь фигуры ABCD это параллелограмм площадь ABCD равна 124 см в квадрате середины AB
CD sunao чтобы решить в этом году мы видно, что мы начертили построение мы построили p перпендикулярно CD напишем построить перпендикуляр на запрос напишем площадь параллелограмма формула площадь параллелограмма равна основанию в высоту найдем площадь параллелограмма площадь параллелограмма
равно видеть на рисунке основание этого снова в один, используя ту же формулу, мы можем найти площадь параллелограмма, если параллелограмм равен в, он остается тем же, что и AP, потому что это не меняет уравнение на теперь мы знаем, что это середина BC и дана нам, поэтому мы можем написать d f равно
BF равно AC, причина в той же точке, что и мы пишем это уравнение 1 2 и 3 и пишем площадь параллелограмма равна площади параллелограмма, потому что в 1 и 2 din к APMC f в него, а в предыдущем через DF равен его, поэтому мы можем сказать, что одно и два уравнения dikhao
напишите годы от 1, чтобы доказать, что это означает, что параллелограмм ABCD был разделен на две равные части, чтобы быть также можно написать площадь параллелограмма площадь параллелограмма ABCD и написать, что это половина площади параллелограмма ABCD значение между быть равно 2124, что равно 62
. (гм)ABCD)
СТРОИТЕЛЬСТВО: Присоединяйтесь к AC
и ВЧ
(гм)ABCD)
СТРОИТЕЛЬСТВО: Присоединяйтесь к AC
и ВЧ
Д, Э, Ж
являются средней точкой
стороны BC, CA и AB
соответственно АВС.
Затем DEF
соответствует
треугольник.
азбука
(б) АЭФ (в)
БФД, CDE
(г)
AFE, BFD, CDE
Дано: D, E, F — середины сторон BC, CA и AB.
1414395
Если ABC и DEF
два таких треугольника
что AB, BC
соответственно равны
и параллельно DE, EF,
затем покажи, что
Четырехугольник ABED
является параллелограммом
Четырехугольник BCFE
является параллелограммом
АС=DF
(4)
ABC ≅ DEF
1414649
Стороны AB и CD параллелограмма ABCD делятся пополам в точках E и F. Докажите, что EBFD является параллелограммом.
1414663
АВСD является параллелограммом, E и F являются серединами AB и CD соответственно. ГХ любая линия пересекает AD, EF и BC в точках G, P и H соответственно. Доказывать что GP=PH
1414705
ABCD
является параллелограммом. Е
это точка
на бакалавриате
такой, что BE=2 EA и F
это точка
в округе Колумбия
такой, что DF=2 FC.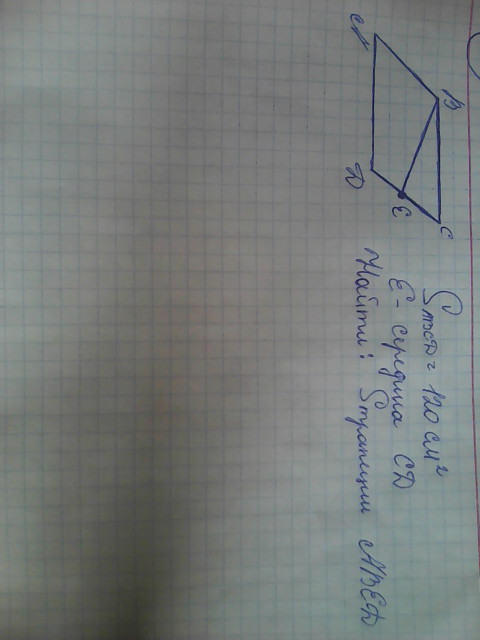 Докажите, что AE CF
это
параллелограмм, площадь которого составляет одну треть площади параллелограмма AB CD.
Докажите, что AE CF
это
параллелограмм, площадь которого составляет одну треть площади параллелограмма AB CD.
1414844
АВСD это параллелограмм, Г это точка на АВ такой, что AG=2GB ,E это точка округа Колумбия такое, что CE=2DE и F это точка Британской Колумбии такой, что BF=2FC. Докажи это: Найти то, что часть площади параллелограмма равна площади EFG
1414852
ABC это треугольник, в котором D это середина BC, E и F являются средние точки DC и AE соответственно. Если площадь ABC 16см2, Найди площадь DEF
1414888
Пусть ABCD — параллелограмм площадью 124 см2. Если Е и Ф являются серединами сторон AB и компакт-диск соответственно, то найти площадь параллелограмма AEFD.
642565211
Д, Э, Ж
являются средней точкой
стороны BC, CA и AB
соответственно △ABC.
Затем DEF
соответствует
треугольник.
(а)АВС
(б) АЭФ
(в)
БФД, CDE
(г)
AFE, BFD, CDE
642572163
Стороны AB и CD
параллелограмма ABCD
делятся пополам в точках E и F. Докажите, что EBFD
является параллелограммом.
Докажите, что EBFD
является параллелограммом.
642572423
АВСD является параллелограммом, E и F являются серединами AB и CD соответственно. ГХ любая линия пересекает AD, EF и BC в точках G, P и H соответственно. Доказывать что GP=PH
642572464
АВСD является параллелограммом и E является серединой BC, DE и AB при производстве встречаются в F. Тогда AF=
642572508
Если E, F, G и H являются соответственно середины сторон параллелограмма ABCD, Покажите, что ar(EFGH)=12ar (ABCD)
642572529
E,F,G,H являются соответственно серединами сторон AB,BC,CD и Д.А. параллелограмма ABCD . Докажите, что четырехугольник EFGH является параллелограммом и его площадь равна половине площадь параллелограмма ABCD. ДАННО: Четырехугольник ABCD. в котором L,F,G,H являются соответственно серединами сторон AB,BC,CD и ДА. ДОКАЗАТЬ: (i) Четырехугольник EFGH является параллелограммом ар(∣∣gmEFGH)=12ар(∣∣gmABCD) СТРОИТЕЛЬСТВО: Присоединяйтесь к AC и ВЧ
642572569
В параллелограмме ABCD E является серединой AB, а AP параллельна EC, которая пересекает DC в точке O и.
 ..
..Перейти к
- Упражнение 12 (А)
- Упражнение 12(Б)
- Глава 1. Рациональные и иррациональные числа
- Глава 2. Сложные проценты [без использования формулы
- Глава 3. Сложные проценты [Использование формулы
- Глава 4- Расширения
- Глава 5.
 Факторизация
Факторизация - Глава 6. Одновременные уравнения
- Глава 7. Индексы [экспоненты]
- Глава 8. Логарифмы
- Глава 9. Треугольники [Конгруэнтность треугольников]
- Глава 10. Равнобедренный треугольник
- Глава 11.
 Неравенства
Неравенства - Глава 12. Середина и ее обратная точка
- Глава 13. Теорема Пифагора.
- Глава 14. Прямолинейные фигуры
- Глава 15. Построение полигонов
- Глава 16. Теоремы площадей
- Глава 17- Круги
- Глава 18- Статистика
- Глава 19.
 Среднее и медиана
Среднее и медиана - Глава 20. Площадь и периметр плоских фигур
- Глава 21- Твердые тела
- Глава 22. Тригонометрические отношения
- Глава 23. Тригонометрические отношения стандартных углов
- Глава 24. Решение прямоугольных треугольников.
- Глава 25.
 Дополнительные углы
Дополнительные углы - Глава 26. Координатная геометрия
- Глава 27. Графическое решение
- Глава 28. Формула расстояния
Главная > Селина Солюшнс Класс 9 Математика > Глава 12. Глава 12. Середина и ее обратная точка. > Упражнение 12(Б) > Вопрос 12
Вопрос 12 Упражнение 12(B)
В параллелограмме ABCD E является серединой AB, а AP параллельна EC, которая пересекает
DC в точке O, а BC получается в P. Докажите, что:
Докажите, что:
(i) BP = 2AD
(ii) O – середина AP.
Ответ:
Решение:
Дан ABCD параллелограмм, поэтому AD = BC, AB = CD.
Рассмотрим треугольник APB, данный EC параллелен AP, а E является серединой стороны AB. Таким образом, по теореме
середина точки C должна быть серединой точки BP.
Таким образом, BP = 2BC, но BC = AD, поскольку ABCD — параллелограмм.
Отсюда BP = 2AD
Рассмотрим треугольник APB, AB || OC как ABCD является параллелограммом. Итак, по теореме о средней точке O должно быть
— середина AP.
Отсюда доказано
Связанные вопросы
Используйте следующий рисунок, чтобы найти: (i) BC, если AB = 7,2 см. (ii) GE, если FE = 4 см. (iii) AE, если BD = 4,1…
На приведенном ниже рисунке 2AD = AB, P — середина AB, Q — середина DR и PR||BS. Докажи, что…
Сторона AC треугольника ABC проведена в точку E, так что D является серединой треугольника BC, а ED. ..
..
В треугольнике ABC проведены медианы BP и CQ до точек M и N соответственно так, что BP = …
В треугольнике ABC угол B тупой. D и E — середины сторон AB и BC соответственно, а F — это…
В параллелограмме ABCD точки E и F являются серединами сторон AB и CD соответственно. Сегменты линии…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 12(A)
Упражнение 12(B)
Главы
Глава 1.

 doc
doc Факторизация
Факторизация Неравенства
Неравенства Среднее и медиана
Среднее и медиана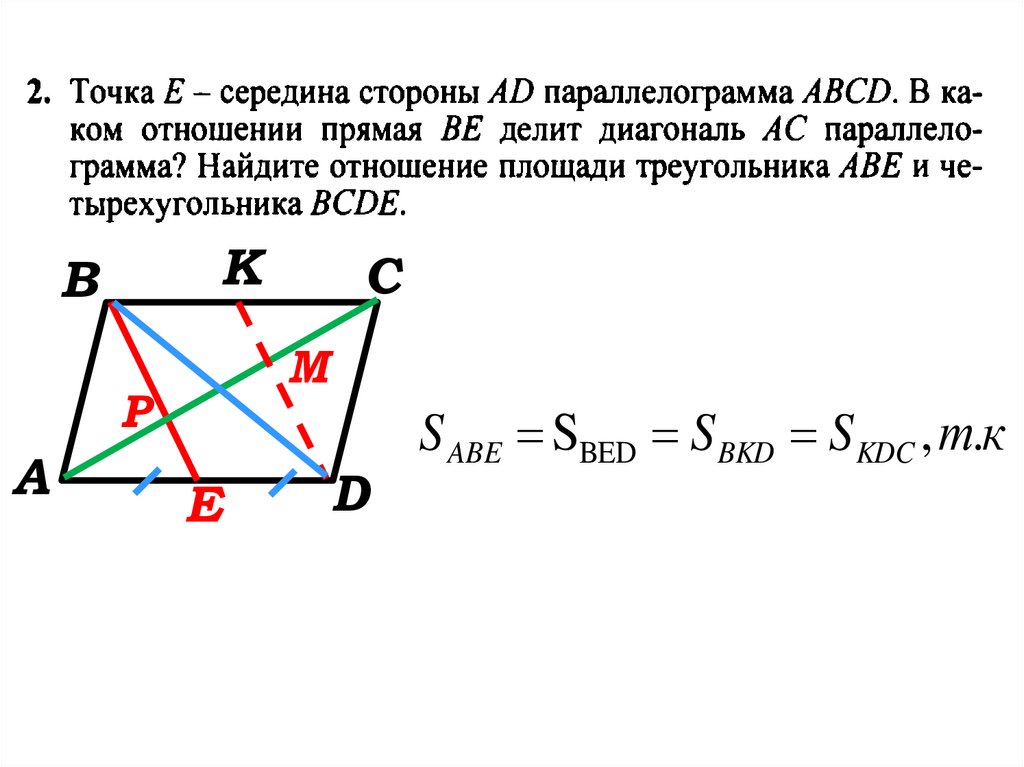 Дополнительные углы
Дополнительные углы
Leave A Comment