Периметр, площадь и объем

Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.

Периметр геометрической фигуры

Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.

Вычислим периметр следующей фигуры:

Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.

У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:

Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:

P = 9 см + 4 см + 9 см + 4 см = 26 см.

Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»

P = 2 × (9 + 4) = 18 + 8 = 26 см.

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»

Чтобы вычислить периметр, сложим все стороны:

P = 5 см + 5 см + 5 см + 5 см = 20 см

Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза

P = 5 см × 4 = 20 см

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь.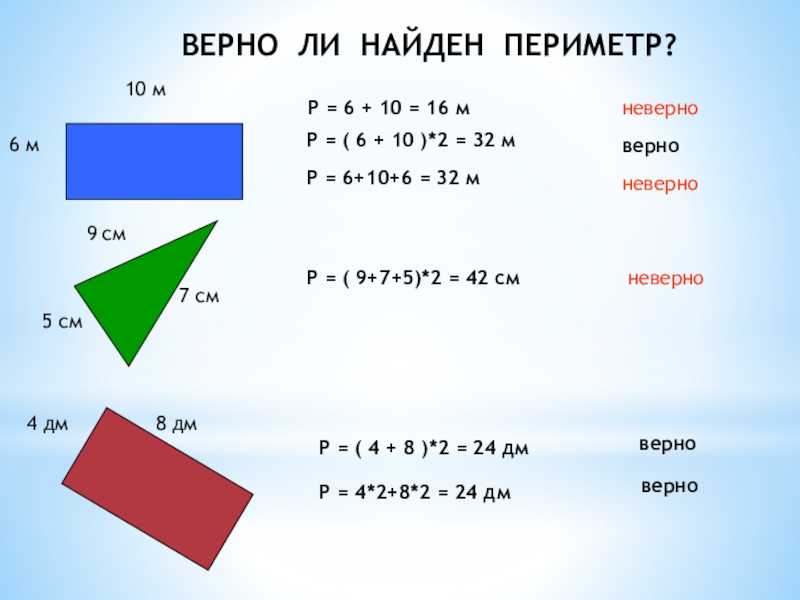 В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

Площадь прямоугольника

В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.

Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.

Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.

Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:

Теперь измерим ширину. Пусть она составила 3 метра:

Умножим длину (4 м) на ширину (3 м).

4 × 3 = 12

Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:

Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:

Площадь квадрата

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

3 × 3 = 9

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см.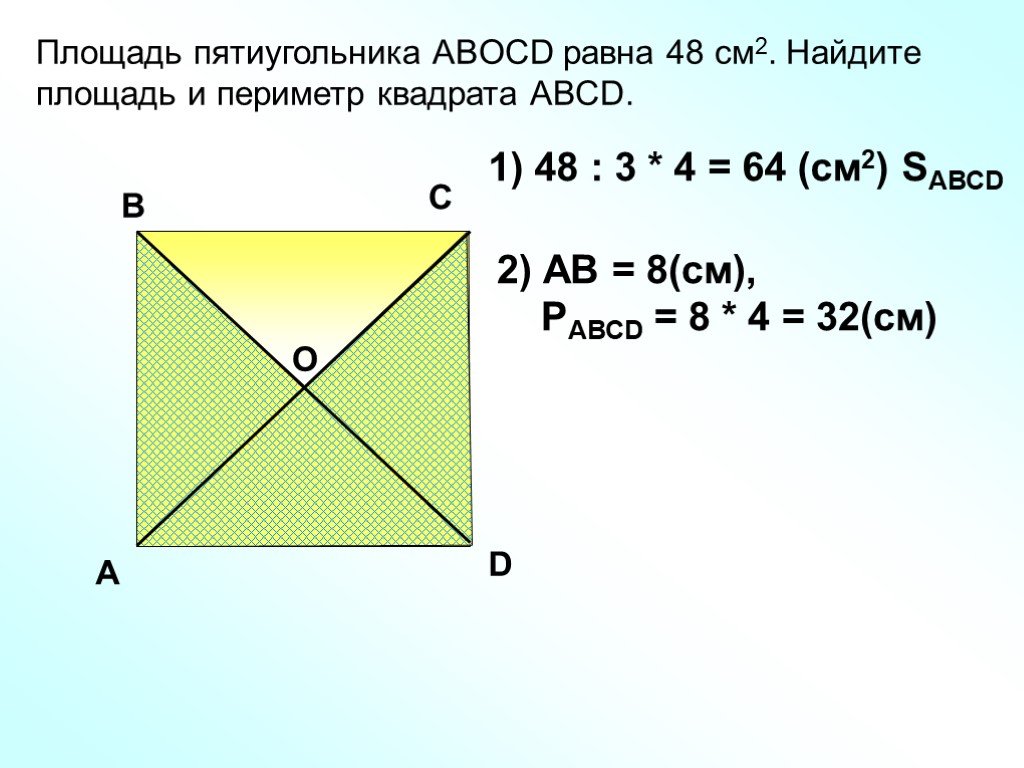 Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.

Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу

S = a2

где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины.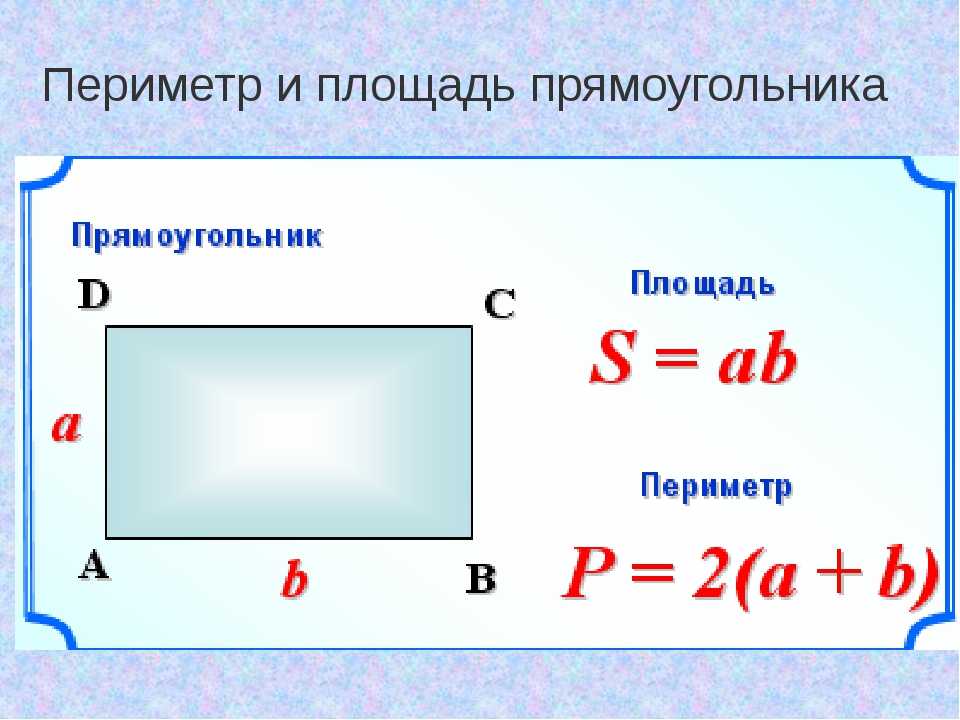 Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.

Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».

Например, вычислим площадь квадрат со стороной 2 см.

Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».

Вычислим площадь квадрата со стороной 3 метра

Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Аналогичные обозначения используются при вычислении площади прямоугольника.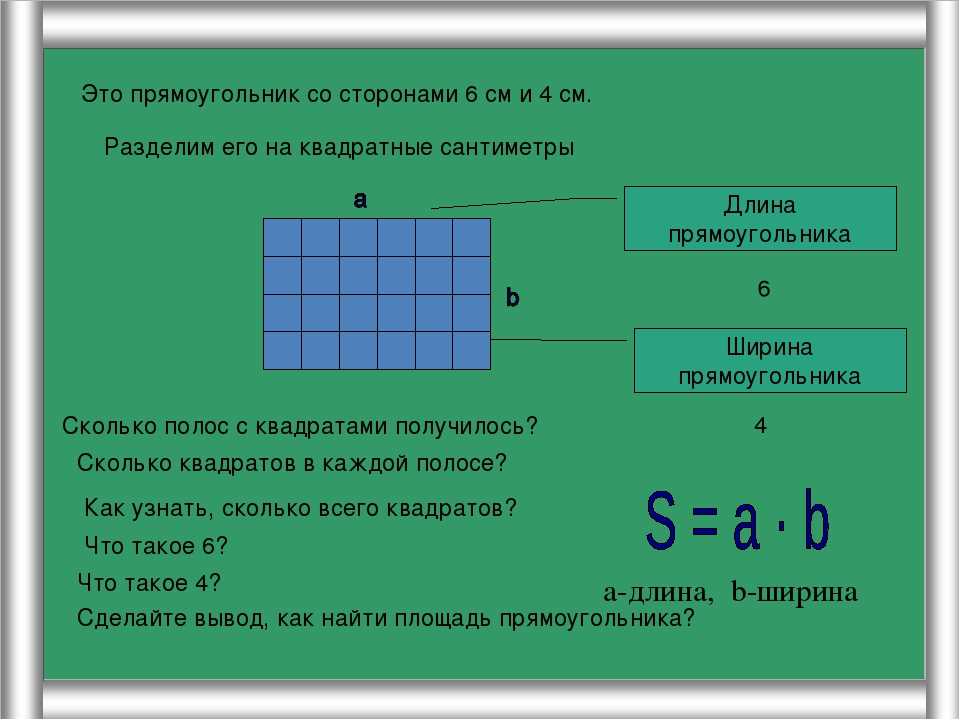 Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

S = a × b

Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).

Перевод единиц измерения площади

Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.

1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100

S = 1002 = 10 000 см2

Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.

1 м2  = 10 000 см2

Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.

Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.

А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.

Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»

100 000 см2 : 10 000 см2 = 10 м2

Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.

Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000

S = 10002 = 1 000 000 м2

Получается, что на один квадратный километр приходится один миллион квадратных метров:

1 км2  = 1 000 000 м2

Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.

Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.

Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000

2 км2 × 1 000 000 = 2 000 000 м2

А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.

Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»

3 500 000 м2 : 1 000 000 м2 = 3,5 км2

Пример 2. Выразить 7 м2 в квадратных сантиметрах.

Умножим 7 м2 на 10 000

7 м2 = 7 м2 × 10 000 = 70 000 см2

Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.

5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2

Пример 4. Выразить 550 000 см2 в квадратных метрах.

Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2

550 000 см2 : 10 000 см2 = 55 м2

Пример 5. Выразить 7 км2 в квадратных метрах.

Умножим 7 км2 на 1 000 000

7 км2 × 1 000 000 = 7 000 000 м2

Пример 6. Выразить 8 500 000 м2 в квадратных километрах.

Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2

8 500 000 м2 × 1 000 000 м2 = 8,5 км2

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:

3 а = 100 м2 × 3 = 300 м2

В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:

1 сотка = 100 м2

2 сотки = 200 м2

10 соток = 1000 м2

Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:

20 га = 10 000 м2 × 20 = 200 000 м2

Прямоугольный параллелепипед и куб

Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:

Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.

Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:

Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:

Объём геометрической фигуры

Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.

Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.

Измерить объём какой-нибудь фигуры означает выяснить сколько  кубических единиц вмещается в данную фигуру.

Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:

Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:

Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3

V = 12 см3

Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .

Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

V = abc

где, a — длина, b — ширина, c — высота

Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат

Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.

Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:

Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:

V = 3 × 3 × 3 = 27 см³

Действительно, в исходный куб вмещается 27 кубиков длиной 1 см

При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.

V = 33 = 27 см3

Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.

Таким образом, объём куба вычисляется по следующему правилу:

V = a3

Где a — длина куба.

Кубический дециметр. Кубический метр

Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).

Другое название одного кубического дециметра – один литр.

1 дм3 = 1 литр

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 1003 = 1 000 000 см3

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м3  = 1 000 000 см3

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.

Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»

300 000 000 см3 : 1 000 000 см3 = 300 м3

Пример 2. Выразить 3 м3 в кубических сантиметрах.

Умножим 3 м3 на 1 000 000

3 м3 × 1 000 000 = 3 000 000 см3

Пример 3. Выразить 60 000 000 см3 в кубических метрах.

Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3

60 000 000 см3 : 1 000 000 см3 = 60 м3

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

1 литр = 1 дм3

Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

5 л × 1 = 5 дм3

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм3

Теперь переведём эти 6000 дм3 в кубические метры.

Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1000 дм3

V = 103= 1000 дм3

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3

6 000 дм3 : 1 000 дм3 = 6 м3

Значит, 6000 л = 6 м3.

Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

242 = 576

Таблица кубов

Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.

Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.

353 = 42875

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Показать решение

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2

Ответ: площадь равна 12 см2.

Показать решение

Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2

Ответ: ширина прямоугольника составляет 2 см.

Показать решение

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2

Показать решение

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3

Показать решение

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Показать решение

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.

Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Показать решение

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м

3 его весит 740 кг.

Решение

a — длина
b — ширина
c — высота

a = 42 м
b = м
c = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м3

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Показать решение

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм3

35 525 л = 35 525 дм3

Переведём кубические дециметры в кубические метры.

Это позволит вычислит объем бассейна:

35 525 дм3 : 1000 дм3 = 35,525 м3

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525
a = 5.8
b = 3.5
c = x

35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано

Что такое периметр? Как найти периметр? Периметр квадрата и прямоугольника.

Способы определения и примеры решения Как посчитать периметр фигуры

Сегодня у нас речь пойдет о том, как вычислить периметр многоугольника . Но сначала поговорим о многообразии фигур. Посмотрите на рисунок. Какие фигуры мы здесь видим? Это прямоугольник и квадрат – многоугольники, которые имеют по четыре стороны, а также треугольник, имеющий три стороны, и пятиугольник с пятью сторонами.

И как же найти периметр этих фигур?

Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .

Периметр обозначается заглавной латинской буквой Р .

Давайте рассмотрим несколько примеров.

Вычислим периметр многоугольника О. Как мы говорили ранее, периметр многоугольника – это сумма длин всех его сторон. Сложим все стороны нашего многоугольника:

Р = 15 + 17 + 10 + 10 + 20 + 15 = 87

Но можно вычислить периметр и другим способом, используя умножение. Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:

Р = 15 × 2 + 10 × 2 + 17 + 20 = 87

Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.

Прямоугольник – это такой четырехугольник, у которого противоположные стороны равны. Например, чтобы вычислить А со сторонами а и б , надо сложить эти стороны и умножить полученный результат на 2 :

Р(прямоугольника) = (а + б) × 2

То есть, если сторона прямоугольника а = 5 см , а сторона прямоугольника б = 3 см , то периметр прямоугольника будет:

Р = (5 + 3) × 2 = 16 см

А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?

Р(прямоугольника) = 2 × а + 2 × б

а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2

Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?

Если мы знаем одну сторону прямоугольника, значит длины двух, из четырех сторон нам известны. Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.

сторона б = (16 – 2 × 5) ÷ 2 = 3 см

Ответ: у прямоугольника две стороны по 5 см и две по 3 см.

Квадрат – это прямоугольник, у которого все стороны равны. Чтобы вычислить надо длину одной стороны умножить на 4:

Р(квадрата) = а × 4

Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:

Р(В) = 5 × 4 = 20 см

А если известен периметр квадрата, как найти длины его сторон? Очень просто, надо его периметр разделить на четыре:

а = Р ÷ 4

Пример: Периметр квадрата 24 см. Чему равны его стороны?

а = 24 ÷ 4 = 6

Ответ: Стороны квадрата равны 6 см.

По подобию вычисления периметра квадрата вычисляется периметр всех равносторонних многоугольников . То есть равен длине одной его стороны умноженной на количество сторон.

Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:

Р(равностороннего многоугольника) = а × n

Например, у пятиугольника Д сторона а = 6 см . Найдем его периметр:

Р(Д) = 6 × 5 = 30 см

Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.

Периметр — это сумма длин всех сторон многоугольника.

  • Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
  • Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника
  • Прямоугольник – это четырехугольник.
  • Все параллельные стороны равны
  • Все углы = 90º.
  • Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

  • 1 способ. Складываем все стороны. P = a + а + b + b
  • 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Запомни формулы вычисления периметра прямоугольника!

Полупериметр — это сумма одной длины и одной ширины.

  • Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
  • Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

  • : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

  1. Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
    • Прямоугольник — это четырехугольник со всеми прямыми углами.
    • Квадрат — прямоугольник, у которого все стороны равны.
  2. Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)

Класс: 2

Цель: ознакомить с приёмом нахождения периметра прямоугольника.

Задачи: формировать умение решать задачи, связанные с нахождением периметра фигур, вырабатывать умения чертить геометрические фигуры, закрепить умение вычислять, применяя с переместительное свойство сложения, развивать навык устного счёта, логическое мышление, воспитывать познавательную активность и умение работать в коллективе.

Оборудование: ИКТ (мультимедийный проектор, презентация к уроку), картинки с геометрическими фигурами для физминутки, модель магического квадрата, у учеников – модели геометрических фигур, маркерные доски, линейки, учебники, тетради.

ХОД УРОКА

1. Организационный момент

Проверка готовности к уроку. Приветствие.

Начинается урок,
Он пойдёт ребятам впрок.
Постарайтесь всё понять –
И внимательно считать.

2. Устный счёт

а) Использование магических фигур. (Приложение 1 )

– Заполним клетки магического квадрата, назовите его особенности (сумма чисел по горизонталям, вертикалям и диагоналям равны) и определите волшебное число. (39)

По цепочке дети заполняют квадрат на доске и в тетрадях .

б) Знакомство со свойствами магических треугольников. (Приложение 2 )

– Суммы чисел в углах, образующие треугольник равны. Найдём волшебные числа у треугольника. Определи пропущенное число. Отметь его на маркерной доске.

3. Подготовка к изучению нового материала

– Перед Вами геометрические фигуры. Назовите их одним словом. (Четырёхугольники).
– Разделите их на 2 группы. (Приложение 3 )
– Что такое прямоугольники. (Прямоугольники – четырехугольники, у которых все углы прямые.)
– Что можно узнать, зная длины сторон четырёхугольников? Периметр – сумма длин сторон фигур.
– Найдите периметр белой фигуры, жёлтой.
– Почему у прямоугольников известны не все стороны?
– Какие свойства у противолежащих сторон прямоугольников? (У прямоугольника противоположные стороны равны).
– Если противоположные стороны равны, надо ли измерять все стороны? (Нет.)
– Правильно, достаточно измерить длину и ширину.
– Как вычислить удобным способом? (Учащиеся работают устно с комментированием.)

4. Изучение новой темы

– Прочитайте тему нашего урока: «Периметр прямоугольника». (Приложение 4 )
– Помогите найти периметр данной фигуры, если её длина равна – а , а ширина – в .

Желающие находят Р у доски. Учащиеся в тетрадях записывают решение.

– Как записать это по-другому?

Р = а + а + в + в ,
Р = а х 2 + в х 2,
Р = (а + в ) х 2.

– Мы получили формулу нахождения периметра прямоугольника. (Приложение 5 )

5. Закрепление

Стр. 44 № 2.

Дети читают и записывают условие, вопрос, чертят фигуру, находят Р разными способами, записывают ответ.

6. Физминутка. Сигнальные карточки

Сколько клеточек зелёных,
Столько выполним наклонов.
Столько раз руками хлопнем.
Столько раз ногами топнем.
Сколько здесь у нас кружков,
Столько сделаем прыжков.
Мы присядем столько раз,
Столь подтянемся сейчас.

7. Практическая работа

– У Вас на партах лежат в конвертах геометрические фигуры. Как мы их назовём?
– Что такое прямоугольники?
– Что вы знаете о противолежащих сторонах прямоугольников?
– Измерьте стороны фигур по вариантам, найдите периметр разными способами.
– Проверяем у соседа.

Взаимопроверка тетрадей .

– Прочитайте: Как нашли периметр? Что можно сказать о периметрах данных фигур? (Они равны) .
– Начертите прямоугольник с таким же Р, но другими сторонами.

Р 1 = (2 + 6) х 2 = 16 Р 1 = 2 х 2 + 6 х 2 = 16
Р 1 = 2 + 2 + 6 + 6 = 16
Р 2 = 3 + 3 + 5 + 5 = 16 Р 2 = (3 + 5) х 2 = 16
Р 3 = 4 + 4 + 4 + 4 = 16 Р 4 = 1 + 1 + 7 + 7 = 16

8. Графический диктант

Слева 6 клеток. Поставили точку. Начинаем движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4 – вправо вверх. Какая фигура? Преврати её в прямоугольник. Дострой. Найди Р разными способами.

Р = (5 + 2) х 2 = 14.
Р = 5 + 5 + 2 + 2 = 14.
Р = 5 х 2 + 2 х 2 = 14.

9. Пальчиковая гимнастика

Умножали, умножали.
Очень, очень мы устали.
Наши пальчики сплетём и соединим ладошки.
А потом, как только можем, крепко накрепко сожмём.
На дверях висит замок.
Кто его открыть не смог?
Мы замочком постучали,
Мы замочек повертели,
Мы замочек покрутили и открыли.

(Слова сопровождаются движениями)

10. Составление и решение задачи по условию (Приложение 8 )

Длина прямоугольника – 12 дм
Ширина – на 3 дм м.
Р – ?
В первом действии найдём ширину: 12 – 3 = 9 (дм) – ширина
Зная длину и ширину, узнаем Р одним из способов.
Р = (12 + 9) х 2 = 42 дм

11. Самостоятельная работа

12. Итог урока

– Чему учились. Как находили Р прямоугольника?

13.Оценивание

Оцениваются ответы учащихся у доски и выборочно в процессе самостоятельной работы.

14.Домашнее задание

С. 44 № 5 (с пояснениями).

Умение находить периметр прямоугольника очень важно для решения многих геометрических задач. Ниже приведена подробная инструкция по нахождению периметра разных прямоугольников.

Как найти периметр обычного прямоугольника

Обычный прямоугольник – четырехугольник, у которого параллельные стороны равны и все углы = 90º. Для нахождения его периметра существует 2 способа:

Складываем все стороны.

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина – 6.

Решение (последовательность действий и рассуждения):

  • Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда. Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
  • Складываем все стороны (3 + 3 + 6 + 6) = 18 см.

Ответ: P = 18 см.

Второй способ заключается в следующем:

Нужно сложить ширину и длину, и умножить на 2. Формула этого способа имеет следующий вид: 2×(a + b), где a – ширина, b – длина.

В рамках данной задачи получим такое решение:

2×(3 + 6) = 2×9 = 18.

Ответ: P = 18.

Как найти периметр прямоугольника – квадрат

Квадрат является правильным четырехугольником. Правильным потому, что все его стороны и углы равны. Для нахождения его периметра так же существует два способа:

  • Сложить все его стороны.
  • Умножить его сторону на 4.

Пример: Найти периметр квадрата, если его сторона = 5 см.

Так как нам известна сторона квадрата, мы сможем найти его периметр.

Складываем все стороны: 5 + 5 + 5 + 5 = 20.

Ответ: P = 20 см.

Умножаем сторону квадрата на 4 (потому что все равны): 4×5 = 20.

Ответ: P = 20 см.


Как найти периметр прямоугольника – онлайн-ресурсы

Несмотря на то, что вышеупомянутые действия легки для понимания и освоения, вам может пригодиться несколько онлайн-калькуляторов, которые помогут вам вычислить периметры (площадь, объем) разных фигур. Просто вбейте необходимые значения и мини-программа рассчитает периметр нужной вам фигуры. Ниже приведен небольшой список.

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.


Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)


Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см


Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)


Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB


Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB


3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?


В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM


Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB


Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Периметр прямоугольника — веб-формулы

В прямоугольнике расстояние вокруг внешней стороны прямоугольника называется периметром. Прямоугольник двумерный; однако периметр является одномерным и измеряется в линейных единицах, таких как футы, метры и т. д.

Периметр прямоугольника представляет собой общую длину всех четырех сторон.
Периметр прямоугольника = 2L + 2W.

Пример 1: Прямоугольник имеет длину 13 см и ширину 8 см. решить периметр прямоугольника.
Решение :
Учитывая, что:
Длина (l) = 13 см
Ширина (w) = 8 см

Периметр прямоугольника = 2 (l + w) единиц
P = 2(13 + 8)
P = 2 (21)
P = 42

Таким образом, периметр прямоугольника равен 42 см.

Пример 2: Если длина прямоугольника 2x + 1, а ширина 2x – 1. Если его площадь 15 см 2 , каковы размеры прямоугольника и каков его периметр?

Решение :
Мы знаем, что размеры прямоугольника в x:
 l = 2x + 1
w = 2x – 1

Поскольку площадь прямоугольника определяется как:
A = l * w

Мы можем подставить выражения для длины и ширины в уравнение для площади, чтобы определить значение x.

A = l * w
15 = (2x + 1) (2x -1)
15 = 4x 2 – 1
16 = 4x 2
x = ± 2

Обратите внимание, что значение x должно быть положительным, и поэтому в нашем случае значение x равно 2. Теперь мы имеем:
l = 5 см
w = 3 см
Следовательно, размеры 5 см и 3 см.

Теперь, подставив эти значения в формулу периметра, получим
P = 2l + 2w
P = 2(5)+2(3)
P = 10+6
P = 16 см

Пример 3: Найдите площадь и периметр прямоугольника, длина которого 24 м, а ширина 12 м?
Решение :
Учитывая, что:
Длина = L = 24 м
Ширина = W = 12 м

Площадь прямоугольника:
A = L × W
A = 24 × 12
A = 188 M 2

Периметр прямоугольника:
P = 2L + 2W
P = 2(24) + 2(12)
P = 48 + 24
P = 72 м

Пример 4: Найдите площадь и периметр прямоугольника, длина которого равна 4 см. и высота 3 см.
Раствор :
Площадь = b×h = 4×3 = 12 см 2 .
Периметр = 2(b) + 2(h) = 2(4) + 2(3) = 8 + 6 = 14.

Пример 5: Вычислите периметр прямоугольника, длина которого 18 см и ширина 7см
Решение :
Учитывая, что:
L = 18 см
B = 7 см

Периметр прямоугольника = 2 (длина + ширина)
P = 2 (L + B)
P = 2 (18 + 7)
P = 50 см

Пример 6: Найдите периметр прямоугольника, длина которого 6 дюймов, а ширина 4 дюйма.
Раствор :
P = 2(L + B)
P = 2(6 + 4)
P = 20 в

Пример 7: Мальчик 5 раз ходит по парку. Если размер парка 100 м на 50 м, найдите расстояние, которое прошел мальчик. Если он пройдет 100 м за 5 минут, сколько времени в общей сложности ему потребуется?
Решение :
Учитывая, что:
Длина = L = 100 м
Ширина = Ш = 50м
Раундов = 5
Время на 100 м = 5 минут.

Периметр парка:
Р = 2 л + 2 Вт.
Р = 2 х 100 + 2 х 50
Р = 200 + 100
P = 300 м

Общее пройденное расстояние = 5 × Периметр парка.
= 5 × 300
= 1500 метров

Общее затраченное время = Общее пройденное расстояние × время, затраченное на прохождение 1 метра.
= 1500 × 5/100
= 75 минут или 1 час 15 минут

Онлайн-калькулятор периметра

Математическая задача: Прямоугольник 3-4-5 — вопрос № 4517, алгебра, выражение переменной из формулы

Стороны прямоугольника находятся в отношении 3: 4. Длина его диагонали 20 см. Вычислите площадь прямоугольника.

Правильный ответ:

Нашли ошибку или неточность? Не стесняйтесь

пишите нам

. Спасибо!

Советы по использованию связанных онлайн-калькуляторов

Воспользуйтесь нашим калькулятором коэффициентов.
См. также наш калькулятор прямоугольного треугольника.
Вы хотите преобразовать единицы длины?
См. также наш калькулятор тригонометрического треугольника.

Для решения этой математической задачи вам необходимо знать следующие знания:

  • алгебра
  • expression of a variable from the formula
  • planimetrics
  • Pythagorean theorem
  • right triangle
  • area of ​​a shape
  • triangle
  • diagonal
  • rectangle
  • basic functions
  • ratio
  • direct отношение
Единицы физических величин:
  • длина
Уровень задачи:
  • практика для 13-летних
  • практика для 14-летних

 

Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: видео1   видео2

  • Длина окружности 7615
    Стороны прямоугольника относятся как 3:5. Его окружность составляет 48 см. Вычислите длину его диагонали.
  • Стороны
    Стороны прямоугольника относятся как 3:5, а его длина окружности составляет 72 см. Вычислите: а) размер обеих сторон прямоугольника б) площадь прямоугольника в) длину диагоналей
  • Прямоугольный 80776
    Периметр прямоугольного сада 42 метра. Его стороны находятся в соотношении 3:4. Вычислите длину тротуара, который является диагональю сада.
  • Прямоугольный 7801
    Длина сторон прямоугольного сада 4:3. Соединение центров смежных сторон имеет длину 20 м. Вычислите площадь сада.
  • Отношение сторон
    Вычислить площадь круга с той же длиной окружности, что и длина окружности прямоугольника, вписанного в окружность радиусом r 9см так, чтобы его стороны находились в соотношении 2 к 7.
  • Прямоугольный сад
    Стороны прямоугольного сада соотносятся 1:2. Диагональ имеет длину 20 метров. Вычислите площадь и периметр сада.
  • Вычислить 70814
    Длины сторон AB и AD прямоугольника ABCD относятся как 3:4. Окружность k диаметром 10 см описывает прямоугольник. Вычислите длины сторон данного прямоугольника.
  • Прямоугольный 4624
    Длины сторон прямоугольного сада находятся в соотношении 1:2. Соединение центров смежных сторон имеет длину 20 м. Вычислите периметр и площадь участка.
  • Прямоугольник — стороны 4
    Периметр прямоугольника 72 см. Вычислите длины сторон, которые находятся в соотношении 3:5.
  • Прямоугольный 6255
    Длины сторон прямоугольного сада находятся в соотношении 1:2. Соединение центров смежных сторон имеет длину 20 м. Вычислите периметр и площадь прямоугольника.
  • Прямоугольник 62854
    Соотношение сторон прямоугольника и его диагонали составляет 9:12:15. Вычислите площадь прямоугольника, если длина диагонали равна 105 см.
  • Прямоугольник — desc окружность
    Длина сторон прямоугольника находится в соотношении 1:3. Радиус окружности, описанной вокруг прямоугольника, равен 10 см. Вычислите периметр прямоугольника.