Что такое угол? Определение, виды, как обозначают, примеры
Поможем понять и полюбить математику
Начать учиться
Знания школьной геометрии пригодятся в самых неожиданных ситуациях: во время ремонта, при рисовании граффити или чтобы нарезать пирог. В этой статье узнаем все про углы.
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
Что такое вершина и стороны угла
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
Иногда встречается обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Прямой угол — это угол, стороны которого перпендикулярны друг другу.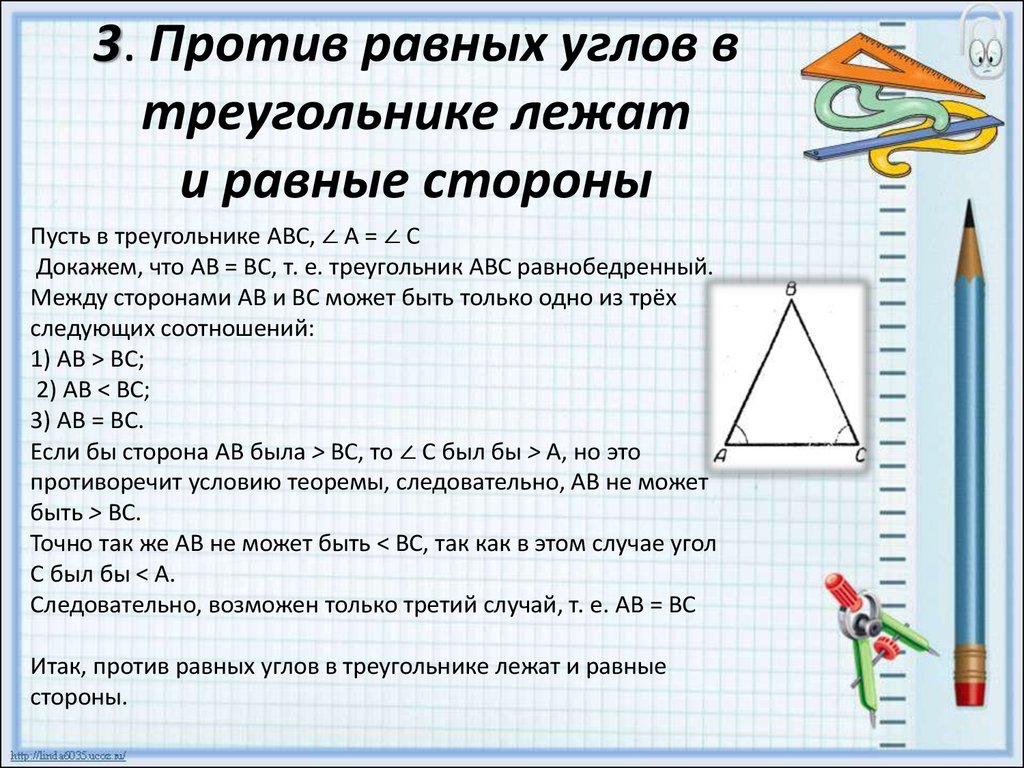 Прямой угол всегда равен 90°.
Прямой угол всегда равен 90°.
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Острый угол — это угол, который меньше прямого угла, то есть < 90°.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:

Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB − ∠COB,
- ∠COB = ∠AOB − ∠AOC.

Запоминаем!
Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.

- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот как он выглядит:
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.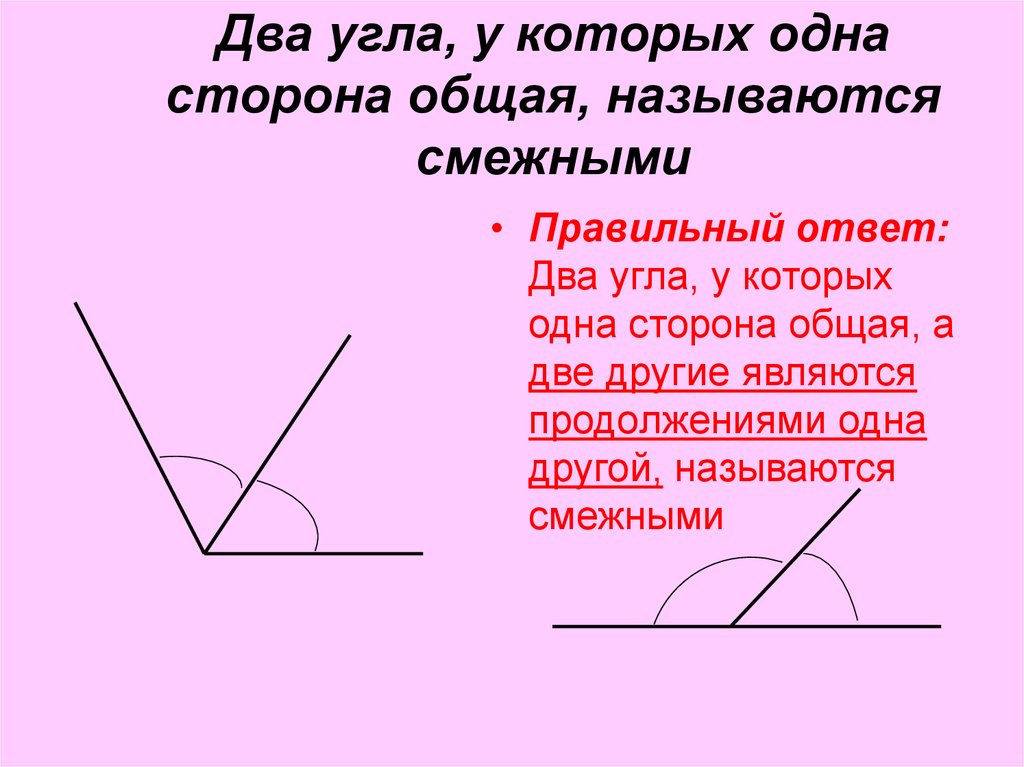
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда — 1/60 часть минуты. Обозначается ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Равные углы имеют равную градусную меру.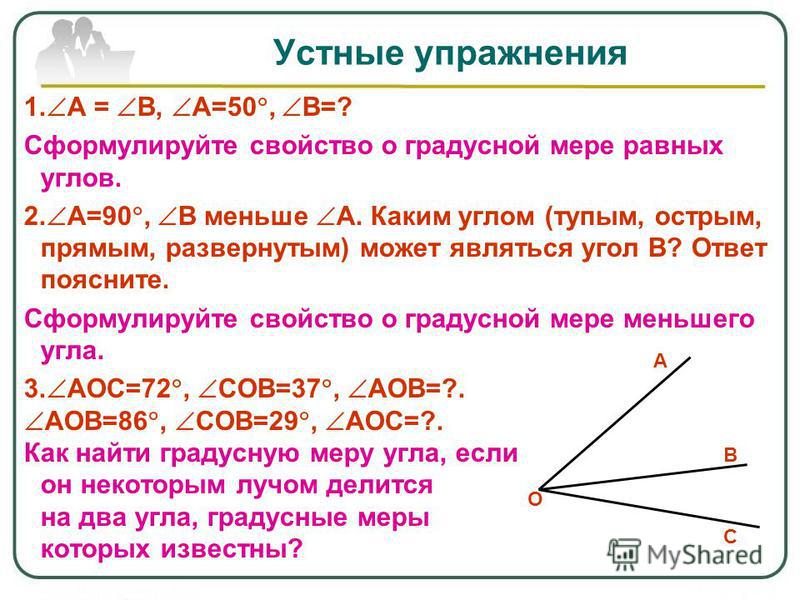
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
На чертеже отмечены три неравных угла:
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
253.2K
Наибольший общий делитель (НОД), свойства и формулы
К следующей статье
204.9K
Неполные квадратные уравнения
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Равные углы треугольника. Дополнительная задача 307 § 4 глава 4 Геометрия 7-9 класс Атанасян Л.С. – Рамблер/класс
Равные углы треугольника. Дополнительная задача 307 § 4 глава 4 Геометрия 7-9 класс Атанасян Л. С. – Рамблер/класс
С. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Привет, я столкнулась вот с какой неразрешимой задачей:
В прямоугольном треугольнике проведена высота из вершины прямого угла. Докажите, что данный треугольник и два образовавшихся треугольника имеют соответственно равные углы.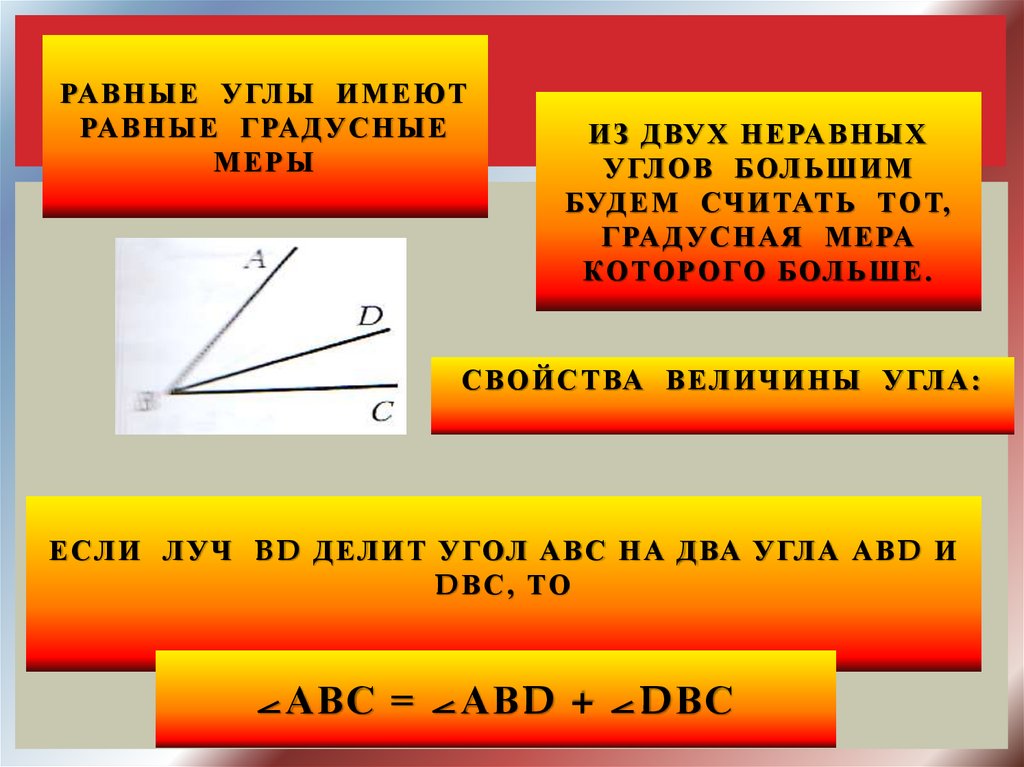
ответы
Дано:
Доказать:
∆АВС. ∆АВH и ∆ВСН имеют равные
углы соответственно.
Доказательство:
103
∆ АВС — прямоугольный, значит
(2) (т.к ∆ СВН — прямоугольный).
вычтем из (3 равенство (2):
Вычтем из (3) (1)
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!
ГИА9 класс
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Стороны равной длины — определение, формы, примеры, факты
Стороны равной длины — введение
Математика — это не только числа, она также включает изучение различных форм, таких как круги, квадраты, овалы, цилиндры, треугольники, прямоугольники и многое другое.
Включает определение размеров сторон или точных углов фигур.
Сегодня мы обсудим фигуры, имеющие сторон одинаковой длины . Мы узнаем факторы, которые отличают их друг от друга, и их соответствующие названия. Давайте начнем!
Родственные игры
Что такое Стороны равной длины?
Стороны одинаковой длины означают, что их размеры одинаковы. Проще говоря, стороны фигуры, имеющие одинаковую длину, являются сторонами равной длины.
Стороны, имеющие одинаковую длину, также называются конгруэнтными сторонами. Эти стороны могут быть частью одной формы или разных форм. Давайте посмотрим на несколько примеров фигур со сторонами одинаковой длины.
Давайте посмотрим на несколько примеров фигур со сторонами одинаковой длины.
В прямоугольнике ниже противоположные стороны конгруэнтны друг другу.
В двух треугольниках ниже стороны конгруэнтны друг другу.
Связанные рабочие листы
Стороны равной длины в одной форме
Треугольники
В зависимости от длины сторон треугольники можно разделить на разносторонние, равнобедренные и равносторонние.
- Разносторонний треугольник:
Это треугольник, в котором каждая сторона имеет разную длину.
- Равнобедренный треугольник:
Это треугольник, в котором две стороны имеют одинаковую длину. Угол, падающий между равными сторонами, называется углом при вершине. Углы, противолежащие двум равным сторонам треугольника, всегда будут равны. Точно так же, если два угла треугольника равны, то их соответствующие противоположные стороны также будут иметь одинаковую длину.
- Равносторонний треугольник:
Это треугольник, в котором все три стороны имеют одинаковую длину.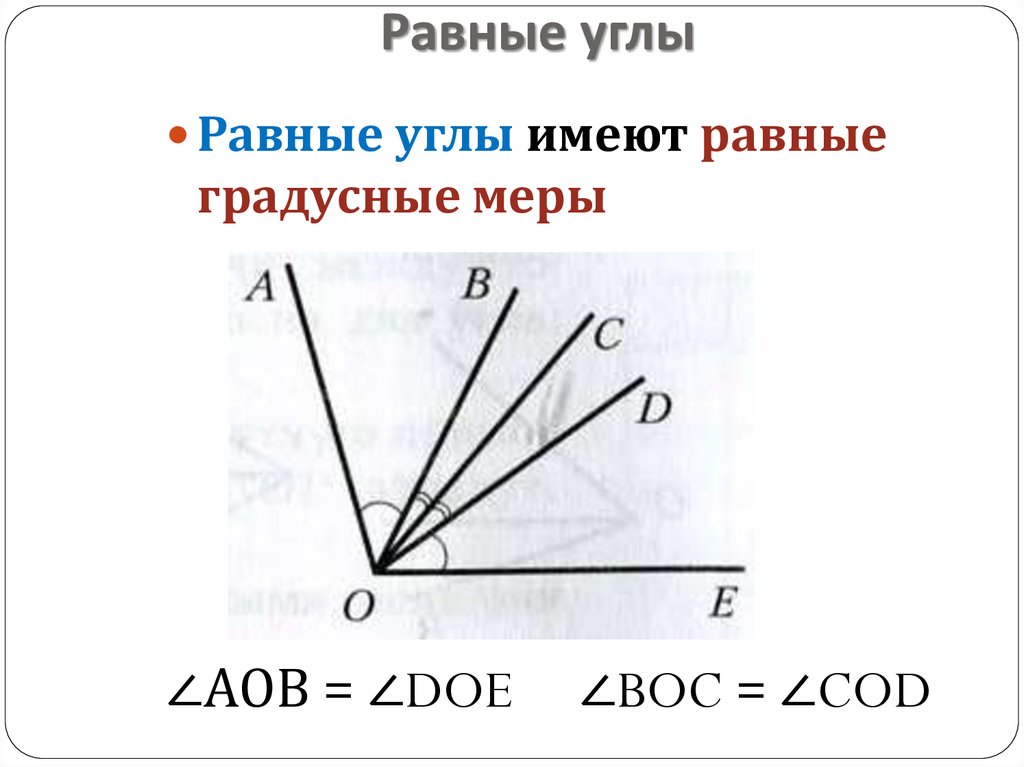 Каждый угол равностороннего треугольника равен 60°. Следовательно, его также называют равноугольным треугольником.
Каждый угол равностороннего треугольника равен 60°. Следовательно, его также называют равноугольным треугольником.
Итак, треугольники с равными сторонами могут быть либо равнобедренными, либо равносторонними.
Четырехугольники
Четырехугольники — это многоугольники с четырьмя сторонами. У них также могут быть равны все или некоторые стороны. Различные категории перечислены ниже:
- Все стороны равны
В этих четырехугольниках все четыре стороны равны. Их еще называют правильными четырехугольниками. Примерами правильных четырехугольников являются квадрат и ромб.
- Три равные стороны
В этих четырехугольниках три стороны равны.
- Одна пара равных сторон
В этих четырехугольниках есть одна пара равных сторон. Стороны могут быть как противоположными, так и примыкающими друг к другу.
- Противоположные стороны равны: Примером этого является равнобедренная трапеция
- Смежные стороны равны: Примером этого является неправильный четырехугольник, у которого две смежные стороны равны.

- Две пары равных сторон
- Равные стороны противоположны: Примеры: прямоугольник и параллелограмм.
- Равные стороны смежные: Пример — воздушный змей.
Многоугольники
Многоугольники — это двумерные замкнутые фигуры, состоящие только из прямых сторон. Многоугольники могут иметь любое количество сторон. Это означает, что треугольники и четырехугольники также являются многоугольниками. Многоугольники также могут иметь равные все или некоторые стороны.
- Правильные многоугольники:
Многоугольники, у которых все стороны и все внутренние углы равны, называются правильными многоугольниками. Все их углы также равны. Обратите внимание, что ромб не имеет равных сторон, а не является правильным многоугольником, потому что все его внутренние углы не равны.
- Неправильные многоугольники:
Многоугольники, у которых все стороны не равны, называются правильными многоугольниками. У них могут быть некоторые стороны одинаковой длины, но не все. Таким образом, даже если прямоугольники и параллелограммы имеют равные противоположные стороны, они являются неправильными многоугольниками.
У них могут быть некоторые стороны одинаковой длины, но не все. Таким образом, даже если прямоугольники и параллелограммы имеют равные противоположные стороны, они являются неправильными многоугольниками.
Стороны одинаковой длины в различных формах
При сравнении различных форм, если сторона одной формы равна стороне другой, говорят, что стороны равны.
Если все стороны одной фигуры равны всем сторонам другой фигуры и углы также одинаковы, то две фигуры называются конгруэнтными.
Например, два треугольника называются конгруэнтными, если все их соответствующие стороны и углы равны.
Критерии конгруэнтности треугольников
Нам не нужно измерять все стороны и углы двух треугольников, чтобы проверить, конгруэнтны они или нет. Если они соответствуют любому из заданных критериев, то они конгруэнтны.
- Критерии SSS (сторона-сторона-сторона)
Два треугольника $\Delta\text{ABC}$ и $\Delta\text{PQR}$ называются конгруэнтными по критерию SSS, если их соответствующие стороны равны.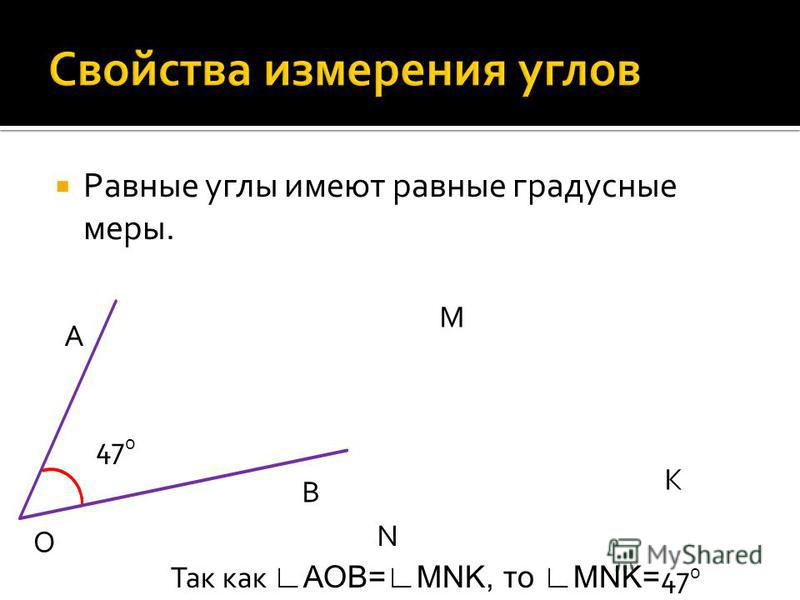
- AB $=$ PQ
- до н.э. $=$ QR
- AC $=$ PR
- Критерии SAS (сторона-угол-сторона)
Два треугольника $\Delta{ABC}$ и $\Delta{PQR}$ называются конгруэнтными по критериям SAS, если две их соответствующие стороны и угол между ними равны.
- AB $=$ PQ
- ∠A $=$ ∠P
- AC $=$ PR
- Критерии AAS (угол-угол-сторона)
Два треугольника $\Delta\text{ABC}$ и $\Delta\text{PQR}$ называются конгруэнтными по критериям ААС, если любые два их соответствующих угла и любая одна сторона равны.
- ∠A $=$ ∠P
- ∠С $=$ ∠Р
- AC $=$ PR
- RHS-критерий (правая сторона гипотенузы)
Два прямоугольных треугольника $\Delta\text{ABC}$ и $\Delta\text{XYZ}$ называются конгруэнтными по RHS-критерию, если их соответствующие гипотенуза и одна пара соответствующих сторон равны.
- ∠B $=$ ∠Y (прямой угол)
- AC $=$ XZ (гипотенуза)
- AB $=$ XY (сторона)
Заключение
У некоторых фигур все стороны равны, а у других ни одна из сторон не равна. Кроме того, есть фигуры, у которых только несколько равных сторон. Мы можем сравнивать стороны и углы различных фигур, чтобы найти конгруэнтные стороны и конгруэнтные формы.
Кроме того, есть фигуры, у которых только несколько равных сторон. Мы можем сравнивать стороны и углы различных фигур, чтобы найти конгруэнтные стороны и конгруэнтные формы.
Решенные примеры
1. Назовите три фигуры, все стороны которых имеют одинаковую длину.
Решение : Три фигуры, все стороны которых имеют одинаковую длину, это ромб, квадрат и равносторонний треугольник.
2. Найдите периметр правильного шестиугольника, если одна из его сторон равна 9 дм.
Решение: Правильный шестиугольник имеет 6 сторон одинаковой длины.
Поскольку сторона равна 9 дюймам, периметр будет:
6$\умножить на 9 = 54$ дюймов.
3. Если две стороны треугольника равны, какой это треугольник?
Решение : Это равнобедренный треугольник. У равнобедренного треугольника две равные стороны.
4. Если одна сторона параллелограмма 10 дюймов, а другая сторона 6 дюймов, каков общий периметр?
Решение : В параллелограмме противоположные стороны равны друг другу.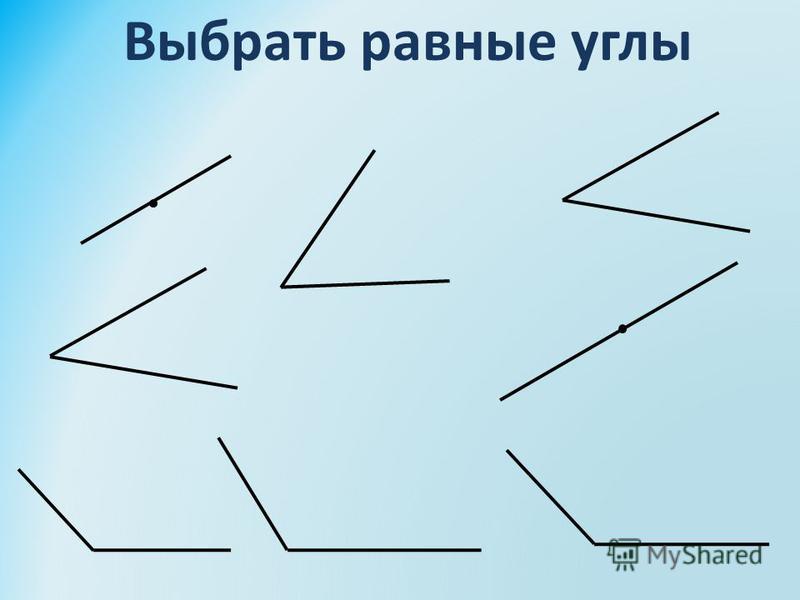
Если одна сторона 10 дюймов, а другая сторона 6 дюймов, общий периметр будет:
10$ + 10 + 6 + 6 = 32$ дюймов.
Практические задачи
1
В $\Delta\text{ABC}$ ∠A $=$ 50°, ∠ B $=$ 80° и ∠ C $=$ 50°. Определите равные стороны.
AC $=$ BC
AB $=$ AC
AB $=$ BC
Стороны не равны
Правильный ответ: AB $=$ BC
Дано, что ∠A $=$∠ В $=$ 50°. Это означает, что стороны, противолежащие этим углам, также равны. То есть AB $=$ BC.
2
$\Delta\text{ABC}$ имеет стороны 6 дюймов, 8 дюймов и 10 дюймов. $\Delta\text{DEF}$ конгруэнтно $\Delta\text{ABC}$. Что за треугольник $\Delta\text{DEF}$?
Разносторонний
Равносторонний
Равнобедренный
Невозможно определить
Правильный ответ: Разносторонний
Если $\Delta\text{DEF}$ конгруэнтно $\Delta\text{ABC}$, стороны $\ Delta\text{DEF}$ также составляет 6 дюймов, 8 дюймов и 10 дюймов.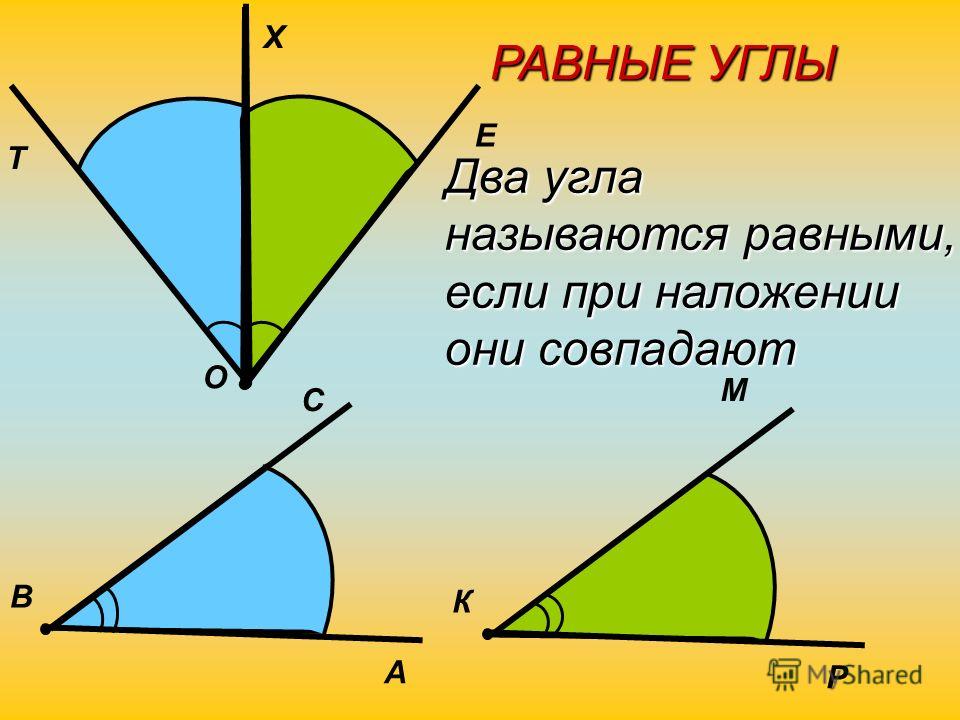 Поскольку все три стороны $\Delta\text{DEF}$ имеют разную длину, это разносторонний треугольник.
Поскольку все три стороны $\Delta\text{DEF}$ имеют разную длину, это разносторонний треугольник.
3
Какие из следующих четырехугольников являются правильными многоугольниками?
Прямоугольник
Квадрат
Воздушный змей
Ромб
Правильный ответ: Квадрат
У правильного многоугольника все стороны равны и все углы равны. Квадрат – это единственный четырехугольник с равными сторонами и равными углами.
4
Определите фигуру, у которой не все стороны равны.
Равносторонний треугольник
Ромб
Прямоугольник
Правильный пятиугольник
Правильный ответ: Прямоугольник
В прямоугольнике смежные стороны имеют разную длину, а противоположные стороны равны.
Часто задаваемые вопросы
Возможны ли конгруэнтные формы с соответствующими сторонами разной длины?
Нет, конгруэнтные фигуры должны иметь стороны одинаковой длины.
Может ли быть неправильный многоугольник со сторонами одинаковой длины?
Да, если стороны равны, но углы разные, или равны только две или некоторые из сторон, то это будет неправильный многоугольник. Например, у ромба равные стороны, но разные углы.
Поскольку все углы равностороннего треугольника равны 60°, можем ли мы сказать, что все равносторонние треугольники конгруэнтны друг другу?
Нет, чтобы треугольники были равны, все их стороны и углы должны быть равны.
геометрия. Обязательно ли равные углы означают, что многоугольник правильный?
спросил
Изменено 3 года, 9несколько месяцев назад
Просмотрено 3к раз
$\begingroup$
В многоугольнике, если все стороны равны, это не обязательно означает, что многоугольник правильный (например, ромб). Верно ли это и для углов? То есть можно ли нарисовать многоугольник, внутренние углы которого равны, но форма все равно неправильная? Я не мог вспомнить ни одного примера, но я уверен, что он есть.
Верно ли это и для углов? То есть можно ли нарисовать многоугольник, внутренние углы которого равны, но форма все равно неправильная? Я не мог вспомнить ни одного примера, но я уверен, что он есть.
- геометрия 9\circ$. Только самый большой из них обычный. Обобщение на любой правильный многоугольник должно быть ясным.
$\endgroup$
1
$\begingroup$
Начните с любого многоугольника, имеющего более трех ребер. Немного переместите одно из ребер параллельно самому себе, соответствующим образом удлините или сузьте соседние ребра, и у вас будет новый многоугольник с теми же направлениями ребер, но разными относительными длинами сторон. Если вы начнете с правильного многоугольника, углы останутся прежними.
Идея этой конструкции является общей. Если вы начнете с любой последовательности из $n > 3$ векторов, охватывающих плоскость, получится $n-2$-мерное пространство линейных комбинаций, которые обращаются в нуль.


Leave A Comment